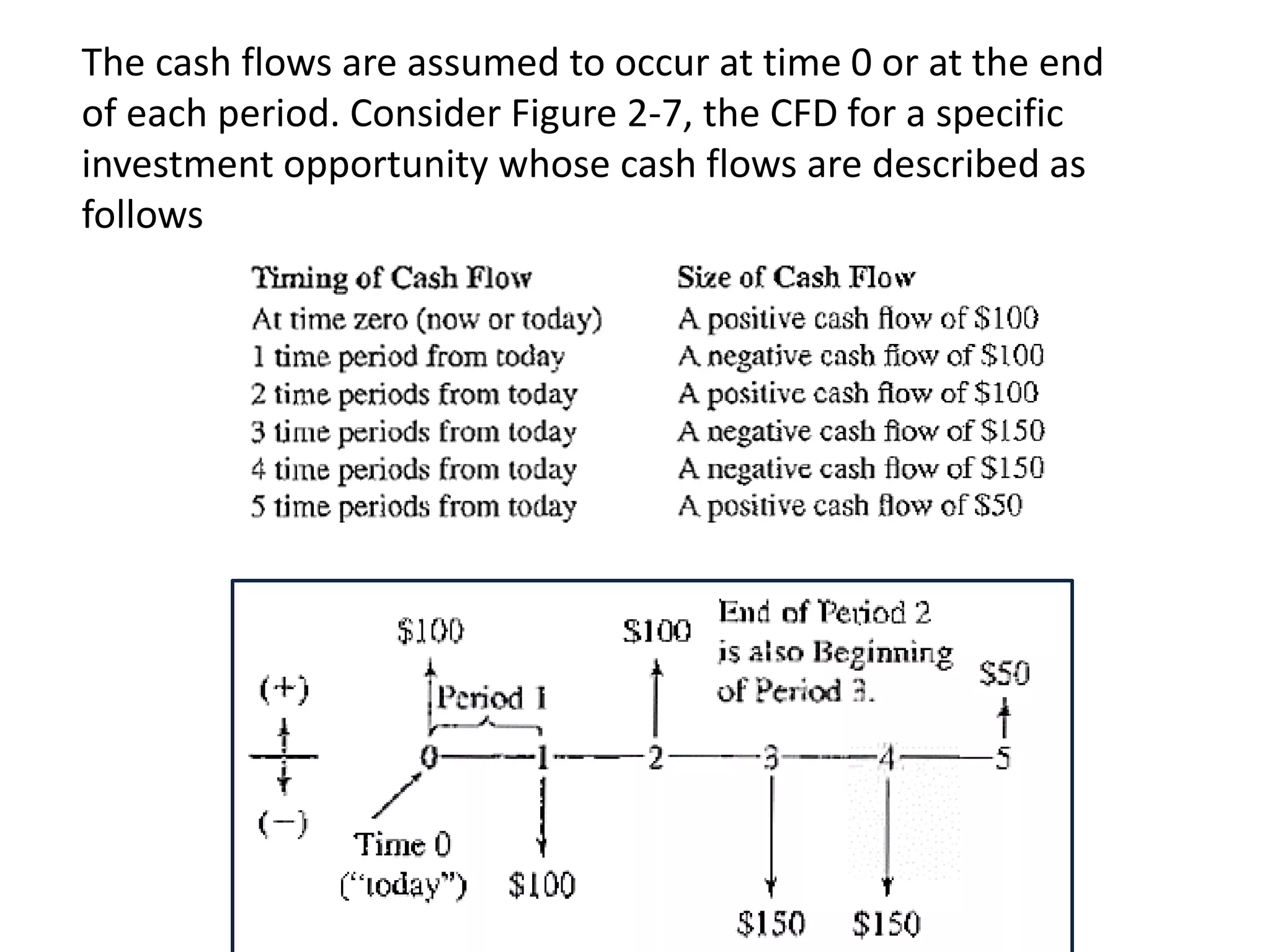
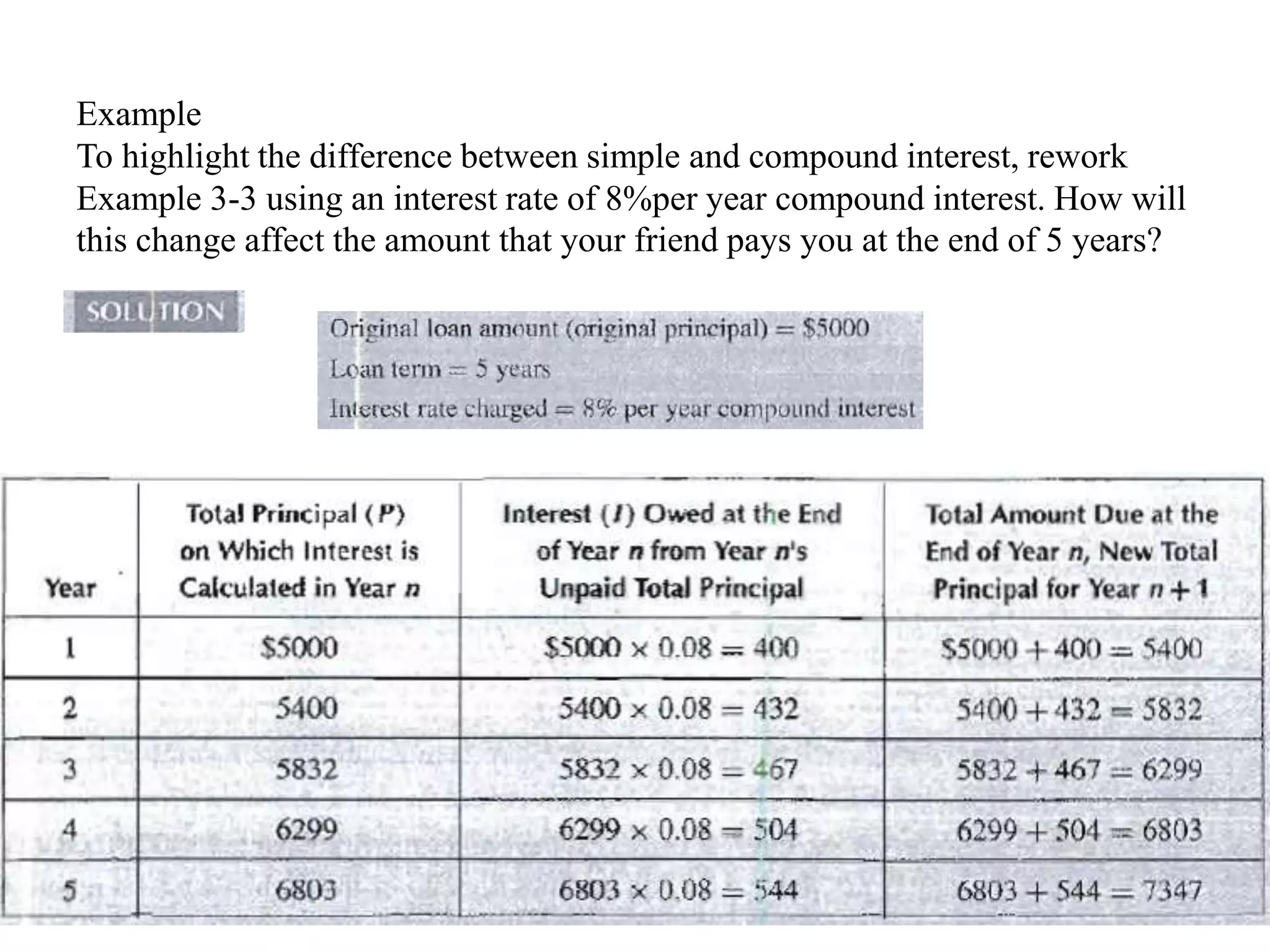
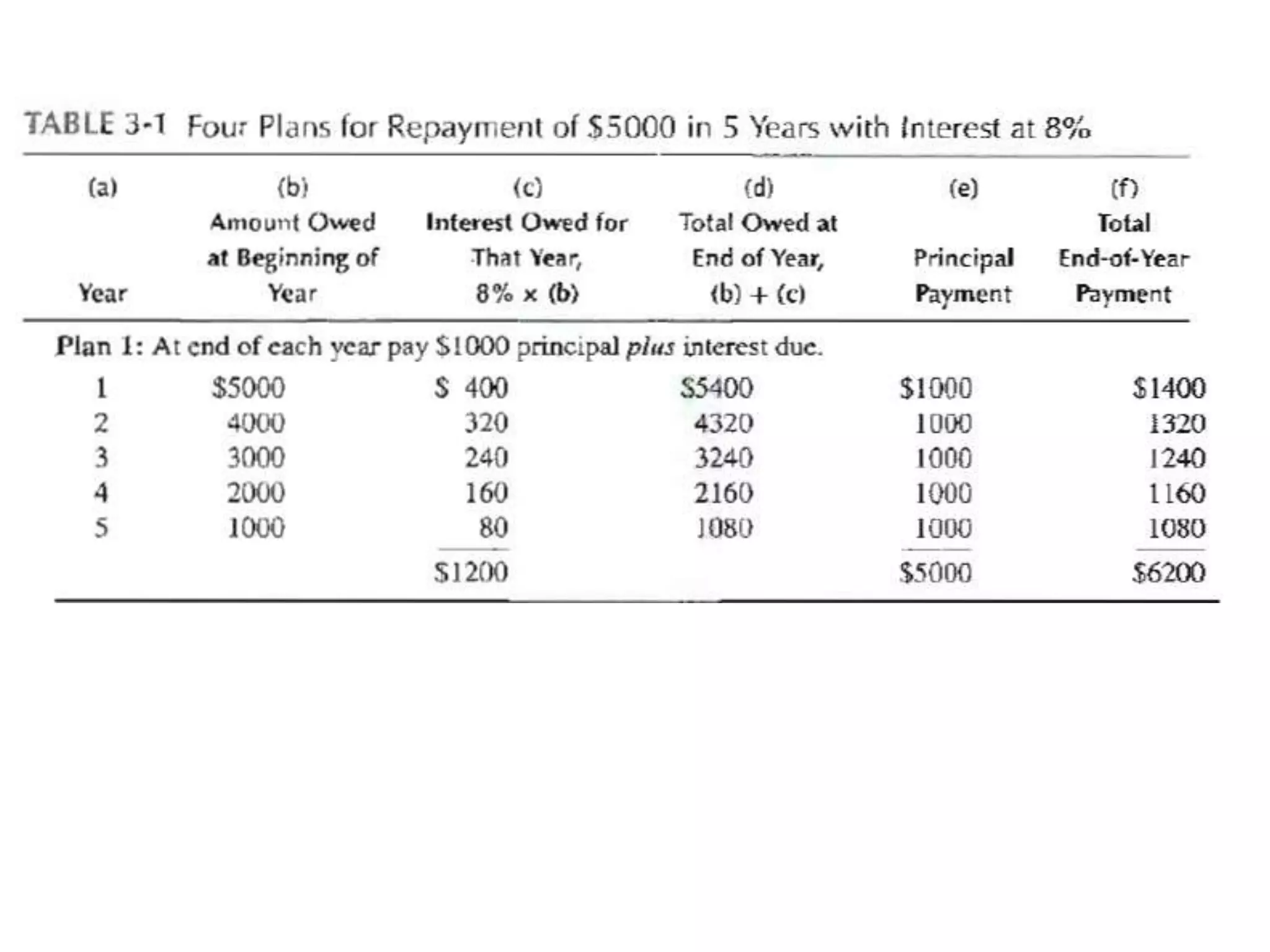
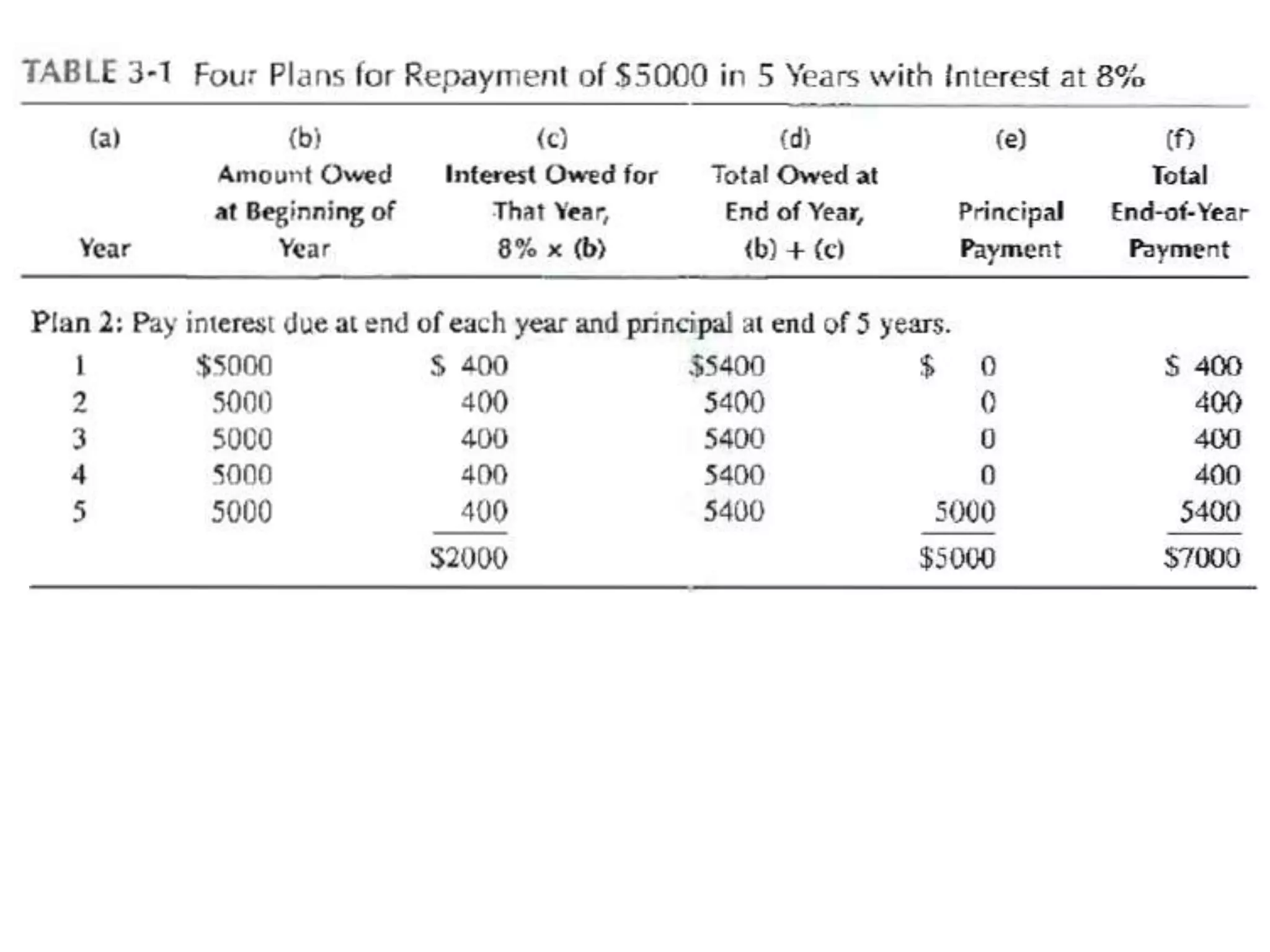
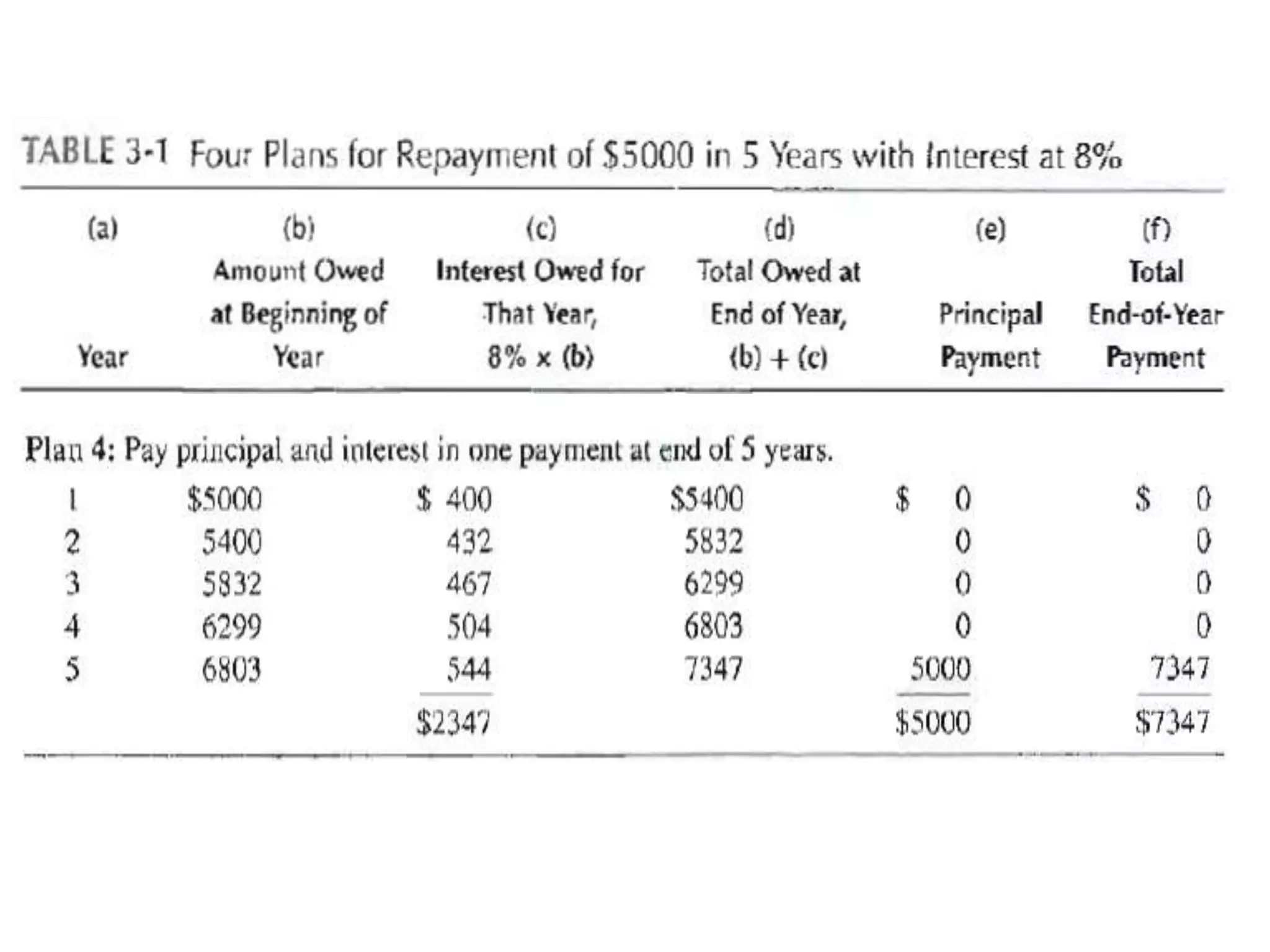
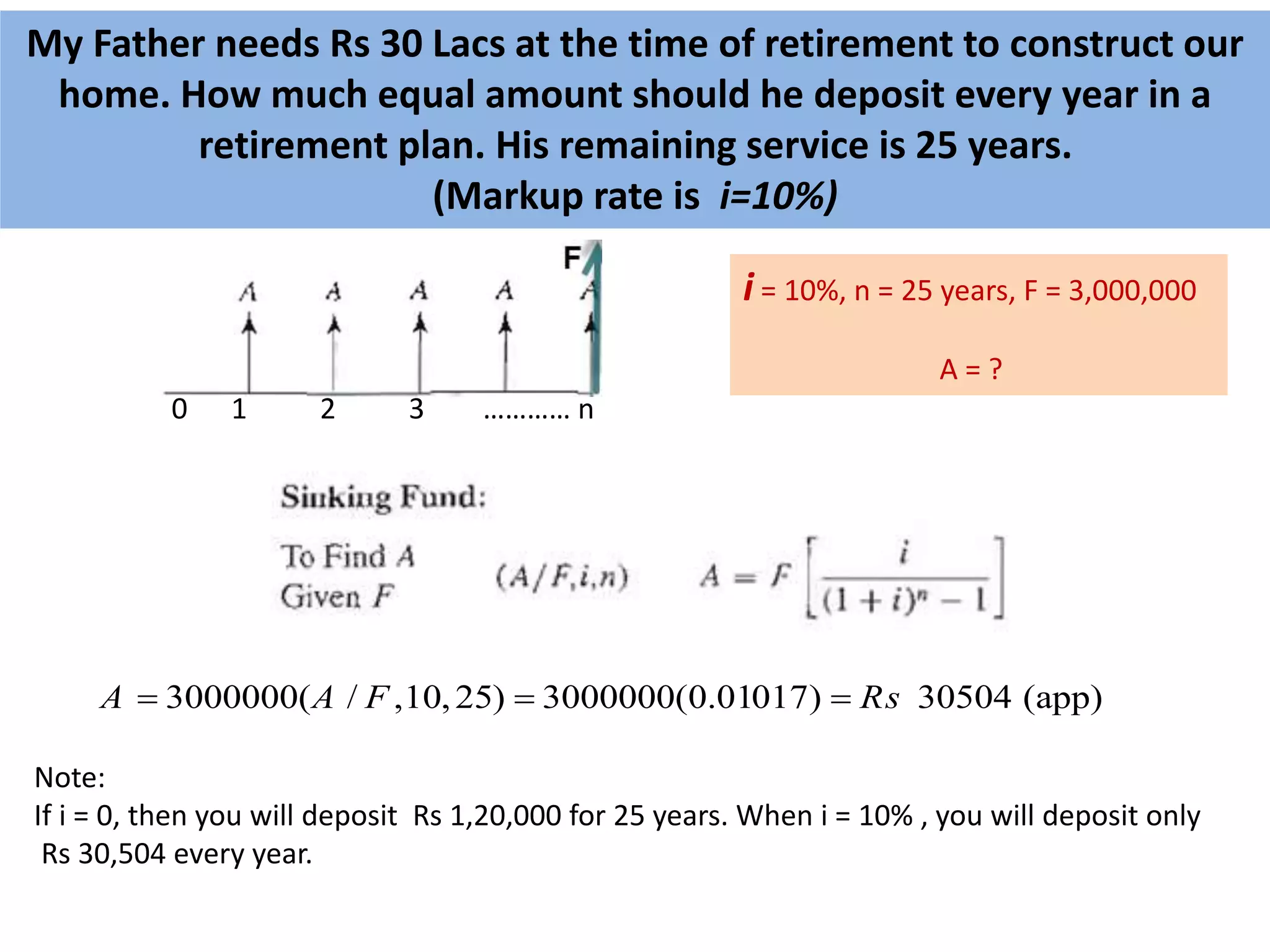
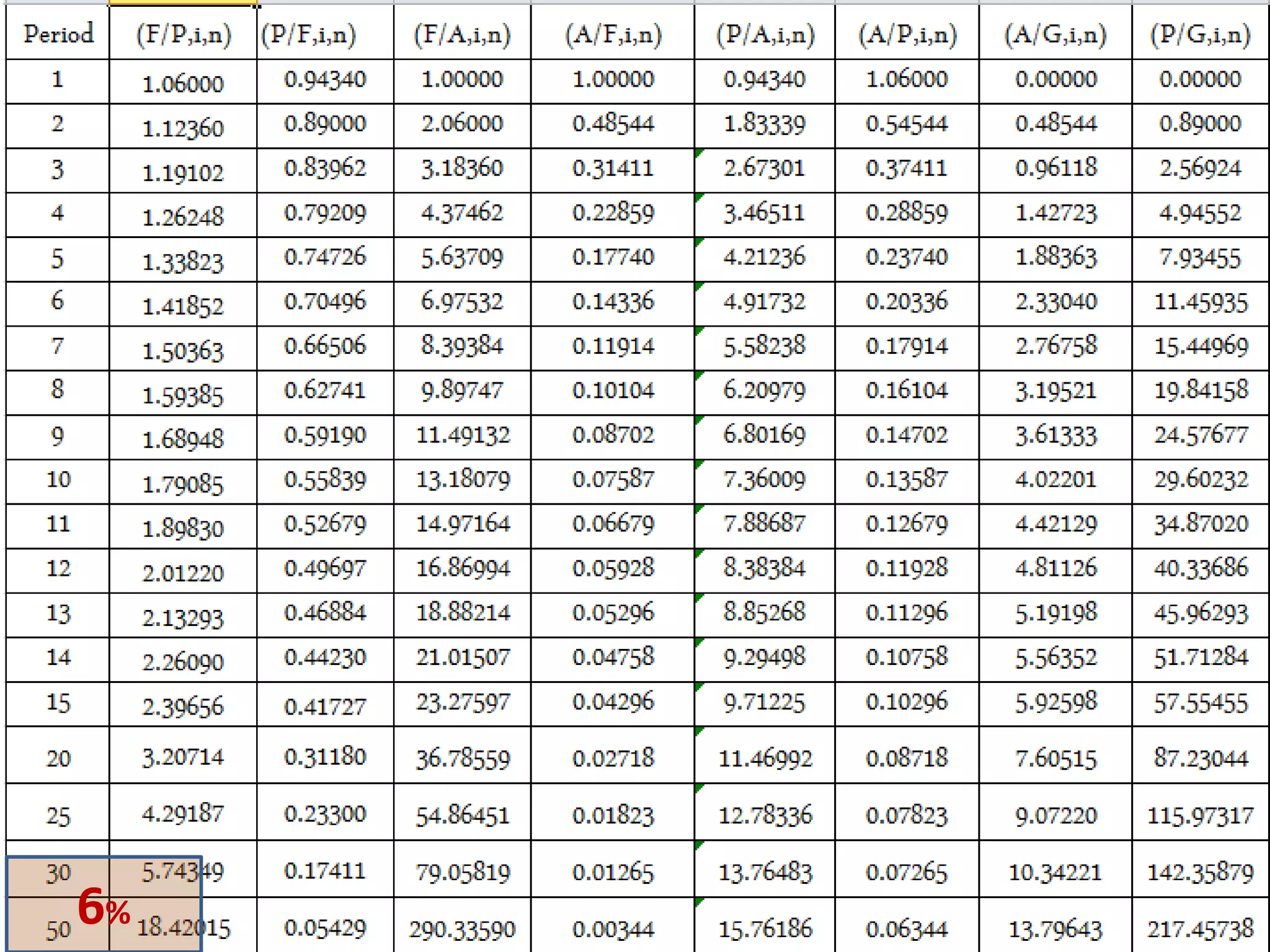
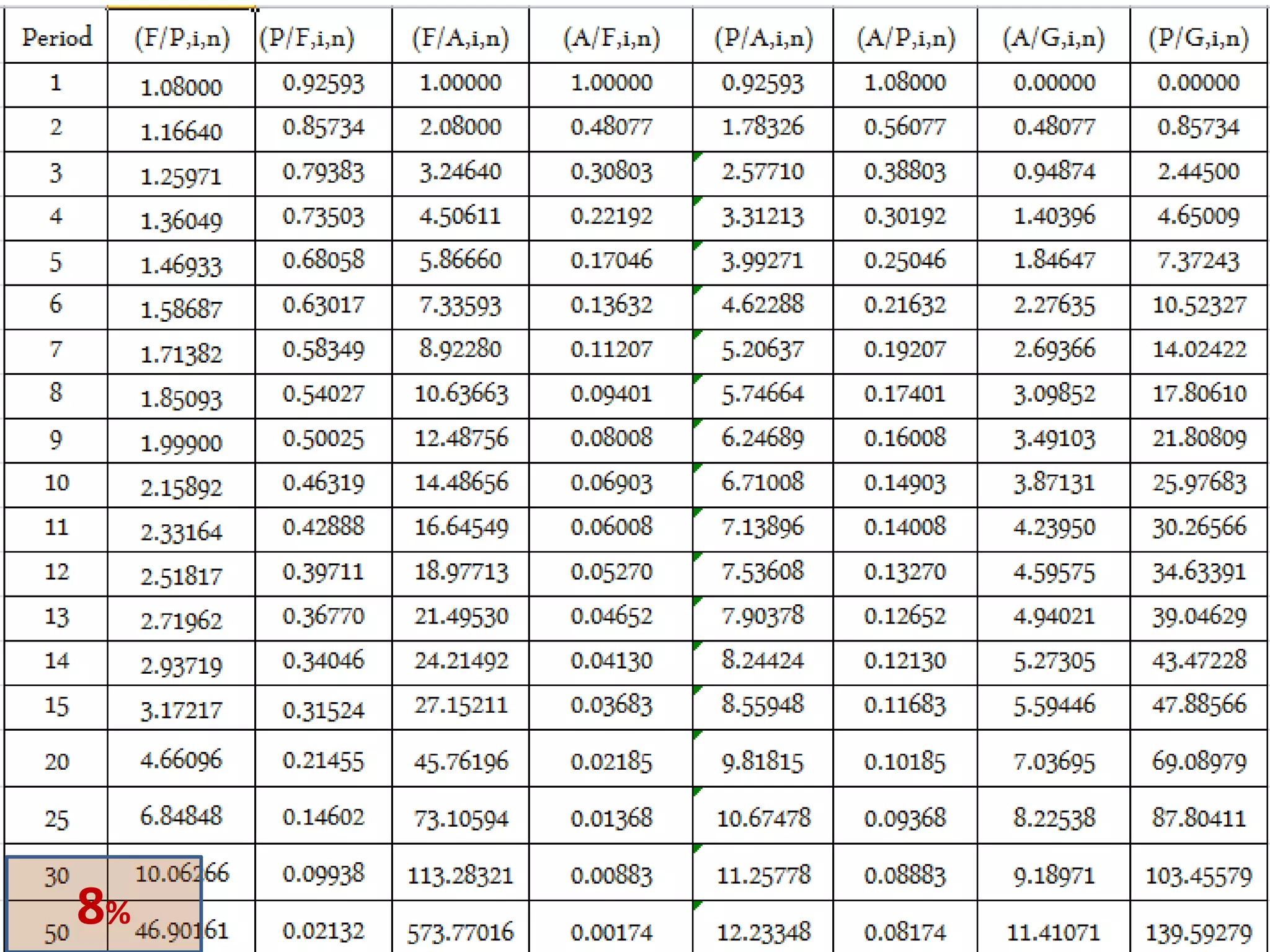
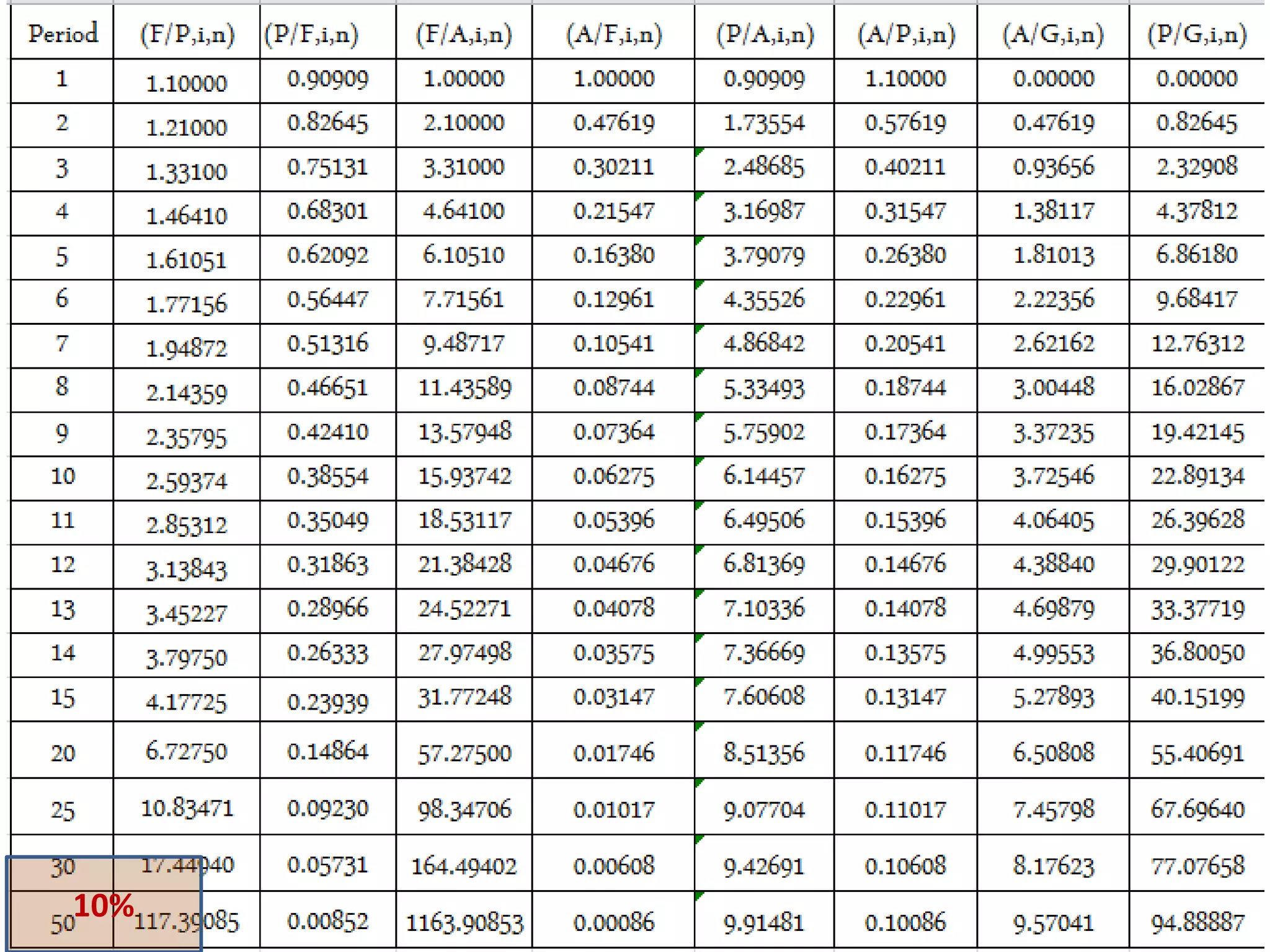
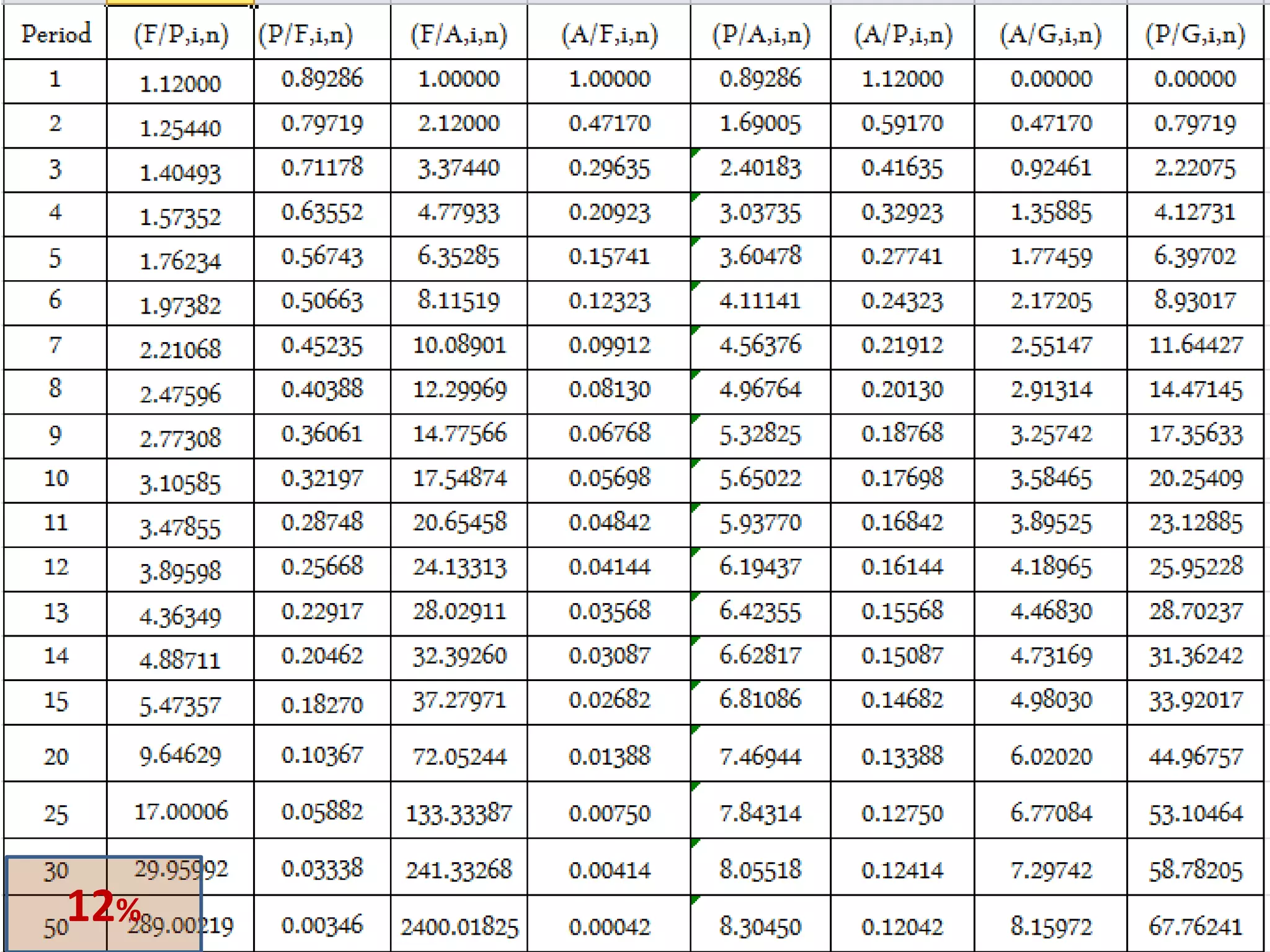
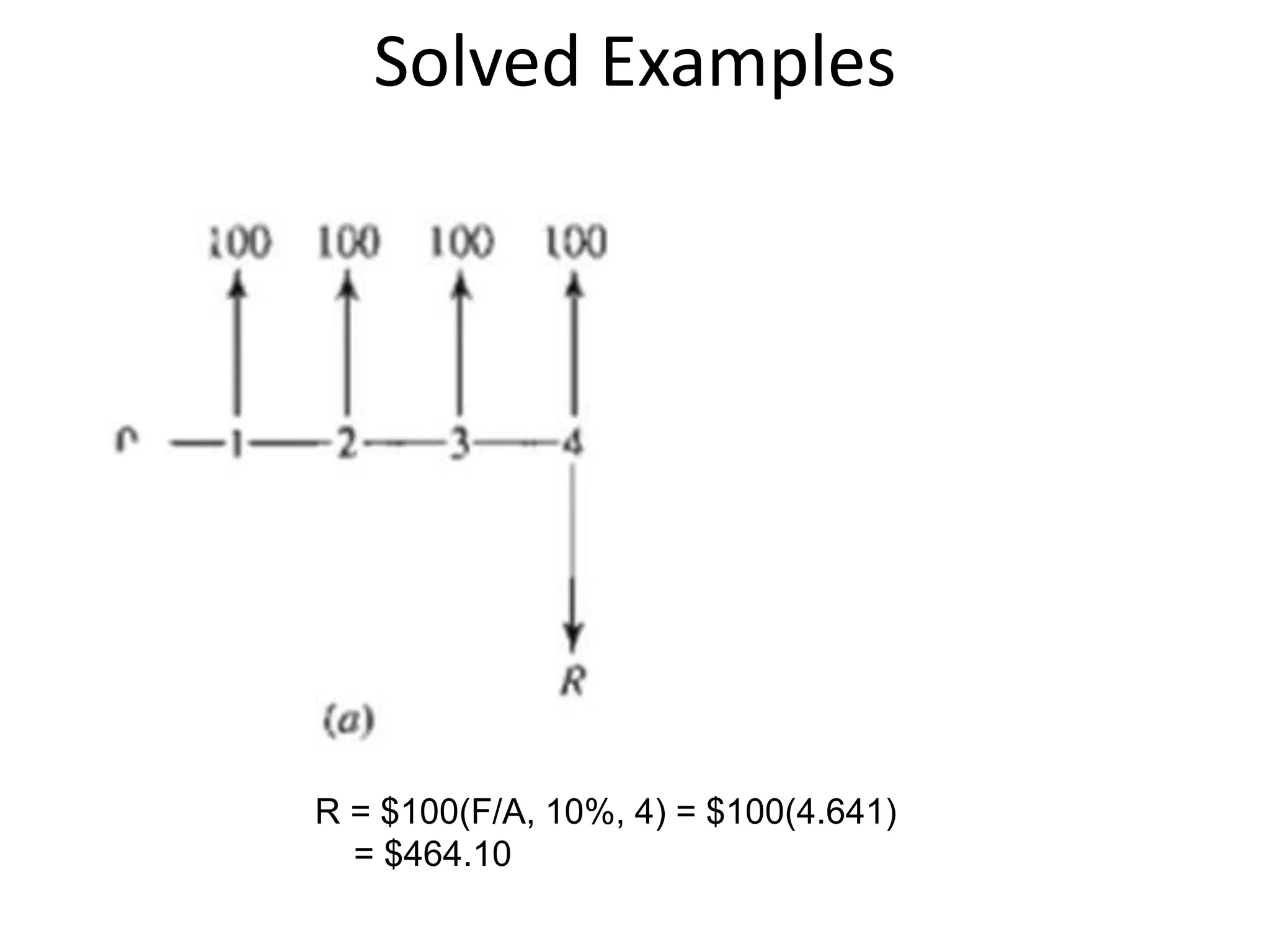
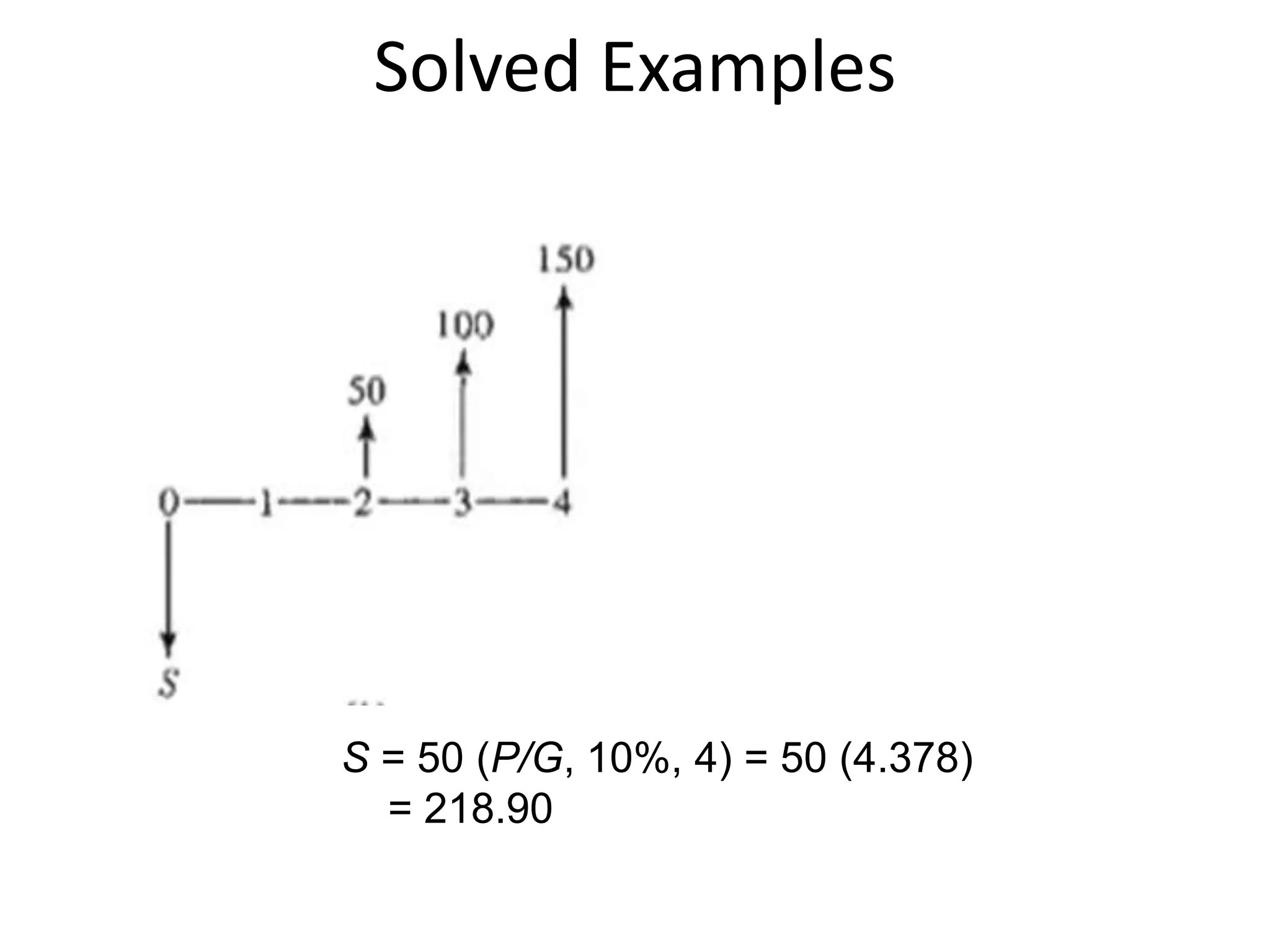
- Cash flow diagrams (CFDs) illustrate the size, timing, and direction (positive or negative) of cash flows from engineering projects over time. - A CFD is created by drawing a segmented time line and adding vertical arrows to represent cash inflows or outflows at each time period. - Common categories of cash flows include first costs, operating/maintenance costs, salvage value, revenues, and overhauls.

1. Engr Muiz Abdur Raqib
Mechanical Engineer

2. TIME VALUE OF MONEY
CASH FLOW DIAGRAMS

3. • CASH FLOW DIAGRAMS
• The costs and benefits of engineering projects occur overtime
and are summarized on a cash flow diagram (CFD).
• Specifically, a CFD illustrates the size, sign, and timing of
individual cash flows.
• In this way the CFD is the basis for engineering economic
analysis.
• A cash flow diagram is created by first drawing a segmented
time-based horizontal line, divided into appropriate time
units. The time units on the CFD can be years, months,
quarters, or any other consistent time unit. Then at each time
at which a cash flow will occur, a vertical arrow is added-
pointing down for costs and up for revenues or benefits.
• These cash flows are drawn to relative scale.

4. The cash flows are assumed to occur at time 0 or at the end
of each period. Consider Figure 2-7, the CFD for a specific
investment opportunity whose cash flows are described as
follows

5. Categories of Cash Flows
The expenses and receipts due to engineering projects usually fall
into one of the following categories.
First cost = expense to build or to buy and install
Operations and maintenance (O&M) = annual expense, such as
electricity, labor, and minor repairs
Salvage value = receipt at project termination for sale or transfer
of the equipment (can be a salvage cost)
Revenues = annual receipts due to sale of products or services
Overhaul = major capital expenditure that occurs during the
asset's life

6. COMPUTING CASH FLOWS
The manager has decided to purchase a new $30,000 mixing machine. The
machine may be paid for in one of two ways:
1. Pay the full price now minus a 3% discount.
2. Pay $5000 now; at the end of one year, pay $8000; at the end of each of
the next four years, pay $6000.
List the alternatives in the form of a table of cash flows

7. A man borrowed $1000 from a bank at 8% interest. He agreed to
repay the loan in two end-of-year payments. At the end of the
first year, he will repay half of the $1000 principal amount plus
the interest that is due. At the end of the second year, he will
repay the remaining half of the principal amount plus the interest
for the second year. Compute the borrower's cash flow.
At the end of the first year, the man pays 8% interest for the use of $1000 for one
year. The interest is 0.08 x $1000 = $80. In addition, he repays half the $1000 loan, or
$500. Therefore, the end-of-year-I cash flow is -$580.
At the end of the second year, the payment is 8% for the use of the balance of the
principal ($500) for the one-year period, or 0.08 x 500 = $40. The $500 principal is
also repaid for a total end-of-year 2cash flow at -$540.

8. TIME VALUE OF MONEY
Which would you prefer, $100 cash today or the assurance
of receiving $100 a year from now?
You might decide you would prefer the $100 now because
that is one way to be certain of receiving it.
If the current interest rate is 9% per year, and you put $100 into
the bank for one year, how much will you receive back at the end
of the year?
You will receive your original $100 together with $9 interest, for
a total of $109.

9. Simple Interest
Simple interest is interest that is computed only on the original sum
and not on accrued interest. Thus if you were to loan a present sum
of money P to someone at a simple annual interest rate i (stated as a
decimal) for a period of n years, the amount of interest you would
receive from the loan would be:
At the end of n years the amount of money due you, F, would
equal the amount of the loan .P plus the total interest earned. That
is, the amount of money due at the end of the loan would be

10. Problem
Bank has agreed to give you a loan of $5000 for 5 years at a simple interest
rate of 8% per year. How much interest will you pay to bank ? How much will
you pay to bank at the end of 5 years?

11. Compound Interest
• With simple interest, the amount earned (for invested money)
or due (for borrowed money) in one period does not affect the
principal for interest calculations in later periods.
• However, this is not how interest is normally calculated.
• In practice, interest is computed using the compound
interest method.

12. Example
To highlight the difference between simple and compound interest, rework
Example 3-3 using an interest rate of 8%per year compound interest. How will
this change affect the amount that your friend pays you at the end of 5 years?

16. SINGLE PAYMENTS
INTEREST FORMULAE

17. What will be future value (F) of P amount deposited now
after n years at markup rate of i
Suppose you deposit Rs 10,000 now (at time = 0 )
in a Bank at a markup rate of 10%. How much
Bank will pay you after 15 years
15
10,000(1 0.1) 10,000( / ,10,15) 10,000(4.177) 41,770F F P    

18. What will be Present Worth (P) of F amount received by you
after n years at markup rate of i
Suppose you are asked to make choice between two alternatives:
(A) Receive Rs 17,000 now
(B) Receive Rs 70, 000 after 15 years (Markup rate is 10%)
So, you find Present worth of Rs 70,000 to make the decision
𝑃 = 𝐹 1 + 𝑖 −𝑛 = 𝐹( 𝑃 𝐹 , 10,15) = 70,000(0.239) = 16,757
So, it is better to opt choice A since it gives you more money than choice B

19. UNIFORM SERIES

20. How much I would receive (F) if I deposit an equal amount
of A rupees every year for n years. (Markup rate is i=10%)
0 1 2 3 ………… n
i = 10%, n = 15 years, A = 1000
F = ?
( / ,10,15) 1000(31.772) 31772F A F A  
If i = 0, then you will receive Rs 15000 after 15 years. When i = 10% , you will get Rs 31,772

21. My Father needs Rs 30 Lacs at the time of retirement to construct our
home. How much equal amount should he deposit every year in a
retirement plan. His remaining service is 25 years.
(Markup rate is i=10%)
0 1 2 3 ………… n
i = 10%, n = 25 years, F = 3,000,000
A = ?
3000000( / ,10,25) 3000000(0.01017) 30504 (app)A A F Rs  
Note:
If i = 0, then you will deposit Rs 1,20,000 for 25 years. When i = 10% , you will deposit only
Rs 30,504 every year.

22. You have invested Rs 10 Lacs now in an investment scheme for 12
years. How much equal amount (A) you will receive every year.
(Markup rate is i=10%)
0 1 2 3 … …… n i = 10%, n = 12 years, P = 1,000,000
A = ?
1000000( / ,10,12) 1000000(0.14676) 146760 (app)A A P Rs  
Note:
If i = 0, then you will receive Rs 83,333 per year for next 12 years. When i = 10% , you will
receive Rs 1,46,760 every year.

23. You need Rs 2,50,000 every year to complete your Four BSc degree
program: How much amount (P) should be deposited by your Father in
a fixed income scheme now. (Markup rate is i=10%)
0 1 2 3 … …… n i = 10%, n = 4 years, A = 2,50,000
P = ?
2,50,000( / ,10,4) 2,50,000(3.16987) 7,92,466 (app)P P A Rs  
Note:
If i = 0, then your father will deposit Rs One Million in fixed income scheme.
When i = 10% , your father will deposit Rs 7,92,466 in fixed income scheme.

24. ARITHMETIC GRADIENT SERIES

25. You are going to deposit in saving scheme as follows:
Year 1 -> 500,
Year 2 -> 1000,
Year 3 -> 1500,
Year 4 -> 2000,
Year 5 -> 2500,
What is equivalent annual amount (A), you will deposit in place of this scheme
(Markup rate is i=10%)
500( / ,10,5) 500(1.81013) 905(app)A A G Rs  
Note:
If i = 0, then you will deposit equivalent annual amount (A) of Rs 1500 per year for next 5
years. When i = 10% , you will deposit equivalent annual amount (A) of Rs 905 per year for
next 5 years.

26. You want withdraw money from fixed income scheme as follows:
Year 1 -> 500,
Year 2 -> 1000,
Year 3 -> 1500,
Year 4 -> 2000,
Year 5 -> 2500,
How much amount (P) you should deposit now in the fixed income scheme.
(Markup rate is i=10%)
500( / ,10,5) 500(6.86180) 3431 (app)P P G Rs  
Note:
If i = 0, then you will deposit (P) now Rs 7500 . When i = 10% , you will deposit Rs 3431 to
receive Rs 500,1000,1500,2000 and 2500 at the end of years 1,2,3,4 and 5 respectively.

27. 6%

28. 8%

29. 10%

30. 12%

31. Solved Examples
Q = $200 (P/F, 10%, 4)
= $200 (0.683)
= $136.60

32. Solved Examples
Using single payment factors:
P = $1400 (P/F, 10%, 1) + $1,320 (P/F, 10%, 2) + $1,240 (P/F, 10%, 3) +
$1,160 (P/F, 10%, 4) + $1,080 (P/F, 10%, 5)
= $1,272.74 + $1,090.85 + $931.61 + $792.28 + $670.57
= $4,758.05

33. Solved Examples
P=$750, n =3 years, i =8%, F =?
F = P (1+ i)n = $750 (1.08)3 = $750 (1.260)
= $945
Using interest tables:
F = $750 (F/P, 8%, 3) = $750 (1.360)
= $945

34. Solved Examples

35. Solved Examples

36. Solved Examples
R = $100(F/A, 10%, 4) = $100(4.641)
= $464.10

37. Solved Examples
S = 50 (P/G, 10%, 4) = 50 (4.378)
= 218.90

38. Solved Examples
T = 30 (A/G, 10%, 5) = 30 (1.810)
= 54.30