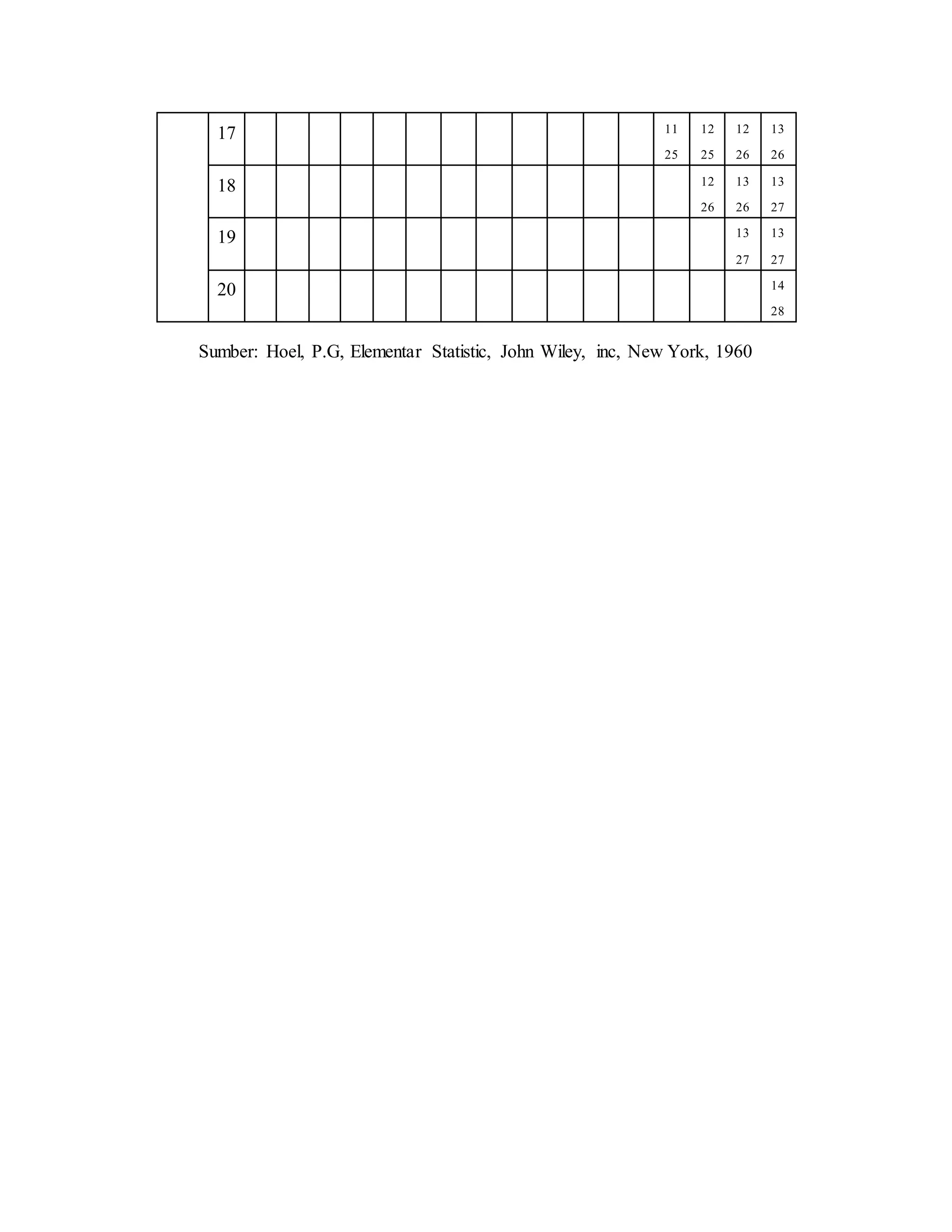
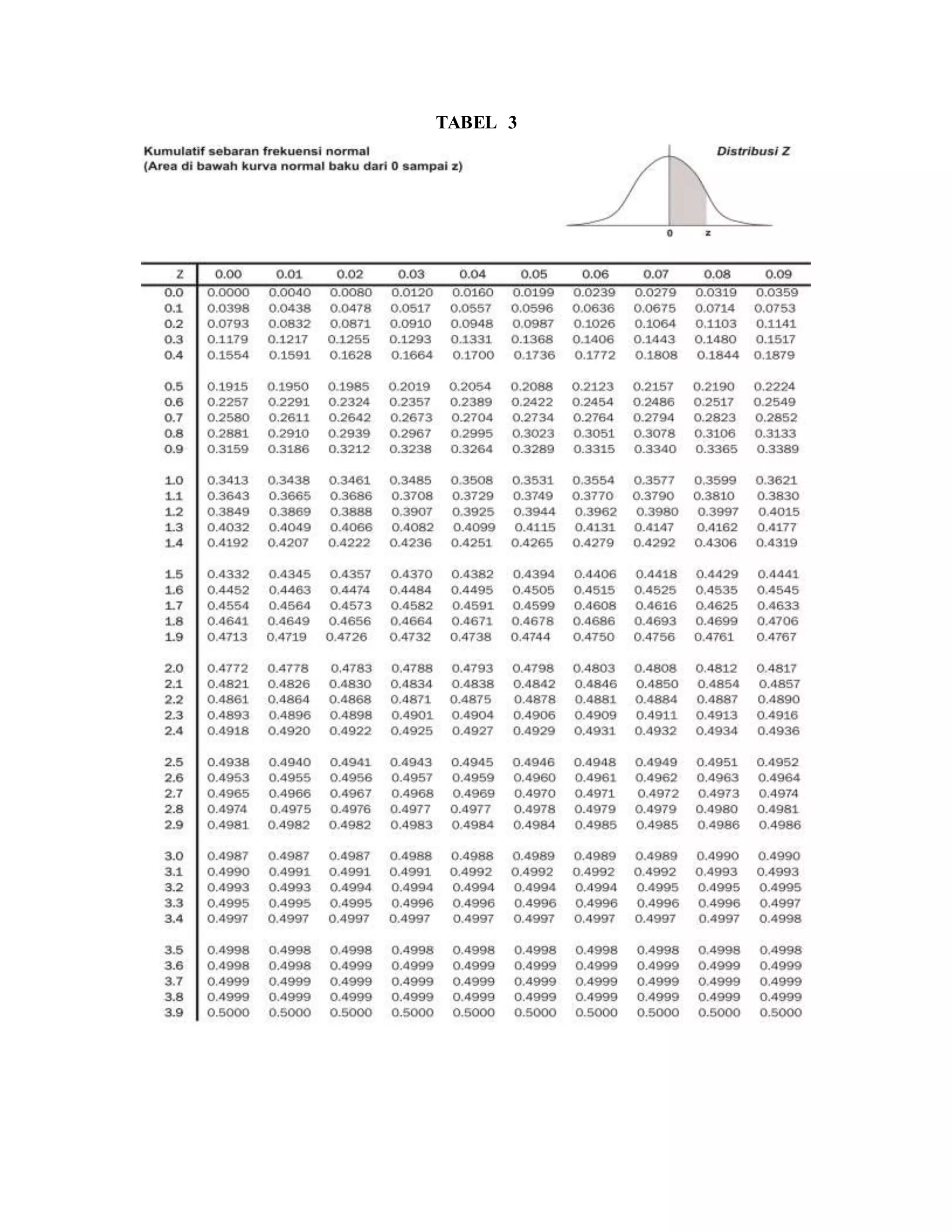
Makalah ini membahas dua pengujian hipotesis statistika nonparametrik yaitu run test untuk satu sampel dan NC Nemar test untuk dua sampel berpasangan. Run test digunakan untuk menguji acak tidaknya suatu sampel dengan menghitung jumlah run dan membandingkannya dengan batas kritis. NC Nemar test digunakan untuk menguji perbedaan antara dua sampel berpasangan dengan menyusun data ke dalam tabel segi empat dan menghitung statistik chi

1. Tugas Mata Kuliah
Statistika Non Parametik
PengujianHipotesis Deskriptiif untuk Satu Sampel (Run Test) dan Pengujian
Hipotesis Komparatif untuk Dua Sampel Berpasangan (N.C Nemar Test)
Oleh:
MUSLIMAH R ( H121 14 005 )
RATRI DWI R ( H121 14 028 )
RESKI WAHYU YANTI ( H121 14 307 )
SUKMA HIDAYANTI NUR ( H121 14 309 )
HANIFAH LAINUN ( H121 13 311 )
PRODI STATISTIKA
JURUSAN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS HASANUDDIN
MAKASSAR
2016

2. i
KATA PENGANTAR
Puji syukur kita panjatkan kepada Allah Subhanahu Wa Ta’ala yang dengan limpahan
rahmat dan nikmat-Nya, baik itu nikmat waktu, nikmat kesehatan, dan nikmat ilmu sehingga
kami dapat menyelesaikan makalah ini dengan baik.
Makalah ini bertujuan untuk memenuhi tugas
Makassar, Februari 2016

3. ii
DAFTAR ISI
KATA PENGANTAR........................................................................................................................... I
DAFTAR ISI...................................................................................................................................... II
BAB I PENDAHULUAN..................................................................................................................... 3
I.1 LATAR BELAKANG ........................................................................................................................ 3
I.2 RUMUSAN MASALAH ................................................................................................................... 3
I.3 TUJUAN..................................................................................................................................... 3
BAB II TINJAUAN PUSTAKA............................................................................................................ 5
II.1 JENIS-JENIS DATA....................................................................................................................... 5
II.2 BENTUK HIPOTESIS ..................................................................................................................... 5
II.3 PEDOMAN UMUM MEMILIH STATISTIK NONPARAMETIS UNTUK PENGUJIAN HIPOTESIS............................. 7
BAB III PEMBAHASAN..................................................................................................................... 8
III.1 PENGUJIAN HIPOTESIS DESKRIPTIF UNTUK SATU SAMPEL (RUN TEST).................................................. 8
III.2 PENGUJIAN HIPOTESIS KOMPARATIF UNTUK DUA SAMPEL BERPASANGAN (N.C NEMAR TEST)............... 10
BAB IV PENUTUP .......................................................................................................................... 14
IV.1 KESIMPULAN.......................................................................................................................... 14
DAFTAR PUSTAKA......................................................................................................................... 15
LAMPIRAN .................................................................................................................................... 16

4. 3
BAB I
PENDAHULUAN
I.1 Latar Belakang
Terdapat dua macam teknik statistik inferensial yang dapat digunakan untuk menguji hipotesis
penelitian, yaitu statistik parametis dan statistik non parametis. Keduanya bekerja dengan data
sampel dan pengambilan sampel harus dilakukan secara random (Sugiyono, 2012).
Statistika Parametis lebih banyak digunakan untuk menganalisis data yang berbentuk interval
dan ratio degan dilandasi beberapa persyaratan tertentu antara lain misalnya: data variabel yang
akan dianalisis harus berdistribui normal. Statistik Non Parametis digunakan untuk menganalisis
data yang berbentuk nominal dan ordinal dan tidak dilandasi persyaratan data harus berdistribusi
normal (Sugiyono, 2012). Oleh karena itu Statistik Non Parametrik sering disebut sebagai Distribusi
Bebas (Free Distribution).
Pemilihan teknik uji statistik Non Parametis didasarkan pada bentuk data yang akan dianalisis
dan bentuk Hipotesisnya. Oleh karena itu, penting untuk mengetahui bentuk-bentuk data dan
bentuk-bentuk hipotesis terlebih dahulu kemudian memahami langkah-langkah pengujian suatu
hipotesis tersebut.
I.2 Rumusan Masalah
1. Bagaimana pengujian hipotesis deskriptif untuk satu sampel menggunakan uji run
(kerandoman)?
2. Bagaimana pengujian hipotesis komparatif untuk dua sampel berpasangan menggunakan
uji NC Nemar?
I.3 Tujuan
1. Mengetahui pengujian hipotesis deskriptif untuk satu sampel menggunakan uji run
(kerandoman).

5. 4
2. Mengetahui pengujian hipotesis komparatif untuk dua sampel berpasangan menggunakan
uji NC Nemar.

6. 5
BAB II
TINJUAN PUSTAKA
II.1 Jenis-jenis Data
Jenis data ada dua yaitu data kualitatif dan data kuantitatif. Data kuanlitatif adalah data yang
dinyatakan dalam bentuk kata, kalimat, dan gambar. Data Kuatitatif adalah data yang berbentuk
angka, atau data kualitatif yang diangkakan (skoring: baik sekali=4, baik=3, kurang baik=2, tidak
baik=1) (sugiyono, 2012).
Data kuantitatif dibagi menjadi dua, yaitu data diskrit (nominal) dan data kontinum. Data diskrit
merupakan hasil perhitungan, sehingga tidak dijumpai bilangan pecahan. Data ini adalah data
yang paling sederhana yang disusun menurut jenisnya atau kategorinya (Husaini dan Purnomo
2006). Misalnya mahasiswa Universitas Hasanuddin yang menyelesaikan program S1 tahun ini
ialah sebanyak 150 orang dimana 30 orang lulus dengan peringkat cum laude, 80 orang lulus
dengan peringkat sangat memuaskan, dan 40 orang lulus dengan peringkat memuaskan.
Data kontinum adalah data yang bervariasi menurut tingkatan dan diperoleh dari hasil
pengukuran. Data ini dibagi menjadi data ordinal, data interval, dan data ratio. Data ordinal
adalah data yang berbentuk ranking atau peringkat. Misalnya juara I, II, III dan seterusnya. Data
ini bila dinyatakan dalam skala, maka jarak satu data dengan data yag lain tiak sama. Data
interval adalah data yang jaraknya sama tetapi tidak mempunyai nilai nol (0) absolut/mutlak.
Contoh skala thermometer walaupun ada 0o C tetapi tetap ada nilainya. Data ratio adalah data
yang jaraknya sama, dan mempunyai nilai nol mutlak. Misalya data tentang berat, panjang, dan
volume. Berat 0 Kg berarti tidak ada bobotnya (Sugiyono, 2012).
II.2 Bentuk Hipotesis
II.2.1 Hipotesis Deskripif
Hipotesis deskriptif, merupakan dugaan terhadap nilai satu variable dalam satu sampel
walaupun di dalamnya bisa terdapat beberapa kategori (Sugiyono, 2012). Contoh:

7. 6
H0 : Kecendrungan masyrakat membuang sampah sembarangan
H1 : Kecendrungan masyarakat membuang sampah pada tempatnya
II.2.2 Hipotesis Komparatif
Hipotesis komparatif merupakan dugaan terhadap perbandingan nilai dua sampel atau lebih.
Dalam hal komparasi ini terdapat beberapa macam yaitu:
1.Komparasi berpasangan dalam dua sampel dan lebih (k sampel)
Contoh:
H0 : Tidak terdapat perbedaan nilai penjualan setelah pemotongan harga
H1 : terdapat perbedaan nilai penjualan setelah pemotongan harga
2.Komparasi independen dalam dua sampel dan lebih (k sampel)
Contoh:
H0 : tidak terdapat perbedaan antara birokrat, akademisi, dan pebisnis dalam memilih
partai
H1 : terdapat perbedaan antara birokrat, akademisi, dan pebisnis dalam memilih partai
II.2.3 Hipotesis Asosiatif
Hipotesis asosiatif merupakan dugaan terhadap hubungan antara dua variable atau lebih.
Contoh:
H0 : tidak terdapat hubungan antara jenis profesi dan jenis olah raga yang disenangi
H1 : terdapat hubungan antara jenis profesi dan jenis olah raga yang disenangi

8. 7
II.3 Pedoman umum Memilih statistik Nonparametis untuk Pengujian Hipotesis
Gambar 1 Pedoman umum Memilih statistik Nonparametis untuk Pengujian Hipotesis
(Sugiyono, 2012).

9. 8
BAB III
PEMBAHASAN
III.1 Pengujian Hipotesis Deskriptif untuk Satu Sampel (Run Test)
Seorang peneliti yang ingin sampai pada kesimpulan tertentu mengenai suatu populasi
berdasarkan data sampel, maka sampelnya haruslah sampel acak. Uji Run digunakan untuk
menguji hipotesis bahwa suatu sampel adalah sampel acak.
1. Hipotesis
H0 : urutan ampel bersifat acak
H1 : urutan sampel tidak bersifat acak
2. Defenisi Run
Serangkaian pemunculan yang sama untuk satu jenis yang kemudian diikuti oleh
pemunculan jenis lainnya.
Contoh: Pelemparan mata uang
B MM B MMM  4 run
M BB M B M B  6 run
Dimana, run yang terlalu banyak atau sedikit menunjukkan sampel tidak bersifat acak.
3. Metode
- Hitung banyaknya run (r)
- Hitung n1 dan n2 (misalnya n1=B dan n2=M)
4. Keputusan
- Untuk sampel yang kecil ( 𝑛1,𝑛2 ≤ 20 ) maka gunakan tabel Tabel I (lihat lampiran).
Tolak H0 apabila r <= batas bawah 𝑛1,𝑛2 atau r ≥ batas atas 𝑛1,𝑛2
- Untuk sampel yang besar ( 𝑛1,𝑛2 > 20 ) digunakan pendekatan distribusi normal
(Tabel III ) dengan:
𝑍 =
r − 𝜇 𝑟
𝜎𝑟
………………….. (1)
𝜇 𝑟 =
2𝑛1 𝑛2
𝑛1+ 𝑛2
+ 1
……………….…. (2)

10. 9
𝜎𝑟 = √
2𝑛1 𝑛2 (2𝑛1 𝑛2 − 𝑛1 − 𝑛2)
(𝑛1+𝑛2)2 (𝑛1+𝑛2 − 1)
………….............. (3)
Contoh untuk sampel kecil:
Tempat duduk mahasiswa prodi matemtika (M) dan mahasiswa prodi statistika (S) dalam suatu
pertemuan ialah sebagai berikut:
M S S M M M M S M S M M S S S
H0 : mereka duduk secara acak
H1 : mereka tidak duduk secara acak
Penyelesaian:
M S S M M M M S M S M M S S S  run = 8
n1 (banyak symbol M) = 8
n2 (banyak symbol S) = 7
Berdasarkan batas kritis untuk run test dengan taraf α=5% (Tabel II) diperoleh batas bawah=4
dan batas atas=13. Karena banyaknya run yaitu 8 terletak diantara 4 dan 13 maka dapat
disimpulkan bahwa ke-15 mahasiswa tersebut telah duduk secara acak atau H0 diterima.
Contoh untuk sampel besar:
Misalkan suatu pertemuan dihadiri oleh 100 peserta. 60 diantaranya ialah mahasiswa matematika
dan 40 mahasiswa statistika. Diketahui jumlah run berdasarkan posisi duduk ialah 38.
• H0 : mereka duduk secara acak, H1 : mereka tidak duduk secara acak
• Statistik uji = z
• Uji dua arah
• Taraf Nyata Pengujian = α = 5% → α/2 = 2.5% = 0.025

11. 10
• Daerah Penolakan H0  z < − z0.025 → z < -1.96 dan z > z0.025 → z > 1.96
Penyelesaian:
Run = 8, n1 = 60, dan n2 = 40
Dari rumus (2) dan (3) diperoleh:
𝜇 𝑟 =
2(60)(40)
(60 + 40)
+ 1 = 49
𝜎𝑟 = √
2(60)(40) ((2(60)(40) − 60 − 40)
(60 + 40)2 (60+ 40 − 1)
= 4,77
Jika didistribusikan kedalam rumus (1) maka didapatkan:
𝑍 =
38 − 49
4,77
= −2,31
Berdasarkan daftar normal baku dengan selang kepercayaan α=5%, dapat disimpulkan bahwa
mereka tidak duduk secara acak atau H0 ditolak (-2.31 < -1.96) atau H1 diterima.
III.2 Pengujian Hipotesis Komparatif untuk Dua Sampel Berpasangan (N.C Nemar Test)
Teknik statistik ini digunakan untuk menguji hipotesis komparatif dua sampel yang berkolerasi
bila datanya berbentuk nominal/diskrit. Rancangan penelitian biasanya berbentuk “before after”.
Jadi hipotesis penelitian merupakan perbandingan antara nilai sebelum dan sesudah ada
perlakuan/treatment (Sugiyono, 2012).

12. 11
Sebagai panduan untuk menguji signifikansi setiap perubahan, maka data perlu disusun kedalam
tabel segi empat ABCD seperti berikut:
Sebelum
Sesudah
- +
+ A B
- C D
Tanda (+) dan (-) sekedar dipakai untuk menandai jawaban yang berbeda, jadi tidak harus
bersifat positifdan negative yang sesungguhnya. Kasus-kasus yang menunjukkan perubahan
antara jawaban petama dan kedua muncul pada sel A dan D. Seseorang dicatat di sel A jika
berubah dari tambah ke kurang, dan dicatat pada sel D jika ia berubah dari kurang ke tambah
(Sugiyono, 2012).
A+D adalah jumlah total orang yang berubah, dan B dan C tidak berubah. H0 = ½ (A+D)
berubah dalam satu arah, dan merupakan frekuensi yang diharapkan di bawah H0 pada kedua sel
yaitu A dan D (Sugiyono, 2012).
Test MC Nemar berdistribusi Chi Kuadrat (𝜒2
), oleh karena itu rumus yang digunakan untuk
pengujian hipotesis adalah rumus chi kuadrat. Persamaan dasarnya ditunjukkan pada persamaan
(4) berikut.
𝜒2
= ∑
(𝑓0−𝑓ℎ)2
𝑓ℎ
𝑘
𝑖=1
……………………. (4)
Dimana:
f0 = Banyak frekuensi yang di observasi dalam kategori ke 1
fh = Banyak frekuensi yang diharapkan dibawah H0 dalam kategori 1
Dari persamaan (4) diperoleh:

13. 𝜒2
=
(𝐴 −
𝐴 + 𝐷
2
)2
𝐴 + 𝐷
2
+
(𝐷 −
𝐴 + 𝐷
2
)2
𝐴 + 𝐷
2
𝜒2
=
𝐴2
− 2𝐴 (
𝐴 + 𝐷
2
) + (
𝐴 + 𝐷
2
)2
𝐴 + 𝐷
2
+
𝐷2
− 2𝐷 (
𝐴 + 𝐷
2
) + (
𝐴 + 𝐷
2
)2
𝐴 + 𝐷
2
𝜒2
=
𝐴2
− 𝐴2
− 𝐴𝐷 +
𝐴2
+ 2𝐴𝐷 + 𝐷2
4
𝐴 + 𝐷
2
+
𝐷2
− 𝐷2
− 𝐴𝐷 +
𝐴2
+ 2𝐴𝐷 + 𝐷2
4
𝐴 + 𝐷
2
𝜒2
=
−2𝐴𝐷 + 2(
𝐴2
+ 2𝐴𝐷 + 𝐷2
4
)
𝐴 + 𝐷
2
𝜒2
= (−2𝐴𝐷 +
𝐴2
+ 2𝐴𝐷 + 𝐷2
2
) ×
2
𝐴 + 𝐷
𝜒2
=
−4𝐴𝐷 + 𝐴2
+ 2𝐴𝐷 + 𝐷2
𝐴 + 𝐷
𝜒2
=
𝐴2
− 2𝐴𝐷 + 𝐷2
𝐴 + 𝐷
𝜒2
=
(𝐴 − 𝐷)2
𝐴 + 𝐷
Dengan dk=1. Maka dengan koreksi kontinuitas,
𝜒2
=
(| 𝐴 − 𝐷| − 1)2
𝐴 + 𝐷
Signifikans setiap harga 𝜒2
yang diperoleh dengan rumus diatas ditetapkan dengan
menggunakan Tabel C. Jika harga 𝜒2
observasi sama atau lebih besar dari yang ditunjukkan di
Tabel C untuk suatu tingkat signifikansi tertentu dengan dk=1, maka implikasinya ialah bahwa
suatu efek yang ”signifikansi” telah ditunjukkan dalam jawaban ”sebelum” dan ”sesudah”.

14. Contoh Soal:
Suatu perusahaan ingin mengetahui pengaruh sponsor yang diberikan dalam suatu pertandingan
olah raga terhadap nilai penjualan barangnya. Dalam penelitian ini digunakan sampel yang
diambil secara random yang jumlah anggotanya 200. Sebelum sponsor diberikan, terdapat 50
orang yang membeli barang tersebut, dan 150 orang tidak membeli. Setelah sponsor diberikan
dalam pertandingan olah raga, ternyata dari 200 orang tersebut terdapat 125 orang yang membeli
dan 75 orang tidak membeli. Dari 125 orang tersebut terdiri atas pembeli tetap 40, dan yang
berubah dari tidak membeli menjadi membeli ada 85 orang. Selanjutnya dari 75 orang yang tidak
membeli itu terdiri atas yang berubah dari membeli menjadi tidak membeli ada 10 orang, dan
yang tetap tidak membeli ada 65 orang.
H0 : tidak terdapat perbedaan jumlah penjualan sebelum dan sesudah ada sponsor
H1 : terdapat perbedaan jumlah penjualan sebelum dan sesudah ada sponsor
Penyelesaian:
Prilaku konsumen Membeli Tidak Membeli
Tidak Membeli A = 85 B = 65
Membeli C = 40 D = 10
Sehingga,
𝜒2
=
(| 𝐴 − 𝐷| − 1)2
𝐴 + 𝐷
=
(|85 − 10| − 1)2
85 + 10
= 57,642
Harga hitung 𝜒2
= 57,642
Harga hitung 𝜒2
tersebut kemudian selanjutnya dibandingkan dengan harga 𝜒2
tabel (Tabel II).
Bila dk=1 dan taraf kesalahan 5%, maka harga 𝜒2
tabel = 3,84. Berdasarkan perhitungan diatas
ternyata harga 𝜒2
hitung lebih besar dari pada tabel (57,642 > 3,84). Hal ini berasrti H0 ditolak
dan H1 diterima.

15. BAB IV
PENUTUP
IV.1 Kesimpulan
Terdapat dua macam teknik statistik inferensial yang dapat digunakan untuk menguji hipotesis
penelitian, yaitu statistik parametis dan statistik non parametis. Keduanya bekerja dengan data
sampel dan pengambilan sampel harus dilakukan secara random (Sugiyono, 2012). Dalam
menguji kerandoman suatu sampel dari suatu populasi maka uji statistik yang digunakan ialah uji
run atau uji kerandoman.
Uji run terbagi menjadi dua yaitu (1) pengujian untuk sampel yang kecil ( 𝑛1,𝑛2 ≤ 20 ) dengan
gunakan Tabel I (lihat lampiran). Tolak H0 apabila r ≤ Tabel II atau r ≥ Tabel III (2) pengujian
untuk sampel yang besar ( 𝑛1,𝑛2 > 20 ) digunakan pendekatan distribusi normal (Tabel III )
dengan:
𝑍 =
r − 𝜇 𝑟
𝜎𝑟
𝜇 𝑟 =
2𝑛1 𝑛2
𝑛1+ 𝑛2
+ 1
𝜎𝑟 = √
2𝑛1 𝑛2 (2𝑛1 𝑛2 − 𝑛1 − 𝑛2)
(𝑛1+𝑛2)2 (𝑛1+𝑛2 − 1)
Uji hipotesis komparatif untuk dua sampel berpasangan menggunakan uji NC Nemar digunakan
untuk meneliti perbandingan antara nilai sebelum dan sesudah adanya perlakuan/treatment
terhadap sampel. Rumus yang digunakan dengan koreksi dk=1 :
𝜒2
=
(| 𝐴 − 𝐷| − 1)2
𝐴 + 𝐷
Apabila harga 𝜒2
hitung lebih besar atau sama dengan hasil perhitungan maka H0 ditolak.

16. DAFTAR PUSTAKA
Sudjana. 2005. Metode Statistika. Bandung: Tarsito.
Sugiyono. 2012. Statistik Nonparametis untuk Penelitian. Bandung: Alfabeta.
Usman, Husaini, Purnomo Setiady. 2006. Pengantar Statistika. Jakarta: PT. Bumi Aksara.

17. LAMPIRAN
TABEL 1........................................................................................................................................ 1
TABEL 2........................................................................................................................................ 3
TABEL 3........................................................................................................................................ 4

18. TABEL 1
BATAS KRITIS UNTUK RUN TEST
TARAF NYATA 5%
Harga terbesar antara n1 dan n2
5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Hargaterkecilantaran1dann2
2 2
6
2
6
2
6
2
6
2
6
2
6
2
6
2
6
2
6
3 2
8
2
8
2
8
2
8
2
8
2
8
2
8
2
8
2
8
2
8
2
8
2
8
2
8
2
8
2
8
4 2
9
2
9
2
10
3
10
3
10
3
10
3
10
3
10
3
10
3
10
3
10
4
10
4
10
4
10
4
10
4
10
5 2
10
3
10
3
11
3
11
3
12
3
12
4
12
4
12
4
12
4
12
4
12
4
12
4
12
5
12
5
12
5
12
6 3
11
3
12
3
12
4
13
4
13
4
13
4
13
5
14
5
14
5
14
5
14
5
14
5
14
6
14
6
14
7 3
13
4
13
4
14
5
14
5
14
5
14
5
15
5
15
6
15
6
16
6
16
6
16
6
16
6
16
8 4
14
5
14
5
15
5
15
6
16
6
16
6
16
6
17
6
17
7
17
7
17
7
17
7
17
9 5
16
5
16
6
16
6
16
6
17
7
18
7
18
7
18
7
18
8
18
8
18
8
18
10 6
16
6
17
7
17
7
18
7
18
7
18
8
19
8
19
8
19
8
10
19
20
11 7
17
7
18
7
19
8
19
8
19
8
20
8
20
8
20
9
21
9
21
12 7
19
8
19
8
20
8
20
9
21
9
21
9
21
10
22
10
22
13 8
20
9
20
9
21
9
21
10
22
10
22
10
23
10
23
14 9
21
9
22
10
22
10
23
10
23
11
23
11
24
15 10
22
10
23
11
23
11
24
11
24
12
25
16 11
23
11
24
11
25
12
25
12
25

19. Sumber: Hoel, P.G, Elementar Statistic, John Wiley, inc, New York, 1960
17 11
25
12
25
12
26
13
26
18 12
26
13
26
13
27
19 13
27
13
27
20 14
28

20. TABEL 2
NILAI-NILAI CHI KUADRAT

21. TABEL 3