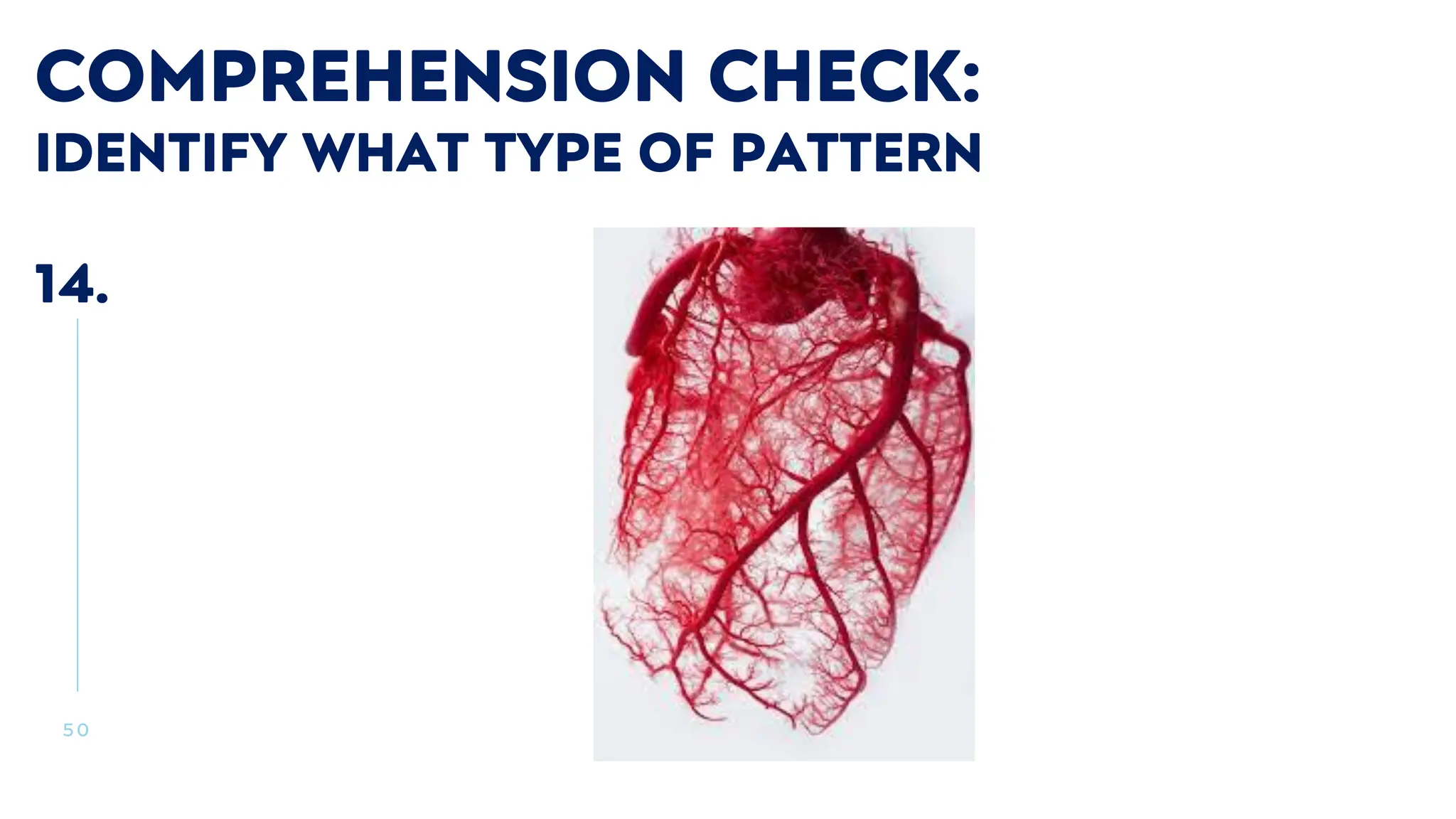
The document outlines a course titled 'Mathematics in the Modern World' which explores the nature and application of mathematics as a practical tool for understanding patterns in nature, employing both inductive and deductive reasoning. It emphasizes the importance of recognizing mathematical concepts in daily life and appreciating mathematics as a human endeavor through the study of various patterns such as symmetry, fractals, spirals, and tessellations. Learning outcomes include developing the ability to articulate the significance of mathematics, identify patterns in nature, and argue its representation and expression in the world.

1. SCIENTIFIC DISCOVERY
MIRJAM NILSSON
MATHEMATICS
IN THE MODERN
WORLD
MATHEMATICS
IN THE MODERN
WORLD

2. SCIENTIFIC DISCOVERY
MIRJAM NILSSON
MATHEMATICS
IN THE MODERN
WORLD
MATHEMATICS
IN THE MODERN
WORLD

3. SCIENTIFIC DISCOVERY
MIRJAM NILSSON
MATHEMATICS
IN THE
MODERN WORLD
COURSE DESCPRIPTION:
This course deals with the
nature of mathematics,
appreciation of its practical,
intellectual and aesthetic
dimensions and application of
mathematical tools in daily life.
This subject discusses the
nature of mathematics as an
exploration of patterns and as an
application of inductive and
deductive reasoning.

4. SCIENTIFIC DISCOVERY
MIRJAM NILSSON
MATHEMATICS
IN THE
MODERN WORLD
By exploring topics in this
subject, students may go beyond
the typical understanding of
mathematics as merely a set of
formulas but as a source of
aesthetics in patterns of nature
and a rich language in itself
governed by logic and reasoning.

5. OUTLINE TOPICS:
5
❑ NATURE OF MATHEMATICS

6. OUTLINE TOPICS:
6
❑ MATHEMATICS AS A PRACTICAL TOOL
❑ NATURE OF MATHEMATICS

7. OUTLINE TOPICS:
7
❑ MATHEMATICS AS A PRACTICAL TOOL
❑ NATURE OF MATHEMATICS
❑ TOOLS FROM ADVANCED
MATHEMATICS

8. LEARNING OUTCOMES:
8
After completing this module, you must be able to:
Identify patterns in nature and regularities in the
world.
Articulate the importance of mathematics in one’s
life.
Argue about the nature of mathematics, what is
it, how it is expressed, represented and used.
Express appreciation for mathematics as a human
endeavor.

9. LEARNING OUTCOMES:
9
After completing this module, you must be able to:
Identify patterns in nature and regularities in the
world.
Articulate the importance of mathematics in one’s
life.
Argue about the nature of mathematics, what is
it, how it is expressed, represented and used.
Express appreciation for mathematics as a human
endeavor.

10. LEARNING OUTCOMES:
1 0
After completing this module, you must be able to:
Identify patterns in nature and regularities in the
world.
Articulate the importance of mathematics in one’s
life.
Argue about the nature of mathematics, what is
it, how it is expressed, represented and used.
Express appreciation for mathematics as a human
endeavor.

11. LEARNING OUTCOMES:
1 1
After completing this module, you must be able to:
Identify patterns in nature and regularities in the
world.
Articulate the importance of mathematics in one’s
life.
Argue about the nature of mathematics, what is
it, how it is expressed, represented and used.
Express appreciation for mathematics as a human
endeavor.

12. WHAT IS MATHEMATICS?

13. WHAT IS MATHEMATICS?
❑ Mathematics is the study of pattern and structure.
Mathematics is fundamental to the physical and
biological sciences, engineering and information
technology, to economics and increasingly to the social
sciences.

14. WHAT IS MATHEMATICS?
❑ Mathematics is a useful way to think about nature
and our world.

15. WHAT IS MATHEMATICS?
❑ Mathematics is a tool to quantify, organize and
control our world, predict phenomena and make life
easier for us.

16. WHAT IS MATHEMATICS?
❑ Mathematics is a form of language. It is also a body
of knowledge.

17. WHAT IS MATHEMATICS?
As language, we use it to name and describe objects or
events that reveal quantity, form, pattern ang change.
As a body of knowledge, it is a set of concepts and
relations among concepts whose properties and
characteristics are obtained through logical reasoning.

18. WHERE IS
MATHEMATICS?
Many patterns and occurrences exists in nature, in our world, in our life.
Mathematics helps make sense of theses patterns and occurrences.

19. WHAT ROLE DOES MATHEMATICS
PLAY IN OUR WORLD?
❑ Mathematics helps organize patterns and regularities in our world.
❑ Mathematics helps control nature and occurrences in the world for
our own ends.
❑ Mathematics helps predict the behavior of nature and phenomena
in the world.
❑ Mathematics has numerous applications in the world making it
indispensable.

20. PATTERNS AND
NUMBERS IN
NATURE AND
THE WORLD

21. PATTERNS
Patterns are regular,
repeated or recurring forms
of designs.
Patters in nature are visible
regularities of form found
in the natural world and can
also be seen in the
universe.

22. PATTERNS
1. Patterns can be observed even in stars which
move in circles across the sky each day.

23. PATTERNS
2. The weather
season cycle each
year. All snowflakes
contains sixfold
symmetry which no
two are exactly the
same.

24. PATTERNS
3. Patterns can be seen in
fish patterns like spotted
trunkfish, spotted puffer,
spotted stingray, coral
grouper, redlion fish, and
angel fish. These fish
stripes and spots attest
to mathematical
regularities in biological
growth and form.

25. PATTERNS
4. Zebras, tigers, cats and
snakes are covered in
patterns of stripes; leopards
and hyenas are covered in
pattern of spots and giraffes
are covered in
pattern of blotches.

26. PATTERNS
6. Other patterns in nature can also be seen in honeycomb formed by bees,
snail’s shell and flower petals.

27. COMMON
TYPES OF
PATTERNS
IN NATURE

28. TYPES OF
PATTERNS IN
NATURE
1. Symmetry
2. Fractal
3. Spiral
4. Tessellation

29. TYPES OF
PATTERNS
1. Symmetry
➢ the quality of being made up of exactly similar
parts facing each other or around an axis.
1.1. Bilateral Symmetry
1.2. Radial Symmetry

30. TYPES OF PATTERNS
1. Symmetry
• A symmetry in which the left and right sides of
the organism can be divided into approximately
mirror image of each other along the midline.
1.1. Bilateral Symmetry

31. TYPES OF PATTERNS
1. Symmetry
• A symmetry around a fixed point known as the
center and it can be classified as either cyclic or
dihedral.
1.2. Radial (or Rotational) Symmetry

32. TYPES OF PATTERNS
2. Fractal
➢ A fractal is a never-ending pattern. Fractals are infinitely
complex patterns that are self-similar across different
scales.
➢ They are created by repeating a simple process over and
over in an ongoing feedback loop.
➢ For example, a tree grows by repetitive branching. This
same kind of branching can be seen in lightning bolts and
the veins in your body.

33. TYPES OF PATTERNS
2. Fractal

34. TYPES OF PATTERNS
3. Spiral
➢ A spiral pattern would be described as a circular pattern beginning
at a center point and circling around the center point as the
pattern moves outward.

35. TYPES OF PATTERNS
4. Tessellation
➢ is a pattern of one or more shapes that fit together with no gaps
or overlaps.
➢ A tessellation can continue on a plane forever.

36. 3 6
COMPREHENSION CHECK:
IDENTIFY WHAT TYPE OF PATTERNS
IN NATURE.
SYMMETRY, SPIRAL,
FRACTAL, TESSELLATION

37. 3 7
COMPREHENSION CHECK:
IDENTIFY WHAT TYPE OF PATTERN
1.

38. 3 8
COMPREHENSION CHECK:
IDENTIFY WHAT TYPE OF PATTERN
2.

39. 3 9
COMPREHENSION CHECK:
IDENTIFY WHAT TYPE OF PATTERN
2.

40. 4 0
COMPREHENSION CHECK:
IDENTIFY WHAT TYPE OF PATTERN
4.

41. 4 1
COMPREHENSION CHECK:
IDENTIFY WHAT TYPE OF PATTERN
5.

42. 4 2
COMPREHENSION CHECK:
IDENTIFY WHAT TYPE OF PATTERN
6.

43. 4 3
COMPREHENSION CHECK:
IDENTIFY WHAT TYPE OF PATTERN
7.

44. 4 4
COMPREHENSION CHECK:
IDENTIFY WHAT TYPE OF PATTERN
8.

45. 4 5
COMPREHENSION CHECK:
IDENTIFY WHAT TYPE OF PATTERN
9.

46. 4 6
COMPREHENSION CHECK:
IDENTIFY WHAT TYPE OF PATTERN
10.

47. 4 7
COMPREHENSION CHECK:
IDENTIFY WHAT TYPE OF PATTERN
11.

48. 4 8
COMPREHENSION CHECK:
IDENTIFY WHAT TYPE OF PATTERN
12.

49. 4 9
COMPREHENSION CHECK:
IDENTIFY WHAT TYPE OF PATTERN
13.

50. 5 0
COMPREHENSION CHECK:
IDENTIFY WHAT TYPE OF PATTERN
14.

51. 5 1
COMPREHENSION CHECK:
IDENTIFY WHAT TYPE OF PATTERN
15.