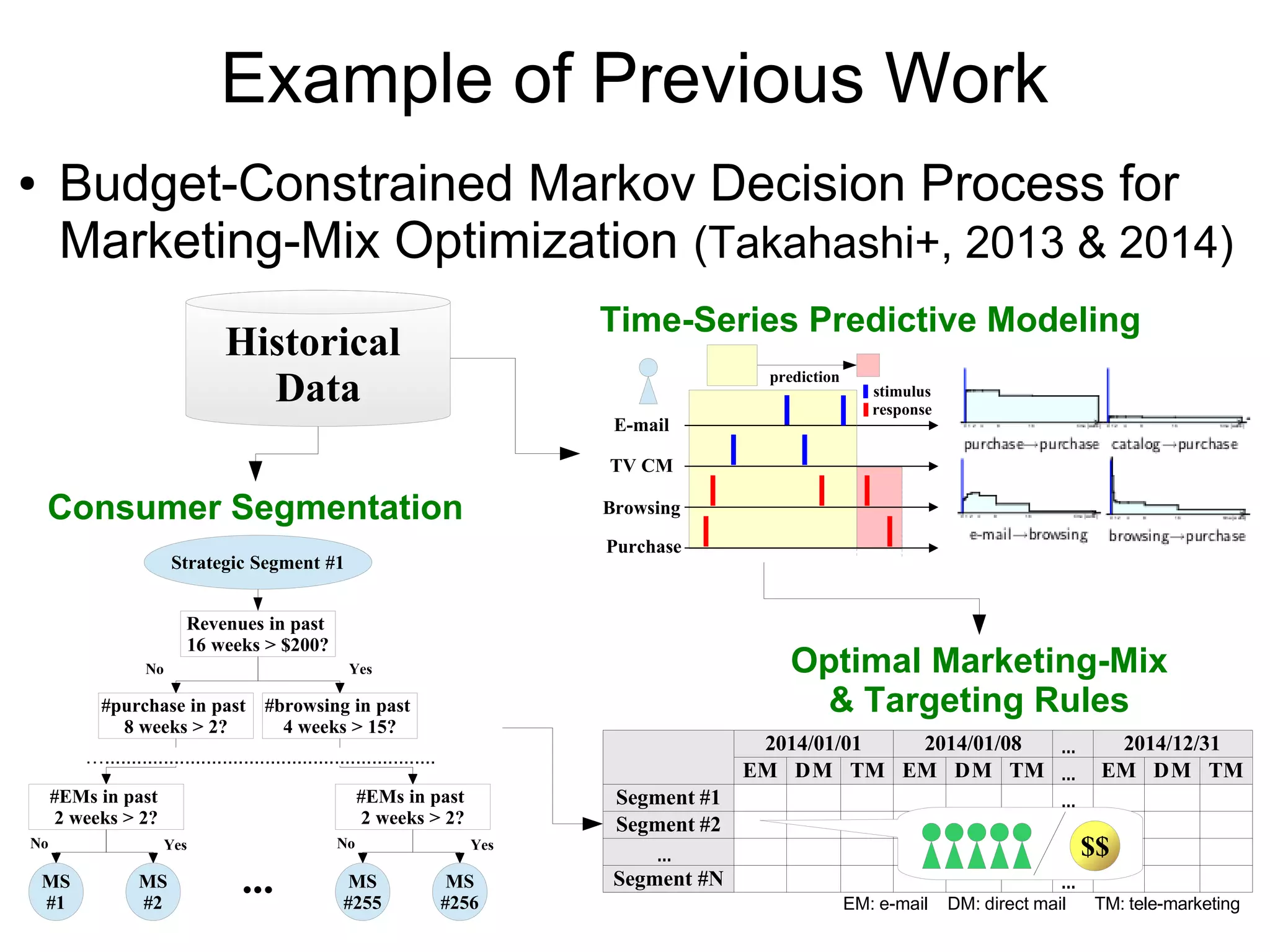
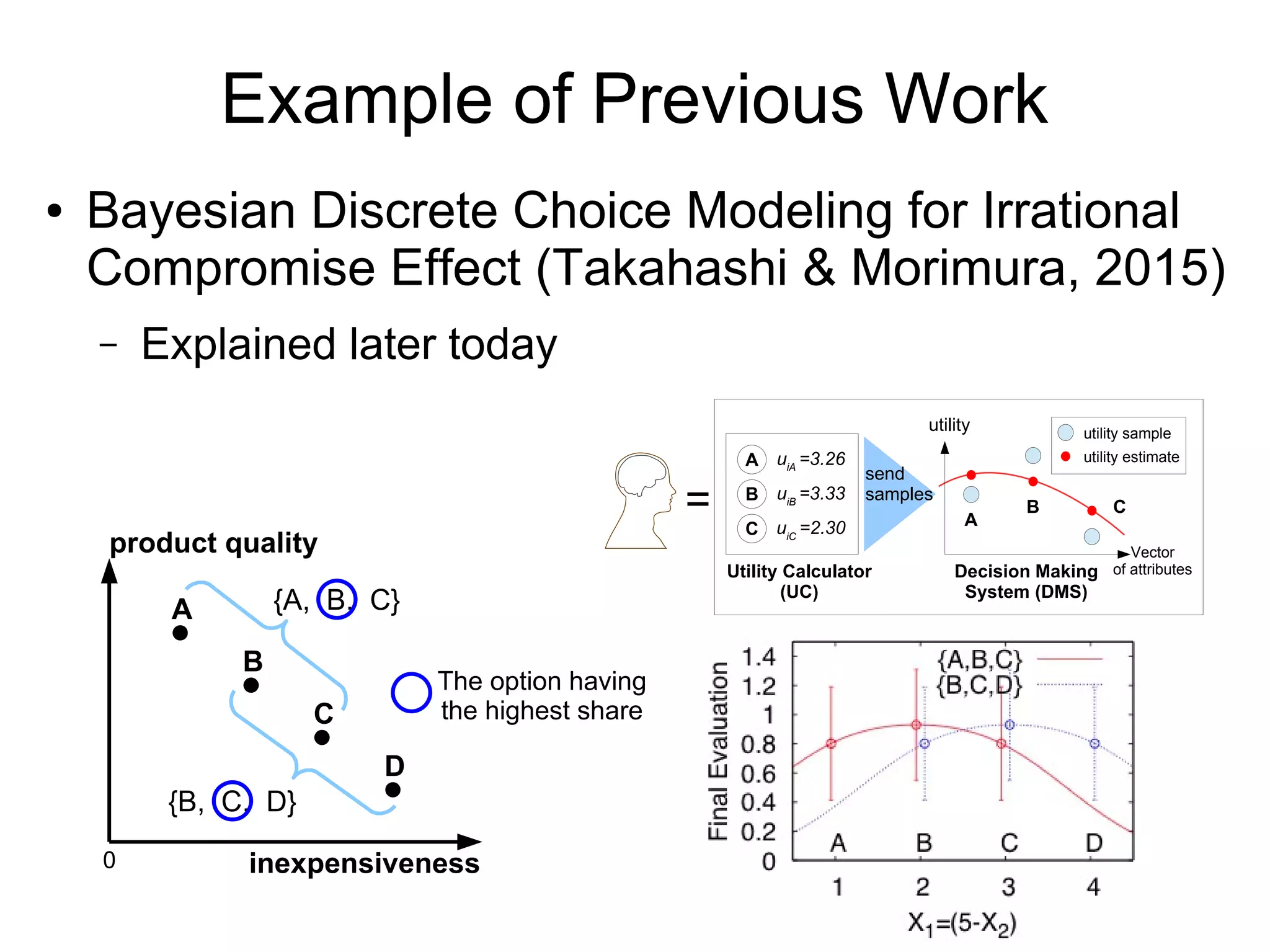
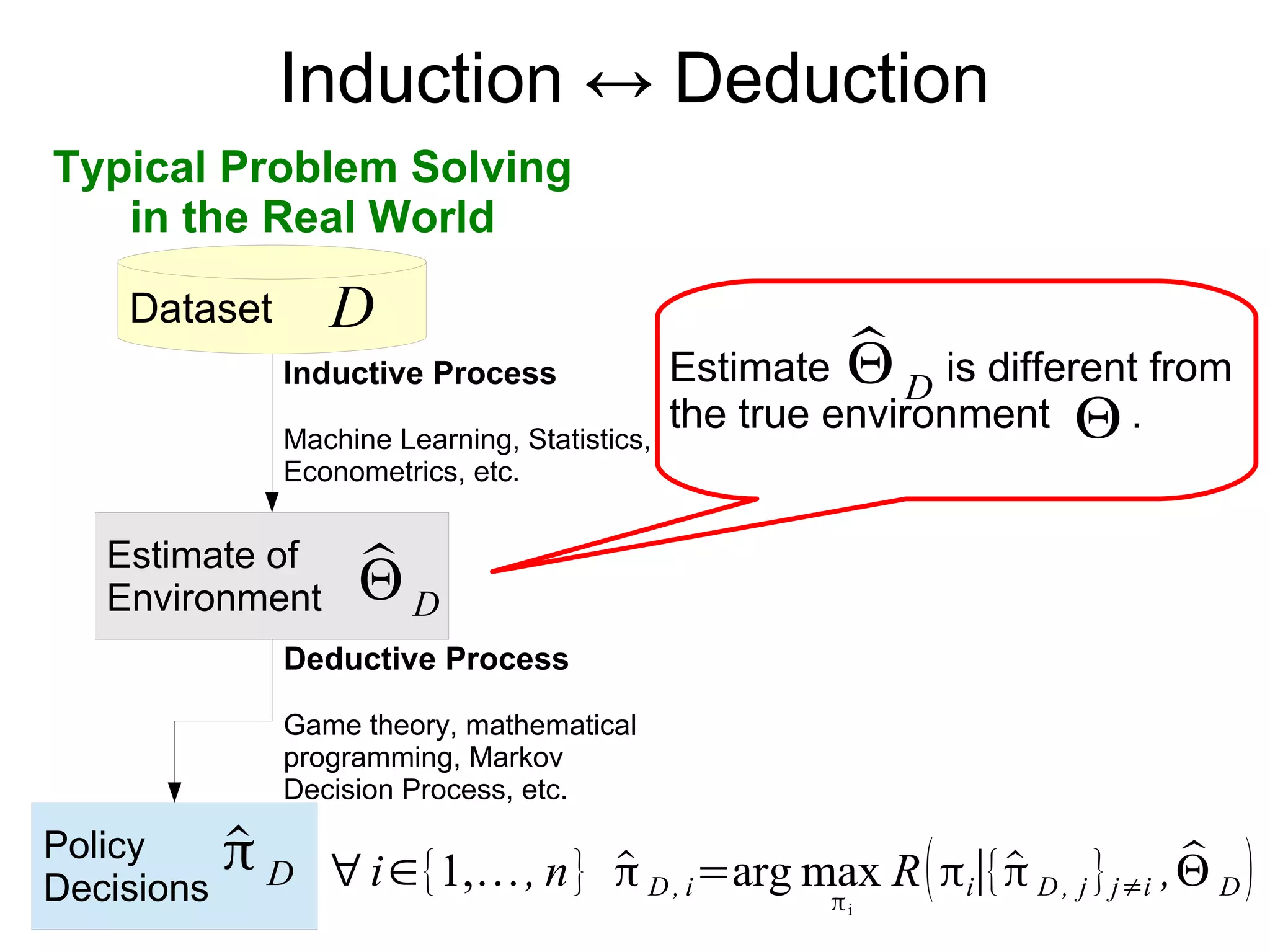
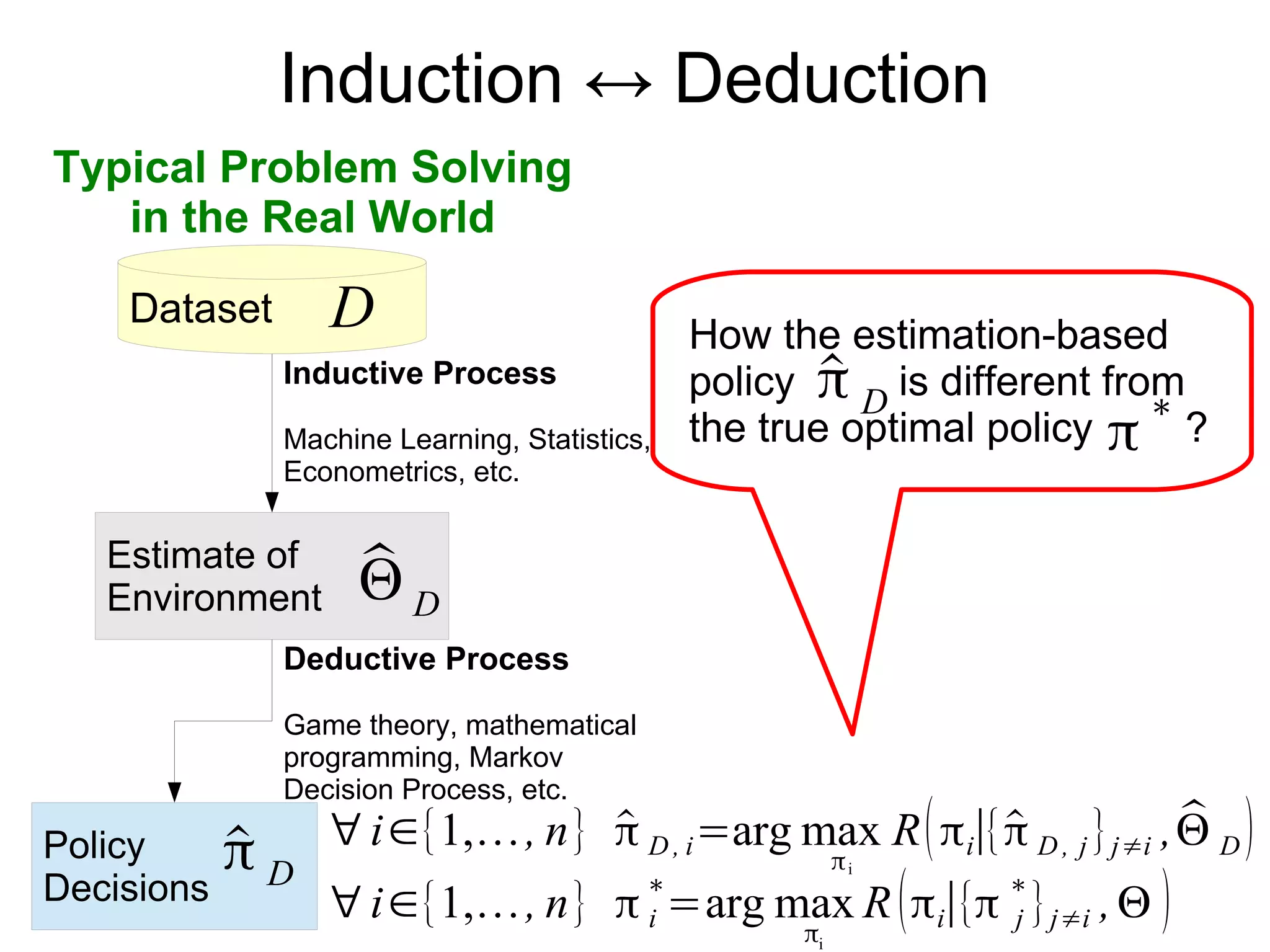
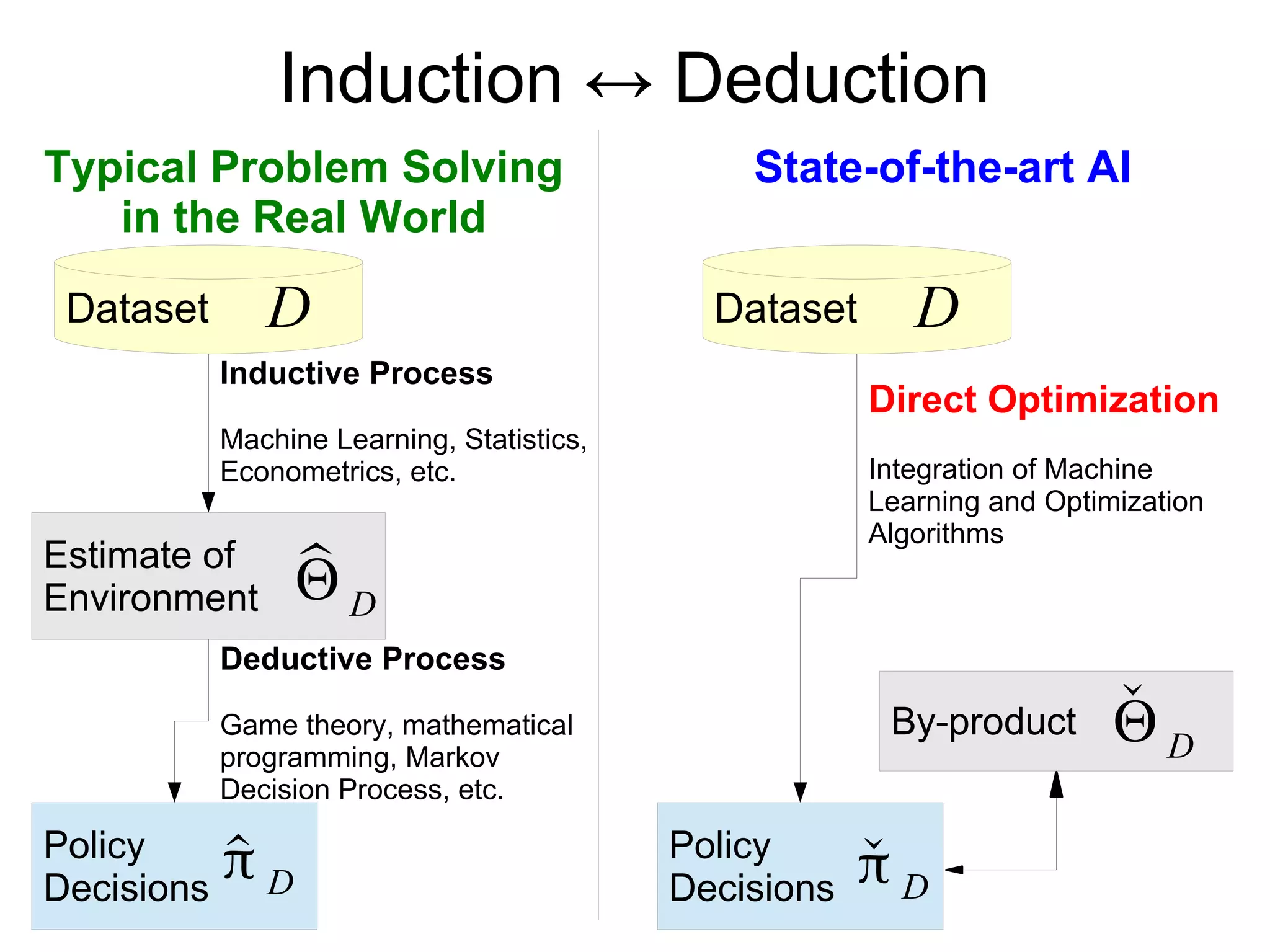
This document discusses integrating machine learning and game theory while accounting for uncertainty. It provides an example of previous work predicting travel time distribution on a road network using taxi data. It also discusses functional approximation in reinforcement learning, noting that techniques like deep learning can better represent functions with fewer parameters compared to nonparametric models like random forests. The document emphasizes avoiding unnecessary intermediate estimation steps and using approaches like fitted Q-iteration that are robust to estimation errors from small datasets.





![Estimation via Bayes' theorem
● Basis behind today's most ML algorithm
posterior distribution: p(θ∣D)=
p(D∣θ ) p(θ)
∫θ
p(D∣θ ) p(θ)d θ
predictive distribution: p( y∗
∣D)=∫θ
p( y∗
∣θ) p(θ∣D)d θ
posterior mode: ̂θ =argmax
θ
[log p(D∣θ )+log p(θ )]
predictive distribution: p( y∗
∣D)≃p( y∗
∣̂θ )
Maximum A
Posteriori
estimation
Bayesian
estimation
p(θ )
approximation
● Q. Why placing a prior ?
– A1. To quantify uncertainty as posterior
– A2. To avoid overfitting
data:D model parameter:θ](https://image.slidesharecdn.com/rtakahashigtw20170305-170226030024/75/Uncertainty-Awareness-in-Integrating-Machine-Learning-and-Game-Theory-8-2048.jpg)






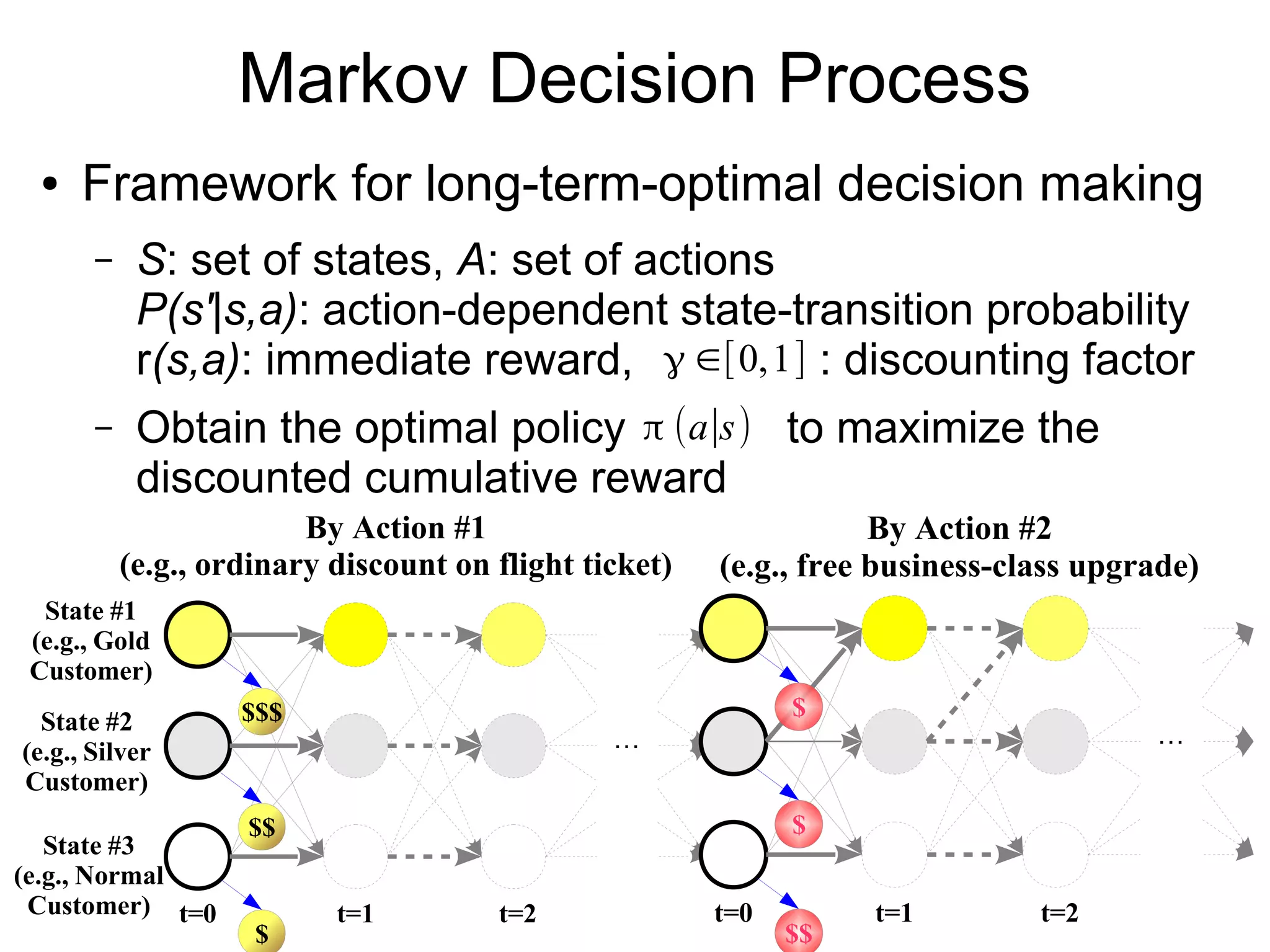
![Markov Decision Process
● Framework for long-term-optimal decision making
– S: set of states, A: set of actions
P(s'|s,a): state-transition probability
r(s,a): immediate reward, : discounting factor
– Optimize policy for maximal cumulative reward
…
State #1
(e.g., Gold
Customer)
State #2
(e.g., Silver
Customer)
State #3
(e.g., Normal
Customer) t=0 t=1 t=2
$
$$
$$$
By Action #1
(e.g., ordinary discount on flight ticket)
…
t=0 t=1 t=2
$$
$
$
By Action #2
(e.g., free business-class upgrade)
γ ∈[0,1]
π (a∣s)](https://image.slidesharecdn.com/rtakahashigtw20170305-170226030024/75/Uncertainty-Awareness-in-Integrating-Machine-Learning-and-Game-Theory-19-2048.jpg)



![Bellman Optimality Equation
● Policy is derived if we have an estimate of Q(s,a).
– Simpler than estimating P(s'|s,a) & r(s,a)
r
Q(s ,a)=E[r(s ,a)]+γ EP (s'∣s,a)
[max
a'
Q(s' ,a' )
]
π (a∣s)=
{1 a=argmax
a'
Q(s ,a' )
0 otherwise
̂Q(s ,a) (si ,ai ,si ' ,ri)i=1
n● Get an estimate from episodes](https://image.slidesharecdn.com/rtakahashigtw20170305-170226030024/75/Uncertainty-Awareness-in-Integrating-Machine-Learning-and-Game-Theory-23-2048.jpg)
![Fitted Q-Iteration (Ernst+, 2005)
● For k=1,2,... iterate 1) value computation and
2) regression as
∀i∈{1,…, n} vi
(k)
:=ri+γ ̂Qk
(1)
(si ' ,argmax
a'
̂Qk
(0)
(si ' ,a')
)
∀ f ∈{0,1} ̂Qk+1
( f )
:=argmin
Q∈H
[1
2
∑i∈J f
(vi
(k )
−Q(si ,ai))
2
+R(Q)]
1)
2)
– H: hypothesis space of function, Q0
≡ 0, R: regularization term
– Indices 1...n are randomly split into sets J0
and J1
, for avoiding
over-estimation of Q values (Double Q-Learning (Hasselt, 2010)).
● Related with Experience Replay in Deep Q-
Network (Mnih+, 2013 & 2015)
– See (Lange+, 2012) for more details.](https://image.slidesharecdn.com/rtakahashigtw20170305-170226030024/75/Uncertainty-Awareness-in-Integrating-Machine-Learning-and-Game-Theory-24-2048.jpg)
![Policy Gradient
●
Accurately fit policy while roughly fit Q(s,a)
– More directness to the final aim
– Applicable for continuous action problem
π θ (a∣s)
∇θ J (θ)⏟
gradient of performance
= Eπ θ
[∇θ logπ θ (a∣s)Q
π
(s ,a)]⏟
expected log-policy times cumulative-reward over s and a
Policy Gradient Theorem (Sutton+, 2000)
● Variations on providing the rough estimate of Q
– REINFORCE (Williams, 1992): reward samples
– Actor-Critic: regression models (e.g., Natural
Gradient (Kakade, 2002), A3C (Mnih+, 2016))](https://image.slidesharecdn.com/rtakahashigtw20170305-170226030024/75/Uncertainty-Awareness-in-Integrating-Machine-Learning-and-Game-Theory-25-2048.jpg)







![Complexity of Real Human’s Choice
An example of choosing PC (Kivetz et al., 2004)
Each subject chooses 1 option from a choice set
A B C D E
CPU [MHz] 250 300 350 400 450
Mem. [MB] 192 160 128 96 64
Choice Set #subjects
{A, B, C} 36:176:144
{B, C, D} 56:177:115
{C, D, E} 94:181:109
Can random utility theory still explain the preference reversals?
B C or C B?
Game Theory Workshop 2017 Uncertainty Awareness](https://image.slidesharecdn.com/rtakahashigtw20170305-170226030024/75/Uncertainty-Awareness-in-Integrating-Machine-Learning-and-Game-Theory-33-2048.jpg)


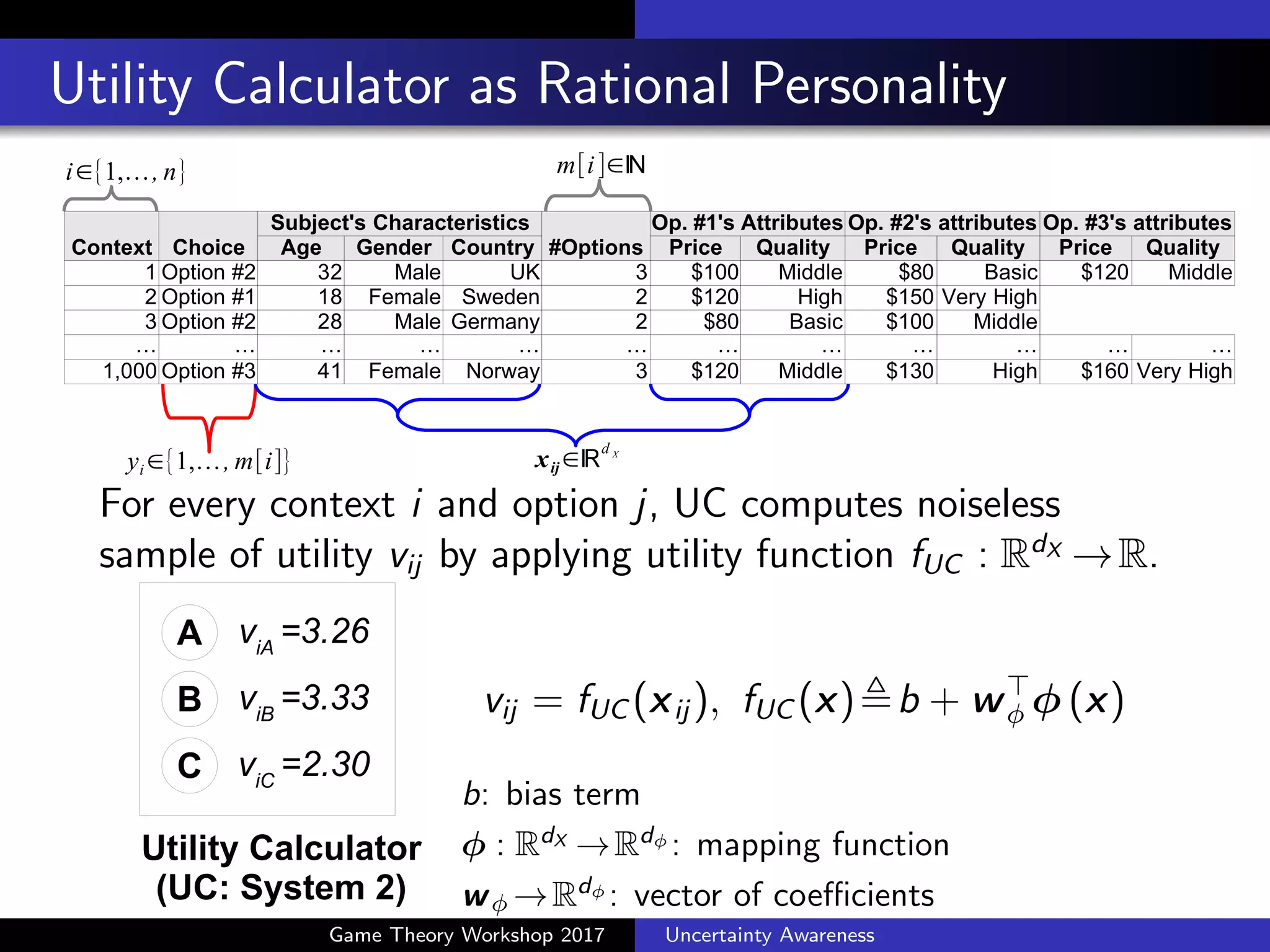


![Key Idea #2: DMS is a Bayesian estimator
DMS does not know fUC but has utility samples {vij }
m[i]
j=1 .
Assumption 2: DMS places a choice-set-dependent Gaussian
Process (GP) prior on regressing the utility function.
µi ⇠ N 0m[i], 2
K(Xi )
K(Xi ) = (K(xij , xij0 ))2Rm[i]⇥m[i]
vi , (vi1, . . ., vim[i])>
⇠N µi , 2
Im[i]
µi 2Rm[i]
: vector of utility
2
: noise level
K(·, ·): similarity function
Xi , (xi1 2RdX
, . . . , xim[i])>
The posterior mean is given as
u⇤
i ,E[µi |vi , Xi , K] = K(Xi ) Im[i]+K(Xi )
1
b1m[i]+ i w .
Game Theory Workshop 2017 Uncertainty Awareness](https://image.slidesharecdn.com/rtakahashigtw20170305-170226030024/75/Uncertainty-Awareness-in-Integrating-Machine-Learning-and-Game-Theory-40-2048.jpg)
![Convex Optimization for Model Parameters
Likelihood of the entire model is tractable, assuming the choice
is given by a logit whose mean utility is the posterior mean u⇤
i .
Thus we can fit the function fUC from the choice data.
Conveniently, MAP estimation of fUC is convex for fixed K.
bb, cw = max
b,w
nX
i=1
`(bHi 1m[i]+Hi i w , yi )
c
2
kw k2
where `(u⇤
i , yi ),log
exp(u⇤
iyi
)
Pm[i]
j0=1exp(u⇤
ij0 )
and Hi ,K(Xi )(Im[i]+K(Xi )) 1
Game Theory Workshop 2017 Uncertainty Awareness](https://image.slidesharecdn.com/rtakahashigtw20170305-170226030024/75/Uncertainty-Awareness-in-Integrating-Machine-Learning-and-Game-Theory-41-2048.jpg)
![Irrationality as Bayesian Shrinkage
Implication from the posterior-mean utility in (1)
Each option’s utility is shrunk into prior mean 0.
Strong shrinkage for an option dissimilar to the others,
due to its high posterior variance (=uncertainty).
u⇤
i = K(Xi ) Im[i]+K(Xi )
1
| {z }
shrinkage factor
b1m[i]+ i w
| {z }
vec. of utility samples
. (1)
Context e↵ects as Bayesian uncertainty aversion
E.g., RBF kernel
K(x, x0
)=exp( kx x0
k2
)
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1 2 3 4
FinalEvaluation
X1=(5-X2)
DCBA
{A,B,C}
{B,C,D}
Game Theory Workshop 2017 Uncertainty Awareness](https://image.slidesharecdn.com/rtakahashigtw20170305-170226030024/75/Uncertainty-Awareness-in-Integrating-Machine-Learning-and-Game-Theory-42-2048.jpg)
![Recovered Context-Dependent Choice Criteria
For a speaker dataset: successfully captured mixture of
objective preference and subjective context e↵ects.
A B C D E
Power [Watt] 50 75 100 125 150
Price [USD] 100 130 160 190 220
Choice Set #subjects
{A, B, C} 45:135:145
{B, C, D} 58:137:111
{C, D, E} 95:155: 91
2
3
4
100 150 200
Evaluation
Price [USD]
EDCBA
Obj. Eval.
{A,B,C}
{B,C,D}
{C,D,E}
-1.1
-1
-0.9
-0.8
AverageLog-Likelihood
Dataset
PC SP SM
LinLogit
NpLogit
LinMix
NpMix
GPUA
Game Theory Workshop 2017 Uncertainty Awareness](https://image.slidesharecdn.com/rtakahashigtw20170305-170226030024/75/Uncertainty-Awareness-in-Integrating-Machine-Learning-and-Game-Theory-43-2048.jpg)
![A Result of p-beauty Contest by Real Humans
Guess 2/3 of all votes (0-100). Mean is apart from the Nash
equilibrium 0 (Camerer et al., 2004; Ho et al., 2006).
Table: Average Choice in (2/3)-beauty Contests
Subject Pool Group Size Sample Size Mean[Yi ]
Caltech Board 73 73 49.4
80 year olds 33 33 37.0
High School Students 20-32 52 32.5
Economics PhDs 16 16 27.4
Portfolio Managers 26 26 24.3
Caltech Students 3 24 21.5
Game Theorists 27-54 136 19.1
Game Theory Workshop 2017 Uncertainty Awareness](https://image.slidesharecdn.com/rtakahashigtw20170305-170226030024/75/Uncertainty-Awareness-in-Integrating-Machine-Learning-and-Game-Theory-44-2048.jpg)





















