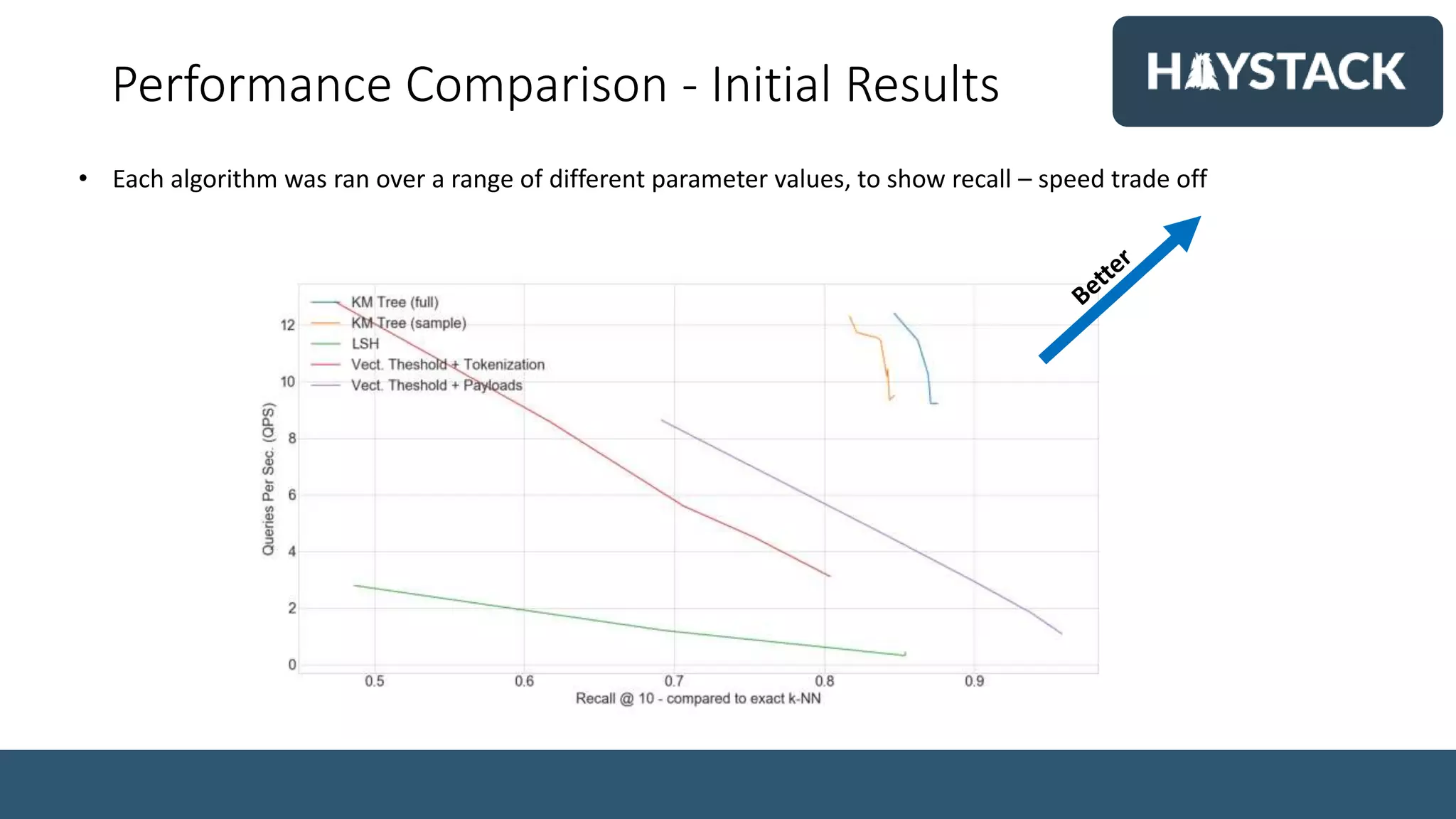
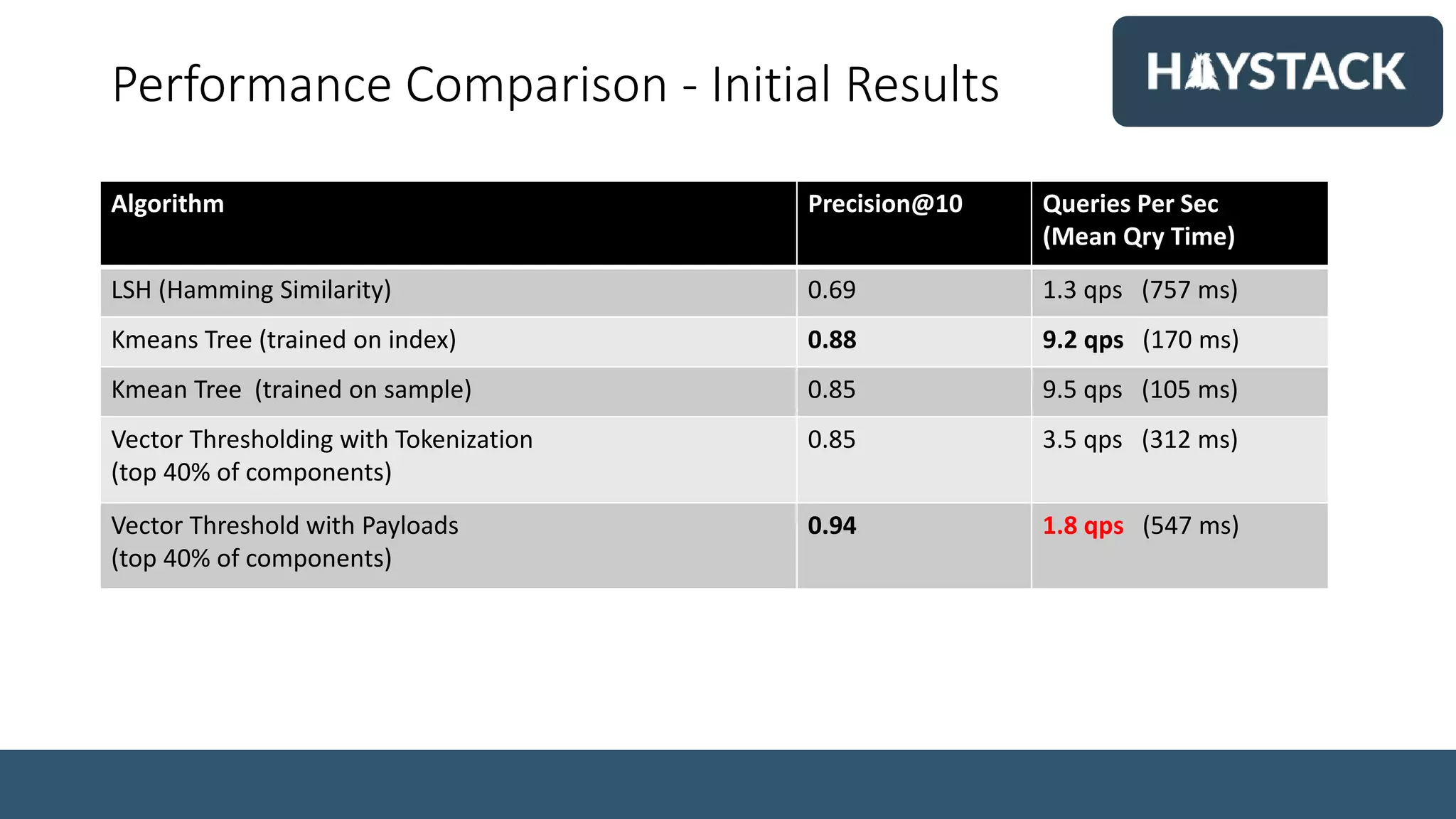
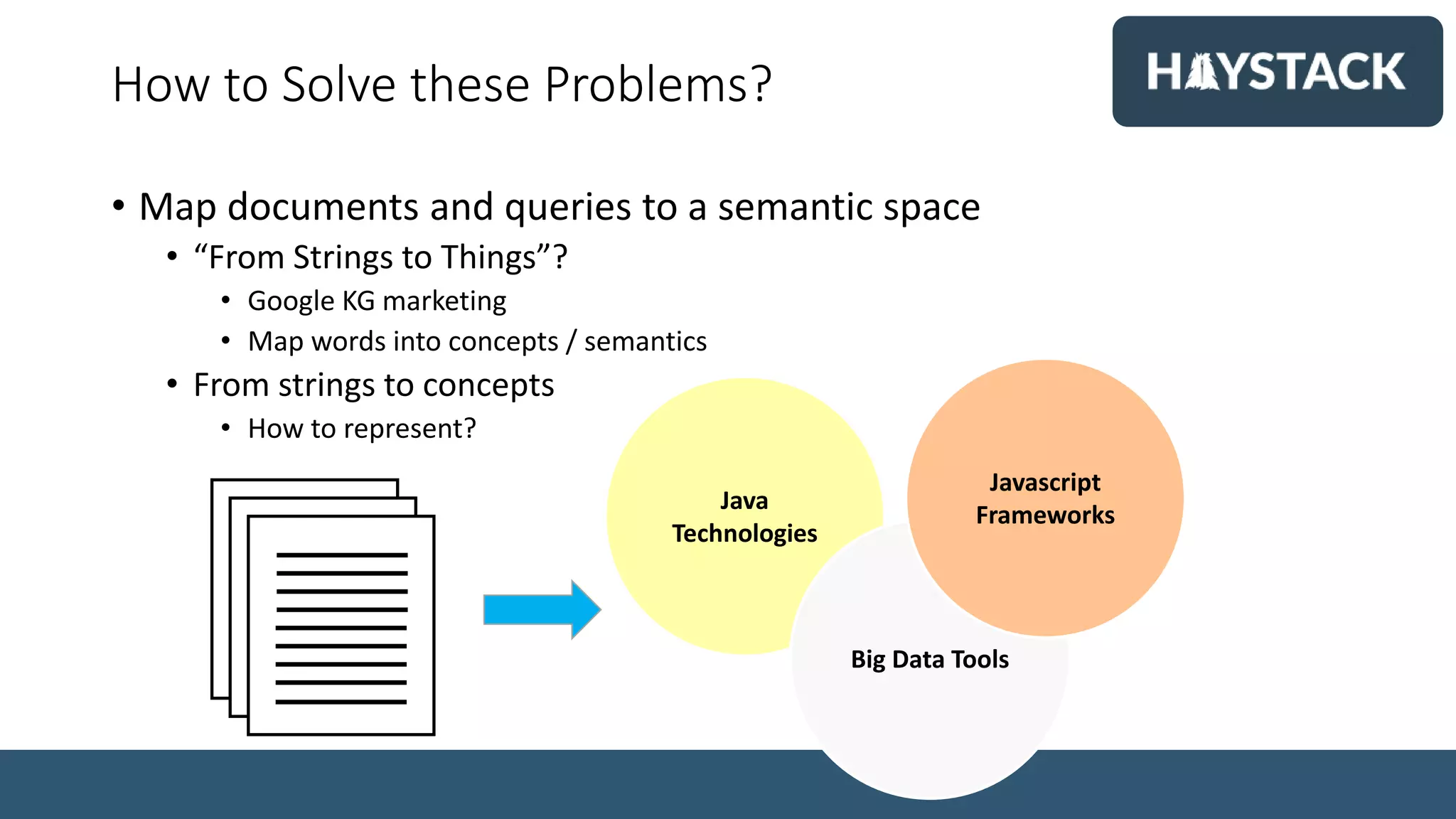
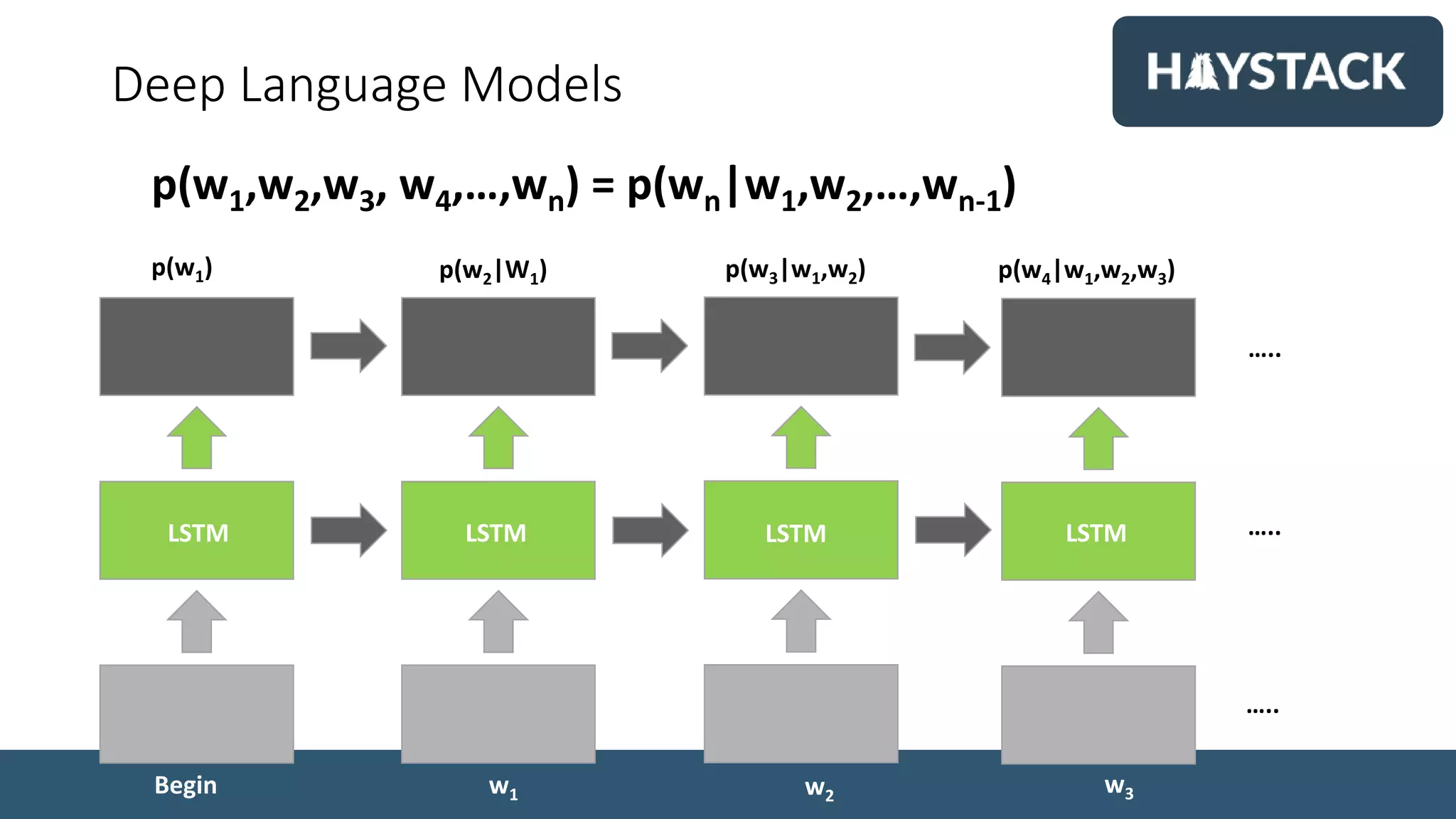
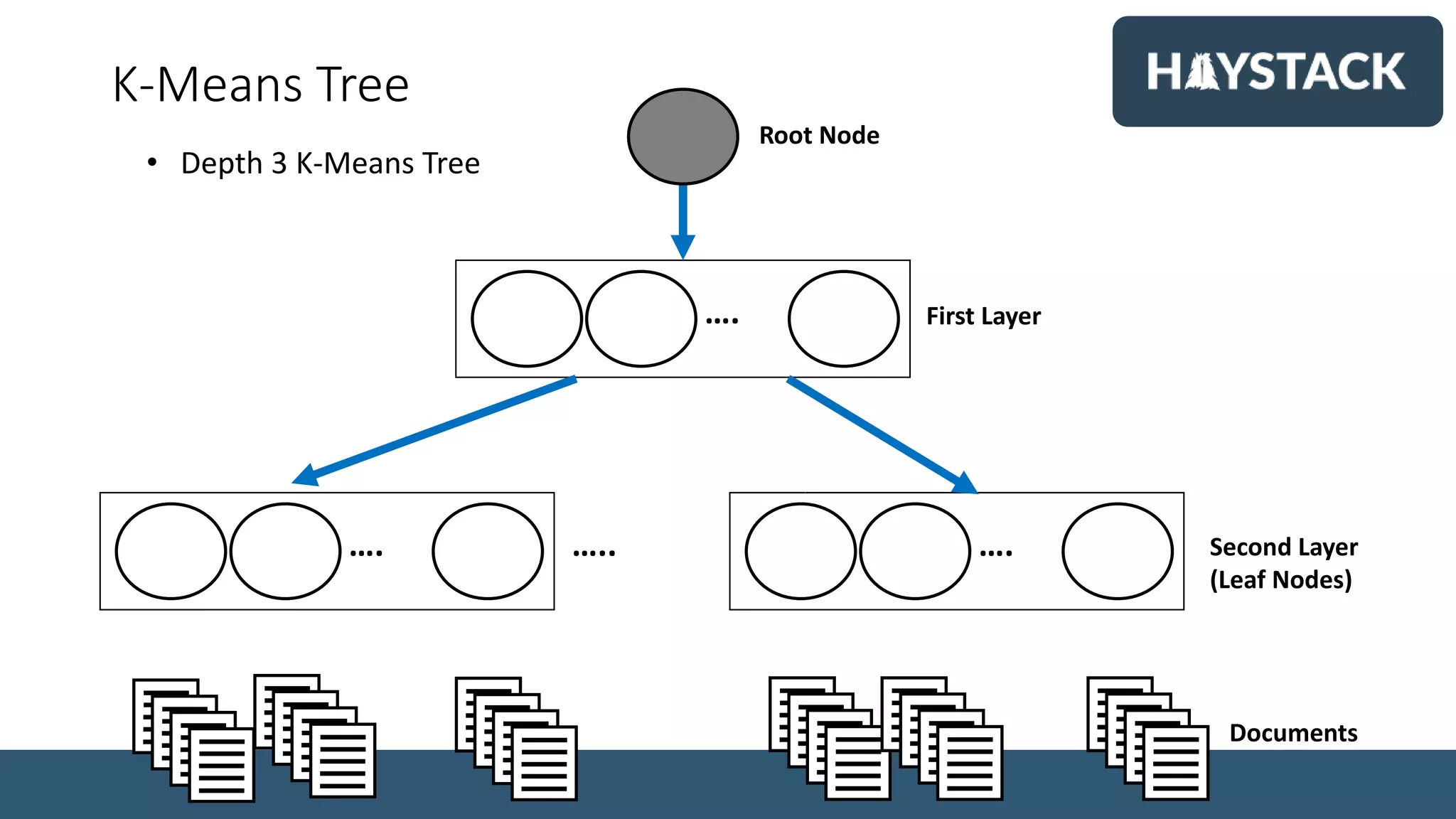
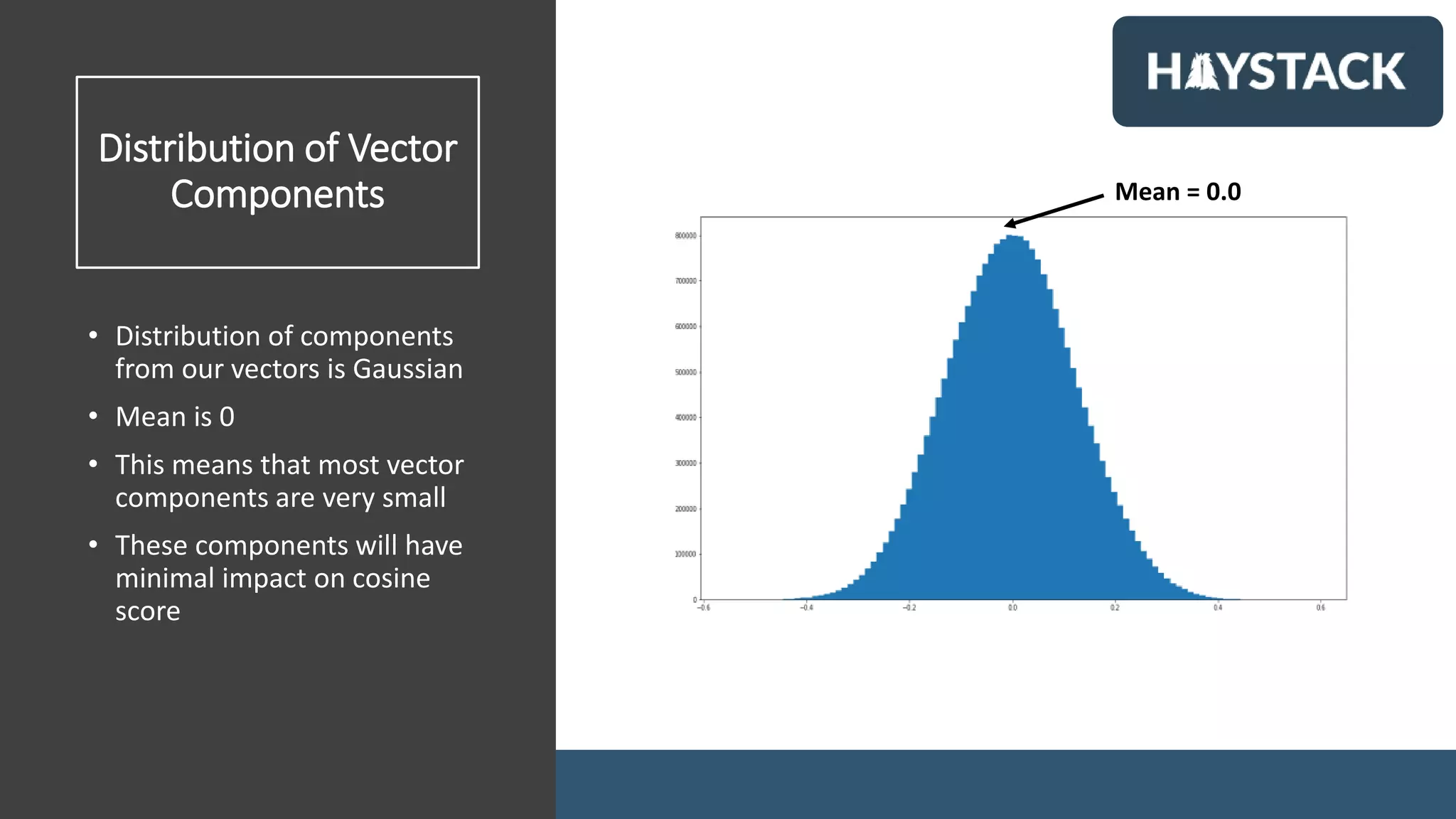
Simon Hughes, Chief Data Scientist at Dice.com, discusses the importance of high-quality content-based recommender engines for job matching in the tech industry. The document covers the challenges of semantic search, vector representations, and advanced NLP techniques, emphasizing the benefits of using deep learning models for better search results. Various methodologies, such as word embeddings and k-NN search, are explored to enhance the job search experience for candidates and employers.






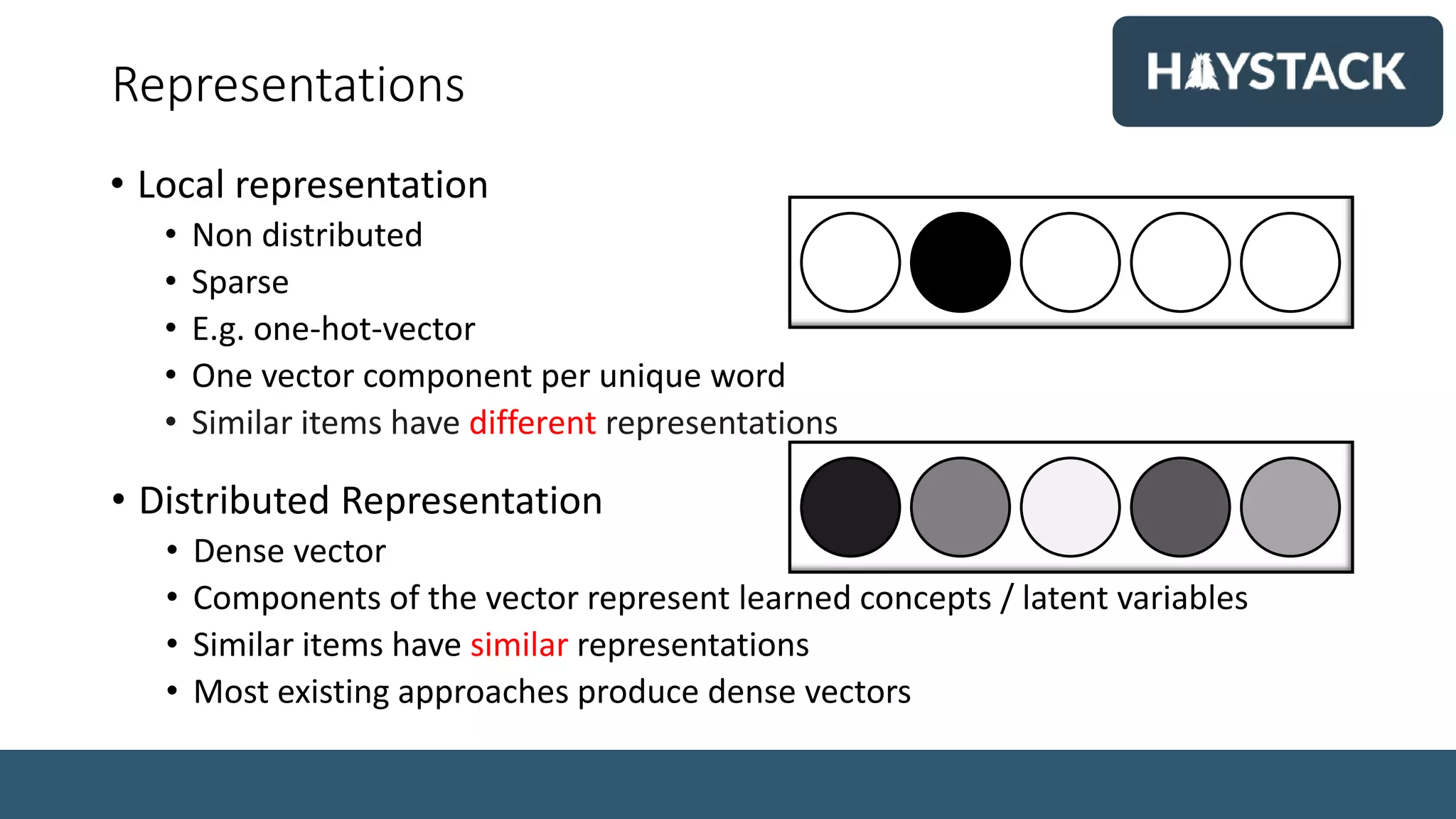



![Word2Vec
• By Aelu013 [CC BY-SA 4.0 (https://creativecommons.org/licenses/by-sa/4.0) ], from Wikimedia Commons](https://image.slidesharecdn.com/searchingwithvectors-190517230738/75/Haystack-2019-Search-with-Vectors-Simon-Hughes-12-2048.jpg)





![Vectors in Search
• Dense Embedding Vector:
• Dense
• D dimensional
• D = 50-1000
• Inverted index:
• Sparse
• Pivoted by term
• V = Vocabulary
• |V| =100k+
• Fast because sparse
[+0.12, -0.34, -0.12, +0.27, +0.63]
Term Posting List
Java 1,5,100,102
.NET 2,4,600,605,1000
C# 2,88,105,800
SQL 130,433,648,899,1200
Html 1,2,10,30,55,202,252,30,598,](https://image.slidesharecdn.com/searchingwithvectors-190517230738/75/Haystack-2019-Search-with-Vectors-Simon-Hughes-19-2048.jpg)



![Zipf’s Law
• The frequency of terms in a
corpus follow a power law
distribution
• Small number of tokens are
very common - filter out
irrelevant docs
• A large number of tokens
are very rare - discriminate
between similar matches
• Distribution of last names - By Thekohser [CC BY-SA 3.0
(https://creativecommons.org/licenses/by-sa/3.0 )], from Wikimedia Commons](https://image.slidesharecdn.com/searchingwithvectors-190517230738/75/Haystack-2019-Search-with-Vectors-Simon-Hughes-23-2048.jpg)



![Encoding LSH Hash into the Index
• Hash into Bits
• Store hash fingerprint as a single token • Store each bit as a token using it’s position and value
• Use mm parameter to speed up search
• Or store shingles of the binary tokens
• This is not sparse!
[+0.08, -0.16, -0.12, +0.27, +0.63, -0.01, +0.16, -0.48]
[1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1]
[“10110110100101”] ["00_1","01_0","02_1","04_1","04_0","05_1","06_1","07_0","08_1","09_0","10_0","11_1","12_0","13_1”]
OR](https://image.slidesharecdn.com/searchingwithvectors-190517230738/75/Haystack-2019-Search-with-Vectors-Simon-Hughes-27-2048.jpg)






![Vector Thresholding with Tokenization
[+0.08, -0.16, -0.12, +0.27, +0.63, -0.01, +0.16, -0.48]
[ 0, 0, 0, 0, +0.63, 0, 0, -0.48]
• Drop all but the largest components
[“04i+0.6”, “07i-0.5”]
• Round weight to lower precision
• Encode position and weight as a single token
• Paper: “Semantic Vector Encoding and Similarity Search Using Fulltext Search Engines”](https://image.slidesharecdn.com/searchingwithvectors-190517230738/75/Haystack-2019-Search-with-Vectors-Simon-Hughes-36-2048.jpg)
![Vector Thresholding with Payloads
[+0.08, -0.16, -0.12, +0.27, +0.63, -0.01, +0.16, -0.48]
[ 0, 0, 0, 0, +0.63, 0, 0, -0.48]
• Drop all but the largest components
• I modified the previous idea, using payload score queries
• Indexing: Store remaining (non zero) tokens in index with payloads
• Querying: Uses custom payload query parser + similarity class
• See Github repo, and solr config in Kmeans tree section
Q=vector:(”3”^-0.0136 ”14”^0.05387 ”56”^-0.070476 ”71”^0.14529 …)
&defType=payloadEdismax](https://image.slidesharecdn.com/searchingwithvectors-190517230738/75/Haystack-2019-Search-with-Vectors-Simon-Hughes-37-2048.jpg)