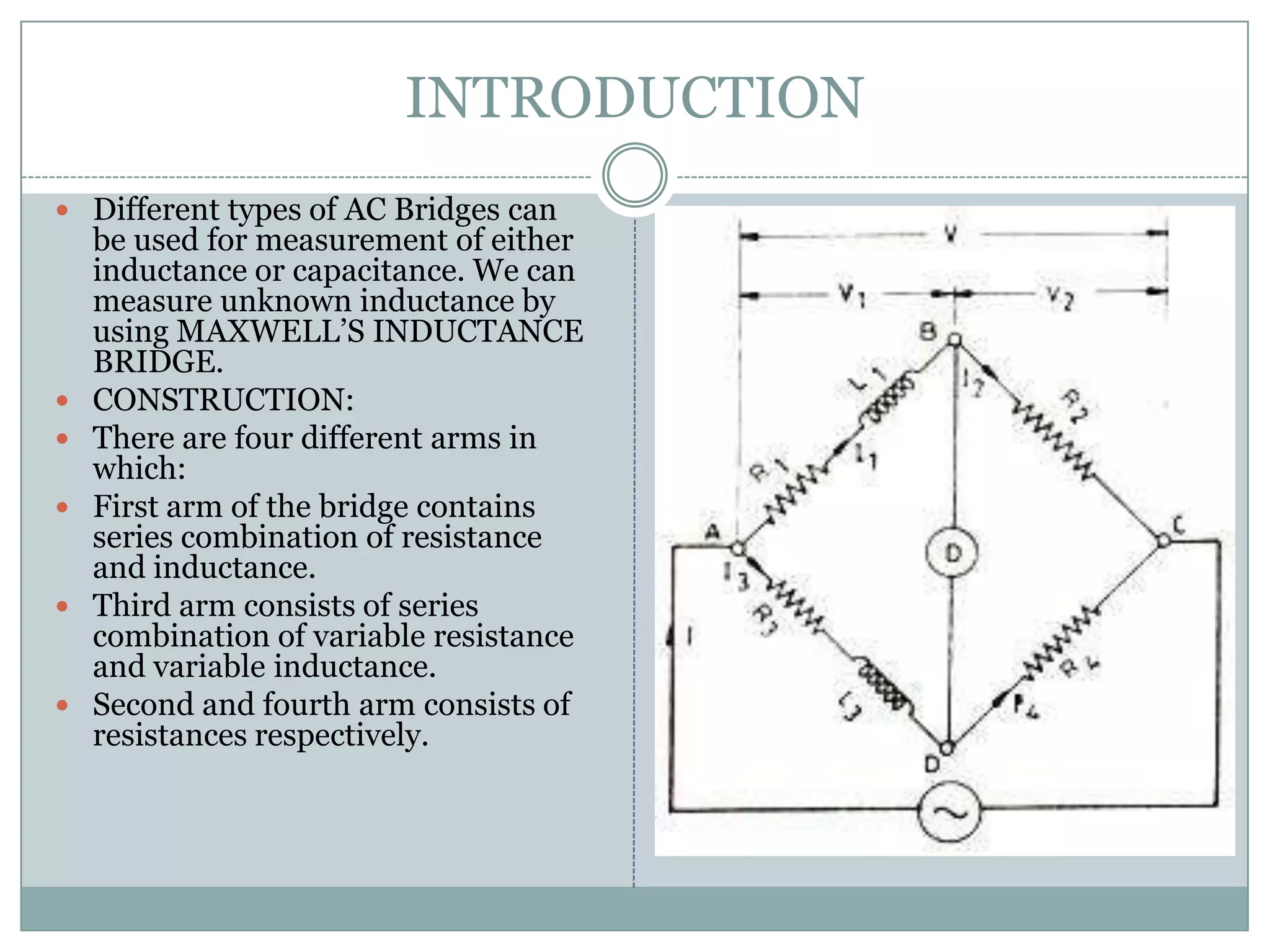
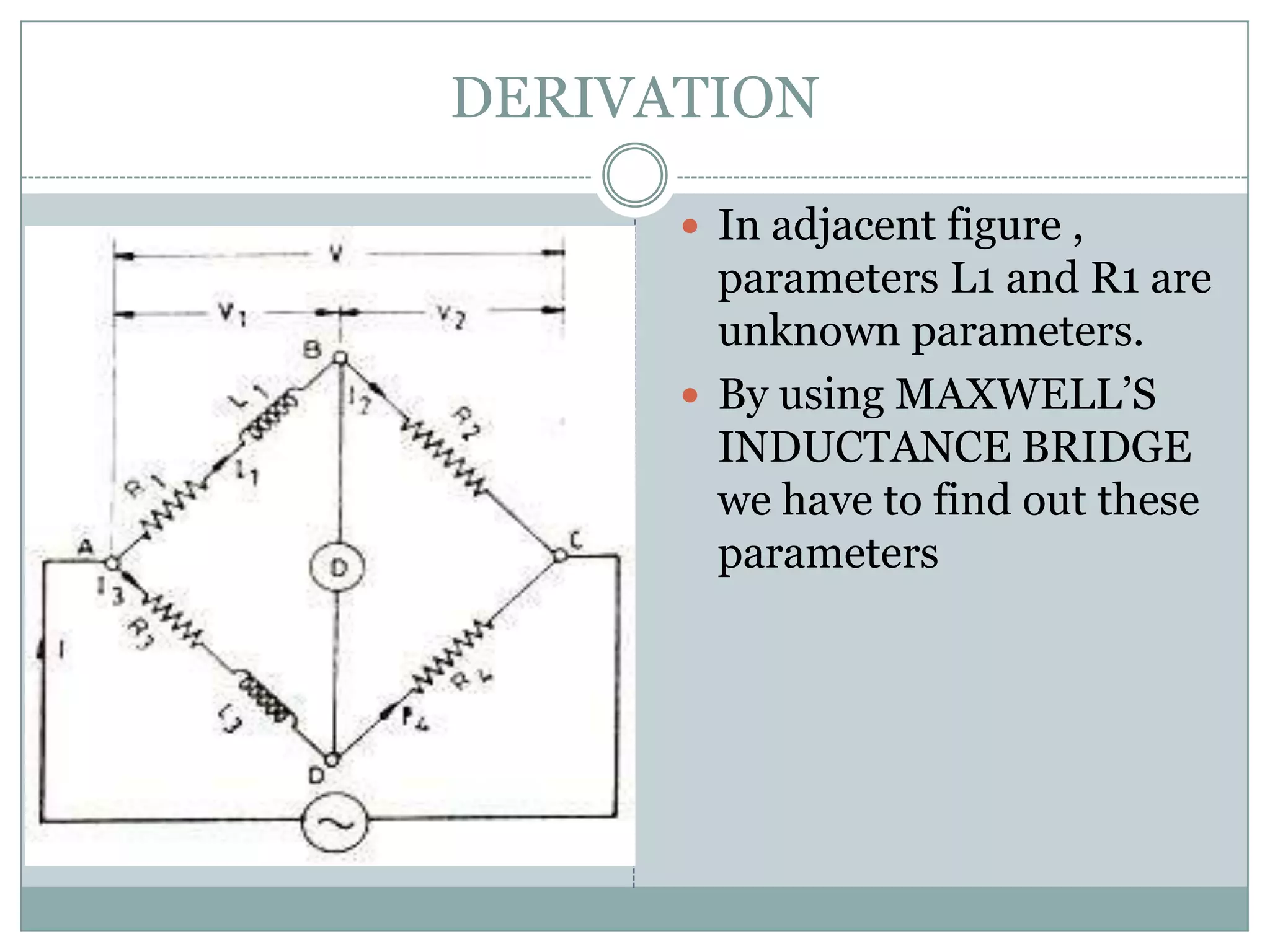
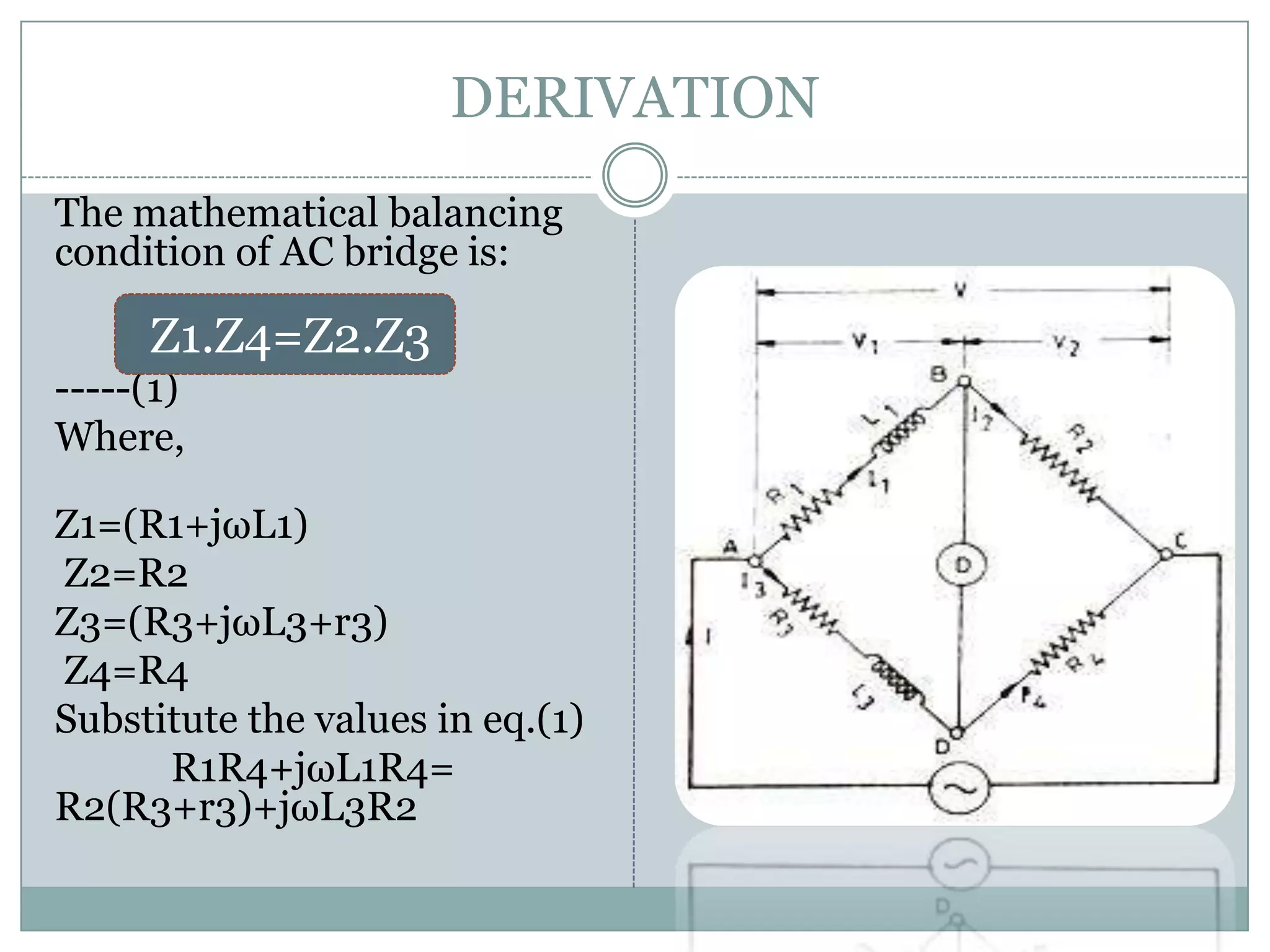
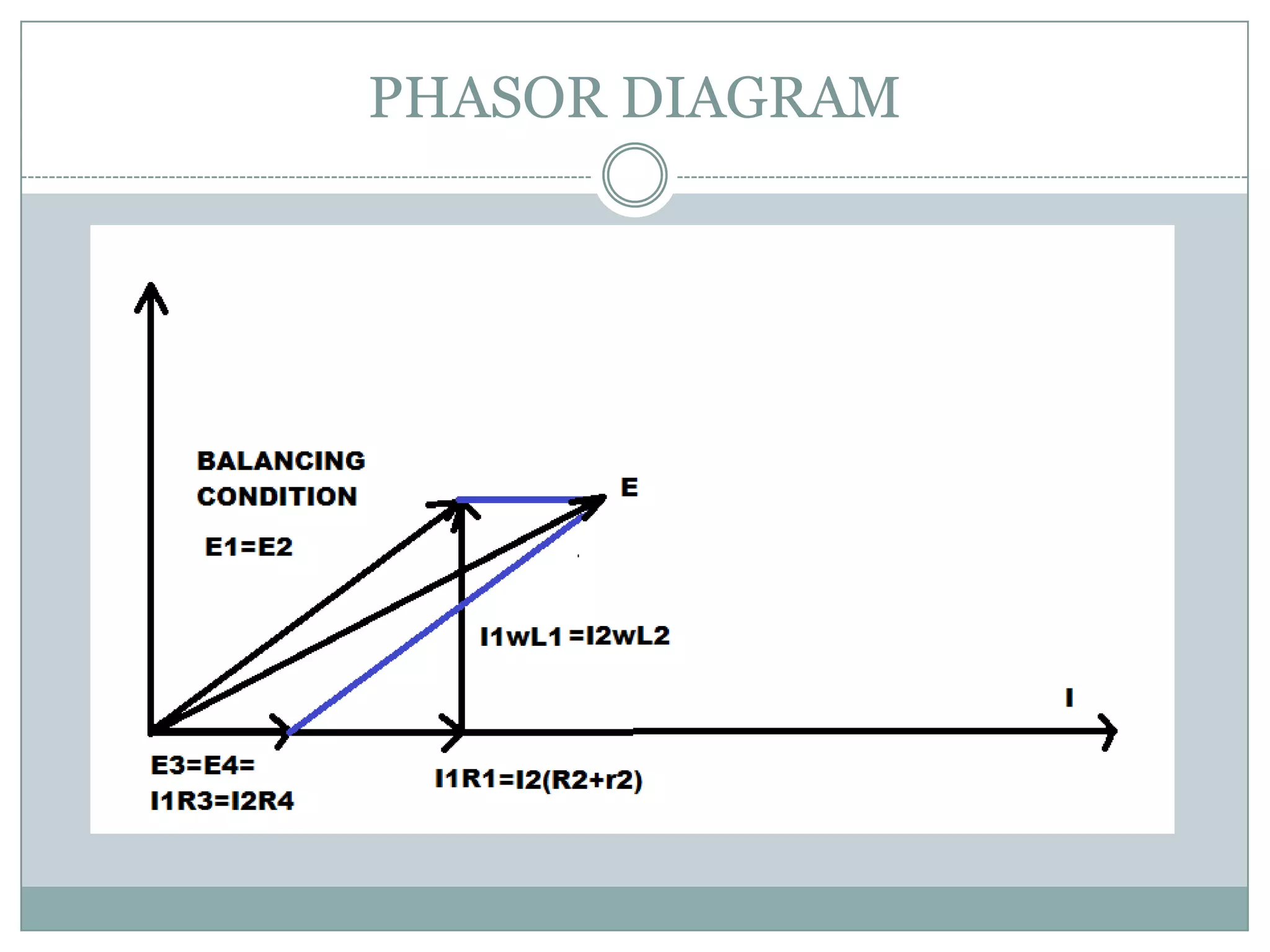
Maxwell's Inductance Bridge is used to measure unknown inductance. It has four arms, with the first containing a series R and L, and third containing variable R and L. When an AC supply is connected to the first coil, it induces an emf in the other coils through electromagnetic induction. By balancing the bridge according to the mathematical equation Z1Z4=Z2Z3, the values of the unknown inductance L1 and resistance R1 in the first arm can be determined from the resulting real and imaginary equations, which are independent of the supply frequency.