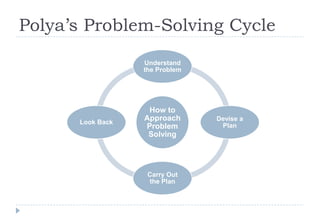
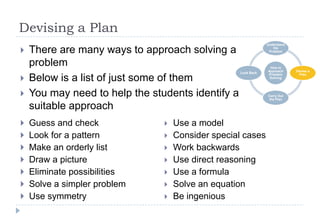
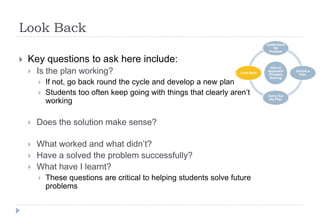
This document outlines George Polya's four-step problem-solving cycle: 1) Understand the problem by clarifying terms, concepts, and requirements; 2) Devise a plan by considering strategies like working backwards or looking for patterns; 3) Carry out the plan by persisting through calculations or experiments; 4) Look back by checking results, evaluating what worked and didn't, and determining if the problem was solved. The document provides examples of applying this cycle in subjects like math, science experiments, and essays. It encourages readers to consider how Polya's approach could work in their own disciplines.

1. Polya’s Problem-Solving Cycle
The Teaching and Learning Group

2. Objectives
 Understand Polya’s Problem-Solving Cycle
 Share some practical ideas for what this might look like in
various subjects.
 Think about how this might be applied in your own
subject

3. What is this about?
 Explicitly teaching students how to solve problems using
the method developed by George Polya
 This is not about problem-based learning

4. Polya’s Problem-Solving Cycle
How to
Approach
Problem
Solving
Understand
the Problem
Devise a
Plan
Carry Out
the Plan
Look Back

5. Understanding the Problem
 The obvious first step, but often not done.
 Ask students questions such as:
 Do you understand all the words used in the problem?
 What are you being asked to do/show/find out?
 Can you put the problem into your own words?
 Can you draw a diagram/picture that would explain what
you have to do?
 Is there enough information to enable you to find a
solution?
 What do we know already, and what do we need to find
out?
How to
Approach
Problem
Solving
Understand
the
Problem
Devise a
Plan
Carry Out
the Plan
Look Back

6. Devising a Plan
 Use a model
 Consider special cases
 Work backwards
 Use direct reasoning
 Use a formula
 Solve an equation
 Be ingenious
 Guess and check
 Look for a pattern
 Make an orderly list
 Draw a picture
 Eliminate possibilities
 Solve a simpler problem
 Use symmetry
 There are many ways to approach solving a
problem
 Below is a list of just some of them
 You may need to help the students identify a
suitable approach
How to
Approach
Problem
Solving
Understand
the
Problem
Devise a
Plan
Carry Out
the Plan
Look Back

7. Carrying Out the Plan
 This is too often where students start!
 Students need persistence and patience (and
perhaps encouragement)
 All the while the students should be keeping
the next step in the cycle at the back of their
minds
How to
Approach
Problem
Solving
Understand
the
Problem
Devise a
Plan
Carry Out
the Plan
Look Back

8. Look Back
 Key questions to ask here include:
 Is the plan working?
 If not, go back round the cycle and develop a new plan
 Students too often keep going with things that clearly aren’t
working
 Does the solution make sense?
 What worked and what didn’t?
 Have a solved the problem successfully?
 What have I learnt?
 These questions are critical to helping students solve future
problems
How to
Approach
Problem
Solving
Understand
the
Problem
Devise a
Plan
Carry Out
the Plan
Look Back

9. For example…
 Solving a complex mathematical problem
 Polya was a mathematician!
 The extended essay!
 Science investigations
 Fulfilling a design-brief
 Writing an essay

10. Over to you….
 Would this work in your subject?
 What might it look like in your subject?

11. References and Further Reading
 ‘How to Solve It’, George Polya, 1945
 ‘Polya’s Problem Solving Techniques,
http://math.berkeley.edu/~gmelvin/math110sp14/polya.pdf
 Wikipedia article:
http://en.wikipedia.org/wiki/How_to_Solve_It