يتناول المستند موضوع الميكانيكا والمواضيع المرتبطة بها في الرياضيات، مع التركيز على قوة الأجسام وتأثيراتها. يتحدث الوثيقة عن المفاهيم الأساسية مثل القوة، أنواعها، وخصائصها، كما يستعرض كيفية حساب المحصلة باستخدام الطريقتين البيانية والجبريه. تركز المادة على التطبيقات العملية ودور هذه المفاهيم في فهم حركة الأجسام واستقرارها.

1. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
1
‫ﻣﻘﺪﻣﺔ‬:
‫اﻟﻤﯿﻜﺎﻧﯿﺎ‬ ‫ﻋﻠﻢ‬:‫ﺑﺎﺳﺘﺨﺪام‬ ‫ذﻟﻚ‬ ‫اﻟﻤﺎدﯾﺔ‬ ‫اﻻﺟﺴﺎم‬ ‫اﺗﺰان‬ ‫أو‬ ‫ﺣﺮﻛﺔ‬ ‫ﺑﺪارﺳﺔ‬ ‫ﯾﻘﻮم‬ ‫اﻟﺬى‬ ‫اﻟﻌﻠﻢ‬ ‫ھﻮ‬
‫ﺑﮭﺎ‬ ‫اﻟﺨﺎﺻﺔ‬ ‫اﻟﻘﻮاﻧﯿﻦ‬.
‫اﻻﺳﺘﺎﺗﯿﻜﺎ‬ ‫ﻋﻠﻢ‬) :‫اﻷﺟﺴﺎم‬ ‫ﺗﻮازن‬ ‫ﻋﻠﻢ‬(‫ﺗﺤﺖ‬ ‫اﻻﺟﺴﺎم‬ ‫ﺳﻜﻮن‬ ‫ﻓﻰ‬ ‫ﯾﺒﺤﺚ‬‫ﻣﻦ‬ ‫ﻣﺠﻤﻮﻋﺔ‬ ‫ﺗﺄﺛﯿﺮ‬
‫ﻧﺴﻤﯿﮭﺎ‬ ‫اﻟﻤﺆﺛﺮات‬"‫اﻟﻘﻮى‬"‫أﯾﻀﺎ‬ ‫و‬‫ﺳﺎﻛﻨﺎ‬ ‫اﻟﺠﺴﻢ‬ ‫ﯾﻈﻞ‬ ‫ﺑﮭﺬا‬ ‫و‬ ‫اﻟﻘﻮى‬ ‫ھﺬه‬ ‫ﺑﯿﻦ‬ ‫اﻟﻌﻼﻗﺎت‬ ‫دراﺳﺔ‬
‫ﻣﺘﻮازﻧﺔ‬ ‫ﻣﺠﻤﻮﻋﺔ‬ ‫ﺑﺄﻧﮭﺎ‬ ‫اﻟﻘﻮى‬ ‫ھﺬه‬ ‫ﻟﻤﺠﻤﻮﻋﺔ‬ ‫ﺣﯿﻨﺌﺬ‬ ‫ﯾﻘﺎل‬ ‫و‬ ،.
‫اﻟﻤﺘﺠﮭﺎت‬ ‫ﻋﻠﻰ‬ ‫ﻋﺎﻣﺔ‬ ‫ﻣﺮاﺟﻌﺔ‬:
*‫اﻟﻘﯿﺎﺳﯿﺔ‬ ‫اﻟﻜﻤﯿﺔ‬:‫ﺗﻤﺎﻣﺎ‬ ‫ﺗﺘﻌﯿﻦ‬ ‫اﻟﺘﻰ‬ ‫اﻟﻜﻤﯿﺔ‬ ‫ھﻰ‬‫ھﻮ‬ ‫ﺣﻘﯿﻘﻰ‬ ‫ﻋﺪد‬ ‫ﺑﻤﻌﺮﻓﺔ‬‫ﻓﻘﻂ‬ ‫ﻣﻘﺪارھﺎ‬
‫ﻣﺜﻞ‬:، ‫اﻟﻄﻮل‬، ‫اﻟﻮزن‬ ، ‫اﻟﺤﺠﻢ‬ ، ‫اﻟﺰﻣﻦ‬ ، ‫اﻟﻜﺘﻠﺔ‬٠٠٠٠
*‫اﻟﻤﺘﺠﮭﺔ‬ ‫اﻟﻜﻤﯿﺔ‬)‫اﻟﻤﺘﺠﺔ‬(:‫اﻟ‬ ‫ھﻰ‬‫ﺑﻤﻌﺮﻓﺔ‬ ‫ﺗﻤﺎﻣﺎ‬ ‫ﺗﺘﻌﯿﻦ‬ ‫اﻟﺘﻰ‬ ‫ﻜﻤﯿﺔ‬‫ﻣﻘﺪارھﺎ‬‫اﺗﺠﺎھﮭﺎ‬ ‫و‬.
‫ﻣﺜﻞ‬:، ‫اﻟﻌﺠﻠﺔ‬ ، ‫اﻟﻘﻮة‬ ، ‫اﻻزاﺣﺔ‬ ، ‫اﻟﺴﺮﻋﺔ‬٠٠٠
*‫اﻟﻤﻮﺟﮭﺔ‬ ‫اﻟﻤﺴﺘﻘﯿﻤﺔ‬ ‫اﻟﻘﻄﻌﺔ‬)‫اﻟﻤﺘﺠﮫ‬:(‫ﻣﺴﺘ‬ ‫ﻗﻄﻌﺔ‬ ‫ھﻰ‬‫ﻧﻘﻄﺔ‬ ‫ﻣﻦ‬ ‫اﺗﺠﺎه‬ ‫ﻟﮭﺎ‬ ‫و‬ ‫ﻃﻮل‬ ‫ﻟﮭﺎ‬ ‫ﻘﯿﻤﺔ‬
‫اﻟﻨﮭﺎﯾﺔ‬ ‫ﻧﻘﻄﺔ‬ ‫اﻟﻰ‬ ‫اﻟﺒﺪاﯾﺔ‬.
‫اﻟﻤﻘﺎﺑﻞ‬ ‫اﻟﺸﻜﻞ‬ ‫ﻓﻰ‬:
‫ا‬‫ﻟﮭﺎ‬ ‫ﻧﮭﺎﯾﺔ‬ ‫ﻧﻘﻄﺔ‬ ‫ب‬ ، ‫ﻣﺴﺘﻘﯿﻤﺔ‬ ‫ﻟﻘﻄﻌﺔ‬ ‫ﺑﺪاﯾﺔ‬ ‫ﻧﻘﻄﺔ‬
‫ﻣﻦ‬ ‫اﻟﻤﻮﺟﮭﺔ‬ ‫اﻟﻘﻄﻌﺔ‬ ‫ﻓﺈن‬‫ا‬‫ب‬ ‫اﻟﻰ‬
‫ﺑﺎﻟﺮﻣﺰ‬ ‫ﻟﮭﺎ‬ ‫ﯾﺮﻣﺰ‬‫ب‬ ‫ا‬‫ﺑــ‬ ‫ﺗﺘﺤﺪد‬:
١(‫ﺑﺪاﯾﺔ‬ ‫ﻧﻘﻄﺔ‬٢(‫ﻧﮭﺎﯾﺔ‬ ‫ﻧﻘﻄﺔ‬٣(‫ﻣﻦ‬ ‫اﺗﺠﺎه‬‫ا‬‫ب‬ ‫اﻟﻰ‬
‫اﻻﺗﺠﺎه‬ ‫ﻧﻔﺲ‬ ‫و‬ ‫اﻟﻄﻮل‬ ‫ﻧﻔﺲ‬ ‫ﻟﮭﻤﺎ‬ ‫ﻛﺎن‬ ‫إذا‬ ‫ﻣﺘﻜﺎﻓﺌﺘﺎن‬ ‫اﻧﮭﻤﺎ‬ ‫ﻣﻮﺟﮭﺘﯿﻦ‬ ‫ﻟﻘﻄﻌﺘﯿﻦ‬ ‫ﯾﻘﺎل‬
*‫اﻟﻤﺘﺠﮫ‬ ‫ﻣﻌﯿﺎر‬:‫ﻛﺎن‬ ‫إذا‬‫ا‬=)‫ص‬ ، ‫س‬(‫ﻓﺈن‬||‫ا‬||=‫؟‬‫س‬٢
+"‫ص‬"٢
"
*‫اﻟﻤﺘ‬‫ﻧﻘﻄﺘﯿﻦ‬ ‫ﺑﯿﻦ‬ ‫اﻟﻮاﺻﻞ‬ ‫ﺠﮫ‬:‫ﻛﺎن‬ ‫إذا‬‫ا‬) =‫س‬١‫ص‬ ،١(‫ب‬ ،) =‫س‬٢‫ص‬ ،٢(
‫ﻓﺈن‬‫ب‬ ‫ا‬=‫ب‬‫ــ‬‫ا‬) =‫س‬٢–‫س‬١‫ص‬ ،٢–‫ص‬١(
‫اﻻول‬ ‫اﻟﻔﺼﻞ‬:‫اﻟﻘ‬‫ــ‬‫ـﻮى‬
‫ا‬
‫ب‬
‫ا‬
‫ب‬
‫ﺏ‬‫ﺍ‬ ‫ﺏ‬‫ﺍ‬

2. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
2
*‫اﻟﻘﻮة‬:‫ﻃﺒﯿﻌﻰ‬ ‫ﺟﺴﻢ‬ ‫ﻋﻠﻰ‬ ‫اﻟﻄﺒﯿﻌﯿﺔ‬ ‫اﻻﺟﺴﺎم‬ ‫أﺣﺪ‬ ‫ﺗﺄﺛﯿﺮ‬ ‫ھﻰ‬‫آ‬‫ﺧﺮ‬.
‫اﻟﺠﺴﻢ‬ ‫ﺣﺎﻟﺔ‬ ‫ﺗﻐﯿﯿﺮ‬ ‫ﻋﻠﻰ‬ ‫ﯾﻌﻤﻞ‬ ‫أو‬ ‫ﯾﻐﯿﺮ‬ ‫ﻣﺆﺛﺮ‬ ‫ﻛﻞ‬ ‫ھﻰ‬‫ﻣﻨﺘﻈﻤﺔ‬ ‫ﺣﺮﻛﺔ‬ ‫أو‬ ‫ﺳﻜﻮن‬ ‫ﻣﻦ‬.
‫ﻣﻌﻠﻮم‬ ‫ﻣﺴﺘﻘﯿﻢ‬ ‫ﺧﻂ‬ ‫ﻓﻰ‬ ‫ﯾﻌﻤﻞ‬ ‫أو‬ ‫ﻣﻌﻠﻮﻣﺔ‬ ‫ﺑﻨﻘﻄﺔ‬ ‫ﯾﻤﺮ‬ ‫ﺑﺄﻧﮫ‬ ‫ﯾﺘﻤﯿﺰ‬ ‫ﻣﺘﺠﮫ‬ ‫ھﻰ‬
‫ﻣﻘﺪارھﺎ‬ ‫اﻟﺘﻰ‬ ‫ﻟﻠﻘﻮة‬ ‫ﯾﺮﻣﺰ‬ ‫و‬‫ق‬‫ﺑﺎﻟﺮﻣﺰ‬‫ق‬‫اﻟﻮﻗﺖ‬ ‫ﻧﻔﺲ‬ ‫ﻓﻰ‬ ‫اﺗﺠﺎھﮭﺎ‬ ‫و‬ ‫ﻣﻘﺪارھﺎ‬ ‫ﻋﻠﻰ‬ ‫ﻟﯿﺪل‬
‫اﻻﺗ‬ ‫ﻣﻊ‬ ‫ھـ‬ ‫ﻗﯿﺎﺳﮭﺎ‬ ‫زاوﯾﺔ‬ ‫ﺗﺼﻨﻊ‬ ‫اﻟﻘﻮة‬ ‫ﻛﺎﻧﺖ‬ ‫إذا‬ ‫و‬‫ﻟﻤﺤ‬ ‫اﻟﻤﻮﺟﺐ‬ ‫ﺠﺎه‬‫ﯾ‬ ‫ﻓﺈﻧﮫ‬ ‫اﻟﺴﯿﻨﺎت‬ ‫ﻮر‬‫ﻤ‬‫ﻜ‬‫ﻛﺘﺎﺑﺔ‬ ‫ﻦ‬
‫ﻣﺮﺗﺐ‬ ‫زوج‬ ‫ﺻﻮرة‬ ‫ﻋﻠﻰ‬ ‫اﻟﻘﻮة‬)‫ق‬‫ھـ‬ ،(‫ﺣﯿﺚ‬‫ق‬=‫ھـ‬ ، ‫اﻟﻘﻮة‬ ‫ﻣﻘﺪار‬=‫اﻟﺰاوﯾﺔ‬ ‫ﻗﯿﺎس‬
*‫اﻟﻘﻮى‬ ‫أﻧﻮاع‬:
)١(‫اﻟﺸﺪ‬ ‫ﻗﻮى‬)٢(‫اﻟﻀﻐﻂ‬ ‫ﻗﻮى‬)٣(‫اﻟﻮزن‬ ‫ﻗﻮة‬)‫اﻟﺘﺜﺎﻗﻞ‬(
)٤(‫اﻟﻔﻌﻞ‬ ‫رد‬ ‫ﻗﻮة‬)٥(‫اﻟﺘﻨﺎﻓﺮ‬ ‫و‬ ‫اﻟﺠﺬب‬ ‫ﻗﻮى‬)‫ﺣﺬب‬ ‫ﻗﻮة‬ ‫ﻣﺜﻞ‬‫ﻟﻸﺟﺴﺎم‬ ‫اﻷرض‬(
*‫اﻟﻘﻮة‬ ‫ﺧﻮاص‬:‫ﻋﻠﻰ‬ ‫اﻟﻘﻮة‬ ‫ﺗﺄﺛﯿﺮ‬ ‫ﯾﺘﻮﻗﻒ‬:
)١(‫اﻟﻘﻮة‬ ‫ﻣﻘﺪار‬)٢(‫اﻟﻘﻮة‬ ‫اﺗﺠﺎه‬)٣(‫ﻋﻤﻠﮭﺎ‬ ‫ﺧﻂ‬ ‫و‬ ‫اﻟﻘﻮة‬ ‫ﺗﺄﺛﯿﺮ‬ ‫ﻧﻘﻄﺔ‬
]١[‫اﻟﻘﻮة‬ ‫ﻣﻘﺪار‬:‫اﻟﻮﺣﺪات‬ ‫ھﺬه‬ ‫اھﻢ‬ ‫و‬ ‫اﻟﻘﻮة‬ ‫وﺣﺪات‬ ‫ﻣﻦ‬ ‫ﺗﺤﺘﻮﯾﺔ‬ ‫ﻣﺎ‬ ‫ﻣﻘﺪار‬ ‫ھﻮ‬.
‫أوﻻ‬:‫اﻟﺘﺜﺎﻗ‬ ‫اﻟﻮﺣﺪات‬‫ﻠﯿﺔ‬:١‫ﻛﺠﻢ‬ ‫ث‬=١٠٠٠‫ﺟﻢ‬ ‫ث‬=١٠٣
‫ﺟﻢ‬ ‫ث‬
‫ﺛﺎﻧﯿﺎ‬:‫اﻟﻤﻄﻠﻘﺔ‬ ‫اﻟﻮﺣﺪات‬:١‫ﻧﯿﻮﺗﻦ‬=٠٠٠١٠٠‫داﯾﻦ‬=١٠٥
‫داﯾﻦ‬
‫ﺛﺎﻟﺜﺎ‬:‫ﺑﺎﻟﻌﻼﻗﺔ‬ ‫اﻟﻤﻄﻠﻘﺔ‬ ‫ﺑﺎﻟﻮﺣﺪات‬ ‫اﻟﺘﺜﺎﻗﻠﯿﺔ‬ ‫اﻟﻮﺣﺪات‬ ‫ﺗﺮﺗﺒﻂ‬:
١‫ﻛﺠﻢ‬ ‫ث‬=٩٫٨، ‫ﻧﯿﻮﯾﻦ‬١‫ﺟﻢ‬ ‫ث‬=٩٨٠‫داﯾﻦ‬]‫ذﻟﻚ‬ ‫ﺧﻼف‬ ‫ﯾﺬﻛﺮ‬ ‫ﻣﺎﻟﻢ‬[
]٢[‫اﻟﻘﻮة‬ ‫اﺗﺠﺎه‬:
‫ھﻮ‬‫اﻟﻘﻮة‬ ‫ھﺬه‬ ‫ﺗﻤﺜﻠﮫ‬ ‫اﻟﺬى‬ ‫اﻟﻤﺘﺠﮫ‬ ‫إﺗﺠﺎه‬‫اﻟﻘﻮة‬ ‫ﻟﻤﺘﺠﮫ‬ ‫اﻟﻘﻄﺒﯿﺔ‬ ‫اﻟﺰاوﯾﺔ‬ ‫ﺑﻘﯿﺎس‬ ‫ﯾﺘﺤﺪد‬.
‫اﻟﻘﻄﺒﯿﺔ‬ ‫اﻟﺰاوﯾﺔ‬:‫اﻟﺴﯿﻨﺎت‬ ‫ﻟﻤﺤﻮر‬ ‫اﻟﻤﻮﺟﺐ‬ ‫اﻻﺗﺠﺎه‬ ‫ﻣﻊ‬ ‫اﻟﻘﻮة‬ ‫ﻋﻤﻞ‬ ‫ﺧﻂ‬ ‫ﯾﺼﻨﻌﮭﺎ‬ ‫اﻟﺘﻰ‬ ‫اﻟﺰاوﯾﺔ‬ ‫ھﻰ‬
)‫ھـ‬(‫اﻟﺴﺎﻋﺔ‬ ‫ﻋﻘﺎب‬ ‫ﻋﻜﺲ‬ ‫ﻓﻰ‬ ‫داﺋﻤﺎ‬ ‫ھﻰ‬ ‫و‬)‫ﻣﻮﺟﺒﺔ‬ ‫داﺋﻤﺎ‬ ‫اى‬(
‫اﻟﻘــــــﻮى‬

3. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
3
]٣[‫ا‬ ‫ﻧﻘﻄﺔ‬‫ﻋﻤﻠﮭﺎ‬ ‫ﺧﻂ‬ ‫و‬ ‫ﻟﺘﺄﺛﯿﺮ‬:‫ﻓﯿﮫ‬ ‫ﺗﻌﻤﻞ‬ ‫ﻋﻤﻞ‬ ‫ﺧﻂ‬ ‫و‬ ‫ﻓﯿﮭﺎ‬ ‫ﺗﺆﺛﺮ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻗﻮة‬ ‫ﻟﻜﻞ‬
‫ﻣﻠﺤﻮﻇﺔ‬:
‫ﺗﺄﺛﯿﺮھﺎ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻣﻮﺿﻊ‬ ‫ﻋﻠﻰ‬ ‫ﯾﺘﻮﻗﻒ‬ ‫ﺟﺴﻢ‬ ‫ﻋﻠﻰ‬ ‫اﻟﻘﻮة‬ ‫ﺗﺄﺛﯿﺮ‬)‫ﻣﻔﺼﻼت‬ ‫ذو‬ ‫ﺑﺎب‬ ‫ﻓﺘﺢ‬ ‫ﻣﺤﺎوﻟﺔ‬ ‫ﻣﺜﻞ‬(
‫اﻟﻘﻮة‬ ‫ﻋﻤﻞ‬ ‫ﺧﻂ‬ ‫ﻻﺗﺠﺎھﮭﺎ‬ ‫اﻟﻤﻮازى‬ ‫و‬ ‫اﻟﻘﻮة‬ ‫ﺗﺄﺛﯿﺮ‬ ‫ﺑﻨﻘﻄﺔ‬ ‫اﻟﻤﺎر‬ ‫اﻟﻤﺴﺘﻘﯿﻢ‬ ‫اﻟﺨﻂ‬ ‫ﯾﺴﻤﻰ‬ ‫و‬.
‫ــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
*‫ﻣﺘﻼﻗ‬ ‫ﻗﻮﺗﯿﻦ‬ ‫ﻣﺤﺼﻠﺔ‬‫ﯿﺘ‬‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﯿﻦ‬:
‫اﻟﻤﺤﺼﻠﺔ‬:‫ﺗﺤﺪﺛﮫ‬ ‫اﻟﺬى‬ ‫اﻟﺘﺄﺛﯿﺮ‬ ‫ﻧﻔﺲ‬ ‫ُﺪث‬‫ﺤ‬‫ﺗ‬ ‫اﻟﺘﻰ‬ ‫اﻟﻘﻮة‬ ‫ھﻰ‬)‫ﻗﻮﺗﯿﻦ‬(‫اﻟﺠﺴﻢ‬ ‫ﻋﻠﻰ‬ ‫ﻗﻮى‬ ‫ﻋﺪة‬ ‫أو‬
‫ﺗﻌﯿﯿﻦ‬‫اﻟﻤﺤﺼﻠﺔ‬:‫اﺗﺠﺎھﮭﺎ‬ ‫و‬ ‫ﻣﻘﺪارھﺎ‬ ‫ﺗﻌﯿﻦ‬ ‫ﯾﺠﺐ‬ ً‫ﺎ‬‫ﺗﺎﻣ‬ ً‫ﺎ‬‫ﺗﻌﯿﯿﻨ‬ ‫اﻟﻤﺤﺼﻠﺔ‬ ‫ﻟﺘﻌﯿﯿﻦ‬
‫ﻃﺮﯾﻘﺘﺎن‬ ‫ﺗﻮﺟﺪ‬ ‫و‬‫اﻟﻤﺤﺼﻠﺔ‬ ‫ﻟﺘﻌﯿﯿﻦ‬:١(‫اﻟﺒﯿﺎﻧﯿﺔ‬٢(‫اﻟﺠﺒﺮﯾﺔ‬)‫ﺗﺤﻠﯿﻠﯿﺔ‬(
]١[‫اﻟﺒﯿﺎﻧﯿﺔ‬ ‫اﻟﻄﺮﯾﻘﺔ‬:
‫ﻣﺘﻮ‬ ‫ﻣﻦ‬ ‫ﻣﺘﺠﺎوران‬ ‫ﺿﻠﻌﺎن‬ ً‫ﺎ‬‫ﺗﺎﻣ‬ ‫ﺗﻤﺜﯿﻼ‬ ‫ﻣﺜﻠﮭﻤﺎ‬ ‫و‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﻣﺘﻼﻗﯿﺘﺎن‬ ‫ﻗﻮﺗﺎن‬ ‫أﺛﺮت‬ ‫إذا‬‫ازى‬
‫اﻻﺿﻼع‬ ‫ﻣﺘﻮازى‬ ‫ﻗﻄﺮ‬ ‫ﺗﺎﻣﺎ‬ ‫ﺗﻤﺜﯿﻼ‬ ‫ﯾﻤﺜﻠﮭﺎ‬ ‫ﻣﺤﺼﻠﺘﮭﻤﺎ‬ ‫ﻓﺈن‬ ‫اﻟﻨﻘﻄﺔ‬ ‫ھﺬه‬ ‫ﻣﻦ‬ ‫ﯾﺒﺪأن‬ ‫اﻷﺿﻼع‬
‫اﻟﻨﻘﻄﺔ‬ ‫ھﺬه‬ ‫ﻣﻦ‬ ‫ﯾﺒﺪأ‬ ‫اﻟﺬى‬.
‫اﻟﻤﻘﺎﺑﻞ‬ ‫اﻟﺸﻜﻞ‬ ‫ﻓﻰ‬:
‫ﻛﺎن‬ ‫إذا‬‫ب‬ ‫ا‬،‫ء‬ ‫ا‬‫ﺗﻤﺜﻼن‬‫ق‬١،‫ق‬٢ً‫ﺎ‬‫ﺗﺎﻣ‬ ‫ﺗﻤﺜﯿﻼ‬
)‫ﻋﻤﻞ‬ ‫ﺧﻂ‬ ‫و‬ ً‫ﺎ‬‫واﺗﺠﺎھ‬ ‫ﻣﻘﺪارا‬(‫ﻓﺈن‬:
‫ح‬=‫ق‬١+‫ق‬٢]=‫ح‬،‫ه‬[
‫ح‬=‫ﺗﺼﻨﻌﮭﺎ‬ ‫اﻟﺘﻰ‬ ‫اﻟﺰاوﯾﺔ‬ ‫ھﻰ‬ ‫ھـ‬ ، ‫اﻟﻤﺤﺼﻠﺔ‬ ‫ﻣﻘﺪار‬
‫ﻣﻊ‬ ‫اﻟﻤﺤﺼﻠﺔ‬‫ق‬١
‫ﺑﺘﻄﺒﯿﻖ‬‫ﯾﺼﻨﻌﮭﺎ‬ ‫اﻟﺘﻰ‬ ‫اﻟﻤﻮﺟﺒﺔ‬ ‫اﻟﺰاوﯾﺔ‬ ‫ھﻰ‬ ‫ھـ‬ ‫ﺣﯿﺚ‬ ‫ﻣﺘﺠﮭﯿﻦ‬ ‫ﻟﺠﻤﻊ‬ ‫اﻻﺿﻼع‬ ‫ﻣﺘﻮازى‬ ‫ﻗﺎﻋﺪة‬‫ح‬
‫اﻟﺴﯿﻨﺎت‬ ‫ﻟﻤﺤﻮر‬ ‫اﻟﻤﻮﺟﺐ‬ ‫اﻻﺗﺠﺎه‬ ‫ﻣﻊ‬)‫اﺗﺠﺎه‬‫ق‬١(
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﻣﻘﺪارھﻤﺎ‬ ‫ﻗﻮﺗﺎن‬٣٠،٤٠‫ﺑﯿﻨﮭﻤﺎ‬ ‫اﻟﺰاوﯾﺔ‬ ‫ﻗﯿﺎس‬ ‫و‬ ‫ﻣﺎدﯾﺔ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﺗﺆﺛﺮان‬ ‫ﺟﻢ‬ ‫ث‬١١٠٥
‫ﺑ‬ ‫أوﺟﺪ‬‫اﻻوﻟﻰ‬ ‫اﻟﻘﻮة‬ ‫و‬ ‫اﻟﻤﺤﺼﻠﺔ‬ ‫ﺑﯿﻦ‬ ‫اﻟﺰاوﯾﺔ‬ ‫و‬ ‫اﻟﻤﺤﺼﻠﺔ‬ ‫ﯿﺎﻧﯿﺎ‬.
‫اﻟﺤﻞ‬:
‫رﺳﻢ‬ ‫ﻣﻘﯿﺎس‬ ‫ﺑﻌﻤﻞ‬١‫ﻟﻜﻞ‬ ‫ﺳﻢ‬١٠‫ﺟﻢ‬ ‫ث‬
B‫و‬‫ا‬=٣‫ب‬ ‫و‬ ، ‫ﺳﻢ‬=٤‫ﺳﻢ‬
‫ا‬ ‫ب‬
‫ج‬‫ء‬
‫و‬
‫ح‬ ‫ق‬٢
‫ق‬١
‫ق‬١
‫ق‬٢
‫ه‬‫ى‬ ‫ى‬

4. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
4
‫ح‬
‫ﺑﺎﻟﻤﺴﻄﺮة‬ ‫ﺑﺎﻟﻘﯿﺎس‬ ‫و‬ ‫اﻻﺿﻼع‬ ‫ﻣﺘﻮازى‬ ‫ﻧﻜﻤـﻞ‬
‫أن‬ ‫ﻧﺠﺪ‬:‫ﺟـ‬ ‫و‬=٤٫٢‫ﺳﻢ‬
B‫ح‬=٤٫٢×١٠=٤٢‫ﺟﻢ‬ ‫ث‬‫ق‬ ،)‫ھـ‬p= (٦٦٥
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
]٢[‫اﻟﺠﺒــــــﺮﯾﺔ‬ ‫اﻟﻄﺮﯾﻘﺔ‬] :‫ﺗﺤﻠﯿﻠﯿﺎ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﻣﺘﻼﻗﯿﺘﯿﻦ‬ ‫ﻗﻮﺗﯿﻦ‬ ‫ﻣﺤﺼﻠﺔ‬ ‫اﯾﺠﺎد‬)‫ﺑﺎﻟﻘﺎﻧﻮن‬:(
‫أن‬ ‫ﺑﻔﺮض‬‫ق‬١،‫ق‬٢‫ﺧﻄﻰ‬ ‫ﺑﯿﻦ‬ ‫اﻟﺰاوﯾﺔ‬ ‫ﺟﺴﻢ‬ ‫ﻓﻰ‬ ‫ﺗﺆﺛﺮان‬
‫ﻋﻤﻠﮭﻤﺎ‬)‫ى‬(‫اﻟﻘﺎﻧﻮ‬ ‫ﻣﻦ‬ ‫ﺗﺘﻌﯿﻦ‬ ‫ﻣﺤﺼﻠﺘﮭﻤﺎ‬ ‫ﻓﺈن‬‫ن‬:
‫اﻟﻤﺤﺼﻠﺔ‬ ‫ﺗﻌﯿﻦ‬:‫ح‬٢
=‫ق‬١
٢
+‫ق‬٢
٢
+٢‫ق‬١‫ق‬٢‫ﺣﺘﺎ‬‫ى‬
‫ﺗﻌ‬‫ﯿﻦ‬‫اﻟﻘﺎﻧﻮن‬ ‫ﻣﻦ‬ ‫اﻟﻤﺤﺼﻠﺔ‬ ‫اﺗﺠﺎه‬:
‫ھـ‬ ‫ﻇﺎ‬=
‫ا‬ ‫ﺑﯿﻦ‬ ‫اﻟﺰاوﯾﺔ‬ ‫ھـ‬ ‫ﺣﯿﺚ‬‫اﻻوﻟﻰ‬ ‫اﻟﻘﻮة‬ ‫و‬ ‫ﻟﻤﺤﺼﻠﺔ‬‫ق‬١
‫آﺧﺮى‬ ‫ﻃﺮﯾﻘﺔ‬:‫اﻟﻘﻮة‬ ‫ﻋﻠﻰ‬ ‫اﻟﻤﺤﺼﻠﺔ‬ ‫ﻣﯿﻞ‬ ‫زاوﯾﺔ‬ ‫ﻻﯾﺠﺎد‬‫ق‬١)‫اﻟﺠﯿﺐ‬ ‫ﻗﺎﻋﺪة‬ ‫اﺳﺘﺨﺪام‬(
*‫اﻟﻤﺤﺼﻠﺔ‬ ‫ﺗﻌﺎﻣﺪ‬ ‫ﺷﺮط‬‫ح‬‫اﻟﻘﻮة‬ ‫ﻋﻠﻰ‬‫ق‬١:
‫اﻟﻤﺤﺼﻠﺔ‬ ‫ﻋﻤﻞ‬ ‫ﺧﻂ‬ ‫ﻛﺎن‬ ‫إذا‬‫ح‬‫اﻟﻘﻮة‬ ‫ﻋﻠﻰ‬ ‫ﻋﻤﻮدﯾﺎ‬‫ق‬١
B‫ق‬١+‫ق‬٢‫ﺣﺘﺎ‬‫ى‬=‫ﺻﻔﺮ‬،‫ح‬٢
=‫ق‬٢
٢
-‫ق‬١
٢
‫و‬
‫ا‬
‫ب‬
‫ج‬
‫ى‬ ‫ه‬
‫ح‬
‫ق‬١
‫ق‬٢
‫ق‬٢‫ﺣﺎ‬‫ى‬
‫ق‬١+‫ق‬٢‫ﺣﺘﺎ‬‫ى‬
‫ق‬١
‫ق‬٢

5. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
5
*‫ﺧﺎﺻﺔ‬ ‫ﺣﺎﻻت‬:
١-‫اﻟﻤﻘﺪار‬ ‫ﻓﻰ‬ ‫ﻣﺘﺴﺎوﯾﺘﺎن‬ ‫اﻟﻘﻮﺗﺎن‬:‫ق‬١=‫ق‬٢=‫ق‬G‫ح‬=٢‫ق‬‫ھـ‬ ، ‫ﺣﺘﺎ‬=
‫أن‬ ‫أى‬‫ح‬‫اﻟﻘﻮﺗﯿﻦ‬ ‫ﺑﯿﻦ‬ ‫اﻟﺰاوﯾﺔ‬ ‫ﺗﻨﺼﻒ‬.
٢-‫ﻣﺘﻌﺎﻣﺪﺗﺎن‬ ‫اﻟﻘﻮﺗﺎن‬:‫ھ‬ ‫ﻓﻰ‬‫ى‬ ‫اﻟﺤﺎﻟﺔ‬ ‫ﺬه‬=٩٠٥
،‫ح‬٢
=‫ق‬١
٢
+‫ق‬٢
٢
‫ھـ‬ ‫ﻇﺎ‬ ،=
٣-‫ﻟﮭﻤﺎ‬ ‫اﻟﻘﻮﺗﺎن‬‫ﻧﻔﺲ‬‫اﻻﺗﺠﺎه‬ ‫ﻧﻔﺲ‬ ‫ﻓﻰ‬ ‫و‬ ‫اﻟﻌﻤﻞ‬ ‫ﺧﻂ‬:
‫ﻋﻈﻤﻰ‬ ‫ﻗﯿﻤﺔ‬ ‫ﻟﮭﺎ‬ ‫اﻟﻤﺤﺼﻠﺔ‬)‫ﻟﻠﻤﺤﺼﻠﺔ‬ ‫ﻗﯿﻤﺔ‬ ‫أﻛﺒﺮ‬ ‫أو‬(
‫ح‬=‫ق‬١+‫ق‬٢،‫ى‬=٠
‫اﻟﻤﺤﺼﻠﺔ‬ ‫اﺗﺠﺎه‬ ‫و‬‫اﺗﺠﺎه‬ ‫ھﻮ‬‫اﻟﻌﻤﻞ‬ ‫ﺧﻂ‬ ‫ﻧﻔﺲ‬ ‫و‬ ‫اﻟﻘﻮﺗﯿﻦ‬
٤-‫ﻣﺘﻀﺎدﯾﻦ‬ ‫اﺗﺠﺎھﯿﻦ‬ ‫ﻓﻰ‬ ‫و‬ ‫اﻟﻌﻤﻞ‬ ‫ﺧﻂ‬ ‫ﻧﻔﺲ‬ ‫ﻟﮭﻤﺎ‬ ‫اﻟﻘﻮﺗﺎن‬:
‫ﺻﻐﺮى‬ ‫ﻗﯿﻤﺔ‬ ‫ﻟﮭﺎ‬ ‫اﻟﻤﺤﺼﻠﺔ‬)‫ﻟﻠﻤﺤﺼﻠﺔ‬ ‫ﻗﯿﻤﺔ‬ ‫أﺻﻐﺮ‬ ‫أو‬(
‫ح‬=|‫ق‬١-‫ق‬٢|،‫ى‬=١٨٠٥
‫و‬‫ﺗﻜﻮن‬‫ح‬‫ﻣﻘﺪارا‬ ‫اﻷﻛﺒﺮ‬ ‫اﻟﻘﻮة‬ ‫اﺗﺠﺎه‬ ‫ﻓﻰ‬
*‫ﻣﻼﺣﻈﺔ‬:‫ق‬١–‫ق‬٢Y‫ح‬Y‫ق‬١+‫ق‬٢‫أو‬]‫ق‬١–‫ق‬٢،‫ق‬١+‫ق‬٢[
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫اﻟﻘﻮى‬ ‫ﻣﻦ‬ ‫زوج‬ ‫ﻟﻜﻞ‬ ‫اﻟﻤﺤﺼﻠﺔ‬ ‫اﺗﺠﺎه‬ ‫و‬ ‫ﻣﻘﺪار‬ ‫أوﺟﺪ‬‫اﻟﺘﺎﻟﯿﺔ‬:
)‫أ‬(٥، ‫ﻧﯿﻮﺗﻦ‬٧‫ﻣﺘﻌﺎﻣﺪﺗﺎن‬ ‫و‬ ‫ﻧﯿﻮﺗﻦ‬
)‫ب‬(٣، ‫ﻧﯿﻮﺗﻦ‬٥‫ﺑﯿﻨﮭﻤﺎ‬ ‫اﻟﺰاوﯾﺔ‬ ‫و‬ ‫ﻧﯿﻮﺗﻦ‬٦٠٥
)‫ﺟـ‬(٥، ‫ﻧﯿﻮﺗﻦ‬٥‫اﻟﺰاوﯾﺔ‬ ‫ﺗﺤﺼﺮان‬ ‫و‬ ‫ﻧﯿﻮﺗﻦ‬١٢٠٥
‫اﻟﺤﻞ‬:
)‫أ‬(A‫ﻣﺘﻌﺎﻣﺪﺗﺎن‬ ‫اﻟﻘﻮﺗﺎن‬
B‫ح‬٢
=‫ق‬٢
١+‫ق‬٢
٢=)٥(٢
) +٧(٢
=٧٤B‫ح‬=‫؟‬٧٤‫ﻧ‬‫ﯿﻮﺗﻦ‬
A‫ﻇﺎ‬‫ھـ‬= =B‫ق‬)‫ھـ‬p= (٢٨/
٥٤٥
)‫ب‬(A‫ح‬٢
=‫ق‬١
٢
+‫ق‬٢
٢
+٢‫ق‬١‫ق‬٢‫ﺣﺘﺎ‬‫ى‬=)٣(٢
) +٥(٢
+٢×٣×٥‫ﺣﺘﺎ‬٦٠=٤٩
B‫ح‬=٧‫ﻧﯿﻮﺗﻦ‬
A‫ھـ‬ ‫ﻇﺎ‬===٠٫٧٨٧٢٩٥٨
B‫ق‬)‫ھـ‬p= (١٣/
٣٨٥
‫ى‬
٢
‫ى‬
٢
‫ق‬٢
‫ق‬١
‫ق‬١‫ق‬٢
‫ق‬٢ ‫ق‬١
‫ق‬٢
‫ق‬١
٧
٥
‫ق‬٢‫ﺣﺎ‬‫ى‬
‫ق‬١+‫ق‬٢‫ﺣﺘﺎ‬‫ى‬
٥‫ﺣﺎ‬٦٠
٣+٥‫ﺣﺘﺎ‬٦٠

6. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
6
)‫ﺟـ‬(A‫ﻣﺘﺴﺎوﯾﺘﺎن‬ ‫اﻟﻘﻮﺗﺎن‬B‫ح‬=٢‫ق‬‫ﺣﺘﺎ‬=٢×٥×‫ﺣﺘﺎ‬٦٠=٥‫ﻧﯿﻮﺗﻦ‬
B‫ق‬)‫ھـ‬p= = = (٦٠٥
‫ـــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫اﻻﺗﯿﺔ‬ ‫اﻟﺤﺎﻻت‬ ‫ﻓﻰ‬ ‫اﻟﻘﻮﺗﯿﻦ‬ ‫ﺑﯿﻦ‬ ‫اﻟﺰاوﯾﺔ‬ ‫أوﺟﺪ‬:
)‫أ‬(٤، ‫ﻧﯿﻮﺗﻦ‬٨‫ح‬ ، ‫ﻧﯿﻮﺗﻦ‬=٤‫؟‬٣
)‫ب‬(٣، ‫ﻧﯿﻮﺗﻦ‬٥‫ﻣﺤﺼﻠﺘﮭﻤﺎ‬ ‫ﻣﻘﺪار‬ ، ‫ﻧﯿﻮﺗﻦ‬٧‫ﻧﯿﻮﺗﻦ‬.
)‫ﺟـ‬(٥، ‫ﻧﯿﻮﺗﻦ‬٦، ‫ﻧﯿﻮﺗﻦ‬‫ح‬=‫؟‬٦١‫ﻧﯿﻮﺗﻦ‬
)‫ء‬(٥٠، ‫ﻧﯿﻮﺗﻦ‬٥٠‫ﻣﺤﺼﻠﺘﮭﻤﺎ‬ ، ‫ﻧﯿﻮﺗﻦ‬=٥٠‫؟‬٣‫ﻧﯿﻮﺗﻦ‬
)‫ھـ‬(١٦، ‫ﻛﺠﻢ‬ ‫ث‬١٢‫ﻣﺤﺼﻠﺘﮭﻤﺎ‬ ، ‫ﻛﺠﻢ‬ ‫ث‬=٤‫؟‬١٣‫ﻛﺠﻢ‬ ‫ث‬
)‫و‬(١٦، ‫ﻛﺠﻢ‬ ‫ث‬١٢‫ﻣﺤﺼﻠﺘﮭﻤﺎ‬ ، ‫ﻛﺠﻢ‬ ‫ث‬=٢٠‫ﻛﺠﻢ‬ ‫ث‬
‫اﻟﺤﻞ‬:
)‫أ‬(٤، ‫ﻧﯿﻮﺗﻦ‬٨‫ح‬ ، ‫ﻧﯿﻮﺗﻦ‬=٤‫؟‬٣
A‫ح‬٢
=‫ق‬١
٢
+‫ق‬٢
٢
+٢‫ق‬١‫ق‬٢‫ﺣﺘﺎ‬‫ى‬B٤٨=١٦+٦٤+٢×٤×٨‫ى‬ ‫ﺣﺘﺎ‬
B٦٤‫ى‬ ‫ﺣﺘﺎ‬=-٣٢B‫ى‬ ‫ﺣﺘﺎ‬=-‫ق‬)‫ى‬‫ﻒ‬‫ﻓ‬= (١٢٠٥
)‫ب‬(٣، ‫ﻧﯿﻮﺗﻦ‬٥‫ﻣﺤﺼﻠﺘﮭﻤﺎ‬ ‫ﻣﻘﺪار‬ ، ‫ﻧﯿﻮﺗﻦ‬٧‫ﻧﯿﻮﺗﻦ‬.
A‫ح‬٢
=‫ق‬١
٢
+‫ق‬٢
٢
+٢‫ق‬١‫ق‬٢‫ﺣﺘﺎ‬‫ى‬B٤٩=٩+٢٥+٢×٣×٥‫ى‬ ‫ﺣﺘﺎ‬
B٣٠‫ى‬ ‫ﺣﺘﺎ‬=١٥B‫ى‬ ‫ﺣﺘﺎ‬=‫ق‬)‫ى‬‫ﻒ‬‫ﻓ‬= (٦٠٥
)‫ﺟـ‬(٥، ‫ﻧﯿﻮﺗﻦ‬٦‫ح‬ ، ‫ﻧﯿﻮﺗﻦ‬=‫؟‬٦١‫ﻧﯿﻮﺗﻦ‬
A‫ح‬٢
=‫ق‬١
٢
+‫ق‬٢
٢
+٢‫ق‬١‫ق‬٢‫ﺣﺘﺎ‬‫ى‬B٦١=٢٥+٣٦+٢×٥×٦‫ى‬ ‫ﺣﺘﺎ‬
B٦٠‫ى‬ ‫ﺣﺘﺎ‬=٠B‫ى‬ ‫ﺣﺘﺎ‬=٠‫ق‬)‫ى‬‫ﻒ‬‫ﻓ‬= (٩٠٥
)‫ء‬(٥٠، ‫ﻧﯿﻮﺗﻦ‬٥٠‫ﻣﺤﺼﻠﺘﮭﻤﺎ‬ ، ‫ﻧﯿﻮﺗﻦ‬=٥٠‫؟‬٣‫ﻧﯿﻮﺗﻦ‬
A‫ح‬=٢‫ق‬‫ﺣﺘﺎ‬B٥٠‫؟‬٣=٢×٥٠‫ﺣﺘﺎ‬
B‫ﺣﺘﺎ‬=B=٣٠B‫ق‬)‫ى‬p= (٦٠٥
‫ى‬
٢ ‫ى‬
٢
١٢٠
٢
١
٢
١
٢
‫ى‬
٢
‫ى‬
٢
‫ى‬
٢
‫؟‬٣
٢
‫ى‬
٢

7. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
7
)‫ھـ‬(١٦، ‫ﻛﺠﻢ‬ ‫ث‬١٢‫ﻣﺤﺼﻠﺘﮭﻤﺎ‬ ، ‫ﻛﺠﻢ‬ ‫ث‬=٤‫؟‬١٣‫ﻛﺠﻢ‬ ‫ث‬
A‫ح‬٢
=‫ق‬١
٢
+‫ق‬٢
٢
+٢‫ق‬١‫ق‬٢‫ﺣﺘﺎ‬‫ى‬B٢٠٨=٢٥٦+١٤٤+٢×١٦×١٢‫ﺣﺘﺎى‬
B٣٨٤‫ى‬ ‫ﺣﺘﺎ‬=-١٩٢B‫ى‬ ‫ﺣﺘﺎ‬=-B‫ق‬)‫ى‬p= (١٢٠٥
)‫و‬(١٦‫ث‬، ‫ﻛﺠﻢ‬١٢‫ﻣﺤﺼﻠﺘﮭﻤﺎ‬ ، ‫ﻛﺠﻢ‬ ‫ث‬=٢٠‫ﻛﺠﻢ‬ ‫ث‬
A‫ح‬٢
=‫ق‬١
٢
+‫ق‬٢
٢
+٢‫ق‬١‫ق‬٢‫ﺣﺘﺎ‬‫ى‬B٤٠٠=٢٥٦+١٤٤+٢×١٦×١٢‫ﺣﺘﺎى‬
B٣٨٤‫ى‬ ‫ﺣﺘﺎ‬=٠B‫ى‬ ‫ﺣﺘﺎ‬=٠B‫ق‬)‫ى‬p= (٩٠٥
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﻣﻘﺪارھﻤﺎ‬ ‫ﻗﻮﺗﺎن‬‫ق‬،٢‫ق‬‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﺗﺆﺛﺮان‬‫ﻣﺎدﯾﺔ‬‫ﻣﻊ‬ ‫ﻗﺎﺋﻤﺔ‬ ‫زاوﯾﺔ‬ ‫ﺗﺼﻨﻊ‬ ‫ﻣﺤﺼﻠﺘﮭﻤﺎ‬ ‫و‬
‫اﻷوﻟﻰ‬ ‫اﻟﻘﻮة‬.‫ﻣﺤﺼﻠﺘﮭﻤﺎ‬ ‫ﻣﻘﺪار‬ ‫أوﺟﺪ‬ ‫ﻛﺬﻟﻚ‬ ‫و‬ ‫اﻟﻘﻮﺗﯿﻦ‬ ‫ﺑﯿﻦ‬ ‫اﻟﺰاوﯾﺔ‬ ‫أوﺟﺪ‬.
‫اﻟﺤﻞ‬:
A‫اﻟﻤﺤﺼ‬‫اﻷوﻟﻰ‬ ‫اﻟﻘﻮة‬ ‫ﻋﻠﻰ‬ ‫ﻋﻤﻮدﯾﺔ‬ ‫ﻠﺔ‬B‫ق‬١+‫ق‬٢‫ى‬ ‫ﺣﺘﺎ‬=٠
B‫ق‬+٢‫ق‬‫ى‬ ‫ﺣﺘﺎ‬=٠B٢‫ق‬‫ى‬ ‫ﺣﺘﺎ‬=-‫ق‬B‫ى‬ ‫ﺣﺘﺎ‬=-B‫ق‬)‫ى‬= (١٢٠
A‫ح‬٢
=‫ق‬٢
٢
-‫ق‬١
٢
B‫ح‬٢
=٤‫ق‬٢
-‫ق‬٢
=٣‫ق‬٢
B‫ح‬=‫؟‬٣‫ق‬
‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﻣﻘﺪارھﻤﺎ‬ ‫ﻗﻮﺗﺎن‬٥،٥‫؟‬٢‫اﻷ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﺗﺆﺛﺮان‬ ‫ﻛﺠﻢ‬ ‫ﺛﻘﻞ‬‫ﻓﻰ‬ ‫اﻟﺜﺎﻧﯿﺔ‬ ‫و‬ ‫اﻟﺸﺮق‬ ‫ﻧﺤﻮ‬ ‫وﻟﻰ‬
‫اﻟﻐﺮﺑﻰ‬ ‫اﻟﺸﻤﺎل‬ ‫اﺗﺠﺎه‬.‫اﻷوﻟﻰ‬ ‫اﻟﻘﻮة‬ ‫ﻣﻘﺪار‬ ‫ﺗﺴﺎوى‬ ‫ﻣﻘﺪارھﺎ‬ ‫ﻣﺤﺼﻠﺘﮭﻤﺎ‬ ‫أن‬ ‫أﺛﺒﺖ‬
‫اﻟﻘﻮﺗﯿﻦ‬ ‫ﻣﻦ‬ ‫ﻛﻞ‬ ‫ﻋﻠﻰ‬ ‫اﻟﻤﺤﺼﻠﺔ‬ ‫ﺑﮭﺎ‬ ‫ﺗﻤﯿﻞ‬ ‫اﻟﺘﻰ‬ ‫اﻟﺰاوﯾﺔ‬ ‫أوﺟﺪ‬ ‫و‬
‫اﻟﺤﻞ‬:
‫ق‬١=٥، ‫ﻛﺠﻢ‬ ‫ث‬‫ق‬٢=٥‫؟‬٢‫ى‬ ، ‫ﻛﺠﻢ‬ ‫ث‬=١٣٥٥
A‫ح‬٢
=‫ق‬١
٢
+‫ق‬٢
٢
+٢‫ق‬١‫ق‬٢‫ﺣﺘﺎ‬‫ى‬
B‫ح‬٢
=٢٥+٥٠+٢×٥×٥‫؟‬٢‫ﺣﺘﺎ‬١٣٥=٢٥
B‫ح‬=٥‫ﻛﺠﻢ‬ ‫ث‬=‫ق‬١
A‫ھـ‬ ‫ﻇﺎ‬= = =
B‫ھـ‬ ‫ﻇﺘﺎ‬=‫ﺻﻔﺮ‬B‫ق‬)‫ھـ‬p= (٩٠
B‫اﻟ‬‫ﺑﺰاوﯾﺔ‬ ‫ﺗﻤﯿﻞ‬ ‫ﻤﺤﺼﻠﺔ‬٩٠٥
‫ﻗﺪرھﺎ‬ ‫ﺑﺰاوﯾﺔ‬ ‫و‬ ‫اﻻوﻟﻰ‬ ‫اﻟﻘﻮة‬ ‫ﻋﻠﻰ‬٤٥٥
‫اﻟﺜﺎﻧﯿﺔ‬ ‫اﻟﻘﻮة‬ ‫ﻋﻠﻰ‬
١
٢
١
٢
٥
٥‫؟‬٢
‫اﻟﺸﺮق‬
‫اﻟﻐﺮب‬
‫اﻟﺸﻤﺎل‬
‫اﻟﺠﻨﻮب‬
٤٥٥
‫ق‬٢‫ﺣﺎ‬‫ى‬
‫ق‬١+‫ق‬٢‫ﺣﺘﺎ‬‫ى‬
٥‫؟‬٢‫ﺣﺎ‬١٣٥
٥+٥‫؟‬٢‫ﺣﺘﺎ‬١٣٥
٥
٠

8. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
8
‫ﻣﺜﺎل‬:‫ﻣﺤﺼﻠﺘﮭﻤﺎ‬ ‫ﻛﺎﻧﺖ‬ ‫ﻗﺎﺋﻤﺔ‬ ‫ﻗﻮﺗﺎن‬ ‫ﺑﯿﻦ‬ ‫اﻟﺰاوﯾﺔ‬ ‫ﻛﺎﻧﺖ‬ ‫إذا‬‫؟‬٣٤‫اﻟﺰاوﯾﺔ‬ ‫ﻛﺎﻧﺖ‬ ‫إذا‬ ‫و‬ ‫ﻧﯿﻮﺗﻦ‬
‫ﺑﯿﻨﮭﻤﺎ‬٦٠٥
‫ﻣﺤﺼﻠﺘﮭﻤﺎ‬ ‫ﻛﺎﻧﺖ‬ ‫و‬٧‫ﻛﺬﻟﻚ‬ ‫و‬ ‫اﻟﻘﻮﺗﯿﻦ‬ ‫ﻣﻦ‬ ‫ﻛﻞ‬ ‫ﻣﻘﺪار‬ ‫أوﺟﺪ‬ ‫ﻧﯿﻮﺗﻦ‬
‫أوﺟ‬‫ﺪ‬‫ﻟﻤﺤﺼﻠﺘﮭﻤﺎ‬ ‫واﻟﺼﻐﺮى‬ ‫اﻟﻌﻈﻤﻰ‬ ‫اﻟﻨﮭﺎﯾﺘﯿﻦ‬.
‫اﻟﺤﻞ‬:
A‫ﻣﺘﻌﺎﻣﺪﺗﺎن‬ ‫اﻟﻘﻮﺗﺎن‬B‫ح‬٢
=‫ق‬١
٢
+‫ق‬٢
٢
B٣٤=‫ق‬١
٢
+‫ق‬٢
٢
)١(
A‫ح‬٢
=‫ق‬١
٢
+‫ق‬٢
٢
+٢‫ق‬١‫ق‬٢‫ﺣﺘﺎ‬‫ى‬
B٤٩=‫ق‬١
٢
+‫ق‬٢
٢
+٢‫ق‬١‫ق‬٢‫ﺣﺘﺎ‬٦٠
B٤٩=‫ق‬١
٢
+‫ق‬٢
٢
+‫ق‬١‫ق‬٢)٢(
‫اﻟﻤﻌﺎدﻟﺘﯿﻦ‬ ‫ﺑﺤﻞ‬ ‫و‬)١(،)٢(ً‫ﺎ‬‫ﻣﻌ‬:‫ﺑﻄﺮح‬)١(‫ﻣﻦ‬)٢(B‫ق‬١‫ق‬٢=١٥
B‫ق‬١=)٣(‫ﻓﻰ‬ ‫ﺑﺎﻟﺘﻌﻮﯾﺾ‬ ‫و‬)١(
B٣٤+ =‫ق‬٢
٢‫ﻓﻰ‬ ‫ﺑﺎﻟﻀﺮب‬‫ق‬٢
٢
B٣٤‫ق‬٢
٢=٢٢٥+‫ق‬٤
٢G‫ق‬٤
٢‫ـ‬‫ـ‬‫ــ‬٣٤‫ق‬٢
٢+٢٢٥
B)‫ق‬٢
٢‫ـ‬‫ـ‬-٩)(‫ق‬٢
٢-٢٥= (٠G‫ق‬٢=٣،‫ق‬٢=٥‫ﻓﻰ‬ ‫ﺑﺎﻟﺘﻌﻮﯾﺾ‬ ‫و‬)٣(
B‫ق‬١=٥،‫ق‬١=٣
B‫ق‬١=٥، ‫ﻧﯿﻮﺗﻦ‬‫ق‬٢=٣‫ﻧﯿﻮﺗﻦ‬‫ﺑﺎﻋﺘﺒﺎر‬ ‫و‬‫ق‬١<‫ق‬٢
B‫ﻟﻠﻤﺤﺼﻠﺔ‬ ‫اﻟﻌﻈﻤﻰ‬ ‫اﻟﻘﯿﻤﺔ‬=٥+٣=٨‫ﻧﯿﻮﺗﻦ‬
B‫ﻟﻠﻤﺤﺼﻠﺔ‬ ‫اﻟﺼﻐﺮى‬ ‫اﻟﻘﯿﻤﺔ‬=٥-٣=٢‫ﻧﯿﻮﺗﻦ‬
‫ــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﻣﻘﺪارھﻤﺎ‬ ‫ﻗﻮﺗﺎن‬‫ق‬١،‫ق‬٢‫ﻣﺤﺼﻠﺘﮭﻤﺎ‬ ‫ﻣﺎدﯾﺔ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﺗﺆﺛﺮان‬ ‫ﻧﯿﻮﺗﻦ‬‫ح‬‫ﺣﯿﺚ‬
‫ح‬g]٢،١٠[‫ﻛ‬ ‫ﻗﯿﻤﺔ‬ ‫أوﺟﺪ‬‫ﻣﻦ‬ ‫ﻞ‬‫ق‬١،‫ق‬٢‫ﻋﻨﺪﻣﺎ‬ ‫اﻟﻤﺤﺼﻠﺔ‬ ‫ﻣﻘﺪار‬ ‫أوﺟﺪ‬ ‫ﺛﻢ‬
‫ﻋﻤﻠﮭﻤﺎ‬ ‫ﺧﻄﻰ‬ ‫ﺑﯿﻦ‬ ‫اﻟﺰاوﯾﺔ‬ ‫ﻗﯿﺎس‬ ‫ﯾﻜﻮن‬١٢٠٥
‫اﻟﺤﻞ‬:
A‫ح‬g]٢،١٠[B‫ق‬١+‫ق‬٢=١٠)١(
B|‫ق‬١-‫ق‬٢|=٢B‫ق‬١-‫ق‬٢=٢)٢(،‫ق‬١-‫ق‬٢=-٢)٣(
‫ﻣﻦ‬)١(،)٢(‫ﯾﻨﺘﺞ‬:‫ق‬١=٦، ‫ﻧﯿﻮﺗﻦ‬‫ق‬٢=٤‫ﻧﯿﻮﺗﻦ‬
‫ﻣﻦ‬)١(،)٣(‫ﯾﻨﺘﺞ‬:‫ق‬١=٤، ‫ﻧﯿﻮﺗﻦ‬‫ق‬٢=٦‫ﻧﯿﻮﺗﻦ‬
A‫ح‬٢
=‫ق‬١
٢
+‫ق‬٢
٢
+٢‫ق‬١‫ق‬٢‫ﺣﺘﺎ‬‫ى‬
B‫ح‬٢
=٣٦+١٦+٢×٦×٤‫ﺣﺘﺎ‬١٢٠=٢٨B‫ح‬=٢‫؟‬٧‫ﻧﯿﻮﺗﻦ‬
١٥
‫ق‬٢
٢٢٥
‫ق‬٢
٢

9. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
9
‫ﻣﺜﺎل‬:‫ﻣﻘﺎدﯾﺮھﺎ‬ ‫ﻣﺴﺘﻮﯾﺔ‬ ‫ﻗﻮى‬ ‫ﺛﻼث‬ ‫ﯾﺘﺄﺛﯿﺮ‬ ‫ﻣﺘﺰن‬ ‫ﺟﺴﻢ‬٥،١٠،٥‫؟‬٣‫اﻟﺘﺮﺗﯿﺐ‬ ‫ﻋﻠﻰ‬ ‫ﻛﺠﻢ‬ ‫ث‬
‫اﻟﻘﻮى‬ ‫ھﺬه‬ ‫ﻣﻦ‬ ‫ﻗﻮﺗﯿﻦ‬ ‫ﻛﻞ‬ ‫ﺑﯿﻦ‬ ‫اﻟﺰاوﯾﺔ‬ ‫ﻗﯿﺎس‬ ‫أوﺟﺪ‬.
‫اﻟﺤﻞ‬:
‫اﻻوﻟﻰ‬ ‫اﻟﺤﺎﻟﺔ‬:
A‫ح‬٢
=‫ق‬١
٢
+‫ق‬٢
٢
+٢‫ق‬١‫ق‬٢‫ﺣﺘﺎ‬‫ى‬
B)٥‫؟‬٣(٢
) =٥(٢
) +١٠(٢
+٢×٥×١٠‫ى‬ ‫ﺣﺘﺎ‬
B‫ى‬ ‫ﺣﺘﺎ‬=‫ــ‬B‫ى‬=١٢٠٥
B‫اﻟ‬ ‫ﺑﯿﻦ‬ ‫اﻟﺰاوﯾﺔ‬ ‫ﻗﯿﺎس‬‫ﻘﻮﺗﯿﻦ‬٥،١٠‫ھﻮ‬ ‫ﻛﺠﻢ‬ ‫ث‬١٢٠٥
‫اﻟﺜﺎﻧﯿﺔ‬ ‫اﻟﺤﺎﻟﺔ‬:
A‫ح‬٢
=‫ق‬٣
٢
+‫ق‬٢
٢
+٢‫ق‬٣‫ق‬٢‫ﺣﺘﺎ‬‫ك‬
B)٥(٢
) =٥‫؟‬٣(٢
) +١٠(٢
+٢×٥‫؟‬٣×١٠‫ﺣﺘﺎ‬‫ك‬
B‫ﺣﺘﺎ‬‫ك‬=‫ــ‬B‫ك‬=١٥٠٥
B‫ﻗﯿﺎس‬‫اﻟﻘﻮﺗﯿﻦ‬ ‫ﺑﯿﻦ‬ ‫اﻟﺰاوﯾﺔ‬٥‫؟‬٣،١٠‫ھﻮ‬ ‫ﻛﺠﻢ‬ ‫ث‬١٥٠٥
B‫ا‬ ‫ﻗﯿﺎس‬‫اﻟﻘﻮﺗﯿﻦ‬ ‫ﺑﯿﻦ‬ ‫ﻟﺰاوﯾﺔ‬٥،٥‫؟‬٣‫ﻛﺠﻢ‬ ‫ث‬=٣٦٠-)١٢٠+١٥٠= (٩٠٥
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﻣﻘﺪارھﻤﺎ‬ ‫ﻗﻮﺗﺎن‬‫ق‬،٢‫ق‬‫ﻛ‬ ‫ث‬‫ﺠﻢ‬‫ﺑﯿﻨﮭﻤﺎ‬ ‫اﻟﺰاوﯾﺔ‬ ‫ﻗﯿﺎس‬ ، ‫ﻣﺎدﯾﺔ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﺗﺆﺛﺮان‬
١٢٠٥
‫ﻣﺤﺼﻠﺘﮭﻤﺎ‬ ‫ﻛﺎﻧﺖ‬ ‫ﻓﺈذا‬٥‫؟‬٣‫اﻟﻘﻮﺗﯿﻦ‬ ‫ﻣﻘﺪار‬ ‫أوﺟﺪ‬ ‫ﻛﺠﻢ‬ ‫ث‬.
‫اﻟﺤﻞ‬:
A‫ح‬٢
=‫ق‬١
٢
+‫ق‬٢
٢
+٢‫ق‬١‫ق‬٢‫ﺣﺘﺎ‬‫ى‬
B)٥‫؟‬٣(٢
=‫ق‬٢
+٤‫ق‬٢
+٢×‫ق‬×٢‫ق‬‫ﺣﺘ‬‫ﺎ‬١٢٠
B٧٥=٣‫ق‬٢
G‫ق‬٢
=٢٥G‫ق‬=٥‫ﻛﺠﻢ‬ ‫ث‬
B‫ھﻤﺎ‬ ‫اﻟﻘﻮﺗﺎن‬ ‫ﻣﻘﺪار‬٥،١٠‫ﻛﺠﻢ‬ ‫ث‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﻣﻘﺪارھﻤﺎ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﻣﺘﻼﻗﯿﺘﺎن‬ ‫ﻗﻮﺗﺎن‬‫ق‬،٢‫ق‬‫ﻣﺤﺼﻠﺘﮭﻤﺎ‬ ‫ﻣﻘﺪار‬ ‫ﻛﺠﻢ‬ ‫ث‬‫ح‬‫زاد‬ ‫إذا‬ ‫و‬
‫اﻷوﻟﻰ‬ ‫اﻟﻘﻮة‬ ‫ﻣﻘﺪار‬٥‫ﯾﺘﻐﯿﺮ‬ ‫ﻻ‬ ‫اﻟﻤﺤﺼﻠﺔ‬ ‫اﺗﺠﺎه‬ ‫ﻓﺈن‬ ‫اﻟﺜﺎﻧﯿﺔ‬ ‫اﻟﻘﻮة‬ ‫ﻣﻘﺪار‬ ‫ﺗﻀﺎﻋﻒ‬ ‫و‬ ‫ﻛﺠﻢ‬ ‫ث‬
‫ﻗﯿﻤﺔ‬ ‫أوﺟﺪ‬‫ق‬
‫اﻟﺤﻞ‬:A‫ﻻ‬ ‫اﻟﻤﺤﺼﻠﺔ‬ ‫اﺗﺠﺎه‬‫ﯾﺘﻐﯿﺮ‬
B‫ﯾﺘﻐﯿﺮ‬ ‫ﻻ‬ ‫اﻷوﻟﻰ‬ ‫اﻟﻘﻮة‬ ‫ﻣﻊ‬ ‫اﻟﻤﺤﺼﻠﺔ‬ ‫ﻋﻤﻞ‬ ‫ﺧﻂ‬ ‫ﻣﯿﻞ‬ ‫زاوﯾﺔ‬ ‫ﻗﯿﺎس‬ ‫ھـ‬
١
٢
‫؟‬٣
٢

10. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
10
B‫ـ‬‫ھ‬‫ھـ‬‫اﻟﺜﺎﻧﯿﺔ‬ ‫اﻟﺤﺎﻟﺔ‬ ‫ﻓﻰ‬ ‫ھـ‬ ‫ﺗﺴﺎوى‬ ‫اﻷوﻟﻰ‬ ‫اﻟﺤﺎﻟﺔ‬ ‫ﻓﻰ‬.
‫ھـ‬ ‫ﻇﺎ‬==
B=
B=
B٢‫ق‬+٤‫ق‬‫ى‬ ‫ﺣﺘﺎ‬=‫ق‬+٥+٤‫ق‬‫ى‬ ‫ﺣﺘﺎ‬B٢‫ق‬=‫ق‬+٥B‫ق‬=٥‫ﻛﺠﻢ‬ ‫ث‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:
‫اﻟﺤﻞ‬:
‫ــــــــــــــــــــــــــــــــــــ‬
٢‫ق‬‫ﺣﺎ‬‫ى‬
‫ق‬+٢‫ق‬‫ﺣﺘﺎ‬‫ى‬
٤‫ق‬‫ﺣﺎ‬‫ى‬
)‫ق‬+٥(+٤‫ق‬‫ﺣﺘﺎ‬‫ى‬
٢‫ق‬‫ﺣﺎ‬‫ى‬
‫ق‬+٢‫ق‬‫ﺣﺘﺎ‬‫ى‬
٤‫ق‬‫ﺣﺎ‬‫ى‬
)‫ق‬+٥(+٤‫ق‬‫ﺣﺘﺎ‬‫ى‬
٢
‫ق‬+٢‫ق‬‫ى‬ ‫ﺣﺘﺎ‬
٤
)‫ق‬+٥(+٤‫ق‬‫ﺣﺘﺎ‬‫ى‬

11. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
11
]١[‫اﻻﻗﻮاس‬ ‫ﺑﯿﻦ‬ ‫ﻣﻦ‬ ‫اﻟﺼﺤﯿﺤﺔ‬ ‫اﻻﺟﺎﺑﺔ‬ ‫اﺧﺘﺮ‬:
١(‫ﻣﻘﺪار‬ ‫ﻗﻮﺗﺎن‬‫ھﻤﺎ‬٦،٨‫اﻟﺰاوﯾﺔ‬ ‫ﻗﯿﺎس‬ ‫و‬ ‫ﻧﯿﻮﺗﻦ‬‫ﺑﯿﻨﮭﻤﺎ‬٩٠٥
‫ﻣﺤ‬ ‫ﻣﻘﺪار‬ ‫ﻓﺈن‬‫ﺼﻠﺘﮭﻤﺎ‬
‫ﺗﺴﺎوى‬..........‫ﻧﯿﻮﺗﻦ‬]١٠،‫أ‬٥،‫أ‬٧،‫أ‬١٢[
٢(‫ﻣﻨﮭﻤﺎ‬ ‫ﻛﻞ‬ ‫ﻣﻘﺪار‬ ‫و‬ ‫ﻣﺘﺴﺎوﯾﺘﺎن‬ ‫ﻗﻮﺗﺎن‬٥‫ﻣﺤﺼﻠﺘﮭﻤﺎ‬ ‫ﻣﻘﺪار‬ ‫و‬ ‫ﻧﯿﻮﺗﻦ‬٥‫ﻗﯿﺎس‬ ‫ﻓﺈن‬ ‫ﻧﯿﻮﺗﻦ‬
‫ﺗﺴﺎوى‬ ‫ﺑﯿﻨﮭﻤﺎ‬ ‫اﻟﺰاوﯾﺔ‬] ...........٠٥
،‫أ‬٩٠٥
،‫أ‬١٢٠،‫أ‬١٨٠٥
[
٣(‫ﻣﺤﺼﻠﺘﮭﻤﺎ‬ ‫و‬ ‫ﻣﺘﻌﺎﻣﺪﺗﺎن‬ ‫و‬ ‫اﻟﻤﻘﺪار‬ ‫ﻓﻰ‬ ‫ﻣﺘﺴﺎوﯾﺘﺎن‬ ‫ﻗﻮﺗﺎن‬٨‫ﻣﻨﮭﻤﺎ‬ ‫ﻗﻮة‬ ‫ﻛﻞ‬ ‫ﻣﻘﺪار‬ ‫ﻓﺈن‬ ‫ﻧﯿﻮﺗﻦ‬
‫ﯾﺴﺎوى‬.........‫ﻧﯿﻮﺗﻦ‬]٤،‫أ‬٨،‫أ‬٢‫؟‬٢،‫أ‬٤‫؟‬٢[
٤(‫ﻣﻘﺪار‬ ‫ﻗﻮﺗﺎن‬‫ھﻤﺎ‬٤،‫ق‬‫ﺑﯿﻨﮭﻤﺎ‬ ‫اﻟﺰاوﯾﺔ‬ ‫ﻗﯿﺎس‬ ‫و‬ ‫ﻧﯿﻮﺗﻦ‬١٢٠٥
‫ﻣﺤﺼﻠﺘﮭﻤﺎ‬ ‫ﻛﺎﻧﺖ‬ ‫ﻓﺈذا‬
‫ﻓﺈن‬ ‫اﻷوﻟﻰ‬ ‫اﻟﻘﻮة‬ ‫ﻋﻠﻰ‬ ‫ﻋﻤﻮدﯾﺔ‬‫ق‬....... =‫ﻧﯿﻮﺗﻦ‬]٢،‫أ‬٤،‫أ‬٨،‫أ‬٤‫؟‬٣[
٥(‫ﻣﻘﺪارھﻤﺎ‬ ‫ﻗﻮﺗﺎن‬٨،‫ق‬‫ﺑﯿﻨﮭﻤﺎ‬ ‫اﻟﺰاوﯾﺔ‬ ‫ﻗﯿﺎس‬ ‫و‬ ‫ﺟﻢ‬ ‫ث‬g[٠‫ط‬ ،]‫ﻣﺤﺼﻠﺘﮭﻤﺎ‬ ‫و‬
‫اﻟﺰاوﯾﺔ‬ ‫ﺗﻨﺼﻒ‬‫ﻓﺈن‬ ‫ﺑﯿﻨﮭﻤﺎ‬‫ق‬......... =‫ﺟﻢ‬ ‫ث‬]٤،‫أ‬٨،‫أ‬١٦،‫أ‬٢‫؟‬٢[
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
]٢[‫ﻣﻘﺪارھﻤﺎ‬ ‫ﻗﻮﺗﺎن‬١٥،٨‫ﻛﺠﻢ‬ ‫ث‬‫ﻣﺤﺼﻠﺘﮭﻤﺎ‬ ‫ﻣﻘﺪار‬ ‫ﻛﺎن‬ ‫إذا‬ ‫ﻣﺎدﯾﺔ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﺗﺆﺛﺮان‬١٣
‫ث‬.‫اﻟﺰاوﯾ‬ ‫ﻗﯿﺎس‬ ‫أوﺟﺪ‬ ‫ﻛﺠﻢ‬‫اﻟﻘﻮﺗﯿﻦ‬ ‫ھﺎﺗﯿﻦ‬ ‫ﺑﯿﻦ‬ ‫ﺔ‬.
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
]٣[‫ﻣﻘﺪارھﻤﺎ‬ ‫ﻗﻮﺗﺎن‬١٢،١٥‫ﯾﺴﺎوى‬ ‫ﺑﯿﻨﮭﻤﺎ‬ ‫اﻟﺰاوﯾﺔ‬ ‫ﻇﻞ‬ ‫و‬ ‫ﻣﺎدﯾﺔ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﺗﺆﺛﺮان‬ ‫ﻧﯿﻮﺗﻦ‬
‫ﻋ‬ ‫ﻣﯿﻠﮭﺎ‬ ‫زاوﯾﺔ‬ ‫ﻗﯿﺎس‬ ‫و‬ ‫ﻣﺤﺼﻠﺘﮭﻤﺎ‬ ‫و‬ ‫ﻣﻘﺪار‬ ‫أوﺟﺪ‬‫اﻷوﻟﻰ‬ ‫اﻟﻘﻮة‬ ‫ﻠﻰ‬.
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــ‬
]٤[‫ﻗﻮﺗﺎن‬‫ق‬،٢‫ق‬‫ﻇﻠﮭﺎ‬ ‫زاوﯾﺔ‬ ‫ﺑﯿﻨﮭﻤﺎ‬ ‫ﺗﺤﺼﺮان‬ ‫و‬ ‫ﻣﺎدﯾﺔ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﺗﺆﺛﺮان‬=-١‫ﻣﻘﺪار‬ ‫و‬
‫ﻣﺤﺼﻠﺘﮭﻤﺎ‬=٤‫أوﺟﺪ‬ ‫ﻧﯿﻮﺗﻦ‬:
)‫أ‬(‫ﻣﻌﯿﺎر‬‫ق‬)‫ب‬(‫اﻟﻤﺤ‬ ‫ﻣﯿﻞ‬ ‫زاوﯾﺔ‬‫ﺼ‬‫اﻷوﻟﻰ‬ ‫اﻟﻘﻮة‬ ‫ﻋﻠﻰ‬ ‫ﻠﺔ‬.
‫اﻟﻘﻮى‬ ‫ﻋﻠﻰ‬ ‫ﺗﻤﺎرﯾﻦ‬
-٣
٤

12. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
12
]٥[‫ﻣﻘﺪارھﻤﺎ‬ ‫ﻗﻮﺗﺎن‬٢،‫ق‬‫ﻧ‬‫ﻗﯿﺎﺳﮭﺎ‬ ‫ﺑﯿﻨﮭﻤﺎ‬ ‫اﻟﺰاوﯾﺔ‬ ‫و‬ ‫ﯿﻮﺗﻦ‬١٢٠٥
‫ﻗﯿﻤﺔ‬ ‫أوﺟﺪ‬‫ق‬‫اﻟﺤﺎﻻت‬ ‫ﻣﻦ‬
)١(‫ﺗﺴﺎوى‬ ‫اﻟﻤﺤﺼﻠﺔ‬ ‫ﻣﻘﺪار‬‫ق‬]٢‫ﻧﯿﻮﺗﻦ‬[
)٢(‫ﻋﻤﻮدى‬ ‫اﻟﻤﺤﺼﻠﺔ‬ ‫اﺗﺠﺎه‬‫اﻟﺜﺎﻧﯿﺔ‬ ‫اﻟﻘﻮة‬ ‫ﻋﻠﻰ‬]١‫ﻧﯿﻮﺗﻦ‬[
)٣(‫ﻗﯿﺎﺳﮭﺎ‬ ‫ﺑﺰاوﯾﺔ‬ ‫ﯾﻤﯿﻞ‬ ‫اﻟﻤﺤﺼﻠﺔ‬ ‫اﺗﺠﺎه‬٤٥٥
‫اﻟﺜﺎﻧﯿﺔ‬ ‫اﻟﻘﻮة‬ ‫ﻋﻠﻰ‬]‫؟‬٣+١‫ﻧﯿﻮﺗﻦ‬[
)٤(‫اﻟﻘﻮﺗﯿﻦ‬ ‫ﺑﯿﻦ‬ ‫اﻟﺰاوﯾﺔ‬ ‫ﺗﻨﺼﻒ‬ ‫اﻟﻤﺤﺼﻠﺔ‬]٢‫ﻧﯿﻮﺗﻦ‬[
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
]٦[‫ﻣﻘﺪارھﻤﺎ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﻣﺘﻼﻗﯿﺘﺎن‬ ‫ﻗﻮﺗﺎن‬‫ق‬١،‫ق‬٢‫وﻣﻘﺪار‬‫ﻣﺤﺼﻠﺘﮭﻤﺎ‬‫ح‬‫اﻟﺰاوﯾﺔ‬ ‫و‬١٢٠٥
‫اﺗﺠﺎه‬ ‫ﻋﻜﺲ‬ ‫إذا‬ ‫و‬‫ق‬٢‫ﯾﺴﺎوى‬ ‫اﻟﻤﺤﺼﻠﺔ‬ ‫ﻣﻘﺪار‬ ‫ﻓﺈن‬‫ح‬‫؟‬٣‫أن‬ ‫أﺛﺒﺖ‬‫ق‬١=‫ق‬٢
‫اﻻوﻟﻰ‬ ‫اﻟﺤﺎﻟﺔ‬ ‫ﻓﻰ‬ ‫اﻟﻤﺤﺼﻠﺔ‬ ‫اﺗﺠﺎه‬ ‫ﻋﻠﻰ‬ ‫ﻋﻤﻮدﯾﺔ‬ ‫اﺗﺠﺎھﮭﺎ‬ ‫ﯾﻜﻮن‬ ‫اﻟﺜﺎﻧﯿﺔ‬ ‫اﻟﺤﺎﻟﺔ‬ ‫ﻓﻰ‬ ‫اﻟﻤﺤﺼﻠﺔ‬ ‫أن‬ ‫و‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
]٧[‫ﻣﺤﺼﻠﺘﮭﻤﺎ‬ ‫أن‬ ‫ﻋﻠﻢ‬ ‫إذا‬ ‫ﯾﺴﺎوى‬ ‫ﺑﯿﻨﮭﻤﺎ‬ ‫اﻟﺰاوﯾﺔ‬ ‫ﻇﻞ‬ ‫و‬ ‫ﻣﺎدﯾﺔ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﺗﺆاﺛﺮان‬ ‫ﻗﻮﺗﺎن‬
‫ﻋﻤﻮد‬‫اﻟﻘﻮة‬ ‫ﻣﻘﺪار‬ ‫أن‬ ‫و‬ ‫اﻟﺼﻐﺮى‬ ‫ﻋﻠﻰ‬ ‫ﯾﺔ‬‫ﯾﺴﺎوى‬ ‫اﻟﻜﺒﺮى‬٣٠‫ﻓﻤﺎ‬ ‫ﻧﯿﻮﺗﻦ‬‫ﻣﻦ‬ ‫ﻛﻞ‬ ‫ﻣﻘﺪار‬ ‫ھﻮ‬
‫اﻟﻘﻮة‬‫اﻟﻤﺤﺼﻠﺔ‬ ‫و‬ ‫اﻷﺧﺮى‬.
]٨[‫ﻛﺎن‬ ‫إذا‬ ‫اﻟﻘﻮﺗﯿﻦ‬ ‫ﻣﻦ‬ ‫ﻛﻞ‬ ‫ﻣﻘﺪار‬ ‫أوﺟﺪ‬:
)١(‫أﻛﺒﺮ‬‫ﻗ‬‫ﻟﻤﺤﺼﻠﺘﮭﻤﺎ‬ ‫ﯿﻤﺔ‬=٢٠‫ﻟﻤﺤﺼﻠﺘﮭﻤﺎ‬ ‫ﻗﯿﻤﺔ‬ ‫أﺻﻐﺮ‬ ‫و‬ ، ‫ﻧﯿﻮﺗﻦ‬=٤‫ﻧﯿﻮﺗﻦ‬
)٢(‫ﻣﺤﺼﻠﺘﮭﻤﺎ‬ ‫و‬ ‫اﻻﺧﺮى‬ ‫ارﺑﺎع‬ ‫ﺛﻼﺛﺔ‬ ‫ﺗﺴﺎوى‬ ‫أﺣﺪھﻤﺎ‬ ‫و‬ ‫ﻣﺘﻌﺎﻣﺪﺗﺎن‬ ‫اﻟﻘﻮﺗﺎن‬٢٠‫ﺟﻢ‬ ‫ث‬
‫ـــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
]٩[‫ﻣﻘﺪارھﻤﺎ‬ ‫ﺑﯿﻦ‬ ‫اﻟﻨﺴﺒﺔ‬ ‫ﻗﻮﺗﺎن‬١:‫؟‬٢‫ﺑﺰاوﯾﺔ‬ ‫اﻟﻜﺒﺮى‬ ‫اﻟﻘﻮة‬ ‫ﻋﻠﻰ‬ ‫ﯾﻤﯿﻞ‬ ‫ﻣﺤﺼﻠﺘﮭﻤﺎ‬ ‫ﻋﻤﻞ‬ ‫ﺧﻂ‬ ‫و‬
٤٥٥
‫ﺑﯿ‬ ‫اﻟﺰاوﯾﺔ‬ ‫ﻗﯿﺎس‬ ‫أوﺟﺪ‬‫ﻣﺤﺼﻠﺘﮭﻤﺎ‬ ‫ﻣﻘﺪار‬ ‫أن‬ ‫ﻋﻠﻢ‬ ‫إذا‬ ‫ﻛﻼھﻤﺎ‬ ‫ﻣﻘﺪار‬ ‫أوﺟﺪ‬ ‫ﺛﻢ‬ ‫ﻨﮭﻤﺎ‬٣‫؟‬٢
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
]١٠[‫ﻣﻘﺪارھﻤﺎ‬ ‫ﻗﻮﺗﺎن‬١٠،٢٠‫ﻧﻘ‬ ‫ﻓﻰ‬ ‫ﺗﺆاﺛﺮان‬ ‫ﺟﻢ‬ ‫ث‬‫اﺳﺘﻘﺎﻣﺔ‬ ‫ﻋﻠﻰ‬ ‫ﻋﻤﻠﮭﻤﺎ‬ ‫ﺧﻂ‬ ‫ﻣﺎدﯾﺔ‬ ‫ﻄﺔ‬
‫ﻛﺎﻧﺖ‬ ‫إذا‬ ‫ﻣﺤﺼﻠﮭﻤﺎ‬ ‫أوﺟﺪ‬ ‫واﺣﺪة‬:
)١(‫اﻻﺗﺠﺎه‬ ‫ﻧﻔﺲ‬ ‫ﻟﮭﻤﺎ‬ ‫اﻟﻘﻮﺗﺎن‬)٢(‫اﻻﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫ﻣﺘﻀﺎدﺗﺎن‬ ‫اﻟﻘﻮﺗﺎن‬
-١
‫؟‬٣

13. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
13
]١١[‫ﻣﻘﺪارھﻤﺎ‬ ‫ﻗﻮﺗﺎن‬١٥،١٠‫واﺣﺪة‬ ‫اﺳﺘﻘﺎﻣﺔ‬ ‫ﻋﻠﻰ‬ ‫ﻋﻤﻠﮭﻤﺎ‬ ‫ﺧﻂ‬ ‫و‬ ‫ﻣﺎدﯾﺔ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﺗﺆاﺛﺮان‬
‫أوﺟﺪ‬:
)١(‫اﺗﺠﺎھﮭﺎ‬ ‫و‬ ‫ﻟﻠﻤﺤﺼﻠﺔ‬ ‫اﻟﻌﻈﻤﻰ‬ ‫اﻟﻨﮭﺎﯾﺔ‬)٢(‫اﺗﺠﺎھﮭﺎ‬ ‫و‬ ‫ﻟﻠﻤﺤﺼﻠﺔ‬ ‫اﻟﺼﻐﺮى‬ ‫اﻟﻨﮭﺎﯾﺔ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
]١٢[‫ﻣﻘﺪارھﻤﺎ‬ ‫ﻗﻮﺗﺎن‬٤،‫ق‬‫ﺑﯿﺘﮭﻤﺎ‬ ‫اﻟﺰاوﯾﺔ‬ ‫ﻣﺎدﯾﺔ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﺗﺆاﺛﺮان‬ ‫ﻧﯿﻮﺗﻦ‬١٣٥٥
‫ﻛﺎن‬ ‫إذا‬
‫ﺑﺰاوﯾﺔ‬ ‫ﯾﻤﯿﻞ‬ ‫ﻣﺤﺼﻠﺘﮭﻤﺎ‬ ‫اﺗﺠﺎه‬٤٥٥
‫اﻟﻘﻮة‬ ‫ﻋﻠﻰ‬‫ق‬‫أوﺟﺪ‬‫ق‬‫ﻣﺤﺼﻠﺘﮭﻤﺎ‬ ‫وﻣﻘﺪار‬
]‫اﻟﻤﺴﺎﺋﻞ‬ ‫ﻟﺒﻌﺾ‬ ‫اﻟﻤﺨﺘﻠﻔﺔ‬ ‫اﻟﺤﻠﻮل‬ ‫ﯾﺮاﻋﻰ‬[
‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
&‫اﻟﻤﺪرﺳﺔ‬ ‫ﻛﺘﺎب‬ ‫ﺗﻤﺎرﯾﻦ‬:

14. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
14
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــ‬

15. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
15

16. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
16
*‫ﻣﺮﻛﺒﺘﯿﻦ‬ ‫اﻟﻰ‬ ‫ﻗﻮة‬ ‫ﺗﺤﻠﯿﻞ‬*
)١(‫ﻗﻮة‬ ‫ﺗﺤﻠﯿﻞ‬‫ﻣﻌﻠﻮﻣﺔ‬‫ﻣﻌﻠﻮﻣﯿﻦ‬ ‫اﺗﺠﺎھﯿﻦ‬ ‫ﻓﻰ‬]‫ﻣﺘﻌﺎﻣﺪﯾﻦ‬ ‫ﻏﯿﺮ‬[:
‫اﻟﻤﻘﺎﺑﻞ‬ ‫اﻟﺸﻜﻞ‬ ‫ﻣﻦ‬:
‫ﻓﻰ‬ ‫اﻟﺠﯿﺐ‬ ‫ﻗﺎﻧﻮن‬ ‫ﺑﺘﻄﺒﯿﻖ‬∆‫ج‬‫ب‬‫ا‬:
==
‫ﯾﻨﺘﺞ‬:‫ق‬١=،‫ق‬٢=
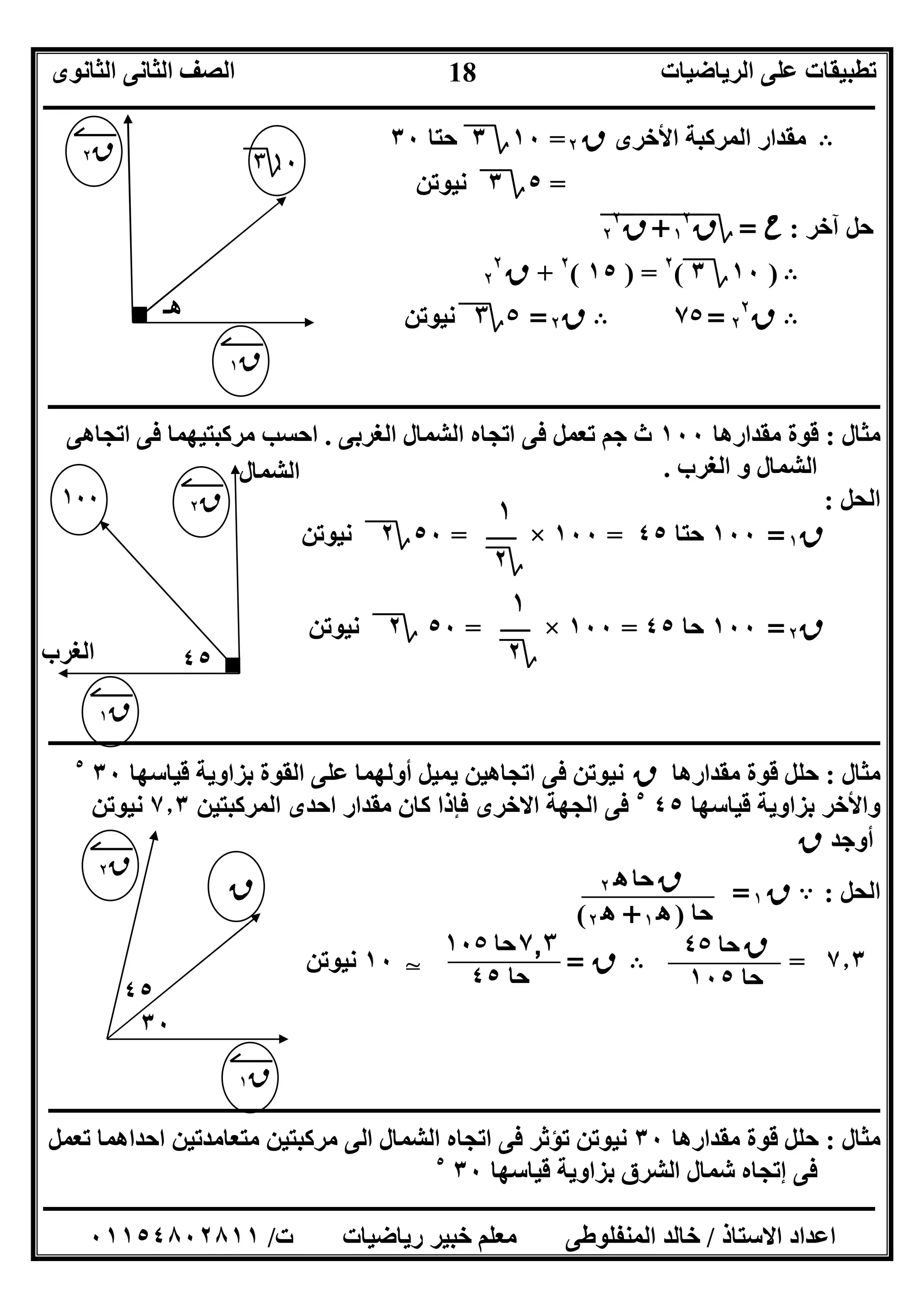
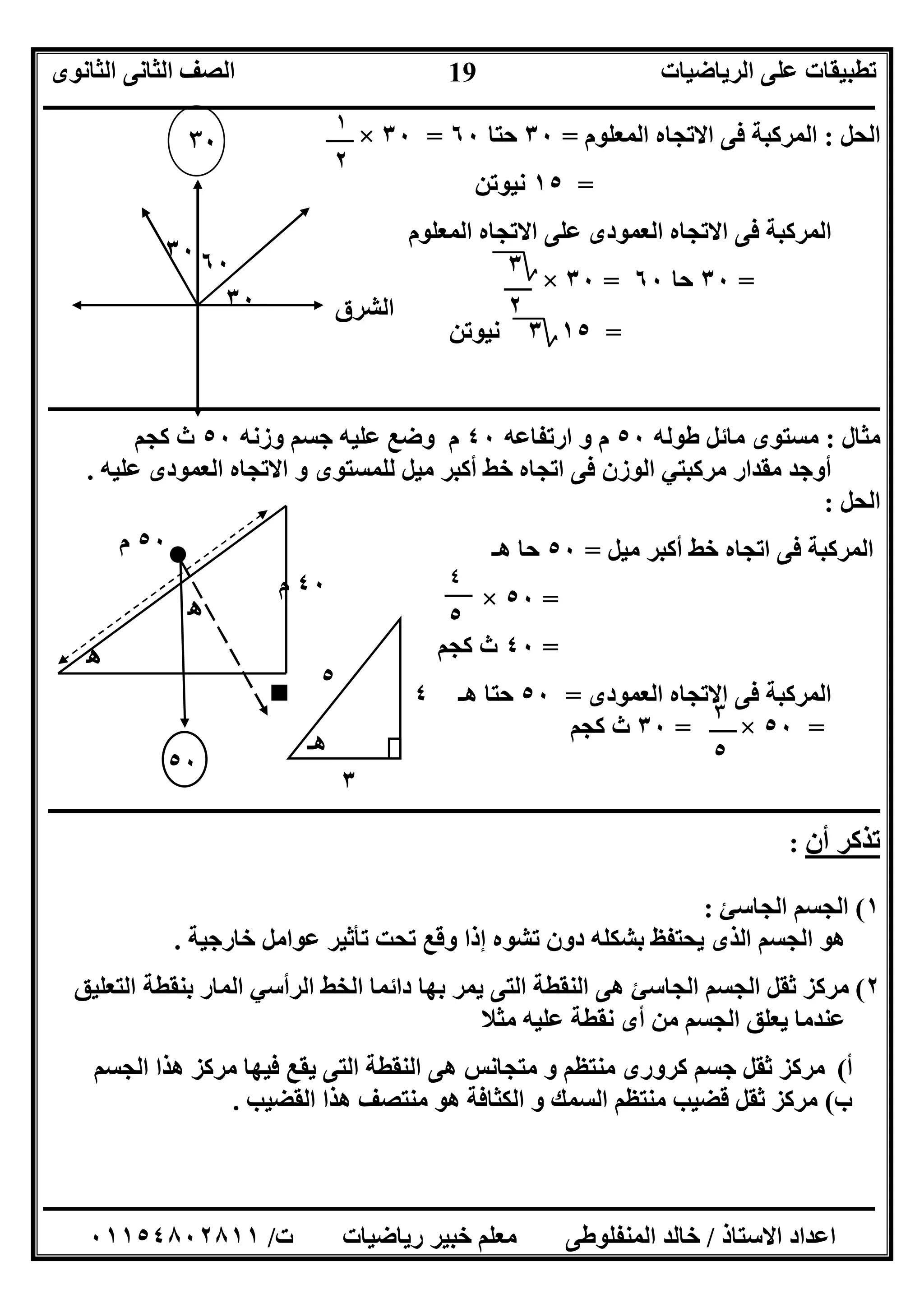
‫ق‬١‫ﻋﻠﻰ‬ ‫ﺗﻤﯿﻞ‬ ‫اﻟﺘﻰ‬ ‫اﻟﻤﺮﻛﺒﺔ‬ ‫ﻣﻘﺪار‬‫ح‬‫ھـ‬ ‫ﺑﺰاوﯾﺔ‬١
،‫ق‬٢‫ﻋﻠﻰ‬ ‫ﺗﻤﯿﻞ‬ ‫اﻟﺘﻰ‬ ‫اﻟﻤﺮﻛﺒﺔ‬ ‫ﻣﻘﺪار‬‫ح‬‫ھـ‬ ‫ﺑﺰاوﯾﺔ‬٢
)٢(‫ﻗﻮة‬ ‫ﺗﺤﻠﯿﻞ‬‫ﻣﻌﻠﻮﻣﺔ‬‫ﻣﺘﻌﺎﻣﺪﯾﻦ‬ ‫اﺗﺠﺎھﯿﻦ‬ ‫ﻓﻰ‬:
‫ق‬١=‫ح‬، ‫ھـ‬ ‫ﺣﺘﺎ‬‫ق‬٢=‫ح‬‫ھـ‬ ‫ﺣﺎ‬
‫ﻣﻼﺣﻈﺔ‬:
‫اﻟﻤﺮﻛﺒﺔ‬ ‫ﻣﻘﺪار‬‫ھـ‬ ‫ﻟﻠﺰاوﯾﺔ‬ ‫اﻟﻤﺠﺎورة‬=‫ح‬‫ھـ‬ ‫ﺣﺘﺎ‬
‫ھـ‬ ‫ﻟﻠﺰاوﯾﺔ‬ ‫اﻻﺧﺮى‬ ‫اﻟﻤﺮﻛﺒﺔ‬ ‫ﻣﻘﺪار‬=‫ح‬‫ھـ‬ ‫ﺣﺎ‬
*‫اﻻﺣﺪاﺛﯿﺎت‬ ‫ﻣﺤﻮرى‬ ‫اﺗﺠﺎھﻰ‬ ‫ﻓﻰ‬ ‫ﻣﻌﻠﻮﻣﺔ‬ ‫ﻗﻮة‬ ‫ﺗﺤﻠﯿﻞ‬:
‫أن‬ ‫ﺑﻔﺮض‬‫ق‬‫و‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﺗﺆﺛﺮ‬ ‫ﻗﻮة‬‫ﻣﺘﻌﺎﻣﺪ‬ ‫اﺣﺪاﺛﻰ‬ ‫ﻧﻈﺎم‬ ‫ﻓﻰ‬
‫ﻣﻌﻠﻮم‬ ‫اﺗﺠﺎه‬ ‫و‬ ‫ﻣﻌﻠﻮم‬ ‫ﻣﻘﺪار‬ ‫ﻟﮭﺎ‬)‫ھـ‬ ‫ﻣﻌﻠﻮﻣﺔ‬ ‫زاوﯾﺔ‬(‫ﻓﺈﻧﮫ‬
‫اﻟﺼﻮرة‬ ‫ﻋﻠﻰ‬ ‫ﻛﺘﺎﺑﺘﮭﺎ‬ ‫ﯾﻤﻜﻦ‬:‫ق‬] =‫ق‬،‫ه‬٥
[
‫ﺗﻜﺘﺐ‬ ‫و‬:) =‫ق‬، ‫ھـ‬ ‫ﺣﺘﺎ‬‫ق‬‫ھـ‬ ‫ﺣﺎ‬(
‫ق‬=‫ق‬‫ھـ‬ ‫ﺣﺘﺎ‬‫ﺳﺲ‬+‫ق‬‫ھـ‬ ‫ﺣﺎ‬‫ﺻﺺ‬
‫ح‬‫ﺣﺎ‬‫ه‬٢
‫ﺣﺎ‬)‫ه‬١+‫ه‬٢(
‫ح‬‫ﺣﺎ‬‫ه‬١
‫ﺣﺎ‬)‫ه‬١+‫ه‬٢(
‫ح‬
‫ﺣﺎ‬)‫ه‬١+‫ه‬٢(
‫ق‬١
‫ﺣﺎ‬‫ه‬٢
‫ق‬٢
‫ﺣﺎ‬‫ه‬١
‫ه‬ ‫س‬
‫ص‬
‫و‬
‫ق‬
‫ق‬‫ھـ‬ ‫ﺣﺘﺎ‬
‫ق‬‫ھـ‬ ‫ﺣﺎ‬
‫ا‬ ‫ب‬
‫ج‬‫ء‬
‫ح‬ ‫ق‬٢
‫ق‬١
‫ق‬١
‫ق‬٢
‫ه‬١
‫ه‬٢
‫ھـ‬٢
‫ا‬ ‫ب‬
‫ج‬‫ء‬
‫ح‬
‫ق‬١
‫ق‬٢
‫ه‬
٩٠–‫ھـ‬

17. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
17
*‫اﻷﻣﻠﺲ‬ ‫اﻟﻤﺎﺋﻞ‬ ‫اﻟﻤﺴﺘﻮى‬:
‫اﻻﻓﻘﻰ‬ ‫ﻋﻠﻰ‬ ‫ﯾﻤﯿﻞ‬ ‫أﻣﻠﺲ‬ ‫ﻣﺎﺋﻞ‬ ‫ﻣﺴﺘﻮى‬ ‫ﻋﻠﻰ‬ ‫ﺟﺴﻢ‬ ‫وﺿﻊ‬ ‫ﻋﻨﺪ‬
‫ﺑﺰا‬‫ھـ‬ ‫ﻗﯿﺎﺳﮭﺎ‬ ‫وﯾﺔ‬‫ﯾﻠﻰ‬ ‫ﻣﺎ‬ ‫ﻓﺘﺬﻛﺮ‬:
)١(‫اﻟﺠﺴﻢ‬ ‫وزن‬ ‫ﻗﻮة‬)‫و‬(‫ﻷﺳﻔﻞ‬ ‫رأﺳﻲ‬ ‫اﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫ﺗﻌﻤﻞ‬ ‫ھﻰ‬ ‫و‬
)٢(‫اﻷﻣﻠﺲ‬ ‫اﻟﻤﺴﺘﻮى‬ ‫ﻓﻌﻞ‬ ‫رد‬ ‫ﻗﻮة‬)‫ر‬(‫ﻋﻤﻮدى‬ ‫اﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫ﺗﻌﻤﻞ‬ ‫و‬
‫اﻷﻣﻠﺲ‬ ‫اﻟﻤﺴﺘﻮى‬ ‫ﻋﻠﻰ‬.
)٣(‫اﻟﺨﻂ‬‫ب‬‫ا‬‫ﻣﯿﻞ‬ ‫أﻛﺒﺮ‬ ‫ﺧﻂ‬ ‫ﯾﺴﻤﻰ‬
)٤(‫اﻟﻤﺴﺘﻮى‬ ‫ﻣﯿﻞ‬ ‫زاوﯾﺔ‬ ‫ﻗﯿﺎس‬ ‫اﯾﺠﺎد‬ ‫ﯾﻤﻜﻦ‬‫ھـ‬ ‫ﺣﺎ‬ ‫ﺣﯿﺚ‬ ‫ھـ‬ ‫اﻻﻓﻘﻰ‬ ‫ﻋﻠﻰ‬=
)٥(‫ﻷﺳﻔﻞ‬ ‫ﻣﯿﻞ‬ ‫أﻛﺒﺮ‬ ‫ﺧﻂ‬ ‫اﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫اﻻوﻟﻰ‬ ‫ﻣﺮﻛﺒﺘﯿﻦ‬ ‫اﻟﻰ‬ ‫اﻟﺠﺴﻢ‬ ‫وزن‬ ‫ﻗﻮة‬ ‫ﺗﺤﻠﯿﻞ‬ ‫ﯾﻤﻜﻦ‬
)‫وﺣﺎھـ‬(‫ﺗﻜﻮن‬ ‫و‬ ‫ﻷﺳﻔﻞ‬ ‫اﻟﻤﺴﺘﻮى‬ ‫ﻋﻠﻰ‬ ‫ﻋﻤﻮدى‬ ‫اﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫اﻟﺜﺎﻧﯿﺔ‬ ‫ﺗﻜﻮن‬)‫ھـ‬ ‫ﺣﺘﺎ‬ ‫و‬(
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:ُ‫ﺣ‬‫ﻠﻠ‬‫ﺖ‬‫ﻣﻘﺪارھﺎ‬ ‫ﻗﻮة‬١٠٠‫ﻧﯿﻮﺗﻦ‬‫ﻣﺮﻛﺒﺘﯿﻦ‬ ‫إﻟﻰ‬‫ﺑﺰاوﯾﺔ‬ ‫اﻻﻓﻘﻰ‬ ‫ﻋﻠﻰ‬ ‫أوﻟﮭﻤﺎ‬ ‫ﯾﻤﯿﻞ‬ ‫اﺗﺠﺎھﯿﻦ‬ ‫ﻓﻰ‬
‫ﻗﯿﺎﺳﮭﺎ‬٣٠٥
‫و‬‫ﻗﯿﺎﺳﮭﺎ‬ ‫ﺑﺰاوﯾﺔ‬ ‫اﻻﺧﺮى‬٤٥٥
‫اﻻﺧﺮى‬ ‫اﻟﻨﺎﺣﯿﺔ‬ ‫ﻓﻰ‬
ً‫ﺗﺤﻠﯿﺎ‬ ‫اﻟﻤﺮﻛﺒﺘﯿﻦ‬ ‫ھﺎﺗﯿﻦ‬ ‫ﻣﻘﺪار‬ ‫أوﺟﺪ‬.
‫اﻟﺤﻞ‬:‫ق‬١= = =٧٣٫٢‫ﻧﯿﻮﺗﻦ‬
‫ق‬٢===٥١٫٨‫ﻧﯿﻮﺗﻦ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــ‬
‫ﻣﺜﺎل‬:‫ﺣﻠﻠ‬‫ﺖ‬‫ﻗﻮة‬‫ﻣﻘﺪارھﺎ‬١٠‫؟‬٣‫ﻧﯿﻮﺗﻦ‬‫ﻣﺮﻛﺒﺘﯿﻦ‬ ‫إﻟﻰ‬‫ﻣﺘﻌﺎﻣﺪﯾﻦ‬‫إ‬ ‫ﻣﻘﺪار‬‫ﺣﺪھﻤﺎ‬١٥‫ﻧﯿﻮﺗﻦ‬
‫اﻷﺧﺮى‬ ‫اﻟﻤﺮﻛﺒﺔ‬ ‫ﻣﻘﺪار‬ ‫ﻓﻤﺎ‬.
‫اﻟﺤﻞ‬:‫اﻟﻤﻘﺪار‬ ‫اﻟﻤﻌﻠﻮﻣﺔ‬ ‫اﻟﻤﺮﻛﺒﺔ‬ ‫أن‬ ‫ﻧﻔﺮض‬)‫ق‬١(‫ھـ‬ ‫ﻗﯿﺎﺳﮭﺎ‬ ‫ﺑﺰاوﯾﺔ‬ ‫اﻟﻘﻮة‬ ‫إﺗﺠﺎه‬ ‫ﻋﻠﻰ‬ ‫ﺗﻤﯿﻞ‬
B‫ق‬١=١٠‫؟‬٣‫ﺣﺘﺎ‬‫ھـ‬
B١٥=١٠‫؟‬٣×‫ھـ‬ ‫ﺣﺘﺎ‬B‫ھـ‬ ‫ﺣﺘﺎ‬==B‫ھـ‬=٣٠٥
‫ا‬
‫ه‬
‫ر‬
‫ه‬
‫و‬
‫ب‬ ‫ج‬
‫اﻟﻤﺴﺘﻮى‬ ‫ارﺗﻔﺎع‬
‫اﻟﻤﺴﺘﻮى‬ ‫ﻃﻮل‬
٣٠
٤٥
١٠٠
‫ق‬١
‫ق‬٢
١٠٠‫ﺣﺎ‬٤٥
‫ﺣﺎ‬٧٥
١٠٠‫ﺣﺎ‬٣٠
‫ﺣﺎ‬٧٥
١٥
١٠‫؟‬٣
‫ح‬‫ﺣﺎ‬‫ه‬٢
‫ﺣﺎ‬)‫ه‬١+‫ه‬٢(
‫ح‬‫ﺣﺎ‬‫ه‬١
‫ﺣﺎ‬)‫ه‬١+‫ه‬٢(
‫؟‬٣
٢

18. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
18
B‫اﻷﺧﺮى‬ ‫اﻟﻤﺮﻛﺒﺔ‬ ‫ﻣﻘﺪار‬‫ق‬٢=١٠‫؟‬٣‫ﺣﺘﺎ‬٣٠
=٥‫؟‬٣‫ﻧﯿﻮﺗﻦ‬
‫آﺧﺮ‬ ‫ﺣﻞ‬:‫ح‬=‫؟‬‫ق‬١
٢
"+"‫ق‬"٢
٢
"
B)١٠‫؟‬٣(٢
) =١٥(٢
+‫ق‬٢
٢
B‫ق‬٢
٢
=٧٥B‫ق‬٢=٥‫؟‬٣‫ﻧﯿﻮﺗﻦ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﻣﻘﺪارھﺎ‬ ‫ﻗﻮة‬١٠٠‫اﻟﻐﺮﺑﻰ‬ ‫اﻟﺸﻤﺎل‬ ‫اﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫ﺗﻌﻤﻞ‬ ‫ﺟﻢ‬ ‫ث‬.‫اﺗﺠﺎھﻰ‬ ‫ﻓﻰ‬ ‫ﻣﺮﻛﺒﺘﯿﮭﻤﺎ‬ ‫اﺣﺴﺐ‬
‫اﻟﻐﺮب‬ ‫و‬ ‫اﻟﺸﻤﺎل‬.
‫اﻟﺤﻞ‬:
‫ق‬١=١٠٠‫ﺣﺘﺎ‬٤٥=١٠٠×=٥٠‫؟‬٢‫ﻧﯿﻮﺗﻦ‬
‫ق‬٢=١٠٠‫ﺣﺎ‬٤٥=١٠٠×=٥٠‫؟‬٢‫ﻧﯿﻮﺗﻦ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﻣﻘﺪارھﺎ‬ ‫ﻗﻮة‬ ‫ﺣﻠﻞ‬‫ق‬‫ﻗﯿﺎﺳﮭﺎ‬ ‫ﺑﺰاوﯾﺔ‬ ‫اﻟﻘﻮة‬ ‫ﻋﻠﻰ‬ ‫أوﻟﮭﻤﺎ‬ ‫ﯾﻤﯿﻞ‬ ‫اﺗﺠﺎھﯿﻦ‬ ‫ﻓﻰ‬ ‫ﻧﯿﻮﺗﻦ‬٣٠٥
‫و‬‫ﺑ‬ ‫اﻷﺧﺮ‬‫ﻗﯿﺎﺳﮭﺎ‬ ‫ﺰاوﯾﺔ‬٤٥٥
‫اﻟﻤﺮﻛﺒﺘﯿﻦ‬ ‫اﺣﺪى‬ ‫ﻣﻘﺪار‬ ‫ﻛﺎن‬ ‫ﻓﺈذا‬ ‫اﻻﺧﺮى‬ ‫اﻟﺠﮭﺔ‬ ‫ﻓﻰ‬٧٫٣‫ﻧﯿﻮﺗﻦ‬
‫أوﺟﺪ‬‫ق‬
‫اﻟﺤﻞ‬:A‫ق‬١=
٧٫٣=B‫ق‬=T١٠‫ﻧﯿﻮﺗﻦ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﺣﻠﻞ‬‫ﻣﻘﺪارھﺎ‬ ‫ﻗﻮة‬٣٠‫ﻣﺮﻛﺒﺘ‬ ‫اﻟﻰ‬ ‫اﻟﺸﻤﺎل‬ ‫اﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫ﺗﺆﺛﺮ‬ ‫ﻧﯿﻮﺗﻦ‬‫ﺗﻌﻤﻞ‬ ‫اﺣﺪاھﻤﺎ‬ ‫ﻣﺘﻌﺎﻣﺪﺗﯿﻦ‬ ‫ﯿﻦ‬
‫ﻓﻰ‬‫ﻗﯿﺎﺳﮭﺎ‬ ‫ﺑﺰاوﯾﺔ‬ ‫اﻟﺸﺮق‬ ‫ﺷﻤﺎل‬ ‫إﺗﺠﺎه‬٣٠٥
‫ھـ‬
١٠‫؟‬٣
‫ق‬١
‫ق‬٢
٤٥
١٠٠
‫ق‬١
‫ق‬٢
‫اﻟﻐﺮب‬
‫اﻟﺸﻤﺎل‬
١
‫؟‬٢
١
‫؟‬٢
‫ق‬‫ﺣﺎ‬٤٥
‫ﺣﺎ‬١٠٥
٧٫٣‫ﺣﺎ‬١٠٥
‫ﺣﺎ‬٤٥
٣٠
‫ق‬
‫ق‬١
‫ق‬٢
٤٥
‫ق‬‫ﺣﺎ‬‫ه‬٢
‫ﺣﺎ‬)‫ه‬١+‫ه‬٢(

19. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
19
‫اﻟﺤﻞ‬:‫اﻟﻤﻌﻠﻮم‬ ‫اﻻﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫اﻟﻤﺮﻛﺒﺔ‬=٣٠‫ﺣﺘﺎ‬٦٠=٣٠×
=١٥‫ﻧﯿﻮﺗﻦ‬
‫اﻟﻤﻌﻠﻮم‬ ‫اﻻﺗﺠﺎه‬ ‫ﻋﻠﻰ‬ ‫اﻟﻌﻤﻮدى‬ ‫اﻻﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫اﻟﻤﺮﻛﺒﺔ‬
=٣٠‫ﺣﺎ‬٦٠=٣٠×
=١٥‫؟‬٣‫ﻧﯿﻮﺗﻦ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﻣﺴﺘﻮى‬‫ﻃﻮﻟﮫ‬ ‫ﻣﺎﺋﻞ‬٥٠‫ارﺗﻔﺎﻋﮫ‬ ‫و‬ ‫م‬٤٠‫وزﻧﮫ‬ ‫ﺟﺴﻢ‬ ‫ﻋﻠﯿﮫ‬ ‫وﺿﻊ‬ ‫م‬٥٠‫ﻛﺠﻢ‬ ‫ث‬
‫أوﺟﺪ‬‫ﻋﻠﯿﮫ‬ ‫اﻟﻌﻤﻮدى‬ ‫اﻻﺗﺠﺎه‬ ‫و‬ ‫ﻟﻠﻤﺴﺘﻮى‬ ‫ﻣﯿﻞ‬ ‫أﻛﺒﺮ‬ ‫ﺧﻂ‬ ‫اﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫اﻟﻮزن‬ ‫ﻣﺮﻛﺒﺘﻲ‬ ‫ﻣﻘﺪار‬.
‫اﻟﺤﻞ‬:
‫ﻣﯿﻞ‬ ‫أﻛﺒﺮ‬ ‫ﺧﻂ‬ ‫اﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫اﻟﻤﺮﻛﺒﺔ‬=٥٠‫ھـ‬ ‫ﺣﺎ‬
=٥٠×
=٤٠‫ﻛﺠﻢ‬ ‫ث‬
‫اﻟﻌﻤﻮدى‬ ‫اﻻﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫اﻟﻤﺮﻛﺒﺔ‬=٥٠‫ھـ‬ ‫ﺣﺘﺎ‬
=٥٠×=٣٠‫ﻛﺠﻢ‬ ‫ث‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــ‬
‫أن‬ ‫ﺗﺬﻛﺮ‬:
١(‫اﻟﺠﺎﺳﺊ‬ ‫اﻟﺠﺴﻢ‬:
‫ﺑﺸﻜﻠ‬ ‫ﯾﺤﺘﻔﻆ‬ ‫اﻟﺬى‬ ‫اﻟﺠﺴﻢ‬ ‫ھﻮ‬‫ﮫ‬‫ﺧﺎرﺟﯿﺔ‬ ‫ﻋﻮاﻣﻞ‬ ‫ﺗﺄﺛﯿﺮ‬ ‫ﺗﺤﺖ‬ ‫وﻗﻊ‬ ‫إذا‬ ‫ﺗﺸﻮه‬ ‫دون‬.
٢(‫اﻟﺘﻌﻠﯿﻖ‬ ‫ﺑﻨﻘﻄﺔ‬ ‫اﻟﻤﺎر‬ ‫اﻟﺮأﺳﻲ‬ ‫اﻟﺨﻂ‬ ‫داﺋﻤﺎ‬ ‫ﺑﮭﺎ‬ ‫ﯾﻤﺮ‬ ‫اﻟﺘﻰ‬ ‫اﻟﻨﻘﻄﺔ‬ ‫ھﻰ‬ ‫اﻟﺠﺎﺳﺊ‬ ‫اﻟﺠﺴﻢ‬ ‫ﺛﻘﻞ‬ ‫ﻣﺮﻛﺰ‬
‫أى‬ ‫ﻣﻦ‬ ‫اﻟﺠﺴﻢ‬ ‫ﯾﻌﻠﻖ‬ ‫ﻋﻨﺪﻣﺎ‬‫ﻣﺜﻼ‬ ‫ﻋﻠﯿﮫ‬ ‫ﻧﻘﻄﺔ‬
‫أ‬(‫اﻟﺠﺴﻢ‬ ‫ھﺬا‬ ‫ﻣﺮﻛﺰ‬ ‫ﻓﯿﮭﺎ‬ ‫ﯾﻘﻊ‬ ‫اﻟﺘﻰ‬ ‫اﻟﻨﻘﻄﺔ‬ ‫ھﻰ‬ ‫ﻣﺘﺠﺎﻧﺲ‬ ‫و‬ ‫ﻣﻨﺘﻈﻢ‬ ‫ﻛﺮورى‬ ‫ﺟﺴﻢ‬ ‫ﺛﻘﻞ‬ ‫ﻣﺮﻛﺰ‬
‫ب‬(‫اﻟﻘﻀﯿﺐ‬ ‫ھﺬا‬ ‫ﻣﻨﺘﺼﻒ‬ ‫ھﻮ‬ ‫اﻟﻜﺜﺎﻓﺔ‬ ‫و‬ ‫اﻟﺴﻤﻚ‬ ‫ﻣﻨﺘﻈﻢ‬ ‫ﻗﻀﯿﺐ‬ ‫ﺛﻘﻞ‬ ‫ﻣﺮﻛﺰ‬.
١
٢
‫؟‬٣
٢٣٠
٣٠
‫اﻟﺸﺮق‬
٣٠٦٠
٥٠‫م‬
‫ه‬
٥٠
‫ه‬
٤٠‫م‬
‫ھـ‬
٤
٣
٥
٤
٥
٣
٥

20. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
20
]١[‫ﻣﻘﺪارھﺎ‬ ‫ﻗﻮة‬ ‫ﺣﻠﻞ‬١٢‫ﺗﺆﺛﺮ‬ ‫إﺣﺪاھﻤﺎ‬ ‫ﻣﺮﻛﺒﺘﯿﻦ‬ ‫اﻟﻰ‬ ‫اﻟﺸﺮﻗﻰ‬ ‫اﻟﺸﻤﺎل‬ ‫اﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫ﺗﺆﺛﺮ‬ ‫ﻛﺠﻢ‬ ‫ث‬
‫واﻻ‬ ‫اﻟﺸﺮق‬ ‫ﻧﺤﻮ‬‫اﻟﻐﺮﺑﻰ‬ ‫اﻟﺸﻤﺎل‬ ‫ﻧﺤﻮ‬ ‫ﺧﺮى‬.‫اﻟﻤﺮﻛﺒﺘﯿﻦ‬ ‫ﻣﻘﺪارھﺎﺗﯿﻦ‬ ‫أوﺟﺪ‬.
]٢[‫ﻣﻘﺪارھﺎ‬ ‫ﻗﻮة‬ ‫ﺣﻠﻞ‬٤٠‫ﺑﺰاوﯾﺔ‬ ‫اﻻﻓﻘﻰ‬ ‫ﻋﻠﻰ‬ ‫ﯾﻤﯿﻞ‬ ‫اﺣﺪھﻤﺎ‬ ‫ﻣﺘﻌﺎﻣﺪﯾﻦ‬ ‫اﺗﺠﺎھﯿﻦ‬ ‫ﻓﻰ‬ ‫ﻧﯿﻮﺗﻦ‬٦٠٥
‫أﺳﻔﻞ‬ ‫اﻟﻰ‬.
]٣[‫وزﻧﮫ‬ ‫ﻣﻘﺪار‬ ‫ﺟﺴﻢ‬٢٠‫ﻣﻮﺿﻮع‬ ‫ﻧﯿﻮﺗﻦ‬‫ﻗﯿﺎﺳﮭﺎ‬ ‫ﺑﺰاوﯾﺔ‬ ‫اﻻﻓﻘﻲ‬ ‫ﻋﻠﻰ‬ ‫ﯾﻤﯿﻞ‬ ‫ﻣﺴﺘﻮى‬ ‫ﻋﻠﻰ‬٣٠
‫اﻟﻮزن‬ ‫ﻣﺮﻛﺒﺘﻲ‬ ‫اﺣﺴﺐ‬)‫و‬(‫ﻋﻠﯿﺔ‬ ‫اﻟﻌﻤﻮدى‬ ‫اﻻﺗﺠﺎه‬ ‫و‬ ‫ﻟﻠﻤﺴﺘﻮى‬ ‫ﻣﯿﻞ‬ ‫أﻛﺒﺮ‬ ‫ﺧﻂ‬ ‫اﺗﺠﺎه‬ ‫ﻓﻰ‬
]٤[‫ﻣﻘﺪارھﺎ‬ ‫ﻗﻮة‬‫ق‬‫اﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫ﺗﺆﺛﺮ‬٣٠‫اﺣﺪاھﻤﺎ‬ ‫ﻣﺘﻌﺎﻣﺪﯾﻦ‬ ‫ﻣﺮﻛﺒﺘﯿﻦ‬ ‫اﻟﻰ‬ ‫ﺣﻠﻠﺖ‬ ‫اﻟﺸﺮق‬ ‫ﺟﻨﻮب‬
‫ﻣﻘﺪارھﺎ‬ ‫و‬ ‫اﻟﺸﺮق‬ ‫ﻧﺤﻮ‬ ‫ﺗﺆﺛﺮ‬٢٥‫؟‬٣‫ﺟﻢ‬ ‫ث‬.‫أوﺟﺪ‬‫ق‬‫اﻻﺧﺮى‬ ‫اﻟﻤﺮﻛﺒﺔ‬ ‫اﺗﺠﺎه‬ ‫و‬ ‫ﻣﻘﺪار‬ ‫و‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﻌﻠﻮﻣﺔ‬ ‫ﻗﻮة‬ ‫ﺗﺤﻠﯿﻞ‬ ‫ﻋﻠﻰ‬ ‫ﺗﻤﺎرﯾﻦ‬

21. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
21

22. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
22
*‫اﯾﺠ‬‫ﺑﯿﺎﻧﯿﺎ‬ ‫ﻗﻮى‬ ‫ﻋﺪة‬ ‫ﻣﺤﺼﻠﺔ‬ ‫ﺎد‬:
‫ﻣﺜﺎل‬:
‫اﻟﺤﻞ‬:
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫أن‬ ‫ﺗﺬﻛﺮ‬:

23. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
23
*‫ﻣﺴﺘﻮﯾﺔ‬ ‫ﻗﻮى‬ ‫ﻋﺪة‬ ‫ﻣﺤﺼﻠﺔ‬‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﻣﺘﻼﻗﯿﺔ‬ ‫و‬)‫ﺗﺤﻠﯿﻠﯿﺎ‬(:
‫اﻟﻤﻌﻄﺎه‬ ‫اﻟﻘﻮى‬ ‫ﻛﺎﻧﺖ‬ ‫إذا‬:
‫ق‬١]=‫ق‬١،‫ه‬١[،‫ق‬٢]=‫ق‬٢،‫ه‬٢[،٠٠٠٠٠
‫اﻟﻤﻮﺟﺒﯿﻦ‬ ‫اﻻﺗﺠﺎھﯿﻦ‬ ‫ﻓﻰ‬ ‫ﻣﺮﻛﺒﺘﯿﻦ‬ ‫اﻟﻰ‬ ‫اﻟﻘﻮى‬ ‫ھﺬه‬ ‫ﻣﻦ‬ ‫ﻗﻮة‬ ‫ﻛﻞ‬ ‫ﺗﺤﻠﻞ‬
‫ھﻤﺎ‬ ‫ﺗﻜﻮﻧﺎن‬ ‫و‬ ‫اﻻﺣﺪاﺛﯿﺎت‬ ‫ﻟﻤﺤﻮرى‬‫ﺳﺲ‬،‫ﺻﺺ‬‫اﻟﺘﺮﺗﯿﺐ‬ ‫ﻋﻠﻰ‬
‫ح‬=)‫ﻣﺤـ‬‫ر‬‫ق‬‫ر‬‫ھـ‬ ‫ﺣﺘﺎ‬‫ر‬(‫ﺳﺲ‬) +‫ﻣﺤــ‬‫ر‬‫ق‬‫ر‬‫ﺣ‬‫ھـ‬ ‫ﺎ‬‫ر‬(‫ﺻﺺ‬
=‫ﺳﺲ‬ ‫س‬+‫ﺻﺺ‬ ‫ص‬] =‫ح‬،‫ه‬[
‫أن‬ ‫أى‬:‫ح‬٢
=‫س‬٢
+‫ص‬٢
،‫ح‬=‫؟‬‫س‬٢
+""‫ص‬"٢
"
‫ھـ‬ ‫ﻇﺎ‬ ،=‫ھـ‬ ‫ﺣﯿﺚ‬g]٠،٢‫ط‬]
‫ﻻﺣﻆ‬:‫ا‬‫ﺑﯿﻦ‬ ‫ﻟﻔﺮق‬‫س‬،‫ﺳﺲ‬
‫س‬=‫ﻟﻤﺮﻛﺒﺎت‬ ‫اﻟﺠﺒﺮى‬ ‫اﻟﻤﺠﻤﻮع‬‫اﻟﺴﯿﻨﺎت‬ ‫ﻟﻤﺤﻮر‬ ‫اﻟﻤﻮﺟﺐ‬ ‫اﻻﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫اﻟﻘﻮى‬
‫ﺳﺲ‬=‫اﻻﺗ‬ ‫ﻓﻰ‬ ‫وﺣﺪة‬ ‫ﻣﺘﺠﮫ‬ ‫ھﻮ‬‫اﻟﺴﯿﻨﺎت‬ ‫ﻟﻤﺤﻮر‬ ‫اﻟﻤﻮﺟﺐ‬ ‫ﺠﺎه‬‫ﻛﺬﻟﻚ‬ ‫و‬‫ص‬،‫ﺻﺺ‬
‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
*‫اﻟﻔﺮﻋﯿﺔ‬ ‫و‬ ‫اﻟﺮﯾﺌﺴﯿﺔ‬ ‫اﻻﺗﺠﺎھﺎت‬ ‫ﺗﻤﺜﯿﻞ‬:
‫ص‬
‫س‬
‫اﻟﺸﻤﺎل‬
٤٥‫اﻟﻐﺮب‬
‫اﻟﺸﺮﻗﻰ‬ ‫اﻟﺠﻨﻮب‬
‫اﻟﺸﺮق‬
‫اﻟﺠﻨﻮب‬
٤٥
‫اﻟﺸﺮﻗﻰ‬ ‫اﻟﺸﻤﺎل‬‫اﻟﻐﺮﺑﻰ‬ ‫اﻟﺸﻤﺎل‬
‫اﻟﻐﺮﺑﻰ‬ ‫اﻟﺠﻨﻮب‬
٤٥ ٤٥
٣٠٥
‫ﺷﻤﺎل‬‫اﻟﺸﺮق‬
٣٠
٦٠
٦٠٥
‫ﺟﻨﻮب‬‫اﻟﻐﺮب‬
‫ھـ‬١
‫ق‬٣
‫س‬
‫ص‬
‫ق‬١
‫ق‬٢
‫ھـ‬٢

24. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
24
‫ﻣﺜﺎل‬:‫ﻣﻘﺎدﯾﺮھﺎ‬ ‫ﻗﻮى‬ ‫أﺛﺮت‬١٦،٤،٨‫؟‬٣،٤‫؟‬٣‫اﺗﺠﺎھﺎت‬ ‫ﻓﻰ‬ ‫ﻣﺎدﯾﺔ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﻧﯿﻮﺗﻦ‬
، ‫اﻟﺸﺮق‬٦٠٥
، ‫اﻟﺸﺮق‬ ‫ﺷﻤﺎل‬٦٠٥
‫اﻟﺘﺮﺗﯿﺐ‬ ‫ﻋﻠﻰ‬ ‫اﻟﺠﻨﻮب‬ ، ‫اﻟﺠﻨﻮب‬ ‫ﻏﺮب‬
‫أوﺟﺪ‬‫اﺗﺠﺎه‬ ‫و‬ ‫ﻣﻘﺪار‬‫اﻟﻘﻮى‬ ‫ھﺬه‬ ‫ﻣﺤﺼﻠﺔ‬.
‫اﻟﺤﻞ‬:
‫اﻟﻘﻮة‬١٦٤٨‫؟‬٣٤‫؟‬٣
‫اﻟﺰاوﯾﺔ‬٠٥
٦٠٢١٠٢٧٠
‫س‬=١٦‫ﺣﺘﺎ‬٠+٤‫ﺣﺘﺎ‬٦٠+٨‫؟‬٣‫ﺣﺘﺎ‬٢١٠+٤‫؟‬٣‫ﺣﺘﺎ‬٢٧٠=٦
‫ص‬=١٦‫ﺣﺎ‬٠+٤‫ﺣﺎ‬٦٠+٨‫؟‬٣‫ﺣﺎ‬٢١٠+٤‫؟‬٣‫ﺣﺎ‬٢٧٠=‫ــ‬٦‫؟‬٣
‫ح‬=)٦‫ــ‬ ،٦‫؟‬٣(B‫ح‬=‫؟‬)٦(٢
"+")"‫ــ‬٦"‫؟‬"٣("٢
"=‫؟‬١٤٤"=١٢‫ﻧﯿﻮﺗﻦ‬
‫ھـ‬ ‫ﻇﺎ‬= ==‫ــ‬‫؟‬٣
A‫س‬<٠،‫ص‬>٠B‫ق‬)‫ھـ‬p= (٣٠٠
B‫اﻟﻤﺤﺼﻠﺔ‬=١٢‫وﺗﺼﻨﻊ‬ ‫ﻧﯿﻮﺗﻦ‬٣٠٠٥
‫ا‬ ‫ﻣﻊ‬‫اﻟﺴﯿﻨﺎت‬ ‫ﻟﻤﺤﻮر‬ ‫اﻟﻤﻮﺟﺐ‬ ‫ﻻﺗﺠﺎه‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫اﻟﻘﻮى‬ ‫أﺛﺮت‬٧،‫ق‬،‫ﻙ‬،٤‫؟‬٣،١١‫؟‬٣‫و‬ ‫ﻣﺎدﯾﺔ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﻛﺠﻢ‬ ‫ث‬‫ﻗﯿﺎس‬ ‫ﻛﺎن‬
‫اﻟﺜﺎﻧﯿﺔ‬ ‫و‬ ‫اﻷوﻟﻰ‬ ‫اﻟﻘﻮﺗﯿﻦ‬ ‫إﺗﺠﺎھﻲ‬ ‫ﺑﯿﻦ‬ ‫اﻟﺰاوﯾﺔ‬٦٠٥
‫اﻟﺜﺎﻟﺜﺔ‬ ‫و‬ ‫اﻟﺜﺎﻧﯿﺔ‬ ‫ﺑﯿﻦ‬ ،٦٠٥
‫ﺑﯿﻦ‬ ،‫اﻟﺜﺎﻟﺜﺔ‬
‫اﻟﺮاﺑﻌﺔ‬ ‫و‬٩٠٥
‫اﻟﺨﺎﻣﺴﺔ‬ ‫و‬ ‫اﻟﺮاﺑﻌﺔ‬ ‫ﺑﯿﻦ‬ ‫و‬ ،٦٠٥
‫ﺗﺴﺎوى‬ ‫اﻟﻘﻮى‬ ‫ﻣﺤﺼﻠﺔ‬ ‫ھﺬه‬ ‫ﻛﺎﻧﺖ‬ ‫ﻓﺈذا‬
٤‫؟‬٣‫و‬‫اﻟﺠﻨﻮب‬ ‫اﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫ﺗﺆﺛﺮ‬‫ﻣﻦ‬ ‫ﻛﻞ‬ ‫ﻗﯿﻤﺔ‬ ‫أوﺟﺪ‬‫ﻕ‬،‫ﻙ‬
‫اﻟﺤﻞ‬:
A‫ﻓ‬ ‫ﺗﺆﺛﺮ‬ ‫اﻟﻤﺤﺼﻠﺔ‬‫اﻟﺠﻨﻮب‬ ‫اﺗﺠﺎه‬ ‫ﻰ‬
B‫س‬=‫ص‬ ، ‫ﺻﻔﺮ‬=‫ــ‬٤‫؟‬٣
‫اﻟﻘﻮة‬٧‫ﻕ‬‫ﻙ‬٤‫؟‬٣١١‫؟‬٣
‫اﻟﺰاوﯾﺔ‬٠٥
٦٠١٢٠٢١٠٢٧٠
‫ص‬
‫س‬
٦٠
٤‫؟‬٣
٤
١٦
٨‫؟‬٣
٦٠
‫ﯾﺴﺘﺨﺪم‬
‫اﻵﻟﺔ‬
‫ﻓﻰ‬ ‫اﻟﺤﺎﺳﺒﺔ‬
‫اﻟﻨﺎﺗﺞ‬ ‫اﯾﺠﺎد‬
‫ص‬
‫س‬
‫ـ‬‫ـ‬-٦‫؟‬٣
٦
‫ص‬
٦٠
‫س‬
١١‫؟‬٣
٤‫؟‬٣
٦٠
‫ك‬
٧٦٠
٩٠
‫ق‬

25. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
25
‫س‬=٧‫ﺣﺘﺎ‬٠+‫ﻕ‬‫ﺣﺘﺎ‬٦٠+‫ﻙ‬‫؟‬٣‫ﺣﺘﺎ‬١٢٠+٤‫؟‬٣‫ﺣﺘﺎ‬٢١٠
+١١‫ة‬٣‫ﺣﺘﺎ‬٢٧٠=‫ﺻﻔﺮ‬
B‫ﻕ‬‫ــ‬‫ﻙ‬=‫ــ‬٢)١(
‫ص‬=٧‫ﺣﺎ‬٠+‫ﻕ‬‫ﺣﺎ‬٦٠+‫ﻙ‬‫؟‬٣‫ﺣﺘﺎ‬١٢٠+٤‫؟‬٣‫ﺣﺘﺎ‬٢١٠+١١‫ة‬٣‫ﺣﺘﺎ‬٢٧٠
=‫ــ‬٤‫؟‬٣
B‫ﻕ‬+‫ﻙ‬=١٨)٢(‫اﻟﻤﻌﺎدﻟﺘﯿﻦ‬ ‫ﺑﺤﻞ‬ ‫و‬)١(،)٢(‫ﻧﺠﺪ‬:
‫ﻕ‬=٨، ‫ﻛﺠﻢ‬ ‫ث‬‫ﻙ‬=١٠‫ﻛﺠﻢ‬ ‫ث‬
‫ــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫د‬ ‫ج‬ ‫ب‬ ‫ا‬‫ﻓﯿﮫ‬ ‫ﻣﺴﺘﻄﯿﻞ‬‫ب‬ ‫ا‬=٦، ‫ﺳﻢ‬‫ج‬ ‫ب‬=٨‫ھـ‬ ‫ﻧﻘﻄﺔ‬ ‫أﺧﺬت‬ ‫ﺳﻢ‬g‫ج‬‫ب‬"‫ﺑﺤﯿﺚ‬
‫ه‬‫ـ‬‫ھ‬‫ب‬=٦‫ﻣﻘﺎدﯾﺮھﺎ‬ ‫ﻗﻮى‬ ‫أﺛﺮت‬ ، ‫ﺳﻢ‬١،١٠،٥‫؟‬٢،٣‫ﻓﻰ‬ ‫ﺟﻢ‬ ‫ث‬‫ء‬ ‫ا‬،‫ج‬‫ا‬،
‫ه‬ ‫ا‬،‫ب‬ ‫ا‬‫اﻟﻘﻮى‬ ‫ھﺬه‬ ‫ﻣﺤﺼﻠﺔ‬ ‫ﻣﻘﺪار‬ ‫أوﺟﺪ‬ ‫اﻟﺘﺮﺗﯿﺐ‬ ‫ﻋﻠﻰ‬.
‫اﻟﺤﻞ‬:
‫اﻟﻘﻮة‬٣٥‫؟‬٢١٠١
‫اﻟﺰاوﯾﺔ‬٠٥
٤٥‫ى‬٩٠
‫س‬=٣‫ﺣﺘﺎ‬٠+٥‫؟‬٢‫ﺣﺘﺎ‬٤٥+١٠‫ى‬ ‫ﺣﺘﺎ‬+١×‫ﺣﺘﺎ‬٩٠
=٣×١+٥‫؟‬٢×+١٠×+١×٠=١٤
‫ص‬=٣‫ﺣﺎ‬٠+٥‫؟‬٢‫ﺣﺎ‬٤٥+١٠‫ى‬ ‫ﺣﺎ‬+١×‫ﺣﺎ‬٩٠=١٤
٦‫ﺳﻢ‬‫ا‬ ‫ب‬
‫ج‬‫ء‬
‫ى‬
‫ى‬
٤٥
‫ه‬
٦‫ﺳﻢ‬
١٠
٥‫؟‬٢
‫ى‬٤٥
١
٣
‫ى‬
٨
٦
١٠
٦
١٠
١
‫؟‬٢

26. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
26
B‫ح‬=)١٤،١٤(B‫ح‬=‫؟‬)١٤(٢
"+")""١٤"(٢
"=‫؟‬١٩٦"×٢"=١٤‫؟‬٢
،‫ھـ‬ ‫ﻇﺎ‬= = =١A‫س‬<٠‫ص‬ ،<٠B‫ھـ‬=٤٥٥
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﻣﻘﺎدﯾﺮھﺎ‬ ‫ﻗﻮى‬ ‫أﺛﺮت‬‫ق‬،٤‫؟‬٣،١٢‫؟‬٣،٣٦‫ﻛﺎﻧﺖ‬ ‫و‬ ‫ﻣﺎدﯾﺔ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﺟﻢ‬ ‫ث‬
، ‫اﻟﺸﻤﺎل‬ ‫اﺗﺠﺎھﺎت‬ ‫ﻓﻰ‬ ‫اﻷﺧﯿﺮة‬ ‫ﻗﻮى‬ ‫اﻟﺜﻼث‬٦٠، ‫اﻟﺸﻤﺎل‬ ‫ﻏﺮب‬٦٠‫ﻋﻠﻰ‬ ‫اﻟﺸﺮق‬ ‫ﺟﻨﻮب‬
‫اﻟﺘﺮﺗﯿﺐ‬‫اﻟﻘﻮى‬ ‫ھﺬه‬ ‫ﻣﺤﺼﻠﺔ‬ ‫ﻛﺎﻧﺖ‬ ‫ﻓﺈذا‬=٨‫اﻟﺸﺮق‬ ‫اﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫ﺟﻢ‬ ‫ث‬‫و‬ ‫ﻣﻘﺪار‬ ‫ﻓﻌﯿﻦ‬‫اﺗﺠﺎه‬‫ق‬
‫اﻟﺤﻞ‬:
‫اﻟﻘﻮة‬‫ق‬٤‫؟‬٣١٢‫؟‬٣٣٦
‫اﻟ‬‫ﺰاوﯾﺔ‬‫ھـ‬٩٠١٥٠٣٠٠
A‫ح‬=٨‫اﻟﺸﺮق‬ ‫اﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫ﺟﻢ‬ ‫ث‬B‫ح‬) =٨،٠(
B٨=‫ق‬‫ھـ‬ ‫ﺣﺘﺎ‬+٤‫؟‬٣‫ﺣﺘﺎ‬٩٠+١٢‫؟‬٣‫ﺣﺘﺎ‬١٥٠+٣٦‫ﺣﺘﺎ‬٣٠٠
٨=‫ق‬‫ھـ‬ ‫ﺣﺘﺎ‬+٤‫؟‬٣×٠+١٢‫؟‬٣×+٣٦×
B‫ق‬‫ھـ‬ ‫ﺣﺘﺎ‬=٨)١(
،٠=‫ق‬‫ھـ‬ ‫ﺣﺎ‬+٤‫؟‬٣‫ﺣﺎ‬٩٠+١٢‫؟‬٣‫ﺣﺎ‬١٥٠+٣٦‫ﺣﺎ‬٣٠٠
B٠=‫ق‬‫ھـ‬ ‫ﺣﺎ‬+٤‫؟‬٣+٦‫؟‬٣‫ــ‬١٨‫؟‬٣
B‫ق‬‫ھـ‬ ‫ﺣﺎ‬=٨‫؟‬٣)٢(
‫ﺑﻘﺴﻤﺔ‬)٢(‫ﻋﻠﻰ‬)١(B=
G‫ظ‬‫ا‬‫ھـ‬=‫؟‬٣B‫ق‬)‫ھـ‬p= (٦٠٥
B‫ق‬‫ﺣﺘﺎ‬٦٠=٨G‫ق‬×=٨
B‫ق‬=١٦
‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﻣﻘﺎدﯾﺮھﺎ‬ ‫ﻗﻮى‬ ‫أﺛﺮت‬‫ق‬،‫ك‬،٦‫اﻟﺸﻤﺎل‬ ، ‫اﻟﺸﺮق‬ ‫اﺗﺠﺎھﺎت‬ ‫ﻓﻰ‬ ‫ﻣﺎدﯾﺔ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﻧﯿﻮﺗﻦ‬
،٣٠‫اﻟﺘﺮﺗﯿﺐ‬ ‫ﻋﻠﻰ‬ ‫اﻟﻐﺮب‬ ‫ﺟﻨﻮب‬‫اﻟﻘﻮى‬ ‫ﻣﺤﺼﻠﺔ‬ ‫ﻛﺎﻧﺖ‬ ‫ﻓﺈذا‬=٨‫اﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫ﺗﻌﻤﻞ‬ ‫و‬ ‫ﻧﯿﻮﺗﻦ‬
٣٠٥
‫اﻟﺸﺮق‬ ‫ﺷﻤﺎل‬‫ﻗﯿﻤﺔ‬ ‫أوﺟﺪ‬‫ق‬،‫ك‬
‫ص‬
‫س‬
١٤
١٤
٣٦
٤‫؟‬٣
٦٠
١٢‫؟‬٣
٦٠
‫؟‬٣
٢
١
٢
‫ق‬‫ھـ‬ ‫ﺣﺎ‬
‫ق‬‫ھـ‬ ‫ﺣﺘﺎ‬
٨‫؟‬٣
٨
١
٢

27. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
27
‫اﻟﺤﻞ‬:
‫ح‬) =٨‫ﺣﺘﺎ‬٣٠،٨‫ﺣﺎ‬٣٠) = (٤‫؟‬٣،٤(
٤‫؟‬٣=‫ق‬‫ﺣﺘﺎ‬٠+‫ك‬‫ﺣﺘﺎ‬٩٠+٦‫ﺣﺘﺎ‬٢١٠
=‫ق‬-٣‫؟‬٣B‫ق‬=٧‫؟‬٣
٤=‫ق‬‫ﺣﺎ‬٠+‫ك‬‫ﺣﺎ‬٩٠+٦‫ﺣﺎ‬٢١٠=٠+‫ك‬-٣B‫ك‬=٧
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ء‬ ‫ج‬‫ب‬‫ا‬‫ﺿﻠﻌﮫ‬ ‫ﻃﻮل‬ ‫ﻣﺮﺑﻊ‬١٢‫ھـ‬ ، ‫ﺳﻢ‬g‫ﺟـ‬ ‫ب‬"‫ھـ‬ ‫ب‬ ‫ﺣﯿﺚ‬=٤‫؟‬٣‫ﻗﻮى‬ ‫أﺛﺮت‬ ‫ﺳﻢ‬
٥،٤‫؟‬٣،٣‫؟‬٢،٢‫؟‬٣‫ب‬ ‫اﻻﺗﺠﺎھﺎت‬ ‫ﻓﻰ‬ ‫ﻣﺎدﯾﺔ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﻧﯿﻮﺗﻦ‬‫ا‬،‫ﺍ‬، ‫ھـ‬‫ج‬‫ا‬
‫ا‬ ‫ء‬‫اﻟﺘﺮﺗﯿﺐ‬ ‫ﻋﻠﻰ‬.‫ھﺬ‬ ‫ﻣﺤﺼﻠﺔ‬ ‫اﺗﺠﺎه‬ ‫و‬ ‫ﻣﻘﺪار‬ ‫أوﺟﺪ‬‫اﻟﻘﻮى‬ ‫ه‬.
‫اﻟﺤﻞ‬:
‫اﻟﻘﻮة‬‫ق‬‫ك‬
٦
‫اﻟﺰاوﯾﺔ‬٠٩٠٢١٠
‫اﻟﻘﻮة‬٢‫؟‬٣٥٣‫؟‬٢٤‫؟‬٣
‫اﻟﺰاوﯾﺔ‬٢٧٠١٨٠٤٥‫ى‬
‫ا‬ ‫ب‬
‫ج‬‫ء‬
‫ه‬
‫ى‬
٣‫؟‬٢
‫ى‬٤٥٥
٢‫؟‬٣
٤‫؟‬٣
‫ى‬
٤‫؟‬٣
١٢
٨‫؟‬٣
‫ق‬
٣٠
‫ك‬
٦
‫ح‬=٨
٣٠

28. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
28
‫س‬=٢‫؟‬٣‫ﺣﺘﺎ‬٢٧٠+٥‫ﺣﺘﺎ‬١٨٠+٣‫؟‬٢‫ﺣﺘﺎ‬٤٥+٤‫؟‬٣‫ى‬ ‫ﺣﺘﺎ‬
=٢‫؟‬٣×٠+٥×)-١+ (٣‫؟‬٢×+٤‫؟‬٣×=-٥+٣+٦=٤
‫ص‬=٢‫؟‬٣‫ﺣﺎ‬٢٧٠+٥‫ﺣﺎ‬١٨٠+٣‫؟‬٢‫ﺣﺎ‬٤٥+٤‫؟‬٣‫ى‬ ‫ﺣﺎ‬
=٢‫؟‬٣×)-١+ (٥×٠+٣‫؟‬٢×+٤‫؟‬٣×
=-٢‫؟‬٣+٣+٢‫؟‬٣=٣
B‫ح‬=)٤،٣(B‫ح‬=‫؟‬١٦+"٩"=‫؟‬٢٥=٥
‫ھـ‬ ‫ﻇﺎ‬= =‫ق‬ ،)‫ھـ‬p= (٥٢/
٣٦٥
‫اﻟﻤﺤﺼﻠﺔ‬=٥‫ﻗﯿﺎﺳﮭﺎ‬ ‫زاوﯾﺔ‬ ‫ﯾﺼﻨﻊ‬ ‫ﻋﻤﻠﮭﺎ‬ ‫ﺧﻂ‬ ‫و‬ ‫ﻧﯿﻮﺗﻦ‬٥٢/
٣٦٥
‫ﻣﻊ‬‫ب‬ ‫ا‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ب‬ ‫ا‬‫ء‬ ‫ج‬‫ﻣﻘﺎدﯾﺮھﺎ‬ ‫ﻗﻮى‬ ‫أﺛﺮت‬ ‫ﻣﻨﺘﻈﻢ‬ ‫ﺷﻜﻞ‬٦،٢‫؟‬٣،٦،٢‫؟‬٣‫اﻻﺗﺠﺎھﺎت‬ ‫ﻓﻰ‬ ‫ﻧﯿﻮﺗﻦ‬
‫ب‬ ‫ا‬،‫ﺝ‬ ‫ﺍ‬،‫ﺍ‬‫ء‬،‫ه‬ ‫ا‬‫اﻟﺘﺮﺗﯿﺐ‬ ‫ﻋﻠﻰ‬.ً‫ﺗﺎﻣﺎ‬ ً‫ﺎ‬‫ﺗﻌﯿﯿﻨ‬ ‫اﻟﻤﺤﺼﻠﺔ‬ ‫ﻋﯿﻦ‬
‫اﻟﺤﻞ‬:
‫س‬=٦‫ﺣﺘﺎ‬٠+٢‫؟‬٣‫ﺣﺘﺎ‬٣٠+٦‫ﺣﺘﺎ‬٦٠+٢‫؟‬٣‫ﺣﺘﺎ‬٩٠
=٦×١+٢‫؟‬٣×+٦×+٢‫؟‬٣×٠
=٦+٣+٣+٠=١٢
‫ص‬=٦‫ﺣﺎ‬٠+٢‫؟‬٣‫ﺣﺎ‬٣٠+٦‫ﺣﺎ‬٦٠+٢‫؟‬٣‫ﺣﺎ‬٩٠
=٦×٠+٢‫؟‬٣×+٦×+٢‫؟‬٣×١
=٠+‫؟‬٣+٣‫؟‬٣+٢‫؟‬٣=٦‫؟‬٣
‫اﻟﻘﻮة‬٦٢‫؟‬٣٦٢‫؟‬٣
‫اﻟﺰاوﯾﺔ‬٠٣٠٦٠٩٠
١
‫؟‬٢
‫؟‬٣
٢
١
‫؟‬٢
١
٢
‫ص‬
‫س‬
٤
٣
٣٠
٣٠
٣٠
‫و‬
‫ا‬ ‫ب‬
‫ج‬
‫ء‬‫ه‬
١
٢
‫؟‬٣
٢
١
٢
‫؟‬٣
٢

29. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
29
‫ح‬=)١٢،٦‫؟‬٣(B‫ح‬=‫؟‬)١٢(٢
"+")""١٢"(٢
"=‫؟‬٢٥٢"=٦‫؟‬٧
‫ھـ‬ ‫ﻇﺎ‬= = =B‫ق‬)‫ھـ‬p(T٤١٥
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﻣﻘﺎدﯾﺮھﺎ‬ ‫ﻗﻮى‬ ‫اﺛﺮت‬٢‫ق‬،٣‫ق‬،٤‫ق‬‫ﻣﻮازﯾﺔ‬ ‫اﺗﺠﺎھﺎت‬ ‫ﻓﻰ‬ ‫ﻣﺎدﯾﺔ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﻧﯿﻮﺗﻦ‬
ً‫ﺎ‬‫واﺗﺠﺎھ‬ ‫ﻣﻘﺪارا‬ ‫اﻟﻘﻮى‬ ‫ھﺬه‬ ‫ﻣﺤﺼﻠﺔ‬ ‫أوﺟﺪ‬ ‫واﺣﺪ‬ ‫دورى‬ ‫ﺗﺮﺗﯿﺐ‬ ‫ﻓﻰ‬ ‫اﻻﺿﻼع‬ ‫ﻣﺘﺴﺎوى‬ ‫ﻣﺜﻠﺚ‬ ‫ﻷﺿﻼع‬
‫اﻟﺤﻞ‬:
‫ﻓﻰ‬ ‫ﺗﺆﺛﺮ‬ ‫اﻟﻘﻮى‬ ‫أن‬ ‫ﻧﻔﺮض‬)‫و‬(‫و‬ ، ‫م‬ ‫و‬ ، ‫وس‬ ‫اﻻﺗﺠﺎھﺎت‬ ‫ﻓﻰ‬‫ن‬
‫ﻟﻼﺗﺠﺎھﺎت‬ ‫اﻟﻤﻮازﯾﺔ‬‫ب‬ ‫ا‬‫ﺟـ‬ ، ‫ﺟـ‬ ‫ب‬ ،‫ا‬‫اﻟﺘﺮﺗﯿﺐ‬ ‫ﻋﻠﻰ‬
‫ﻓﻰ‬∆‫ج‬‫ب‬ ‫ا‬‫اﻟﻘﻮى‬ ‫ﺑﺘﺤﻠﯿﻞ‬ ‫و‬ ‫اﻻﺿﻼع‬ ‫اﻟﻤﺘﺴﺎوى‬
B‫س‬=٢‫ق‬‫ﺣﺘﺎ‬٠+٣‫ق‬‫ﺣﺘﺎ‬١٢٠+٤‫ق‬‫ﺣﺘﺎ‬٢٤٠
=٢‫ق‬×١+٣‫ق‬×+٤‫ق‬×=‫ق‬
‫ص‬ ،=٢‫ق‬‫ﺣﺎ‬٠+٣‫ق‬‫ﺣﺎ‬١٢٠+٤‫ق‬‫ﺣﺎ‬٢٤٠
=٢‫ق‬×٠+٣‫ق‬×+٤‫ق‬×)-(
=-‫ق‬
B‫ح‬٢
=‫س‬٢
+‫ص‬٢
) =‫ق‬(٢
) +-‫ق‬(٢
=‫ق‬٢
+‫ق‬٢
=٣‫ق‬٢
B‫ح‬=‫؟‬٣‫ق‬‫ﻧﯿﻮﺗﻦ‬‫ﻋﻠﻰ‬ ‫ﺗﻤﯿﻞ‬ ‫و‬‫ب‬‫ا‬‫ﻗﯿﺎﺳﮭﺎ‬ ‫ﺑﺰاوﯾﺔ‬٢١٠٥
‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬
‫اﻟﻘﻮة‬٢‫ق‬٣‫ق‬٤‫ق‬
‫اﻟﺰاوﯾﺔ‬٠١٢٠٢٤٠
‫ص‬
‫س‬
٦‫؟‬٣
١٢
‫؟‬٣
٢
‫ج‬
‫ا‬ ‫ب‬
٦٠
٤‫ق‬
٦٠
٢‫ق‬
٣‫ق‬
‫ﺻﺺ‬
‫م‬
‫و‬
‫ن‬
‫ﺳﺲ‬
‫ب‬
-١
٢
-١
٢
-٣
٢
‫؟‬٣
٢
‫؟‬٣
٢
‫؟‬٣
٢
-٣
٢
‫؟‬٣
٢
٩
٤
٣
٤

30. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
30
‫ﻣﺜﺎل‬:‫ء‬‫ج‬‫ب‬ ‫ا‬‫ق‬ ‫ﻓﯿﮫ‬ ‫أﺿﻼع‬ ‫ﻣﺘﻮازى‬)‫ب‬‫ء‬‫ا‬‫ﻒ‬‫ﻓ‬= (٩٠٥
،‫ب‬‫ا‬=٢‫ء‬‫ا‬‫اﻟﺘﻰ‬ ‫اﻟﻘﻮى‬ ‫أﺛﺮت‬
‫ﻣﻘﺎدﯾﺮھﺎ‬٣،١٢،١٥‫؟‬٣‫ﻓﻰ‬ ‫ﻧﯿﻮﺗﻦ‬‫ج‬‫ء‬،‫ء‬‫ا‬‫ب‬ ،‫ء‬‫اﻟﻤﺤﺼﻠﺔ‬ ‫اﺗﺠﺎه‬ ‫و‬ ‫ﻣﻘﺪار‬ ‫أوﺟﺪ‬.
‫اﻟﺤﻞ‬:
‫اﻟﺤﻞ‬ ‫أﻛﻤــــــــﻞ‬٠٠٠٠٠٠٠٠٠٠٠٠٠
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
]١[‫ﻛﺎﻧﺖ‬ ‫إذا‬‫ق‬١=٥‫ﺳﺲ‬+٣‫ﺻﺺ‬،‫ق‬٢=‫ا‬‫ﺳﺲ‬+٦‫ﺻﺺ‬،‫ق‬٣=-١٤‫ﺳﺲ‬+‫ب‬‫ﺻﺺ‬
‫اﻟﻤﺤﺼﻠﺔ‬ ‫ﻛﺎﻧﺖ‬ ‫و‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﻣﺘﻼﻗﯿﺔ‬ ‫و‬ ‫ﻣﺴﺘﻮﯾﺔ‬ ‫ﻗﻮى‬ ‫ﺛﻼث‬‫ح‬=)١٠‫؟‬٢،١٣٥٥
(
‫ﻗﯿﻤﺔ‬ ‫أوﺟﺪ‬‫ا‬،‫ب‬
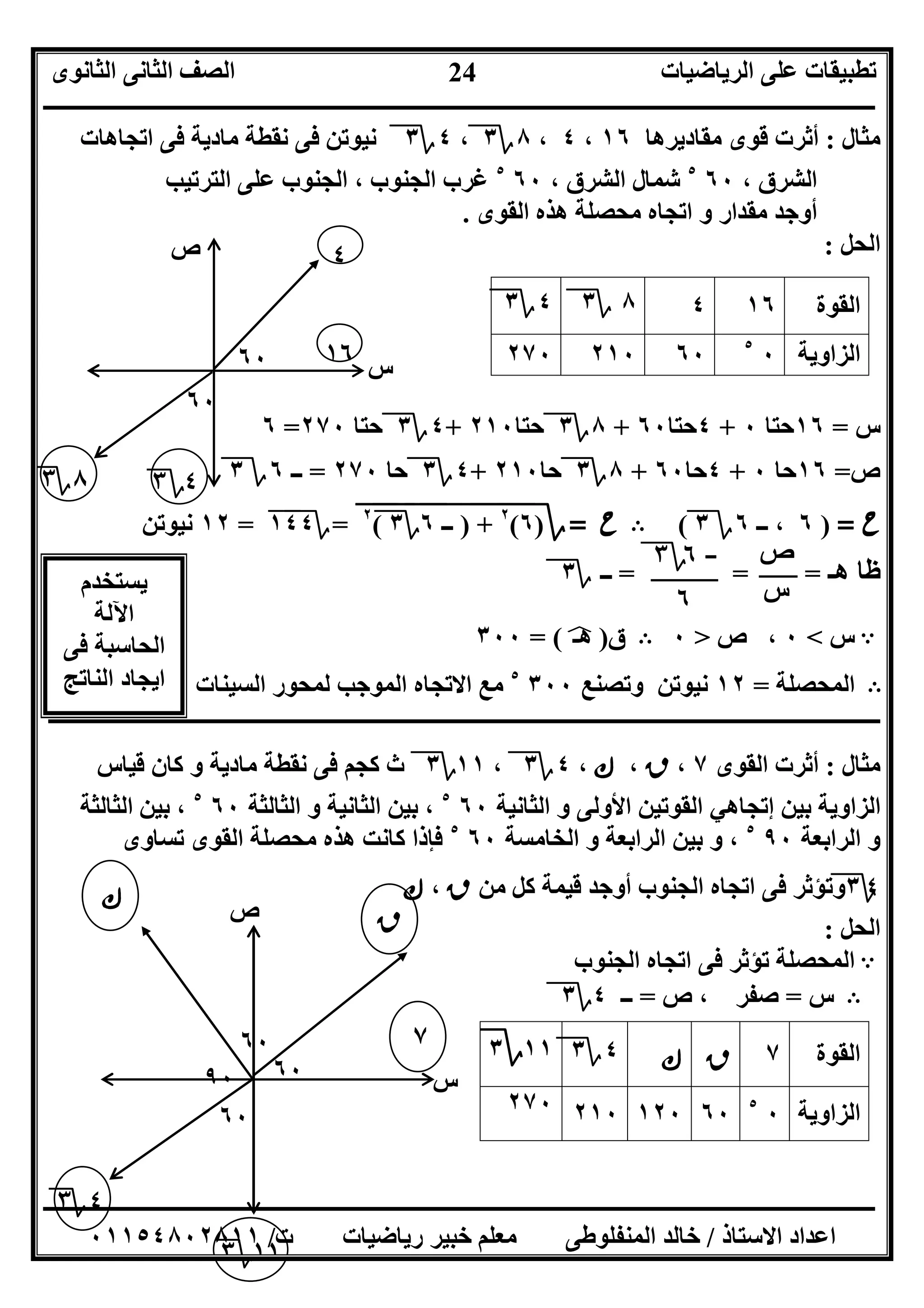
]٢[‫ﻣﻘﺎدﯾﺮھﺎ‬ ‫اﻟﺘﻰ‬ ‫اﻟﻘﻮى‬ ‫أﺛﺮت‬٧،٤‫؟‬٣،٨،٦،٩‫؟‬٣‫اﻻوﻟﻰ‬ ‫ﻣﺎدﯾﺔ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﺟﻢ‬ ‫ث‬
‫اﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫اﻟﺜﺎﻧﯿﺔ‬ ، ‫اﻟﺸﺮق‬ ‫اﺗﺠﺎه‬ ‫ﻓﻰ‬٣٠٥
‫اﻟﺜﺎﻟﺜﺔ‬ ، ‫اﻟﺸﺮق‬ ‫ﺷﻤﺎل‬٦٠٥
، ‫اﻟﻐﺮب‬ ‫ﺷﻤﺎل‬
‫اﻟﺮاﺑﻌﺔ‬٣٠٥
، ‫اﻟﺠﻨﻮب‬ ‫ﻏﺮب‬‫اﻟﻤﺤﺼﻠﺔ‬ ‫أوﺟﺪ‬ ‫اﻟﺠﻨﻮب‬ ‫اﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫اﻟﺨﺎﻣﺴﺔ‬.
]٣[‫ﻣﻘﺎدﯾﺮھﺎ‬ ‫اﻟﺘﻰ‬ ‫اﻟﻤﺴﺘﻮﯾﺔ‬ ‫اﻟﻘﻮى‬ ‫أﺛﺮت‬٣،٦،٩‫؟‬٣،١٢‫ﻛﺎن‬ ‫و‬ ‫ﻣﺎدﯾﺔ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﻛﺠﻢ‬ ‫ث‬
‫اﻟﺜﺎﻧﯿﺔ‬ ‫و‬ ‫اﻷوﻟﻰ‬ ‫ﺑﯿﻦ‬ ‫اﻟﺰاوﯾﺔ‬ ‫ﻗﯿﺎس‬٦٠‫اﻟﺜﺎﻟﺜﺔ‬ ‫و‬ ‫اﻟﺜﺎﻧﯿﺔ‬ ‫ﺑﯿﻦ‬ ‫و‬٩٠‫اﻟﺮاﺑﻌﺔ‬ ‫و‬ ‫اﻟﺜﺎﻟﺜﺔ‬ ‫وﺑﯿﻦ‬
١٥٠‫ﻣﺤﺼﻠﺔ‬ ‫اﺗﺠﺎه‬ ‫و‬ ‫ﻣﻘﺪار‬ ‫أوﺟﺪ‬‫اﻻرﺑﻌﺔ‬ ‫اﻟﻘﻮى‬.
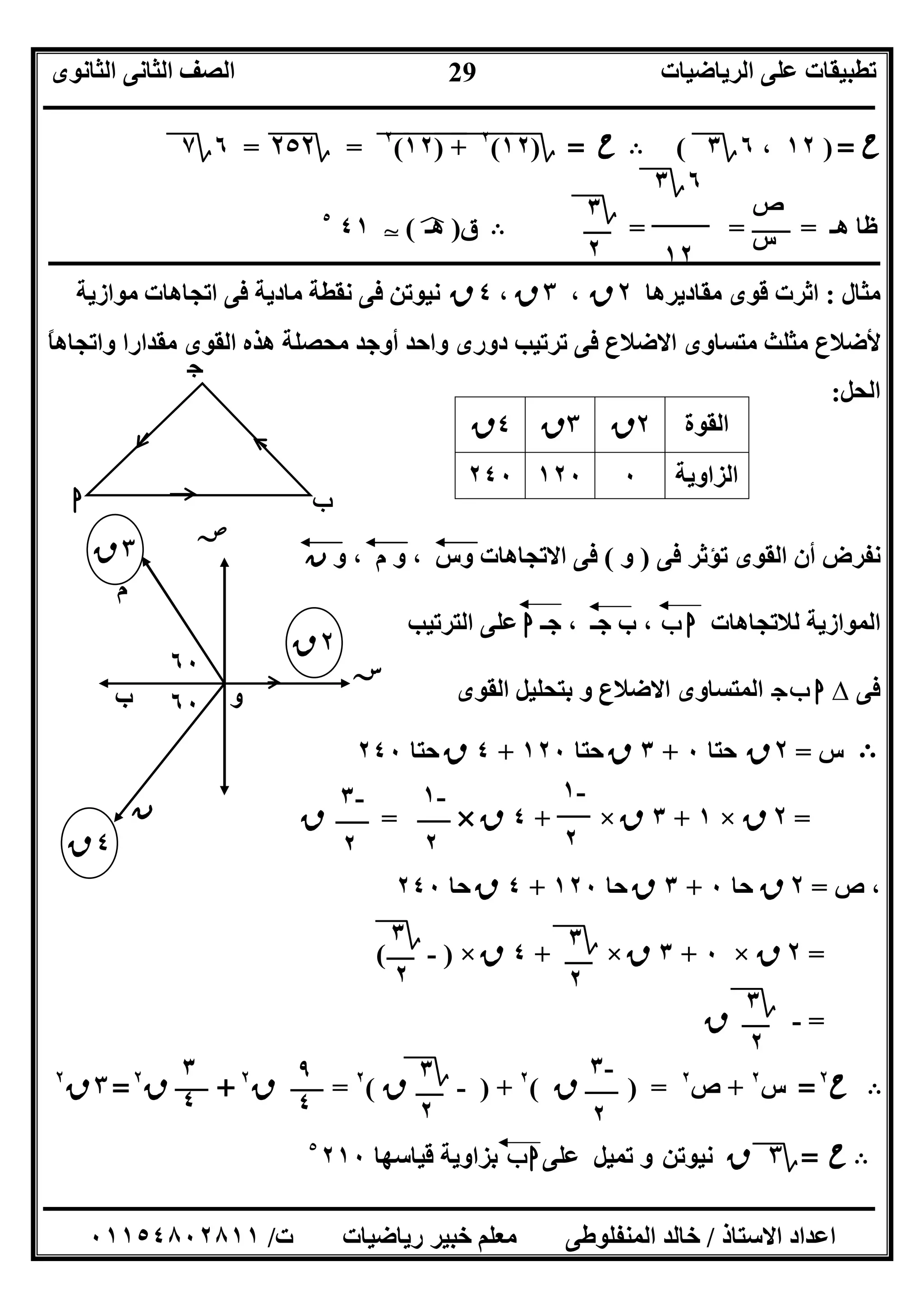
]٤[‫ج‬‫ب‬‫ا‬‫ﻣﻘﺎدﯾﺮھﺎ‬ ‫اﻟﺘﻰ‬ ‫اﻟﻘﻮى‬ ‫أﺛﺮت‬ ‫ﻣﺘﻮﺳﻄﺎﺗﮫ‬ ‫ﺗﻼﻗﻰ‬ ‫ﻧﻘﻄﺔ‬ ‫م‬ ، ‫اﻷﺿﻼع‬ ‫ﻣﺘﺴﺎوى‬ ‫ﻣﺜﻠﺚ‬
٦،٨،١٠‫م‬ ، ‫ب‬ ‫م‬ ، ‫ﺟـ‬ ‫م‬ ‫اﻻﺗﺠﺎھﺎت‬ ‫ﻓﻰ‬ ‫ﻣﺎدﯾﺔ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﻧﯿﻮﺗﻦ‬‫ا‬
‫اﻟﻘﻮى‬ ‫ھﺬه‬ ‫ﻣﺤﺼﻠﺔ‬ ‫اﺗﺠﺎه‬ ‫و‬ ‫ﻣﻘﺪار‬ ‫أوﺟﺪ‬.
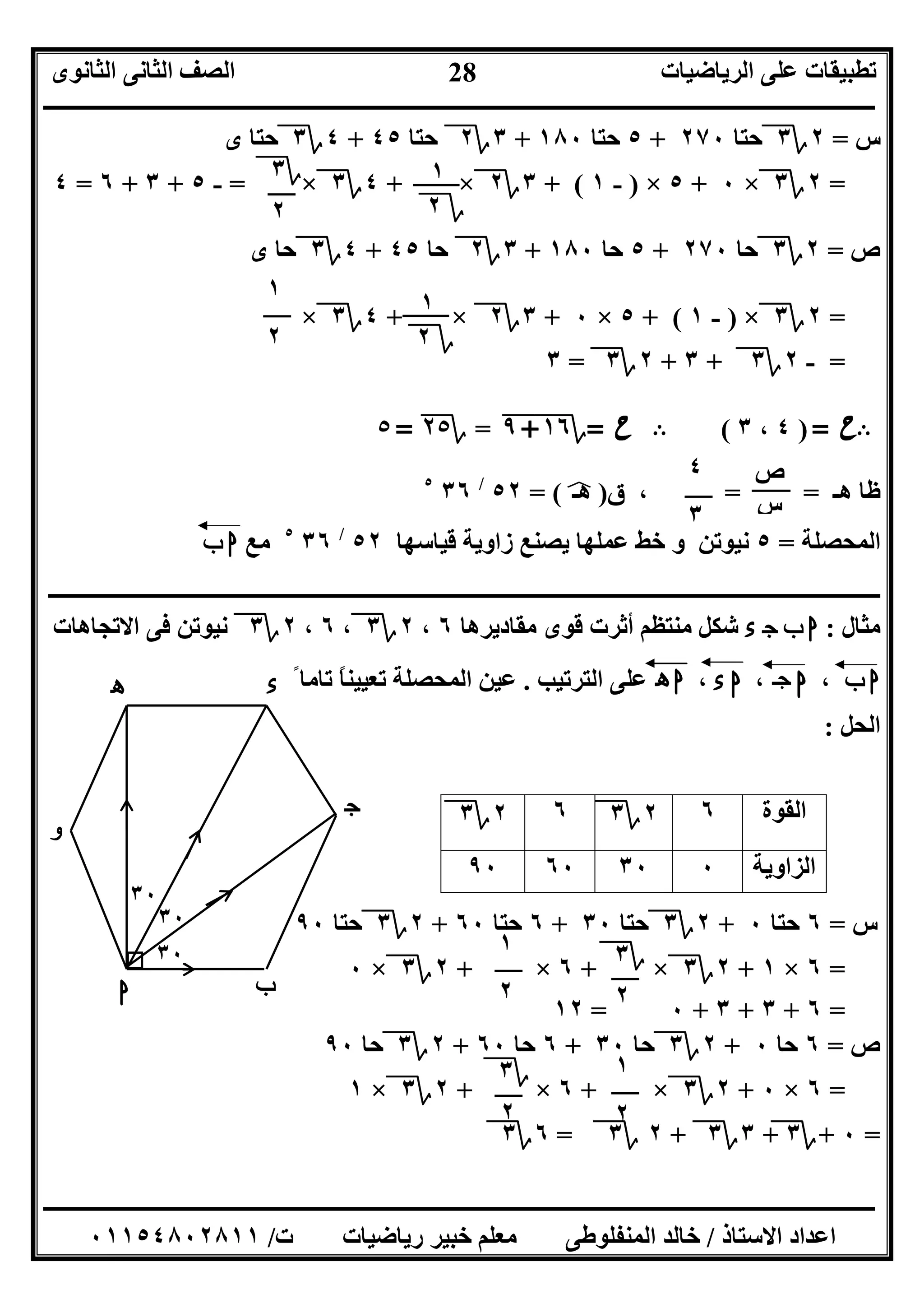
]٥[‫ه‬ ‫ء‬ ‫ج‬ ‫ب‬ ‫ا‬‫و‬‫اﻟﻘﻮى‬ ‫ﺗﺆﺛﺮ‬ ‫ﻣﻨﺘﻈﻢ‬ ‫ﻣﺴﺪس‬٢،٤‫؟‬٣،٨،٢‫؟‬٣،٤‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﻛﺠﻢ‬ ‫ث‬
‫اﻻﺗﺠﺎھﺎت‬ ‫ﻓﻰ‬ ‫ﻣﺎدﯾﺔ‬‫ب‬‫ا‬،‫ج‬‫ا‬،‫ء‬‫ا‬،‫ه‬‫ا‬،‫ا‬‫و‬‫اﻟﻘﻮى‬ ‫ھﺬه‬ ‫ﻣﺤﺼﻠﺔ‬ ‫أوﺟﺪ‬ ‫اﻟﺘﺮﺗﯿﺐ‬ ‫ﻋﻠﻰ‬
‫اﻟﻘﻮة‬٣١٢١٥‫؟‬٣
‫اﻟﺰاوﯾﺔ‬٠٦٠١٥٠
٦٠
‫ا‬ ‫ب‬
‫ج‬‫ء‬
‫؟‬٣١
٢
٣٠
٣٠ ٦٠
١٢
٣
١٥‫؟‬٣
‫ﻗﻮى‬ ‫ﻋﺪة‬ ‫ﻣﺤﺼﻠﺔ‬ ‫ﻋﻠﻰ‬ ‫ﺗﻤﺎرﯾﻦ‬

31. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
31
]٦[‫و‬ ‫ه‬ ‫ء‬ ‫ج‬ ‫ب‬ ‫ا‬‫اﻟﻘﻮى‬ ‫ﺗﺆﺛﺮ‬ ‫أﻗﻄﺎره‬ ‫ﺗﻘﺎﻃﻊ‬ ‫ﻧﻘﻄﺔ‬ ‫ھﻰ‬ ‫م‬ ، ‫ﻣﻨﺘﻈﻢ‬ ‫ﻣﺴﺪس‬٤،١،٤،٥،٢
٣‫اﻻﺗﺠﺎھﺎت‬ ‫ﻓﻰ‬ ‫ﻣﺎدﯾﺔ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﺟﻢ‬ ‫ث‬‫ا‬ ‫م‬‫م‬ ، ‫ﺟـ‬ ‫م‬ ، ‫ب‬ ‫م‬ ،‫ء‬‫و‬ ‫م‬ ، ‫ھـ‬ ‫م‬ ،
‫م‬ ‫اﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫ﺗﺆﺛﺮ‬ ‫أﻧﮭﺎ‬ ‫أﺛﺒﺖ‬ ‫و‬ ‫اﻟﻘﻮى‬ ‫ھﺬه‬ ‫ﻣﺤﺼﻠﺔ‬ ‫ﻣﻘﺪار‬ ‫أوﺟﺪ‬‫ء‬
]٧[‫ء‬ ‫ج‬ ‫ب‬ ‫ا‬‫ﻓﯿﮫ‬ ‫ﻣﺴﺘﻄﯿﻞ‬‫ب‬‫ا‬=٤‫ب‬ ، ‫ﺳﻢ‬‫ﺟـ‬=٣‫اﻟﻘﻮى‬ ‫أﺛﺮت‬ ‫ﺳﻢ‬٢،٥،٣‫ﻓﻰ‬ ‫ﻛﺠﻢ‬ ‫ث‬
‫اﻻﺗﺠﺎھﺎت‬ ‫ﻓﻰ‬ ‫ﻣﺎدﯾﺔ‬ ‫ﻧﻘﻄﺔ‬‫ب‬‫ا‬،‫ج‬‫ا‬،‫ء‬‫ا‬‫اﻟﺘﺮﺗﯿﺐ‬ ‫ﻋﻠﻰ‬.
‫ﻣﯿ‬ ‫زاوﯾﺔ‬ ‫ﻗﯿﺎس‬ ‫و‬ ‫اﻟﻘﻮى‬ ‫ھﺬه‬ ‫ﻣﺤﺼﻠﺔ‬ ‫ﻣﻘﺪار‬ ‫أوﺟﺪ‬‫ﻋﻠﻰ‬ ‫ﻠﮭﺎ‬‫ب‬‫ا‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
*‫اﻟﻤﺪرﺳﺔ‬ ‫ﻛﺘﺎب‬ ‫ﻣﻦ‬ ‫ﺗﻤﺎرﯾﻦ‬:

32. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
32

33. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
33
‫اﻟﻘﻮﺗﯿﻦ‬ ‫ﻣﺤﺼﻠﺔ‬ ‫ﺗﻜﻮن‬=‫ﺻﻔﺮ‬
‫ﻗﺎ‬‫ﻋﺪة‬:‫ﺟﺴﻢ‬ ‫اﺗﺰن‬ ‫إذا‬‫ﺟﺎﺳﺊ‬‫اﻟﻘﻮﺗﺎن‬ ‫ﻛﺎﻧﺖ‬ ‫ﻓﻘﻂ‬ ‫ﻗﻮﺗﯿﻦ‬ ‫ﺗﺄﺛﯿﺮ‬ ‫ﺗﺤﺖ‬:
١(‫اﻟﻤﻘﺪار‬ ‫ﻓﻰ‬ ‫ﻣﺘﺴﺎوﯾﺘﯿﻦ‬٢(‫اﻻﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫ﻣﺘﻀﺎدﺗﯿﻦ‬٣(‫واﺣﺪة‬ ‫اﺳﺘﻘﺎﻣﺔ‬ ‫ﻋﻠﻰ‬ ‫ﻋﻤﻠﮭﻤﺎ‬ ‫ﺧﻂ‬
‫ﻗﻮﺗﯿﻦ‬ ‫ﺗﺄﺛﯿﺮ‬ ‫ﺗﺤﺖ‬ ‫ﺟﺴﻢ‬ ‫ﺗﻮازن‬ ‫أﻣﺜﻠﺔ‬ ‫ﻣﻦ‬:
)١(‫ﺛﻘﻞ‬ ‫ﻋﻠﻖ‬ ‫إذا‬)‫و‬(‫ﯾﺘﺰن‬ ‫ﻓﺈﻧﮫ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻣﻦ‬ ‫ﺧﻔﯿﻒ‬ ‫ﺑﺤﺒﻞ‬
‫ﻗﻮﺗﯿﻦ‬ ‫ﺗﺄﺛﯿﺮ‬ ‫ﺗﺤﺖ‬‫اﻟﺤﺒﻞ‬ ‫ﻓﻰ‬ ‫واﻟﺸﺪ‬ ‫اﻟﺠﺴﻢ‬ ‫وزن‬ ‫ھﻤﺎ‬
)٢(‫ﯾﺘﺰن‬ ‫ﻓﺈﻧﮫ‬ ‫أﻣﻠﺲ‬ ‫أﻓﻘﻰ‬ ‫ﻧﻀﺪ‬ ‫ﻋﻠﻰ‬ ‫ﺟﺴﻢ‬ ‫وﺿﻊ‬ ‫إذا‬
‫اﻟﺠﺴﻢ‬ ‫ﻋﻠﻰ‬ ‫اﻟﻨﻀﺪ‬ ‫ﻓﻌﻞ‬ ‫ورد‬ ‫اﻟﻮزن‬ ‫ھﻤﺎ‬ ‫ﻗﻮﺗﯿﻦ‬ ‫ﺗﺄﺛﯿﺮ‬ ‫ﺗﺤﺖ‬
‫ھﺎﻣﺔ‬ ‫ﻣﻼﺣﻈﺎت‬:
)١(‫ﻧﻔﺲ‬ ‫وﻓﻰ‬ ‫ﻣﺘﻀﺎدﯾﻦ‬ ‫إﺗﺠﺎھﯿﻦ‬ ‫وﻓﻰ‬ ‫اﻟﻤﻘﺪار‬ ‫ﻓﻰ‬ ‫ﻣﺘﺴﺎوﯾﺘﺎن‬ ‫ﻗﻮﺗﺎن‬ ‫ﻣﺘﻤﺎﺳﻚ‬ ‫ﺟﺴﻢ‬ ‫ﻋﻠﻰ‬ ‫أﺛﺮ‬ ‫إذا‬
‫اﻟﺨﻂ‬‫ﻓ‬ ‫اﻟﻤﺴﺘﻘﯿﻢ‬‫اﻟﺤﺮﻛﺔ‬ ‫أو‬ ‫اﻟﺴﻜﻮن‬ ‫ﻧﺎﺣﯿﺔ‬ ‫ﻣﻦ‬ ‫اﻟﺠﺴﻢ‬ ‫ﻋﻠﻰ‬ ‫ﺗﺄﺛﯿﺮ‬ ‫أى‬ ‫ﻟﮭﻤﺎ‬ ‫ﯾﻜﻮن‬ ‫ﻻ‬ ‫ﺈﻧﮫ‬
)٢(‫وﻣﺘﻀﺎدة‬ ‫اﻟﻤﻘﺪار‬ ‫ﻓﻰ‬ ‫ﻣﺘﺴﺎوﯾﺔ‬ ‫داﺋﻤﺎ‬ ‫ﺗﻜﻮن‬ ‫أﺧﺮ‬ ‫ﻋﻠﻰ‬ ‫ﺟﺴﻢ‬ ‫ﺗﺄﺛﯿﺮ‬ ‫ﻋﻦ‬ ‫اﻟﻨﺎﺗﺠﺔ‬ ‫اﻟﻤﺘﺒﺎدﻟﺔ‬ ‫اﻟﻘﻮى‬
‫أﻧﮫ‬ ‫ﻋﻠﻰ‬ ‫ﯾﻨﺺ‬ ‫واﻟﺬى‬ ‫ﻟﻨﯿﻮﺗﻦ‬ ‫اﻟﺜﺎﻟﺚ‬ ‫اﻟﻘﺎﻧﻮن‬ ‫ھﻮ‬ ‫وھﺬا‬ ‫اﻻﺗﺠﺎه‬ ‫ﻓﻰ‬
)٣(‫ﻣﻠﺴﺎء‬ ‫ﺑﻜﺮة‬ ‫ﻋﻠﻰ‬ ‫ﺧﻔﯿﻒ‬ ‫ﺧﯿﻂ‬ ‫ﻣﺮ‬ ‫إذا‬‫ﻣﻘﺪار‬ ‫ﻓﺎن‬
‫اﻟﺒﻜﺮة‬ ‫ﻋﻠﻰ‬ ‫ﺑﻤﺮوره‬ ‫ﯾﺘﻐﯿﺮ‬ ‫ﻻ‬ ‫اﻟﺨﯿﻂ‬ ‫ﻓﻰ‬ ‫اﻟﺸﺪ‬
)٤(‫ﻣﻘﺪار‬ ‫ﻓﺈن‬ ‫ﻣﻠﺴﺎء‬ ‫ﺣﻠﻘﺔ‬ ‫ﻓﻰ‬ ‫ﺧﻔﯿﻒ‬ ‫ﺧﯿﻂ‬ ‫ﻣﺮ‬ ‫إذا‬
‫اﻟﺤﻠﻘﺔ‬ ‫داﺧﻞ‬ ‫ﺑﻤﺮوره‬ ‫ﯾﺘﻐﯿﺮ‬ ‫ﻻ‬ ‫اﻟﺨﯿﻂ‬ ‫ﻓﻰ‬ ‫اﻟﺸﺪ‬
‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﻔﺼﻞ‬:‫اﻻﺗــﺰان‬
)١(‫ﻗﻮﺗﯿﻦ‬ ‫ﺗﺄﺛﯿﺮ‬ ‫ﺗﺤﺖ‬ ‫ﺟﺎﺳﺊ‬ ‫ﺟﺴﻢ‬ ‫اﺗﺰان‬
‫اﻻﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫ﻟﮫ‬ ‫وﻣﻀﺎد‬ ‫اﻟﻤﻘﺪار‬ ‫ﻓﻰ‬ ‫ﻟﮫ‬ ‫ﻣﺴﺎو‬ ‫ﻓﻌﻞ‬ ‫رد‬ ‫ﻓﻌﻞ‬ ‫ﻟﻜﻞ‬
‫ش‬
‫و‬
‫و‬
‫ر‬
‫ش‬ ‫ش‬
‫ش‬ ‫ش‬

34. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
34
‫ﻣﺜﺎل‬:
‫اﻟﺤﻞ‬:
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
A‫ق‬١،‫ق‬٢،‫ق‬٣‫واﺣﺪ‬ ‫دورى‬ ‫اﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫ﻗﻮى‬ ‫ﺛﻼث‬
B‫ﻣﺘﺰﻧﺔ‬ ‫اﻟﺜﻼث‬ ‫اﻟﻘﻮى‬
*‫ﻣﻼﺣﻈﺎت‬:
١(‫ﻣﺜﻠﺚ‬ ‫ﻷﺿﻼع‬ ‫أﻃﻮال‬ ‫ﺗﻜﻮن‬ ‫ﻷن‬ ‫ﺗﺼﻠﺢ‬ ‫ﻣﻘﺎدﯾﺮھﺎ‬ ‫ﺗﻜﻮن‬ ‫أن‬ ‫ﯾﺠﺐ‬ ‫اﻟﺜﻼث‬ ‫اﻟﻘﻮى‬ ‫ﺗﺘﺰن‬ ‫ﻟﻜﻰ‬
‫ﻣﺜﻼ‬:‫ﻣﻘﺎدﯾﺮھﺎ‬ ‫اﻟﺘﻰ‬ ‫اﻟﺜﻼث‬ ‫اﻟﻘﻮى‬٤،٣،٧‫اﻻﻋﺪاد‬ ‫ﻷن‬ ‫ﺗﺘﺰن‬ ‫أن‬ ‫ﯾﻤﻜﻦ‬ ‫ﻻ‬ ‫ﻗﻮة‬ ‫وﺣﺪة‬
٤،٣،٧‫ﻷن‬ ‫ﻣﺜﻠﺚ‬ ‫ﻷﺿﻼع‬ ‫أﻃﻮاﻻ‬ ‫ﺗﻜﻮن‬ ‫ﻷن‬ ‫ﺗﺼﻠﺢ‬ ‫ﻻ‬٤+٣<٧
٢(‫اﻟﺼﻔﺮى‬ ‫اﻟﻤﺘﺠﮫ‬ ‫ھﻮ‬ ‫ﻣﺤﺼﻠﺘﮭﺎ‬ ‫ﻣﺘﺠﮫ‬ ‫ﻓﺈن‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﻣﺘﻼﻗﯿﺔ‬ ‫ﻗﻮى‬ ‫ﺛﻼث‬ ‫اﺗﺰﻧﺖ‬ ‫إذا‬
‫ح‬=‫ق‬١+‫ق‬٢+‫ق‬٣=٠
٣(‫ﻣﺴﺎوﯾﺔ‬ ‫ﺗﻜﻮن‬ ‫ﻣﻨﮭﺎ‬ ‫ﻗﻮﺗﯿﻦ‬ ‫أى‬ ‫ﻣﺤﺼﻠﺔ‬ ‫ﻓﺈن‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﻣﺘﻼﻗﯿﺔ‬ ‫و‬ ‫ﻣﺴﺘﻮﯾﺔ‬ ‫ﻗﻮى‬ ‫ﺛﻼث‬ ‫إﺗﺰﻧﺖ‬ ‫إذا‬
‫اﻟﻌﻤﻞ‬ ‫ﺧﻂ‬ ‫ﻧﻔﺲ‬ ‫ﻟﮭﻤﺎ‬ ‫و‬ ‫اﻻﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫ﻟﮭﺎ‬ ‫ﻣﻀﺎدة‬ ‫و‬ ‫اﻟﺜﺎﻟﺜﺔ‬ ‫اﻟﻘﻮة‬ ‫ﻟﻤﻘﺪار‬ ‫اﻟﻤﻘﺪار‬ ‫ﻓﻰ‬.
)٢(‫ﻗﻮى‬ ‫ﺛﻼث‬ ‫ﺗﺄﺛﯿﺮ‬ ‫ﺗﺤﺖ‬ ‫ﺟﺴﻢ‬ ‫إﺗﺰان‬
‫ﻣﺘﻼﻗﯿ‬ ‫و‬ ‫ﻣﺴﺘﻮﯾﺔ‬ ‫ﻗﻮى‬ ‫ﺛﻼث‬ ‫ﺗﻤﺜﯿﻞ‬ ‫أﻣﻜﻦ‬ ‫إذا‬‫ﻣﺄﺧﻮذة‬ ‫ﻣﺜﻠﺚ‬ ‫ﺑﺄﺿﻼع‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﺔ‬‫اﺗﺠﺎه‬ ‫ﻓﻰ‬
‫ﻣ‬ ‫ﺗﻜﻮن‬ ‫اﻟﻘﻮى‬ ‫ھﺬه‬ ‫ﻓﺈن‬ ‫واﺣﺪ‬ ‫دورى‬‫ﺘﺰﻧﺔ‬.
‫ﻗﺎﻋﺪة‬
‫ق‬١
‫ق‬٣
‫ق‬٢
‫ج‬
‫ا‬
‫ب‬

35. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
35
‫أﻧﮫ‬ ‫ﯾﻼﺣﻆ‬‫ﻣﻌﺮﻓﺔ‬ ‫أﻣﻜﻦ‬ ‫إذا‬ ‫ﺗﺴﺘﺨﺪم‬‫اﻟﻘﻮ‬ ‫إﺣﺪى‬ ‫ﻣﻘﺪار‬‫وﻋﻠﻤﺖ‬ ‫اﻟﺜﻼث‬ ‫ى‬‫أﺿﻼع‬ ‫أﻃﻮال‬‫ﻣﺜﻠﺚ‬
‫اﻟﻘﻮى‬)‫اﻟﻨﺴﺒ‬ ‫أو‬‫ﺔ‬‫اﻟﻘﻮى‬ ‫ﻣﺜﻠﺚ‬ ‫أﺿﻼع‬ ‫أﻃﻮال‬ ‫ﺑﯿﻦ‬(
= =
‫اﻟﻤﻘﺎﺑﻞ‬ ‫اﻟﺸﻜﻞ‬ ‫ﻓﻰ‬:
‫ج‬‫ب‬‫ا‬‫اﻟﻘﻮى‬ ‫ﻣﺜﻠﺚ‬:
= =
‫ﻣﻼﺣﻈﺎت‬‫ھﺎﻣﺔ‬:
١(‫اﻟﺜﻼث‬ ‫اﻟﻘﻮى‬ ‫ﻋﻤﻞ‬ ‫ﺧﻄﻮط‬ ‫ﺗﻮازى‬ ‫أﺿﻼﻋﮫ‬ ‫اﻟﺬى‬ ‫اﻟﻤﺜﻠﺚ‬
‫ﯾﺴﻤﻰ‬)‫اﻟﻘﻮى‬ ‫ﻣﺜﻠﺚ‬(
٢(‫أﺿﻼﻋﮫ‬ ‫ﻣﻦ‬ ‫ﺿﻠﻌﺎن‬ ‫ﯾﻜﻮن‬ ‫ﺑﺤﯿﺚ‬ ‫اﻟﻘﻮى‬ ‫ﻣﺜﻠﺚ‬ ‫رﺳﻢ‬ ‫اﻟﻤﻤﻜﻦ‬ ‫ﻣﻦ‬
‫ﺧﻂ‬ ‫ﯾﻮازى‬ ‫اﻟﺜﺎﻟﺚ‬ ‫اﻟﻀﻠﻊ‬ ‫و‬ ‫ﻗﻮﺗﯿﻦ‬ ‫ﻋﻤﻞ‬ ‫ﺧﻄﻰ‬ ‫ﻋﻠﻰ‬ ‫ﻣﺤﻤﻮﻟﯿﻦ‬
‫اﻟﺜﺎﻟﺜﺔ‬ ‫اﻟﻘﻮة‬ ‫ﻋﻤﻞ‬.
٣(‫ﻣﺘﺰ‬ ‫ﻗﻮى‬ ‫ﻟﺜﻼث‬ ‫اﻟﻘﻮى‬ ‫ﻣﺜﻠﺚ‬ ‫ﻛﺎن‬ ‫إذا‬‫ﻛﺎﻧﺖ‬ ‫ﺳﺘﯿﻨﻰ‬ ‫ﺛﻼﺛﯿﻨﻰ‬ ‫ﻣﺜﻠﺚ‬ ‫ھﻮ‬ ‫ﻧﺔ‬
‫أﺿﻼﻋﮫ‬ ‫أﻃﻮال‬ ‫ﺑﯿﻦ‬ ‫اﻟﻨﺴﺒﺔ‬١:٢:‫؟‬٣
٤(‫اﻟﺴﺎﻗﯿﻦ‬ ‫ﻣﺘﺴﺎوى‬ ‫و‬ ‫اﻟﺰاوﯾﺔ‬ ‫ﻗﺎﺋﻢ‬ ‫اﻟﻘﻮى‬ ‫ﻣﺜﻠﺚ‬ ‫ﻛﺎن‬ ‫إذا‬
‫أﺿﻼﻋﮫ‬ ‫ﺑﯿﻦ‬ ‫ﻓﺎﻟﻨﺴﺒﺔ‬١:١:‫؟‬٢
‫ﻣﺜ‬ ‫ورﺳﻢ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﻣﺘﻼﻗﯿﺔ‬ ‫ﻗﻮى‬ ‫ﺛﻼث‬ ‫ﺗﺄﺛﯿﺮ‬ ‫ﺗﺤﺖ‬ ‫ﺟﺴﻢ‬ ‫أﺗﺰن‬ ‫إذا‬‫أﺿﻼﻋﮫ‬ ‫ﻠﺚ‬
‫اﻟﻤﺜﻠﺚ‬ ‫أﺿﻼع‬ ‫أﻃﻮال‬ ‫ﻓﺈن‬ ‫واﺣﺪ‬ ‫دورى‬ ‫أﺗﺠﺎه‬ ‫وﻓﻰ‬ ‫اﻟﻘﻮى‬ ‫ﻋﻤﻞ‬ ‫ﺧﻄﻮط‬ ‫ﺗﻮازى‬
‫اﻟﻤﻨﺎﻇﺮة‬ ‫اﻟﻘﻮى‬ ‫ﻣﻘﺎدﯾﺮ‬ ‫ﻣﻊ‬ ‫ﻣﺘﻨﺎﺳﺒﺔ‬ ‫ﺗﻜﻮن‬
‫ﻗﺎﻋﺪة‬‫اﻟﻘﻮى‬ ‫ﻣﺜﻠﺚ‬
‫ش‬١
‫ب‬ ‫ج‬
‫ش‬٢
‫ا‬‫ب‬
‫و‬
‫ج‬ ‫ا‬
‫ق‬١
‫ج‬‫ب‬
‫ق‬٢
‫ا‬‫ب‬
‫ق‬٣
‫ج‬ ‫ا‬
‫ج‬
‫ا‬
‫ب‬
‫ق‬١
‫ق‬٣
‫ق‬٢
‫؟‬٣
٣٠
٦٠
٤٥
٤٥
١
١
١
٢‫؟‬٢

36. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
36
‫أﻧﮫ‬ ‫ﯾﻼﺣﻆ‬‫اﻟﺜﻼث‬ ‫اﻟﻘﻮى‬ ‫ﺧﻄﻮط‬ ‫ﺑﯿﻦ‬ ‫اﻟﺰواﯾﺎ‬ ‫ﻗﯿﺎﺳﺎت‬ ‫ﻣﻌﺮﻓﺔ‬ ‫أﻣﻜﻦ‬ ‫إذا‬ ‫ﺗﺴﺘﺨﺪم‬
‫اﻟﻘﻮى‬ ‫أﺛﺮت‬ ‫إذا‬‫ق‬١،‫ق‬٢،‫ق‬٣‫ﻣﺎدﯾﺔ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫اﻟﺜﻼث‬
‫ھـ‬ ‫ﻛﺎﻧﺖ‬ ‫و‬١‫ھـ‬ ،٢‫ھـ‬ ،٣‫ﻟﮭﺎ‬ ‫اﻟﻤﻘﺎﺑﻠﺔ‬ ‫اﻟﺰواﯾﺎ‬ ‫ﻗﯿﺎﺳﺎت‬ ‫ھﻰ‬
‫ﻓﺈن‬ ‫اﻟﺘﺮﺗﯿﺐ‬ ‫ﻋﻠﻰ‬:
==
‫ــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﻣﻘﺪاره‬ ‫ﺛﻘﻞ‬ ‫ﻋﻠﻖ‬١٠٠‫ﻃﻮﻟﯿﮭﻤﺎ‬ ‫ﺑﺨﯿﻄﯿﻦ‬ ‫ﺟﻢ‬ ‫ث‬٣٠، ‫ﺳﻢ‬٤٠‫ﺳﻢ‬‫اﻵﺧﺮان‬ ‫اﻟﻄﺮﻓﺎن‬ ‫ﺛﺒﺖ‬ ‫و‬
‫ﻓﻰ‬ ‫ﻟﻠﺨﯿﻄﺎن‬‫ﻧﻘﻄﺘﯿﻦ‬‫ﻣﺘﻌﺎﻣﺪ‬ ‫اﻟﺨﯿﻄﺎن‬ ‫ﻛﺎن‬ ‫ﺑﺤﯿﺚ‬ ‫أﻓﻘﻰ‬ ‫ﺧﻂ‬ ‫ﻣﻦ‬‫ﯾﻦ‬
.‫اﻟﺨﯿﻄﯿﻦ‬ ‫ﻣﻦ‬ ‫ﻛﻼ‬ ‫ﻓﻰ‬ ‫اﻟﺸﺪ‬ ‫ﻣﻘﺪار‬ ‫أوﺟﺪ‬
‫اﻟﺤﻞ‬:A‫ق‬)‫ب‬ ‫ج‬‫ا‬‫ﻒ‬‫ﻓ‬= (٩٠٥
B)‫ب‬‫ا‬(٢
) =‫ج‬‫ا‬(٢
) +‫ج‬‫ب‬(٢
A)‫ب‬‫ا‬(٢
) =٤٠(٢
) +٣٠(٢
B‫ب‬‫ا‬=٥‫ﺳﻢ‬
B‫ھـ‬ ‫ﺣﺎ‬١= =‫ھـ‬ ‫ﺣﺎ‬ ،٢==
‫ﺑﺎﺳﺘﺨﺪ‬‫ﻻﻣﻰ‬ ‫ﻗﺎﻋﺪة‬ ‫ام‬:
= =
= =
B‫ش‬١= ==٦٠‫ﺟﻢ‬ ‫ث‬
‫ﻣﻘﺪار‬ ‫ﻓﺎن‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﻣﺘﻼﻗﯿﺔ‬ ‫ﻗﻮى‬ ‫ﺛﻼث‬ ‫ﺗﺄﺛﯿﺮ‬ ‫ﺗﺤﺖ‬ ‫ﺟﺴﻢ‬ ‫أﺗﺰن‬ ‫إذا‬‫ﻗﻮة‬ ‫ﻛﻞ‬
‫اﻻﺧﺮﯾﯿﻦ‬ ‫اﻟﻘﻮﺗﯿﻦ‬ ‫ﺑﯿﻦ‬ ‫اﻟﻤﺤﺼﻮرة‬ ‫اﻟﺰاوﯾﺔ‬ ‫ﺟﯿﺐ‬ ‫ﻣﻊ‬ ‫ﯾﺘﻨﺎﺳﺐ‬.
‫ﻗﺎﻋﺪة‬‫ﻻﻣﻰ‬
‫ق‬١
‫ق‬٣‫ق‬٢
‫ه‬١
‫ه‬٣
‫ه‬٢
‫ق‬١
‫ھـ‬ ‫ﺣﺎ‬١
‫ق‬٢
‫ھـ‬ ‫ﺣﺎ‬٢
‫ق‬٣
‫ھـ‬ ‫ﺣﺎ‬٣
‫ش‬١
‫ھـ‬٢
‫ﺟـ‬
‫ھـ‬١
‫ا‬‫ب‬
٥٠‫ﺳﻢ‬
‫ھـ‬٢ ‫ھـ‬١
‫و‬
‫ش‬٢
٤٠‫ﺳﻢ‬٣٠‫ﺳﻢ‬
٣٠
٥٠
٣
٥
٤٠
٥٠
٤
٥
‫ش‬١
‫ھـ‬ ‫ﺣﺎ‬١
‫ش‬٢
‫ھـ‬ ‫ﺣﺎ‬٢
‫و‬
‫ﺣﺎ‬)‫ھـ‬١+‫ھـ‬٣(
‫ش‬١
‫ھـ‬ ‫ﺣﺎ‬١
‫ش‬٢
‫ھـ‬ ‫ﺣﺎ‬٢
١٠٠
‫ﺣﺎ‬٩٠
١٠٠‫ھـ‬ ‫ﺣﺎ‬١
‫ﺣﺎ‬٩٠
١٠٠×
١
٣
٥

37. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
37
،‫ش‬٢===٨٠‫ﺟﻢ‬ ‫ث‬
‫أﺧﺮ‬ ‫ﺣﻞ‬:‫اﻟﻘﻮى‬ ‫ﻣﺜﻠﺚ‬ ‫ﻗﺎﻋﺪة‬ ‫ﺑﺎﺳﺘﺨﺪام‬:
‫ﻧﺮﺳﻢ‬‫و‬‫ء‬"//‫ب‬‫ج‬"
‫ﻓﯿﻜﻮن‬´‫ج‬‫و‬‫ء‬‫اﻟﻘﻮى‬ ‫ﻣﺜﻠﺚ‬
==
B‫ش‬١=١٠٠×=١٠٠×‫ھـ‬ ‫ﺣﺎ‬١=١٠٠×=٦٠‫ﺟﻢ‬ ‫ث‬
،B‫ش‬٢=١٠٠×=١٠٠×‫ھـ‬ ‫ﺣﺎ‬٢=١٠٠×=٨٠‫ﺟﻢ‬ ‫ث‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫وزﻧﮭ‬ ‫ﺑﻨﺪول‬ ‫ﻛﺮة‬ ‫أزﯾﺤﺖ‬‫ﺎ‬١‫ﯾﺼﻨﻊ‬ ‫اﻟﺨﯿﻂ‬ ‫ﺻﺎر‬ ‫ﺣﺘﻰ‬ ‫ﻧﯿﻮﺗﻦ‬٣٠‫ﻗﻮة‬ ‫ﺗﺄﺛﯿﺮ‬ ‫ﺗﺤﺖ‬ ‫اﻟﺮأﺳﻰ‬ ‫ﻣﻊ‬ ْ
‫ا‬ ‫ﻋﻠﻰ‬‫اﻟﺨﯿﻂ‬ ‫ﻋﻠﻰ‬ ‫ﻋﻤﻮدى‬ ‫أﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫ﻟﻜﺮة‬‫اﻟﺨﯿﻂ‬ ‫ﻓﻰ‬ ‫واﻟﺸﺪ‬ ‫اﻟﻘﻮة‬ ‫أوﺟﺪ‬
‫اﻟﺤﻞ‬:
‫ﻻﻣﻰ‬ ‫ﻗﺎﻋﺪة‬ ‫ﺑﺎﺳﺘﺨﺪام‬
= =
‫ق‬=١×‫ﺟﺎ‬١٥٠=١×=‫ﻧﯿﻮﺗﻦ‬
‫ش‬=١×‫ﺟﺎ‬١٢٠=١×=‫ﻧﯿﻮﺗﻦ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﻃﻮﻟﮫ‬ ‫ﺧﻔﯿﻒ‬ ‫ﺧﯿﻂ‬٢٤‫ﻃﺮﻓﮫ‬ ‫ﺛﺒﺖ‬ ‫ﺳﻢ‬‫ا‬‫ﻣﻘﺪاره‬ ‫وزن‬ ‫وﻋﻠﻖ‬ ‫ﺛﺎﺑﺘﺔ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬١٠٠‫ﺟ‬ ‫ث‬‫ﻣﻦ‬ ‫ﻢ‬
‫ب‬ ‫اﻻﺧﺮ‬ ‫ﻃﺮﻓﮫ‬‫ﺑﻌﺪ‬ ‫ﻋﻠﻰ‬ ‫اﻟﻮزن‬ ‫ﻟﺤﻔﻆ‬ ‫اﻟﻼزﻣﺔ‬ ‫اﻟﻘﻮة‬ ‫ﻣﻘﺪار‬ ‫أوﺟﺪ‬١٢‫اﻻﻓﻘﻰ‬ ‫اﻟﺨﻂ‬ ‫ﻣﻦ‬ ‫ﺳﻢ‬
‫ﺑﻨﻘﻄﺔ‬ ‫اﻟﻤﺎر‬‫ا‬‫اﻟﺤﺎﻟﺘﯿﻦ‬ ‫ﻓﻰ‬‫اﻻﺗﯿﺘﯿﻦ‬:
)١(‫اﻟﻘﻮة‬ ‫ﻛﺎﻧﺖ‬ ‫إذا‬‫أﻓﻘﯿﺔ‬ ‫اﻟﻤﺆﺛﺮة‬)٢(‫ﻛﺎن‬ ‫إذا‬‫ﻣﻊ‬ ‫ﻣﺘﻌﺎﻣﺪا‬ ‫اﻟﻘﻮة‬ ‫اﺗﺠﺎه‬‫ا‬‫ب‬
١٠٠‫ھـ‬ ‫ﺣﺎ‬٢
‫ﺣﺎ‬٩٠
١٠٠×
١
٤
٥
‫ش‬١
‫و‬ ‫ج‬
‫ش‬٢
‫ء‬‫و‬
١٠٠
‫ج‬‫ء‬‫ﺟـ‬
‫ھـ‬١
‫ا‬‫ب‬
٥٠‫ﺳﻢ‬
‫ھـ‬٢ ‫ھـ‬١
‫و‬
‫ش‬٢
٤٠‫ﺳﻢ‬٣٠‫ﺳﻢ‬ ‫و‬
‫ء‬
‫ھـ‬٢
‫ش‬١
‫و‬ ‫ج‬
‫ج‬‫ء‬
٣
٥
‫و‬ ‫ء‬
‫ج‬‫ء‬
٤
٥
٣٠
٦٠٣٠
‫ق‬
١
‫ش‬
١
٢
١
٢
‫ق‬
‫ﺟﺎ‬١٥٠
‫ش‬
‫ﺟﺎ‬١٢٠
١
‫ﺟﺎ‬٩٠
٣ ‫؟‬
٢
٣ ‫؟‬
٢

38. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
38
‫اﻟﺤﻞ‬:
‫اﻻوﻟﻰ‬ ‫اﻟﺤﺎﻟﺔ‬:‫أﻓﻘﯿﺔ‬ ‫اﻟﻤﺆﺛﺮة‬ ‫اﻟﻘﻮة‬:
)‫ج‬‫ا‬(٢
) =٢٤(٢
–)١٢(٢
=٤٣٢B‫ج‬‫ا‬=١٢‫؟‬٣‫ﺳﻢ‬
´‫ج‬‫ب‬‫ا‬‫اﻟﻘﻮى‬ ‫ﻣﺜﻠﺚ‬
B= =
B= =
B‫ق‬=×١٢‫؟‬٣=١٠٠‫؟‬٣‫ﺟﻢ‬ ‫ث‬،‫ش‬=×٢٤=٢٠٠‫ﺟﻢ‬ ‫ث‬
‫ا‬ ‫اﻟﺤﺎﻟﺔ‬‫ﻟﺜﺎﻧﯿﺔ‬:‫ﻛﺎن‬ ‫إذا‬‫ﻣﻊ‬ ‫ﻣﺘﻌﺎﻣﺪا‬ ‫اﻟﻘﻮة‬ ‫اﺗﺠﺎه‬‫ا‬‫ب‬
‫ﻻﻣﻰ‬ ‫ﻗﺎﻋﺪة‬ ‫ﺑﺎﺳﺘﺨﺪام‬:
= =
B‫ق‬= =٥٠‫؟‬٣،‫ش‬= =٥٠‫ﺟﻢ‬ ‫ث‬
‫أﺧﺮ‬ ‫ﺣﻞ‬:‫اﻟﺜﺎﻧ‬ ‫ﻟﻠﺤﺎﻟﺔ‬‫ﯿﺔ‬) :‫ﺑﺎﻟﺘﺤﻠﯿﻞ‬(
A‫ﻣﺘﺰﻧﺔ‬ ‫اﻟﻘﻮى‬B‫ﻣﺤﺼﻠﺔ‬‫ق‬،‫ش‬=١٠٠‫اﺗﺠﺎھﺎ‬ ‫ﺗﻀﺎدھﺎ‬ ‫و‬
B‫ق‬=١٠٠‫ﺣﺘﺎ‬٣٠=١٠٠×=٥٠‫؟‬٣‫ﺟﻢ‬ ‫ث‬
،‫ش‬=١٠٠‫ﺣﺎ‬٣٠=١٠٠×=٥٠‫ﺟﻢ‬ ‫ث‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﻣﻘﺪاره‬ ‫ﺛﻘﻞ‬ ‫ﻋﻠﻖ‬٨٠‫أزﯾﺢ‬ ، ‫رأﺳﻲ‬ ‫ﺣﺎﺋﻂ‬ ‫ﻓﻰ‬ ‫اﻷﺧﺮ‬ ‫ﻃﺮﻓﮫ‬ ‫ﻣﺜﺒﺖ‬ ‫ﺧﯿﻂ‬ ‫ﻃﺮف‬ ‫ﻓﻰ‬ ‫ﺟﻢ‬ ‫ث‬
‫ﺑﺰاوﯾﺔ‬ ‫اﻟﺤﺎﺋﻂ‬ ‫ﻋﻠﻰ‬ ‫ﻣﺎﺋﻼ‬ ‫اﻟﺨﯿﻂ‬ ‫أﺻﺒﺢ‬ ‫ﺣﺘﻰ‬ ‫اﻟﺨﯿﻂ‬ ‫ﻋﻠﻰ‬ ‫ﻋﻤﻮدﯾﺔ‬ ‫ﺑﻘﻮة‬ ‫اﻟﺜﻘﻞ‬‫ﻗ‬‫ﯿﺎﺳﮭﺎ‬٣٠٥
‫ﻋﻨﺪﺋﺬ‬ ‫اﻟﺨﯿﻂ‬ ‫ﻓﻰ‬ ‫اﻟﺸﺪ‬ ‫ﻛﺬﻟﻚ‬ ‫و‬ ‫اﻟﻘﻮة‬ ‫ﻣﻘﺪار‬ ‫اﻻﺗﺰان‬ ‫وﺿﻊ‬ ‫ﻓﻰ‬ ‫أوﺟﺪ‬
١٠٠
‫ق‬
٢٤ ١٢
‫ج‬‫ا‬
‫ب‬
‫ق‬
‫ج‬ ‫ا‬
‫ش‬
‫ا‬‫ب‬
١٠٠
‫ب‬ ‫ج‬
‫ق‬
١٢‫؟‬٣
‫ش‬
٢٤
١٠٠
١٢
١٠٠
١٢
١٠٠
١٢
٣٠
‫ب‬
٦٠
‫ء‬‫ا‬
٣٠ ٦٠
‫ش‬
١٠٠
‫ق‬
‫ﺟـ‬
١٥٠
١٢٠
‫ق‬
‫ﺣﺎ‬١٢٠
‫ش‬
‫ﺣﺎ‬١٥٠
١٠٠
‫ﺣﺎ‬٩٠
١٠٠‫ﺣﺎ‬١٢٠
‫ﺣﺎ‬٩٠
١٠٠‫ﺣﺎ‬١٥٠
‫ﺣﺎ‬٩٠
١
٢
٣ ‫؟‬
٢

39. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
39
‫اﻟﺤﻞ‬:
‫ﻻﻣﻰ‬ ‫ﻗﺎﻋﺪة‬ ‫ﺣﺴﺐ‬:
= =
B‫ق‬=٨٠‫ﺣﺎ‬١٥٠=٨٠×=٤٠‫ﺟﻢ‬ ‫ث‬
‫ش‬=٨٠‫ﺣﺎ‬١٢٠=٨٠×=٤٠‫؟‬٣‫ﺟﻢ‬ ‫ث‬
‫أﺧﺮ‬ ‫ﺣﻞ‬:
‫اﻟﻘﻮى‬ ‫ﻣﺜﻠﺚ‬ ‫ﺑﺎﺳﺘﺨﺪام‬‫ج‬‫ب‬‫ا‬:
= =
A´‫ب‬ ‫ج‬‫ا‬‫ﺳﺘﯿﻨﻰ‬ ‫ﺛﻼﺛﯿﻨﻰ‬B‫ب‬‫ج‬:‫ب‬‫ا‬:‫ج‬ ‫ا‬=١:‫؟‬٣:٢
B= =
B‫ق‬=٤٠، ‫ﺟﻢ‬ ‫ث‬‫ش‬=٤٠‫؟‬٣‫ﺟﻢ‬ ‫ث‬
‫ــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫وزن‬ ‫ﻋﻠﻖ‬‫و‬‫ﺑﺰاوﯾﺔ‬ ‫اﻟﺮأﺳﻲ‬ ‫ﻋﻠﻰ‬ ‫أوﻟﮭﻤﺎ‬ ‫ﯾﻤﯿﻞ‬ ‫ﺧﯿﻄﯿﻦ‬ ‫ﺑﻮاﺳﻄﺔ‬ ‫ﻧﯿﻮﺗﻦ‬‫ھـ‬‫ﺑﻜﺮة‬ ‫ﯾﻤﺮﻋﻠﻰ‬ ‫و‬
‫ﻣﻘﺪارة‬ ‫وزﻧﺎ‬ ‫اﻻﺧﺮى‬ ‫ﻧﮭﺎﯾﺘﮫ‬ ‫ﻓﻰ‬ ‫ﯾﺤﻤﻞ‬ ‫و‬ ‫ﻣﻠﺴﺎء‬ ‫ﺻﻐﯿﺮة‬٨‫و‬ ‫ﻧﯿﻮﺗﻦ‬‫ﻋﻠﻰ‬ ‫اﻟﺜﺎﻧﻰ‬ ‫ﯾﻤﯿﻞ‬
‫ﺑﺰاوﯾﺔ‬ ‫اﻟﺮاﺳﻲ‬٣٠٥
‫وزﻧﺎ‬ ‫اﻻﺧﺮى‬ ‫ﻧﮭﺎﯾﺘﺔ‬ ‫ﻓﻰ‬ ‫ﯾﺤﻤﻞ‬ ‫و‬ ‫ﻣﻠﺴﺎء‬ ‫ﺻﻐﯿﺮ‬ ‫ﺑﻜﺮة‬ ‫ﻋﻠﻰ‬ ‫ﯾﻤﺮ‬ ‫و‬
‫ﻣﻘﺪارة‬١٢‫ﻧﯿﻮﺗﻦ‬.‫اﻟﻮزن‬ ‫ﻣﻘﺪار‬ ‫أوﺟﺪ‬‫و‬‫ھـ‬ ‫ﻗﯿﻤﺔ‬ ،
٨٠
‫ق‬
‫ش‬
١٢٠
٣٠
١٥٠
‫ق‬
‫ﺣﺎ‬١٥٠
‫ش‬
‫ﺣﺎ‬١٢٠
٨٠
‫ﺣﺎ‬٩٠
١
٢
٣ ‫؟‬
٢
‫ش‬
٨٠
‫ق‬
‫ج‬
٣٠
٦٠
‫ا‬
‫ب‬
‫ق‬
‫ج‬ ‫ب‬
‫ش‬
‫ا‬‫ب‬
٨٠
‫ج‬‫ا‬
‫ق‬
١
‫ش‬
‫؟‬٣
٨٠
٢

40. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
40
٣٠
‫اﻟﺤﻞ‬:
‫اﻟﺒﻜﺮة‬ ‫ﺣﻮل‬ ‫اﻟﻤﺎﺋﻞ‬ ‫اﻟﺨﯿﻂ‬ ‫ﻓﺮﻋﻰ‬ ‫ﻓﻰ‬ ‫اﻟﺸﺪ‬ ‫ﯾﺘﺴﺎوى‬ ‫ﻣﻠﺴﺎء‬ ‫اﻟﺒﻜﺮة‬ ‫ﺗﻜﻮن‬ ‫ﻋﻨﺪﻣﺎ‬ ‫أﻧﮫ‬ ‫ﻻﺣﻆ‬
B‫ھـ‬ ‫ﺣﺎ‬= =B‫ق‬)‫ھـ‬= (٢٨/
١٩٥
B٣٠+‫ھـ‬=٣٠+٢٨/
١٩ْ=٢٨/
٤٩ْ
B‫و‬==١٨٫٤‫ﻧﯿﻮﺗﻦ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﻣﻠﺴﺎء‬ ‫ﻛﺮة‬‫وزﻧﮭﺎ‬١٥‫ﻓﻰ‬ ‫ﻃﺮﻓﯿﺔ‬ ‫أﺣﺪ‬ ‫ﻣﺜﺒﺖ‬ ‫ﺑﺨﯿﻂ‬ ‫ﻣﻌﻠﻘﺔ‬ ‫و‬ ‫أﻣﻠﺲ‬ ‫ﺣﺎﺋﻂ‬ ‫ﻋﻠﻰ‬ ‫ﺗﺴﺘﻨﺪ‬ ‫ﻧﯿﻮﺗﻦ‬
‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﺣﺎﺋﻂ‬ ‫ﻓﻰ‬ ‫ﻣﺮﺑﻮط‬ ‫اﻻﺧﺮ‬ ‫ﻃﺮﻓﮫ‬ ‫و‬ ‫ﺳﻄﺤﮭﺎ‬ ‫ﻋﻠﻰ‬ ‫ﻧﻘﻄﺔ‬‫ا‬‫ﺗﻤﺎﻣﺎ‬ ‫اﻟﻜﺮة‬ ‫ﺗﻤﺎس‬ ‫ﻧﻘﻄﺔ‬ ‫أﻋﻠﻰ‬.
‫ﻧﺼ‬ ‫ﻃﻮل‬ ‫ﯾﺴﺎوى‬ ‫اﻟﺨﯿﻂ‬ ‫ﻃﻮل‬ ‫ﻛﺎن‬ ‫ﻓﺈذا‬‫اﻟﻜﺮة‬ ‫ﻗﻄﺮ‬ ‫ﻒ‬.‫اﻟﺨﯿﻂ‬ ‫ﻓﻰ‬ ‫اﻟﺸﺪ‬ ‫و‬ ‫اﻟﺤﺎﺋﻂ‬ ‫ﻋﻠﻰ‬ ‫اﻟﻀﻐﻂ‬ ‫أوﺟﺪ‬
‫اﻟﺤﻞ‬:
٨‫ﺣﺎ‬٣٠
١٢
١
٣
١٢‫ﺟﺎ‬٢٨/
٤٩ْ
‫ﺣﺎ‬١٥٠

41. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
41
٦٠
٣٠٣٠
‫م‬
==B= =B= =
B‫ر‬= =٥‫؟‬٣، ‫ﻧﯿﻮﺗﻦ‬‫ش‬= =١٠‫؟‬٣‫ﻧﯿﻮﺗﻦ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:
‫اﻟﺤﻞ‬:
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﺑﯿﻨﮭﻤﺎ‬ ‫واﻟﺒﻌﺪ‬ ‫واﺣﺪ‬ ‫أﻓﻘﻰ‬ ‫ﻣﺴﺘﻮى‬ ‫ﻓﻰ‬ ‫ﯾﻘﻌﺎن‬ ‫ﻣﺘﻮازﯾﯿﻦ‬ ‫ﻗﻀﯿﺒﯿﻦ‬ ‫ﻋﻠﻰ‬ ‫ﺗﺮﺗﻜﺰ‬ ‫ﻣﺼﻤﺘﺔ‬ ‫ﻛﺮة‬
‫اﻟﻜﺮة‬ ‫ﻗﻄﺮ‬ ‫ﻧﺼﻒ‬ ‫ﻃﻮل‬ ‫ﯾﺴﺎوى‬.‫اﻟﻜﺮة‬ ‫وزن‬ ‫ﻛﺎن‬ ‫إذا‬ ‫اﻟﻘﻀﯿﺒﯿﻦ‬ ‫ﻣﻦ‬ ‫ﻛﻼ‬ ‫ﻋﻠﻰ‬ ‫اﻟﻀﻐﻂ‬ ‫أوﺟﺪ‬
‫ﯾﺴﺎوى‬١٠‫ﻧﯿﻮﺗﻦ‬.
‫اﻟﺤﻞ‬:
´‫ب‬‫م‬‫ا‬‫اﻻﺿﻼع‬ ‫ﻣﺘﺴﺎوى‬B‫ق‬)‫ب‬ ‫م‬‫ا‬‫ﻒ‬‫ﻓ‬(=٦٠‫ﯾﻨﺼﻔﮭﺎ‬ ‫اﻟﻮزن‬ ‫ﺧﻂ‬ ،
‫اﻟﻘﻮى‬ ‫ﺗﺄﺛﯿﺮ‬ ‫ﺗﺤﺖ‬ ‫ﻣﺘﺰﻧﺔ‬ ‫اﻟﻜﺮة‬:
)١(‫اﻟﻮزن‬١٠‫ﻷﺳﻔﻞ‬ ‫رأﺳﻲ‬ ‫ﻧﯿﻮﺗﻦ‬
)٢(‫ر‬١‫رد‬‫اﻟﻘﻀﯿﺐ‬ ‫ﻓﻌﻞ‬‫ا‬
)٣(‫ر‬٢‫ب‬ ‫اﻟﻘﻀﯿﺐ‬ ‫ﻓﻌﻞ‬ ‫رد‬
‫ر‬
‫ب‬‫م‬
‫ش‬
‫ا‬‫م‬
١٥
‫ب‬‫ا‬
‫ر‬
‫ﻧﻖ‬
‫ش‬
٢‫ﻧﻖ‬
١٥
‫ﻧﻖ‬‫؟‬٣
‫ر‬
١
‫ش‬
٢
١٥
‫؟‬٣
١٥
‫؟‬٣
٣٠
‫؟‬٣

42. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
42
)٣(‫أﻣﻠﺲ‬ ‫ﻣﺎﺋﻞ‬ ‫ﻣﺴﺘﻮ‬ ‫ﻋﻠﻰ‬ ‫ﺟﺴﻢ‬ ‫اﺗﺰان‬
‫ﻻﻣﻰ‬ ‫ﻗﺎﻋﺪة‬ ‫ﺑﺘﻄﺒﯿﻖ‬= = :
= =
B‫ر‬١=‫ر‬٢===٥٫٨‫ﻧﯿﻮﺗﻦ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬‫ـ‬
‫ﻣﺜﺎل‬:‫ﻧﻘﻄﺘﯿﻦ‬ ‫ﻓﻰ‬ ‫ﻃﺮﻓﯿﮫ‬ ‫ﻣﻦ‬ ‫رﺑﻂ‬ ‫ﺧﻔﯿﻒ‬ ‫ﺧﯿﻂ‬‫ب‬ ‫ﻛﺎن‬ ‫ﺑﺤﯿﺚ‬ ‫ﺟـ‬ ، ‫ب‬"‫ﺟـ‬"‫ﻋﻠﻰ‬ ‫اﻧﺰﻟﻘﺖ‬ ‫ﺛﻢ‬ ‫اﻓﻘﯿﺎ‬
‫وزﻧﮭﺎ‬ ‫ﻣﻠﺴﺎء‬ ‫ﺻﻐﯿﺮة‬ ‫ﺣﻠﻘﺔ‬ ‫اﻟﺨﯿﻂ‬٢٠‫وﺿﻊ‬ ‫ﻋﻨﺪ‬ ‫اﻟﺨﯿﻂ‬ ‫ﻓﺮﻋﻰ‬ ‫ﺑﯿﻦ‬ ‫اﻟﺰاوﯾﺔ‬ ‫ﻗﯿﺎس‬ ‫ﻓﺄﺻﺒﺢ‬ ‫ﺟﻢ‬ ‫ث‬
‫اﻟﺘﻮ‬‫ازن‬٩٠٥
‫ﻣﻨﮭﻤﺎ‬ ‫ﻛﻞ‬ ‫ﻓﻰ‬ ‫اﻟﺸﺪ‬ ‫ﻗﯿﻤﺔ‬ ‫أوﺟﺪ‬ ‫ﺛﻢ‬ ‫اﻟﻄﻮل‬ ‫ﻓﻰ‬ ‫ﻣﺘﺴﺎوﯾﺎن‬ ‫اﻟﺨﯿﻂ‬ ‫ﻓﺮﻋﻰ‬ ‫أن‬ ‫أﺛﺒﺖ‬
‫اﻟﺤﻞ‬:
A‫ﻣﻠﺴﺎء‬ ‫اﻟﺤﻠﻘﺔ‬B‫ﻣﺘﺴﺎوى‬ ‫اﻟﺨﯿﻂ‬ ‫ﻓﺮﻋﻰ‬ ‫ﻓﻰ‬ ‫اﻟﺸﺪ‬
‫ﻻﻣﻰ‬ ‫ﻗﺎﻋﺪة‬ ‫ﺑﺎﺳﺘﺨﺪام‬ ‫و‬:
B= =B‫ھـ‬ ‫ﺣﺎ‬١=‫ھـ‬ ‫ﺣﺎ‬٢
B‫ھـ‬١=‫ھـ‬٢= =٤٥٥
B‫ش‬=
B‫ش‬=١٠‫؟‬٢
A‫ء‬‫ا‬"M‫ج‬‫ب‬"،‫ق‬)‫ھـ‬١(‫ﻒ‬‫ﻓ‬=‫ق‬)‫ھـ‬٢(‫ﻒ‬‫ﻓ‬B‫ب‬‫ا‬=‫ج‬‫ا‬
B‫اﻟﻄﻮل‬ ‫ﻓﻰ‬ ‫ﻣﺘﺴﺎوﯾﺎن‬ ‫اﻟﺨﯿﻂ‬ ‫ﻓﺮﻋﺎ‬
‫ــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫وزﻧﮫ‬ ‫ﺟﺴﻢ‬ ‫وﺿﻊ‬ ‫إذا‬)‫و‬(‫ھـ‬ ‫ﻗﯿﺎﺳﮭﺎ‬ ‫ﺑﺰاوﯾﺔ‬ ‫اﻻﻓﻘﻰ‬ ‫ﻋﻠﻰ‬ ‫ﯾﻤﯿﻞ‬ ‫أﻣﻠﺲ‬ ‫ﻣﺎﺋﻞ‬ ‫ﻣﺴﺘﻮ‬ ‫ﻋﻠﻰ‬
‫ﻓﺈن‬‫ﻗﻮﺗﯿﻦ‬ ‫ﺗﺄﺛﯿﺮ‬ ‫ﺗﺤﺖ‬ ‫ﯾﻜﻮن‬ ‫اﻟﺠﺴﻢ‬:
١(‫اﻟﻮزن‬ ‫ﻗﻮة‬)‫و‬(‫واﺗ‬‫أﺳﻔﻞ‬ ‫اﻟﻰ‬ ‫رأﺳﻲ‬ ‫ﺠﺎھﮭﺎ‬
٢(‫اﻻﻣﻠﺲ‬ ‫اﻟﻤﺴﺘﻮى‬ ‫ﻓﻌﻞ‬ ‫رد‬ ‫ﻗﻮة‬)‫ر‬(
‫ﻷﻋﻠﻰ‬ ‫اﻟﻤﺴﺘﻮى‬ ‫ﻋﻠﻰ‬ ‫ﻋﻤﻮدى‬
‫ر‬١
‫ﺟﺎ‬١٥٠
‫ر‬٢
‫ﺟﺎ‬١٥٠
١٠
‫ﺟﺎ‬٦٠
‫ر‬١
‫ﺟﺎ‬٣٠
‫ر‬٢
‫ﺟﺎ‬٣٠
١٠
‫ﺟﺎ‬٦٠
١٠‫ﺣﺎ‬٣٠
‫ﺣﺎ‬٦٠
١٠‫؟‬٣
٣
‫ه‬٢ ‫ش‬‫ش‬
٢٠
‫ا‬
‫ب‬‫ج‬
‫ه‬١
‫ر‬
‫ھـ‬
‫ھـ‬
‫و‬
٢٠
‫ﺟﺎ‬٩٠
‫ش‬
‫ﺟﺎھـ‬١
‫ش‬
‫ﺟﺎھـ‬٢
٩٠
٢
٢٠‫ﺟﺎ‬‫ھـ‬١
‫ﺟﺎ‬٩٠

43. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
43
‫ق‬
‫ﺗﺆﺛﺮ‬ ‫ﺛﺎﻟﺜﺔ‬ ‫ﻗﻮة‬ ‫وﺟﻮد‬ ‫ﻣﻦ‬ ‫ﻻﺑﺪ‬ ‫اﻟﺠﺴﻢ‬ ‫ﯾﺘﺰن‬ ‫ﻟﻜﻰ‬ ‫و‬
‫اﻻﺗﯿﺔ‬ ‫اﻟﺤﺎﻻت‬ ‫أﺣﺪ‬ ‫ﻓﻰ‬ ‫اﻟﺠﺴﻢ‬ ‫ﻋﻠﻰ‬:
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬

44. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
44
*‫ﻣﻼﺣﻈﺎت‬:
)١(‫اﻟﻤﻨﺘﻈﻢ‬ ‫اﻟﻘﻀﯿﺐ‬:‫ﻣﻨﺘﺼﻔﮫ‬ ‫ﻓﻰ‬ ‫ﯾﺆﺛﺮ‬ ‫وزﻧﮫ‬ ‫اﻟﺬى‬ ‫اﻟﻘﻀﯿﺐ‬ ‫ھﻮ‬.
)٢(‫اﻟﺨﺸﻦ‬ ‫اﻟﻤﺴﺘﻮى‬ ‫أو‬ ً‫ا‬‫ﺣﺮ‬ ً‫ﺎ‬‫ﺗﻌﻠﯿﻘ‬ ‫ﻣﻌﻠﻖ‬ ‫اﻟﻘﻀﯿﺐ‬ ‫ﯾﻜﻮن‬ ‫ﻋﻨﺪھﺎ‬ ‫اﻟﺘﻰ‬ ‫اﻟﻨﻘﻄﺔ‬ ‫أو‬ ‫اﻟﻤﻔﺼﻞ‬ ‫ﻓﻌﻞ‬ ‫رد‬
‫ﯾﻜﻮن‬‫اﻟﻘﺎﻋﺪة‬ ‫ﺑﻮاﺳﻄﺔ‬ ‫اﺗﺠﺎھﮫ‬ ‫ﻧﺤﺪد‬ ‫و‬ ‫اﻻﺗﺠﺎه‬ ‫ﻣﺠﮭﻮل‬.
)‫اﻟﻨﻘﻄﺔ‬ ‫ﺑﻨﻔﺲ‬ ‫ﯾﻤﺮ‬ ‫أن‬ ‫ﻻﺑﺪ‬ ‫اﻟﺜﺎﻟﺜﺔ‬ ‫اﻟﻘﻮة‬ ‫ﻋﻤﻞ‬ ‫ﺧﻂ‬ ‫ﻓﺈن‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﻗﻮﺗﯿﻦ‬ ‫ﻋﻤﻞ‬ ‫ﺧﻄﻰ‬ ‫ﺗﻼﻗﻰ‬ ‫إذا‬(
)٣(‫ﻟﻠﻘﻀﯿﺐ‬ ‫اﻟﺤﺮ‬ ‫اﻟﺘﻌﻠﯿﻖ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻣﻊ‬ ‫واﺣﺪ‬ ‫رأﺳﻲ‬ ‫ﺧﻂ‬ ‫ﺗﻜﻮن‬ ‫أن‬ ‫ﻻﺑﺪ‬ ‫اﻟﻘﻀﯿﺐ‬ ‫وزن‬ ‫ﺗﺄﺛﯿﺮ‬ ‫ﻧﻘﻄﺔ‬
)٤(‫اﻟﻘﻀ‬ ‫ﻓﯿﮫ‬ ‫ﯾﺘﺰن‬ ‫اﻟﺬى‬ ‫اﻟﻮﺿﻊ‬ ‫ﻣﻨﺎ‬ ‫ﻃﻠﺐ‬ ‫إذا‬‫ﻋﻠﻰ‬ ‫اﻟﻘﻀﯿﺐ‬ ‫ﻣﯿﻞ‬ ‫زاوﯾﺔ‬ ‫اﯾﺠﺎد‬ ‫ﻣﻌﻨﺎه‬ ‫ﻓﮭﺬا‬ ‫ﯿﺐ‬
‫اﻷﻓﻘﻰ‬ ‫أو‬ ‫اﻟﺮأﺳﻲ‬)‫ﺑﺈﺧﺘﯿﺎرك‬(
)٥(‫اﻟﮭﻨﺪﺳﻲ‬ ‫ﻣﺮﻛﺰھﺎ‬ ‫ﻓﻰ‬ ‫ﯾﻘﻊ‬ ‫اﻟﻤﻨﺘﻈﻤﺔ‬ ‫اﻟﻜﺮة‬ ‫ﺛﻘﻞ‬ ‫ﻣﺮﻛﺰ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫وزﻧﮭﺎ‬ ‫اﻟﺤﺪﯾﺪ‬ ‫ﻣﻦ‬ ‫ﻣﻠﺴﺎء‬ ‫ﻛﺮة‬٣٠‫أﻣﻠﺲ‬ ‫ﻣﺴﺘﻮى‬ ‫و‬ ‫أﻣﻠﺲ‬ ‫رأﺳﻲ‬ ‫ﺣﺎﺋﻂ‬ ‫ﺑﯿﻦ‬ ‫ﻣﺴﺘﻘﺮة‬ ‫ﻧﯿﻮﺗﻦ‬
‫ﺑﺰاوﯾﺔ‬ ‫اﻻﻓﻘﻰ‬ ‫ﻋﻠﻰ‬ ‫ﯾﻤﯿﻞ‬٦٠٥
‫اﻟﻤﺴﺘﻮى‬ ‫و‬ ‫اﻟﺤﺎﺋﻂ‬ ‫ﻣﻦ‬ ‫ﻛﻞ‬ ‫ﻋﻠﻰ‬ ‫اﻟﻀﻐﻂ‬ ‫أوﺟﺪ‬،
‫اﻟﺤﻞ‬:
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫وزﻧﮫ‬ ‫ﺟﺴﻢ‬ ‫وﺿﻊ‬٦‫ﻗﯿﺎﺳﮭﺎ‬ ‫ﺑﺰاوﯾﺔ‬ ‫اﻻﻓﻘﻰ‬ ‫ﻋﻠﻰ‬ ‫ﯾﻤﯿﻞ‬ ‫أﻣﻠﺲ‬ ‫ﻣﺎﺋﻞ‬ ‫ﻣﺴﺘﻮى‬ ‫ﻋﻠﻰ‬ ‫ﻛﺠﻢ‬ ‫ث‬٣٠ْ
‫اﻻ‬ ‫اﻟﺤﺎﻟﺘﯿﻦ‬ ‫ﻓﻰ‬ ‫اﻟﻤﺴﺘﻮى‬ ‫ﻓﻌﻞ‬ ‫ورد‬ ‫اﻟﻘﻮة‬ ‫ھﺬه‬ ‫أوﺟﺪ‬ ‫ﻗﻮة‬ ‫ﺑﻮاﺳﻄﺔ‬ ‫ﺗﻮازﻧﮫ‬ ‫وﺣﻔﻆ‬‫ﺗﯿﺘﯿﻦ‬:
)‫أوﻻ‬(‫اﻟﻘﻮة‬‫أﻓﻘﯿﺔ‬)‫ﺛﺎﻧﯿﺎ‬(‫ﻗﯿﺎﺳﮭﺎ‬ ‫ﺑﺰاوﯾﺔ‬ ‫اﻟﻤﺴﺘﻮى‬ ‫ﻋﻠﻰ‬ ‫ﺗﻤﯿﻞ‬ ‫اﻟﻘﻮة‬٣٠ْ

45. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
45
‫اﻟﺤﻞ‬:
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫وزﻧﮫ‬ ‫ﺟﺴﻢ‬ ‫وﺿﻊ‬٦٠‫ﻗﯿﺎﺳﮭﺎ‬ ‫ﺑﺰاوﯾﺔ‬ ‫اﻻﻓﻘﻰ‬ ‫ﻋﻠﻰ‬ ‫ﯾﻤﯿﻞ‬ ‫أﻣﻠﺲ‬ ‫ﻣﺴﺘﻮى‬ ‫ﻋﻠﻰ‬ ‫ﻧﯿﻮﺗﻦ‬٣٠ْ
‫وﺷﺪ‬‫ﻻﻋﻠﻰ‬ ‫ﻟﻠﻤﺴﺘﻮى‬ ‫ﻣﯿﻞ‬ ‫أﻛﺒﺮ‬ ‫ﺧﻂ‬ ‫أﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫ﺑﺨﯿﻂ‬ ‫اﻟﻤﺴﺘﻮى‬ ‫أﻋﻠﻰ‬ ‫اﻟﻰ‬
‫اﻟﺨﯿﻂ‬ ‫ﻓﻰ‬ ‫اﻟﺸﺪ‬ ‫ﻣﻘﺪار‬ ‫أوﺟﺪ‬‫و‬‫اﻟﻤﺴﺘﻮى‬ ‫ﻓﻌﻞ‬ ‫رد‬
‫اﻟﺤﻞ‬:

46. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
46
‫ﻣﺜﺎل‬:‫ﻣﻨﺘ‬ ‫ﻗﻀﯿﺐ‬ ‫ﻋﻠﻖ‬‫ووزﻧﮫ‬ ‫ﻣﺘﺮ‬ ‫ﻃﻮﻟﮫ‬ ‫ﻈﻢ‬٣٠‫ﻓﻰ‬ ‫ﻃﺮﻓﺎھﻤﺎ‬ ‫ﺛﺒﺖ‬ ‫ﺑﺨﯿﻄﯿﻦ‬ ‫ﻃﺮﻓﯿﮫ‬ ‫ﻣﻦ‬ ‫ﻧﯿﻮﺗﻦ‬
‫واﺣﺪ‬ ‫ﻧﻘﻄﺔ‬‫ﻣﺘﻌﺎ‬ ‫اﻟﺨﯿﻄﯿﻦ‬ ‫ﻛﺎن‬ ‫ﻓﺈذا‬ ‫اﻟﺴﻘﻒ‬ ‫ﻓﻰ‬ ‫ة‬‫أﺣﺪھﻤﺎ‬ ‫ﻃﻮل‬ ‫وﻛﺎن‬ ‫ﻣﺪﯾﻦ‬٦٠‫ﺳﻢ‬
‫اﻟﺸﺪ‬ ‫ﻣﻘﺪار‬ ‫ھﻮ‬ ‫ﻓﻤﺎ‬‫ﺣﺎﻟﺔ‬ ‫وﻓﻰ‬ ‫ﻣﻄﻠﻘﺎ‬ ‫ﺗﻌﻠﯿﻘﺎ‬ ‫ﻣﻌﻠﻘﺎ‬ ‫اﻟﻘﻀﯿﺐ‬ ‫ﯾﻜﻮن‬ ‫ﻋﻨﺪﻣﺎ‬ ‫اﻟﺨﯿﻄﯿﻦ‬ ‫ﻣﻦ‬ ‫ﻛﻼ‬ ‫ﻓﻰ‬‫أﺗﺰان‬
‫اﻟﺤﻞ‬:
‫ـــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﻃﺮﻓﮭﺎ‬ ‫ﻓﻰ‬ ‫ﺗﺆﺛﺮ‬ ‫أﻓﻘﯿﺔ‬ ‫ﺑﻘﻮة‬ ‫ﺟﺎﻧﺒﺎ‬ ‫ﺷﺪت‬ ‫ﻃﺮﻓﯿﮭﺎ‬ ‫أﺣﺪ‬ ‫ﺣﻮل‬ ‫ﻟﻠﺤﺮﻛﺔ‬ ‫ﻗﺎﺑﻠﺔ‬ ‫ﻣﻨﺘﻈﻤﺔ‬ ‫ﺳﺎق‬
‫اﻻﺧﺮ‬‫ا‬ ‫ﺛﻘﻞ‬ ‫ﻧﺼﻒ‬ ‫وﺗﺴﺎوى‬‫ﺗﺘﺰن‬ ‫ﻋﻨﺪﻣﺎ‬ ‫اﻟﺮأﺳﻰ‬ ‫ﻋﻠﻰ‬ ‫اﻟﺴﺎق‬ ‫ﻣﯿﻞ‬ ‫زاوﯾﺔ‬ ‫ﻗﯿﺎس‬ ‫أوﺟﺪ‬ ‫ﻟﺴﺎق‬
‫اﻻول‬ ‫اﻟﻄﺮف‬ ‫ﻋﻨﺪ‬ ‫اﻟﻔﻌﻞ‬ ‫رد‬ ‫وﻛﺬﻟﻚ‬
‫اﻟﺤﻞ‬:

47. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
47
A‫د‬‫ﻣﻨﺘﺼﻒ‬‫ا‬‫ب‬"،‫د‬‫م‬"//‫ا‬‫ﺟـ‬"‫ﻣﻨﺘﺼﻒ‬ ‫م‬‫ب‬"‫ﺟـ‬"‫م‬ ‫ب‬=‫ﺟـ‬ ‫م‬
‫ا‬‫ﺟـ‬=‫ﺟـ‬ ‫ب‬‫ق‬)‫ب‬‫ا‬‫ﺟـ‬‫ﻒ‬‫ﻓ‬= (‫ق‬)‫ا‬‫ب‬‫ﺟـ‬‫ﻒ‬‫ﻓ‬= (٤٥ْ
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫وزﻧﮫ‬ ‫ﻣﻨﺘﻈﻢ‬ ‫ﻗﻀﯿﺐ‬ ‫وﺿﻊ‬٢٤‫اﻻﻓﻘﻰ‬ ‫ﻋﻠﻰ‬ ‫وﯾﻤﯿﻼن‬ ‫ﻣﺘﻘﺎﺑﻠﯿﻦ‬ ‫أﻣﻠﺴﯿﻦ‬ ‫ﻣﺴﺘﻮﯾﯿﻦ‬ ‫ﻋﻠﻰ‬ ‫ﻧﯿﻮﺗﻦ‬
‫ﺑﺎﻟﺰاوﯾﺘﯿﻦ‬٣٠، ْ٦٠‫أوﺟﺪ‬ ‫واﺣﺪ‬ ‫ﻣﺴﺘﻮى‬ ‫ﻓﻰ‬ ‫ﻟﻠﻤﺴﺘﻮﯾﯿﻦ‬ ‫ﻣﯿﻞ‬ ‫أﻛﺒﺮ‬ ‫وﺧﻄﺎ‬ ‫اﻟﻘﻀﯿﺐ‬ ‫ﯾﻘﻊ‬ ‫ﺑﺤﯿﺚ‬ ْ:
‫اﻟﺘﻮازن‬ ‫ﺣﺎﻟﺔ‬ ‫ﻓﻰ‬ ‫اﻻﻓﻘﻰ‬ ‫ﻋﻠﻰ‬ ‫اﻟﻘﻀﯿﺐ‬ ‫ﻣﯿﻞ‬ ‫زاوﯾﺔ‬ ‫وﻛﺬا‬ ‫اﻟﻤﺴﺘﻮﯾﯿﻦ‬ ‫ﻣﻦ‬ ‫ﻛﻼ‬ ‫ﻋﻠﻰ‬ ‫اﻟﻀﻐﻂ‬ ‫ﻣﻘﺪار‬.
‫اﻟﺤﻞ‬:
‫ﻗﻮى‬ ‫ﺛﻼث‬ ‫ﺑﺘﺄﺛﯿﺮ‬ ‫ﻣﺘﺰن‬ ‫اﻟﻘﻀﯿﺐ‬:
١(‫اﻟﻮزن‬٢٤‫ﻣﻨﺘﺼﻒ‬ ‫ﻓﻰ‬ ‫ﯾﺆﺛﺮ‬ ‫و‬ ‫ﻷﺳﻔﻞ‬ ‫راﺳﯿﺎ‬ ‫ﻧﯿﻮﺗﻦ‬‫ا‬‫ب‬"
٢(‫اﻟﻤ‬ ‫ﻓﻌﻞ‬ ‫رد‬‫اﻻول‬ ‫ﺴﺘﻮى‬‫ر‬١
٣(‫اﻻول‬ ‫اﻟﻤﺴﺘﻮى‬ ‫ﻓﻌﻞ‬ ‫رد‬‫ر‬٢
‫ﻻﻣﻰ‬ ‫ﻗﺎﻋﺪة‬ ‫ﺑﺘﻄﺒﯿﻖ‬:
= =
B‫ر‬١==١٢، ‫ﻧﯿﻮﺗﻦ‬‫ر‬٢=١٢‫؟‬٣
‫ر‬٢
‫ر‬١
‫ء‬
٦٠٣٠
٦٠
٣٠
٣٠ ٦٠
‫م‬
‫ا‬
‫ب‬
‫ج‬
٢٤
‫ر‬١
‫ﺟﺎ‬١٥٠
‫ر‬٢
‫ﺟﺎ‬١٢٠
٢٤
‫ﺟﺎ‬٩٠
٢٤‫ﺣﺎ‬١٥٠
‫ﺟﺎ‬٩٠

48. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
48
‫اﻟﻤﻌﻄﺎ‬ ‫اﻟﻘﻮى‬ ‫ﻣﻦ‬ ‫ﻗﻮة‬ ‫ﻛﻞ‬ ‫ﻧﺤﻠﻞ‬‫اﻟﻤ‬ ‫اﻻﺗﺠﺎھﯿﻦ‬ ‫ﻓﻰ‬ ‫ﻣﺮﻛﺒﺘﯿﻦ‬ ‫اﻟﻰ‬ ‫ة‬‫اﻻﺣﺪاﺛﯿﺎت‬ ‫ﻟﻤﺤﻮرى‬ ‫ﻮﺟﺒﯿﻦ‬
‫ھﻤﺎ‬ ‫ﺗﻜﻮن‬ ‫و‬‫ﺳﺲ‬،‫ﺻﺺ‬‫ﻧﻀﻊ‬ ‫ﺛﻢ‬ ‫اﻟﺘﺮﺗﯿﺐ‬ ‫ﻋﻠﻰ‬‫ﺳﺲ‬=٠،‫ﺻﺺ‬=٠‫اﻟﻤﻄﻠﻮب‬ ‫ﻧﻮﺟﺪ‬ ‫ﺛﻢ‬
*‫ﻧﺘﯿﺠﺔ‬:
‫ﯾﺘﻼﺷﻰ‬ ‫أن‬ ‫ھﻮ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫اﻟﻤﺘﻼﻗﯿﺔ‬ ‫اﻟﻤﺴﺘﻮﯾﺔ‬ ‫اﻟﻘﻮى‬ ‫ﻣﻦ‬ ‫ﻣﺠﻤﻮﻋﺔ‬ ‫ﺗﺄﺛﯿﺮ‬ ‫ﺗﺤﺖ‬ ‫ﺟﺴﻢ‬ ‫اﺗﺰان‬ ‫ﺷﺮط‬
‫اﺗﺠﺎه‬ ‫أى‬ ‫ﻓﻰ‬ ‫اﻟﻘﻮى‬ ‫ﻟﮭﺬه‬ ‫اﻟﺠﺒﺮﯾﺔ‬ ‫ﻟﻠﻤﺮﻛﺒﺎت‬ ‫اﻟﺠﺒﺮى‬ ‫اﻟﻤﺠﻤﻮع‬.
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:
)٤(‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫اﻟﻤﺘﻼﻗﯿﺔ‬ ‫اﻟﻤﺴﺘﻮﯾﺔ‬ ‫اﻟﻘﻮى‬ ‫ﻣﻦ‬ ‫ﻣﺠﻤﻮﻋﺔ‬ ‫ﺗﺄﺛﯿﺮ‬ ‫ﺗﺤﺖ‬ ‫ﺟﺴﻢ‬ ‫اﺗﺰان‬
‫اﻟﻤﺘﻼﻗﯿ‬ ‫اﻟﻤﺴﺘﻮﯾﺔ‬ ‫اﻟﻘﻮى‬ ‫ﻣﻦ‬ ‫ﻣﺠﻤﻮﻋﺔ‬ ‫ﺗﺄﺛﯿﺮ‬ ‫ﺗﺤﺖ‬ ‫ﺟﺴﻢ‬ ‫اﺗﺰان‬ ‫ﺷﺮط‬‫أن‬ ‫ھﻮ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﺔ‬
‫اﻟﻤﺘﻌﺎﻣﺪﯾﻦ‬ ‫اﻻﺗﺠﺎھﯿﻦ‬ ‫ﻓﻰ‬ ‫اﻟﻘﻮى‬ ‫ﻟﮭﺬه‬ ‫اﻟﺠﺒﺮﯾﺔ‬ ‫ﻟﻠﻤﺮﻛﺒﺎت‬ ‫اﻟﺠﺒﺮى‬ ‫اﻟﻤﺠﻤﻮع‬ ‫ﯾﺘﻼﺷﻰ‬.
‫ﻗﺎﻋﺪة‬

49. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
49
‫ﻣﺜﺎل‬:
‫ـــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:

50. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
50
‫ﻣﺜﺎل‬:
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:

51. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
51
‫اﻟﻘﻮى‬ ‫ﻛﺎﻧﺖ‬ ‫إذا‬‫ق‬١=٤‫ﺳﺲ‬–٣‫ﺻﺺ‬،‫ق‬٢=-‫ا‬‫ﺳﺲ‬–٢‫ﺻﺺ‬،‫ق‬٣=-٦‫ﺳﺲ‬+‫ب‬‫ﺻﺺ‬
‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﻣﺘﻼﻗﯿﺔ‬‫ﻣﻦ‬ ‫ﻗﯿﻤﺔ‬ ‫ﻓﺄوﺟﺪ‬ ‫ﻣﺘﺰﻧﺔ‬ ‫و‬‫ا‬‫ب‬ ،
‫اﻟﺤﻞ‬:
A‫ﻣﺘﺰﻧﺔ‬ ‫و‬ ‫ﻣﺘﻼﻗﯿﺔ‬ ‫اﻟﻘﻮى‬
B‫ﻓﻰ‬ ‫اﻟﻤﺮﻛﺒﺎت‬ ‫ﻣﺠﻤﻮع‬‫اﺗﺠﺎة‬‫ﺳﺲ‬=٠‫اﺗﺠﺎة‬ ‫ﻓﻰ‬ ‫اﻟﻤﺮﻛﺒﺎت‬ ‫ﻣﺠﻤﻮع‬ ،‫ﺻﺺ‬=٠
B٤‫ــ‬‫ا‬–٦=٠B‫ا‬=‫ــ‬٢‫ــ‬ ،٣‫ــ‬٢+‫ب‬=٠B‫ب‬=٥
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــ‬
‫اﻟﺤﻞ‬:
A‫ﻣﺘﺰﻧﺔ‬ ‫اﻟﻘﻮى‬B‫س‬=٠‫ص‬ ،=٠‫أﻛﻤــــﻞ‬..........
B‫ق‬=٢‫ك‬ ، ‫ﻧﯿﻮﺗﻦ‬=١٥‫ﻧﯿﻮﺗﻦ‬
٥
‫ھـ‬١
‫ھـ‬٢
‫ھـ‬٢
‫ق‬
×
٢‫؟‬١٠
٢‫؟‬١٠
‫ﺳﺲ‬
‫ﺳﺺ‬
‫ك‬ ‫ھـ‬٢
‫ھـ‬١
٢‫ﺳﻢ‬
٦‫ﺳﻢ‬
٨‫ﺳﻢ‬
٢‫ﺳﻢ‬
٦‫ﺳﻢ‬
‫ھـ‬٢ ‫ھـ‬١

52. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
52
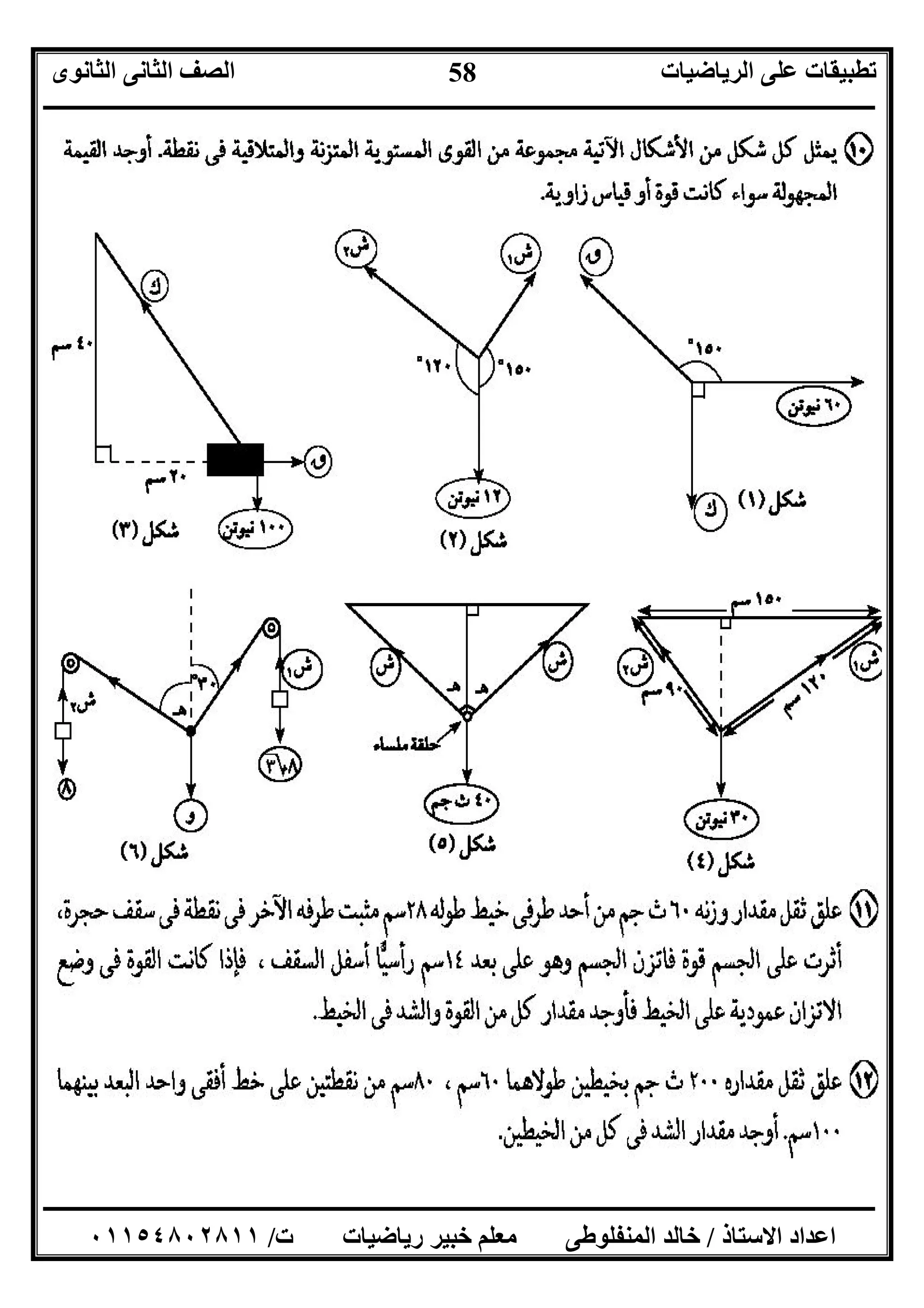
]١[‫ﯾﺄﺗﻰ‬ ‫ﻣﺎ‬ ‫أﻛﻤـــــﻞ‬:
١(‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﻣﺘﻼﻗﯿﺔ‬ ‫ﻣﺴﺘﻮﯾﺔ‬ ‫ﻗﻮى‬ ‫ﺛﻼث‬ ‫ﺗﺄﺛﯿﺮ‬ ‫ﺗﺤﺖ‬ ‫ﺟﺴﻢ‬ ‫اﺗﺰن‬ ‫إذا‬‫ﻣﻨﮭﺎ‬ ‫ﻗﻮﺗﯿﻦ‬ ‫أى‬ ‫ﻣﺤﺼﻠﺔ‬ ‫ﻓﺈن‬
‫اﻟﻤﻘﺪار‬ ‫ﻓﻰ‬ ‫ﺗﺴﺎوى‬..............‫ﻓﻰ‬ ‫اﺳﺘﻘﺎﻣﺘﮭﺎ‬ ‫ﻋﻠﻰ‬ ‫ﺗﻜﻮن‬ ‫و‬.............‫اﻟﻤﻀﺎد‬.
٢(‫ﺧﻄﻮط‬ ‫ﺗﻮازى‬ ‫أﺿﻼﻋﮫ‬ ‫ﻣﺜﻠﺚ‬ ‫رﺳﻢ‬ ‫و‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﻣﺘﻼﻗﯿﺔ‬ ‫ﻗﻮى‬ ‫ﺛﻼث‬ ‫ﺗﺄﺛﯿﺮ‬ ‫ﺗﺤﺖ‬ ‫ﺟﺴﻢ‬ ‫اﺗﺰن‬ ‫إذا‬
‫ا‬ ‫أﺿﻼع‬ ‫أﻃﻮال‬ ‫ﻓﺈن‬ ‫واﺣﺪ‬ ‫دورى‬ ‫اﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫و‬ ‫اﻟﺜﻼﺛﺔ‬ ‫اﻟﻘﻮى‬ ‫ﻋﻤﻞ‬‫ﺗﻜﻮن‬ ‫ﻟﻤﺜﻠﺚ‬..................
٣(‫اﻟﻤﻘﺎﺑﻞ‬ ‫اﻟﺸﻜﻞ‬ ‫ﻓﻰ‬:
‫وزﻧﮫ‬ ‫ﺟﺴﻢ‬٩‫ﻣﻘﺪارھﺎ‬ ‫أﻓﻘﯿﺔ‬ ‫ﻗﻮة‬ ‫ﺑﺘﺄﺛﯿﺮ‬ ‫اﺗﺰن‬ ‫ﺧﯿﻂ‬ ‫ﻧﮭﺎﯾﺔ‬ ‫ﻓﻰ‬ ‫ﻣﻌﻠﻖ‬ ‫ﻧﯿﻮﺗﻦ‬‫ق‬‫اﻟﺨﯿﻂ‬ ‫ﻛﺎن‬ ‫ﻋﻨﺪﻣﺎ‬
‫ﻗﯿﺎﺳﮭﺎ‬ ‫ﺑﺰاوﯾﺔ‬ ‫اﻟﺮأﺳﻲ‬ ‫ﻋﻠﻰ‬ ‫ﯾﻤﯿﻞ‬٣٠٥
‫أ‬= = (
‫ب‬(‫ق‬=......، ‫ﻧﯿﻮﺗﻦ‬‫ش‬=.......‫ﻧﯿﻮﺗﻦ‬
٤(‫اﻟﻤﻘﺎﺑﻞ‬ ‫اﻟﺸﻜﻞ‬ ‫ﻓﻰ‬:
‫وزﻧﮫ‬ ‫ﺟﺴﻢ‬٩٠‫ﻃﻮﻟﮫ‬ ‫ﺧﯿﻂ‬ ‫ﻧﮭﺎﯾﺔ‬ ‫ﻓﻰ‬ ‫ﻣﻌﻠﻖ‬ ‫ﺟﻢ‬ ‫ث‬٣٠‫أﻓﻘﯿﺔ‬ ‫ﻗﻮة‬ ‫ﺑﺘﺄﺗﯿﺮ‬ ‫اﻟﺠﺴﻢ‬ ‫ﺟﺬب‬ ‫ﺳﻢ‬
‫ﺑﻌﺪ‬ ‫ﻋﻠﻰ‬ ‫ھﻮ‬ ‫و‬ ‫اﺗﺰن‬ ‫ﺣﺘﻰ‬٢٤‫ﻓﺈن‬ ‫اﻟﺤﺎﺋﻂ‬ ‫ﻣﻦ‬ ‫ﺳﻢ‬:
‫أ‬= = (
‫ب‬(‫ق‬......... =، ‫ﺟﻢ‬ ‫ث‬‫ش‬........ =‫ﺟﻢ‬ ‫ث‬
‫ﺗﺄﺛﯿﺮ‬ ‫ﺗﺤﺖ‬ ‫ﺟﺴﻢ‬ ‫اﺗﺰان‬ ‫ﻋﻠﻰ‬ ‫ﺗﻤﺎرﯾﻦ‬
‫اﻟﻘﻮى‬ ‫ﻣﻦ‬ ‫ﻣﺠﻤﻮﻋﺔ‬
٩
‫ق‬
‫ش‬
٣٠
‫ج‬
‫ا‬
‫ب‬
‫ق‬
.....
‫ش‬
......
٩
.....
٩٠
‫ق‬
‫ش‬
٣٠‫ﺳﻢ‬
٢٤‫ﺳﻢ‬
‫ق‬
.....
‫ش‬
......
٩
.....

53. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
53
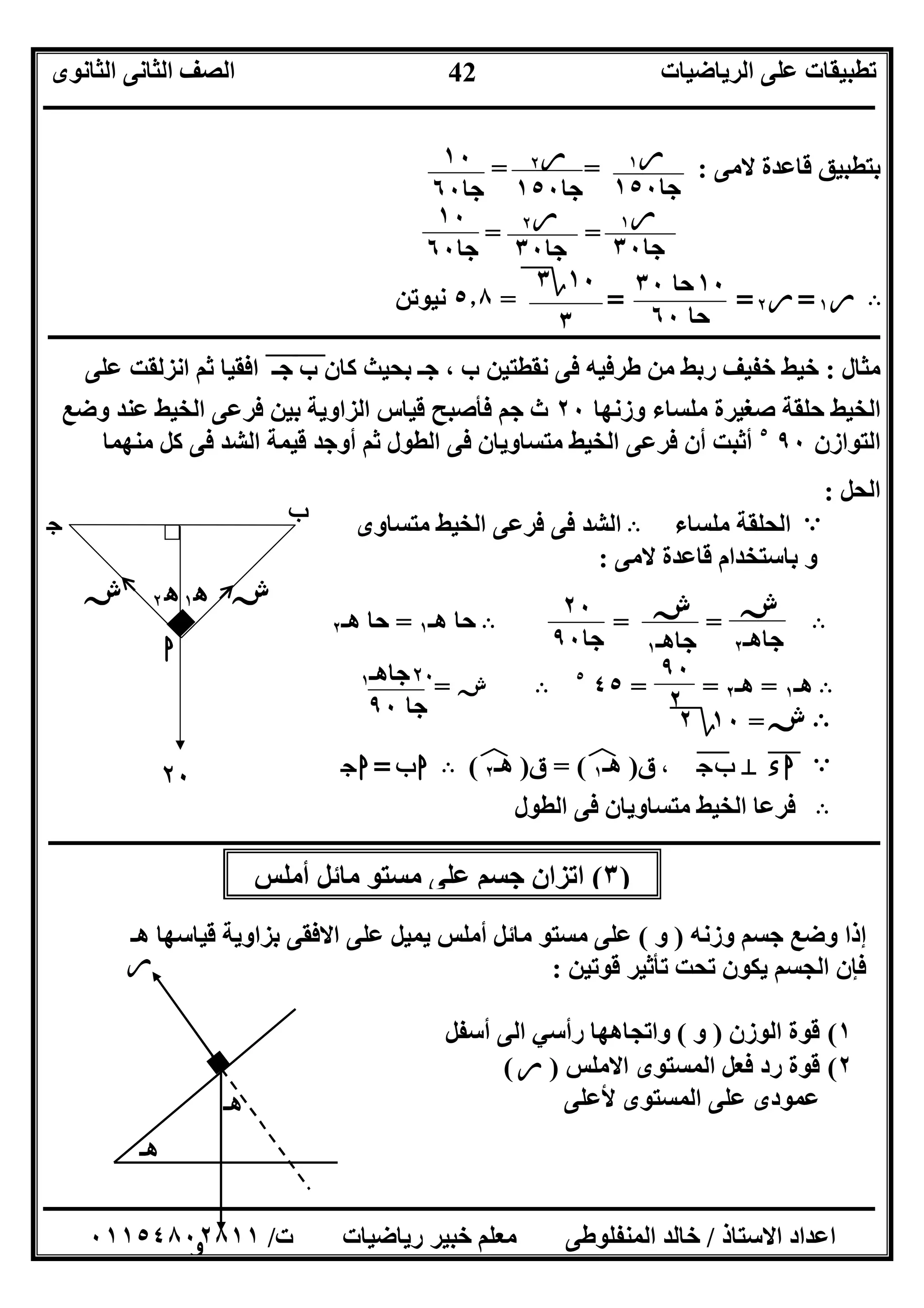
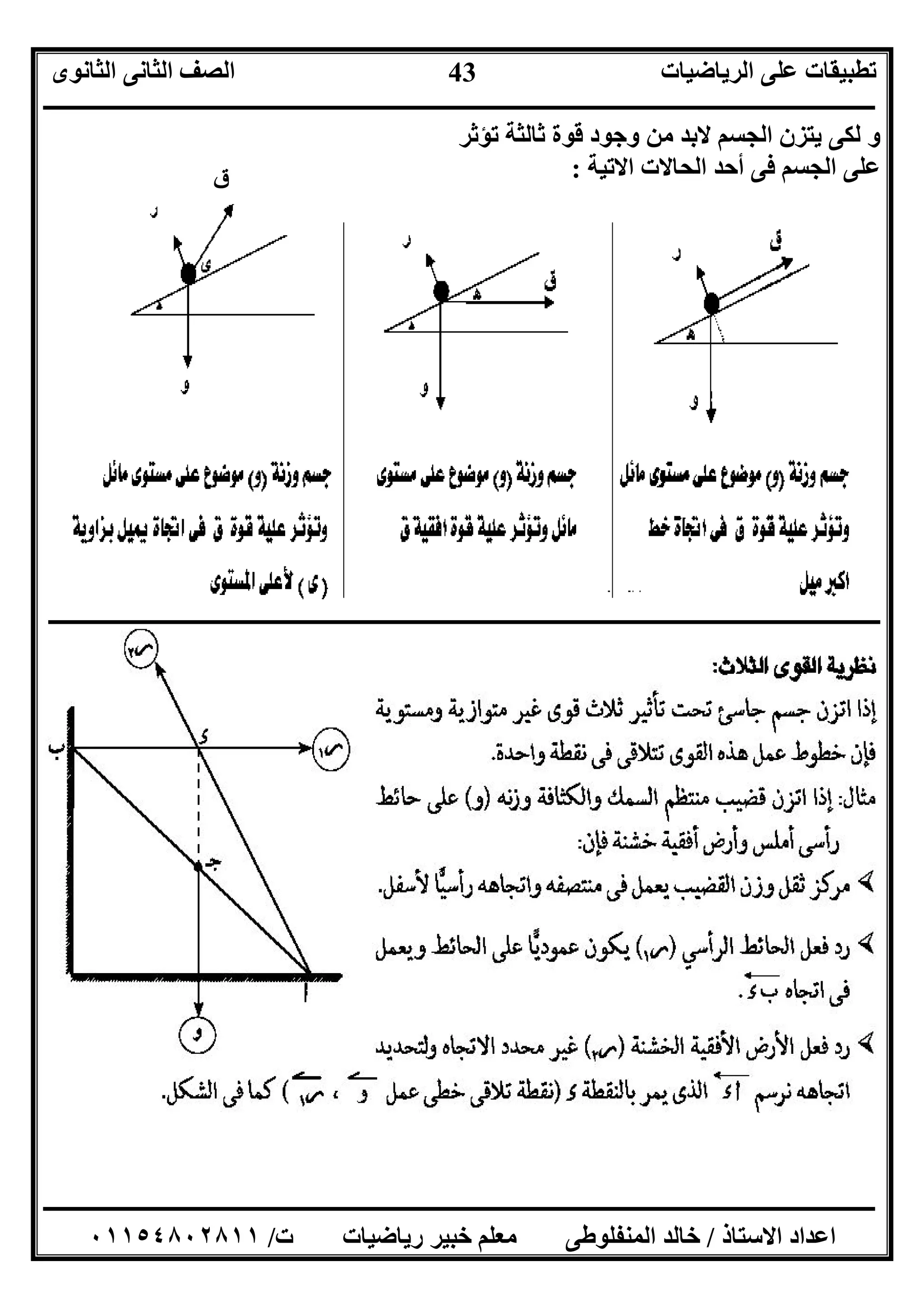
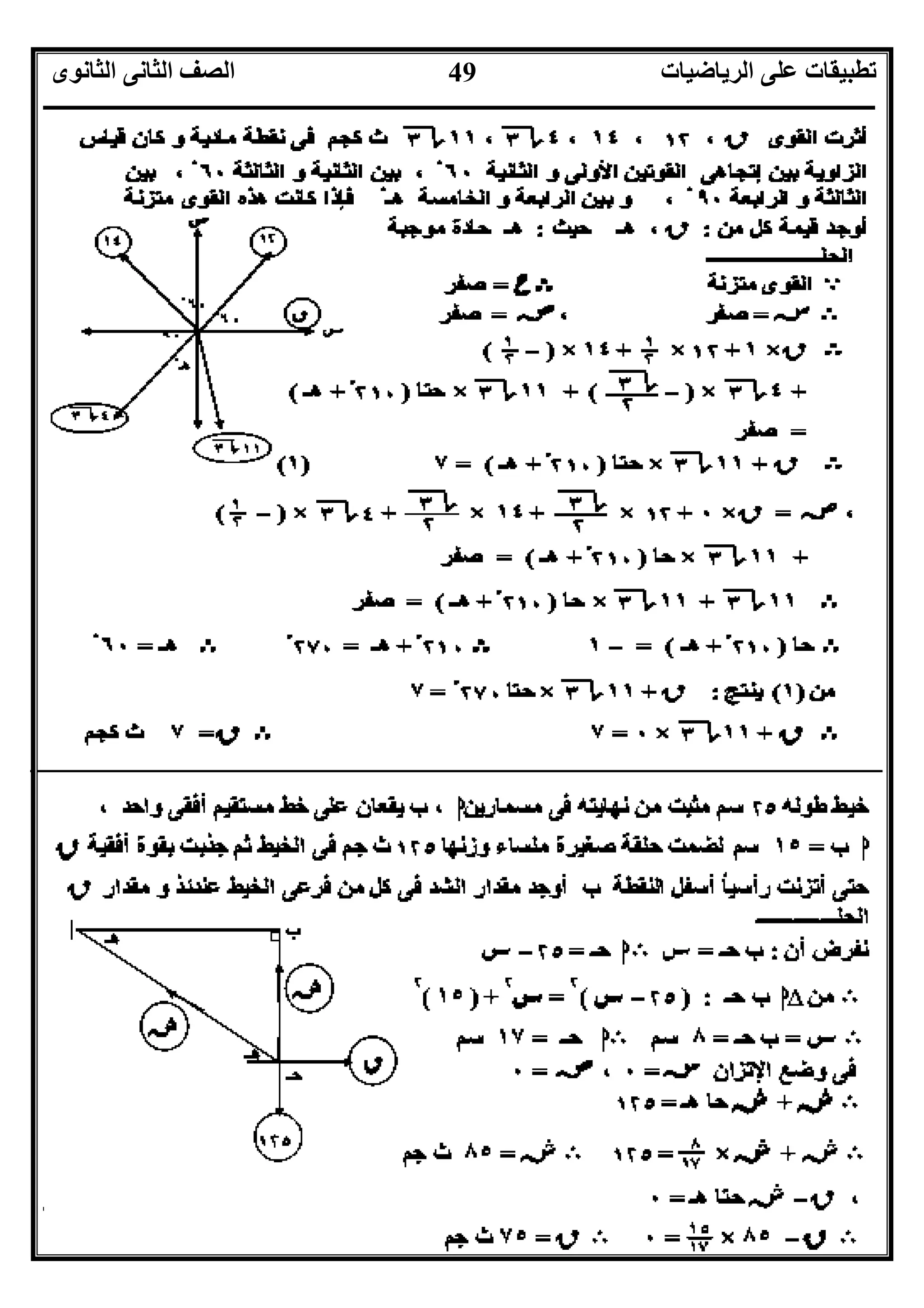
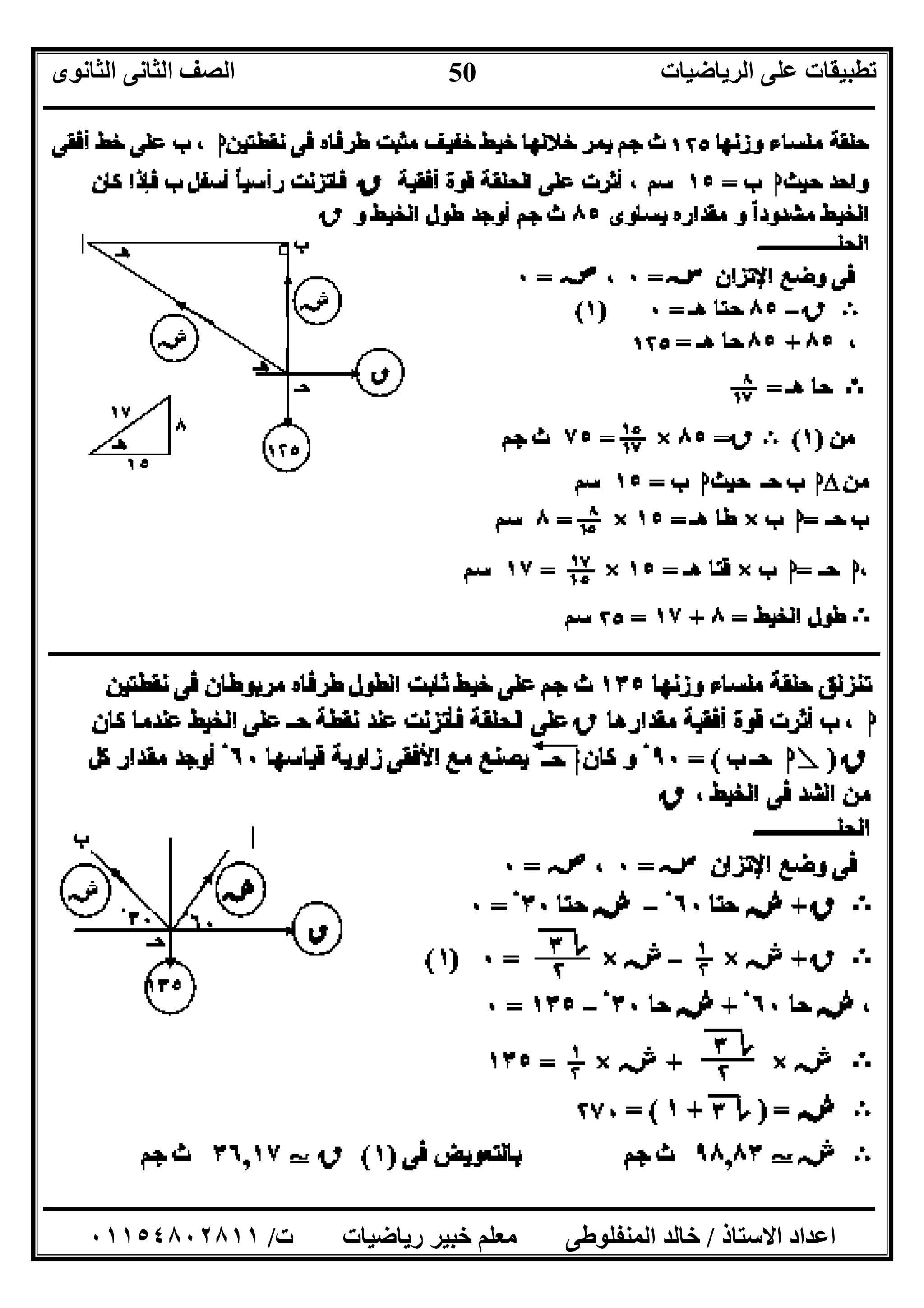
٥(‫اﻟﻤﻘﺎﺑﻞ‬ ‫اﻟﺸﻜﻞ‬ ‫ﻓﻰ‬:
‫ﻣﻠﺴﺎء‬ ‫ﺣﻠﻘﺔ‬ ‫ﺧﻼل‬ ‫ﯾﻤﺮ‬ ‫ﺧﻔﯿﻒ‬ ‫ﺧﯿﻂ‬
‫وزﻧﮭﺎ‬١٠٠، ‫داﯾﻦ‬‫ش‬١M‫ش‬٢
‫ﻓﺈن‬:‫ش‬١=............‫داﯾﻦ‬
،‫ش‬٢=............‫داﯾﻦ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
]٢[‫ﻣﻘﺎدﯾﺮھﺎ‬ ‫ﻣﺴﺘﻮﯾﺔ‬ ‫ﻗﻮى‬ ‫ﺛﻼث‬٨،١٠،١٢‫اﻟﻘﻮى‬ ‫ﻛﺎﻧﺖ‬ ‫ﻓﺈذا‬ ، ‫ﻣﺎدﯾﺔ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﺗﺆﺛﺮ‬ ‫ﻧﯿﻮﺗﻦ‬
‫ﻣﺘﺰﻧﺔ‬.‫؟‬ ‫اﻷﺧﺮﺗﯿﻦ‬ ‫اﻟﻘﻮﺗﯿﻦ‬ ‫ﺑﯿﻦ‬ ‫اﻟﺰاوﯾﺔ‬ ‫ﻗﯿﺎس‬ ‫ﻓﻤﺎ‬
‫ـــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
]٣[‫ﻣﻘﺎدﯾﺮھﺎ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﻣﺘﻼﻗﯿﺔ‬ ‫و‬ ‫ﻣﺴﺘﻮﯾﺔ‬ ‫ﻗﻮى‬ ‫ﺛﻼث‬‫ق‬١=٨، ‫ﺟﻢ‬ ‫ث‬‫ق‬٢=٤‫؟‬٣‫ﺟﻢ‬ ‫ث‬
،‫ق‬٣=٤‫ﺟﻢ‬ ‫ث‬.‫ﻗﯿﺎﺳﺎت‬ ‫أوﺟﺪ‬‫ﻋﻠﻤﺎ‬ ‫اﻟﺜﻼﺛﺔ‬ ‫اﻟﻘﻮى‬ ‫ﻋﻤﻞ‬ ‫ﺧﻄﻮط‬ ‫ﺑﯿﻦ‬ ‫اﻟﺜﻼﺛﺔ‬ ‫اﻟﺰواﯾﺎ‬
‫ﻣﺘﺰﻧﺔ‬ ‫اﻟﻤﺠﻤﻮﻋﺔ‬ ‫ﺑﺄن‬.
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــ‬
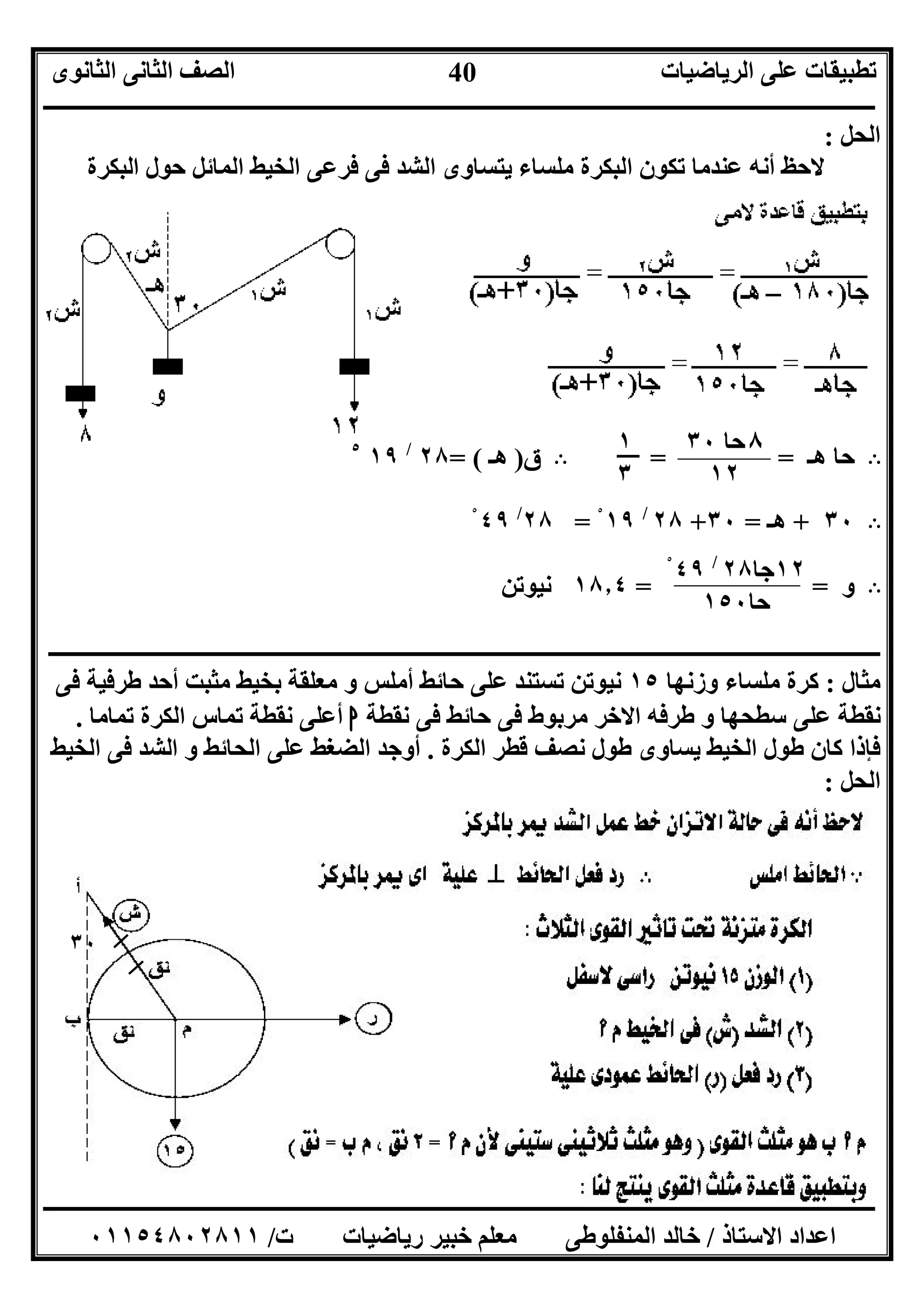
]٤[‫ﻣﻘﺪاره‬ ‫ﺛﻘﻞ‬ ‫ﻋﻠﻖ‬٣٤٠‫ﻃﻮﻻھﻤﺎ‬ ‫ﺧﯿﻄﯿﻦ‬ ‫ﺑﻮاﺳﻄﺔ‬ ‫ﺟﻢ‬ ‫ث‬١٦، ‫ﺳﻢ‬٣٠‫ﻓﻰ‬ ‫ﻧﻘﻄﺘﯿﻦ‬ ‫ﻣﻦ‬ ‫ﺳﻢ‬
‫ﺑﯿﻨﮭﻤﺎ‬ ‫اﻟﺒﻌﺪ‬ ‫أﻓﻘﻰ‬ ‫ﺧﻂ‬١٠٠‫اﻟﺨﯿﻄ‬ ‫ﻣﻦ‬ ‫ﻛﻞ‬ ‫ﻓﻰ‬ ‫اﻟﺸﺪ‬ ‫أوﺟﺪ‬ ‫ﺳﻢ‬‫ﯿﻦ‬.
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
]٥[‫وزﻧﮫ‬ ‫ﺟﺴﻢ‬ ‫ﻋﻠﻖ‬٦٫٥‫أﺣﺪھﻤﺎ‬ ‫ﻃﻮل‬ ‫ﺧﯿﻄﯿﻦ‬ ‫ﺑﻮاﺳﻄﺔ‬ ‫ﻧﯿﻮﺗﻦ‬٠٫٥‫اﻻﺧﺮ‬ ‫ﻃﻮل‬ ‫و‬ ‫ﻣﺘﺮ‬١٫٢
‫ﻣﺘﻌﺎﻣﺪﯾﻦ‬ ‫ﻛﺎﻧﺎ‬ ‫ﺑﺤﯿﺚ‬ ‫أﻓﻘﻰ‬ ‫ﻣﺴﺘﻘﯿﻢ‬ ‫ﻣﻦ‬ ‫ﻧﻘﻄﺘﯿﻦ‬ ‫ﻓﻰ‬ ‫اﻟﺨﯿﻄﺎن‬ ‫ورﺑﻂ‬ ‫ﻣﺘﺮ‬.
‫اﻟﺸﺪ‬ ‫ﻣﻘﺪار‬ ‫أوﺟﺪ‬‫اﻟﺨﯿﻄﯿﻦ‬ ‫ﻣﻦ‬ ‫ﻛﻞ‬ ‫ﻓﻰ‬.
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
]٦[‫ﻣﻘﺪاره‬ ‫ﺛﻘﻞ‬ ‫ﻋﻠﻖ‬٢٠٠‫ﺧ‬ ‫ﻃﺮف‬ ‫ﻣﻦ‬ ‫ﺟﻢ‬ ‫ث‬‫ﺟﺬب‬ ‫ﺛﻢ‬ ‫ﺣﺠﺮة‬ ‫ﺳﻘﻒ‬ ‫ﻓﻰ‬ ‫اﻷﺧﺮ‬ ‫ﻃﺮﻓﮫ‬ ‫ﻣﺜﺒﺖ‬ ‫ﯿﻂ‬
‫ﻗﯿﺎﺳﮭﺎ‬ ‫ﺑﺰاوﯾﺔ‬ ‫اﻟﺮأﺳﻲ‬ ‫ﻋﻠﻰ‬ ‫ﻣﺎﺋﻼ‬ ‫اﻟﺨﯿﻂ‬ ‫أﺻﺒﺢ‬ ‫ﺣﺘﻰ‬ ‫أﻓﻘﯿﺔ‬ ‫ﺑﻘﻮة‬ ‫اﻟﺜﻘﻞ‬٣٠٥
‫اﻟﺨﯿﻂ‬ ‫ﻓﻰ‬ ‫اﻟﺸﺪ‬ ‫و‬ ‫اﻷﻓﻘﯿﺔ‬ ‫اﻟﻘﻮة‬ ‫ﻣﻦ‬ ‫ﻛﻞ‬ ‫ﻣﻘﺪار‬ ‫ﻋﯿﻦ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
]٧[‫ﻣﻘﺪاره‬ ‫وزن‬ ‫ﻋﻠﻖ‬٧٢‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﻟﻠﺨﯿﻂ‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﻄﺮف‬ ‫ﺛﺒﺖ‬ ‫و‬ ‫ﺧﯿﻂ‬ ‫ﻃﺮﻓﻰ‬ ‫أﺣﺪ‬ ‫ﻓﻰ‬ ‫ﺟﺮام‬ ‫ﺛﻘﻞ‬‫ا‬
‫ﺣﺎﺋﻂ‬ ‫ﻋﻠﻰ‬‫اﻷو‬ ‫اﻟﺨﯿﻂ‬ ‫ﻣﻦ‬ ‫ب‬ ‫ﻧﻘﻄﺔ‬ ‫ﻋﻨﺪ‬ ‫ﺛﺄن‬ ‫ﺧﯿﻂ‬ ‫رﺑﻂ‬ ‫ز‬ ‫رأﺳﻲ‬‫ﻋﻦ‬ ‫ﺗﺒﻌﺪ‬ ‫ل‬‫ا‬‫ﺑﻤﻘﺪار‬٢٥‫ﺳﻢ‬
‫اﻟﺤﺎﺋﻂ‬ ‫ﻋﻦ‬ ‫ﺗﺒﻌﺪ‬ ‫ب‬ ‫اﻟﻨﻘﻄﺔ‬ ‫ﺻﺎرت‬ ‫ﺣﺘﻰ‬ ‫اﻓﻘﻰ‬ ‫اﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫ﺷﺪ‬ ‫و‬٧‫ﺳﻢ‬.
‫اﻟﺨﯿﻂ‬ ‫ﺟﺰأى‬ ‫ﻣﻦ‬ ‫ﻛﻞ‬ ‫ﻓﻰ‬ ‫و‬ ‫اﻻﻓﻘﻰ‬ ‫اﻟﺨﯿﻂ‬ ‫ﻓﻰ‬ ‫اﻟﺸﺪ‬ ‫ﻗﻮة‬ ‫أوﺟﺪ‬‫اﻟﺜﺎﻧﻰ‬
١٠٠
**
‫ش‬١‫ش‬٢

54. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
54
]٨[‫وزﻧﮫ‬ ‫ﺟﺴﻢ‬ ‫ﻋﻠﻖ‬٢٠٠‫ﺑﺰاوﯾﺔ‬ ‫اﻟﺮأﺳﻲ‬ ‫ﻋﻠﻰ‬ ‫أﺣﺪھﻤﺎ‬ ‫ﯾﻤﯿﻞ‬ ‫ﺧﻔﯿﻔﯿﻦ‬ ‫ﺧﯿﻄﯿﻦ‬ ‫ﺑﻮاﺳﻄﺔ‬ ‫ﺟﻢ‬ ‫ث‬
‫ﺑﺰاوﯾﺔ‬ ‫اﻟﺮأﺳﻲ‬ ‫ﻋﻠﻰ‬ ‫اﻷﺧﺮ‬ ‫اﻟﺨﯿﻂ‬ ‫ﯾﻤﯿﻞ‬ ‫و‬ ‫ھـ‬ ‫ﻗﯿﺎﺳﮭﺎ‬٣٠٥
‫ﻓﻰ‬ ‫اﻟﺸﺪ‬ ‫ﻣﻘﺪار‬ ‫ﻛﺎن‬ ‫ﻓﺈذا‬ ،
‫ﯾﺴﺎوى‬ ‫اﻷول‬ ‫اﻟﺨﯿﻂ‬١٠٠‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺨﯿﻂ‬ ‫ﻓﻰ‬ ‫اﻟﺸﺪ‬ ‫ﻣﻘﺪار‬ ، ‫ھـ‬ ‫ﻓﺄوﺟﺪ‬ ، ‫ﺟﻢ‬ ‫ث‬.
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
]٩[‫وزن‬ ‫ﻋﻠﻖ‬)‫و‬(‫أوﻟﮭ‬ ‫ﯾﻤﯿﻞ‬ ‫ﺧﯿﻄﯿﻦ‬ ‫ﺑﻮاﺳﻄﺔ‬ ‫ﻧﯿﻮﺗﻦ‬‫و‬ ‫ھـ‬ ‫ﻗﯿﺎﺳﮭﺎ‬ ‫ﺑﺰاوﯾﺔ‬ ‫اﻟﺮأﺳﻲ‬ ‫ﻋﻠﻰ‬ ‫ﻤﺎ‬‫ﯾﻤﺮ‬
‫ﻣﻘﺪاره‬ ‫وزﻧﺎ‬ ‫اﻷﺧﺮى‬ ‫ﻧﮭﺎﯾﺘﮫ‬ ‫ﻓﻰ‬ ‫ﯾﺤﻤﻞ‬ ‫و‬ ‫ﻣﻠﺴﺎء‬ ‫ﺻﻐﯿﺮة‬ ‫ﺑﻜﺮة‬ ‫ﻋﻠﻰ‬١٢‫اﻟﺜﺎﻧﻰ‬ ‫ﯾﻤﯿﻞ‬ ‫و‬ ‫ﻧﯿﻮﺗﻦ‬
‫ﺑﺰا‬ ‫اﻟﺮأﺳﻲ‬ ‫ﻋﻠﻰ‬‫ﻗﯿﺎﺳﮭﺎ‬ ‫وﯾﺔ‬٣٠٥
‫ﻧﮭﺎﯾﺘﮫ‬ ‫ﻓﻰ‬ ‫ﯾﺤﻤﻞ‬ ‫و‬ ‫ﻣﻠﺴﺎء‬ ‫ﺻﻌﯿﺮة‬ ‫ﺑﻜﺮة‬ ‫ﻋﻠﻰ‬ ‫ﯾﻤﺮ‬ ‫و‬
‫ﻣﻘﺪاره‬ ‫وزﻧﺎ‬ ‫اﻷﺧﺮى‬٨‫ھـ‬ ‫ﻗﯿﻤﺔ‬ ‫و‬ ‫اﻟﻮزن‬ ‫ﻣﻘﺪار‬ ‫أوﺟﺪ‬ ‫ز‬ ‫ﻧﯿﻮﺗﻦ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــ‬
]١٠[‫وزﻧﮫ‬ ‫ﺟﺴﻢ‬٤٠٠‫ﻧﻘﻄﺔ‬ ‫ﻣﻦ‬ ‫ﻣﻌﻠﻖ‬ ‫ﺟﺮام‬ ‫ﺛﻘﻞ‬‫ا‬‫ﻣﻦ‬ ‫ب‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﺧﯿﻂ‬ ‫رﺑﻂ‬ ، ‫ﺧﯿﻂ‬ ‫ﺑﻮاﺳﻄﺔ‬
‫ﺣـ‬ ‫ب‬ ‫ﺛﺎن‬ ‫ﺑﺨﯿﻂ‬ ‫أﻓﻘﯿﺎ‬ ‫ﺷﺪ‬ ‫و‬ ‫اﻟﺨﯿﻂ‬"‫ﻓﻰ‬ ‫ﯾﺘﺪﻟﻰ‬ ‫و‬ ‫ﻣﺜﺒﺘﮫ‬ ‫ﻣﻠﺴﺎء‬ ‫ﺻﻐﯿﺮة‬ ‫ﺑﻜﺮة‬ ‫ﻋﻠﻰ‬ ‫ﯾﻤﺮ‬
‫ﻣﻘﺪاره‬ ‫ﺛﻘﻞ‬ ‫ﻧﮭﺎﯾﺘﮫ‬٣٠٠‫ﺟﺮام‬ ‫ﺛﻘﻞ‬.‫ﻣﯿﻞ‬ ‫أوﺟﺪ‬‫ب‬‫ا‬"‫اﻟﺮأﺳ‬ ‫ﻋﻠﻰ‬‫ﻣﻦ‬ ‫ﻛﻞ‬ ‫ﻓﻰ‬ ‫اﻟﺸﺪ‬ ‫و‬ ‫ﻲ‬
‫اﻟﺨﯿﻄﯿﻦ‬‫ب‬‫ا‬"‫ﺣـ‬ ‫ب‬ ،"
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫أﻣﻠﺲ‬ ‫ﻣﺎﺋﻞ‬ ‫ﻣﺴﺘﻮ‬ ‫ﻋﻠﻰ‬ ‫ﺟﺴﻢ‬ ‫اﺗﺰان‬ ‫ﻋﻠﻰ‬ ‫ﻣﺴﺎﺋﻞ‬:
]١[‫ﻋﻠ‬ ‫ﺟﺴﻢ‬ ‫وﺿﻊ‬‫ﻗﯿﺎﺳﮭﺎ‬ ‫ﺑﺰاوﯾﺔ‬ ‫اﻷﻓﻘﻰ‬ ‫ﻋﻠﻰ‬ ‫ﯾﻤﯿﻞ‬ ‫أﻣﻠﺲ‬ ‫ﻣﺎﺋﻞ‬ ‫ﻣﺴﺘﻮى‬ ‫ﻰ‬٣٠٥
‫اﻟﺠﺴﻢ‬ ‫ﺣﻔﻆ‬ ‫إذا‬
‫ﻗﻮة‬ ‫ﺑﻮاﺳﻄﺔ‬ ‫ﺗﻮازن‬ ‫ﺣﺎﻟﺔ‬ ‫ﻓﻰ‬‫ق‬‫ﻣﻘﺪارھﺎ‬ ‫و‬ ‫أﻋﻠﻰ‬ ‫اﻟﻰ‬ ‫ﻟﻠﻤﺴﺘﻮى‬ ‫ﻣﯿﻞ‬ ‫أﻛﺒﺮ‬ ‫اﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫ﺗﻌﻤﻞ‬٢٠٠
‫اﻟﺠﺴﻢ‬ ‫ﻋﻠﻰ‬ ‫اﻟﻤﺴﺘﻮى‬ ‫ﻓﻌﻞ‬ ‫رد‬ ‫و‬ ‫اﻟﺠﺴﻢ‬ ‫وزن‬ ‫ﻓﺄوﺟﺪ‬ ‫ﺟﻢ‬ ‫ث‬.
‫ــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
]٢[‫وزﻧﮫ‬ ‫ﺟﺴﻢ‬ ‫وﺿﻊ‬٦‫ﺣﻔﻆ‬ ‫و‬ ‫ھـ‬ ‫ﻗﯿﺎﺳﮭﺎ‬ ‫ﺑﺰاوﯾﺔ‬ ‫اﻷﻓﻘﻰ‬ ‫ﻋﻠﻰ‬ ‫ﯾﻤﯿﻞ‬ ‫أﻣﻠﺲ‬ ‫ﻣﺴﺘﻮى‬ ‫ﻋﻠﻰ‬ ‫ﻧﯿﻮﺗﻦ‬
‫ﻣﻘﺪارھﺎ‬ ‫ﻗﻮة‬ ‫ﺑﻮاﺳﻄﺔ‬ ‫ﺗﻮازﻧﮫ‬٢‫؟‬٣‫ﺑ‬ ‫ﻟﻠﻤﺴﺘﻮى‬ ‫ﻣﯿﻞ‬ ‫أﻛﺒﺮ‬ ‫ﺧﻂ‬ ‫ﻋﻠﻰ‬ ‫ﺗﻤﯿﻞ‬ ‫و‬ ‫ﻧﯿﻮﺗﻦ‬‫ﻧﻔﺲ‬ ‫ﻟﮭﺎ‬ ‫ﺰاوﯾﺔ‬
‫ﻷﻋﻠﻰ‬ ‫ھـ‬ ‫اﻟﻘﯿﺎس‬.‫اﻟﺠﺴﻢ‬ ‫ﻋﻠﻰ‬ ‫اﻟﻤﺴﺘﻮى‬ ‫ﻓﻌﻞ‬ ‫رد‬ ‫و‬ ‫ھـ‬ ‫ﻗﯿﻤﺔ‬ ‫أوﺟﺪ‬.

55. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
55
]٣[‫وزﻧﮫ‬ ‫ﺟﺴﻢ‬٩‫أﻣﻠﺲ‬ ‫ﻣﺎﺋﻞ‬ ‫ﻣﺴﺘﻮى‬ ‫ﻋﻠﻰ‬ ‫ﻣﻮﺿﻮع‬ ‫ﻛﺠﻢ‬ ‫ث‬
‫ﺑﺰاوﯾﺔ‬ ‫اﻻﻓﻘﻰ‬ ‫ﻋﻠﻰ‬ ‫ﯾﻤﯿﻞ‬٣٠٥
‫ﺗﻮازﻧﮫ‬ ‫ﺣﻔﻆ‬ ‫و‬
‫ﺷﺪ‬ ‫ﻗﻮة‬ ‫ﺑﻮاﺳﻄﺔ‬‫ش‬‫ﻣﻘﺪارھﺎ‬٣‫؟‬٣‫ﻛﺠﻢ‬ ‫ث‬
‫ﻃﺮ‬ ‫أﺣﺪ‬ ‫ﻣﻦ‬ ‫ﻣﺜﺒﺖ‬ ‫ﺧﯿﻂ‬ ‫ﻓﻰ‬ ‫ﺗﻌﻤﻞ‬‫ﺑﺎﻟﺠﺴﻢ‬ ‫ﻓﯿﮫ‬
‫رأﺳﻲ‬ ‫ﺣﺎﺋﻂ‬ ‫ﻓﻰ‬ ‫اﻵﺧﺮ‬ ‫اﻟﻄﺮف‬ ‫و‬.
‫اﻻﻓﻘﻰ‬ ‫اﻟﺨﯿﻄﻤﻊ‬ ‫ﯾﺼﻨﻌﮭﺎ‬ ‫اﻟﺘﻰ‬ ‫اﻟﺰاوﯾﺔ‬ ‫ﻗﯿﺎس‬ ‫أوﺟﺪ‬
‫اﻟﺠﺴﻢ‬ ‫ﻋﻠﻰ‬ ‫اﻟﻤﺴﺘﻮى‬ ‫ﻓﻌﻞ‬ ‫رد‬ ‫ﻣﻘﺪار‬ ‫و‬.
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــ‬
]٤[‫وزﻧﮫ‬ ‫ﺟﺴﻢ‬ ‫وﺿﻊ‬٩٠‫ﻗﯿﺎﺳﮭﺎ‬ ‫ﺑﺰاوﯾﺔ‬ ‫اﻻﻓﻘﻰ‬ ‫ﻋﻠﻰ‬ ‫ﯾﻤﯿﻞ‬ ‫أﻣﻠﺲ‬ ‫ﻣﺴﺘﻮى‬ ‫ﻋﻠﻰ‬ ‫ﺟﻢ‬ ‫ث‬٣٠٥
‫ﻗﻮة‬ ‫ﺑﻮاﺳﻄﺔ‬ ‫ﺗﻮازن‬ ‫ﺣﺎﻟﺔ‬ ‫ﻓﻰ‬ ‫اﻟﺠﺴﻢ‬ ‫ﺣﻔﻆ‬ ‫إذا‬ ‫و‬.‫اﻟﻤﺴﺘﻮى‬ ‫ﻓﻌﻞ‬ ‫رد‬ ‫و‬ ‫اﻟﻘﻮة‬ ‫ھﺬه‬ ‫أوﺟﺪ‬:
)١(‫أﻓﻘﯿﺔ‬ ‫ﻛﺎﻧﺖ‬ ‫إذا‬)٢(‫ﻗ‬ ‫زاوﯾﺔ‬ ‫ﺗﺼﻨﻊ‬ ‫ﻛﺎﻧﺖ‬ ‫إذا‬‫ﯿﺎﺳﮭﺎ‬٦٠٥
‫اﻻﻓﻘﻰ‬ ‫ﻣﻊ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺘﺰﻧﺔ‬ ‫ﻗﻮى‬ ‫ﺛﻼث‬ ‫ﻋﻤﻞ‬ ‫ﺧﻄﻮط‬ ‫ﺗﻼﻗﻰ‬ ‫ﻋﻠﻰ‬ ‫ﻣﺴﺎﺋﻞ‬:
]١[‫ﻗﻄﺮھﺎ‬ ‫ﻧﺼﻒ‬ ‫ﻃﻮل‬ ‫ﻣﻠﺴﺎء‬ ‫ﻛﺮة‬٦‫وزﻧﮭ‬ ‫و‬ ‫ﺳﻢ‬‫ﺎ‬٢٤‫ﻋﻠﻰ‬ ‫ﻣﺴﺘﻨﺪة‬ ‫ﻣﺮﻛﺰھﺎ‬ ‫ﻓﻰ‬ ‫ﯾﺆﺛﺮ‬ ‫ﻧﯿﻮﺗﻦ‬
‫ﻃﻮﻟﮫ‬ ‫ﺑﺨﯿﻂ‬ ‫ﻣﻌﻠﻘﺔ‬ ‫و‬ ‫أﻣﻠﺲ‬ ‫رأﺳﻲ‬ ‫ﺣﺎﺋﻂ‬٤‫ﺳﻢ‬.‫و‬ ‫ﺳﻄﺤﮭﺎ‬ ‫ﻋﻠﻰ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﻃﺮﻓﯿﮫ‬ ‫أﺣﺪ‬ ‫ﺛﺒﺖ‬
‫ﺗﻤﺎس‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻮق‬ ‫اﻵﺧﺮ‬ ‫اﻟﻄﺮف‬ ‫ﺛﺒﺖ‬ً‫ﺎ‬‫ﺗﻤﺎﻣ‬ ‫ﺑﺎﻟﺤﺎﺋﻂ‬ ‫اﻟﻜﺮة‬.‫اﻟﺨﯿﻂ‬ ‫ﻓﻰ‬ ‫اﻟﺸﺪ‬ ‫و‬ ‫اﻟﺤﺎﺋﻂ‬ ‫ﻓﻌﻞ‬ ‫رد‬ ‫أوﺟﺪ‬
]٢[‫وزﻧﮭﺎ‬ ‫ﻣﻠﺴﺎء‬ ‫ﻛﺮة‬١٥‫ﻓﻰ‬ ‫ﻃﺮﻓﯿﮫ‬ ‫أﺣﺪ‬ ‫ﻣﺜﺒﺖ‬ ‫ﺑﺨﯿﻂ‬ ‫ﻣﻌﻠﻘﺔ‬ ‫و‬ ‫أﻣﻠﺲ‬ ‫ﺣﺎﺋﻂ‬ ‫ﻋﻠﻰ‬ ‫ﺗﺴﺘﻨﺪ‬ ‫ﻧﯿﻮﺗﻦ‬
‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫اﻟﺤﺎﺋﻂ‬ ‫ﻓﻰ‬ ‫ﻣﺮﺑﻮط‬ ‫اﻻﺧﺮ‬ ‫ﻃﺮﻓﮫ‬ ‫و‬ ‫ﺳﻄﺤﮭﺎ‬ ‫ﻋﻠﻰ‬ ‫ﻧﻘﻄﺔ‬‫ا‬‫ﺗﻤﺎﻣﺎ‬ ‫اﻟﻜﺮة‬ ‫ﺗﻤﺎس‬ ‫ﻧﻘﻄﺔ‬ ‫ﻋﻠﻰ‬
‫اﻟﻜﺮة‬ ‫ﻗﻄﺮ‬ ‫ﻧﺼﻒ‬ ‫ﻃﻮل‬ ‫ﯾﺴﺎوى‬ ‫اﻟﺨﯿﻂ‬ ‫ﻃﻮل‬ ‫ﻛﺎن‬ ‫ﻓﺈذا‬.‫اﻟﺨﯿﻂ‬ ‫ﻓﻰ‬ ‫اﻟﺸﺪ‬ ‫و‬ ‫اﻟﺤﺎﺋﻂ‬ ‫ﻋﻠﻰ‬ ‫اﻟﻀﻐﻂ‬ ‫أوﺟﺪ‬
]٣[‫ﻃﻮﻟﮫ‬ ‫ﻣﻨﺘﻈﻢ‬ ‫ﻗﻀﯿﺐ‬ ‫ﻋﻠﻖ‬١٣٠‫ووزﻧﮫ‬ ‫ﺳﻢ‬٢٦‫ﺧﯿﻄﯿﻦ‬ ‫ﻓﻰ‬ ‫ﻣﻄﻠﻘﺎ‬ ‫ﺗﻌﻠﯿﻘﺎ‬ ‫ﻃﺮﻓﯿﮫ‬ ‫ﻣﻦ‬ ‫ﻧﯿﻮﺗﻦ‬
‫أﺣﺪھﻤﺎ‬ ‫ﻃﻮل‬ ‫ﻛﺎن‬ ‫و‬ ‫واﺣﺪة‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﻣﺮﺑﻮﻃﯿﻦ‬٥٠‫ﻃﻮل‬ ‫و‬ ‫ﺳﻢ‬١٢٠‫ﺳﻢ‬.‫اﻟﺬى‬ ‫اﻟﻮﺿﻊ‬ ‫ھﻮ‬ ‫ﻣﺎ‬
‫اﻟﺨﯿﻄﯿﻦ‬ ‫ﻣﻦ‬ ‫ﻛﻞ‬ ‫ﻓﻰ‬ ‫اﻟﺸﺪ‬ ‫ﻣﻘﺪار‬ ‫ھﻮ‬ ‫ﻣﺎ‬ ‫ز‬ ‫؟‬ ‫ﻣﺘﺰﻧﺎ‬ ‫اﻟﻘﻀﯿﺐ‬ ‫ﻓﯿﮫ‬ ‫ﯾﻜﻮن‬‫؟‬
٩
‫ر‬
٣‫؟‬٣
٣٠
‫ھـ‬

56. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
56
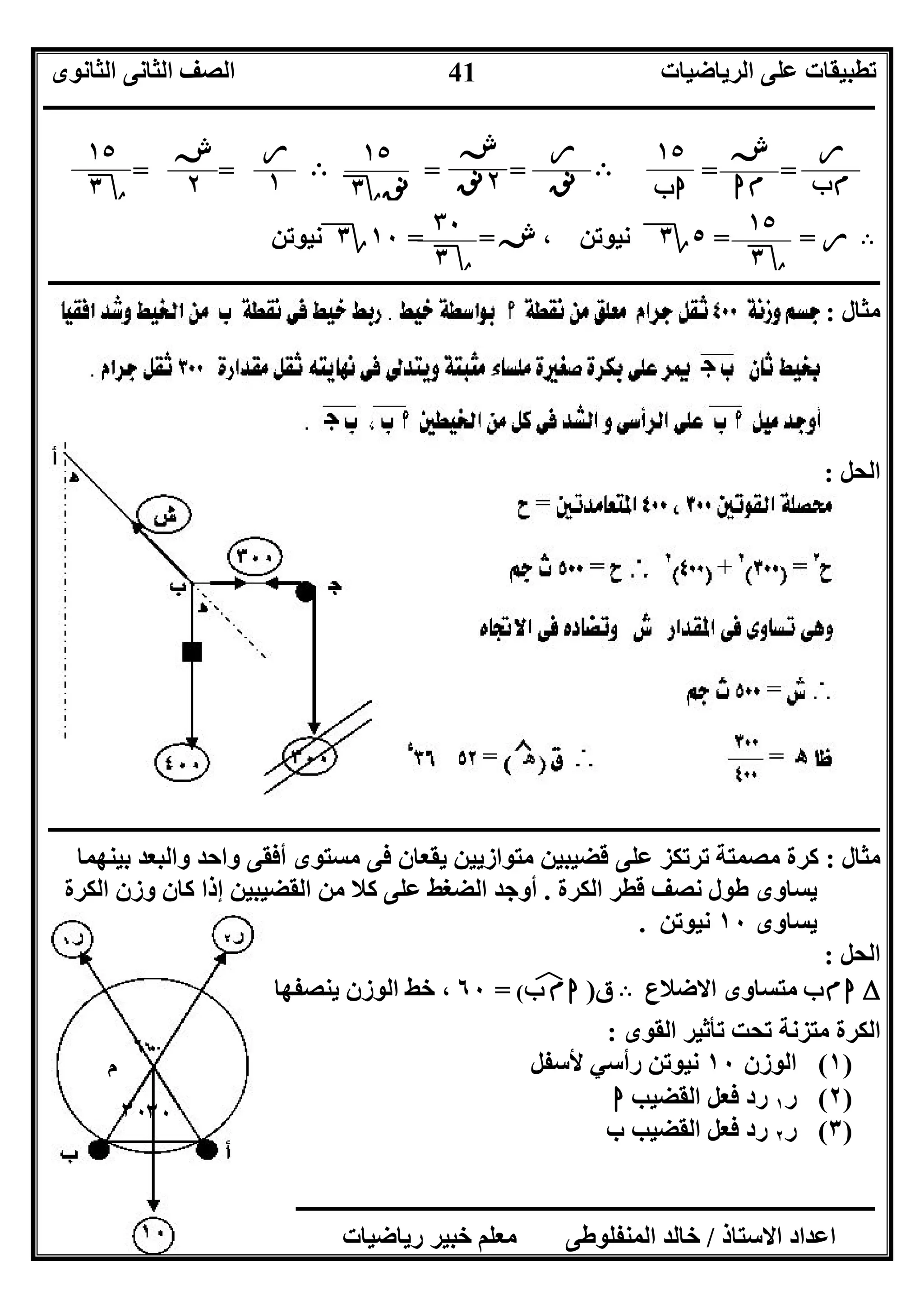
]٤[‫ﺑﯿﻨﮭﻤﺎ‬ ‫اﻟﺒﻌﺪ‬ ‫و‬ ‫واﺣﺪ‬ ‫أﻓﻘﻰ‬ ‫ﻣﺴﺘﻮى‬ ‫ﻓﻰ‬ ‫ﯾﻘﻌﺎن‬ ‫ﻣﺘﻮازﯾﯿﻦ‬ ‫ﻓﻀﯿﺒﯿﻦ‬ ‫ﻋﻠﻰ‬ ‫ﺗﺮﺗﻜﺰ‬ ‫ﻣﺼﻤﺘﺔ‬ ‫ﻛﺮة‬
‫اﻟﻜﺮة‬ ‫ﻗﻄﺮ‬ ‫ﻧﺼﻒ‬ ‫ﻃﻮل‬ ‫ﯾﺴﺎوى‬.‫ﯾﺴﺎوى‬ ‫اﻟﻜﺮة‬ ‫وزن‬ ‫ﻛﺎن‬ ‫إذا‬ ‫اﻟﻘﻀﯿﺒﯿﻦ‬ ‫ﻣﻦ‬ ‫ﻛﻞ‬ ‫ﻋﻠﻰ‬ ‫اﻟﻀﻐﻂ‬ ‫أوﺟﺪ‬
١٠‫ﻧﯿﻮﺗﻦ‬
]٥[‫ﻃﻮﻟﮫ‬ ‫ﻣﻨﺘﻈﻢ‬ ‫ﻗﻀﯿﺐ‬٨٠‫ووزﻧﮫ‬ ‫ﺳﻢ‬١٢‫ﺑﺤﺒﻠﯿﻦ‬ ‫ﻃﺮﻓﯿﮫ‬ ‫ﻣﻦ‬ ‫ﻋﻠﻖ‬ ‫ﻣﻨﺘﺼﻔﮫ‬ ‫ﻓﻰ‬ ‫ﯾﺆﺛﺮ‬ ‫ﻧﯿﻮﺗﻦ‬
‫أﺣﺪھﻤﺎ‬ ‫ﻃﻮل‬ ‫و‬ ‫ﻣﺘﻌﺎﻣﺪﯾﻦ‬ ‫اﻟﺤﺒﻼن‬ ‫ﻛﺎن‬ ‫ﻓﺈذا‬ ‫اﻟﺴﻘﻒ‬ ‫ﻓﻰ‬ ‫ﻣﺴﻤﺎر‬ ‫ﻓﻰ‬ ‫ﻃﺮﻓﺎھﻤﺎ‬ ‫ﺛﺒﺖ‬٤٨‫ﺳﻢ‬
‫ﯾﻜﻮ‬ ‫ﻋﻨﺪﻣﺎ‬ ‫اﻟﺤﺒﻠﯿﻦ‬ ‫ﻣﻦ‬ ‫ﻛﻞ‬ ‫ﻓﻰ‬ ‫اﻟﺸﺪ‬ ‫ﻣﻘﺪار‬ ‫ﻓﻤﺎ‬‫ﺗﻮازن‬ ‫ﺣﺎﻟﺔ‬ ‫ﻓﻰ‬ ‫و‬ ً‫ﺎ‬‫ﻣﻄﻠﻘ‬ ً‫ﺎ‬‫ﺗﻌﻠﯿﻘ‬ ً‫ﺎ‬‫ﻣﻌﻠﻘ‬ ‫اﻟﻘﻀﯿﺐ‬ ‫ن‬
]٦[‫ﻣﻨﺘﻈﻢ‬ ‫ﻗﻀﯿﺐ‬‫ب‬‫ا‬"‫ﻓﻰ‬ ‫ﻣﻔﺼﻞ‬ ‫ﺣﻮل‬ ‫رأﺳﻲ‬ ‫ﻣﺴﺘﻮى‬ ‫ﻓﻰ‬ ‫ﻋﺎﺋﻖ‬ ‫ﺑﻐﯿﺮ‬ ‫اﻟﺪوران‬ ‫ﯾﻤﻜﻨﮫ‬‫ا‬‫رﺑﻂ‬ ،
‫أﻋﻠﻰ‬ ‫ﺟـ‬ ‫ﻋﻨﺪ‬ ‫ﻣﻠﺴﺎء‬ ‫ﺑﻜﺮة‬ ‫ﻋﻠﻰ‬ ‫ﯾﻤﺮ‬ ‫ﺑﺨﯿﻂ‬ ‫ب‬ ‫اﻻﺧﺮ‬ ‫ﻃﺮﻓﮫ‬‫ا‬‫ﺛﻘﻞ‬ ‫ﻧﺼﻒ‬ ‫ﯾﺴﺎوى‬ ‫ﺛﻘﻼ‬ ‫ﯾﺤﻤﻞ‬ ‫و‬ ً‫ﺎ‬‫ﺗﻤﺎﻣ‬
‫اﻟﻘﻀﯿﺐ‬.‫ا‬ ‫ﻋﻠﻰ‬ ‫اﻟﻘﻀﯿﺐ‬ ‫ﻣﯿﻞ‬ ‫زاوﯾﺔ‬ ‫ﻗﯿﺎس‬ ‫أوﺟﺪ‬‫أن‬ ‫ﻋﻠﻢ‬ ‫إذا‬ ‫اﻟﺘﻮازن‬ ‫ﺣﺎﻟﺔ‬ ‫ﻓﻰ‬ ‫ﻻﻓﻘﻰ‬‫ج‬‫ا‬=‫ب‬‫ا‬
]٧[‫ب‬ ‫ا‬"‫ﻃﻮﻟﮫ‬ ‫ﻣﻨﺘﻈﻢ‬ ‫ﻗﻀﯿﺐ‬٤٠‫ووزﻧﮫ‬ ‫ﺳﻢ‬١٢‫ﺑﻄﺮﻓﮫ‬ ‫ﯾﺴﻨﺪ‬ ‫ﻧﯿﻮﺗﻦ‬‫ا‬‫أﻣﻠﺲ‬ ‫رأﺳﻲ‬ ‫ﺣﺎﺋﻂ‬ ‫ﻋﻠﻰ‬
‫ﻣﺮﺑ‬ ‫ﺧﻔﯿﻒ‬ ‫ﺧﯿﻂ‬ ‫ﺑﻮاﺳﻄﺔ‬ ‫ﻣﺤﻤﻮل‬ ‫و‬‫ج‬ ‫ب‬ ‫ﺣﯿﺚ‬ ‫اﻟﻘﻀﯿﺐ‬ ‫ﻧﻘﻂ‬ ‫ﻣﻦ‬ ‫ﺟـ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﻃﺮﻓﯿﮫ‬ ‫أﺣﺪ‬ ‫ﻮط‬=
١٠‫ﻓﻮق‬ ً‫ﺎ‬‫راﺳﯿ‬ ‫اﻟﺤﺎﺋﻂ‬ ‫ﻋﻠﻰ‬ ‫ﺗﻘﻊ‬ ‫ء‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫اﻻﺧﺮ‬ ‫ﻃﺮﻓﮫ‬ ‫ﻣﺮﺑﻮط‬ ‫و‬ ‫ﺳﻢ‬‫ا‬‫ﯾﻤﯿﻞ‬ ‫اﻟﻘﻀﯿﺐ‬ ‫ﻛﺎن‬ ‫إذا‬
‫ﺑﺰاوﯾﺔ‬ ‫اﻟﺮأﺳﻲ‬ ‫ﻋﻠﻰ‬٦٠٥
‫اﻟﺤﺎﺋﻂ‬ ‫ﻓﻌﻞ‬ ‫رد‬ ، ‫اﻟﺨﯿﻂ‬ ‫ﻓﻰ‬ ‫اﻟﺸﺪ‬ ‫ﻣﻘﺪار‬ ‫ﻓﺄوﺟﺪ‬ ‫اﻟﺘﻮازن‬ ‫وﺿﻊ‬ ‫ﻓﻰ‬.
‫ـــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻟﻘﻮى‬ ‫ﻣﻦ‬ ‫ﻣﺠﻤﻮﻋﺔ‬ ‫ﺗﺄﺛﯿﺮ‬ ‫ﺗﺤﺖ‬ ‫ﺟﺴﻢ‬ ‫اﺗﺰان‬ ‫ﻋﻠﻰ‬ ‫ﻣﺴﺎﺋﻞ‬:
]١[‫اﻟﻤﻘﺎﺑﻞ‬ ‫اﻟﺸﻜﻞ‬ ‫ﻓﻰ‬:
‫ﻣﻘﺎدﯾﺮھﺎ‬ ‫ﻗﻮى‬‫ق‬١،‫ق‬٢،٥‫؟‬٣،٧‫؟‬٣‫ﻧﯿﻮﺗﻦ‬
‫اﻟﻨﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﺗﺆﺛﺮ‬)‫و‬(‫اﻟﺴﯿﻨﺎت‬ ‫ﻣﺤﻮر‬ ‫ﻣﻊ‬ ‫ﺗﺼﻨﻊ‬ ‫و‬
‫ﺑﺎﻟﺸﻜﻞ‬ ‫ﻣﺒﯿﻨﺔ‬ ‫ﻗﯿﺎﺳﺎﺗﮭﺎ‬ ‫زواﯾﺎ‬.
‫أوﺟﺪ‬‫ق‬١،‫ق‬٢‫ﻣﺘﺰﻧﺔ‬ ‫اﻟﻤﺠﻤﻮﻋﺔ‬ ‫ﺑﺄن‬ ‫ﻋﻠﻤﺎ‬
]٢[
٣٠
٦٠
‫ص‬/
‫ق‬١‫ق‬٢
٧‫؟‬٣٥‫؟‬٣
٣٠
٦٠
‫س‬
‫ص‬
‫و‬‫س‬/

57. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
57
*‫اﻟﻤﺪرﺳﺔ‬ ‫ﻛﺘﺎب‬ ‫ﻣﻦ‬ ‫ﺗﻤﺎرﯾﻦ‬*

58. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
58

59. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
59

60. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
60

61. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
61

62. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
62

63. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
63
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬

64. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
64
‫اﻟﺜﺎﻧﯿﺔ‬ ‫اﻟﻮﺣﺪة‬:
*‫اﻟﺪﯾﻨﺎﻣﯿﻜﺎ‬*
‫اﺳﺔ‬‫ر‬‫ﺑد‬ ‫ﯾﺧﺗص‬ ‫ﻋﻠم‬ ‫ﻫﻰ‬‫ﺗﻌرﺿﻬﺎ‬ ‫ﻋن‬ ‫اﻟﻧﺎﺗﺟﺔ‬ ‫اﻷﺟﺳﺎم‬ ‫ﺣرﻛﺔ‬‫ﻋﻠﯾﻬﺎ‬ ‫ﻧطﻠق‬ ‫ات‬‫ر‬‫اﻟﻣؤﺛ‬ ‫ﻣن‬ ‫ﻟﻣﺟﻣوﻋﺔ‬
‫اﻟﻘوى‬ ‫اﺳم‬‫اﻟﻬﻧدﺳﯾﺔ‬ ‫اﻟوﺟﻬﺔ‬ ‫ﻣن‬ ‫اﻟﺣرﻛﺔ‬ ‫ﺧﺻﺎﺋص‬ ‫ﻓﻰ‬ ‫ﺗﺑﺣث‬ ‫و‬.
*‫اﻟﻣﺳﺗﻘﯾﻣﺔ‬ ‫اﻟﺣرﻛﺔ‬:
‫اﻟﻤﻮﺿﻊ‬ ‫ﻣﺘﺠﮫ‬‫ر‬:
‫ﻫﻮ‬‫اﳌﺘﺠﻪ‬‫اﻟﺬي‬‫ﺑﺪاﻳﺘﻪ‬‫ﻣﻮﺿﻊ‬‫اﻟﺮاﺻﺪ‬‫وﳖﺎﻳﺘﻪ‬‫ﻣﻮﺿﻊ‬‫اﳉﺴﻢ‬‫اﳌﺮﺻﻮد‬.
‫اﻻزاﺣﺔ‬ ‫ﻣﺘﺠﮫ‬‫ف‬:
‫ﻣﻮﺿﻊ‬ ‫ﻣﻦ‬ ‫ﺟﺴﻢ‬ ‫اﻧﺘﻘﺎل‬ ‫ھﻮ‬)‫ا‬(‫ﻣﻌﯿﻨﺔ‬ ‫ﻟﺤﻈﺔ‬ ‫ﻓﻰ‬ ‫اﺑﺘﺪاﺋﻰ‬
‫ﻟﮫ‬ ‫أﺧﺮ‬ ‫ﻣﻮﺿﻊ‬ ‫إﻟﻰ‬)‫ب‬(‫ﺗﺎﻟﯿﺔ‬ ‫ﻟﺤﻈﺔ‬ ‫ﻓﻰ‬
‫اﻟﻤﺴﺘﻘﯿﻤﺔ‬ ‫ﺑﺎﻟﻘﻄﻌﺔ‬ ‫ﯾﻤﺜﻞ‬ ‫و‬‫ا‬‫ب‬
‫ﻣﻌﯿﺎ‬‫اﻹزاﺣﺔ‬ ‫ر‬)‫اﻟﻤﺴﺎﻓﺔ‬ ‫ﻣﻘﺪار‬(:
||‫ا‬‫ب‬||‫اﻟﻤﺴﺘﻘﯿﻤﺔ‬ ‫اﻟﻘﻄﻌﺔ‬ ‫ﻃﻮل‬ ‫ھﻮ‬‫ا‬‫اﻟﺤﻘﯿﻘﯿﺔ‬ ‫اﻟﻤﺴﺎﻓﺔ‬ ‫ﯾﺴﺎوى‬ ‫ﻻ‬ ‫أو‬ ‫ﯾﺴﺎوى‬ ‫ﻗﺪ‬ ‫ﻟﻜﻨﮫ‬ ‫و‬ ‫ب‬
‫ﻣﻦ‬ ‫ﺑﺎﻧﺘﻘﺎﻟﮫ‬ ‫اﻟﺠﺴﻢ‬ ‫ﻗﻄﻌﮭﺎ‬ ‫اﻟﺘﻰ‬)‫ا‬(‫إﻟﻰ‬)‫ب‬(‫اﻟﺠﺴﻢ‬ ‫ﺣﺮﻛﺔ‬ ‫ﻋﻠﻰ‬ ‫ﯾﺘﻮﻗﻒ‬ ‫ذﻟﻚ‬ ‫ﻻن‬
‫اﻻزاﺣﺔ‬ ‫ﻣﻌﯿﺎر‬ ‫وﺣﺪات‬:‫ﻣﻢ‬-‫ﺳﻢ‬–‫م‬-‫ﻛﻢ‬
*‫ﻣ‬ ‫ﺑﯿﻦ‬ ‫اﻟﻌﻼﻗﺔ‬‫اﻻزاﺣﺔ‬ ‫و‬ ‫اﻟﻤﻮﺿﻊ‬ ‫ﺘﺠﮭﻰ‬:
‫ﻛﺎﻧﺖ‬ ‫إذا‬)‫و‬(، ‫اﻟﻤﺸﺎھﺪ‬ ‫ﻣﻮﺿﻊ‬ ‫ھﻰ‬‫ا‬)‫س‬١‫ص‬ ،١(‫ب‬ ،)‫س‬٢‫ص‬ ،٢(
‫ﻓﺈن‬ ‫ﻣﺘﺘﺎﻟﯿﺘﯿﻦ‬ ‫ﻟﺤﻈﺘﯿﻦ‬ ‫ﻋﻨﺪ‬ ‫اﻟﺠﺴﯿﻢ‬ ‫ﻣﻮﺿﻌﺎ‬ ‫ھﻤﺎ‬
‫ب‬‫ا‬‫ﻟﯿﻜﻦ‬ ‫و‬ ‫ﻟﻠﺠﺴﯿﻢ‬ ‫اﻻزاﺣﺔ‬ ‫ﻣﺘﺠﺔ‬ ‫ھﻮ‬‫ف‬
‫ف‬=‫ر‬-‫ر‬.
،||‫ف‬||=‫؟‬)‫س‬٢"–"‫س‬١"(٢
"+")"‫ص‬"٢"‫ــ‬"‫ص‬"١(٢
"
B‫ف‬=||‫ف‬||‫ى‬،‫ى‬‫اﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫وﺣﺪة‬ ‫ﻣﺘﺠﺔ‬‫ف‬)‫اﻟﺤﺮﻛﺔ‬ ‫اﺗﺠﺎه‬(

65. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
65
‫ﻣﺜﺎل‬:‫ﻣﻮﺿﻌﮫ‬ ‫ﻣﺘﺠﺔ‬ ‫ﻛﺎن‬ ‫ﺑﺤﯿﺚ‬ ‫ﺟﺴﯿﻢ‬ ‫ﯾﺘﺤﺮك‬‫ر‬‫اﻟﻮﺣﺪة‬ ‫ﻣﺘﺠﮭﻰ‬ ‫ﺑﺪﻻﻟﺔ‬ ‫اﻟﺰﻣﻦ‬ ‫ﻓﻰ‬ ‫ﻛﺪاﻟﺔ‬ ‫ﯾﻌﻄﻰ‬
‫اﻷﺳﺎﺳﯿﯿﻦ‬‫ﺳﺲ‬،‫ﺻﺺ‬‫ﺑﺎﻟﻌﻼﻗﺔ‬:‫ر‬) =٣‫ن‬+٢(‫ﺳﺲ‬) +٤‫ن‬–١(‫ﺻﺺ‬
‫ن‬ ‫اﻟﻠﺤﻈﺔ‬ ‫ﺣﺘﻰ‬ ‫اﻟﻤﻘﻄﻮﻋﺔ‬ ‫اﻟﻤﺴﺎﻓﺔ‬ ‫أوﺟﺪ‬=٤
]‫أوﺟﺪ‬ ‫اﻟﻤﺜﺎل‬ ‫ﻧﻔﺲ‬ ‫ﻓﻰ‬‫ف‬‫ن‬ ‫ﻣﻦ‬=١‫ن‬ ‫اﻟﻰ‬=٣[
‫اﻟﺤﻞ‬:‫ر‬)٠= (٢‫ﺳﺲ‬‫ــ‬‫ﺻﺺ‬
،‫ر‬)٤) = (٣×٤+٢(‫ﺳﺲ‬) +٤×٤–١(‫ﺻﺺ‬=١٤‫ﺳﺲ‬+١٥‫ﺻﺺ‬
B‫ف‬=‫ر‬)٤(‫ــ‬‫ر‬)٠) = (١٤،١٥(‫ــ‬)٢،-١= (١٢‫ﺳﺲ‬+١٥‫ﺻﺺ‬
B||‫ف‬||=‫؟‬)١٢"(٢
"+")"١٥"(٢
"=٢٠‫ﻣﺴﺎﻓﺔ‬ ‫وﺣﺪة‬
‫اﻟﻤﺜﺎل‬ ‫ﻧﻔﺲ‬ ‫ﻓﻰ‬:‫ر‬)١= (٥‫ﺳﺲ‬‫ــ‬٣‫ﺻﺺ‬،،‫ر‬)٣= (١١‫ﺳﺲ‬+١١‫ﺻﺺ‬
B‫ف‬=‫ر‬)٣(‫ــ‬‫ر‬)١) = (١١،١١(‫ــ‬)٥،-٣= (٦‫ﺳﺲ‬+١٤‫ﺻﺺ‬
B||‫ف‬||=‫؟‬)٦"(٢
"+")"١٤"(٢
"=٢‫؟‬٥٨‫ﻣﺴﺎﻓﺔ‬ ‫وﺣﺪة‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
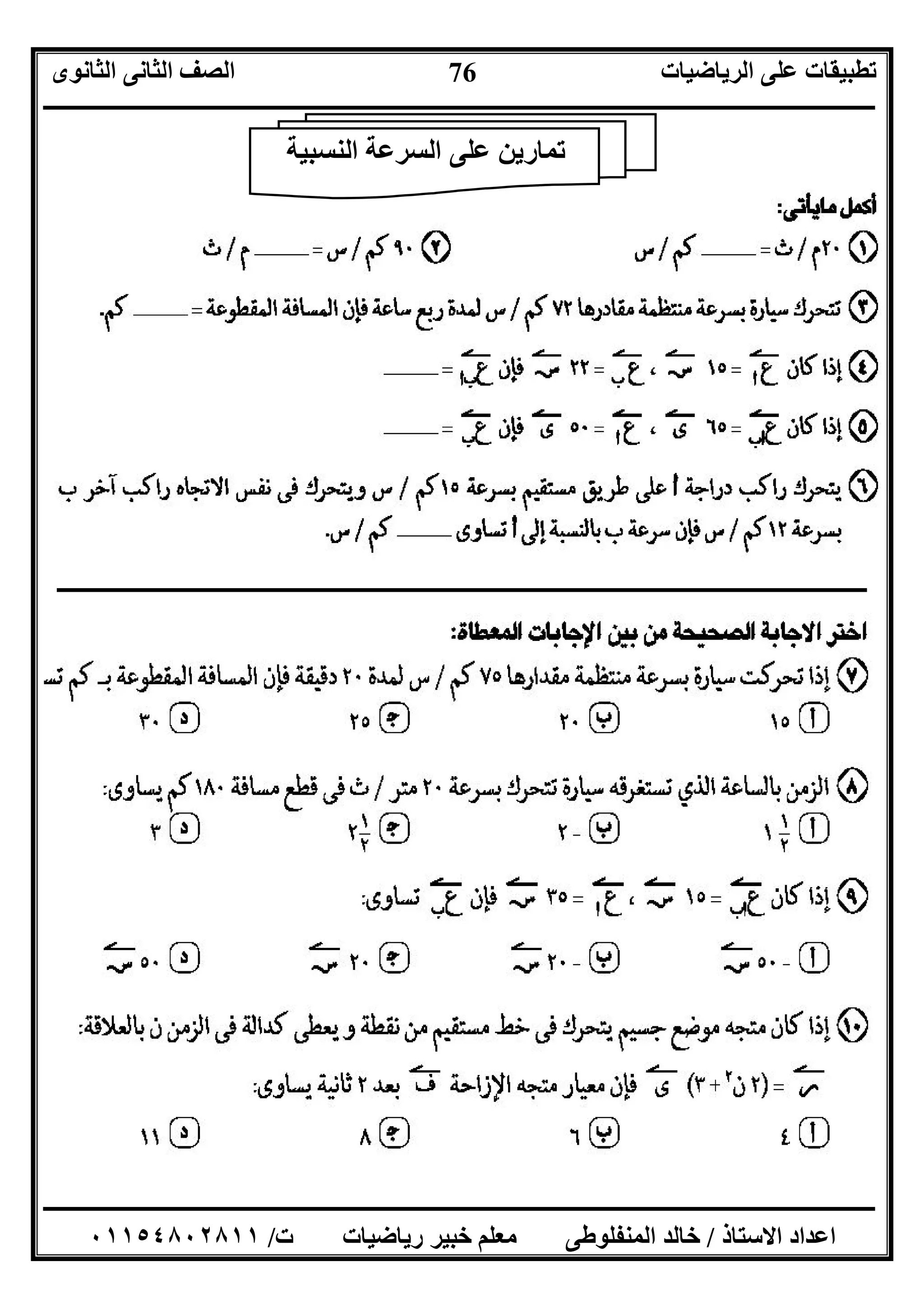
‫ﻣﻘﺪار‬‫اﻟﺴﺮ‬‫ﻋﺔ‬:‫ﺳﯿﺎرة‬ ‫ﺳﺮﻋﺔ‬ ‫ﻛﺎﻧﺖ‬ ‫إذا‬٥٠‫اﻟﺴﺎﻋﺔ‬ ‫ﻓﻰ‬ ‫ﻛﻢ‬)‫ﺗﻜﺘﺐ‬٥٠‫ﻛﻢ‬/‫س‬(‫ﺑﺬﻟﻚ‬ ‫وﯾﻘﺼﺪ‬
‫ﻣﺤﺪدة‬ ‫زﻣﻨﯿﺔ‬ ‫ﻓﺘﺮة‬ ‫ﺧﻼل‬ ‫اﻟﻤﻘﻄﻮﻋﺔ‬ ‫ﺑﺎﻟﻤﺴﺎﻓﺔ‬ ‫اﻟﺴﺮﻋﺔ‬ ‫ﻣﻘﺪار‬ ‫أن‬
‫إﺗﺠﺎھﮭﺎ‬ ‫ﺗﺤﺪﯾﺪ‬ ‫ﯾﻠﺰم‬ ‫ﺑﻞ‬ ‫ﻓﻘﻂ‬ ‫اﻟﺴﺮﻋﺔ‬ ‫ﻣﻘﺪار‬ ‫ﯾﻜﻔﻰ‬ ‫ﻻ‬ ‫اﻻﺣﯿﺎن‬ ‫ﻣﻦ‬ ‫ﻛﺜﯿﺮ‬ ‫وﻓﻰ‬.
‫ﻋﺔ‬‫ﺳر‬ ‫ﻣﺗﺟﻪ‬:
‫ﻣﺘﺠ‬‫اﺗﺠﺎه‬ ‫ﻋﻠﻰ‬ ‫اﺗﺠﺎھﮫ‬ ‫وﯾﻨﻄﺒﻖ‬ ‫اﻟﺴﺮﻋﺔ‬ ‫ﻗﯿﻤﺔ‬ ‫ﯾﺴﺎوى‬ ‫ﻣﻌﯿﺎره‬ ‫اﻟﺬى‬ ‫اﻟﻤﺘﺠﮫ‬ ‫ھﻮ‬ ‫اﻟﺠﺴﯿﻢ‬ ‫ﺳﺮﻋﺔ‬ ‫ﮫ‬
‫اﻟﺤﺮﻛﺔ‬.
‫اﻟﺴﺮﻋﺔ‬ ‫ﻣﻌﯿﺎر‬ ‫ﻗﯿﺎس‬ ‫وﺣﺪات‬:‫ﻛم‬/‫ﺳﺎﻋﺔ‬،‫ﻣﺗر‬/‫ث‬،‫ﺳم‬/‫ث‬
‫ﻧﻘﺳم‬ ‫اﻟﻌﻛس‬ ‫و‬ ‫ﻧﺿرب‬ ‫ﺻﻐﯾر‬ ‫اﻟﻰ‬ ‫ة‬‫ﻛﺑﯾر‬ ‫وﺣدات‬ ‫ﻣن‬ ‫اﻟﺗﺣوﯾل‬
١‫ﻛﻢ‬/‫س‬=‫م‬/‫ث‬E١‫م‬/‫ث‬=‫ﻛﻢ‬/‫س‬
،١‫ﻛﻢ‬/‫س‬=‫ﺳﻢ‬/‫ث‬E١‫ﺳﻢ‬/‫ث‬=‫ﻛﻢ‬/‫س‬
‫ﻣﺜﻼ‬:٩٠‫ﻛﻢ‬/‫س‬=٩٠×=٢٥‫م‬/، ‫ث‬١٥‫م‬/‫ث‬=١٥×=٥٤‫ﻛﻢ‬/‫س‬
٥
١٨
٢٥٠
٩
١٨
٥
٩
٢٥٠
٥
١٨
١٨
٥

66. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
66
*‫اﻟﻤﻨﺘﻈﻤﺔ‬ ‫اﻟﺤﺮﻛﺔ‬:
‫اﻟﺴ‬ ‫ﻣﺘﺠﺔ‬ ‫واﺗﺠﺎه‬ ‫ﻣﻌﯿﺎر‬ ‫ﻣﻦ‬ ‫ﻛﻞ‬ ‫ﻓﯿﮭﺎ‬ ‫ﯾﻜﻮن‬ ‫اﻟﺘﻰ‬ ‫اﻟﺤﺎﻟﺔ‬ ‫ھﻰ‬ً‫ﺎ‬‫ﺛﺎﺑﺘ‬ ‫ﺮﻋﺔ‬)‫ﻓﻰ‬ ‫ﯾﺘﺤﺮك‬ ‫اﻟﺠﺴﯿﻢ‬ ‫أى‬
‫ﻣﺘﺴﺎوﯾﺔ‬ ‫زﻣﻨﯿﺔ‬ ‫ﻓﺘﺮات‬ ‫ﻓﻰ‬ ‫ﻣﺘﺴﺎوﯾﺔ‬ ‫ﻣﺴﺎﻓﺎت‬ ‫ﯾﻘﻄﻊ‬ ‫ﺣﯿﺚ‬ ‫ﺛﺎﺑﺖ‬ ‫اﺗﺠﺎه‬(
‫ﺑﯿﻦ‬ ‫اﻟﻌﻼﻗﺔ‬ ‫ﺗﻜﻮن‬ ‫و‬‫ف‬،‫ع‬:‫ف‬=‫ن‬‫ع‬‫أو‬‫ف‬=‫ع‬‫ن‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻟﻤﺘﻮﺳﻄﺔ‬ ‫اﻟﺴﺮﻋﺔ‬ ‫ﻣﻘﺪار‬:
‫ﻛﺎن‬ ‫و‬ ‫ف‬ ‫اﻟﻤﺪﯾﻨﺘﯿﻦ‬ ‫ﺑﯿﻦ‬ ‫اﻟﻤﺴﺎﻓﺔ‬ ‫ﻛﺎﻧﺖ‬ ‫و‬ ‫ﻣﺪﯾﻨﺘﯿﻦ‬ ‫ﺑﯿﻦ‬ ‫ﻣﺘﻔﺎوﺗﺔ‬ ‫ﺑﺴﺮﻋﺎت‬ ‫ﺗﺘﺤﺮك‬ ‫ﺳﯿﺎرة‬ ‫ﻛﺎﻧﺖ‬ ‫إذا‬
‫ﻓﺈن‬ ‫ن‬ ‫اﻟﺮﺣﻠﺔ‬ ‫ﺧﻼل‬ ‫اﻟﻤﻘﻄﻮع‬ ‫اﻟﺰﻣﻦ‬
‫اﻟﻤﺘ‬ ‫اﻟﺴﺮﻋﺔ‬‫ﻮﺳﻄﺔ‬‫ع‬‫م‬=
‫ﻣﺜﺎل‬:‫أﺻﺒﺢ‬ ‫ﺳﺎﻋﺔ‬ ‫رﺑﻊ‬ ‫ﺑﻌﺪ‬ ‫و‬ ، ‫اﻟﺼﻔﺮ‬ ‫إﻟﻰ‬ ‫ﯾﺸﯿﺮ‬ ‫اﻟﺴﯿﺎرات‬ ‫إﺣﺪى‬ ‫ﻓﻰ‬ ‫اﻟﻤﺴﺎﻓﺎت‬ ‫ﻋﺪاد‬ ‫ﻛﺎن‬ ‫إذا‬
‫إﻟﻰ‬ ‫ﯾﺸﯿﺮ‬١٨‫ﻛﻢ‬.‫اﻟﻤﺘﻮﺳﻄﺔ‬ ‫اﻟﺴﺮﻋﺔ‬ ‫ﻓﺄﺣﺴﺐ‬.‫ﺛﺎﺑﺖ‬ ‫اﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫ﺗﺤﺮﻛﺖ‬ ‫اﻟﺴﯿﺎرة‬ ‫ﺑﺄن‬ ً‫ﺎ‬‫ﻋﻠﻤ‬
‫اﻟﺤﻞ‬:
‫ع‬ ‫اﻟﻤﺘﻮﺳﻄﺔ‬ ‫اﻟﺴﺮﻋﺔ‬‫م‬= ==٧٢‫ﻛﻢ‬/‫س‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻟﻤﺘﻮﺳﻄﺔ‬ ‫اﻟﺴﺮﻋﺔ‬ ‫ﻣﺘﺠﮫ‬:
‫ن‬ ‫ﻣﺗﺗﺎﻟﯾﺗﯾن‬ ‫زﻣﻧﯾﺗﯾن‬ ‫ﻟﺣظﺗﯾن‬ ‫ﺑﯾن‬ ‫ﻟﻠﺟﺳم‬ ‫اﻟﻣﺗوﺳطﺔ‬ ‫ﻋﺔ‬‫اﻟﺳر‬ ‫ﻣﺗﺟﻪ‬١
‫ن‬ ،٢
‫و‬‫ﻟﻪ‬ ‫ﻧرﻣز‬‫ع‬‫م‬‫ﻋﻠﻰ‬
‫اﻟزﻣﻧﯾﺔ‬ ‫ة‬‫اﻟﻔﺗر‬ ‫ﻋﻠﻰ‬ ‫اﻟﻠﺣظﺗﯾن‬ ‫ﻫﺎﺗﯾن‬ ‫ﺑﯾن‬ ‫اﻟﺟﺳم‬ ‫اﺣﺔ‬‫ز‬‫إ‬ ‫ﻣﺗﺟﻪ‬ ‫ﻗﺳﻣﺔ‬ ‫ﺧﺎرج‬ ‫أﻧﻪ‬)‫ن‬٢
–‫ن‬١
(
‫ﻛﺎن‬ ‫إذا‬:‫ر‬١‫ن‬ ‫اﻟﻠﺣظﺔ‬ ‫ﻋﻧد‬ ‫اﻟﺟﺳم‬ ‫ﻣوﺿﻊ‬ ‫ﻣﺗﺟﻪ‬١
‫ر‬٢‫ن‬ ‫اﻟﻠﺣظﺔ‬ ‫ﻋﻧد‬ ‫اﻟﺟﺳم‬ ‫ﻣوﺿﻊ‬ ‫ﻣﺗﺟﻪ‬٢
‫ع‬‫م‬==
‫ذﻟك‬ ‫وﻋﻠﻰ‬:
١(‫اﻟﻣﺗوﺳطﺔ‬ ‫ﻋﺔ‬‫اﻟﺳر‬:‫ع‬‫م‬==‫ى‬
‫اﻟﻜﻠﯿﺔ‬ ‫اﻟﻤﺴﺎﻓﺔ‬
‫اﻟﻜﻠﻰ‬ ‫اﻟﺰﻣﻦ‬
‫ف‬
‫ن‬٢
-‫ن‬١
‫ر‬٢
-‫ر‬١
‫ن‬٢
-‫ن‬١
‫ف‬
‫ن‬
‫ف‬
‫ن‬
‫ى‬
+
‫ف‬
‫ن‬
‫ا‬‫اﻟﻜﻠﯿﺔ‬ ‫ﻟﻤﺴﺎﻓﺔ‬
‫اﻟﻜﻠﻰ‬ ‫اﻟﺰﻣﻦ‬
١٨
٠٫٢٥

67. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
67
٢(‫ﻣن‬ ‫ﺟﺳم‬ ‫ﻟﺣرﻛﺔ‬ ‫اﻟﻣﺧﺗﻠﻔﺔ‬ ‫اﻟﺣﺎﻻت‬)‫ا‬(‫ف‬ ‫ﻣﺴﺎﻓﺔ‬١‫إﻟﻰ‬)‫ب‬(‫إﻟﻰ‬ ‫ﺛﻢ‬)‫ﺟـ‬(‫ف‬ ‫ﻣﺴﺎﻓﺔ‬٢
‫ن‬ ‫اﻟﺰﻣﻨﯿﺘﯿﻦ‬ ‫اﻟﻔﺘﺮﺗﯿﻦ‬ ‫ﺧﻼل‬١‫ن‬ ،٢‫اﻟﺘﺮﺗﯿﺐ‬ ‫ﻋﻠﻰ‬:
*‫واﺣﺪ‬ ‫اﺗﺠﺎه‬ ‫ﻓﻰ‬:‫ع‬‫م‬=‫ى‬
*‫اﻟﺠﺴﻢ‬ ‫ﺗﻮﻗﻒ‬ ‫إذا‬‫ﻋﻨﺪ‬)‫ب‬(‫ن‬ ‫زﻣﻨﯿﺔ‬ ‫ﻓﺘﺮة‬ ‫ﻓﻰ‬٣‫ﻓﺈن‬:‫ع‬‫م‬=‫ى‬
*‫ﻣﺘﻀﺎدﯾﻦ‬ ‫إﺗﺠﺎھﯿﻦ‬ ‫ﻓﻰ‬:
‫ع‬‫م‬=‫ى‬
‫ھﺎﻣﺔ‬ ‫ﻣﻼﺣﻈﺔ‬:١-‫ﺗﺤﺪﯾﺪ‬ ‫ﯾﺠﺐ‬‫ى‬‫ف‬ ‫إﺗﺠﺎه‬ ‫ﻧﻔﺲ‬ ‫ﻟﮫ‬ ‫وﺣﺪة‬ ‫ﻣﺘﺠﮫ‬١
٢-‫اﻟﺤﺮﻛﺔ‬ ‫اﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫ﻛﺎن‬ ‫إذا‬ ‫ﻣﻮﺟﺐ‬ ‫ﯾﻜﻮن‬ ‫ﻗﺪ‬ ‫اﻟﻤﺘﻮﺳﻄﺔ‬ ‫اﻟﺴﺮﻋﺔ‬ ‫ﻣﺘﺠﺔ‬
‫اﻟﺤﺮﻛﺔ‬ ‫اﺗﺠﺎه‬ ‫ﻋﻜﺲ‬ ‫ﻓﻰ‬ ‫ﻛﺎن‬ ‫إذا‬ ‫ﺳﺎﻟﺐ‬ ‫و‬
٣-‫ﻓﺈن‬ ‫اﻟﺒﺪاﯾﺔ‬ ‫ﻧﻘﻄﺔ‬ ‫إﻟﻰ‬ ‫اﻟﺠﺴﻢ‬ ‫ﻋﺎد‬ ‫إذا‬:‫ف‬١=‫ف‬٢=‫ف‬
،‫ع‬‫م‬=٠‫اﻟ‬ ،‫اﻟﻤﻘﻄﻮﻋﺔ‬ ‫ﻤﺴﺎﻓﺔ‬=٢‫ف‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻟﺤﻞ‬:
‫ف‬١
+‫ف‬٢
‫ن‬١
+‫ن‬٢
‫ى‬
+
‫ب‬
‫ا‬ ‫ج‬
‫ف‬١
+‫ف‬٢
‫ن‬١
+‫ن‬٢
+‫ن‬٣
‫ف‬١
-‫ف‬٢
‫ن‬١
+‫ن‬٢

68. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
68
‫اﻟﻠﺣظﯾﺔ‬ ‫ﻋﺔ‬‫اﻟﺳر‬ ‫ﻣﺗﺟﻪ‬:
‫اﻟزﻣﻧﯾﺔ‬ ‫ة‬‫اﻟﻔﺗر‬ ‫ﻛﺎﻧت‬ ‫إذا‬)‫ن‬٢–‫ن‬١(‫ة‬‫ﺻﻐﯾر‬‫ﺟدا‬ً
‫و‬‫ن‬ ‫اﻟﻠﺣظﺔ‬ ‫ﻣﺗوﺳطﻬﺎ‬‫ﻓﺈن‬‫ﻋﺔ‬‫اﻟﺳر‬ ‫ﻣﺗﺟﻪ‬‫ﻫذﻩ‬ ‫ﻓﻰ‬
‫ﻋﺔ‬‫اﻟﺳر‬ ‫ﺑﻣﺗﺟﻪ‬ ‫ﯾﻌرف‬ ‫اﻟﺣﺎﻟﺔ‬‫اﻟﻠﺣظﯾﺔ‬‫ن‬ ‫اﻟﻠﺣظﺔ‬ ‫ﻋﻧد‬
‫ع‬ ‫ﺑﺎﻟرﻣز‬ ‫ﻟﻪ‬ ‫وﯾرﻣز‬
‫ﻣﻼﺣﻈﺔ‬:‫ھﻮ‬ ‫اﻟﻤﺘﻮﺳﻄﺔ‬ ‫اﻟﺴﺮﻋﺔ‬ ‫ﻣﺘﺠﮫ‬ ‫ﻓﺈن‬ ‫ﻣﺤﺪدة‬ ‫ﻓﺘﺮة‬ ‫ﻓﻰ‬ ‫ﻣﻨﺘﻈﻤﺔ‬ ‫ﺣﺮﻛﺔ‬ ‫ﺟﺴﯿﻢ‬ ‫ﺗﺤﺮك‬ ‫إذا‬
‫ﻟﮭﺎ‬ ‫اﻟﻤﻨﺘﻈﻤﺔ‬ ‫اﻟﺴﺮﻋﺔ‬ ‫ﻣﺘﺠﮫ‬ ‫ﻧﻔﺴﮫ‬.
‫ﻣﺜﻼ‬:‫ﺑﺎﻟﻜﻢ‬ ‫اﻟﻠﺤﻈﯿﺔ‬ ‫اﻟﺴﺮﻋﺔ‬ ‫ﻗﯿﻤﺔ‬ ‫ﯾﻌﻄﻰ‬ ‫ﻟﻠﺴﯿﺎرة‬ ‫اﻟﺴﺮﻋﺔ‬ ‫ﻋﺪاد‬/‫س‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﻣﺴﺎﻓﺔ‬ ‫ﺳﯿﺎرة‬ ‫ﻗﻄﻌﺖ‬٨٠‫ﻣﺴ‬ ‫ﻃﺮﯾﻖ‬ ‫ﻋﻠﻰ‬ ‫ﻛﻢ‬‫ﺑﺴﺮﻋﺔ‬ ‫ﺘﻘﯿﻢ‬٦٠‫ﻛﻢ‬/‫ﻓﻘﻄﻌﺖ‬ ‫ﻋﺎدت‬ ‫ﺛﻢ‬ ‫س‬
‫ﻣﺴﺎﻓﺔ‬٦٠‫ﺑﺴﺮﻋﺔ‬ ‫ﻛﻢ‬٤٥‫ﻛﻢ‬/‫اﻟﻤﻀﺎد‬ ‫اﻻﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫س‬.
‫ﻛﻠﮭﺎ‬ ‫اﻟﺮﺣﻠﺔ‬ ‫ﺧﻼل‬ ‫اﻟﻤﺘﻮﺳﻄﺔ‬ ‫ﺳﺮﻋﺘﮭﺎ‬ ‫أوﺟﺪ‬.
‫اﻟﺤﻞ‬:
‫إﺗﺠﺎه‬ ‫ﻧﻔﺲ‬ ‫ﻟﮫ‬ ‫وﺣﺪة‬ ‫ﻣﺘﺠﮫ‬ ‫ى‬ ‫ﻧﻔﺮض‬‫ا‬‫ب‬
‫ن‬١= =‫ن‬ ، ‫ﺳﺎﻋﺔ‬٢==‫ﺳﺎﻋﺔ‬
‫ن‬=‫ن‬١+‫ن‬٢= + =‫ﺳﺎﻋﺔ‬
‫ف‬=٨٠‫ــ‬ ‫ى‬٦٠‫ى‬=٢٠‫ى‬
B‫ع‬‫م‬=‫ى‬=٢٠×‫ى‬=٧٫٥‫ى‬
‫أن‬ ‫أى‬:‫ﻣﻘﺪارھﺎ‬ ‫اﻟﻤﺘﻮﺳﻄﺔ‬ ‫اﻟﺴﯿﺎرة‬ ‫ﺳﺮﻋﺔ‬٧٫٥‫ﻛﻢ‬/‫اﻷ‬ ‫ﺣﺮﻛﺘﮭﺎ‬ ‫إﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫س‬‫وﻟﻰ‬
٨٠
٦٠
٤
٣
٦٠
٤٥
٤
٣
٤
٣
٤
٣
٨
٣
٣
٨
‫ف‬
‫ن‬

69. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
69
‫ﻣﺛﺎل‬:‫ﻓﻰ‬ ‫ب‬ ‫اﻟﻣدﯾﻧﺔ‬ ‫إﻟﻰ‬ ‫أ‬ ‫اﻟﻣدﯾﻧﺔ‬ ‫ﻣن‬ ‫اﻟﻣﺳﺎﻓﺔ‬ ‫ﻗطﺎر‬ ‫ﻗطﻊ‬٣٦‫ﻣﺗوﺳطﺔ‬ ‫ﻋﺔ‬‫ﺑﺳر‬ ‫دﻗﯾﻘﺔ‬
٧٠‫ﻛم‬/‫اﻟـ‬ ‫ﻗطﻊ‬ ‫ﻓﺈذا‬ ‫ﺳﺎﻋﺔ‬١٥‫ﻋﺔ‬‫ﺑﺳر‬ ‫اﻷوﻟﻰ‬ ‫ﻛم‬٧٥‫ﻛم‬/‫اﻟـ‬ ، ‫ﺳﺎﻋﺔ‬١٥‫ﻛم‬
‫ﻋﺔ‬‫ﺑﺳر‬ ‫اﻟﺗﺎﻟﯾﺔ‬٦٠‫ﻛم‬/‫ﺳﺎﻋﺔ‬.‫اﻟﺑﺎﻗﯾﺔ‬ ‫اﻟﻣﺳﺎﻓﺔ‬ ‫ﻓﻰ‬ ‫اﻟﻣﺗوﺳطﺔ‬ ‫ﻋﺗﻪ‬‫ﺳر‬ ‫ﻓﻣﺎ‬.
‫اﻟﺣل‬:
‫ا‬‫ﺑﯾن‬ ‫ﻟﻣﺳﺎﻓﺔ‬‫اﻟﻣدﯾﻧﺗﯾن‬=‫اﻟﻣﺗوﺳطﺔ‬ ‫ﻋﺔ‬‫اﻟﺳر‬×‫اﻟزﻣن‬=٧٠×=٤٢‫ﻛم‬
∴‫اﻟﺑﺎﻗﯾﺔ‬ ‫اﻟﻣﺳﺎﻓﺔ‬=٤٢–)١٥+١٥= (١٢‫ﻛم‬
‫ن‬١
= =‫ﺳﺎﻋﺔ‬=×٦٠=١٢‫دﻗﯾﻘﺔ‬
‫ن‬٢
= =‫ﺳﺎﻋﺔ‬=×٦٠=١٥‫دﻗﯾﻘﺔ‬
∴‫اﻟﺑﺎﻗﯾﺔ‬ ‫اﻟﻣﺳﺎﻓﺔ‬ ‫زﻣن‬=٣٦–)١٢+١٥= (٩‫دﻗﯾﻘﺔ‬= =‫ﺳﺎﻋﺔ‬
∴‫اﻟﺑﺎﻗﯾﺔ‬ ‫اﻟﻣﺳﺎﻓﺔ‬ ‫ﻓﻰ‬ ‫اﻟﻣﺗوﺳطﺔ‬ ‫ﻋﺔ‬‫اﻟﺳر‬=١٢÷=٢×=٨٠‫ﻛم‬/‫ﺳﺎﻋﺔ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـ‬‫ـــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺛﺎل‬:‫اﺟ‬‫ر‬‫د‬ ‫ﻋﻠﻰ‬ ‫ﺑرﺣﻠﺔ‬ ‫طﺎﻟب‬ ‫ﻗﺎم‬‫ﻋﺔ‬‫ﺑﺳر‬ ‫ﻣﻧﻬﺎ‬ ‫اﻟﻧﺻف‬ ‫ﻓﻘطﻊ‬ ‫ﺔ‬١٢‫ﻛم‬/‫ﻟﻣدة‬ ‫اح‬‫ر‬‫اﺳﺗ‬ ‫ﺛم‬ ‫ﺳﺎﻋﺔ‬
‫ﻋﺔ‬‫ﺑﺳر‬ ‫اﻟﺛﺎﻧﻰ‬ ‫اﻟﻧﺻف‬ ‫ﻗطﻊ‬ ‫ﺛم‬ ‫ﺳﺎﻋﺔ‬٨‫ﻛم‬/‫ﺳﺎﻋﺔ‬.‫اﺳﺗﻐ‬ ‫ﻓﺈذا‬‫ﻛﻠﻬﺎ‬ ‫اﻟرﺣﻠﺔ‬ ‫ﻓﻰ‬ ‫رق‬
٣‫ﺳﺎﻋﺎت‬.‫اﻟﻛﻠﯾﺔ‬ ‫اﻟﻣﺳﺎﻓﺔ‬ ‫أوﺟد‬.
‫اﻟﺣل‬:‫اﻟﻣﺳﺎﻓﺔ‬ ‫أن‬ ‫ﻧﻔرض‬=٢‫ﻛم‬ ‫ف‬
‫اﻷول‬ ‫اﻟﻧﺻف‬ ‫ﻗطﻊ‬ ‫زﻣن‬=‫ﺳﺎﻋﺔ‬
‫اﻟﺛﺎﻧﻰ‬ ‫اﻟﻧﺻف‬ ‫ﻗطﻊ‬ ‫زﻣن‬=‫ﺳﺎﻋﺔ‬
‫اﺣﺔ‬‫ر‬‫اﻻﺳﺗ‬ ‫زﻣن‬=‫ﺳﺎﻋﺔ‬
∴+ +=٣∴=
∴‫ف‬=×=١٢‫ﻛم‬∴‫اﻟﻛﻠﯾﺔ‬ ‫اﻟﻣﺳﺎﻓﺔ‬=٢٤‫ﻛم‬
٣٦
٦٠
١٥
٧٥
١
٥
١
٥
١٥
٦٠
١
٤
١
٤
٩
٦٠
٣
٢٠ ٣
٢٠
٢٠
٣
١
٢
‫ف‬
١٢
١‫ف‬
٨
‫ف‬
٨
‫ف‬
١٢
١
٢
٨‫ف‬+١٢‫ف‬
١٢×٨
٥
٢
١٢×٨
٢٠
٥
٢
١
٢

70. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
70
‫ﻣﺛﺎل‬:‫ﺳﯿﺎرﺗﺎن‬ ‫ﺗﺘﺤﺮك‬‫ﻣﺴﺎﻓﺔ‬ ‫ﻣﺴﺘﻘﯿﻢ‬ ‫ﻃﺮﯾﻖ‬ ‫ﻋﻠﻰ‬ ‫ب‬ ، ‫أ‬٢٧‫ﺑﺴﺮﻋﺔ‬ ‫ﻛﻢ‬١٨‫ﻛﻢ‬/‫ﻗﻄﻊ‬ ‫ﺛﻢ‬ ‫س‬
‫ﻣﺴﺎﻓﺔ‬٩‫ﺑﺴﺮﻋﺔ‬ ‫ﻛﻢ‬١٢‫ﻛﻢ‬/‫س‬.‫ﻛﺎﻧﺖ‬ ‫إذا‬ ‫ﻛﻠﮭﺎ‬ ‫اﻟﺮﺣﻠﺔ‬ ‫ﺧﻼل‬ ‫اﻟﻤﺘﻮﺳﻄﺔ‬ ‫اﻟﺴﺮﻋﺔ‬ ‫أوﺟﺪ‬:
)١(‫واﺣﺪ‬ ‫أﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫اﻻزاﺣﺘﺎن‬)٢(‫ﻣﺘﻀﺎدﯾﻦ‬ ‫أﺗﺠﺎھﯿﻦ‬ ‫ﻓﻰ‬ ‫اﻻزاﺣﺘﺎن‬
‫اﻟﺤﻞ‬:
‫ﻓﻰ‬ ‫اﻻزاﺣﺘﺎن‬ ‫ﻛﺎﻧﺖ‬ ‫إذا‬‫واﺣﺪ‬ ‫أﺗﺠﺎه‬‫ﻣﺘﻀﺎدﯾﻦ‬ ‫أﺗﺠﺎھﯿﻦ‬ ‫ﻓﻰ‬ ‫اﻻزاﺣﺘﺎن‬ ‫ﻛﺎﻧﺖ‬ ‫إذا‬
‫ف‬=٢٧+٩=٣٦‫ف‬ ‫ﻛﻢ‬=٢٧–٩=١٨‫ﻛﻢ‬
‫اﻟﻜﻠﻰ‬ ‫اﻟﺰﻣﻦ‬= + =٢٫٢٥‫اﻟﺰ‬ ‫ﺳﺎﻋﺔ‬‫اﻟﻜﻠﻰ‬ ‫ﻣﻦ‬= + =٢٫٢٥
‫ع‬)‫اﻟﻤﺘﻮﺳﻄﺔ‬= = (‫ــــــــ‬‫ع‬)‫اﻟﻤﺘﻮﺳﻄﺔ‬= (=‫ــــــــــ‬=٨‫ﻛﻢ‬/‫س‬
=١٦‫ﻛﻢ‬/‫س‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــ‬
‫ﻣﺜﺎل‬:‫زﻣﻨﯿﺘﯿﻦ‬ ‫ﻟﺤﻈﺘﯿﻦ‬ ‫ﻋﻨﺪ‬ ‫ﺟﺴﯿﻢ‬ ‫ﺗﻮاﺟﺪ‬٣،٨‫اﻟﻤﻮﺿﻌﯿﻦ‬ ‫ﻋﻨﺪ‬ ‫ﺛﻮان‬‫ا‬)٧،٢(‫ب‬ ،)٤،٦(
‫اﻟﺘﺮﺗﯿﺐ‬ ‫ﻋﻠﻰ‬.‫ﻟﻠﺠﺴﯿﻢ‬ ‫اﻟﻤﺘﻮﺳﻄﺔ‬ ‫اﻟﺴﺮﻋﺔ‬ ‫ﻣﺘﺠﺔ‬ ‫أوﺟﺪ‬‫اﻟﺰﻣﻨﯿﺔ‬ ‫اﻟﻔﺘﺮة‬ ‫ھﺬه‬ ‫ﺧﻼل‬
‫اﺗﺠﺎه‬ ‫و‬ ‫ﻣﻌﯿﺎر‬ ‫أوﺟﺪ‬ ‫ﺛﻢ‬ ،‫اﻟﺴﺮﻋﺔ‬ ‫ھﺬه‬.
‫اﻟﺤﻞ‬:
‫و‬ ‫اﻻﺑﺘﺪاﺋﻰ‬ ‫اﻟﻤﻮﺿﻊ‬ ‫ﻣﺘﺠﺔ‬‫ا‬)‫ر‬١(
‫ب‬ ‫و‬ ‫اﻟﻨﮭﺎﺋﻰ‬ ‫اﻟﻤﻮﺿﻊ‬ ‫ﻣﺘﺠﺔ‬)‫ر‬٢(
‫اﻻزاﺣﺔ‬ ‫ﻣﺘﺠﺔ‬‫ب‬ ‫ا‬)‫ف‬(
‫ف‬=‫ر‬٢-‫ر‬‫ـ‬‫ـ‬١
) =٧،٢(‫ــ‬)٤،٦(
) =٣،-٤(
A‫ع‬‫م‬==
) =٣،-٤(
) =،(
||‫ع‬‫م‬||=‫ﰈ‬( )‫ﱂ‬
٢
‫ﱂ‬+‫ﱂ‬)‫ﱂ‬(‫ﱂ‬
٢
=١‫ﻇﺎ‬ ، ‫ﺳﺮﻋﺔ‬ ‫وﺣﺪة‬‫ــ‬١
=١٢//
٥٢/
١٢٦٥
٢٧
١٨
٩
١٢
‫اﻟﻜﻠﯿﺔ‬ ‫اﻻزاﺣﺔ‬
‫اﻟﻜﻠﻰ‬ ‫اﻟﺰﻣﻦ‬
٣٦
٢٫٢٥
٢٧
١٨
٩
١٢
‫اﻟﻜﻠﯿﺔ‬ ‫اﻻزاﺣﺔ‬
‫اﻟﻜﻠﻰ‬ ‫اﻟﺰﻣﻦ‬
١٨
٢٫٢٥
×
×
-١ ١ ٢ ٣ ٤ ٥ ٦ ٧ ٨ 
٧
٦
٥
٤
٣
٢
١
-١

‫ا‬
‫ب‬
‫و‬
‫ف‬
‫ن‬٢
-‫ن‬١
)٣،-٤(
٨–٣
١
٥
٤-
٥
٣
٥
٣
٥
٤-
٥
٤-
٣

71. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
71
* ‫اﻟﻧﺳﺑﯾﺔ‬ ‫ﻋﺔ‬‫اﻟﺳر‬ *
‫ا‬ ‫ﺑﺗﻐﯾـر‬ ‫وﺻـﻔﻬﺎ‬ ‫ﯾﺗﻐﯾر‬ ‫ﻗد‬ ‫ﻧﺳﺑﻰ‬ ‫ﻣﻔﻬوم‬ ‫اﻟﺣرﻛﺔ‬‫ﻟﻣـﺷﺎﻫد‬.‫أن‬ ‫اﺣـدة‬‫و‬ ‫ة‬‫ﻣـر‬ ‫وﻟـو‬ ‫ﯾﺗﺧﯾـل‬ ‫ﻟـم‬ ‫ﻣﻧـﺎ‬ ‫ﻓﻣـن‬
‫إذا‬ ‫أﻣـﺎ‬ ‫ﺑﺑطء‬ ‫اﻟﻣﺣطﺔ‬ ‫ﻣن‬ ‫ﺣرﻛﺗﻪ‬ ‫ﺑدأ‬ ‫ﻗطﺎر‬ ‫ﻓﻰ‬ ‫ﺟﺎﻟس‬ ‫ﻫو‬ ‫ﺑﯾﻧﻣﺎ‬ ‫ﺗﺗﺣرك‬ ‫وﻛﺄﻧﻬﺎ‬ ‫ﺗﺑدو‬ ‫ة‬‫اﻹﻧﺎر‬ ‫أﻋﻣدة‬
‫ﻓﺈﻧﻬـﺎ‬ ‫ﻧﻔـﺳﻬﺎ‬ ‫اﻟﻘطـﺎر‬ ‫ﺣرﻛـﺔ‬ ‫اﺗﺟﺎﻩ‬ ‫ﻧﻔس‬ ‫ﻓﻰ‬ ‫اﻟﻣﺗﺣرﻛﺔ‬ ‫ات‬‫ر‬‫اﻟﺳﯾﺎ‬ ‫إﻟﻰ‬ ‫اﻟﻘطﺎر‬ ‫ﻧﺎﻓذة‬ ‫ﺧﻼل‬ ‫ﻣن‬ ‫ﻧظرت‬
‫ﯾﺣـدث‬ ‫ﺑﯾﻧﻣﺎ‬ ‫ﺷدﯾد‬ ‫ﺑﺑطء‬ ‫ﻣﺗﺣرﻛﺔ‬ ‫أﻧﻬﺎ‬ ‫ﻟك‬ ‫ﺗﺑدو‬‫اﻻﺗﺟـﺎﻩ‬ ‫ﻋﻛـس‬ ‫ﻓـﻰ‬ ‫ﺗﺗﺣـرك‬ ‫ة‬‫اﻟـﺳﯾﺎر‬ ‫أن‬ ‫ﻟـو‬ ‫اﻟﻌﻛـس‬
‫اﻟﻘطﺎر‬ ‫ﻟﺣرﻛﺔ‬.‫اﻟﺣرﻛﺔ‬ ‫ﻧﺳﺑﯾﺔ‬ ‫ﻣﻔﻬوم‬ ‫ﺗؤﻛد‬ ‫اﻫر‬‫و‬‫اﻟظ‬ ‫وﻫذﻩ‬.
‫اﻟﻧﺳﺑﯾﺔ‬ ‫ﻋﺔ‬‫اﻟﺳر‬ ‫ﻣﻔﻬوم‬:
‫ﻟﺟﺳﯾم‬ ‫اﻟﻧﺳﺑﯾﺔ‬ ‫ﻋﺔ‬‫اﻟﺳر‬)‫ا‬(‫آﺧﺮ‬ ‫ﻟﺠﺴﯿﻢ‬ ‫ﺑﺎﻟﻨﺴﺒﺔ‬)‫ب‬(‫ﻟﻠﺠﺴﯿﻢ‬ ‫ﯾﺒﺪو‬ ‫اﻟﺘﻰ‬ ‫اﻟﺴﺮﻋﺔ‬ ‫ھﻰ‬)‫ا‬(‫أن‬
‫اﻟﺠﺴﯿﻢ‬ ‫اﻋﺘﺒﺮﻧﺎ‬ ‫ﻟﻮ‬ ‫ﺑﮭﺎ‬ ‫ﯾﺘﺤﺮك‬)‫ب‬(‫ﺳﻜﻮن‬ ‫ﺣﺎﻟﺔ‬ ‫ﻓﻰ‬.
‫اﻟ‬ ‫ﻣﺗﺟﻪ‬‫اﻟﻧﺳﺑﯾﺔ‬ ‫ﻋﺔ‬‫ﺳر‬:
‫ـﺳﻣﯾن‬‫ـ‬‫اﻟﺟ‬ ‫ـر‬‫ـ‬‫ﻧﻌﺗﺑ‬‫ا‬‫أن‬‫و‬ ‫ب‬ ،‫ع‬‫ا‬
،‫ع‬‫ب‬‫ـﺷﺎﻫد‬‫ـ‬‫ﻟﻣ‬ ‫ـﺳﺑﺔ‬‫ـ‬‫ﺑﺎﻟﻧ‬ ‫ـﺳﻣﯾن‬‫ـ‬‫اﻟﺟ‬ ‫ﻋﺗﻰ‬‫ـر‬‫ـ‬‫ﺳ‬ ‫ـﻰ‬‫ـ‬‫ﻣﺗﺟﻬ‬)‫و‬(
‫اﻟﺟــــــــــــﺳﯾم‬ ‫ﻋﻠــــــــــــﻰ‬ ‫ﻣوﺟــــــــــــودا‬ ‫ﺷﺧــــــــــــﺻﺎ‬ ‫أن‬ ‫ﻓرﺿــــــــــــﻧﺎ‬ ‫ــــﺈذا‬‫ـ‬‫ﻓـــــــ‬ ‫اﻷرض‬ ‫ﺳــــــــــــطﺢ‬ ‫ـــــــــــﻰ‬‫ـ‬‫ﻋﻠ‬ً ً
‫ا‬‫ﻫـﻰ‬ ‫ب‬ ‫اﻟﺟـﺳﯾم‬ ‫ﻋﺔ‬‫ﺳـر‬ ‫ﻣﺗﺟـﻪ‬ ‫أن‬ ‫وﺟـد‬ ‫أﻧـﻪ‬‫و‬ ‫ب‬ ‫اﻟﺟـﺳﯾم‬ ‫ﺣرﻛـﺔ‬ ‫ورﺻد‬ ‫ﻣﻌﻪ‬ ‫ﻣﺗﺣرك‬‫ع‬‫ب‬‫ا‬
‫ﺣﯾـث‬
‫إﻟﻰ‬ ‫ﺑﺎﻟﻧﺳﺑﺔ‬ ‫ب‬ ‫ﻋﺔ‬‫ﺳر‬ ‫ﻣﺗﺟﻪ‬ ‫ﺗﺳﻣﻰ‬‫ا‬
‫وﺗﻛون‬‫ﺑﯾن‬ ‫اﻟﻌﻼﻗﺔ‬‫ع‬‫ا‬
،‫ع‬‫ب‬،‫ع‬‫ب‬‫ا‬
‫ﻫﻰ‬:
‫ع‬‫ب‬‫ا‬
=‫ع‬‫ب‬‫ـــ‬‫ع‬‫ا‬
)١(
‫اﻟﻰ‬ ‫ﺑﺎﻟﻧﺳﺑﺔ‬ ‫ب‬ ‫ﻋﺔ‬‫ﺳر‬‫ا‬]‫اﺻد‬‫ر‬‫اﻟ‬)‫ا‬(‫اﻟﻣرﺻود‬ ،)‫ب‬[ (
‫ع‬‫ا‬‫ب‬
=‫ع‬‫ا‬
‫ـــ‬‫ع‬‫ب‬
‫ﻋﺔ‬‫ﺳر‬‫ا‬‫ب‬ ‫اﻟﻰ‬ ‫ﺑﺎﻟﻧﺳﺑﺔ‬]‫اﺻد‬‫ر‬‫اﻟ‬)‫ب‬(‫اﻟﻣرﺻود‬ ،)‫ا‬[ (

72. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
72
**‫اﻟﻣ‬ ‫اﻟﺣﺎﻻت‬‫اﻟﺟﺳﻣﯾن‬ ‫ﻟﺣرﻛﺔ‬ ‫ﺧﺗﻠﻔﺔ‬)‫ا‬(‫و‬)‫ب‬: (
‫اﺣد‬‫و‬ ‫اﺗﺟﺎﻩ‬ ‫ﻓﻰ‬ ‫ﯾﺗﺣرﻛﺎن‬ ‫ﻛﺎﻧﺎ‬ ‫إذا‬ ‫ﻟﺟﺳﻣﯾن‬ ‫اﻟﻧﺳﺑﯾﺔ‬ ‫ﻋﺔ‬‫اﻟﺳر‬:
‫إﻟﻰ‬ ‫ﺑﺎﻟﻧﺳﺑﺔ‬ ‫ب‬ ‫ﻋﺔ‬‫ﺳر‬ ‫ﻣﺗﺟﻪ‬ ‫أن‬ ‫أى‬‫ا‬=‫ب‬ ‫ﻋﺔ‬‫ﺳر‬ ‫ﻣﺗﺟﻪ‬-‫ﻋﺔ‬‫ﺳر‬ ‫ﻣﺗﺟﻪ‬‫ا‬
‫ع‬‫ب‬‫ا‬
=‫ع‬‫ب‬‫ـــ‬‫ع‬‫ا‬
)١(
‫ﺗﻛون‬ ‫وﺑﺎﻟﺗﺎﻟﻰ‬
‫ع‬‫ب‬=‫ع‬‫ا‬
+‫ع‬‫ب‬‫ا‬
)٢(
‫ﻣﻼﺣظﺔ‬:‫ﻛﺎن‬ ‫إذا‬‫ع‬‫ا‬
=‫ع‬‫ب‬‫ﻓﺈن‬‫ع‬‫ا‬‫ب‬
=٠،‫ع‬‫ب‬‫ا‬=٠
‫ﻣﺗﺿﺎدﯾن‬ ‫اﺗﺟﺎﻫﯾن‬ ‫ﻓﻰ‬ ‫ﯾﺗﺣرﻛﺎن‬ ‫اﻟﺟﺳﻣﯾن‬ ‫ﻛﺎن‬ ‫إذا‬:
‫ﻓﺈن‬:‫ع‬‫ب‬‫ا‬
=‫ع‬‫ب‬–)-‫ع‬‫ا‬
(
‫أن‬ ‫أى‬:‫ع‬‫ب‬‫ا‬
=‫ع‬‫ب‬+‫ع‬‫ا‬
‫ﻣﻼﺣظﺔ‬:‫ﻛﺎن‬ ‫إذا‬‫ع‬‫ا‬
=‫ع‬‫ب‬‫ﻓﺈن‬‫ع‬‫ا‬‫ب‬
=٢‫ع‬‫ا‬=٢‫ع‬‫ب‬
‫ــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـ‬‫ــــــــــ‬
‫اﻟﺤﻞ‬:
‫ا‬ ‫ب‬
‫ى‬ +
‫ا‬ ‫ب‬
‫ى‬ +

73. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
73
‫ـــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻟﺤﻞ‬:
‫اﻟﺰﻣﻦ‬= = =٢‫ﺳﺎﻋﺔ‬ ‫اﻟﻤﺴﺎﻓﺔ‬
‫اﻟﺴﺮﻋﺔ‬
١٠٠
٥٠

74. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
74
‫ﻣﺛﺎل‬:‫ﻋ‬‫اﻟـﺳر‬ ‫اﻗﺑـﺔ‬‫ر‬‫ﻟﻣ‬ ‫اﻟﻣﺧﺻـﺻﺔ‬ ‫ادار‬‫ر‬‫اﻟ‬ ‫ة‬‫ﺳﯾﺎر‬ ‫ﺗﺗﺣرك‬‫ﺔ‬‫ﻋﺔ‬‫ﺑـﺳر‬ ‫اوﯾﺔ‬‫ر‬‫اﻟـﺻﺣ‬ ‫اﻟطـرق‬ ‫ﻋﻠـﻰ‬٣٠‫ﻛـم‬/
‫ﻋﺔ‬‫ﺑـﺳر‬ ‫ﺗﺗﺣـرك‬ ‫وﻛﺄﻧﻬـﺎ‬ ‫ﻓﺑـدت‬ ‫اﻟﻣـﺿﺎد‬ ‫اﻻﺗﺟـﺎﻩ‬ ‫ﻓـﻰ‬ ‫ﻗﺎدﻣـﺔ‬ ‫ﺷـﺎﺣﻧﺔ‬ ‫ﺣرﻛﺔ‬ ‫ة‬‫اﻟﺳﯾﺎر‬ ‫ﻫذﻩ‬ ‫اﻗﺑت‬‫ر‬ ‫ﺳﺎﻋﺔ‬
١١٠‫ﻛم‬/‫ﺳﺎﻋﺔ‬.‫اﻟﺷﺎﺣﻧﺔ‬ ‫ﻟﺣرﻛﺔ‬ ‫اﻟﻔﻌﻠﯾﺔ‬ ‫ﻋﺔ‬‫اﻟﺳر‬ ‫ﻫﻰ‬ ‫ﻓﻣﺎ‬.
‫اﻟﺣل‬:
‫ﺑﻔرض‬‫ى‬‫ع‬ ‫ﻋﺗﻬﺎ‬‫ﺳر‬ ‫أن‬‫و‬ ‫اﻟﺷﺎﺣﻧﺔ‬ ‫ﺣرﻛﺔ‬ ‫اﺗﺟﺎﻩ‬ ‫ﻓﻰ‬ ‫وﺣدة‬ ‫ﻣﺗﺟﻪ‬‫ب‬
‫ﺳ‬ ‫ﻣﺗﺟﻪ‬ ‫وﺑﺎﻟﺗﺎﻟﻰ‬‫ع‬ ‫ادار‬‫ر‬‫اﻟ‬ ‫ة‬‫ﺳﯾﺎر‬ ‫ﻋﺔ‬‫ر‬‫أ‬=-٣٠‫ى‬
∵‫ع‬‫أ‬ ‫ب‬
=‫ع‬‫ب‬
-‫ع‬‫أ‬
∴١١٠‫ى‬=‫ع‬‫ب‬
-)-٣٠‫ى‬(
١١٠‫ى‬=‫ع‬‫ب‬
+٣٠‫ى‬∴‫ع‬‫ب‬
=١١٠‫ى‬–٣٠‫ى‬=٨٠‫ى‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــ‬
‫ﻣﺜﺎل‬:‫ﺳﯿﺎرﺗﯿﻦ‬ ‫ﺗﺘﺤﺮك‬‫ا‬‫ﻋﻠﻰ‬ ‫ب‬ ،‫ﻧﻔﺲ‬‫ﺑﺎﻟﺴﺮﻋﺘﯿﻦ‬ ‫ﻣﺴﺘﻘﯿﻢ‬ ‫ﻃﺮﯾﻖ‬٦٠‫ﻛﻢ‬/، ‫س‬٩٠‫ﻛﻢ‬/‫س‬
‫ب‬ ‫أﺗﺠﺎه‬ ‫وﻓﻰ‬‫ا‬‫ﲔ‬‫ﺑ‬‫أوﺟﺪ‬) :١(‫ﺳﺮ‬‫اﻟﻰ‬ ‫ﺑﺎﻟﻨﺴﺒﺔ‬ ‫ب‬ ‫ﻋﺔ‬‫ا‬)٢(‫ﺳﺮﻋﺔ‬‫ا‬‫ب‬ ‫ﻟـ‬ ‫ﺑﺎﻟﻨﺴﺒﺔ‬
‫ﺑﯿﻨﮭﻤﺎ‬ ‫اﻟﻤﺴﺎﻓﺔ‬ ‫ﻛﺎﻧﺖ‬ ‫وإذا‬١٠‫ﯾﻠﺘﻘﯿﺎ‬ ‫أن‬ ‫ﯾﻤﻜﻦ‬ ‫دﻗﯿﻘﺔ‬ ‫ﻛﻢ‬ ‫ﻓﺒﻌﺪ‬ ‫ﻛﻢ‬
‫اﻟﺤﻞ‬:
‫ع‬‫ب‬‫ا‬=‫ع‬‫ب‬–‫ع‬‫ا‬=٩٠–٦٠=٣٠‫ﻛﻢ‬/‫س‬
‫أن‬ ‫أى‬:‫اﻟﺴﯿﺎرة‬‫ا‬‫ﺑﺴﺮﻋﺔ‬ ‫ﺗﺴﺒﻘﮭﺎ‬ ‫و‬ ‫أﻣﺎﻣﮭﺎ‬ ‫ﺗﺴﯿﺮ‬ ‫ب‬ ‫اﻟﺴﯿﺎرة‬ ‫ﻛﺄن‬ ‫و‬ ‫ﺗﺸﻌﺮ‬٣٠‫ﻛﻢ‬/‫س‬
‫ع‬‫ا‬‫ب‬=‫ع‬‫ا‬–‫ع‬‫ب‬=٦٠–٩٠=-٣٠‫ﻛﻢ‬/‫س‬
‫أن‬ ‫أى‬:‫اﻟﺴﯿﺎرة‬ ‫ﻛﺄن‬ ‫و‬ ‫ﺗﺸﻌﺮ‬ ‫ب‬ ‫اﻟﺴﯿﺎرة‬‫ا‬‫ﻧﺤﻮھﺎ‬ ‫ﺗﺴﯿﺮ‬)‫ﺗﺘﻘﮭﻘﺮ‬(‫ﺑﺴﺮﻋﺔ‬٣٠‫ﻛﻢ‬/‫س‬
‫ﻟﻼﻟﺘﻘﺎء‬ ‫اﻟﻼزم‬ ‫اﻟﺰﻣﻦ‬= = =‫ﺳﺎﻋﺔ‬=٢٠‫دﻗﯿﻘﺔ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــ‬‫ــــ‬
‫ﻣﺜﺎل‬:‫اﻟﻤﺴﺎﻓﺔ‬ ‫ﻛﺎﻧﺖ‬ ‫ﻓﺈذا‬ ‫ﻣﺘﻀﺎدﯾﻦ‬ ‫أﺗﺠﺎھﯿﻦ‬ ‫ﻓﻰ‬ ‫اﻟﻤﺴﺘﻘﯿﻢ‬ ‫اﻟﺨﻂ‬ ‫ﻧﻔﺲ‬ ‫ﻋﻠﻰ‬ ‫ﺳﯿﺎرﺗﺎن‬ ‫ﺗﺘﺤﺮك‬
‫ﺑﯿﻨﮭﻤﺎ‬٤‫ﻛﻢ‬‫اﻟﺴﯿﺎرﺗﯿﻦ‬ ‫أﺣﺪى‬ ‫وﺳﺮﻋﺔ‬٧٠‫ﻛﻢ‬/‫دﻗﯿﻘﺘﯿﻦ‬ ‫ﺑﻌﺪ‬ ‫وﺗﻘﺎﺑﻠﺘﺎ‬ ‫س‬
‫اﻻﺧﺮى‬ ‫ﻟﻠﺴﯿﺎرة‬ ‫اﻟﻔﻌﻠﯿﺔ‬ ‫اﻟﺴﺮﻋﺔ‬ ‫ھﻰ‬ ‫ﻓﻤﺎ‬٠
‫اﻟﺤ‬‫ﻞ‬:
‫ع‬‫ب‬‫ا‬= =٤÷=٤×٣٠=١٢٠‫ﻛﻢ‬/‫س‬
‫ا‬ ‫ب‬‫ى‬ +
‫اﻟﻤﺴﺎﻓﺔ‬
‫اﻟﺴﺮﻋﺔ‬
١٠
٣٠
١
٣
‫ا‬‫ب‬
‫اﻟﻤﺴﺎﻓﺔ‬
‫اﻟﺰﻣﻦ‬
٢
٦٠

75. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
75
‫ع‬‫ب‬+‫ع‬‫أ‬=١٢٠B‫ع‬‫ب‬+٧٠=١٢٠B‫ع‬‫ب‬=١٢٠–٧٠=٥٠‫ﻛﻢ‬/‫س‬
‫ـــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﺑﻌﺪ‬ ‫ﻋﻠﻰ‬ ‫ﺻﺎرت‬ ‫وﻟﻤﺎ‬ ‫ﻣﯿﻨﺎء‬ ‫ﻧﺤﻮ‬ ‫ﻣﺴﺘﻘﯿﻢ‬ ‫ﻣﺴﺎر‬ ‫ﻓﻰ‬ ‫ﺑﺎﺧﺮة‬ ‫ﺗﺘﺤﺮك‬٤٥‫ﻣﺮت‬ ‫اﻟﻤﯿﻨﺎء‬ ‫ﻣﻦ‬ ‫ﻛﻢ‬
‫ﺑﺴ‬ ‫اﻟﻤﻀﺎد‬ ‫اﻻﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫ﻃﺎﺋﺮة‬ ‫ﻓﻮﻗﮭﺎ‬‫ﺮﻋﺔ‬٢٥٠‫ﻛﻢ‬/‫ﻟﮭﺎ‬ ‫ﻓﺒﺪت‬ ‫اﻟﺒﺎﺧﺮة‬ ‫ﺣﺮﻛﺔ‬ ‫ورﺻﺪت‬ ‫س‬
‫ﺑﺴﺮﻋﺔ‬ ‫ﻣﺘﺤﺮﻛﺔ‬٢٦٥‫ﻛﻢ‬/‫أﺣﺴﺐ‬ ‫س‬‫وﺻﻮل‬ ‫ﺣﺘﻰ‬ ‫ﯾﻤﻀﻲ‬ ‫اﻟﻮﻗﺖ‬ ‫ﻣﻦ‬ ‫ﻛﻢ‬‫اﻟﺒﺎﺧﺮة‬‫إﻟ‬‫اﻟﻤﯿﻨﺎء‬ ‫ﻰ‬.
‫اﻟﺤﻞ‬:
‫ع‬‫ﻟﻠﻄﺎﺋﺮة‬ ‫ﺑﺎﻟﻨﺴﺒﺔ‬ ‫اﻟﺒﺎﺧﺮة‬=‫ع‬‫اﻟﻄﺎﺋﺮة‬+‫ع‬‫اﻟﺒﺎﺧﺮة‬
٢٦٥=٢٥٠+‫ع‬‫اﻟﺒﺎﺧﺮة‬
‫ع‬‫اﻟﺒﺎﺧﺮة‬=٢٦٥–٢٥٠=١٥‫ﻛﻢ‬/‫س‬
‫اﻟﺰﻣﻦ‬= = =٣‫ﺳﺎﻋﺎت‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﻣ‬ ‫ﺧﻂ‬ ‫ﻋﻠﻰ‬ ‫ﻣﺘﺤﺮﻛﺔ‬ ‫ﺷﺮﻃﺔ‬ ‫ﺳﯿﺎرة‬ ‫ﻗﺎﻣﺖ‬‫اﻻﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫ﻗﺎدﻣﺔ‬ ‫ﻧﻘﻞ‬ ‫ﺳﯿﺎرة‬ ‫ﺳﺮﻋﺔ‬ ‫ﺑﻘﯿﺎس‬ ‫ﺴﺘﻘﯿﻢ‬
‫ﻓﻮﺟﺪﺗﮭﺎ‬ ‫اﻟﻄﺮﯾﻖ‬ ‫ﻧﻔﺲ‬ ‫وﻋﻠﻰ‬ ‫اﻟﻤﻀﺎد‬١٨٠‫ﻛﻢ‬/‫ﺳﺮﻋﺘﮭﺎ‬ ‫اﻟﺸﺮﻃﺔ‬ ‫ﺳﯿﺎرة‬ ‫ﺧﻔﻀﺖ‬ ‫وﻟﻤﺎ‬ ‫س‬
‫ﻓﻮﺟﺪﺗﮭﺎ‬ ‫اﻟﻨﻘﻞ‬ ‫ﻟﺴﯿﺎرة‬ ‫اﻟﻨﺴﺒﯿﺔ‬ ‫اﻟﺴﺮﻋﺔ‬ ‫ﻗﯿﺎس‬ ‫وأﻋﺎدت‬ ‫اﻟﺴﺎﺑﻘﺔ‬ ‫ﺳﺮﻋﺘﮭﺎ‬ ‫ﺛﻠﺜﻰ‬ ‫اﻟﻰ‬١٥٠
‫ﻛﻢ‬/‫س‬.‫ﻟﻜﻼ‬ ‫اﻟﻔﻌﻠﯿﺔ‬ ‫اﻟﺴﺮﻋﺔ‬ ‫أﺣﺴﺐ‬‫اﻟﺴﯿﺎرﺗﯿﻦ‬ ‫ﻣﻦ‬.
‫اﻟﺤﻞ‬:‫ع‬ ‫ﺑﻔﺮض‬‫أ‬‫اﻟﺸﺮﻃﺔ‬ ‫ﺳﯿﺎرة‬ ‫ﺳﺮﻋﺔ‬
‫ع‬‫ب‬‫اﻟﻨﻘﻞ‬ ‫ﺳﯿﺎرة‬ ‫ﺳﺮﻋﺔ‬
‫ع‬‫أ‬ ‫ب‬=١٨٠B‫ع‬‫ب‬+‫ع‬‫أ‬=١٨٠)١(
‫ع‬‫أ‬ ‫ب‬=١٥٠B‫ع‬‫ب‬+‫ع‬‫أ‬=١٥٠)٢(
‫ﺑطرح‬٢‫ﻣن‬١‫ﻧﺟد‬:
‫ع‬‫أ‬=٣٠B‫ع‬‫أ‬=٩٠‫ﻛم‬/‫س‬
B‫ع‬‫ب‬=١٨٠–٩٠=٩٠‫ﻛم‬/‫س‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــ‬
‫ﻗﺎدﻣﺔ‬ ‫ب‬ ‫ة‬‫ﻟﺳﯾﺎر‬ ‫اﻟﻧﺳﺑﯾﺔ‬ ‫ﻋﺔ‬‫اﻟﺳر‬ ‫وﺑﻘﯾﺎس‬ ‫ﻣﺳﺗﻘﯾم‬ ‫طرﯾق‬ ‫ﻋﻠﻰ‬ ‫ﻣﺗﺣرﻛﺔ‬ ‫أ‬ ‫ة‬‫ﺳﯾﺎر‬ ‫ﻗﺎﻣت‬ : ‫ﺗدرﯾب‬
‫ﻓوﺟـدﺗﻬﺎ‬ ‫اﻟﻣـﺿﺎد‬ ‫اﻻﺗﺟـﺎﻩ‬ ‫ﻓﻰ‬١٤٠‫ﻛـم‬/‫ﺳـﺎﻋﺔ‬.‫إﻟـﻰ‬ ‫ﻋﺗﻬﺎ‬‫ﺳـر‬ ‫أ‬ ‫ة‬‫اﻟـﺳﯾﺎر‬ ‫ﺧﻔـﺿت‬ ‫وﻟﻣـﺎ‬
‫اﻟﻧﺳﺑﯾﺔ‬ ‫ﻋﺔ‬‫اﻟﺳر‬ ‫أن‬ ‫وﺟدت‬ ‫اﻟﻘﯾﺎس‬ ‫أﻋﺎدت‬‫و‬ ‫اﻟﻧﺻف‬‫أﺻﺑﺣت‬ ‫ب‬ ‫ة‬‫ﻟﻠﺳﯾﺎر‬١٢٠‫ﻛم‬/‫ﺳﺎﻋﺔ‬
‫؟‬ ‫اﻟﺳﯾﺎرﺗﯾن‬ ‫ﻣن‬ ‫ﻟﻛل‬ ‫اﻟﻔﻌﻠﯾﺔ‬ ‫ﻋﺔ‬‫اﻟﺳر‬ ‫ﻓﻣﺎ‬
‫اﻟﻤﺴﺎﻓﺔ‬
‫اﻟﺴﺮﻋﺔ‬
٤٥
١٥
‫ا‬
‫ب‬ ‫ى‬
‫ﺷﺮﻃﺔ‬ ‫ﻧﻘﻞ‬
‫ب‬‫أ‬
٢
٣
١
٣

76. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
76
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻟﻨﺴﺒﯿﺔ‬ ‫اﻟﺴﺮﻋﺔ‬ ‫ﻋﻠﻰ‬ ‫ﺗﻤﺎرﯾﻦ‬

77. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
77
‫ـــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــ‬

78. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
78
*‫ﻰ‬ ‫ﻨ‬ ‫ﺤ‬ ‫ﻨ‬ ‫ﻣ‬)‫ﺔ‬ ‫ﻋ‬ ‫ﺮ‬ ‫ﺴ‬ ‫ﻟ‬ ‫ا‬–‫ﻦ‬ ‫ﻣ‬ ‫ﺰ‬ ‫ﻟ‬ ‫ا‬(:
‫اﻟﺘﺴﺎرع‬ ‫ﻣﻔﮭﻮم‬ ‫ﯾﺮﺗﺒﻂ‬)‫اﻟﻌﺠﻠﺔ‬(‫اﻟﺴﺮﻋﺔ‬ ‫ﺑﺘﻐﯿﺮ‬
‫ﻓﻰ‬‫اﻟﻤ‬ ‫اﻟﺸﻜﻞ‬‫ﻘﺎﺑﻞ‬:
‫اﻟﺴﺮﻋﺔ‬ ‫ﻗﯿﻤﺔ‬ ‫ﺗﺰداد‬‫ﻣﺘﺴﺎرﻋﺔ‬ ‫اﻟﺤﺮﻛﺔ‬ ‫ﺗﻜﻮن‬ ‫و‬ ‫اﻟﺰﻣﻦ‬ ‫ﻣﻊ‬
‫اﻟﺘﺴﺎرع‬ ‫ﯾﻜﻮن‬ ‫و‬)‫اﻟﻌﺠﻠﺔ‬(ً‫ﺎ‬‫ﻣﻮﺟﺒ‬)‫ﻣﻮﺟﺒﺔ‬ ‫اﻟﺴﺮﻋﺔ‬ ‫ﺑﺎﻋﺘﺒﺎر‬(
‫ﻓﻰ‬‫اﻟﻤﻘﺎﺑﻞ‬ ‫اﻟﺸﻜﻞ‬:
‫ﺗﻘﺼﯿﺮﯾﺔ‬ ‫اﻟﺤﺮﻛﺔ‬ ‫ﺗﻜﻮن‬ ‫و‬ ‫اﻟﺰﻣﻦ‬ ‫ﻣﻊ‬ ‫اﻟﺴﺮﻋﺔ‬ ‫ﻗﯿﻤﺔ‬ ‫ﺗﻨﺎﻗﺺ‬
ً‫ﺎ‬‫ﺳﺎﻟﺒ‬ ‫اﻟﺘﺴﺎرع‬ ‫وﯾﻜﻮن‬)‫ﺳﺎﻟﺒﺔ‬ ‫اﻟﺴﺮﻋﺔ‬ ‫ﺑﺎﻋﺘﺒﺎر‬(
‫ﺛﺎﺑﺘﺔ‬ ‫اﻟﺴﺮﻋﺔ‬ ‫ﻛﺎﻧﺖ‬ ‫وإذا‬‫ﻣﻨﺘﻈﻤﺔ‬ ‫اﻟﺤﺮﻛﺔ‬ ‫ﺗﻜﻮن‬ ‫اﻟﺰﻣﻦ‬ ‫ﻣﻊ‬.
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﺗﺬﻛﺮ‬‫اﻟﺤﺮﻛﺔ‬ ‫اﻧﻮاع‬:
*‫اﻟﻤﻨﺘﻈﻤﺔ‬ ‫اﻟﺤﺮﻛﺔ‬:
‫ﻣﻌ‬ ‫ﻣﻦ‬ ‫ﻛﻞ‬ ‫ﻓﯿﮭﺎ‬ ‫ﯾﻜﻮن‬ ‫اﻟﺘﻰ‬ ‫اﻟﺤﺎﻟﺔ‬ ‫ھﻰ‬ً‫ﺎ‬‫ﺛﺎﺑﺘ‬ ‫اﻟﺴﺮﻋﺔ‬ ‫ﻣﺘﺠﺔ‬ ‫واﺗﺠﺎه‬ ‫ﯿﺎر‬)‫ﻓﻰ‬ ‫ﯾﺘﺤﺮك‬ ‫اﻟﺠﺴﯿﻢ‬ ‫أى‬
‫ﻣﺘﺴﺎوﯾﺔ‬ ‫زﻣﻨﯿﺔ‬ ‫ﻓﺘﺮات‬ ‫ﻓﻰ‬ ‫ﻣﺘﺴﺎوﯾﺔ‬ ‫ﻣﺴﺎﻓﺎت‬ ‫ﯾﻘﻄﻊ‬ ‫ﺣﯿﺚ‬ ‫ﺛﺎﺑﺖ‬ ‫اﺗﺠﺎه‬(‫اﻟﻌﺠﻠﺔ‬ ‫ﺗﻜﻮن‬ ‫و‬=‫ﺻﻔﺮ‬
‫ﺑﯿﻦ‬ ‫اﻟﻌﻼﻗﺔ‬ ‫ﺗﻜﻮن‬ ‫و‬‫ف‬،‫ع‬:‫ف‬=‫ن‬‫ع‬

79. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
79
*‫ة‬‫اﻟﻣﺗﻐﯾر‬ ‫اﻟﺣرﻛﺔ‬:
‫ﻋﺔ‬‫ﺳر‬ ‫ﻣﺗﺟﻪ‬ ‫ﻓﯾﻬﺎ‬ ‫ﯾﺗﻐﯾر‬ ‫اﻟﺗﻰ‬ ‫اﻟﺣرﻛﺔ‬ ‫ﻫﻰ‬‫اﻟﻣ‬ ‫ﻓﻰ‬ ‫اﻟﺟﺳﯾم‬‫اﻻﺗﺟﺎﻩ‬ ‫ﻓﻰ‬ ‫أو‬ ‫ﻘدار‬‫أو‬‫ﻣن‬ ‫ﻛﻠﯾﻬﻣﺎ‬ ‫ﻓﻰ‬
‫ى‬‫أﺧر‬ ‫إﻟﻰ‬ ‫ﻟﺣظﺔ‬.‫ﯾﺗﺣرك‬ ‫اﻟﺟﺳﯾم‬ ‫ﻫذا‬ ‫أن‬ ‫ﻧﻘول‬ ‫ﻓﺈﻧﻧﺎ‬‫ﺑﻌﺟﻠﺔ‬ ‫ﯾﺗﺣرك‬ ‫أﻧﻪ‬ ‫أو‬ ‫ة‬‫ﻣﺗﻐﯾر‬ ‫ﺣرﻛﺔ‬‫ة‬‫ﻣﺗﻐﯾر‬
*‫اﻟﺘﻐﯿﺮ‬ ‫ﻣﻨﺘﻈﻤﺔ‬ ‫اﻟﺤﺮﻛﺔ‬:
‫ﺑﺘﺴﺎرع‬ ‫أو‬ ‫اﻟﺘﻐﯿﺮ‬ ‫ﻣﻨﺘﻈﻤﺔ‬ ‫ﺣﺮﻛﺔ‬ ‫ﯾﺘﺤﺮك‬ ‫اﻟﺠﺴﻢ‬ ‫أن‬ ‫ﯾﻘﺎل‬)‫ﻋﺠﻠﺔ‬(‫اﻟﻌﺠﻠﺔ‬ ‫ﻣﺘﺠﺔ‬ ‫ﻛﺎن‬ ‫إذا‬ ‫ﻣﻨﺘﻈﻢ‬
‫واﺗ‬ ً‫ا‬‫ﻣﻘﺪار‬ ً‫ﺎ‬‫ﺛﺎﺑﺘ‬‫اﻷزﻣﻨﺔ‬ ‫ﻟﺠﻤﯿﻊ‬ ً‫ﺎ‬‫ﺠﺎھ‬.
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﺳﯿﺎرة‬ ‫ﺳﺮﻋﺔ‬ ‫ﺗﻐﯿﺮت‬ ‫إذا‬)‫ا‬(‫ﻣﻦ‬ ‫ﻣﺴﺘﻘﯿﻢ‬ ‫ﺧﻂ‬ ‫ﻓﻰ‬ ‫ﺗﺘﺤﺮك‬٢٤‫ﻛﻢ‬/‫إﻟﻰ‬ ‫س‬٣٦‫ﻛﻢ‬/‫س‬
‫ﺧﻼل‬٥‫ﺳﯿﺎرة‬ ‫ﺳﺮﻋﺔ‬ ‫ﺗﻐﯿﺮت‬ ‫و‬ ، ‫ﺛﻮاﻧﻰ‬)‫ب‬(‫اﻟﻤﺴﺘﻘﯿﻢ‬ ‫اﻟﺨﻂ‬ ‫ﻧﻔﺲ‬ ‫ﻓﻰ‬ ‫ﺗﺘﺤﺮك‬‫ﻣﻦ‬
١٢‫ﻛﻢ‬/‫اﻟﻰ‬ ‫س‬٣٠‫ﻛﻢ‬/‫اﻟﻤﺪة‬ ‫ﻧﻔﺲ‬ ‫ﺧﻼل‬ ‫س‬.‫ذﻟﻚ‬ ‫ﻓﺴﺮ‬ ‫؟‬ ‫أﻛﺒﺮ‬ ‫ﺑﺘﺴﺎرع‬ ‫ﯾﺘﺤﺮك‬ ‫أﯾﮭﻤﺎ‬
‫اﻟﺤﻞ‬:
‫اﻟﺰﯾﺎدة‬‫اﻟﺴﯿﺎرة‬ ‫ﺳﺮﻋﺔ‬ ‫ﻓﻰ‬‫ا‬=٣٦–٢٤=١٢‫ﻛﻢ‬/‫س‬=٣٫٣‫م‬/‫ث‬
‫ﺳﺮﻋ‬ ‫ﻓﻰ‬ ‫اﻟﺰﯾﺎدة‬‫ب‬ ‫اﻟﺴﯿﺎرة‬ ‫ﺔ‬=٣٠–١٢=١٨‫ﻛﻢ‬/‫س‬=٥‫م‬/‫ث‬
‫ـ‬‫ﺟ‬‫ﺝ‬‫ﻟﻠﺴﯿﺎرة‬‫ا‬= = =٠٫٦٦‫م‬/‫ث‬٢
‫ﺝ‬‫ب‬ ‫ﻟﻠﺴﯿﺎرة‬= =١‫م‬/‫ث‬٢
‫اﻟﺴﯿﺎرة‬ ‫ﺳﺮﻋﺔ‬ ‫ﻋﻦ‬ ‫ﺗﺰﯾﺪ‬ ‫ب‬ ‫اﻟﺴﯿﺎرة‬ ‫ﺳﺮﻋﺔ‬ ‫أن‬ ‫واﺿﺢ‬‫ا‬
‫ﺑﻌﺠﻠﺔ‬ ‫ﺗﺘﺤﺮك‬ ‫ب‬ ‫اﻟﺴﯿﺎرة‬ ‫ﺑﺎﻟﺘﺎﻟﻰ‬ ‫و‬‫اﻟﺴﯿﺎرة‬ ‫ﻣﻦ‬ ‫أﻛﺒﺮ‬‫ا‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻟﻤﻨﺘ‬ ‫اﻟﺤﺮﻛﺔ‬ ‫ﻓﻰ‬ ‫واﻟﺰﻣﻦ‬ ‫واﻟﻌﺠﻠﺔ‬ ‫واﻟﺴﺮﻋﺔ‬ ‫اﻟﻤﺴﺎﻓﺔ‬ ‫ﺑﯿﻦ‬ ‫ﺗﺮﺑﻂ‬ ‫أﺳﺎﺳﯿﺔ‬ ‫ﻣﻌﺎدﻻت‬ ‫ﺛﻼث‬ ‫ﺗﻮﺟﺪ‬‫ﻈﻤﺔ‬
‫اﻟﺴﺮﻋﺔ‬ ‫ﻓﻰ‬ ‫اﻟﺘﻐﯿﺮ‬
‫اﻟﺰﻣﻦ‬
٥
٥
٣٫٣
٥
‫اﻟﺘﻐﯿﺮ‬ ‫ﻣﻨﺘﻈﻤﺔ‬ ‫اﻟﺤﺮﻛﺔ‬ ‫ﻣﻌﺎدﻻت‬

80. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
80
‫ھﺎﻣﺔ‬ ‫ﻣﻼﺣﻈﺎت‬:
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﺑﺴﺮﻋﺔ‬ ‫ﺛﺎﺑﺖ‬ ‫اﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫ﺣﺮﻛﺘﮫ‬ ‫ﺟﺴﯿﻢ‬ ‫ﺑﺪأ‬٢٠‫ﺳﻢ‬/‫ﻣﻨﺘﻈﻤﺔ‬ ‫ﺑﻌﺠﻠﺔ‬ ‫و‬ ‫ث‬٥‫ﺳﻢ‬/‫ث‬٢
‫ﺗﻌﻤﻞ‬
‫اﻻﺑﺘﺪاﺋﯿﺔ‬ ‫اﻟﺴﺮﻋﺔ‬ ‫ﻣﺘﺠﮫ‬ ‫اﺗﺠﺎه‬ ‫ﻧﻔﺲ‬ ‫ﻓﻰ‬.‫أوﺟﺪ‬:
)‫أ‬(‫اﻟﺤﺮﻛﺔ‬ ‫ﺑﺪأ‬ ‫ﻣﻦ‬ ‫واﺣﺪة‬ ‫دﻗﯿﻘﺔ‬ ‫ﻧﮭﺎﯾﺔ‬ ‫ﻓﻰ‬ ‫ﺳﺮﻋﺘﮫ‬.
)‫ب‬(‫ﺳﺮﻋﺘﮫ‬ ‫ﺗﺼﺒﺢ‬ ‫ﺣﺘﻰ‬ ‫اﻟﺤﺮﻛﺔ‬ ‫ﺑﺪء‬ ‫ﻣﻦ‬ ‫ﯾﻤﻀﻰ‬ ‫اﻟﺬى‬ ‫اﻟﺰﻣﻦ‬١٨‫ﻛﻢ‬/‫س‬
‫اﻟﺤﻞ‬:
‫اﻟﺠﺴﯿﻢ‬ ‫ﺣﺮﻛﺔ‬ ‫اﺗﺠﺎه‬ ‫ھﻮ‬ ‫اﻟﻤﻮﺟﺐ‬ ‫اﻻﺗﺠﺎه‬ ‫ﻧﻔﺮض‬
‫ع‬٠=٢٠‫ﺳﻢ‬/، ‫ث‬‫ﺝ‬=٥‫ﺳﻢ‬/‫ث‬٢
‫ن‬ ،=٦٠‫ﺛﺎﻧﯿﺔ‬
)‫أ‬(A‫ع‬=‫ع‬٠+‫ﺟـ‬‫ن‬B‫ع‬=٢٠+٥×٦٠=٣٢٠‫ﺳﻢ‬/‫ث‬
)‫ب‬(‫ع‬٠=٢٠‫ﺳﻢ‬/‫ع‬ ، ‫ث‬=١٨×=٥٠٠‫ﺳﻢ‬/، ‫ث‬‫ﺝ‬=٥‫ﺳﻢ‬/‫ث‬٢
A‫ع‬=‫ع‬٠+‫ﺟـ‬‫ن‬B٥٠٠=٢٠+٥×‫ن‬B٥‫ن‬=٤٨٠
B‫ن‬=٩٦‫ﺛﺎﻧﯿﺔ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﻣﻦ‬ ‫ﺳﺮﻋﺘﮫ‬ ‫ﻓﺘﻐﯿﺮت‬ ‫ﺟﺴﯿﻢ‬ ‫ﯾﺘﺤﺮك‬٥٤‫ﻛﻢ‬/‫اﻟﻰ‬ ‫س‬٣‫م‬/‫ﻗﺪره‬ ‫زﻣﻦ‬ ‫ﻓﻰ‬ ‫ث‬‫دﻗﯿﻘﺔ‬ ‫ﻧﺼﻒ‬.
‫اﻟﺤﺮﻛﺔ‬ ‫ﻋﺠﻠﺔ‬ ‫ﻣﻘﺪار‬ ‫أوﺟﺪ‬.‫اﻟﺠﺴﯿﻢ‬ ‫ﻟﮭﺬا‬ ‫ﯾﻤﻜﻦ‬ ‫ھﻞ‬‫إﺟﺎﺑﺘﻚ‬ ‫ﻓﺴﺮ‬ ‫؟‬ ً‫ﺎ‬‫ﻟﺤﻈﯿ‬ ‫ﯾﺴﻜﻦ‬ ‫أن‬.
‫اﻟﺤﻞ‬:
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـ‬
‫ﺗﺪرﯾﺐ‬:‫ﻣﻨﺘﻈﻤﺔ‬ ‫ﺑﻌﺠﻠﺔ‬ ‫ﻣﺴﺘﻘﯿﻢ‬ ‫ﺧﻂ‬ ‫ﻓﻰ‬ ‫ﺣﺮﻛﺘﮫ‬ ‫ﺟﺴﯿﻢ‬ ‫ﺑﺪأ‬٥‫ﺳﻢ‬/‫ث‬٢‫اﺑﺘﺪاﺋﯿﺔ‬ ‫وﺑﺴﺮﻋﺔ‬
٢٠‫ﺳﻢ‬/‫اﻟﻌﺠﻠﺔ‬ ‫اﺗﺠﺎه‬ ‫ﻋﻜﺲ‬ ‫ﻓﻰ‬ ‫ث‬.‫ﺑﻌﺪ‬ ‫ﺳﺮﻋﺘﮫ‬ ‫أوﺟﺪ‬:
)١(‫ﺛﻮاﻧﻰ‬ ‫ﺛﻼث‬ ‫ﻣﺮور‬)٢(‫ﺛﻮاﻧﻰ‬ ‫ﺧﻤﺲ‬ ‫ﻣﺮور‬
٢٥٠
٩

81. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
81
‫ﺛﺎﻧﯿﺎ‬‫اﻟﺰﻣﻦ‬ ‫و‬ ‫اﻟﻤﺴﺎﻓﺔ‬ ‫ﺑﯿﻦ‬ ‫اﻟﻌﻼﻗﺔ‬:
‫اﺑﺘﺪا‬ ‫ﺑﺴﺮﻋﺔ‬ ‫ﻣﻨﺘﻈﻤﺔ‬ ‫ﺑﻌﺠﻠﺔ‬ ‫ﺟﺴﯿﻢ‬ ‫ﯾﺘﺤﺮك‬‫ﺋﯿﺔ‬‫ع‬٠‫ﺳﺮﻋﺘﮫ‬ ‫أﺻﺒﺤﺖ‬ ‫ن‬ ‫زﻣﻦ‬ ‫ﺑﻌﺪ‬‫ع‬‫ﻓﺈن‬:
‫ف‬=‫ع‬٠‫ن‬+‫ن‬ ‫ﺟـ‬٢
‫ﻣﻨﺤﻨﻰ‬ ‫ﺗﺤﺖ‬ ‫اﻟﻤﺴﺎﺣﺔ‬)‫اﻟﺴﺮﻋﺔ‬–‫اﻟﺰﻣﻦ‬= (‫اﻟﺠﺴﯿﻢ‬ ‫ازاﺣﺔ‬
‫ﻣﻼﺣﻈﺎت‬‫ھﺎﻣﺔ‬:
١(‫ﻓﺈن‬ ‫ﺳﻜﻮن‬ ‫ﻣﻦ‬ ‫ﯾﺘﺤﺮك‬ ‫اﻟﺠﺴﯿﻢ‬ ‫ﻛﺎن‬ ‫إذا‬:‫ف‬=‫ن‬ ‫ﺟـ‬٢
٢(‫ﺟـ‬ ‫ﻛﺎن‬ ‫إذا‬=٠‫ﻓﺈن‬:‫ف‬=‫اﻟﻌﺠﻠ‬ ‫أى‬ ‫ن‬ ‫ع‬‫ﻣﻨﺘﻈﻤﺔ‬ ‫ﺔ‬
٣(‫اﻟﻮﻗﻮد‬ ‫دواﺳﺔ‬ ‫ﺳﯿﺎرة‬ ‫ﺳﺮﻋﺔ‬ ‫ﻋﻠﻰ‬ ‫ﺗﺆﺛﺮ‬ ‫ادوات‬ ‫ﺛﻼث‬
‫اﻟﺤﺮﻛﺔ‬ ‫اﺗﺠﺎه‬ ‫ﺗﺤﺪﯾﺪ‬ ‫ﻓﻰ‬ ‫اﻟﻘﯿﺎدة‬ ‫ﻋﺠﻠﺔ‬ ‫ﺛﻢ‬ ‫اﻟﻔﺮاﻣﻞ‬ ‫دواﺳﺔ‬ ‫و‬
٤(‫ع‬ ‫ﺗﻜﻮن‬ ‫اﻟﺠﺴﻢ‬ ‫ﯾﻘﻒ‬ ‫ﻋﻨﺪﻣﺎ‬=٠
٥(‫ﯾﺘﻮﻗﻒ‬ ‫ﺛﻢ‬ ‫ﻣﺤﺪودة‬ ‫زﻣﻨﯿﺔ‬ ‫ﻟﻔﺘﺮة‬ ‫اﻟﺤﺮﻛﺔ‬ ‫ﻓﻰ‬ ‫ﯾﺴﺘﻤﺮ‬ ‫ﻓﺈﻧﮫ‬ ‫ﻣﻨﺘﻈﻢ‬ ‫ﺑﺘﻘﺼﯿﺮ‬ ‫ﺟﺴﯿﻢ‬ ‫ﺗﺤﺮك‬ ‫إذا‬
‫أو‬‫ﺑﻌﺪھﺎ‬‫ﻣﺘﺴﺎرﻋ‬ ‫ﺣﺮﻛﺔ‬ ‫ﯾﺘﺤﺮك‬‫اﻟﻤﻀﺎد‬ ‫اﻻﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫ﺔ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﺑﺴﺮﻋﺔ‬ ‫ﺗﺘﺤﺮك‬ ‫ﺳﯿﺎرة‬٩٠‫ﻛﻢ‬/‫ﺗﻨﺎﻗﺼﺖ‬ ‫ﺑﺤﯿﺚ‬ ‫اﻟﻔﺮاﻣﻞ‬ ‫دواﺳﺔ‬ ‫ﻋﻠﻰ‬ ‫اﻟﺴﺎﺋﻖ‬ ‫ﺿﻐﻂ‬ ، ‫س‬
‫ﻣﺮور‬ ‫ﺑﻌﺪ‬ ‫ﺗﻮﻗﻔﺖ‬ ‫ﺣﺘﻰ‬ ‫ﺛﺎﺑﺖ‬ ‫ﺑﻤﻌﺪل‬ ‫اﻟﺴﺮﻋﺔ‬٥‫ﺛﻮان‬.‫اﺣﺴﺐ‬:
)‫أ‬(‫اﻟﺴﺮﻋﺔ‬ ‫ﺗﻨﺎﻗﺺ‬ ‫ﺧﻼل‬ ‫اﻟﺴﯿﺎرة‬ ‫ﻋﺠﻠﺔ‬.
)‫ب‬(ً‫ﺎ‬‫ﺗﻤﺎﻣ‬ ‫ﺣﺮﻛﺘﮭﺎ‬ ‫ﺗﻮﻗﻔﺖ‬ ‫ﺣﺘﻰ‬ ‫اﻟﺴﯿﺎرة‬ ‫ﻗﻄﻌﺘﮭﺎ‬ ‫اﻟﺘﻰ‬ ‫اﻟﻤﺴﺎﻓﺔ‬
‫اﻟﺤﻞ‬:
)‫أ‬(٩٠‫ﻛﻢ‬/‫س‬=٩٠×=٢٥‫م‬/‫ث‬
‫ع‬٠=٢٥‫م‬/، ‫ث‬‫ع‬=٠‫ن‬ ،=٥‫ﺛﻮان‬
A‫ع‬=‫ع‬٠+‫ن‬ ‫ﺟـ‬B٠=٢٥+‫ﺟـ‬×٥B‫ﺟـ‬=‫ــ‬٥‫م‬/‫ث‬٢
‫ﻣﻘﺪاره‬ ‫ﻣﻨﺘﻈﻢ‬ ‫ﺑﺘﻘﺼﯿﺮ‬ ‫ﺗﺘﺤﺮك‬ ‫اﻟﺴﯿﺎرة‬ ‫أن‬ ‫أى‬٥‫م‬/‫ث‬٢
)‫ب‬(A‫ف‬=‫ع‬٠‫ن‬+‫ن‬ ‫ﺟـ‬٢
B‫ف‬=٢٥×٥+×)-٥(×)٥(٢
=٦٢٫٥‫ﻣﺘﺮ‬
١
٢
١
٢
٥
١٨
١
٢
١
٢

82. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
82
‫ﻣﺜﺎل‬:‫ﺻﻐ‬ ‫ﻛﺮة‬ ‫ﻗﺬﻓﺖ‬‫ﺑﺴﺮﻋﺔ‬ ‫ﯿﺮة‬٢٠‫م‬/‫ﺗﻘﺼﯿﺮﯾﺔ‬ ‫ﺣﺮﻛﺔ‬ ‫ﻣﺴﺘﻘﯿﻢ‬ ‫ﺧﻂ‬ ‫ﻓﻰ‬ ‫ﻓﺘﺤﺮﻛﺖ‬ ً‫ﺎ‬‫أﻓﻘﯿ‬ ‫ث‬
‫م‬ ‫ﻣﻨﺘﻈﻤﺔ‬ ‫ﺑﻌﺠﻠﺔ‬/‫ث‬٢
‫ﻣﺮور‬ ‫ﺑﻌﺪ‬ ‫ﺳﺮﻋﺘﮭﺎ‬ ‫و‬ ، ‫اﻟﻜﺮة‬ ‫ﻣﻮﺿﻊ‬ ‫ﻋﯿﻦ‬٢‫اﻟﺤﺮﻛﺔ‬ ‫ﺑﺪء‬ ‫ﻣﻦ‬ ‫ﺛﺎﻧﯿﺔ‬
‫اﻟﺤﻞ‬:
‫ع‬٠=٢٠‫م‬/‫ﺟـ‬ ، ‫ث‬=‫م‬ ‫ــ‬/‫ث‬٢
‫ن‬ ،=٢‫ف‬ ، ‫ﺛﺎﻧﯿﺔ‬=‫ع‬ ، ‫؟‬=‫؟‬
‫ف‬=‫ع‬٠‫ن‬+‫ن‬ ‫ﺟـ‬٢
=٢٠×٢+×‫ــ‬×)٢(٢
=٤٠‫ــ‬١=٣٩‫ﻣﺘﺮا‬
‫ﺑﻌﺪ‬ ‫ﻋﻠﻰ‬ ‫ﺗﻜﻮن‬ ‫اﻟﻜﺮة‬٣٩‫اﻟﺤﺮﻛﺔ‬ ‫ﺑﺪء‬ ‫ﻣﻦ‬ ‫ﻣﺘﺮا‬.
‫ع‬=‫ع‬٠+‫ن‬ ‫ﺟـ‬=٢٠‫ــ‬×٢=١٩‫م‬/‫ث‬
‫ﺑﻌﺪ‬ ‫اﻟﻜﺮة‬ ‫ﺳﺮﻋﺔ‬٢‫ﺗﺴﺎوى‬ ‫ﺛﺎﻧﯿﺔ‬١٩‫م‬/‫ث‬
‫ــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﺛﺎﻟﺜﺎ‬:‫اﻻزاﺣﺔ‬ ‫و‬ ‫اﻟﺴﺮﻋﺔ‬ ‫ﺑﯿﻦ‬ ‫اﻟﻌﻼﻗﺔ‬:
A‫ع‬=‫ع‬٠+‫اﻟﻄﺮﻓﯿﻦ‬ ‫ﺑﺘﺮﺑﯿﻊ‬ ‫ن‬ ‫ﺟـ‬
B‫ع‬٢
=‫ع‬٠
٢
+٢‫ع‬٠‫ن‬+‫ﺟـ‬٢
‫ن‬٢
=‫ع‬٠
٢
+٢‫ﺟـ‬)‫ع‬٠+‫ن‬ ‫ﺟـ‬٢
(
‫ﺑﺎﻟﺘﻌﻮﯾﺾ‬‫اﻟﻌﻼﻗﺔ‬ ‫ﻓﻰ‬:‫ف‬=‫ع‬٠‫ن‬+‫ن‬ ‫ﺟـ‬٢
B‫ع‬٢
=‫ع‬٠
٢
+٢‫ﺟـ‬‫ف‬
‫ع‬٠‫اﻟﻤﻨﺘﻈﻤﺔ‬ ‫اﻟﻌﺠﻠﺔ‬ ‫ﺟـ‬ ، ‫اﻟﻨﮭﺎﺋﯿﺔ‬ ‫اﻟﺴﺮﻋﺔ‬ ‫ع‬ ، ‫اﻻﺑﺘﺪاﺋﯿﺔ‬ ‫اﻟﺴﺮﻋﺔ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﻣﻦ‬ ‫ﺑﺎﻧﺘﻈﺎم‬ ‫ﺳﯿﺎرة‬ ‫ﺳﺮﻋﺔ‬ ‫ﻧﻘﺼﺖ‬٤٥‫ﻛﻢ‬/‫اﻟﻰ‬ ‫س‬١٨‫ﻛﻢ‬/‫ﻣﺴﺎﻓﺔ‬ ‫ﻗﻄﻌﺖ‬ ‫أن‬ ‫ﺑﻌﺪ‬ ‫س‬
٦٢٥‫ﻣﺘﺮا‬.‫ﺗﺴﻜﻦ‬ ‫ﺣﺘﻰ‬ ‫ذﻟﻚ‬ ‫ﺑﻌﺪ‬ ‫ﺗﻘﻄﻌﮭﺎ‬ ‫اﻟﺘﻰ‬ ‫اﻟﻤﺴﺎﻓﺔ‬ ‫أوﺟﺪ‬.
‫اﻟﺤﻞ‬:
‫اﻻوﻟﻰ‬ ‫اﻟﺤﺎﻟﺔ‬:‫ع‬٠=٤٥×=١٢٫٥‫م‬/‫ث‬‫ع‬ ،=١٨×=٥‫م‬/‫ث‬
١
٢
١
٢
١
٢
١
٢
١
٢
١
٢
١
٢
١
٢
‫ع‬٠=٤٥‫ﻛﻢ‬/‫س‬
٦٢٥‫ﻣﺘﺮ‬
‫ا‬
‫ب‬
‫ء‬
‫ع‬=١٨‫ﻛﻢ‬/‫س‬
‫ف‬=‫؟‬
‫ع‬=٠‫ﺣـ‬
٥
١٨
٥
١٨

83. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
83
A‫ع‬٢
=‫ع‬٠
٢
+٢‫ف‬ ‫ﺟـ‬B)٥(٢
) =١٢٫٥(٢
+٢×‫ﺟـ‬×٦٢٥
B‫ﺟـ‬=‫ــ‬٠٫١٠٥‫م‬/‫ث‬٢
‫اﻟﺜﺎﻧﯿﺔ‬ ‫اﻟﺤﺎﻟﺔ‬:‫ع‬٠=٥‫م‬/‫ث‬‫ع‬ ،=٠‫ﺟـ‬ ،=‫ــ‬٠٫١٠٥‫م‬/‫ث‬٢
A‫ع‬٢
=‫ع‬٠
٢
+٢‫ف‬ ‫ﺟـ‬B٠=)٥(٢
‫ــ‬٢×٠٫١٠٥‫ف‬
B‫ف‬=١١٩٫٠٤‫ﻣﺘﺮا‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫أﻓﻘﯿﺎ‬ ‫رﺻﺎﺻﺔ‬ ‫أﻃﻠﻘﺖ‬‫ﺑﺴﺮﻋﺔ‬ ‫ﺧﺸﺒﯿﺔ‬ ‫ﻛﺘﻠﺔ‬ ‫ﻋﻠﻰ‬١٠٠‫م‬/‫ﻣﺴﺎﻓﺔ‬ ‫ﻓﯿﮭﺎ‬ ‫ﻓﻐﺎﺻﺖ‬ ‫ث‬٥٠‫ﺳﻢ‬
‫ﻰ‬‫ﻋﻠ‬ ‫ﺎ‬‫إﻃﻼﻗﮭ‬ ‫ﻢ‬‫ﺗ‬ ‫إذا‬ ‫و‬ ‫ﺔ‬‫ﻣﻨﺘﻈﻤ‬ ‫ﺔ‬‫اﻟﻌﺠﻠ‬ ‫أن‬ ‫ﻢ‬‫ﻋﻠ‬ ‫إذا‬ ‫ﺔ‬‫اﻟﺮﺻﺎﺻ‬ ‫ﺎ‬‫ﺑﮭ‬ ‫ﺮك‬‫ﺗﺘﺤ‬ ‫اﻟﺘﻰ‬ ‫اﻟﻌﺠﻠﺔ‬ ‫أوﺟﺪ‬‫ﺔ‬‫ﻛﺘﻠ‬
‫ﻤﻜﮭﺎ‬‫ﺳ‬ ‫ﻟﻼوﻟﻰ‬ ‫ﻣﻤﺎﺛﻠﺔ‬ ‫أﺧﺮى‬ ‫ﺧﺸﺒﯿﺔ‬١٨‫ﻢ‬‫ﺳ‬.‫ﻦ‬‫ﻣ‬ ‫ﺔ‬‫اﻟﺮﺻﺎﺻ‬ ‫ﺎ‬‫ﺑﮭ‬ ‫ﺮج‬‫ﺗﺨ‬ ‫ﻰ‬‫اﻟﺘ‬ ‫ﺴﺮﻋﺔ‬‫اﻟ‬ ‫ﻰ‬‫ھ‬ ‫ﺎ‬‫ﻓﻤ‬
‫اﻟﺨﺸﺒﯿﺔ‬ ‫اﻟﻜﺘﻠﺔ‬.
‫اﻟﺤﻞ‬:
‫اﻟﻤﻮﺟﺐ‬ ‫اﻻﺗﺠﺎه‬ ‫ھﻮ‬ ‫اﻟﺮﺻﺎﺻﺔ‬ ‫ﺣﺮﻛﺔ‬ ‫اﺗﺠﺎه‬ ‫ﻧﻔﺮض‬
‫اﻻوﻟﻰ‬ ‫اﻟﺤﺎﻟﺔ‬:‫ع‬=٠‫ع‬ ،٠=١٠٠‫م‬/‫ف‬ ، ‫ث‬=٥٠‫ﺳﻢ‬=٠٫٥‫م‬
A‫ع‬٢
=‫ع‬٠
٢
+٢‫ف‬ ‫ﺟـ‬B٠) =١٠٠(٢
+٢‫ﺟـ‬×٠٫٥
B‫ﺟـ‬=‫ــ‬١٠٠٠٠‫م‬/‫ث‬٢
‫اﻟﺜﺎﻧﯿﺔ‬ ‫اﻟﺤﺎﻟﺔ‬:‫ع‬٠=١٠٠‫م‬/‫ﺟـ‬ ، ‫ث‬=‫ــ‬١٠٠٠٠‫م‬/‫ث‬٢
‫ف‬ ،=٠٫١٨‫م‬
A‫ع‬٢
=‫ع‬٠
٢
+٢‫ف‬ ‫ﺟـ‬B‫ع‬٢
) =١٠٠(٢
‫ــ‬٢×١٠٠٠٠×٠٫١٨
B‫ع‬٢
=٦٤٠٠B‫ع‬=٨٠‫م‬/‫اﻟﺮﺻﺎﺻﺔ‬ ‫ﺑﮭﺎ‬ ‫ﺗﺨﺮج‬ ‫اﻟﺘﻰ‬ ‫اﻟﺴﺮﻋﺔ‬ ‫ھﻰ‬ ‫ث‬
‫ــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:
‫ف‬=٠٫١٨‫ﻣﺘﺮ‬
‫ع‬٠=١٠٠‫م‬/‫ث‬
‫ف‬=٠٫٥‫ﻣﺘﺮ‬
‫ﺟـ‬=‫؟‬ ‫ع‬=‫؟‬

84. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
84
‫اﻟﺤﻞ‬:
‫اﻟﻤﻮﺟﺐ‬ ‫اﻻﺗﺠﺎه‬ ‫ھﻮ‬ ‫اﻟﺮﺻﺎﺻﺔ‬ ‫ﺣﺮﻛﺔ‬ ‫اﺗﺠﺎة‬ ‫ﻧﻔﺮض‬
‫اﻻوﻟﻰ‬ ‫اﻟﺤﺎﻟﺔ‬:A‫ع‬٢
=‫ع‬٠
٢
+٢‫ف‬ ‫ﺟـ‬
B)١٥(٢
) =٢٠(٢
+٢‫ﺟـ‬×٠٫١٤
B‫ﺟـ‬=‫ــ‬٦٢٥‫م‬/‫ث‬٢
‫اﻟﺜﺎﻧﯿﺔ‬ ‫اﻟﺤﺎﻟﺔ‬:
A‫ع‬٢
=‫ع‬٠
٢
+٢‫ف‬ ‫ﺟـ‬
B٠) =٢٠(٢
‫ــ‬٢×٦٢٥‫ف‬
B‫ف‬=٠٫٣٢‫ﻣﺘﺮا‬
B‫ﻣﺴﺎﻓﺔ‬ ‫اﻟﺤﺎﺋﻂ‬ ‫ﻓﻰ‬ ‫ﺗﻐﻮص‬ ‫اﻟﺮﺻﺎﺻﺔ‬٣٢‫ﯾﺴﻜﻦ‬ ‫ﺣﺘﻰ‬ ‫ﺳﻢ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
*‫اﻟﻨﻮﻧﯿﺔ‬ ‫اﻟﺜﺎﻧﯿﺔ‬ ‫ﺧﻼل‬ ‫اﻟﺴﺮﻋﺔ‬:
‫ﻣﻠﺤﻮﻇﺔ‬:
‫ﺧﻼ‬ ‫ﻟﺟﺳﯾم‬ ‫اﻟﻣﺗوﺳطﺔ‬ ‫ﻋﺔ‬‫اﻟﺳر‬‫زﻣﻧﯾﺔ‬ ‫ة‬‫ﻓﺗر‬ ‫ل‬=‫ﻋﺗﻪ‬‫ﺳر‬‫اﻟﻠﺣظﯾﺔ‬‫اﻟزﻣﻧﯾﺔ‬ ‫ة‬‫اﻟﻔﺗر‬ ‫ﻫذﻩ‬ ‫ﻣﻧﺗﺻف‬ ‫ﻓﻰ‬
‫ﻣﺜﻼ‬:‫اﻟﺮاﺑﻌﺔ‬ ‫اﻟﺜﺎﻧﯿﺔ‬ ‫ﺧﻼل‬ ‫اﻟﻤﺘﻮﺳﻄﺔ‬ ‫اﻟﺴﺮﻋﺔ‬=‫ع‬٠+٣٫٥‫ﺟـ‬
‫اﻟﺘﺎﺳﻌﺔ‬ ‫و‬ ‫اﻟﺜﺎﻣﻨﺔ‬ ‫اﻟﺜﺎﻧﯿﺘﯿﻦ‬ ‫ﺧﻼل‬ ‫اﻟﻤﺘﻮﺳﻄﺔ‬ ‫اﻟﺴﺮﻋﺔ‬=‫ع‬٠+٨‫ﺟـ‬
‫اﻟﺘﺎﺳﻌ‬ ‫و‬ ‫اﻟﺜﺎﻣﻨﺔ‬ ‫و‬ ‫اﻟﺴﺎﺑﻌﺔ‬ ‫اﻟﺜﻮاﻧﻰ‬ ‫ﺧﻼل‬ ‫اﻟﻤﺘﻮﺳﻄﺔ‬ ‫اﻟﺴﺮﻋﺔ‬‫ﺔ‬=‫ع‬٠+٧٫٥‫ﺟـ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺛﺎل‬:‫ﻋﺔ‬‫ﺑﺳر‬ ‫ﺛﺎﺑت‬ ‫اﺗﺟﺎﻩ‬ ‫ﻓﻰ‬ ‫ﺣرﻛﺗﻪ‬ ‫ﺟﺳﯾم‬ ‫ﺑدأ‬١٢‫ﺳم‬/‫ﻣﻧﺗظﻣﺔ‬ ‫وﻋﺟﻠﺔ‬ ‫ث‬٦‫ﺳم‬/‫ث‬٢
‫ﻓﻰ‬
‫اﺗﺟﺎﻩ‬‫ﻋﺗﻪ‬‫ﺳر‬.‫أﺣﺳب‬:
‫أوﻻ‬:‫ﻗد‬ ‫اﻟﺟﺳﯾم‬ ‫ﯾﻛون‬ ‫اﻟﺗﻰ‬ ‫اﻟﻣﺳﺎﻓﺔ‬‫ﻓﻘط‬ ‫اﻟﺧﺎﻣﺳﺔ‬ ‫اﻟﺛﺎﻧﯾﺔ‬ ‫ﺧﻼل‬ ‫ﻗطﻌﻬﺎ‬
‫ﺛﺎﻧﯾﺎ‬ً:‫ﻣﻌﺎ‬ ‫اﻟﺛﺎﻣﻧﺔ‬‫و‬ ‫اﻟﺳﺎﺑﻌﺔ‬ ‫اﻟﺛﺎﻧﯾﺗﯾن‬ ‫ﺧﻼل‬ ‫ﻗطﻌﻬﺎ‬ ‫ﻗد‬ ‫اﻟﺟﺳﯾم‬ ‫ﯾﻛون‬ ‫اﻟﺗﻰ‬ ‫اﻟﻣﺳﺎﻓﺔ‬ً.
‫اﻟﺣل‬:
‫اﻟﺣرﻛﺔ‬ ‫اﺗﺟﺎﻩ‬ ‫ﻫو‬ ‫اﻟﻣوﺟب‬ ‫اﻻﺗﺟﺎﻩ‬ ‫ﻧﻌﺗﺑر‬
‫ع‬
٠
=١٢‫ﺳم‬/‫ﺟـ‬ ، ‫ث‬=٦‫ﺳم‬/‫ث‬٢
‫ع‬٠=٢٠‫م‬/‫ث‬
‫ف‬=٠٫١٤‫ﻣﺘﺮ‬
‫ﺟـ‬=‫؟‬
‫ع‬=١٥‫م‬/‫ث‬
‫ف‬=‫؟‬
‫ع‬٠=٢٠‫م‬/‫ث‬
‫ع‬=٠

85. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
85
. ‫ﻓﻘط‬ ‫اﻟﺧﺎﻣﺳﺔ‬ ‫اﻟﺛﺎﻧﯾﺔ‬ ‫ﺧﻼل‬ ‫ﻗطﻌﻬﺎ‬ ‫ﻗد‬ ‫اﻟﺟﺳﯾم‬ ‫ﯾﻛون‬ ‫اﻟﺗﻰ‬ ‫اﻟﻣﺳﺎﻓﺔ‬ ‫ﻹﯾﺟﺎد‬ : ‫أوﻻ‬
‫اﻟﺧﺎﻣﺳﺔ‬ ‫ﻟﻠﺛﺎﻧﯾﺔ‬ ‫اﻟﻣﺗوﺳطﺔ‬ ‫ﻋﺔ‬‫اﻟﺳر‬=‫اﻟزﻣﻧﯾﺔ‬ ‫ة‬‫اﻟﻔﺗر‬ ‫ﻫذﻩ‬ ‫ﻣﻧﺗﺻف‬ ‫ﻓﻰ‬ ‫ﻋﺔ‬‫اﻟﺳر‬
=‫ﺑﻌد‬ ‫ﻋﺔ‬‫اﻟﺳر‬٤.٥‫ﺛﺎﻧﯾﺔ‬‫اﻟﺣرﻛﺔ‬ ‫ﺑدء‬ ‫ﻣن‬
‫ع‬
‫م‬
=١٢+٦×٤.٥=١٢+٢٧=٣٩‫ﺳم‬/‫ث‬ B ‫ع‬
‫م‬
=‫ع‬
٠
+‫ن‬ ‫ﺟـ‬ A
‫اﻟ‬‫ﻣﺳﺎﻓﺔ‬=‫اﻟﻣﺗوﺳطﺔ‬ ‫ﻋﺔ‬‫اﻟﺳر‬×‫اﻟزﻣن‬
‫ف‬=٣٩×١=٣٩‫ﺳم‬
. ‫ﻣﻌﺎ‬ ‫اﻟﺛﺎﻣﻧﺔ‬‫و‬ ‫اﻟﺳﺎﺑﻌﺔ‬ ‫اﻟﺛﺎﻧﯾﺗﯾن‬ ‫ﺧﻼل‬ ‫ﻗطﻌﻬﺎ‬ ‫ﻗد‬ ‫اﻟﺟﺳﯾم‬ ‫ﯾﻛون‬ ‫اﻟﺗﻰ‬ ‫اﻟﻣﺳﺎﻓﺔ‬ً ‫ﻹﯾﺟﺎد‬ : ‫ﺛﺎﻧﯾﺎ‬ً
‫ﻣﻌﺎ‬ ‫اﻟﺛﺎﻣﻧﺔ‬‫و‬ ‫اﻟﺳﺎﺑﻌﺔ‬ ‫ﻟﻠﺛﺎﻧﯾﺗﯾن‬ ‫اﻟﻣﺗوﺳطﺔ‬ ‫ﻋﺔ‬‫اﻟﺳر‬ً=‫أى‬ ‫اﻟزﻣﻧﯾﺔ‬ ‫ة‬‫اﻟﻔﺗر‬ ‫ﻫذﻩ‬ ‫ﻣﻧﺗﺻف‬ ‫ﻓﻰ‬ ‫ﻋﺔ‬‫اﻟﺳر‬
‫ﻣﺿﻰ‬ ‫ﺑﻌد‬ ‫ﻋﺔ‬‫اﻟﺳر‬ ‫ﺗﺳﺎوى‬٧‫اﻟﺣرﻛﺔ‬ ‫ﺑدء‬ ‫ﻣن‬ ‫اﻧﻰ‬‫و‬‫ﺛ‬
‫ع‬
‫م‬
=‫ع‬
٠
+‫ن‬ ‫ﺟـ‬
‫ع‬
‫م‬
=١٢+٦×٧=١٢+٤٢=٥٤‫ﺳم‬/‫ث‬
‫اﻟﻤﺴﺎﻓﺔ‬=‫اﻟﻤﺘﻮﺳﻄﺔ‬ ‫اﻟﺴﺮﻋﺔ‬×‫اﻟﺰﻣﻦ‬ B
‫ف‬=٥٤×٢=١٠٨‫ﺳﻢ‬ B
‫ــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــ‬‫ــــــــــــــــــ‬‫ـــــــــــــ‬
‫ﻣﺛﺎل‬:‫ﻋﺔ‬‫ﺑﺳر‬ ‫ﺛﺎﺑت‬ ‫اﺗﺟﺎﻩ‬ ‫ﻓﻰ‬ ‫ﺣرﻛﺗﻪ‬ ‫ﺟﺳﯾم‬ ‫ﺑدأ‬٣٠‫ﺳم‬/‫ﻣﻧﺗظﻣﺔ‬ ‫ﺑﻌﺟﻠﺔ‬ ‫و‬ ‫ث‬٦‫ﺳم‬/‫ث‬٢
‫اﺣﺳب‬ ‫ﻋﺗﻪ‬‫ﺳر‬ ‫اﺗﺟﺎﻩ‬ ‫ﻧﻔس‬ ‫ﻓﻰ‬ ‫ﺗﻌﻣل‬:
‫أوﻻ‬:‫اﻟﻣﺳﺎ‬‫ﺑﻌد‬ ‫اﻟﻣﻘطوﻋﺔ‬ ‫ﻓﺔ‬٥‫اﻟﺣرﻛﺔ‬ ‫ﺑدء‬ ‫ﻣن‬ ‫ان‬‫و‬‫ﺛ‬.
‫ﺛﺎﻧﯾﺎ‬:‫ﻓﻘط‬ ‫اﻟﺧﺎﻣﺳﺔ‬ ‫اﻟﺛﺎﻧﯾﺔ‬ ‫ﻓﻰ‬ ‫اﻟﻣﻘطوﻋﺔ‬ ‫اﻟﻣﺳﺎﻓﺔ‬.
‫اﻟﺤﻞ‬:
‫أوﻻ‬:‫ﺑﻌﺪ‬ ‫اﻟﻤﻘﻄﻮﻋﺔ‬ ‫اﻟﻤﺴﺎﻓﺔ‬٥‫اﻟﺤﺮﻛﺔ‬ ‫ﺑﺪء‬ ‫ﻣﻦ‬ ‫ﺛﻮان‬
‫ف‬=‫ع‬٠‫ن‬+‫ن‬ ‫ﺟـ‬٢
=٣٠×٥+×٦×)٥(٢
=٢٢٥‫ﺳﻢ‬
‫ﺛﺎﻧﯿﺎ‬:‫اﻟﻤ‬‫ﻓﻘﻂ‬ ‫اﻟﺨﺎﻣﺴﺔ‬ ‫اﻟﺜﺎﻧﯿﺔ‬ ‫ﻓﻰ‬ ‫اﻟﻤﻘﻄﻮﻋﺔ‬ ‫ﺴﺎﻓﺔ‬.
‫ﺳﺮﻋﺔ‬‫اﻟﻤﺘﻮﺳﻄﺔ‬ ‫اﻟﺠﺴﯿﻢ‬=‫ﺑﻌﺪ‬ ‫ﺳﺮﻋﺘﮫ‬٤٫٥‫اﻟﺤﺮﻛﺔ‬ ‫ﺑﺪء‬ ‫ﻣﻦ‬ ‫ﺛﺎﻧﯿﺔ‬
١
٢
١
٢

86. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
86
‫ع‬‫م‬=‫ع‬٠+‫ن‬ ‫ﺟـ‬=٣٠+٦×٤٫٥=٥٧‫ﺳﻢ‬/‫ث‬
B‫اﻟﻤﺴﺎﻓﺔ‬=‫ع‬‫م‬×‫ن‬=٥٧×١=٥٧‫ﺳﻢ‬/‫ث‬
‫ـــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫اﻟﺜﺎﻧﯿﺔ‬ ‫ﻓﻰ‬ ‫ﻗﻄﻊ‬ ‫ﻓﺈذا‬ ، ‫ﻣﻨﺘﻈﻤﺔ‬ ‫ﺑﻌﺠﻠﺔ‬ ‫و‬ ‫ﺛﺎﺑﺖ‬ ‫اﺗﺠﺎه‬ ‫ﻓﻰ‬ ‫ﻣﺎ‬ ‫اﺑﺘﺪاﺋﯿﺔ‬ ‫ﺑﺴﺮﻋﺔ‬ ‫ﺟﺴﯿﻢ‬ ‫ﺗﺤﺮك‬
‫ﻣﺴﺎﻓﺔ‬ ‫ﺣﺮﻛﺘﮫ‬ ‫ﻣﻦ‬ ‫اﻟﺜﺎﻟﺜﺔ‬٢٠‫ﻣﺘﺮا‬‫ﻣﺴﺎﻓﺔ‬ ً‫ﺎ‬‫ﻣﻌ‬ ‫اﻟﺴﺎدﺳﺔ‬ ‫و‬ ‫اﻟﺨﺎﻣﺴﺔ‬ ‫اﻟﺜﺎﻧﯿﺘﯿﻦ‬ ‫ﻓﻰ‬ ‫ﻗﻄﻊ‬ ‫ﺛﻢ‬ ،
٦٠‫ﻣﺘﺮا‬.‫اﻻﺑﺘﺪاﺋﯿﺔ‬ ‫ﺳﺮﻋﺘﮫ‬ ‫و‬ ‫اﻟﺠﺴﯿﻢ‬ ‫ﺑﮭﺎ‬ ‫ﺗﺤﺮك‬ ‫اﻟﺘﻰ‬ ‫اﻟﻌﺠﻠﺔ‬ ‫اﺣﺴﺐ‬.
‫اﻟﺤﻞ‬:
‫اﯾﻀﺎ‬ ‫ﻣﻮﺟﺐ‬ ‫اﻟﻌﺠﻠﺔ‬ ‫اﺗﺠﺎه‬ ‫ﻓﯿﻜﻮن‬ ‫اﻻﺑﺘﺪاﺋﯿﺔ‬ ‫اﻟﺴﺮﻋﺔ‬ ‫اﺗﺠﺎه‬ ‫ھﻮ‬ ‫اﻟﻤﻮﺟﺐ‬ ‫اﻻﺗﺠﺎه‬ ‫ﻧﻔﺮض‬
‫اﻟﺛﺎ‬ ‫اﻟﺛﺎﻧﯾﺔ‬ ‫ﺧﻼل‬ ‫اﻟﻣﺗوﺳطﺔ‬ ‫ﻋﺔ‬‫اﻟﺳر‬‫ﻟﺛﺔ‬= = =٢٠‫م‬/‫ث‬
=‫ﺑﻌد‬ ‫ﻋﺗﻪ‬‫ﺳر‬٢.٥‫اﻟﺣرﻛﺔ‬ ‫ﺑدء‬ ‫ﻣن‬ ‫ﺛﺎﻧﯾﺔ‬
‫اﻟﺳﺎدﺳﺔ‬ ‫و‬ ‫اﻟﺧﺎﻣﺳﺔ‬ ‫اﻟﺛﺎﻧﯾﺗﯾن‬ ‫ﺧﻼل‬ ‫اﻟﻣﺗوﺳطﺔ‬ ‫ﻋﺔ‬‫اﻟﺳر‬= =٣٠‫م‬/‫ث‬
=‫ﺑﻌد‬ ‫ﻋﺗﻪ‬‫ﺳر‬٥‫اﻟﺣرﻛﺔ‬ ‫ﺑدء‬ ‫ﻣن‬ ‫ان‬‫و‬‫ﺛ‬
A‫اﻟﻌ‬‫ﺟﻠﺔ‬=== =‫ــ‬٤‫م‬/‫ث‬٢
‫ﺑﻌﺟﻠﺔ‬ ‫ﺗﻘﺻﯾرﯾﺔ‬ ‫ﺣرﻛﺔ‬ ‫ﯾﺗﺣرك‬ ‫اﻟﺟﺳﯾم‬٤‫م‬/‫ث‬٢
A‫ع‬=‫ع‬٠+‫ن‬ ‫ﺟـ‬B٢٠=‫ع‬٠‫ـــ‬٤×٢.٥B‫ع‬٠=٣٠‫م‬/‫ث‬
‫اﺑﺘﺪاﺋﯿﺔ‬ ‫ﺑﺴﺮﻋﺔ‬ ‫ﯾﺘﺤﺮك‬ ‫اﻟﺠﺴﯿﻢ‬٣٠‫م‬/‫ث‬
‫ع‬‫م‬
‫ع‬٠
‫ى‬
‫ع‬‫م‬/
٢٠‫م‬ ٦٠‫م‬
‫ع‬٢
– ‫ع‬١
‫ن‬٢
– ‫ن‬١
‫اﻟﻤﺴﺎﻓﺔ‬
‫اﻟﺰﻣﻦ‬
٢٠
١
٦٠
٢
‫اﻟﺴﺮﻋﺔ‬ ‫ﻓﻰ‬ ‫اﻟﺘﻐﯿﺮ‬
‫اﻟﺰﻣﻦ‬ ‫اﻟﻔﺘﺮة‬
٢٠‫ــ‬٣٠
٥‫ــ‬٢٫٥

87. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
87
‫ـــﺎل‬‫ـ‬‫ﻣﺛ‬:‫ـــ‬‫ـ‬‫ﻓﻘط‬ ‫ـــﺔ‬‫ـ‬‫ﻣﻧﺗظﻣ‬ ‫ـــﺔ‬‫ـ‬‫ﺑﻌﺟﻠ‬ ‫ـــﺳم‬‫ـ‬‫ﺟ‬ ‫ـــرك‬‫ـ‬‫ﯾﺗﺣ‬‫ـــﺳﺎﻓﺔ‬‫ـ‬‫ﻣ‬ ‫ـــﺎ‬‫ـ‬‫ﻣﻌ‬ ‫ـــﺳﺔ‬‫ـ‬‫اﻟﺧﺎﻣ‬‫و‬ ‫ـــﺔ‬‫ـ‬‫اﺑﻌ‬‫ر‬‫اﻟ‬ ‫ـــﺔ‬‫ـ‬‫اﻟﺛﺎﻧﯾ‬ ‫ـــﻰ‬‫ـ‬‫ﻓ‬ ‫ﻊ‬ً
٦٠‫ﻟﻬﺎ‬ ‫اﻟﺗﺎﻟﯾﺔ‬ ‫ان‬‫و‬‫ﺛ‬ ‫اﻟﺛﻼث‬ ‫ﻓﻰ‬ ‫وﻗطﻊ‬ ‫ﺳم‬١٢٠‫ﺳم‬.‫أوﺟد‬‫اﻻﺑﺗداﺋﯾﺔ‬ ‫ﻋﺗﻪ‬‫وﺳر‬ ‫اﻟﺟﺳم‬ ‫ﻋﺟﻠﺔ‬
‫اﻟﺣل‬:
‫اﻟﺧﺎﻣﺳﺔ‬‫و‬ ‫اﺑﻌﺔ‬‫ر‬‫اﻟ‬ ‫اﻟﺛﺎﻧﯾﺔ‬ ‫ﻓﻰ‬ ‫اﻟﻣﺗوﺳطﺔ‬ ‫ﻋﺔ‬‫اﻟﺳر‬= =٣٠‫ﺳم‬/‫ث‬
‫ﺑﻌد‬ ‫اﻟﺟﺳم‬ ‫ﻋﺔ‬‫ﺳر‬ ‫وﻫﻰ‬٤‫ث‬‫اﻟﺣرﻛﺔ‬ ‫ﺑدء‬ ‫ﻣن‬
‫ﻓﻰ‬ ‫اﻟﻣﺗوﺳطﺔ‬ ‫ﻋﺔ‬‫اﻟﺳر‬‫اﻟﺳﺎد‬ ‫اﻟﺛﺎﻧﯾﺔ‬‫اﻟﺛﺎﻣﻧﺔ‬‫و‬ ‫اﻟﺳﺎﺑﻌﺔ‬‫و‬ ‫ﺳﺔ‬==٤٠‫ﺳم‬/‫ث‬
‫ﺑﻌد‬ ‫اﻟﺟﺳم‬ ‫ﻋﺔ‬‫ﺳر‬ ‫وﻫﻰ‬٦.٥‫ث‬‫اﻟﺣرﻛﺔ‬ ‫ﺑدء‬ ‫ﻣن‬.
A‫ع‬=‫ع‬
٠
+‫ن‬ ‫ﺟـ‬
B٤٠=٣٠+‫ﺟـ‬×‫ﺟـ‬=١٠×‫ﺳم‬/‫ث‬٢
B‫ﺟـ‬=٤‫ﺳم‬/‫ث‬٢
A‫ع‬=‫ع‬٠+‫ن‬ ‫ﺣـ‬B٣٠=‫ع‬
٠
+٤×٤
B‫ع‬
٠
=٣٠–١٦=١٤‫ﺳم‬/‫ث‬
‫ـــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
*‫ﻣﻨﺘﻈﻤﺔ‬ ‫ﺑﻌﺠﻠﺔ‬ ‫اﻟﺤﺮﻛﺔ‬ ‫ﻗﻮاﻧﯿﻦ‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬:
‫ﻣﺜﺎل‬:‫ﻣﻨﺘﻈﻤﺔ‬ ‫ﺑﺴﺮﻋﺔ‬ ‫ﺳﯿﺎرة‬ ‫ﺗﺘﺤﺮك‬٧٢‫ﻛﻢ‬/‫س‬.‫ﺑﺴﯿﺎرة‬ ‫ﻣﺮت‬‫ﺳﯿ‬ ‫ﻓﺒﺪأت‬ ‫ﺳﺎﻛﻨﺔ‬‫ﺎرة‬‫اﻟﺸﺮﻃﺔ‬
‫ﻓﻰ‬‫ﺑﻌﺪ‬ ‫ﻣﺘﺎﺑﻌﺘﮭﺎ‬١٠‫ﻣﺘ‬ ‫ﻣﺮورھﺎ‬ ‫ﻣﻦ‬ ‫ﺛﻮان‬‫ﻣﺴﺎﻓﺔ‬ ‫ﻣﻨﺘﻈﻤﺔ‬ ‫ﺑﻌﺠﻠﺔ‬ ‫ﺤﺮﻛﺔ‬١٠٠‫ﻣﺘﺮ‬‫ﺑﻠﻐﺖ‬ ‫ﺣﺘﻰ‬
‫ﺳﺮﻋﺘﮭﺎ‬٩٠‫ﻛﻢ‬/‫اﻷوﻟﻰ‬ ‫ﺑﺎﻟﺴﯿﺎرة‬ ‫ﻟﺤﻘﺖ‬ ‫ﺣﺘﻰ‬ ‫اﻟﺴﺮﻋﺔ‬ ‫ﺑﮭﺬه‬ ‫ﺳﺎرت‬ ‫ﺛﻢ‬ ، ‫س‬.
‫واﻟﻤﺴﺎﻓﺔ‬ ‫اﻟﺸﺮﻃﺔ‬ ‫ﺳﯿﺎرة‬ ‫ﺗﺤﺮك‬ ‫ﻟﺤﻈﺔ‬ ‫ﻣﻨﺬ‬ ‫اﻟﻤﻄﺎردة‬ ‫ﻋﻤﻠﯿﺔ‬ ‫اﺳﺘﻐﺮﻗﺘﮫ‬ ‫اﻟﺬى‬ ‫اﻟﺰﻣﻦ‬ ‫أوﺟﺪ‬
‫اﻟﺴﯿﺎرة‬ ‫ھﺬه‬ ‫ﻗﻄﻌﺘﮭﺎ‬ ‫اﻟﺘﻰ‬.
‫اﻟﺤﻞ‬:
٦٠
٢
١٢٠
٣
٥
٢
٢
٥

88. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
88
‫و‬ ‫ﻧﻘﻄﺔ‬ ‫ﻋﻨﺪ‬ ‫ﺳﺎﻛﻨﺔ‬ ‫ﻛﺎﻧﺖ‬ ‫اﻟﺸﺮﻃﺔ‬ ‫ﺳﯿﺎرة‬ ‫أن‬ ‫و‬ ‫اﻟﻤﻨﺘﻈﻤﺔ‬ ‫اﻟﺴﺮﻋﺔ‬ ‫اﺗﺠﺎه‬ ‫ھﻮ‬ ‫اﻟﻤﻮﺟﺐ‬ ‫اﻻﺗﺠﺎه‬ ‫ﻧﻌﺘﺒﺮ‬
‫ﻣﺴﺎﻓﺔ‬ ‫ﻗﻄﻌﺖ‬ ‫ﺛﻢ‬١٠٠‫اﻟﻰ‬ ‫وﺻﻠﺖ‬ ‫ﺣﺘﻰ‬ ‫ﻣﺘﺮ‬‫ا‬‫ﺳﺮﻋﺘﮭﺎ‬ ‫أﺻﺒﺤﺖ‬ ‫ﺣﯿﺚ‬٩٠‫ﻛﻢ‬/‫ﺑﮭﺎ‬ ‫ﺳﺎرت‬ ‫ﺛﻢ‬ ‫س‬
‫ب‬ ‫ﻋﻨﺪ‬ ‫اﻻوﻟﻰ‬ ‫ﺑﺎﻟﺴﯿﺎرة‬ ‫ﻟﺤﻘﺖ‬ ‫ﺣﺘﻰ‬ ‫ﺑﺎﻧﺘﻈﺎم‬.
٧٢‫ﻛﻢ‬/‫س‬=٧٢×=٢٠‫م‬/، ‫ث‬٩٠‫ﻛﻢ‬/‫س‬=٩٠×=٢٥‫م‬/‫ث‬
‫اﻟﻰ‬ ‫و‬ ‫ﻣﻦ‬ ‫اﻟﻔﺘﺮة‬ ‫ﻓﻰ‬ ‫اﻟﺸﺮﻃﺔ‬ ‫ﻟﺴﯿﺎرة‬ ‫ﺑﺎﻟﻨﺴﺒﺔ‬‫ا‬:‫ع‬٠=٠‫ع‬ ،=٢٥‫م‬/‫ف‬ ، ‫ث‬=١٠٠‫ﻣﺘﺮ‬
A‫ع‬٢
=‫ع‬٠
٢
+٢‫ف‬ ‫ﺟـ‬B)٢٥(٢
=٠+٢×‫ﺟـ‬×١٠٠B‫ﺟـ‬=‫م‬/‫ث‬٢
A‫ع‬=‫ع‬٠+‫ن‬ ‫ﺟـ‬B٢٥=٠+‫ن‬B‫ن‬=٨‫ﺛﺎﻧﯿﺔ‬
B‫ﻣﻨﺘﻈﻤﺔ‬ ‫ﺑﺴﺮﻋﺔ‬ ‫اﻟﺸﺮﻃﺔ‬ ‫ﺳﯿﺎرة‬ ‫ﺗﺘﺤﺮﻛﮭﺎ‬ ‫اﻟﺘﻰ‬ ‫اﻟﻤﺴﺎﻓﺔ‬=٢٥×)‫ن‬–٨(‫ﻣﺘﺮ‬
‫ﻗﺪره‬ ‫زﻣﻦ‬ ‫ﻓﻰ‬ ‫ب‬ ‫و‬ ‫اﻟﻤﺴﺎﻓﺔ‬ ‫ﻗﻄﻌﺖ‬ ‫اﻟﻤﻄﺎدرة‬ ‫اﻟﺴﯿﺎرة‬ ‫ﺗﻜﻮن‬ ،) =‫ن‬+١٠(‫ﺛﺎﻧﯿﺔ‬
‫ﻗﺪره‬ ‫زﻣﻦ‬ ‫ﻓﻰ‬ ‫ب‬ ‫و‬ ‫اﻟﻤﺴﺎﻓﺔ‬ ‫ﻧﻔﺲ‬ ‫ﻗﻄﻌﺖ‬ ‫اﻟﺸﺮﻃﺔ‬ ‫ﺳﯿﺎرة‬ ‫ﺗﻜﻮن‬ ،=‫ﺛ‬ ‫ن‬‫ﺎﻧﯿﺔ‬
B٢٠)‫ن‬+١٠= (١٠٠+٢٥)‫ن‬–٨(B‫ن‬=٦٠‫ﺛﺎﻧﯿﺔ‬
B‫اﻟﻤﻘﻄﻮﻋﺔ‬ ‫اﻟﻤﺴﺎﻓﺔ‬=٢٠×٧٠=١٤٠٠‫ﻣﺘﺮ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــ‬
‫ﻣﺛﺎل‬:‫ﻓﻘطﻊ‬ ‫ﺛﺎﺑت‬ ‫اﺗﺟﺎﻩ‬ ‫ﻓﻰ‬ ‫ﺟﺳﯾم‬ ‫ﺗﺣرك‬١٨‫اﻟﺛو‬ ‫ﻓﻰ‬ ‫ا‬‫ر‬‫ﻣﺗ‬ً‫ﺣرﻛﺗـﻪ‬ ‫ﻣـن‬ ‫اﻷوﻟـﻰ‬ ‫اﻟﺛﻼﺛﺔ‬ ‫اﻧﻰ‬١٢‫ا‬‫ر‬‫ﻣﺗـ‬ً
‫اﻟﺧﺎﻣﺳﺔ‬ ‫اﻟﺛﺎﻧﯾﺔ‬ ‫ﻓﻰ‬٢٠‫اﻟﺗﺎﺳـﻌﺔ‬ ‫اﻟﺛﺎﻧﯾـﺔ‬ ‫ﻓـﻰ‬ ‫ا‬‫ر‬‫ﻣﺗـ‬ً.‫ﺑـﺄن‬ ‫اﻟﻔـرض‬‫و‬ ‫ﺗﺗﻔـق‬ ‫اﻟﻣـﺳﺎﻓﺎت‬ ‫ﻫـذﻩ‬ ‫أن‬ ‫اﺛﺑـت‬
‫و‬ ‫ﻣﻧﺗظﻣﺔ‬ ‫ﺑﻌﺟﻠﺔ‬ ‫ﯾﺗﺣرك‬ ‫اﻟﺟﺳﯾم‬ ‫ﻫذا‬‫اﻟﺣرﻛﺔ‬ ‫ﺑدء‬ ‫ﻋﻧد‬ ‫ﻋﺗﻪ‬‫ﺳر‬ ‫اﺣﺳب‬.
‫اﻟﺣل‬:
‫اﻟﻣﺗو‬ ‫ﻋﺔ‬‫اﻟﺳر‬‫ﺳ‬‫اﻷوﻟﻰ‬ ‫ة‬‫اﻟﻔﺗر‬ ‫ﺧﻼل‬ ‫طﺔ‬==٦‫م‬/‫ث‬
)‫اﻟزﻣن‬ ‫ﻣﻧﺗﺻف‬ ‫ﻋﻧد‬ ‫ﻋﺔ‬‫اﻟﺳر‬(‫ع‬
١.٥‫ث‬
=٦‫م‬/‫ث‬
‫اﻟﺧﺎﻣﺳﺔ‬ ‫اﻟﺛﺎﻧﯾﺔ‬ ‫ﺧﻼل‬ ‫اﻟﻣﺗوﺳطﺔ‬ ‫ﻋﺔ‬‫اﻟﺳر‬:
‫ع‬
٤.٥
==١٢‫م‬/‫ث‬
٥
١٨
٥
١٨
٢٥
٨
٢٥
٨
١٨
٣
١٢
١
٩
١٨‫ﻣﺘﺮ‬ ١٢‫ﻣﺘﺮ‬ ٢٠‫ﻣﺘﺮ‬
٣ ٥

89. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
89
‫اﻟﺗﺎﺳﻌﺔ‬ ‫اﻟﺛﺎﻧﯾﺔ‬ ‫ﺧﻼل‬ ‫اﻟﻣﺗوﺳطﺔ‬ ‫ﻋﺔ‬‫اﻟﺳر‬:
‫ع‬
٨.٥
==٢٠‫م‬/‫ث‬
‫ن‬ ‫ﻣن‬=١.٥‫ن‬ ‫إﻟﻰ‬ ‫ث‬=٤.٥‫ث‬
B‫ﺗﻐﯾ‬ ‫ﻣﻌدل‬‫ﻟﻠزﻣن‬ ‫ﺑﺎﻟﻧﺳﺑﺔ‬ ‫ﻋﺔ‬‫اﻟﺳر‬ ‫ر‬=‫اﻟﻌﺟﻠﺔ‬
‫ﺟـ‬===٢‫م‬/‫ث‬٢
‫ن‬ ‫ﻣن‬=٤.٥‫ن‬ ‫إﻟﻰ‬ ‫ث‬=٨.٥‫ث‬
B‫ﻟﻠزﻣن‬ ‫ﺑﺎﻟﻧﺳﺑﺔ‬ ‫ﻋﺔ‬‫اﻟﺳر‬ ‫ﺗﻐﯾر‬ ‫ﻣﻌدل‬====٢‫م‬/‫ث‬٢
B‫ﻟﻠزﻣن‬ ‫ﺑﺎﻟﻧﺳﺑﺔ‬ ‫ﺛﺎﺑت‬ ‫ﺑﻣﻌدل‬ ‫ﺗﺗﻐﯾر‬ ‫ﻋﺔ‬‫اﻟﺳر‬
B‫ﯾﺗ‬ ‫اﻟﺟﺳم‬‫ﺟـ‬ ‫ﻣﻧﺗظﻣﺔ‬ ‫ﺑﻌﺟﻠﺔ‬ ‫ﺣرك‬=٢‫م‬/‫ث‬٢
B‫ع‬=‫ع‬
٠
+‫ن‬ ‫ﺟـ‬
B‫ع‬
١.٥
=‫ع‬
٠
+٢×١.٥B٦=‫ع‬
٠
+٣
B‫ع‬
٠
=٣‫م‬/‫ث‬‫اﻟﺣرﻛﺔ‬ ‫ﺑدء‬ ‫ﻋﻧد‬ ‫ﻋﺔ‬‫اﻟﺳر‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــ‬
٢٠
١
‫ع‬
٤.٥
-‫ع‬
١.٥
٤.٥ –١.٥
٢٠-١٢
٤
‫ع‬
٨.٥
-‫ع‬
٤.٥
٨.٥–٤.٥
٨
٤
١٢-٦
٢
‫اﻟﻤﻨﺘﻈﻤﺔ‬ ‫اﻟﺤﺮﻛﺔ‬ ‫ﻗﻮاﻧﯿﻦ‬ ‫ﻋﻠﻰ‬ ‫ﺗﻤﺎرﯾﻦ‬

90. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
90
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬

91. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
91

92. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
92
*‫اﻟ‬‫اﻟﺤــــﺮ‬ ‫ﺴﻘﻮط‬*
‫ـــــــﺎ‬‫ـ‬‫ﻫ‬‫ﻣﻌﯾﺎر‬ ‫ـــــــﺔ‬‫ـ‬‫ﻣﻧﺗظﻣ‬ ‫ـــــــﺔ‬‫ـ‬‫ﺑﻌﺟﻠ‬ ‫ـــــــﺎ‬‫ـ‬‫ﺣرﻛﺗﻬ‬ ‫ـــــــون‬‫ـ‬‫ﺗﻛ‬ ‫ة‬‫ـــــــر‬‫ـ‬‫ﺣ‬ ‫ـــــــﺔ‬‫ـ‬‫ﺣرﻛ‬ ‫ـــــــﯾﺎ‬‫ـ‬‫أﺳ‬‫ر‬ ‫ـــــــﺔ‬‫ـ‬‫اﻟﻣﺗﺣرﻛ‬ ‫ـــــــﺳﺎم‬‫ـ‬‫اﻷﺟ‬ً
‫ء‬=٩.٨‫ﻣﺗر‬/‫ث‬٢
‫أ‬،‫ء‬=٩٨٠‫ﺳﻢ‬/‫ث‬٢
،‫ء‬‫اﻷرﺿﯿﺔ‬ ‫اﻟﺠﺎذﺑﯿﺔ‬ ‫ﻋﺠﻠﺔ‬ ‫ﻋﻠﻰ‬ ‫ﺗﺪل‬
‫وﺑﺎﻟﺗﺎﻟﻰ‬ ‫اﻟﻣﻧﺗظﻣﺔ‬ ‫اﻟﻌﺟﻠﺔ‬ ‫ذات‬ ‫اﻟﻣﺳﺗﻘﯾﻣﺔ‬ ‫اﻟﺣرﻛﺔ‬ ‫اﻧﯾن‬‫و‬‫ﻗ‬ ‫ﻟﻧﻔس‬ ‫ﺗﺧﺿﻊ‬ ‫ﻓﻬﻰ‬ ‫وﺑﺎﻟﺗﺎﻟﻰ‬:
‫أوﻻ‬:‫اﻟ‬ ‫ﻛﺎن‬ ‫إذا‬‫أﺳﻔل‬ ‫إﻟﻰ‬ ‫ﻣﻘذوﻓﺎ‬ ‫أو‬ ‫ﺳﺎﻗطﺎ‬ ‫ﺟﺳﯾم‬ً ً:
‫اﻟﻣوﺟب‬ ‫اﻻﺗﺟﺎﻩ‬ ‫ﻫو‬ ‫اﻟﺣرﻛﺔ‬ ‫اﺗﺟﺎﻩ‬ ‫ﺑﻔرض‬
‫ﺛﺎﻧﯾﺎ‬:‫أﻋﻠﻰ‬ ‫إﻟﻰ‬ ‫ﻣﻘذوﻓﺎ‬ ‫اﻟﺟﺳﯾم‬ ‫ﻛﺎن‬ ‫إذا‬:
‫اﻟﻣوﺟب‬ ‫اﻻﺗﺟﺎﻩ‬ ‫ﻫو‬ ‫اﻟﺣرﻛﺔ‬ ‫اﺗﺟﺎﻩ‬ ‫ﺑﻔرض‬
‫اﻷرﺿﯾﺔ‬ ‫اﻟﺟﺎذﺑﯾﺔ‬ ‫ﺗﺄﺛﯾر‬ ‫ﺗﺣت‬ ‫أﺳﯾﺔ‬‫ر‬‫اﻟ‬ ‫اﻟﺣرﻛﺔ‬
/////////////////////////
+
+
+
‫اﻟﺴﻘﻮط‬ ‫ﻣﻜﺎن‬
‫ﻻﺳﻔﻞ‬ ‫اﻟﻘﺬف‬ ‫أو‬
‫اﻻرض‬ ‫ﺳﻄﺢ‬
‫اﻻﺗﺠﺎ‬‫اﻟﻤﻮﺟﺐ‬ ‫ه‬‫ف‬‫ء‬
‫ب‬
‫اﻟﮭﺒﻮط‬ ‫ﺣﺮﻛﺔ‬
‫ا‬
‫ج‬
‫ء‬
‫ع‬‫ا‬
‫ع‬‫ج‬
‫ء‬
‫ع‬٠
‫ع‬=٠‫ارﺗﻔﺎع‬ ‫أﻗﺼﻰ‬
‫اﻟﻘﺬف‬ ‫ﻣﻜﺎن‬ ‫و‬ ‫و‬
‫اﻟﻤﻮﺟﺐ‬ ‫اﻻﺗﺠﺎه‬
‫ع‬‫ء‬
‫ــ‬
+
+
‫ع‬٠‫ــ‬
‫ع‬=‫ع‬٠+‫ء‬‫ن‬
‫ف‬=‫ع‬٠‫ن‬+‫ء‬‫ن‬٢
‫ع‬٢=‫ع‬٠
٢+٢‫ء‬‫ف‬
١
٢
‫ع‬=‫ع‬٠‫ـــ‬‫ء‬‫ن‬
‫ف‬=‫ع‬٠‫ن‬‫ــــ‬‫ء‬‫ن‬٢
‫ع‬٢=‫ع‬٠
٢‫ــــ‬٢‫ء‬‫ف‬
١
٢

93. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
93
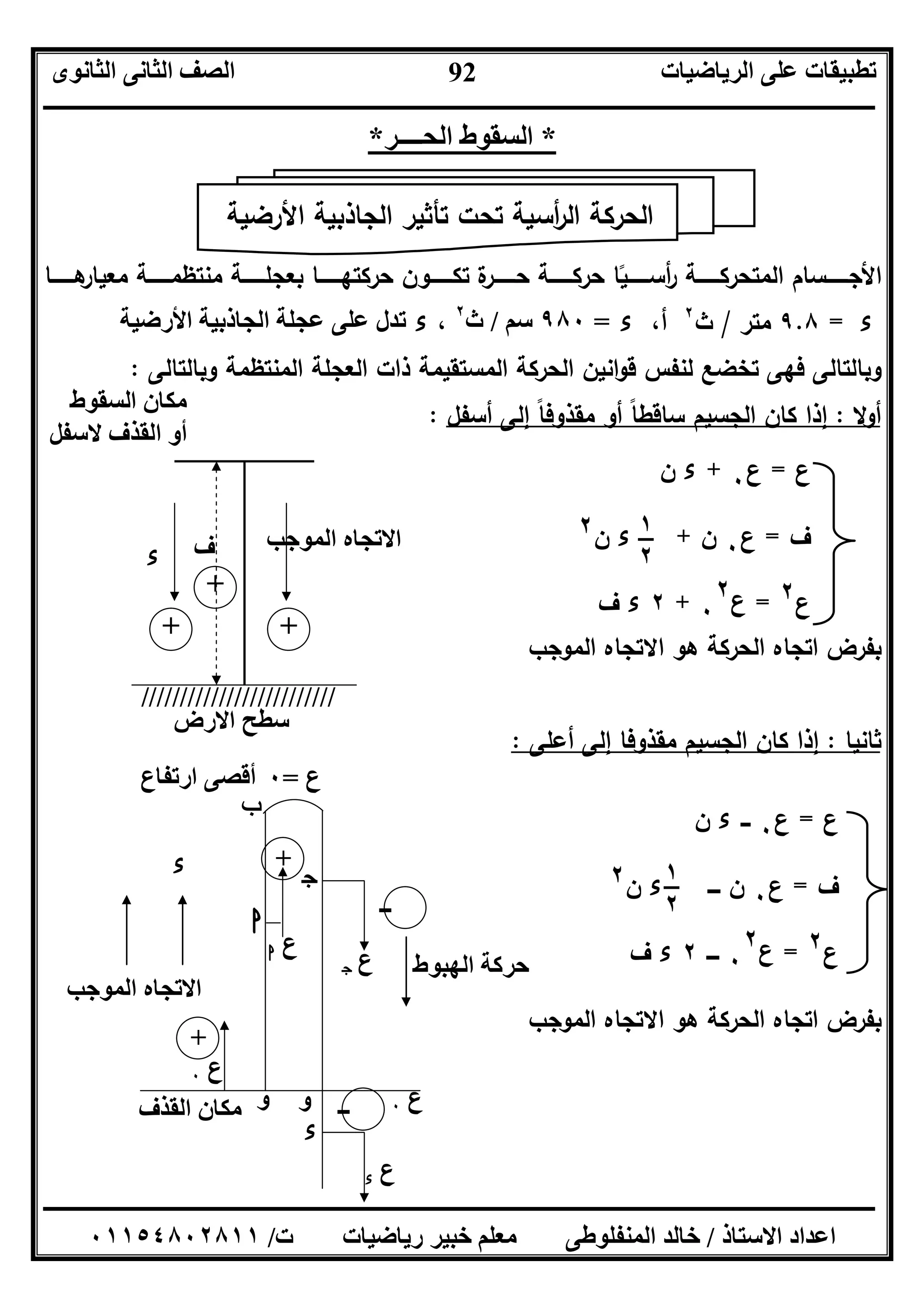
‫زﻣن‬ ‫إﯾﺟﺎد‬‫و‬‫أﻋﻠﻰ‬ ‫إﻟﻰ‬ ‫اﺳﯾﺎ‬‫ر‬ ‫ﻣﻘذوف‬ ‫ﻟﺟﺳﯾم‬ ‫ارﺗﻔﺎع‬ ‫أﻗﺻﻰ‬ ‫ﻣﺳﺎﻓﺔ‬:
‫ارﺗﻔﺎع‬ ‫ﻻﻗﺻﻰ‬ ‫اﻟوﺻول‬ ‫زﻣن‬:
‫ع‬=‫ع‬٠-‫ء‬‫ن‬‫ع‬ ‫ارﺗﻔﺎع‬ ‫أﻗﺻﻰ‬ ‫ﻋﻧد‬=‫ﺻﻔر‬
B‫ع‬٠=‫ء‬‫ن‬B‫ن‬==
‫ارﺗﻔﺎع‬ ‫أﻗﺻﻰ‬ ‫ﻣﺳﺎﻓﺔ‬:٠=‫ع‬٠
٢
‫ــ‬٢‫ف‬ ‫ﺟـ‬
‫ف‬==
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـ‬‫ــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـ‬‫ــــــــــــــــــــــــــــــــ‬
‫ﻣﻼﺣظﺎت‬:
‫ﻓﺈن‬ ‫أﻋﻠﻰ‬ ‫إﻟﻰ‬ ‫أﺳﯾﺎ‬‫ر‬ ‫ﺟﺳﯾم‬ ‫ﻗذف‬ ‫إذا‬ً:
)١(‫اﻟﺻﻌود‬ ‫زﻣن‬=‫اﻟﻬﺑوط‬ ‫زﻣن‬
)٢(‫اﻟﻘـذف‬ ‫ﻧﻘطـﺔ‬ ‫إﻟـﻰ‬ ‫اﻟﺟـﺳﯾم‬ ‫ﺑﻬـﺎ‬ ‫ﯾﻌـود‬ ‫اﻟﺗـﻰ‬ ‫ﻋﺔ‬‫اﻟﺳر‬ ‫ﻣﻘدار‬=‫ﻣ‬‫ﺑﺈﺷـﺎرﺗﯾن‬ ‫اﻟﻘـذف‬ ‫ﻋﺔ‬‫ﺳـر‬ ‫ﻘـدار‬
‫ﻣﺧﺗﻠﻔﺗﯾن‬]‫ﻋﺗﻪ‬‫ﺳـر‬ ‫ﻟﻣﻘـدار‬ ‫ﻣـﺳﺎوﯾﺔ‬ ‫ﺗﻛـون‬ ‫ﺻـﺎﻋد‬ ‫وﻫـو‬ ‫ﻧﻘطـﺔ‬ ‫أى‬ ‫ﻋﻧـد‬ ‫اﻟﺟﺳﯾم‬ ‫ﻋﺔ‬‫ﺳر‬ ‫ﻣﻘدار‬
‫ﻋﺗﯾن‬‫اﻟﺳر‬ ‫اﺗﺟﺎﻫﻰ‬ ‫اﺧﺗﻼف‬ ‫ﻣﻊ‬ ‫ﻫﺎﺑط‬ ‫وﻫو‬ ‫اﻟﻧﻘطﺔ‬ ‫ﺑﻧﻔس‬ ‫ﻩ‬‫ﻣرور‬ ‫ﻋﻧد‬[
)٣(‫زﻣﻧﯾﺔ‬ ‫ة‬‫ﻓﺗر‬ ‫ﻓﻰ‬ ‫اﺣﺔ‬‫ز‬‫اﻻ‬ ‫ﺗﻛون‬ ‫ى‬‫اﻟﺿرور‬ ‫ﻣن‬ ‫ﻟﯾس‬ ‫ﻻﻋﻠﻰ‬ ‫اﺳﯾﺎ‬‫ر‬ ‫اﻟﻣﻘذوﻓﺔ‬ ‫اﻻﺟﺳﺎم‬ ‫ﺣﺎﻟﺔ‬ ‫ﻓﻰ‬
‫ﻣﺳﺎوﯾ‬ ‫ﻣﺎ‬‫ة‬‫اﻟﻔﺗر‬ ‫ﺧﻼل‬ ‫اﻟﺟﺳم‬ ‫ﻗطﻌﻬﺎ‬ ‫اﻟﺗﻰ‬ ‫ﻟﻠﻣﺳﺎﻓﺔ‬ ‫ﺔ‬.
)٤(‫ﻣوﺟﺑﺔع‬ ‫ﺗﻛون‬ ‫ﺻﺎﻋد‬ ‫وﻫو‬ ‫اﻟﺟﺳﯾم‬ ‫ﻋﺔ‬‫ﺳر‬<٠‫ع‬ ‫ﺳﺎﻟب‬ ‫ﺗﻛون‬ ‫ﻫﺎﺑط‬ ‫وﻫو‬>٠
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﺳﻘﺎﻟﺔ‬ ‫ﻣﻦ‬ ‫ﺧﺮﺳﺎﻧﯿﺔ‬ ‫ﻗﻄﻌﺔ‬ ‫ﺑﻨﺎء‬ ‫ﻋﺎﻣﻞ‬ ‫أﺳﻘﻂ‬)‫ﻣﻨﺼﺔ‬(‫ﻋﺎﻟﯿﺔ‬.
)‫أ‬(‫ﺛﺎﻧﯿﺔ‬ ‫ﻧﺼﻒ‬ ‫ﺑﻌﺪ‬ ‫اﻟﺒﻨﺎء‬ ‫ﻗﻄﻌﺔ‬ ‫ﺳﺮﻋﺔ‬ ‫ﻣﺎ‬.
)‫ب‬(‫اﻟﺰﻣﻦ‬ ‫ھﺬا‬ ‫ﺧﻼل‬ ‫اﻟﺒﻨﺎء‬ ‫ﻛﺘﻠﺔ‬ ‫ﺗﻘﻄﻌﮭﺎ‬ ‫اﻟﺘﻰ‬ ‫اﻟﻤﺴﺎﻓﺔ‬ ‫ﻣﺎ‬.
‫ع‬٠
‫ء‬
‫اﻟﻘذف‬ ‫ﻋﺔ‬‫ﺳر‬ ‫ﻣﻘدار‬
‫اﻷرﺿﯾﺔ‬ ‫اﻟﺟﺎذﺑﯾﺔ‬ ‫ﻋﺟﻠﺔ‬ ‫ﻣﻘدار‬
‫ع‬٠
٢
٢‫ء‬
‫ﻣرﺑﻊ‬‫اﻟﻘذف‬ ‫ﻋﺔ‬‫ﺳر‬
‫اﻷرﺿﯾﺔ‬ ‫اﻟﺟﺎذﺑﯾﺔ‬ ‫ﻋﺟﻠﺔ‬ ‫ﺿﻌف‬

94. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
94
‫اﻟﺤﻞ‬:
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:
‫اﻟﺤﻞ‬:
)‫أ‬(‫ﺑﺎﻻرض‬ ‫ارﺗﻄﺎﻣﮭﺎ‬ ‫ﻟﺤﻈﺔ‬ ‫اﻟﺘﻔﺎﺣﺔ‬ ‫ﺳﺮﻋﺔ‬:‫ع‬٠=٠،‫ء‬=٩٫٨‫م‬/‫ث‬٢
‫ن‬ ،=١‫ﺛﺎﻧﯿﺔ‬
A‫ع‬=‫ع‬٠+‫ء‬‫ن‬B‫ع‬=٠+٩٫٨×١=٩٫٨‫م‬/‫ث‬٢
‫اﻟﺜﺎﻧﯿﺔ‬ ‫ﺧﻼل‬ ‫اﻟﻤﺘﻮﺳﻄﺔ‬ ‫اﻟﺴﺮﻋﺔ‬=‫ﺛﺎﻧﯿﺔ‬ ‫ﻧﺼﻒ‬ ‫ﺑﻌﺪ‬ ‫اﻟﺘﻔﺎﺣﺔ‬ ‫ﺳﺮﻋﺔ‬
=٩٫٨×٠٫٥=٤٫٩‫م‬/‫ث‬٢
)‫ب‬(‫ف‬=‫ع‬٠‫ن‬+‫ء‬‫ن‬٢
=٠+×٩٫٨×)١(٢
=٩٫٨‫ﻣﺘﺮا‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﺑﺴﺮﻋﺔ‬ ‫ﺑﺌﺮ‬ ‫ﻓﻰ‬ ‫ﺻﻐﯿﺮ‬ ‫ﺣﺠﺮ‬ ‫ﻗﺬف‬٤‫م‬/‫ﺑﻌﺪ‬ ‫ﻗﺎﻋﮫ‬ ‫اﻟﻰ‬ ‫ﻓﻮﺻﻞ‬ ‫ث‬٢‫أوﺟ‬ ‫ﺛﺎﻧﯿﺔ‬‫اﻟﺒﺌﺮ‬ ‫ﻋﻤﻖ‬ ‫ﺪ‬
‫ﺑﺎﻟﻘﺎع‬ ‫اﺻﻄﺪاﻣﮫ‬ ‫ﻋﻨﺪ‬ ‫اﻟﺤﺠﺮ‬ ‫وﺳﺮﻋﺔ‬
‫اﻟﺤﻞ‬:
A‫ف‬=‫ع‬٠‫ن‬+‫ء‬‫ن‬٢
=٤×٢+×٩٫٨×٤=٢٧٫٦‫م‬
B‫ع‬=‫ع‬٠+‫ء‬‫ن‬=٤+٩٫٨×٢=٢٣٫٦‫م‬/‫ث‬
١
٢
١
٢
١
٢
١
٢

95. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
95
‫ﻣﺜﺎل‬:‫ﺑﺴﺮﻋﺔ‬ ‫ﻻﻋﻠﻰ‬ ‫رأﺳﯿﺎ‬ ‫ﺟﺴﯿﻢ‬ ‫ﻗﺬف‬١٩٫٦‫م‬/‫أرﺗﻔﺎع‬ ‫أﻗﺼﻰ‬ ‫اﻟﻰ‬ ‫وﺻﻮﻟﮫ‬ ‫زﻣﻦ‬ ‫أوﺟﺪ‬ ‫ث‬
‫اﻟﯿﮭﺎ‬ ‫وﺻﻞ‬ ‫اﻟﺘﻰ‬ ‫واﻟﻤﺴﺎﻓﺔ‬
‫اﻟﺤﻞ‬:
‫ع‬٠=١٩٫٦‫ع‬ ،=٠،‫ء‬=٩٫٨
B‫ع‬=‫ع‬٠‫ــ‬‫ء‬‫ن‬B٠=١٩٫٦–٩٫٨‫ن‬
٩٫٨‫ن‬=١٩٫٦B‫ن‬=٢‫ﺛﺎﻧﯿﺔ‬
B‫ارﺗﻔﺎع‬ ‫أﻗﺼﻰ‬ ‫اﻟﻰ‬ ‫اﻟﻮﺻﻮل‬ ‫زﻣﻦ‬=٢‫ﺛﺎﻧﯿﺔ‬
‫اﻟﻤﺴ‬ ‫ﻻﯾﺠﺎد‬‫اﻟﯿﮭﺎ‬ ‫وﺻﻞ‬ ‫اﻟﺘﻰ‬ ‫ﺎﻓﺔ‬:
‫ف‬=‫ع‬٠‫ن‬‫ــ‬‫ء‬‫ن‬٢
=١٩٫٦×٢‫ــ‬×٩٫٨×٤=١٩٫٦‫ﻣﺘﺮا‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﻻ‬ ‫رأﺳﯿﺎ‬ ‫ﺟﺴﯿﻢ‬ ‫ﻗﺬف‬‫ﺑﺴﺮﻋﺔ‬ ‫ﻋﻠﻰ‬٢٤٫٥‫م‬/‫اﻟﻘﺬف‬ ‫ﻧﻘﻄﺔ‬ ‫اﻟﻰ‬ ‫ﯾﻌﻮد‬ ‫ﺛﺎﻧﯿﺔ‬ ‫ﻛﻢ‬ ‫ﻓﺒﻌﺪ‬ ‫ث‬
‫اﻟﺤﻞ‬:
‫أرﺗﻔﺎع‬ ‫ﻻﻗﺼﻰ‬ ‫اﻟﻮﺻﻮل‬ ‫زﻣﻦ‬ ‫ﻧﻮﺟﺪ‬
‫ع‬٠=٢٤٫٥‫ع‬ ،=٠،‫ء‬=٩٫٨
A‫ع‬=‫ع‬٠‫ــ‬‫ء‬‫ن‬B٠=٢٤٫٥–٩٫٨‫ن‬B٩٫٨‫ن‬=٢٤٫٥
B‫ن‬=٢٫٥‫ﺛﺎﻧﯿﺔ‬B‫ا‬ ‫زﻣﻦ‬‫واﻟﮭﺒﻮط‬ ‫ﻟﺼﻌﻮد‬=٢×٢٫٥=٥‫ﺛﻮان‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﺑﺴﺮﻋﺔ‬ ‫ﻻﻋﻠﻰ‬ ‫رأﺳﯿﺎ‬ ‫ﺟﺴﯿﻢ‬ ‫ﻗﺬف‬١٤‫م‬/‫اﻟ‬ ‫ﯾﺼﻞ‬ ‫ﺣﺘﻰ‬ ‫ﯾﺄﺧﺬه‬ ‫اﻟﺬى‬ ‫اﻟﺰﻣﻦ‬ ‫أوﺟﺪ‬ ‫ث‬‫ﻧﻘﻄﺔ‬ ‫ﻰ‬
‫ﺗﺒﻌﺪ‬٣٥٠‫اﻟﻘﺬف‬ ‫ﻧﻘﻄﺔ‬ ‫أﺳﻔﻞ‬ ‫م‬
‫اﻟﺤﻞ‬:
‫ف‬=-٣٥٠٤٩‫ن‬٢
–١٤٠‫ن‬–٣٥٠٠=٠÷٧
‫ع‬٠‫ن‬+‫ء‬‫ن‬٢
=-٣٥٠٧‫ن‬٢
–٢٠‫ن‬–٥٠٠=٠
١٤‫ن‬+×-٩٫٨‫ن‬٢
=-٣٥٠)٧‫ن‬+٥٠)(‫ن‬–١٠= (٠
١٤‫ن‬–٤٫٩‫ن‬٢
=-٣٥٠×١٠B‫ن‬=١٠‫ن‬ ،=‫ﻣﺮﻓﻮض‬ ‫ــ‬
١
٢
١
٢
١
٢
١
٢
٥٠
٧

96. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
96
‫ـﺎل‬‫ـ‬‫ﻣﺛ‬:‫ﻋﺔ‬‫ﺑــﺳر‬ ‫ﺻــﻐﯾر‬ ‫ـر‬‫ـ‬‫ﺣﺟ‬ ‫ﻗــذف‬١٩.٦‫ـر‬‫ـ‬‫ﻣﺗ‬/‫ارﺗﻔﺎﻋــﻪ‬ ‫ﺑــرج‬ ‫ـﺔ‬‫ـ‬‫ﻗﻣ‬ ‫ﻣــن‬ ‫أﻋﻠــﻰ‬ ‫ـﻰ‬‫ـ‬‫إﻟ‬ ‫أﺳــﯾﺎ‬‫ر‬ ‫ث‬ً
١٥٦.٨‫اﻷرض‬ ‫ﺳطﺢ‬ ‫ﻋن‬ ‫ﻣﺗر‬.‫إﻟﻰ‬ ‫اﻟﺣﺟر‬ ‫ﯾﺻل‬ ‫ﻣﺗﻰ‬‫ﻫﻰ‬ ‫وﻣﺎ‬ ‫؟‬ ‫اﻷرض‬ ‫ﺳطﺢ‬‫ﻋﻧدﺋذ‬ ‫ﻋﺗﻪ‬‫ﺳر‬
‫اﻟﺣل‬:
‫ع‬ ‫ارﺗﻔﺎع‬ ‫أﻗﺻﻰ‬ ‫ﻋﻧد‬=٠
‫ف‬== =١٩.٦‫ﻣﺗر‬
B‫ﻣﺳﺎﻓﺔ‬ ‫أﻗﺻﻰ‬=١٥٦.٨+١٩.٦=١٧٦.٤‫ﻣﺗر‬
A‫ف‬=‫ع‬٠‫ن‬+‫ء‬‫ن‬٢‫ع‬ ‫ﺣﯾث‬٠‫اﻟﻬﺑوط‬ ‫ﺣﺎﻟﺔ‬ ‫ﻓﻰ‬ ‫اﻻﺑﺗداﺋﯾﺔ‬ ‫ﻋﺗﻪ‬‫ﺳر‬.
١٧٦.٤=٠×‫ن‬+×٩.٨‫ن‬٢
١٧٦.٤=٤.٩‫ن‬٢B‫ن‬٢==٣٦B‫ن‬=٦‫ث‬
‫ارﺗﻔﺎع‬ ‫ﻻﻗﺻﻰ‬ ‫اﻟوﺻول‬ ‫زﻣن‬ ،= =٢‫ث‬
B‫اﻟﻘذف‬ ‫ﻟﺣظﺔ‬ ‫ﻣن‬ ‫اﻷرض‬ ‫ﺳطﺢ‬ ‫إﻟﻰ‬ ‫اﻟوﺻول‬ ‫زﻣن‬=٦+٢=٨‫ث‬
A‫ع‬=‫ع‬٠+‫ء‬‫ن‬
B‫ع‬=٠+٩.٨×٦=٥٨.٨‫ﻣﺗر‬/‫ث‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــﺎل‬‫ـ‬‫ﻣﺛ‬:‫ة‬‫ـــر‬‫ـ‬‫اﻟﻛ‬ ‫ـــوﻫدت‬‫ـ‬‫وﺷ‬ ، ‫ـــﺎزل‬‫ـ‬‫اﻟﻣﻧ‬ ‫ـــد‬‫ـ‬‫أﺣ‬ ‫ـــذة‬‫ـ‬‫ﻧﺎﻓ‬ ‫ـــن‬‫ـ‬‫ﻣ‬ ‫ـــﻰ‬‫ـ‬‫أﻋﻠ‬ ‫ـــﻰ‬‫ـ‬‫إﻟ‬ ‫ـــﯾﺎ‬‫ـ‬‫أﺳ‬‫ر‬ ‫ة‬‫ـــﻐﯾر‬‫ـ‬‫ﺻ‬ ‫ة‬‫ـر‬‫ـ‬‫ـ‬‫ـ‬‫ﻛ‬ ‫ـــذﻓت‬‫ـ‬‫ﻗ‬ً
‫ــــد‬‫ـ‬‫ﺑﻌ‬ ‫ــــذة‬‫ـ‬‫اﻟﻧﺎﻓ‬ ‫ــــﺎم‬‫ـ‬‫أﻣ‬ ‫ــــﺔ‬‫ـ‬‫ﻫﺎﺑط‬ ‫ــــﻰ‬‫ـ‬‫وﻫ‬٤‫اﻷرض‬ ‫ــــطﺢ‬‫ـ‬‫ﺳ‬ ‫ــــﻰ‬‫ـ‬‫إﻟ‬ ‫ــــﻠت‬‫ـ‬‫وﺻ‬ ‫ــــم‬‫ـ‬‫ﺛ‬ ‫ــــذﻓﻬﺎ‬‫ـ‬‫ﻗ‬ ‫ــــن‬‫ـ‬‫ﻣ‬ ‫اﻧﻰ‬‫و‬‫ــــ‬‫ـ‬‫ﺛ‬
‫ﺑﻌد‬٥‫اﻟﻘذف‬ ‫ﻟﺣظﺔ‬ ‫ﻣن‬ ‫اﻧﻰ‬‫و‬‫ﺛ‬.‫اﻷرض‬ ‫ﺳطﺢ‬ ‫ﻋن‬ ‫اﻟﻧﺎﻓذة‬ ‫ارﺗﻔﺎع‬ ‫أوﺟد‬.
‫اﻟﺣل‬:‫اﻟﺻﻌود‬ ‫ﺣﺎﻟﺔ‬ ‫ﻓﻰ‬:‫ع‬=‫ع‬٠-‫ء‬‫ن‬
‫ﺻﻔر‬ ‫ارﺗﻔﺎع‬ ‫أﻗﺻﻰ‬ ‫ﺣﺎﻟﺔ‬ ‫ﻓﻰ‬=‫ع‬٠–٩.٨×٢
A‫اﻟﺻﻌود‬ ‫زﻣن‬=‫اﻟﻬﺑوط‬ ‫زﻣن‬B‫اﻟﺻﻌود‬ ‫زﻣن‬==٢‫ث‬
‫ع‬٠
٢
٢‫ء‬
)١٩.٦(٢
٢×٩.٨
١٧٦٫٤
٤٫٩
٤
٢
١
٢
١
٢
١٩٫٦
٩٫٨

97. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
97
‫ﺑﻌد‬ ‫اﻷرض‬ ‫ﺳطﺢ‬ ‫إﻟﻰ‬ ‫وﺻﻠت‬ ‫ة‬‫اﻟﻛر‬٥‫اﻟﻘذف‬ ‫ﻟﺣظﺔ‬ ‫ﻣن‬ ‫اﻧﻰ‬‫و‬‫ﺛ‬
‫ﺗﺄﺧذ‬ ‫ة‬‫اﻟﻛر‬١‫اﻟﻬﺑوط‬ ‫أﺛﻧﺎء‬ ‫اﻷرض‬ ‫ﺳطﺢ‬ ‫ﺣﺗﻰ‬ ‫اﻟﻧﺎﻓذة‬ ‫أﻣﺎم‬ ‫ﻣن‬ ‫ث‬.
A‫ف‬=‫ع‬٠‫ن‬+‫ء‬‫ن‬٢
B‫ف‬=١٩.٦×١+×٩.٨)١(٢
‫ف‬=١٩.٦+٤.٩=٢٤.٥‫ﻣﺗر‬)‫اﻟﻧﺎﻓذة‬ ‫ارﺗﻔﺎع‬(
‫ـــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـ‬‫ــــــــــــ‬
‫ﻣﺛﺎل‬:‫ﻋﺔ‬‫ﺑﺳر‬ ‫أﻋﻠﻰ‬ ‫إﻟﻰ‬ ‫أﺳﯾﺎ‬‫ر‬ ‫ﺟﺳﯾم‬ ‫ﻗذف‬ً١٩.٦‫ﻣﺗر‬/‫ﻣﺗﻰ‬ ‫اﻷرض‬ ‫ﺳطﺢ‬ ‫ﻋﻠﻰ‬ ‫ﻧﻘطﺔ‬ ‫ﻣن‬ ‫ث‬
‫ارﺗﻔﺎع‬ ‫ﻋﻠﻰ‬ ‫اﻟﺟﺳﯾم‬ ‫ﯾﻛون‬١٤.٧‫اﻷرض‬ ‫ﺳطﺢ‬ ‫ﻓوق‬ ‫ﻣﺗر‬
‫؟‬ ‫اﺑﯾن‬‫و‬‫اﻟﺟ‬ ‫ﻣﻌﻧﻰ‬ ‫ﻓﺳر‬ ‫ﻋﻧدﺋذ‬ ‫ﻋﺗﻪ‬‫ﺳر‬ ‫ﻫﻰ‬ ‫وﻣﺎ‬
‫اﻟﺣل‬:A‫ف‬=‫ع‬٠‫ن‬-‫ء‬‫ن‬٢)‫ﺻﺎﻋدا‬ ‫اﻟﺟﺳﯾم‬ً(
B١٤.٧=١٩.٦‫ن‬-×٩.٨‫ن‬٢
١٤.٧=١٩.٦‫ن‬–٤.٩‫ن‬٢‫ﻋﻠﻰ‬ ‫ﺑﺎﻟﻘﺳﻣﺔ‬٤.٩
٣=٤‫ن‬–‫ن‬٢B‫ن‬٢-٤‫ن‬+٣=٠
)‫ن‬-٣) (‫ن‬-١= (٠C‫ن‬=٣‫ن‬ ، ‫ث‬=١‫ث‬
‫ن‬=١‫ﻩ‬‫ﻣﻘدار‬ ‫زﻣن‬ ‫ﯾﺄﺧذ‬ ‫اﻟﺟﺳﯾم‬ ‫أن‬ ‫أى‬ ‫ث‬١‫ن‬ ‫اﻟﻘذف‬ ‫ﻟﺣظﺔ‬ ‫ﻣن‬ ‫اﻟﺻﻌود‬ ‫ﺣﺎﻟﺔ‬ ‫ﻓﻰ‬ ‫ث‬=٣‫ث‬
‫ﯾﻌود‬ ‫ﺛم‬ ‫ارﺗﻔﺎع‬ ‫أﻗﺻﻰ‬ ‫إﻟﻰ‬ ‫وﯾﺻل‬ ‫اﻻرﺗﻔﺎع‬ ‫ﻫذا‬ ‫ﺑﻌد‬ ‫ﺣﺗﻰ‬ ‫اﻟﺻﻌود‬ ‫ﻓﻰ‬ ‫ﯾﺳﺗﻣر‬ ‫اﻟﺟﺳﯾم‬ ‫أن‬ ‫أى‬
‫اﻟﺟ‬‫اﻻرﺗﻔﺎع‬ ‫إﻟﻰ‬ ‫ﻟﯾﺻل‬ ‫ى‬‫أﺧر‬ ‫ة‬‫ﻣر‬ ‫اﻟﻬﺑوط‬ ‫ﻓﻰ‬ ‫ﺳﯾم‬١٤.٧‫ﻣﺿﻰ‬ ‫ﺑﻌد‬ ‫ى‬‫أﺧر‬ ‫ة‬‫ﻣر‬ ‫ﻣﺗر‬٣‫ﻣن‬ ‫ث‬
‫اﻟﻘذف‬ ‫ﻟﺣظﺔ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـ‬‫ــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺛﺎل‬:‫ﻋﺔ‬‫ﺑﺳر‬ ‫أﻋﻠﻰ‬ ‫إﻟﻰ‬ ‫أﺳﯾﺎ‬‫ر‬ ‫ﺟﺳﯾم‬ ‫ﻗذف‬١٤.٧‫ﻣﺗر‬/‫اﻷرض‬ ‫ﺳطﺢ‬ ‫ﻋﻧد‬ ‫ﻧﻘطﺔ‬ ‫ﻣن‬ ‫ث‬
‫ارﺗﻔﺎع‬ ‫ﻋﻠﻰ‬ ‫ﯾﻛون‬ ‫ﻋﻧدﻣﺎ‬ ‫اﻟﺟﺳﯾم‬ ‫ﻋﺔ‬‫ﺳر‬ ‫اﺣﺳب‬٩.٨‫اﻷرض‬ ‫ﺳطﺢ‬ ‫ﻋن‬ ‫ا‬‫ر‬‫ﻣﺗ‬ً
١
٢
١
٢
١
٢
١
٢

98. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
98
‫اﺑﯾن‬‫و‬‫اﻟﺟ‬ ‫ﻣﻌﻧﻰ‬ ‫ﻓﺳر‬ ‫و‬.
‫اﻟﺣل‬:‫ﺑ‬‫أﻋﻠﻰ‬ ‫اﻟﻰ‬ ‫اﻟﻣوﺟب‬ ‫اﻻﺗﺟﺎﻩ‬ ‫ﻔرض‬
B‫ع‬٠=١٤.٧‫ﻣﺗر‬/‫ف‬ ، ‫ث‬=٩.٨‫ا‬‫ر‬‫ﻣﺗ‬
A‫ع‬٢
=‫ع‬٢
٠‫ـــ‬٢‫ء‬‫ف‬
) =١٤٫٧(٢
‫ــ‬٢×٩٫٨×٩٫٨=٢٤٫٠١
B‫ع‬=±٤٫٩‫ﻣﺘﺮ‬/‫ث‬
‫ع‬ ‫ﺗﻜﻮن‬ ‫و‬=٤٫٩‫ﻣﺘﺮ‬/‫ﺻﺎﻋﺪا‬ ‫اﻟﺠﺴﯿﻢ‬ ‫ﻋﻨﺪﻣﺎ‬ ‫ث‬
‫ع‬ ،=‫ــ‬٤٫٩‫ﻣﺘﺮ‬/‫ﻋﻨﺪﻣﺎ‬ ‫ث‬ً‫ﺎ‬‫ھﺎﺑﻄ‬ ‫اﻟﺠﺴﯿﻢ‬
‫ارﺗﻔﺎع‬ ‫ﻋﻠﻰ‬ ‫ﯾﻜﻮن‬ ‫اﻟﺠﺴﯿﻢ‬ ‫ھﺬا‬ ‫أن‬ ‫ﻣﻌﻨﻰ‬ ‫و‬٩٫٨‫ﻣﺮﺗﯿﻦ‬ ‫اﻻرض‬ ‫ﻋﻦ‬ ‫ﻣﺘﺮا‬:
‫اﻻوﻟﻰ‬:‫ﻋﺔ‬‫ﺑﺳر‬ ‫ﺻﺎﻋد‬ ‫وﻫو‬٤.٩‫ﻣﺗر‬/‫ب‬ ‫ﻋﻧد‬ ‫ث‬
‫اﻟﺛﺎﻧﯾﺔ‬ ‫و‬:‫ب‬ ‫ﻋن‬ ‫ﻋﺔ‬‫اﻟﺳر‬ ‫ﺑﻧﻔس‬ ‫ﻫﺎﺑط‬ ‫ﻫو‬ ‫و‬)‫ب‬ ‫ﻣﺣﺎذاة‬ ‫ﻓﻰ‬ ‫اﻟﺗﻰ‬(
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺛﺎل‬:‫ﻋﺔ‬‫ﺑﺳر‬ ‫أﻋﻠﻰ‬ ‫إﻟﻰ‬ ‫أﺳﯾﺎ‬‫ر‬ ‫ﺟﺳﯾم‬ ‫ﻗذف‬٢٤‫ﻣﺗر‬/‫اﻷرض‬ ‫ﺳطﺢ‬ ‫أﻋﻠﻰ‬ ‫ﻧﻘطﺔ‬ ‫ﻣن‬ ‫ث‬.
‫اﻟزﻣن‬ ‫أوﺟد‬‫ﺗﺑﻌد‬ ‫ﻧﻘطﺔ‬ ‫إﻟﻰ‬ ‫ﯾﺻل‬ ‫ﺣﺗﻰ‬ ‫ﯾﺄﺧذﻩ‬ ‫اﻟذى‬٣٢.٤‫اﻟﻘذف‬ ‫ﻧﻘطﺔ‬ ‫أﺳﻔل‬ ‫ا‬‫ر‬‫ﻣﺗ‬ً.
‫اﻟﺣل‬:
‫ﻣوﺟﺑﺎ‬ ‫اﺗﺟﺎﻩ‬ ‫أﻋﻠﻰ‬ ‫اﻟﻰ‬ ‫أﺳﻲ‬‫ر‬‫اﻟ‬ ‫اﻻﺗﺟﺎﻩ‬ ‫ﻧﺗﺧذ‬ً
B‫ع‬٠+ =٢٤‫ﻣﺗر‬/‫ث‬‫ف‬ ،=‫ــ‬٣٢.٤‫ﻣﺗر‬
A‫ف‬=‫ع‬٠‫ـــ‬ ‫ن‬‫ء‬‫ن‬٢
B‫ــ‬٣٢٫٤=٢٤‫ــ‬ ‫ن‬×٩٫٨‫ن‬٢
B٤.٩‫ن‬٢
‫ـــ‬٢٤‫ـــ‬ ‫ن‬٣٢.٤=٠
B٤٩‫ن‬٢
‫ــ‬٢٤٠‫ــ‬ ‫ن‬٣٢٤=٠
B)‫ــ‬ ‫ن‬٦)(٤٩‫ن‬+٥٤= (٠
B‫ن‬=٦‫ن‬ ،‫أ‬=‫ــ‬)‫ﻣرﻓوض‬(
‫اﻟﻣطﻠوب‬ ‫اﻟزﻣن‬=٦‫ان‬‫و‬‫ﺛ‬
/////////////////////////
+
+
‫ـــ‬
‫ب‬
‫اﻻرض‬ ‫ﺳﻄﺢ‬
‫اﻟﻤﻮﺟﺐ‬ ‫اﻻﺗﺠﺎه‬‫ف‬‫ء‬
///////////////////////////
+
‫ع‬٠=٢٤‫ﻣﺘﺮ‬/‫ث‬
‫اﻻرض‬ ‫ﺳﻄﺢ‬
‫اﻟﻤﻮﺟﺐ‬ ‫اﻻﺗﺠﺎه‬‫ف‬=-٣٢٫٤‫ﻣﺘﺮا‬
‫اﻟﻘﺬف‬ ‫ﻧﻘﻄﺔ‬
‫ب‬‫ب‬ ١
٢١
٢
٥٤
٤٩

99. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
99
‫ﻣﺛﺎل‬:‫ارﺗﻔﺎع‬ ‫ﻣن‬ ‫اﻟﻣطﺎط‬ ‫ﻣن‬ ‫ة‬‫ﻛر‬ ‫ﺳﻘطت‬١٩.٦‫اﻟﻰ‬ ‫ﻓﺄرﺗدت‬ ‫ﺻﻠﺑﺔ‬ ‫اﻓﻘﯾﺔ‬ ‫أرض‬ ‫ﺳطﺢ‬ ‫ﻋﻠﻰ‬ ‫ﻣﺗر‬
‫أﻋﻠﻰ‬‫اﻟﺗﺻﺎدم‬ ‫ﻧﺗﯾﺟﺔ‬ ‫ﻋﺗﻬﺎ‬‫ﺳر‬ ‫ﻧﺻف‬ ‫ﻓﻘدت‬ ‫ة‬‫اﻟﻛر‬ ‫ﺑﺄن‬ ‫ﻋﻠﻣﺎ‬ ‫ة‬‫اﻟﻛر‬ ‫إﻟﯾﻪ‬ ‫ﺗﺻل‬ ‫ارﺗﻔﺎع‬ ‫اﻗﺻﻰ‬ ‫ﻓﺄوﺟد‬
‫اﻟﺣل‬:‫ﺑﺎﻻرض‬ ‫اﻻﺻطدام‬ ‫ﻗﺑل‬:
A‫ع‬٢
=‫ع‬٠
٢
+٢‫ف‬ ‫ء‬B‫ع‬٢
=٠+٢×٩٫٨×١٩٫٦
B‫ع‬=١٩٫٦‫م‬/‫ث‬
B‫ﻣﺒﺎﺷﺮة‬ ‫اﻻﺻﻄﺪام‬ ‫ﻗﺒﻞ‬ ‫اﻟﻜﺮة‬ ‫ﺳﺮﻋﺔ‬=١٩٫٦‫م‬/‫ث‬
B‫ﻣﺒﺎﺷﺮة‬ ‫اﻻﺻﻄﺪام‬ ‫ﺑﻌﺪ‬ ‫اﻟﻜﺮة‬ ‫ﺳﺮﻋﺔ‬=٩٫٨‫م‬/‫ث‬
‫ﺑﺎﻻرض‬ ‫اﻻﺻطدام‬ ‫ﺑﻌد‬:
‫ارﺗﻔﺎع‬ ‫أﻗﺻﻰ‬= ==٤.٩‫ا‬‫ر‬‫ﻣﺗ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـ‬‫ــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺛﺎل‬:‫ارﺗﻔﺎع‬ ‫ﻣن‬ ‫اﻟﻣطﺎط‬ ‫ﻣن‬ ‫ة‬‫ﻛر‬ ‫ﺳﻘطت‬١٠‫أﻋﻠﻰ‬ ‫اﻟﻰ‬ ‫أﺳﯾﺎ‬‫ر‬ ‫ارﺗدت‬‫و‬ ‫ﺑﺎﻻرض‬ ‫ﻓﺎﺻطدﻣت‬ ‫ﻣﺗر‬
‫ﻣﺳﺎﻓﺔ‬٢‫ﻣﺗر‬.‫ﺑﺎﻻرض‬ ‫اﺻطداﻣﻬﺎ‬ ‫ﺑﻌد‬ ‫و‬ ‫ﻗﺑل‬ ‫ة‬‫اﻟﻛر‬ ‫ﻋﺔ‬‫ﺳر‬ ‫اﺣﺳب‬‫ة‬‫ﻣﺑﺎﺷر‬
‫اﻟﺣل‬:‫ﺑﺎﻻرض‬ ‫اﻻﺻطدام‬ ‫ﻗﺑل‬:
A‫ع‬٢
=‫ع‬٠
٢
+٢‫ف‬ ‫ء‬B‫ع‬٢
=٠+٢×٩٫٨×١٠
B‫ع‬=١٤‫م‬/‫ث‬
‫ﻣﺒﺎﺷﺮة‬ ‫اﻻﺻﻄﺪام‬ ‫ﻗﺒﻞ‬ ‫اﻟﺴﺮﻋﺔ‬ ‫ان‬ ‫أى‬=١٤‫م‬/‫ث‬
‫ﺑﺎﻻرض‬ ‫اﻻﺻطدام‬ ‫ﺑﻌد‬:
A‫ع‬٢
=‫ع‬٠
٢
-٢‫ف‬ ‫ء‬B٠=‫ع‬٠
٢
-٢×٩٫٨×٢٫٥
B‫ع‬٠=٧‫م‬/‫ث‬
‫ة‬‫ﻣﺑﺎﺷر‬ ‫اﻻﺻطدام‬ ‫ﺑﻌد‬ ‫ﻋﺔ‬‫اﻟﺳر‬ ‫أن‬ ‫أى‬=٧‫م‬/‫ث‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺛﺎل‬:‫ارﺗﻔﺎع‬ ‫ﻣن‬ ‫اﻟﺳﻛون‬ ‫ﻣن‬ ‫ﺣﺟر‬ ‫ﺳﻘط‬١٠‫ﻣﺳﺎﻓﺔ‬ ‫ﻓﯾﻬﺎ‬ ‫ﻓﻐﺎص‬ ‫اﻟرﻣل‬ ‫ﻣن‬ ‫ﻛوﻣﺔ‬ ‫ﻓوق‬ ‫ﻣﺗر‬
١٩٦‫اﻟرﻣل‬ ‫داﺧل‬ ‫اﻟﺟﺳم‬ ‫ﺑﻬﺎ‬ ‫ﺗﺣرك‬ ‫اﻟﺗﻰ‬ ‫اﻟﻌﺟﻠﺔ‬ ‫أوﺟد‬ ‫ﺳم‬.
‫ع‬٠=٠
‫ع‬=٠
١٩٫٦‫م‬
‫ع‬٠
٢
٢‫د‬
)٩.٨(٢
٢×٩.٨
١
٢
‫ع‬٠=٠
‫ع‬=٠
١٠‫م‬
٢٫٥‫م‬

100. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
100
‫اﻟﺣل‬:‫ع‬٠=٠‫ف‬ ،=١٠، ‫ﻣﺗر‬‫ء‬=٩٫٨‫م‬/‫ث‬٢
A‫ع‬٢
=‫ع‬٠
٢
+٢‫ف‬ ‫ء‬B‫ع‬٢
=٠+٢×٩٫٨×١٠=١٩٦
B‫ع‬=١٤‫م‬/‫ث‬
‫اﻟﺮﻣﻞ‬ ‫ﻓﻰ‬ ‫اﻟﻐﻮص‬ ‫ﺑﻌﺪ‬:‫ع‬٠=١٤‫م‬/‫ع‬ ، ‫ث‬=٠‫ف‬ ،=١٫٩٦‫م‬
‫ع‬٢
=‫ع‬٠
٢
+٢‫ف‬ ‫ج‬B‫ﺻﻔﺮ‬) =١٤(٢
+٢‫ﺟـ‬×١٫٩٦
B‫ﺟـ‬=‫ــ‬=‫ــ‬٥٠‫م‬/‫ث‬٢
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻟﺮأﺳﯿﺔ‬ ‫اﻟﺤﺮﻛﺔ‬ ‫ﻋﻠﻰ‬ ‫ﺗﻤﺎرﯾﻦ‬
‫اﻷرﺿﯿﺔ‬ ‫اﻟﺠﺎذﺑﯿﺔ‬ ‫ﺗﺄﺛﯿﺮ‬ ‫ﺗﺤﺖ‬
)١٤(٢
٢×١.٩٦

101. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
101

102. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
102
‫ﻣﺒﺎﺷﺮة‬ ‫ﻗﻮة‬ ‫ﺑﺘﺄﺛﯿﺮ‬ ‫اﻵﺧﺮى‬ ‫اﻻﺟﺴﺎم‬ ‫ﻣﻊ‬ ‫ﺗﺘﺠﺎذب‬ ‫اﻟﻜﻮن‬ ‫ﻓﻰ‬ ‫اﻻﺟﺴﺎم‬ ‫ﻛﻞ‬
‫ﻣﺮﻛﺰﯾﮭﻤﺎ‬ ‫ﺑﯿﻦ‬ ‫اﻟﻤﺴﺎﻓﺔ‬ ‫ﻣﺮﺑﻊ‬ ‫ﻣﻊ‬ ‫ﻋﻜﺴﯿﺎ‬ ‫و‬ ‫ﻛﺘﻠﺘﯿﮭﻤﺎ‬ ‫ﻣﻊ‬ ‫ﻃﺮدﯾﺎ‬ ‫ﺗﺘﻨﺎﺳﺐ‬
‫ق‬=‫ث‬×
‫ق‬‫اﻟﺘ‬ ‫ﻋﻦ‬ ‫ﻧﺎﺗﺠﺔ‬ ‫ﻗﻮة‬‫ﺠﺎذب‬
‫اﻟﻌﺎم‬ ‫اﻟﺠﺬب‬ ‫ﺛﺎﺑﺖ‬ ‫ث‬ ،=٦٫٦٧×١٠‫ـ‬‫ـ‬‫ــ‬١١
‫ﻧﯿﻮﺗﻦ‬.‫م‬٢
/‫ﻛﺠﻢ‬٢
‫ك‬١‫ك‬ ، ‫اﻷول‬ ‫اﻟﺠﺴﻢ‬ ‫ﻛﺘﻠﺔ‬ ‫ھﻰ‬٢‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺠﺴﻢ‬ ‫ﻛﺘﻠﺔ‬ ‫ھﻰ‬
‫اﻟﺒﻌﺪ‬ ‫ھﻮ‬ ‫ف‬)‫اﻟﻤﺴﺎﻓﺔ‬(‫اﻟﺠﺴﻤﯿﻦ‬ ‫ﺑﯿﻦ‬
*‫ﺗﻌﺮﯾﻒ‬
*‫ﺟﺴﻤﯿﻦ‬ ‫ﺑﯿﻦ‬ ‫اﻟﺘﺠﺎذب‬ ‫ﻗﻮة‬ ‫ﻋﻠﯿﮭﺎ‬ ‫ﺗﺘﻮﻗﻒ‬ ‫اﻟﺘﻰ‬ ‫اﻟﻌﻮاﻣﻞ‬:
١(‫اﻟﻤﺘﺠﺎذﺑﺔ‬ ‫اﻻﺟﺴﺎم‬ ‫ﻛﺘﻞ‬٢(‫اﻟﻜﺘﻞ‬ ‫ﺑﯿﻦ‬ ‫اﻟﻔﺎﺻﻠﺔ‬ ‫اﻟﻤﺴﺎﻓﺔ‬
‫ﻣﻼﺣﻈﺎت‬:
١-‫ﺳﺮﯾﻌﺎ‬ ‫ﺗﻨﻘﺺ‬ ‫ﻟﻜﻨﮭﺎ‬ ‫و‬ ‫اﻻﺟﺴﺎم‬ ‫ﺑﯿﻦ‬ ‫اﻟﻮﺳﻂ‬ ‫ﻋﻦ‬ ‫اﻟﻨﻈﺮ‬ ‫ﺑﻐﺾ‬ ‫اﻻﺟﺴﺎم‬ ‫ﺑﯿﻦ‬ ‫ﻣﻮﺟﻮدة‬ ‫اﻟﺠﺬب‬ ‫ﻗﻮة‬
‫اﻟ‬ ‫ﺑﯿﻦ‬ ‫اﻟﻤﺴﺎﻓﺔ‬ ‫ﺑﺰﯾﺎدة‬‫ﺠﺴﻤﯿﻦ‬.
٢-‫اﻟﻤﺴﺎﻓﺔ‬ ‫ﻣﺮﺑﻊ‬ ‫ﻣﻊ‬ ‫ﻋﻜﺴﯿﺎ‬ ‫ﺗﺘﻨﺎﺳﺐ‬ ‫اﻟﻘﻮة‬ ‫ﻻن‬ ‫اﻟﻌﻜﺴﻲ‬ ‫اﻟﺘﺮﺑﯿﻊ‬ ‫ﺑﻘﺎﻧﻮن‬ ‫اﻟﻌﺎم‬ ‫اﻟﺠﺬب‬ ‫ﻗﺎﻧﻮن‬ ‫ﯾﺴﻤﻰ‬
‫اﻟﻜﺘﻠﺘﯿﻦ‬ ‫ﻣﺮﻛﺰى‬ ‫ﺑﯿﻦ‬.
‫اﻟﻌﺎم‬ ‫اﻟﺠـﺬب‬ ‫ﻗﺎﻧﻮن‬
‫ك‬١‫ك‬٢
‫ق‬٢١‫ق‬١٢
‫ف‬
‫ك‬١×‫ك‬٢
‫ف‬٢
‫اﻟﻌﺎم‬ ‫اﻟﺠﺬب‬ ‫ﺛﺎﺑﺖ‬:
‫ﻣﻨﮭﻤﺎ‬ ‫ﻛﻞ‬ ‫ﻣﻘﺪار‬ ‫ﻛﺘﻠﺘﯿﻦ‬ ‫ﺑﯿﻦ‬ ‫اﻟﻤﺘﺒﺎدﻟﺔ‬ ‫اﻟﺠﺬب‬ ‫ﻗﻮة‬ ‫ھﻮ‬١‫ﻣﺮﻛﺰﯾﮭﻤﺎ‬ ‫ﺑﯿﻦ‬ ‫اﻟﻤﺴﺎﻓﺔ‬ ‫و‬ ‫ﺟﺮام‬ ‫ﻛﯿﻠﻮ‬
١‫ﻣﺘ‬‫ﯾﺴﺎوى‬ ‫و‬ ‫ﺮ‬٦٫٦٧×١٠‫ــ‬١١
‫ﻧﯿﻮﺗﻦ‬.‫م‬٢
/‫ﻛﺠﻢ‬٢
.

103. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
103
٣-‫اﻟﺠﺎذﺑﯿﺔ‬ ‫ﻋﺠﻠﺔ‬ ‫ﺑﯿﻦ‬ ‫ﻓﺮق‬ ‫ھﻨﺎك‬)‫أﺧﺮ‬ ‫ﻣﻜﺎن‬ ‫اﻟﻰ‬ ‫ﻣﻜﺎن‬ ‫ﻣﻦ‬ ‫ﺗﺘﻐﯿﺮ‬ ‫و‬ ‫ﺑﺎﻻرض‬ ‫ﺧﺎﺻﺔ‬(
‫اﻟﺠﺬب‬ ‫وﺛﺎﺑﺖ‬)‫أو‬ ‫اﻟﺼﻐﯿﺮة‬ ‫ﻟﻼﺟﺴﺎم‬ ‫ﺑﺎﻟﻨﺴﺒﺔ‬ ‫ﻋﺎم‬ ‫ﻃﺒﯿﻌﻰ‬ ‫ﺛﺎﺑﺖ‬‫اﻟﺴﻤﺎوﯾﺔ‬ ‫اﻻﺟﺮام‬(
‫اﻟﺜﺎﺑﺘﺎن‬ ‫وﺣﺪﺗﻰ‬ ‫وﺗﺨﺘﻠﻒ‬.‫م‬ ‫اﻟﺠﺬﺑﯿﺔ‬ ‫ﻋﺠﻠﺔ‬/‫ث‬٢
‫ﻧﯿﻮﺗﻦ‬ ‫اﻟﺠﺬب‬ ‫ﺛﺎﺑﺖ‬ ‫أﻣﺎ‬.‫م‬٢
/‫ﻛﺠﻢ‬٢
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎ‬‫ل‬:‫ﻛﺘﻠﺘﺎھﻤﺎ‬ ‫ﻛﺮﺗﯿﻦ‬ ‫ﺑﯿﻦ‬ ‫اﻟﺠﺬب‬ ‫ﻗﻮة‬ ‫اﺣﺴﺐ‬١٠، ‫ﻛﺠﻢ‬٥‫ﻣﺮﻛﺰﯾﮭﻤﺎ‬ ‫ﺑﯿﻦ‬ ‫اﻟﻤﺴﺎﻓﺔ‬ ‫و‬ ‫ﻛﺠﻢ‬
٠٫٥‫ﻣﺘﺮ‬.‫اﻟﻌﺎم‬ ‫اﻟﺠﺬب‬ ‫ﺛﺎﺑﺖ‬ ‫ﺑﺄن‬ ً‫ﺎ‬‫ﻋﻠﻤ‬٦٫٦٧×١٠‫ــ‬١١
‫ﻧﯿﻮﺗﻦ‬.‫م‬٢
/‫ﻛﺠﻢ‬٢
.
‫اﻟﺤﻞ‬:
‫ك‬١=١٠‫ك‬ ، ‫ﻛﺠﻢ‬٢=٥‫ف‬ ، ‫ﻛﺠﻢ‬=٠٫٥‫ث‬ ، ‫م‬=٦٫٦٧×١٠‫ــ‬١١
‫ﻧﯿﻮﺗﻦ‬.‫م‬٢
/‫ﻛﺠﻢ‬٢
‫ﻗ‬‫اﻟﻌﺎم‬ ‫اﻟﺠﺬب‬ ‫ﺎﻧﻮن‬:
‫ق‬=‫ث‬×=٦٫٦٧×١٠‫ــ‬١١
×=١٫٣٣٤×١٠‫ــ‬٨
‫ﻧﯿﻮﺗﻦ‬
‫ﻣﻠﺤﻮﻇﺔ‬:‫اﺳﮭﻞ‬ ‫ھﺬا‬ ‫و‬ ‫اﻟﺤﺴﺎب‬ ‫ﻓﻰ‬ ‫اﻻﻟﺔ‬ ‫ﻧﺴﺘﺨﺪم‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﻛﺘﻠﺘﯿﮭﻤﺎ‬ ‫ﻛﺮﺗﯿﻦ‬٥٫٢، ‫ﻛﺠﻢ‬٠٫٢٥‫ﺑﯿﻦ‬ ‫اﻟﻤﺴﺎﻓﺔ‬ ‫ﻛﺎﻧﺖ‬ ‫ﺑﺤﯿﺚ‬ ‫اﻟﻜﺮﺗﺎن‬ ‫وﺿﻌﺖ‬ ‫ﻛﺠﻢ‬
‫ﻣﺮﻛﺰﯾﮭﻤﺎ‬٥٠‫ﺳﻢ‬.‫ﺑﯿﻨﮭﻤﺎ‬ ‫اﻟﺘﺠﺎذب‬ ‫ﻗﻮة‬ ‫اﺣﺴﺐ‬.‫ث‬ ‫ﺑﺄن‬ ‫ﻋﻠﻤﺎ‬=٦٫٦٧×١٠‫ــ‬١١
‫ن‬٠‫م‬٢
/‫ﻛﺠﻢ‬٢
‫اﻟﺤﻞ‬:
‫ف‬=٥٠‫ﺳﻢ‬=٠٫٥‫ك‬ ، ‫ﻣﺘﺮ‬١=٥٫٢‫ك‬ ، ‫ﻛﺠﻢ‬٢=٠٫٢٥‫ﻛﺠﻢ‬
‫اﻟﻌﺎم‬ ‫اﻟﺠﺬب‬ ‫ﻗﺎﻧﻮن‬:‫ق‬=‫ث‬×
=٦٫٦٧×١٠‫ــ‬١١
×
=٣٫٤٦٨٤×١٠‫ــ‬١٠
‫ﻧﯿﻮﺗﻦ‬)‫ﺟﺪا‬ ‫ﺻﻐﯿﺮة‬ ‫ﻗﻮة‬ ‫ھﻰ‬(
‫ـ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫اﻻرض‬ ‫ﻛﺘﻠﺔ‬ ‫أن‬ ‫ﻋﻠﻤﺖ‬ ‫إذا‬٦×١٠٢٤
‫اﻟﻘﻤﺮ‬ ‫ﻛﺘﻠﺔ‬ ‫و‬ ‫ﻛﺠﻢ‬٧×١٠٢٢
‫اﻟﻤﺴﺎﻓﺔ‬ ‫و‬ ‫ﻛﺠﻢ‬
‫ﺑﯿﻨﮭﻤﺎ‬٣×١٠٦
‫اﻟﻌﺎم‬ ‫اﻟﺠﺬب‬ ‫ﺛﺎﺑﺖ‬ ‫و‬ ‫ﻣﺘﺮ‬٦٫٦٧×١٠‫ــ‬١١
‫ﻧﯿﻮﺗﻦ‬.‫م‬٢
/‫ﻛﺠﻢ‬٢
‫ﻟﻠﻘﻤﺮ‬ ‫اﻻرض‬ ‫ﺟﺬب‬ ‫ﻗﻮة‬ ‫أوﺟﺪ‬.
‫اﻟﺤﻞ‬:
‫اﻟﻌﺎم‬ ‫اﻟﺠﺬب‬ ‫ﻗﺎﻧﻮن‬:‫ق‬=‫ث‬×
=٦٫٦٧×١٠‫ــ‬١١
×
=٣٫١١٢٦×١٠٢٤
‫ﻧﯿﻮﺗﻦ‬)‫ﻛﺒﯿﺮة‬ ‫ﻗﻮة‬ ‫ھﻰ‬(
‫ك‬١×‫ك‬٢
‫ف‬٢
١٠×٥
)٠٫٥(٢
‫ك‬١×‫ك‬٢
‫ف‬٢
٥٫٢×٠٫٢٥
)٠٫٥(٢
‫ك‬١×‫ك‬٢
‫ف‬٢
٦×١٠٢٤
×٧×١٠٢٢
)٣×١٠٦
(٢

104. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
104
‫ﻣﺜﺎل‬:‫ارﺗﻔﺎع‬ ‫ﻋﻠﻰ‬ ‫ﯾﺪور‬ ‫ﻛﺠﻢ‬ ‫ك‬ ‫ﻛﺘﻠﺘﮫ‬ ‫ﺻﻨﺎﻋﻰ‬ ‫ﻗﻤﺮ‬٤٤٠‫ﻛﺘﻠﺘﮭﺎ‬ ‫اﻟﺘﻰ‬ ‫اﻻرض‬ ‫ﺳﻄﺢ‬ ‫ﻣﻦ‬ ‫ﻛﻢ‬
٦×١٠٢٤
‫ﻗﻄﺮھﺎ‬ ‫ﻧﺼﻒ‬ ‫و‬ ‫ﻛﺠﻢ‬٦٣٦٠‫ﻛﻢ‬.‫ﻛﺠﻢ‬ ‫ﻷﻗﺮب‬ ‫ك‬ ‫ﻗﯿﻤﺔ‬ ‫أوﺟﺪ‬.‫ﺛﺎﺑﺖ‬ ‫ﺑﺄن‬ ً‫ﺎ‬‫ﻋﻠﻤ‬
‫ﯾﺴﺎوى‬ ‫اﻟﻌﺎم‬ ‫اﻟﺠﺬب‬٦٫٦٧×١٠‫ــ‬١١
‫ﻧﯿﻮﺗﻦ‬.‫م‬٢
/‫ﻛﺠﻢ‬٢
‫ﺟﺬب‬ ‫ﻗﻮة‬ ،‫ھﻰ‬ ‫ﻟﻠﻘﻤﺮ‬ ‫اﻻرض‬
١٧٣١٠‫ﻧﯿﻮﺗﻦ‬.
‫اﻟﺤﻞ‬:
‫ك‬١‫ﻟﻠﻘﻤﺮ‬=‫ك‬ ، ‫ﻛﺠﻢ‬ ‫ك‬٢‫ﻟﻼرض‬=٦×١٠٢٤
‫ﻛﺠﻢ‬
‫ف‬ ،) =٦٣٦٠+٤٤٠(×١٠٠٠‫ﻣﺘﺮ‬=٦٨٠٠×١٠٠٠‫م‬
‫اﻟﻌﺎم‬ ‫اﻟﺠﺬب‬ ‫ﻗﺎﻧﻮن‬:‫ق‬=‫ث‬×
١٧٣١٠=٦٫٦٧×١٠‫ــ‬١١
×
B‫ك‬)‫اﻟﻘﻤﺮ‬ ‫ﻛﺘﻠﺔ‬= (
=٢٠٠٠٫٣٥٩٨٢
٢٠٠٠‫ﻛﺠﻢ‬ T
: ‫ﻣﻠﺤﻮﻇﺔ‬
‫ﻓ‬ ‫س‬ ‫ﻗﺪرھﺎ‬ ‫ﻣﺴﺎﻓﺔ‬ ‫ﯾﺒﻌﺪ‬ ‫اﻟﺠﺴﻢ‬ ‫ﻛﺎن‬ ‫إذا‬‫ﻣﺮﻛﺰ‬ ‫ﻋﻦ‬ ‫ف‬ ‫ﻣﺴﺎﻓﺔ‬ ‫أو‬ ‫اﻻرض‬ ‫ﺳﻄﺢ‬ ‫ﻮق‬‫اﻻرض‬
‫ﻓ‬‫ﺈن‬:‫ف‬=‫س‬+‫اﻻرض‬ ‫ﻗﻄﺮ‬ ‫ﻧﺼﻒ‬ ‫ﻧﻖ‬ ‫ﺣﯿﺚ‬ ‫ﻧﻖ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
: ‫ء‬ ‫اﻻرﺿﯿﺔ‬ ‫اﻟﺠﺎذﺑﯿﺔ‬ ‫ﻋﺠﻠﺔ‬ ‫و‬ ‫اﻻرض‬ ‫ﻛﺘﻠﺔ‬ ‫ﺣﺴﺎب‬ *
‫ك‬ ‫ﻛﺘﻠﺘﮫ‬ ‫ﻟﺠﺴﻢ‬ ‫اﻻرض‬ ‫ﺟﺬب‬ ‫ﻗﻮة‬ : ‫أن‬ ‫ﺗﺬﻛﺮ‬
‫ھﻰ‬‫ق‬=‫ك‬×‫ء‬‫ﺣﯿﺚ‬‫ء‬‫ﺗﺴﺎوى‬ ‫و‬ ‫اﻻرﺿﯿﺔ‬ ‫اﻟﺠﺎذﺑﯿﺔ‬ ‫ﻋﺠﻠﺔ‬٩٫٨‫م‬/‫ث‬٢
‫اﻟﻘﻤﺮ‬ ‫ﺳﻄﺢ‬ ‫ﻋﻠﻰ‬ ‫ﺗﺨﺘﻠﻒ‬ ‫و‬ ‫ﻟﻼرض‬ ‫ﺑﺎﻟﻨﺴﺒﺔ‬ ‫ﺛﺎﺑﺘﺔ‬ ‫اﻟﺠﺎذﺑﯿﺔ‬ ‫ﻋﺠﻠﺔ‬ ‫ﻏﺎﻟﺒﺎ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﻛﺘﻠﺘﮫ‬ ‫ﺟﺴﯿﻤﺎ‬ ‫أن‬ ‫ﺑﻔﺮض‬ ‫ﻛﺠﻢ‬ ‫ﺑﻮﺣﺪة‬ ‫اﻻرض‬ ‫ﻛﺘﻠﺔ‬ ‫اﺣﺴﺐ‬١‫ﺳﻄﺤﮭﺎ‬ ‫ﻓﻮق‬ ‫وﺿﻊ‬ ‫ﻛﺠﻢ‬
‫اﻻرض‬ ‫ﻗﻄﺮ‬ ‫ﻧﺼﻒ‬ ‫ﻃﻮل‬ ‫ﺑﺄن‬ ً‫ﺎ‬‫ﻋﻠﻤ‬٦٣٦٠‫ث‬ ، ‫ﻛﻢ‬=٦٫٦٧×١٠‫ــ‬١١
‫ﻧﯿﻮﺗﻦ‬
‫اﻟﺤﻞ‬:
‫اﻟﺠﺴﻢ‬ ‫ﻛﺘﻠﺔ‬ ‫أن‬ ‫ﺑﻔﺮض‬‫ك‬١=١، ‫ﻛﺠﻢ‬‫ﻛﺘﻠﺔ‬‫ك‬ ‫اﻻرض‬٢=‫ك‬
‫ق‬ ‫ﻟﻠﺠﺴﻢ‬ ‫اﻻرض‬ ‫ﺟﺬب‬ ‫ﻗﻮة‬=‫ك‬١×‫ء‬=١×٩٫٨=٩٫٨‫ﻧﯿﻮﺗﻦ‬
A‫ق‬=‫ث‬×B٩٫٨=٦٫٦٧×١٠‫ــ‬١١
×
٦٣٦٠‫ﻛﻢ‬=‫ﻧﻖ‬
‫اﻟﻘﻤﺮ‬
‫اﻻرض‬
٤٤٠‫ﻛﻢ‬ ‫ك‬١×‫ك‬٢
‫ف‬٢
‫ك‬×٦×١٠٢٤
)٦٨٠٠×١٠٠٠(٢
١٧٣١٠×)٦٨٠٠×١٠٠٠(٢
٦٫٦٧×١٠‫ــ‬١١
×٦×١٠٢٤
‫ك‬١×‫ك‬٢
‫ف‬٢
١×‫ﻟﻼرض‬ ‫ك‬
)٦٣٦٠×١٠٠٠(٢

105. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
105
‫ك‬= =٦×١٠٢٤
‫ﻛ‬‫ﺠﻢ‬ B
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫اﻟﺴﺎﺑﻖ‬ ‫اﻟﻤﺜﺎل‬ ‫ﻧﻔﺲ‬ ‫ﻓﻰ‬‫اﻟﺠﺴﻢ‬ ‫ﻛﺘﻠﺔ‬ ‫ﻛﺎﻧﺖ‬ ‫إذا‬١٠٠٠‫ﻓﺈن‬ ‫ﻛﺠﻢ‬:
‫ﻟﻠﺠﺴﻢ‬ ‫اﻻرض‬ ‫ﺟﺬب‬ ‫ﻗﻮة‬=٩٨٠٠‫اﻻرض‬ ‫ﻛﺘﻠﺔ‬ ‫و‬ ‫ﻧﯿﻮﺗﻦ‬=٦×١٠١٧
‫ﻛﺠﻢ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫م‬ ‫ﺑﻮﺣﺪة‬ ‫اﻻرﺿﯿﺔ‬ ‫اﻟﺠﺎذﺑﯿﺔ‬ ‫ﻋﺠﻠﺔ‬ ‫اﺣﺴﺐ‬/‫ث‬٢
‫ﻛﺘﻠﮫ‬ ‫ﻟﺠﺴﻢ‬١‫ﻛﺠﻢ‬‫ﺳﻄﺤﮭﺎ‬ ‫ﻓﻮق‬ ‫وﺿﻊ‬
‫ﺗﺴﺎوى‬ ‫اﻻرض‬ ‫ﻛﺘﻠﺔ‬ ‫ﺑﺄن‬ ً‫ﺎ‬‫ﻋﻠﻤ‬٦×١٠٢٤
‫اﻻرض‬ ‫ﻗﻄﺮ‬ ‫ﻧﺼﻒ‬ ، ‫ﻛﺠﻢ‬٦٣٦٠‫ﻛﻢ‬.
‫اﻟﺤﻞ‬:
‫ق‬ ‫ﻟﻠﺠﺴﻢ‬ ‫اﻻرض‬ ‫ﺟﺬب‬ ‫ﻗﻮة‬=‫ك‬×‫ء‬=١×‫ء‬=‫ء‬ A
‫ء‬=٦٫٦٧×١٠‫ــ‬١١
× B ‫ق‬=‫ث‬× A
٩٫٨٩٣٧٩‫م‬/‫ث‬٢
T ‫ء‬ B
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﻗﺪر‬ ‫اﻻرض‬ ‫ﻛﺘﻠﺔ‬ ‫ﻛﺎﻧﺖ‬ ‫إذا‬‫اﻟﻘﻤﺮ‬ ‫ﻛﺘﻠﺔ‬٨١‫ﻗﻄﺮﯾﮭﻤﺎ‬ ‫و‬ ‫ﻣﺮة‬٦٣٧٨، ‫ﻛﻢ‬١٧٣٨‫ﻋﻠﻰ‬ ‫ﻛﻢ‬
‫اﻟﺘﺮﺗﯿﺐ‬.‫ﻟﻼرض‬ ‫اﻟﺠﺎذﺑﯿﺔ‬ ‫ﻋﺠﻠﺔ‬ ‫ﻛﺎﻧﺖ‬ ‫ﻓﺈذا‬٩٫٨‫م‬/‫ث‬٢
‫ﻋﻠﻰ‬ ‫اﻟﺠﺎذﺑﯿﺔ‬ ‫ﺗﺴﺎرع‬ ‫ﯾﻜﻮن‬ ‫ﻓﻜﻢ‬
‫اﻟﻘﻤﺮ‬ ‫ﺳﻄﺢ‬.
‫اﻟﺤﻞ‬:
‫اﻟﻘﻤﺮ‬ ‫ﻛﺘﻠﺔ‬ ‫أن‬ ‫ﺑﻔﺮض‬=‫اﻻرض‬ ‫ﻛﺘﻠﺔ‬ ‫ﻓﺈن‬ ‫ﻛﺠﻢ‬ ‫ك‬=٨١‫ﻛﺠﻢ‬ ‫ك‬
‫ﻧﻖ‬١=٦٣٧٨، ‫ﻛﻢ‬‫ﻧﻖ‬٢=١٧٣٨، ‫ﻛﻢ‬‫ء‬١=٩٫٨‫م‬/‫ث‬٢
،‫ء‬٢=‫؟‬
=×)(٢
B =×
١٫٦٣‫م‬/‫ث‬٢
T ‫ء‬٢‫ﻟ‬‫ﻠ‬‫ﻘﻤﺮ‬=
٩٫٨×)٦٣٦٠×١٠٠٠(٢
٦٫٦٧×١٠‫ــ‬١١
‫ك‬١×‫ك‬٢
‫ف‬٢
١×٦×١٠٢٤
)٦٣٦٠×١٠٠٠(٢
: ‫ﻛﻮﻛﺒﯿﻦ‬ ‫ﺳﻄﺤﻰ‬ ‫ﻋﻠﻰ‬ ‫اﻟﺠﺎذﺑﯿﺔ‬ ‫ﻋﺠﻠﺘﻰ‬ ‫ﺑﯿﻦ‬ ‫اﻟﻤﻘﺎرﻧﺔ‬
=×
‫ﺣﯿﺚ‬‫ء‬١،‫ء‬٢‫اﻟﻜﻮﻛﺒﯿﻦ‬ ‫ﻣﻦ‬ ‫ﻟﻜﻞ‬ ‫اﻟﺠﺎذﺑﯿﺔ‬ ‫ﻋﺠﻠﺘﻰ‬
،‫ك‬١،‫ك‬٢‫ﺑﺎﻟﻜﺠﻢ‬ ‫ﻛﺘﻠﺘﯿﮭﻤﺎ‬
‫ﻧﻖ‬١،‫ﻧﻖ‬٢‫اﻟﺘﺮﺗﯿﺐ‬ ‫ﻋﻠﻰ‬ ‫ﺑﺎﻟﻤﺘﺮ‬ ‫ﻗﻄﺮﯾﮭﻤﺎ‬ ‫ﻧﺼﻔﻰ‬
،
‫ء‬١
‫ء‬٢
‫ك‬١
‫ك‬٢
‫ﻧﻖ‬٢
٢
‫ﻧﻖ‬٢
١
‫ء‬١
‫ء‬٢
‫ك‬١
‫ك‬٢
‫ﻧﻖ‬٢
٢
‫ﻧﻖ‬٢
١
٨٠‫ك‬
‫ك‬
٩٫٨
‫ء‬٢
١٧٣٨
٦٣٧٨
٥٫٩٤٠٤٦
٩٫٨

106. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
106
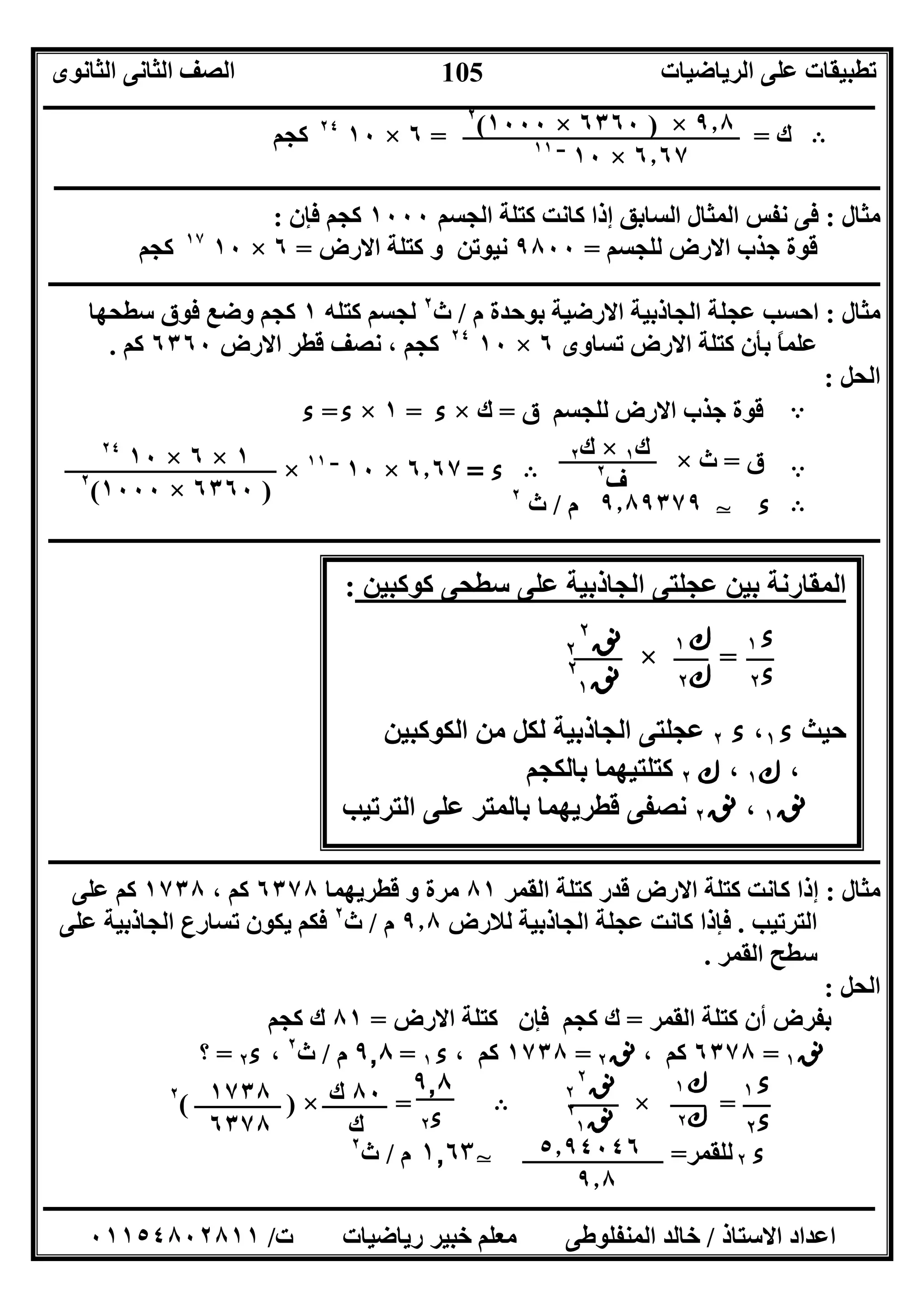
‫ﻣﺜﺎل‬:‫اﻻرض‬ ‫ﻛﺘﻠﺔ‬ ‫أن‬ ‫ﻋﻠﻤﺖ‬ ‫إذا‬٥٫٩٧×١٠٢٤
‫ﻗﻄﺮھﺎ‬ ‫ﻧﺼﻒ‬ ‫و‬ ‫ﻛﺠﻢ‬٦٫٣٤×١٠٦
‫ﻣﺘﺮ‬
‫ﻛﺘﻠ‬ ‫و‬‫اﻟﻘﻤﺮ‬ ‫ﺔ‬٧٫٣٦×١٠٢٢
‫ﻗﻄﺮه‬ ‫ﻧﺼﻒ‬ ‫و‬ ‫ﻛﺠﻢ‬١٫٧٤×١٠٦
‫ﻣﺘﺮ‬
‫اﻻرض‬ ‫ﺳﻄﺢ‬ ‫اﻟﻰ‬ ‫اﻟﻘﻤﺮ‬ ‫ﺳﻄﺢ‬ ‫ﻋﻠﻰ‬ ‫اﻟﺠﺎذﺑﯿﺔ‬ ‫ﺑﯿﻦ‬ ‫اﻟﻨﺴﺒﺔ‬ ‫ﻓﺄوﺟﺪ‬.
‫اﻟﺤﻞ‬:
=×=×( )٢
=×١٣٫٢٧٦٣٩=٠٫١٦ً‫ﺎ‬‫ﺗﻘﺮﯾﺒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﺗﻨﺒﯿﺔ‬:‫اﻟﻌﺎم‬ ‫اﻟﺠﺬب‬ ‫ﺛﺎﺑﺖ‬ ‫اﻋﺘﺒﺮ‬‫ﻟﻨﯿﻮﺗﻦ‬:‫ث‬=٦٫٦٧×١٠‫ــ‬١١
‫ﻧﯿﻮﺗﻦ‬.‫م‬٢
/‫ﻛﺠﻢ‬٢
]١[‫اﻟﺼﺤﯿﺤﺔ‬ ‫اﻻﺟﺎﺑﺔ‬ ‫اﺧﺘﺮ‬:
]٢[
]٣[
]٤[
‫ء‬١
‫ء‬٢
‫ك‬١
‫ك‬٢
‫ﻧﻖ‬٢
٢
‫ﻧﻖ‬٢
١
٧٫٣٦×١٠٢٢
٥٫٩٧×١٠٢٤
٦٫٣٤×١٠٦
١٫٧٤×١٠٦
١٨٤
١٤٩٢٥
‫اﻟﻌﺎم‬ ‫اﻟﺠﺬب‬ ‫ﻋﻠﻰ‬ ‫ﺗﻤﺎرﯾﻦ‬

107. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
107
]٥[
]٦[
]٧[
]٨[
]٩[
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
]١٠[
]١١[
]١٢[

108. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
108
: ‫أن‬ ‫ﺗﺬﻛﺮ‬
. ‫ﻣﻨﺤﻨﻰ‬ ‫و‬ ‫ﻣﺴﺘﻘﯿﻢ‬ ‫أو‬ ‫ﻣﻨﺤﻨﯿﻦ‬ ‫أو‬ ‫ﻣﺴﺘﻘﯿﻤﯿﻦ‬ ‫ﺧﻄﯿﻦ‬ ‫ﺗﻘﺎﻃﻊ‬ ‫ﻣﻦ‬ ‫ﻧﺎﺗﺞ‬ ‫ﻣﻜﺎن‬ ‫ھﻰ‬ ‫اﻟﻨﻘﻄﺔ‬ (١
‫اﻟﻤﻨﺘﮭﯿﺔ‬ ‫ﻏﯿﺮ‬ ‫اﻟﻨﻘﻂ‬ ‫ﻣﻦ‬ ‫ﻣﺠﻤﻮﻋﺔ‬ : ‫اﻟﻤﺴﺘﻘﯿﻢ‬ ‫اﻟﺨﻂ‬ (٢
‫ﻣ‬ ‫ﻣﻤﺘﺪ‬‫ﻋﻠﯿﮫ‬ ‫ﺑﻨﻘﻄﺘﯿﻦ‬ ‫ﯾﺘﻌﯿﻦ‬ ‫ﺟﮭﺘﯿﺔ‬ ‫ﻦ‬.
‫ﯾﻘﺮأ‬ ‫و‬‫ب‬ ‫ا‬‫اﻟﻤﺴﺘﻘﯿﻢ‬‫ب‬‫ا‬
‫ﯾﻨﻄﺒﻖ‬ ‫اﻟﻤﻨﺘﮭﯿﺔ‬ ‫ﻏﯿﺮ‬ ‫اﻟﻨﻘﻂ‬ ‫ﻣﻦ‬ ‫ﻣﺠﻤﻮﻋﺔ‬ : ‫اﻟﻤﺴﺘﻮى‬ (٣
‫ﺟﮭﺎﺗﮫ‬ ‫ﺟﻤﯿﻊ‬ ‫ﻣﻦ‬ ‫ﻣﻤﺘﺪ‬ ‫و‬ ‫ﺣﺎﻻﺗﮫ‬ ‫ﺟﻤﯿﻊ‬ ‫ﻓﻰ‬ ‫اﻟﻤﺴﺘﻘﯿﻢ‬ ‫ﻋﻠﯿﺔ‬
‫و‬ ‫اﺳﺘﻘﺎﻣﺔ‬ ‫ﻋﻠﻰ‬ ‫ﻟﯿﺴﺖ‬ ‫ﻧﻘﻂ‬ ‫ﺑﺜﻼث‬ ‫ﯾﺘﻌﯿﻦ‬ ‫و‬ ‫ﻧﮭﺎﯾﺔ‬ ‫ﺑﻼ‬‫اﺣﺪة‬.
‫أو‬ ‫اﻻﻗﻞ‬ ‫ﻋﻠﻰ‬ ‫ﻋﻠﯿﮫ‬ ‫ﻧﻘﺎط‬ ‫ﺑﺜﻼث‬ ‫ﯾﻘﺮأ‬ ‫و‬‫اﻟﺤﺮوف‬ ‫ﺑﺄﺣﺪ‬ ‫ﻟﮫ‬ ‫ﻧﺮﻣﺰ‬
‫اﻟﻜﺒﯿﺮة‬‫ﺳﺲ‬،‫ﺻﺺ‬،.....
‫اﻟﺘﻰ‬ ‫اﻟﺸﺎﻣﻠﺔ‬ ‫اﻟﻤﺠﻤﻮﻋﺔ‬ ‫ﯾﻌﺘﺒﺮ‬ ‫و‬ ‫اﻟﻤﻨﺘﮭﯿﺔ‬ ‫ﻏﯿﺮ‬ ‫اﻟﻨﻘﻂ‬ ‫ﻣﻦ‬ ‫ﻣﺠﻤﻮﻋﺔ‬ : ( ‫اﻟﻔﻀﺎء‬ ) ‫اﻟﻔﺮاغ‬ (٤
‫اﻟﻤﺠﺴﻤﺎت‬ ‫و‬ ‫اﻟﻤﺴﺘﻮﯾﺎت‬ ‫و‬ ‫اﻟﻤﺴﺘﻘﯿﻤﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﺤﺘﻮى‬.
‫ــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
: ‫ﻣﺴﻠﻤﺎت‬ ‫و‬ ‫ﻣﻔﺎھﯿﻢ‬ *
)١(‫وﺣﯿﺪ‬ ‫ﻣﺴﺘﻘﯿﻢ‬ ‫ﺑﮭﻤﺎ‬ ‫ﯾﻤﺮ‬ ‫ﻣﺨﺘﻠﻔﺘﯿﻦ‬ ‫ﻧﻘﻄﺘﯿﻦ‬ ‫أى‬.
)٢(‫ﯾﻤ‬ ‫واﺣﺪة‬ ‫اﺳﺘﻘﺎﻣﺔ‬ ‫ﻋﻠﻰ‬ ‫ﻟﯿﺴﺖ‬ ‫ﻧﻘﻂ‬ ‫ﺛﻼث‬ ‫ﻛﻞ‬‫وﺣﯿﺪ‬ ‫ﻣﺴﺘﻮى‬ ‫ﺑﮭﺎ‬ ‫ﺮ‬.
)٣(‫اﻟﻤﺴﺘﻮى‬ ‫ﻓﻰ‬ ‫ﺑﺄﻛﻤﻠﮫ‬ ‫ﯾﻘﻊ‬ ‫اﻟﻤﺴﺘﻘﯿﻢ‬ ‫ﻓﺈن‬ ‫ﻧﻘﻄﺔ‬ ‫ﻣﻦ‬ ‫أﻛﺜﺮ‬ ‫ﻓﻰ‬ ‫ﻣﺴﺘﻮى‬ ‫و‬ ‫ﻣﺴﺘﻘﯿﻢ‬ ‫اﺷﺘﺮك‬ ‫إذا‬.
‫اﻟﺜﺎﻟﺜﺔ‬ ‫اﻟﻮﺣﺪة‬:‫اﻟﻘﯿﺎس‬ ‫و‬ ‫اﻟﮭﻨﺪﺳﺔ‬
‫اﻟﻔﺮاغ‬ ‫ﻓﻰ‬ ‫اﻟﻤﺴﺘﻮﯾﺎت‬ ‫و‬ ‫اﻟﻤﺴﺘﻘﯿﻤﺎت‬
‫ا‬
‫ب‬
‫ج‬
‫ﺳﺲ‬

109. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
109
: ‫ﻣﻼﺣﻈﺎت‬
١-‫ﯾﻤﺮ‬ ‫اﻟﻤﺴﺘﻮى‬ ‫ﻓﻰ‬ ‫ﻧﻘﻄﺔ‬ ‫أى‬‫اﻟﻤﺴﺘﻘﯿﻤﺎت‬ ‫ﻣﻦ‬ ‫ﻧﮭﺎﺋﻰ‬ ‫ﻻ‬ ‫ﻋﺪد‬ ‫ﺑﮭﺎ‬.
٢-‫اﻟﻤﺴﺘﻮﯾﺎت‬ ‫ﻣﻦ‬ ‫ﻧﮭﺎﺋﻰ‬ ‫ﻻ‬ ‫ﻋﺪد‬ ‫ﺑﮭﺎ‬ ‫ﯾﻤﺮ‬ ‫اﻟﻔﺮاغ‬ ‫ﻓﻰ‬ ‫ﻧﻘﻄﺔ‬ ‫أى‬.
٣-‫ﻣﺴﺘﻘ‬ ‫أى‬‫اﻟﻤﺴﺘﻮﯾﺎت‬ ‫ﻣﻦ‬ ‫ﻧﮭﺎﺋﻰ‬ ‫ﻻ‬ ‫ﻋﺪد‬ ‫ﺑﮭﺎ‬ ‫ﯾﻤﺮ‬ ‫اﻟﻔﺮاغ‬ ‫ﻓﻰ‬ ‫ﯿﻢ‬.
٤-‫ﻓﻘﻂ‬ ‫واﺣﺪ‬ ‫و‬ ‫واﺣﺪ‬ ‫ﻣﺴﺘﻮ‬ ‫ﺑﮭﺎ‬ ‫ﯾﻤﺮ‬ ‫واﺣﺪة‬ ‫اﺳﺘﻘﺎﻣﺔ‬ ‫ﻋﻠﻰ‬ ‫ﻟﯿﺴﺖ‬ ‫ﻧﻘﻂ‬ ‫ﺛﻼث‬ ‫ﻛﻞ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــ‬
‫ﻣﺜﺎل‬:‫أﺟﺐ‬ ‫ﺛﻢ‬ ‫أﻣﺎﻣﻚ‬ ‫اﻟﺬى‬ ‫اﻟﺸﻜﻞ‬ ‫ﺗﺄﻣﻞ‬
١-‫؟‬ ‫ﺑﺎﻟﺸﻜﻞ‬ ‫اﻟﻤﺴﺘﻘﯿﻤﺎت‬ ‫ﻋﺪد‬ ‫ﻛﻢ‬
٢-‫ﺑﻨﻘﻄﺔ‬ ‫ﺗﻤﺮ‬ ‫اﻟﺘﻰ‬ ‫اﻟﻤﺴﺘﻘﯿﻤﺎت‬ ‫اذﻛﺮ‬‫م‬‫ب‬ ‫ﻧﻘﻄﺔ‬ ،
٣-‫؟‬ ‫ﺑﺎﻟﺸﻜﻞ‬ ‫اﻟﻤﺴﺘﻮﯾﺎت‬ ‫ﻋﺪد‬ ‫ﻛﻢ‬
٤-‫ﺑﺎﻟﻨﻘﻄﺔ‬ ‫ﺗﻤﺮ‬ ‫ﻣﺴﺘﻮﯾﺎت‬ ‫ﺛﻼﺛﺔ‬ ‫اذﻛﺮ‬‫ا‬
٥-‫ﺑﻨﻘﻄﺔ‬ ‫ﺗﻤﺮ‬ ‫اﻟﺘﻰ‬ ‫اﻟﻤﺴﺘﻘﯿﻤﺎت‬ ‫اذﻛﺮ‬‫ا‬‫ﻣﻌﺎ‬ ‫ب‬ ،
٦-‫اﻟﻤﺴﺘﻮﯾﺎ‬ ‫اذﻛﺮ‬‫ﺑﺎﻟﻨﻘﻄﺔ‬ ‫ﺗﻤﺮ‬ ‫اﻟﺘﻰ‬ ‫ت‬‫ا‬‫ﻣﻌﺎ‬ ‫ب‬ ،

110. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
110
‫اﻟﺤﻞ‬:١-‫ﺑﺎﻟﺸﻜﻞ‬ ‫اﻟﻤﺴﺘﻘﯿﻤﺎت‬ ‫ﻋﺪد‬=٩
٢-‫ﺑﻨﻘﻄﺔ‬ ‫ﺗﻤﺮ‬ ‫اﻟﺘﻰ‬ ‫اﻟﻤﺴﺘﻘﯿﻤﺎت‬‫م‬‫ھﻰ‬‫ا‬‫م‬،‫ب‬‫م‬،‫ج‬‫م‬،‫ء‬‫م‬
‫ﺑﻨﻘﻄﺔ‬ ‫ﺗﻤﺮ‬ ‫اﻟﺘﻰ‬ ‫اﻟﻤﺴﺘﻘﯿﻤﺎت‬‫ب‬‫ھﻰ‬‫ب‬‫م‬،‫ب‬‫ا‬،‫ج‬‫ب‬
٣-‫ﺑﺎﻟﺸﻜﻞ‬ ‫اﻟﻤﺴﺘﻮﯾﺎت‬ ‫ﻋﺪد‬=٥
٤-‫ﺑﺎﻟﻨﻘﻄﺔ‬ ‫ﺗﻤﺮ‬ ‫ﻣﺴﺘﻮﯾﺎت‬ ‫ﺛﻼﺛﺔ‬‫ا‬‫ھﻰ‬‫ء‬‫ا‬‫م‬،‫ا‬‫م‬‫ب‬،‫ا‬‫ب‬‫ج‬‫ء‬
٥-‫ﺑﻨﻘﻄﺔ‬ ‫ﺗﻤﺮ‬ ‫اﻟﺘﻰ‬ ‫اﻟﻤﺴﺘﻘﯿﻤﺎت‬‫ا‬‫ھﻰ‬ ‫ﻣﻌﺎ‬ ‫ب‬ ،‫ا‬‫ب‬
٦-‫ﺑﺎﻟﻨﻘﻄﺔ‬ ‫ﺗﻤﺮ‬ ‫اﻟﻤﺴﺘﻮﯾﺎت‬‫ا‬‫ھﻰ‬ ‫ﻣﻌﺎ‬ ‫ب‬ ،‫ا‬‫م‬‫ب‬،‫ا‬‫ب‬‫ج‬‫ء‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
: ‫اﻟﻔﺮاغ‬ ‫ﻓﻰ‬ ‫ﻣﺴﺘﻘﯿﻤﯿﻦ‬ ‫ﺑﯿﻦ‬ ‫اﻟﻌﻼﻗﺔ‬ *
‫اﻟﺸﻜﻞ‬)٣( ‫اﻟﺸﻜﻞ‬)٢( ‫اﻟﺸﻜﻞ‬)١(
‫ﻟﻸو‬ ‫ﻣﺨﺘﻠﻔﺔ‬ ‫ﺣﺎﻻت‬ ‫ﺛﻼث‬ ‫ﺗﻮﺟﺪ‬‫ل‬ ‫ﻟﻤﺴﺘﻘﯿﻤﯿﻦ‬ ‫اﻟﻨﺴﺒﯿﺔ‬ ‫ﺿﺎع‬١‫ل‬ ،٢‫ھﻰ‬ ‫اﻟﻔﺮاغ‬ ‫ﻓﻰ‬:
. ‫واﺣﺪ‬ ‫ﻣﺴﺘﻮى‬ ‫ﯾﺤﺘﻮﯾﮭﻤﺎ‬ ‫أن‬ ‫ﯾﻤﻜﻦ‬ ‫اﻟﺤﺎﻟﺔ‬ ‫ھﺬه‬ ‫ﻓﻰ‬ ‫و‬ : ‫ﻣﺘﻘﺎﻃﻌﺎن‬ ‫اﻟﻤﺴﺘﻘﯿﻤﺎن‬ (١)
‫ل‬ ،١‫ل‬ ،٢‫واﺣﺪ‬ ‫ﻣﺴﺘﻮى‬ ‫ﻓﻰ‬ ‫ﯾﻘﻌﺎن‬ ‫اﻟﺸﻜﻞ‬ ‫ﻓﻰ‬)١: (‫ل‬١‫ﺑﻼ‬‫ل‬٢=}‫ا‬{
. ‫واﺣﺪ‬ ‫ﻣﺴﺘﻮى‬ ‫ﯾﺤﺘﻮﯾﮭﻤﺎ‬ ‫أن‬ ‫ﯾﻤﻜﻦ‬ ‫اﻟﺤﺎﻟﺔ‬ ‫ھﺬه‬ ‫ﻓﻰ‬ ‫و‬ : ‫ﻣﺘﻮازﯾﺎن‬ ‫اﻟﻤﺴﺘﻘﯿﻤﺎن‬ (٢)
‫اﻟﺸﻜﻞ‬ ‫ﻓﻰ‬)٢: (‫ل‬١‫ﺑﻼ‬‫ل‬٢=T‫ل‬ ،١‫ل‬ ،٢‫واﺣﺪ‬ ‫ﻣﺴﺘﻮى‬ ‫ﻓﻰ‬ ‫ﯾﻘﻌﺎن‬
. ‫واﺣﺪ‬ ‫ﻣﺴﺘﻮى‬ ‫ﯾﺤﺘﻮﯾﮭﻤﺎ‬ ‫أن‬ ‫ﯾﻤﻜﻦ‬ ‫ﻻ‬ ‫اﻟﺤﺎﻟﺔ‬ ‫ھﺬه‬ ‫وﻓﻰ‬ : ‫ﻣﺘﺨﺎﻟﻔﺎن‬ ‫اﻟﻤﺴﺘﻘﯿﻤﺎن‬ (٣)
‫اﻟﺸﻜﻞ‬ ‫ﻓﻰ‬)٣: (‫ل‬١‫ﺑﻼ‬‫ل‬٢=T،‫ل‬١‫ﻣﻦ‬ ‫ﺟﺰء‬‫ﺳﺲ‬‫ﻣﺴﺘﻮﯾﯿﻦ‬ ‫ﻏﯿﺮ‬ ‫أو‬ ‫ﻣﺘﺨﺎﻟﻔﺎن‬ ‫أﻧﮭﻤﺎ‬ ‫وﯾﻘﺎل‬
: ‫ﻣﻼﺣﻈﺔ‬
١-‫ل‬ ‫ﻛﺎن‬ ‫إذا‬١‫ﺑﻼ‬‫ل‬٢=T‫ﻓﺈن‬ ‫واﺣﺪ‬ ‫ﻣﺴﺘﻮى‬ ‫ﯾﺤﺘﻮﯾﮭﻤﺎ‬ ‫أن‬ ‫ﯾﻤﻜﻦ‬ ‫و‬:‫ل‬١//‫ل‬٢
٢-‫ل‬ ‫ﻛﺎن‬ ‫إذا‬١‫ﺑﻼ‬‫ل‬٢=T‫ﻓﺈن‬ ‫واﺣﺪ‬ ‫ﻣﺴﺘﻮى‬ ‫ﯾﺤﺘﻮﯾﮭﻤﺎ‬ ‫أن‬ ‫ﯾﻤﻜﻦ‬ ‫وﻻ‬:‫ل‬١‫ل‬ ،٢‫ﻣﺘﺨﺎﻟﻔﺎن‬
٣-‫ﻣﺘﻮازﯾﺎن‬ ‫اﻟﻔﺮاغ‬ ‫ﻓﻰ‬ ‫ﻟﺜﺎﻟﺚ‬ ‫اﻟﻤﻮزﯾﺎن‬ ‫اﻟﻤﺴﺘﻘﯿﻤﺎن‬
٤-‫ﻣﻌﺎ‬ ‫ﻣﺴﺘﻮﯾﯿﻦ‬ ‫ﯾﻜﻮﻧﺎ‬ ‫أن‬ ‫إﻣﺎ‬ ‫اﻟﻔﺮاغ‬ ‫ﻓﻰ‬ ‫ﻣﺴﺘﻘﯿﻤﺎن‬ ‫أى‬‫واﺣ‬ ‫ﻣﺴﺘﻮى‬ ‫ﻓﻰ‬‫ﺪ‬)‫أو‬ ‫ﻣﺘﻮزاﯾﺎن‬
‫ﻣﺘﻘﺎﻃﻌﯿﻦ‬(‫واﺣﺪ‬ ‫ﻣﺴﺘﻮى‬ ‫ﻓﻰ‬ ‫ﯾﻘﻌﺎن‬ ‫ﻻ‬ ‫ﻣﻌﺎ‬ ‫ﻏﯿﺮﻣﺴﺘﻮﯾﯿﻦ‬ ‫أو‬)‫ﻣﺘﺨﺎﻟﻔﯿﻦ‬(

111. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
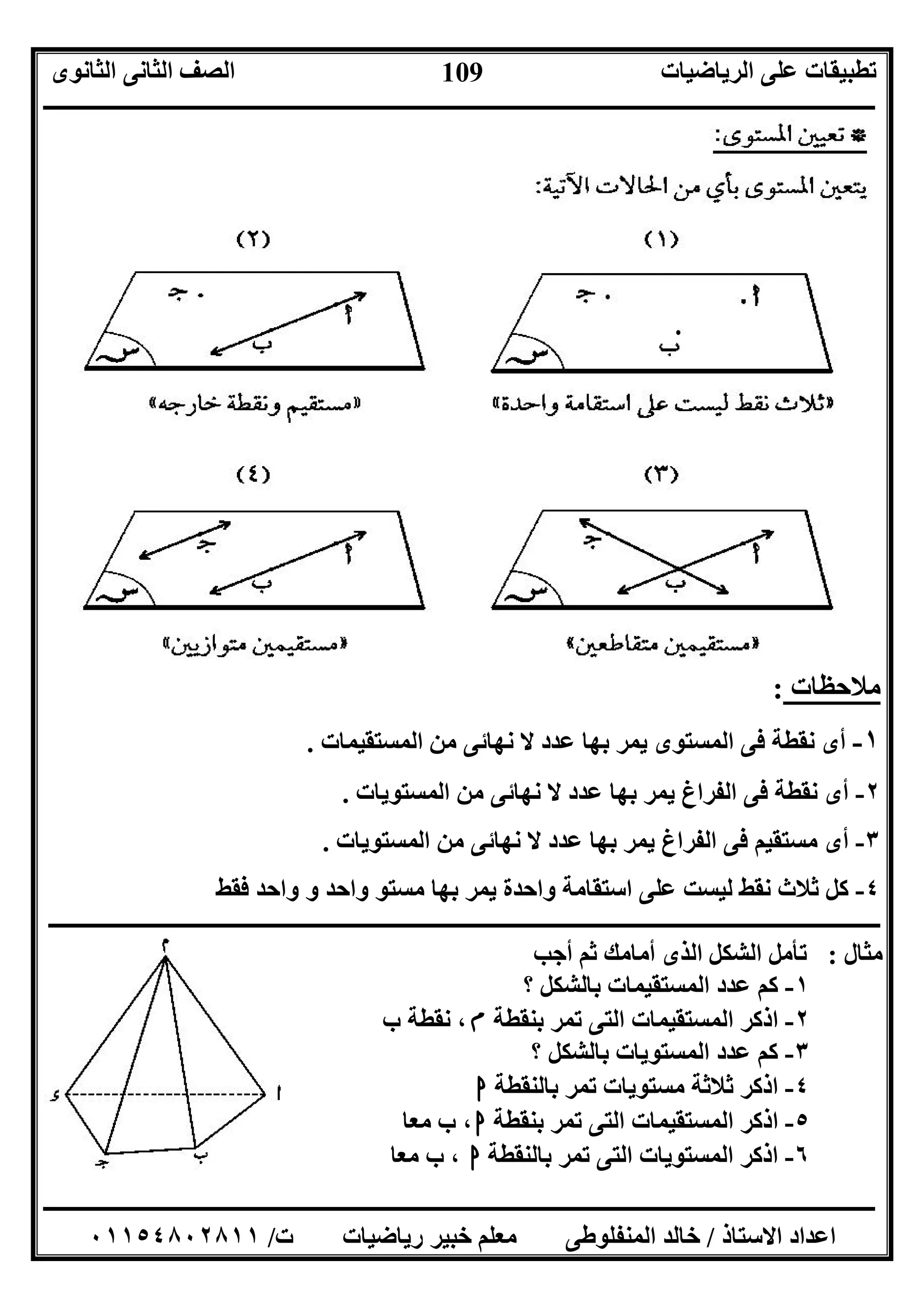
111
: ‫اﻟﻔﺮاغ‬ ‫ﻓﻰ‬ ‫ﻣﺴﺘﻮى‬ ‫و‬ ‫ﻣﺴﺘﻘﯿﻢ‬ ‫ﺑﯿﻦ‬ ‫اﻟﻌﻼﻗﺔ‬ *
‫ھﻰ‬ ‫أوﺿﺎع‬ ‫ﺛﻼث‬ ‫اﻟﻔﺮاغ‬ ‫ﻓﻰ‬ ‫اﻟﻤﺴﺘﻮى‬ ‫و‬ ‫ﻟﻠﻤﺴﺘﻘﯿﻢ‬:
]‫اﻟﻤﺴﺘﻮى‬ ‫ﻓﻰ‬ ‫ﻣﺤﺘﻮى‬ ‫اﻟﻤﺴﺘﻘﯿﻢ‬] [‫ﻟﻠﻤﺴﺘﻮى‬ ‫ﻗﺎﻃﻊ‬ ‫اﻟﻤﺴﺘﻘﯿﻢ‬] [‫ﻟﻠﻤﺴﺘﻮى‬ ‫ﻣﻮاز‬ ‫اﻟﻤﺴﺘﻘﯿﻢ‬[
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
: ‫اﻟﻔﺮاغ‬ ‫ﻓﻰ‬ ‫ﻟﻤﺴﺘﻮﯾﯿﻦ‬ ‫اﻟﻨﺴﺒﯿﺔ‬ ‫اﻻوﺿﺎع‬ *
‫ﯾﻮﺟﺪ‬‫ﺛﻼﺛﺔ‬ ‫ﻣﺨﺘﻠﻔﯿﻦ‬ ‫ﻟﻤﺴﺘﻮﯾﯿﻦ‬‫أوﺿﺎع‬‫ﻓﻰ‬‫ھﻰ‬ ‫اﻟﻔﺮاغ‬:

112. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
112
‫ﻣﺜﺎل‬:
}‫ء‬{
}‫ء‬{
}‫ء‬{
‫ء‬‫ب‬
‫ء‬ ‫ج‬
‫ء‬ ‫ا‬
}‫ء‬{
)‫ب‬‫ا‬،‫ج‬‫ء‬(،)‫ج‬‫ا‬،‫ء‬‫ب‬(،)‫ء‬‫ا‬،‫ج‬‫ب‬(
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﯾﺄﺗﻰ‬ ‫ﻣﺎ‬ ‫أﻛﻤـﻞ‬ ‫ﺛﻢ‬ ‫اﻟﻤﻘﺎﺑﻞ‬ ‫اﻟﺸﻜﻞ‬ ‫ﺗﺄﻣﻞ‬:
)‫أ‬(‫اﻟﻤﺴﺘﻮى‬‫ب‬ ‫ب‬ ‫ا‬/
‫ا‬/
‫ﺑﻼ‬‫اﻟﻤﺴﺘﻮى‬‫ج‬ ‫ج‬‫ب‬/
‫ب‬/
=‫ب‬ ‫ب‬/
)‫ب‬(‫اﻟﻤﺴﺘﻮى‬‫ج‬‫ب‬‫ا‬‫ﺑﻼ‬‫اﻟﻤﺴﺘﻮى‬‫ا‬/
‫ب‬/
‫ج‬/
=T
)‫ﺟـ‬(‫ج‬ ‫ا‬‫ﺑﻼ‬‫ا‬/
‫ج‬/
=T
)‫د‬(‫ب‬ ‫ب‬/
‫ﺑﻼ‬‫اﻟﻤﺴﺘﻮى‬‫ج‬ ‫ب‬ ‫ا‬=}‫ب‬{
)‫ھـ‬(‫ب‬ ‫ب‬/
‫ﺑﻼ‬‫ا‬‫ج‬=T
)‫ط‬(‫اﻟﻤﺴﺘﻮى‬‫ا‬/
‫ب‬ ‫ب‬‫ا‬/
‫ﺑﻼ‬‫اﻟﻤﺴﺘﻮى‬‫ج‬‫ب‬‫ا‬=‫ب‬ ‫ا‬
)‫و‬(‫اﻟﻤﺴﺘﻮى‬‫ج‬‫ب‬‫ا‬‫ﺑﻼ‬‫اﻟﻤﺴﺘﻮى‬‫ج‬ ‫ج‬‫ا‬/
‫ا‬/
‫ﺑﻼ‬‫اﻟﻤﺴﺘﻮى‬‫ب‬‫ب‬‫ا‬/
‫ا‬/
=}‫ا‬{
‫ج‬/
‫ا‬
‫ب‬
‫ا‬/
‫ج‬
‫ب‬/

113. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
113
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
]١[‫ﯾﺄﺗﻰ‬ ‫ﻣﺎ‬ ‫أﻛﻤﻞ‬:
١(‫ل‬ ‫اﻟﻤﺴﺘﻘﯿﻢ‬ ‫ﻛﺎن‬ ‫إذا‬//‫اﻟﻤﺴﺘﻮى‬‫ﺳﺲ‬‫ل‬ ‫ﻓﺈن‬‫ﺑﻼ‬‫ﺳﺲ‬...... =
٢(‫ل‬ ‫اﻟﻤﺴﺘﻘﯿﻢ‬ ‫ﻛﺎن‬ ‫إذا‬G‫اﻟﻤﺴﺘﻮى‬‫ﺳﺲ‬‫ل‬ ‫ﻓﺈن‬‫ﺑﻼ‬‫ﺳﺲ‬...... =
٣(‫ل‬ ‫اﻟﻤﺴﺘﻘﯿﻢ‬ ‫ﻛﺎن‬ ‫إذا‬١//‫ل‬ ‫اﻟﻤﺴﺘﻘﯿﻢ‬٢‫ل‬ ‫ﻓﺈن‬١‫ﺑﻼ‬‫ل‬٢..... =
٤(‫ﻛﺎن‬ ‫إذا‬‫ﺳﺲ‬،‫ﺻﺺ‬‫ﺣﯿﺚ‬ ‫ﻣﺴﺘﻮﯾﺎن‬‫ﺳﺲ‬‫ﺑﻼ‬‫ﺻﺺ‬=T‫ﻓﺈن‬‫ﺳﺲ‬.....‫ﺻﺺ‬
٥(‫ﻟﯿﺴﺎ‬ ‫ﻣﺴﺘﻘﯿﻤﺎن‬ ‫ھﻤﺎ‬ ‫اﻟﻤﺘﺨﺎﻟﻔﺎن‬ ‫اﻟﻤﺴﺘﻘﯿﻤﺎن‬..............‫أو‬................
]٢[‫ﻣﻦ‬ ‫ﺑﻜﻞ‬ ‫ﺗﻤﺮ‬ ‫اﻟﺘﻰ‬ ‫اﻟﻤﺴﺘﻮﯾﺎت‬ ‫ﻋﺪد‬ ‫اذﻛﺮ‬:
‫أ‬(‫ﻣﻌﻠﻮﻣﺔ‬ ‫واﺣﺪة‬ ‫ﻧﻘﻄﺔ‬‫ب‬(‫ﻣﺨﺘﻠﻔﺘﯿﻦ‬ ‫ﻧﻘﻄﺘﯿﻦ‬.
‫ﺟـ‬(‫د‬ ‫واﺣﺪة‬ ‫اﺳﺘﻘﺎﻣﺔ‬ ‫ﻋﻠﻰ‬ ‫ﻧﻘﻂ‬ ‫ﺛﻼث‬(‫واﺣﺪة‬ ‫اﺳﺘﻘﺎﻣﺔ‬ ‫ﻋﻠﻰ‬ ‫ﻟﯿﺴﺖ‬ ‫ﻧﻘﻂ‬ ‫ﺛﻼث‬
‫ھـ‬(‫و‬ ‫واﺣﺪ‬ ‫ﻣﺴﺘﻮى‬ ‫ﻓﻰ‬ ‫ﻟﯿﺴﺖ‬ ‫ﻧﻘﻂ‬ ‫أرﺑﻊ‬(‫واﺣﺪ‬ ‫ﻣﺴﺘﻮى‬ ‫ﻓﻰ‬ ‫ﻟﯿﺴﺖ‬ ‫ﻧﻘﻂ‬ ‫ﺛﻼث‬
]٣[‫اﻟﺮﻣﻮز‬ ‫أﺣﺪ‬ ‫ﺑﺎﺳﺘﺨﺪام‬ ‫أﻛﻤـﻞ‬ ‫ﺛﻢ‬ ‫اﻟﻤﻘﺎﺑﻞ‬ ‫اﻟﺸﻜﻞ‬ ‫ﺗﺄﻣﻞ‬)g،h،
‫أ‬(‫ل‬.......‫ﺳﺲ‬‫ب‬(‫ا‬.......‫ﺳﺲ‬
‫ﺟـ‬(‫ﺟـ‬.......‫ﺻﺺ‬‫ء‬(‫ﺟـ‬ ‫ب‬.........‫ﺻﺺ‬
‫اﻟﻤﺴﺘﻘﯿ‬ ‫ﻋﻠﻰ‬ ‫ﺗﻤﺎرﯾﻦ‬‫اﻟﻤﺴﺘﻮﯾﺎت‬ ‫و‬ ‫ﻤﺎت‬
(: f ، e

114. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
114
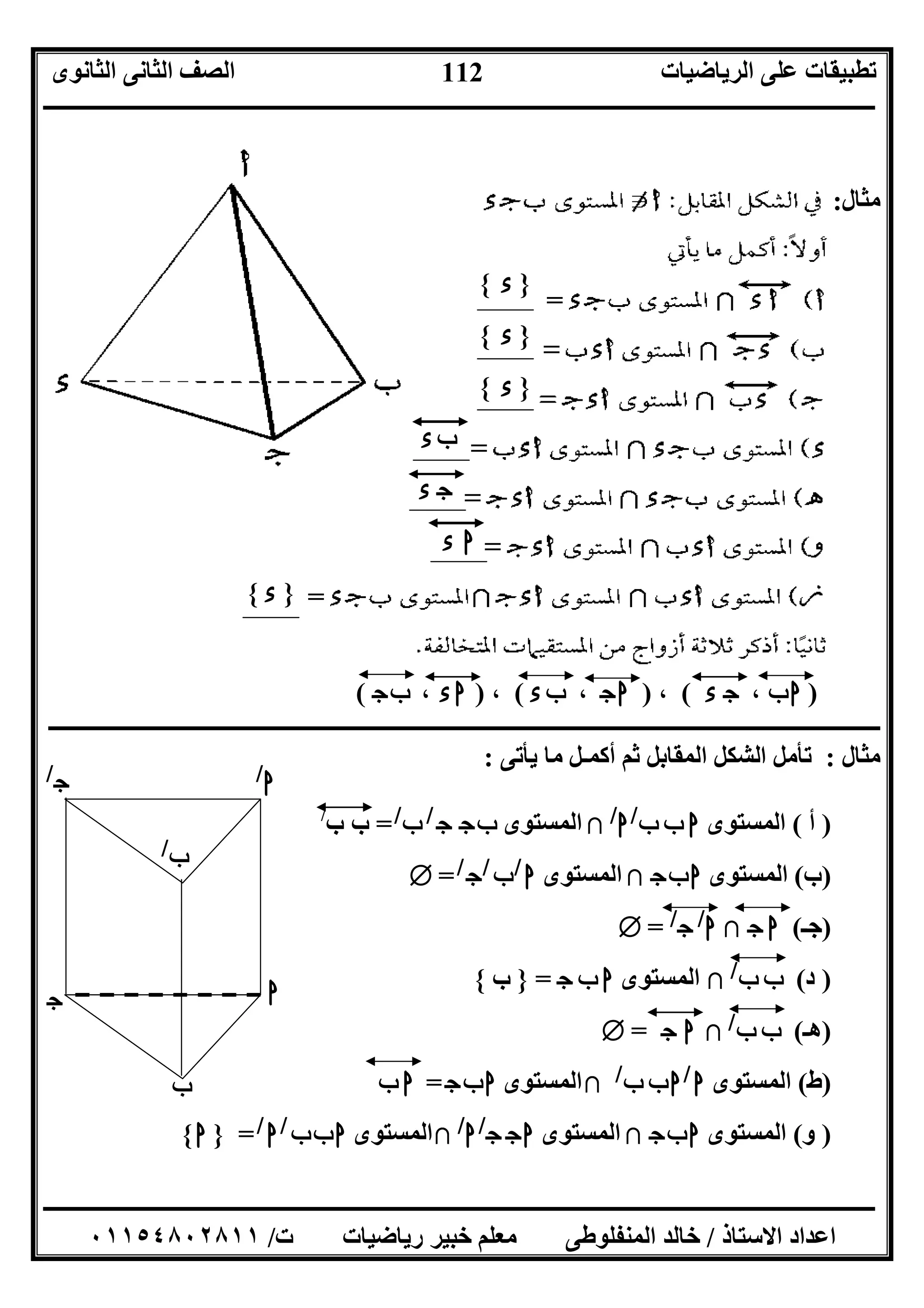
]٤[‫اﻟﻤﻘﺎﺑﻞ‬ ‫اﻟﺸﻜﻞ‬ ‫ﻓﻰ‬:
‫ﺳﺲ‬،‫ﺻﺺ‬، ‫ل‬ ‫اﻟﻤﺴﺘﻘﯿﻢ‬ ‫ﻓﻰ‬ ‫ﻣﺘﻘﺎﻃﻌﺎن‬ ‫ﻣﺴﺘﻮﯾﺎن‬‫ا‬g، ‫ل‬‫ب‬g‫ﺳﺲ‬‫ب‬ ،h‫ﺻﺺ‬
‫ج‬g‫ﺻﺺ‬،‫ج‬h‫ﺳﺲ‬‫ﯾﺄﺗﻰ‬ ‫ﻣﺎ‬ ‫أﻛﻤـﻞ‬:
١(‫اﻟﻤﺴﺘﻮى‬‫ﺳﺲ‬‫ﺑﻼ‬‫اﻟﻤﺴﺘﻮى‬‫ج‬‫ب‬‫ا‬........... =
٢(‫اﻟﻤﺴﺘﻮى‬‫ﺻﺺ‬‫ﺑﻼ‬‫اﻟﻤﺴﺘﻮى‬‫ج‬‫ب‬‫ا‬........... =
٣(‫اﻟﻤﺴﺘﻮى‬‫ﺳﺲ‬‫ﺑﻼ‬‫اﻟﻤﺴﺘﻮى‬‫ج‬‫ب‬‫ا‬........... =
٤(‫اﻟﻤﺴﺘﻮى‬‫ﺳﺲ‬‫ﺑﻼ‬‫اﻟﻤﺴﺘﻮى‬‫ﺻﺺ‬‫ﺑﻼ‬‫اﻟﻤﺴﺘﻮى‬‫ج‬‫ب‬‫ا‬............. =
]٥[
]٦[
‫ﺻﺺ‬(
)‫ﺻﺲ‬
‫ل‬
‫ا‬
‫ج‬
‫ب‬
‫ج‬/
‫ا‬
‫ب‬
‫ا‬/
‫ء‬
‫ب‬/
‫ء‬/
‫ج‬

115. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
115
‫ﯾﺄﺗﻰ‬ ‫ﻣﻤﺎ‬ ‫ﻟﻜﻞ‬ ‫اﻟﺼﺤﯿﺤﺔ‬ ‫اﻹﺟﺎﺑﺔ‬ ‫اﺧﺘﺮ‬:
١(‫ﻟﻨﺎ‬ ‫ﺗﻌﯿﻦ‬ ‫واﺣﺪ‬ ‫ﻣﺴﺘﻮى‬ ‫ﻓﻰ‬ ‫ﻟﯿﺴﺖ‬ ‫ﻧﻘﻂ‬ ‫أرﺑﻊ‬ ‫أى‬:
‫أ‬(‫ب‬ ‫ﻣﺴﺘﻮﯾﺎن‬(‫ﺟـ‬ ‫ﻣﺴﺘﻮﯾﺎت‬ ‫ﺛﻼث‬(‫د‬ ‫ﻣﺴﺘﻮﯾﺎت‬ ‫ارﺑﻊ‬(‫ﻣﺴﺘﻮ‬ ‫ﺗﻌﯿﻦ‬ ‫ﻻ‬
٢(‫إذا‬‫ﻧﻘﻄﺘﯿﻦ‬ ‫ﻓﻰ‬ ‫ﻣﺴﺘﻮﯾﺎن‬ ‫اﺷﺘﺮك‬‫ا‬‫ﻓﺈﻧﮭﻤﺎ‬ ‫ب‬ ،:
‫أ‬(‫ب‬ ‫ﻣﺘﻄﺎﺑﻘﺎن‬(‫ﻓﻰ‬ ‫ﻣﺘﻘﺎﻃﻌﺎن‬‫ا‬‫ب‬
‫ﺟـ‬(ِ‫ز‬‫ﻣﻮا‬ ‫ﻣﺴﺘﻘﯿﻢ‬ ‫ﻓﻰ‬ ‫ﻣﺘﻘﺎﻃﻌﺎن‬‫ب‬ ‫ا‬‫د‬(‫ﻋﻠﻰ‬ ‫ﺗﻘﻊ‬ ‫ﻻ‬ ‫ﺛﺎﻟﺜﺔ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﯾﺸﺘﺮﻛﺎن‬‫ب‬‫ا‬
٣(‫ب‬‫ا‬‫ﺗﻮا‬‫اﻟﻤﺴﺘﻮى‬ ‫زى‬‫ﺳﺲ‬‫ﻛﺎن‬ ‫إذا‬:
‫أ‬(‫ا‬‫ب‬‫ﺑﻼ‬‫ﺳﺲ‬=T‫ب‬(‫ب‬‫ا‬‫ﺑﻼ‬‫ﺳﺲ‬=T
‫ﺟـ‬(‫ا‬‫اﻟﻤﺴﺘﻮى‬ ‫ﻣﻦ‬ ‫ﻣﺨﺘﻠﻔﯿﻦ‬ ‫ﺑﻌﺪﯾﻦ‬ ‫ﻋﻠﻰ‬ ‫ب‬ ،‫ﺳﺲ‬
‫د‬(‫ا‬‫ﻣﻦ‬ ‫ﻣﺨﺘﻠﻔﺘﯿﻦ‬ ‫ﺟﮭﺘﯿﻦ‬ ‫ﻓﻰ‬ ‫ﺗﻘﻌﺎن‬ ‫ب‬ ،‫ﺳﺲ‬
]٤[‫ل‬ ‫اﻟﻤﺴﺘﻘﯿﻤﺎن‬١‫ل‬ ،٢‫ﻛﺎﻧﺎ‬ ‫إذا‬ ‫ﻣﺘﻮازﯾﺎن‬:
‫أ‬(‫ل‬١‫ﺑﻼ‬‫ل‬٢=T‫ب‬(‫ل‬١‫ﺑﻶ‬‫ل‬٢‫ﯾﻘﻌﺎن‬‫واﺣﺪ‬ ‫ﻣﺴﺘﻮى‬ ‫ﻓﻰ‬
‫ﺟـ‬(‫ل‬ ‫ﻛﺎن‬ ‫إذا‬١‫ﺑﻼ‬‫ل‬٢=T‫ل‬ ،١‫ل‬ ،٢‫واﺣﺪ‬ ‫ﻣﺴﺘﻮى‬ ‫ﯾﺠﻤﻌﮭﻤﺎ‬
‫د‬(‫ل‬ ‫ﻛﺎن‬ ‫إذا‬١‫ﺑﻼ‬‫ل‬٢=T‫ل‬ ،١‫ل‬ ،٢‫واﺣﺪ‬ ‫ﻣﺴﺘﻮى‬ ‫ﯾﺠﻤﻌﮭﻤﺎ‬ ‫ﻻ‬
]٥[‫ﻛﺎﻧ‬ ‫إذا‬ ‫ﻣﺘﺨﺎﻟﻔﯿﻦ‬ ‫اﻟﻤﺴﺘﻘﯿﻤﺎن‬ ‫ﯾﻜﻮن‬‫ﺎ‬:
‫أ‬(‫ﻣﺘﻮازﯾﯿﻦ‬ ‫ﻏﯿﺮ‬.‫ب‬(‫ﻣﻨﻄﺒﻘﯿﻦ‬ ‫ﻏﯿﺮ‬.
‫ﺟـ‬(‫د‬ ‫واﺣﺪ‬ ‫ﻣﺴﺘﻮى‬ ‫ﯾﺠﻤﻌﮭﻤﺎ‬ ‫ﻻ‬(‫واﺣﺪ‬ ‫ﻣﺴﺘﻮى‬ ‫ﻓﻰ‬ ‫ﯾﻘﻌﺎن‬
: ‫ﻟﻠﺘﻔﻜﯿﺮ‬ ‫ﺳﺆال‬ [٦]
‫أن‬ ‫إﻣﺎ‬ ‫ﺗﻘﺎﻃﻌﮭﺎ‬ ‫ﻣﺴﺘﻘﯿﻤﺎت‬ ‫ﻓﺈن‬ ‫ﻣﺜﻨﻰ‬ ‫ﻣﺜﻨﻰ‬ ‫ﻣﺴﺘﻮﯾﺎت‬ ‫ﺛﻼﺛﺔ‬ ‫ﺗﻘﺎﻃﻌﺖ‬ ‫إذا‬ ‫أﻧﮫ‬ ‫ﺑﺎﻟﺮﺳﻢ‬ ‫ﺑﯿﻦ‬
‫ﺗﺘﻮا‬‫واﺣﺪة‬ ‫ﻧﻘﻄﺔ‬ ‫ﻓﻰ‬ ‫ﺗﺘﻼﻗﻰ‬ ‫أو‬ ‫زى‬.
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬

116. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
116
‫ص‬
‫س‬
: ‫أن‬ ‫ﺗﺬﻛﺮ‬
‫ﺗﺴﺎوت‬ ‫ﻣﺴﺘﻄﯿﻼت‬ ‫ﻣﺘﻮازى‬ ‫ھﻮ‬ : ‫اﻟﻤﻜﻌﺐ‬ (١
‫ل‬ ‫ﻣﻨﮭﺎ‬ ‫ﻛﻞ‬ ‫ﻃﻮل‬ ، ‫اﻟﺜﻼﺛﺔ‬ ‫أﺑﻌﺎده‬
*‫ﻣﺮﺑﻊ‬ ‫اﻟﺴﺘﮫ‬ ‫أوﺟﮭﮫ‬ ‫ﻣﻦ‬ ‫وﺟﺔ‬ ‫ﻛﻞ‬
‫اﻟﺠﺎﻧﺒﯿﺔ‬ ‫ﻣﺴﺎﺣﺘﮫ‬=٤‫ل‬٢
*
*‫اﻟﻜﻠﯿﺔ‬ ‫ﻣﺴﺎﺣﺘﮫ‬=٦‫ل‬٢
*‫ﺣﺠﻤـﮫ‬=‫ل‬٣
*‫ﻗﻄــﺮه‬ ‫ﻃﻮل‬=‫ل‬‫؟‬٣
. ‫اﻟﻤﺠﺴﻢ‬ ‫ﻟﺘﻜﻮﯾﻦ‬ ‫ﻃﯿﮫ‬ ‫ﯾﻤﻜﻦ‬ ‫اﻟﺬى‬ ‫اﻟﺸﻜﻞ‬ ‫ھﻮ‬ : ‫اﻟﻤﺠﺴﻢ‬ ‫ﺷﺒﻜﺔ‬ (٢
‫ﺷﺒﻜﺔ‬ ‫ﻣﻦ‬ ‫أﻛﺜﺮ‬ ‫رﺳﻢ‬ ‫ﯾﻤﻜﻦ‬ ‫و‬‫ﻟﻠﻤﺠﺴﻢ‬.
: ‫اﻟﻘﺎﺋﻤﺔ‬ ‫اﻟﺪاﺋﺮﯾﺔ‬ ‫اﻻﺳﻄﻮاﻧﺔ‬ (٣
‫ﻗﺎﺋﻤﺔ‬ ‫داﺋﺮﯾﺔ‬ ‫اﺳﻄﻮاﻧﺔ‬ ‫ﺷﺒﻜﺔ‬ ‫اﻟﻤﻘﺎﺑﻞ‬ ‫اﻟﺸﻜﻞ‬.
‫أ‬–‫داﺋﺮة‬ ‫ﺷﻜﻞ‬ ‫ﻋﻠﻰ‬ ‫ﻣﻨﮭﻤﺎ‬ ‫ﻛﻞ‬ ‫و‬ ‫ﻣﺘﻄﺎﺑﻘﺘﯿﻦ‬ ‫اﻻﺳﻄﻮاﻧﺔ‬ ‫ﻗﺎﻋﺪﺗﺎ‬
‫ب‬-‫ﺑﻌﺪاه‬ ‫ﻣﺴﺘﻄﯿﻞ‬ ‫ھﻮ‬ ‫ﻃﯿﮫ‬ ‫ﻗﺒﻞ‬ ‫ﻟﻼﺳﻄﻮاﻧﺔ‬ ‫اﻟﺠﺎﻧﺒﻰ‬ ‫اﻟﺴﻄﺢ‬
‫ﻃﻮل‬ ‫وﺣﺪة‬ ‫ص‬ ‫اﻻﺳﻄﻮاﻧﺔ‬ ‫ارﺗﻔﺎع‬ ، ‫ص‬ ، ‫س‬
‫زواﯾﺎه‬ ‫و‬ ‫اﻟﻄﻮل‬ ‫ﻣﺘﺴﺎوﯾﺔ‬ ‫أﺿﻼﻋﮫ‬ ‫ﻣﻀﻠﻊ‬ ‫ھﻮ‬ ‫اﻟﻤﻨﺘﻈﻢ‬ ‫اﻟﻤﻀﻠﻊ‬ (٤
‫ﺧﺎرﺟﮫ‬ ‫أو‬ ‫داﺧﻠﮫ‬ ‫اﻟﻤﺮﺳﻮﻣﺔ‬ ‫اﻟﺪاﺋﺮة‬ ‫ﻣﺮﻛﺰ‬ ‫ھﻮ‬ ‫ﻣﺮﻛﺰه‬ ‫اﻟﻘﯿﺎس‬ ‫ﻣﺘﺴﺎوﯾﺔ‬
٥(‫رﺑﺎﻋﻰ‬ ‫ھﺮم‬ ‫ھﻮ‬ ‫اﻟﻤﻘﺎﺑﻠﺔ‬ ‫اﻟﺸﺒﻜﺔ‬ ‫ﻃﻰ‬ ‫ﻣﻦ‬ ‫ﺗﻜﻮﯾﻨﮫ‬ ‫ﯾﻤﻜﻦ‬ ‫اﻟﺬى‬ ‫اﻟﻤﺠﺴﻢ‬
٦(‫اﻟﻤﺜﻠﺚ‬ ‫ﻣﺴﺎﺣﺔ‬=‫اﻟﻘﺎﻋﺪة‬ ‫ﻃﻮل‬×‫اﻟﻤﻨﺎﻇﺮ‬ ‫اﻻرﺗﻔﺎع‬
٧(‫ﻣﺴﺎﺣﺔ‬‫اﻟﻤﺮﺑﻊ‬=‫ﺿﻠﻌﮫ‬ ‫ﻃﻮل‬ ‫ﻣﺮﺑﻊ‬=‫ﺿﻠﻌﮫ‬ ‫ﻃﻮل‬ ‫ﻣﺮﺑﻊ‬
‫ﻣﺤﯿﻄﮫ‬=٤×‫ﺿﻠﻌﮫ‬ ‫ﻃﻮل‬
٨(‫اﻟﻤﺴﺘﻄﯿﻞ‬ ‫ﻣﺴﺎﺣﺔ‬=‫اﻟﻄﻮل‬×، ‫اﻟﻌﺮض‬‫ﻣﺤﯿﻄﮫ‬) =‫اﻟﻄﻮل‬+‫اﻟﻌﺮض‬(×٢
‫اﻟﻤﺨﺮوط‬ ‫و‬ ‫اﻟﮭـــــــﺮم‬
١
٢
١
٢

117. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
117
‫س‬
‫واﺣﺪة‬ ‫رأس‬ ‫ﻓﻰ‬ ‫ﺗﺸﺘﺮك‬ ‫ﻣﺜﻠﺜﺎت‬ ‫اﻷﺧﺮى‬ ‫أوﺟﮭﺔ‬ ‫ﺟﻤﯿﻊ‬ ‫و‬ ‫واﺣﺪة‬ ‫ﻗﺎﻋﺪة‬ ‫ﻟﮫ‬ ‫ﻣﺠﺴﻢ‬ ‫ھﻮ‬
‫ﻗﺎﻋﺪﺗﮫ‬ ‫ﻣﻀﻠﻊ‬ ‫أﺿﻼع‬ ‫ﻋﺪد‬ ‫ﺣﺴﺐ‬ ‫ﯾﺴﻤﻰ‬ ‫و‬‫أو‬ ‫ﺛﻼﺛﻰ‬‫أو‬ ‫رﺑﺎﻋﻰ‬٠٠٠٠.
*‫اﻟﻨﻘﻄﺔ‬ ‫ﺗﺴﻤﻰ‬‫م‬‫رأﺳﮫ‬ ‫ﻣﻦ‬ ‫اﺑﺘﺪاء‬ ‫ﯾﻜﺘﺐ‬ ‫و‬ ‫اﻟﮭﺮم‬ ‫ﯾﻘﺮأ‬ ‫و‬ ‫اﻟﮭﺮم‬ ‫رأس‬
*‫اﻟﻘﻄﻊ‬ ‫ﺗﺴﻤﻰ‬‫ا‬‫م‬"،‫م‬‫ب‬"،‫ج‬‫م‬"،‫ء‬‫م‬"،٠٠٠٠‫ﻟﻠﮭﺮم‬ ‫اﻟﺠﺎﻧﺒﯿﺔ‬ ‫اﻷﺣﺮف‬
*‫ﻣﺜﻠﺚ‬ ‫ﻋﻦ‬ ‫ﻋﺒﺎرة‬ ‫اﻟﺠﺎﻧﺒﯿﺔ‬ ‫اﻟﮭﺮم‬ ‫أوﺟﮫ‬ ‫ﻣﻦ‬ ‫وﺟﮫ‬ ‫ﻛﻞ‬.
*‫اﻟﮭﺮم‬ ‫ارﺗﻔﺎع‬‫ﻣﺴﺘﻮى‬ ‫ﻋﻦ‬ ‫اﻟﮭﺮم‬ ‫رأس‬ ‫ﺑﻌﺪ‬ ‫ھﻮ‬‫ﻗﺎﻋﺪﺗﮫ‬.‫ﻣﺜﻞ‬‫م‬‫ن‬"
*‫ﻗﺎﻋﺪﺗﮫ‬ ‫أﺿﻼع‬ ‫أﺣﺪ‬ ‫ﻋﻦ‬ ‫اﻟﮭﺮم‬ ‫رأس‬ ‫ﺑﻌﺪ‬ ‫ھﻮ‬ ‫اﻟﺠﺎﻧﺒﻰ‬ ‫اﻟﻮﺟﺔ‬ ‫ارﺗﻔﺎع‬
‫ﻣﺜﻞ‬‫م‬"‫س‬"
‫ﻋﻠﯿﮭﺎ‬ ‫اﻟﮭﺮم‬ ‫رأس‬ ‫ﻣﻦ‬ ‫اﻟﻤﺮﺳﻮم‬ ‫اﻟﻌﻤﻮد‬ ‫ﻣﻮﻗﻊ‬ ‫ﻣﺮﻛﺰه‬ ‫ﻣﻨﺘﻈﻢ‬ ‫ﻣﻀﻠﻊ‬ ‫ﻗﺎﻋﺪﺗﮫ‬ ‫اﻟﺬى‬ ‫اﻟﮭﺮم‬ ‫ھﻮ‬
: ‫اﻟﻤﻨﺘﻈﻢ‬ ‫اﻟﮭﺮم‬ ‫ﺧﻮاص‬ *
١-‫اﻟﻄﻮل‬ ‫ﻣﺘﺴﺎوﯾﺔ‬ ‫اﻟﺠﺎﻧﺒﯿﺔ‬ ‫أﺣﺮﻓﮫ‬.
٢-‫ﻣﺜ‬ ‫ﺳﻄﻮح‬ ‫اﻟﺠﺎﻧﺒﯿﺔ‬ ‫أوﺟﮭﮫ‬‫ﻣﺘﻄﺎﺑﻘﺔ‬ ‫و‬ ‫اﻟﺴﺎﻗﯿﻦ‬ ‫ﻣﺘﺴﺎوﯾﺔ‬ ‫ﻠﺜﺎت‬
٣-‫ﻣﺘﺴﺎوﯾﺔ‬ ‫اﻟﺠﺎﻧﺒﯿﺔ‬ ‫اﻻرﺗﻔﺎﻋﺎت‬‫اﻟﻄﻮل‬ ‫ﻓﻰ‬.
٤-‫ﻣﻨﺘﻈﻢ‬ ‫ﻣﻀﻠﻊ‬ ‫اﻟﮭﺮم‬ ‫ﻗﺎﻋﺪة‬)، ‫ﻣﺮﺑﻊ‬ ، ‫اﻻﺿﻼع‬ ‫ﻣﺘﺴﺎوى‬ ‫ﻣﺜﻠﺚ‬٠٠
: ‫ھﺎﻣﺔ‬ ‫ﻣﻠﺤﻮﻇﺔ‬
‫ﯾﻜﻮن‬ ‫ﻗﺎﻋﺪﺗﮫ‬ ‫ﻣﺴﺘﻮى‬ ‫ﻋﻠﻰ‬ ‫اﻟﮭﺮم‬ ‫رأس‬ ‫ﻣﻦ‬ ‫اﻟﻌﻤﻮدى‬ ‫اﻟﻤﺴﺘﻘﯿﻢ‬
‫ﻓﯿﮭﺎ‬ ‫ﻣﺴﺘﻘﯿﻢ‬ ‫أى‬ ‫ﻋﻠﻰ‬ ‫ﻋﻤﻮدﯾﺎ‬.
‫اﻟﻤﻘﺎﺑﻞ‬ ‫اﻟﺸﻜﻞ‬ ‫ﻓﻰ‬:‫ن‬ ‫م‬ ‫ﻛﺎن‬ ‫إذا‬"‫ﻓﺈن‬ ‫اﻟﻘﺎﻋﺪة‬ ‫ﻣﺴﺘﻮى‬ ‫ﻋﻠﻰ‬ ‫ﻋﻤﻮدى‬:
‫ن‬ ‫م‬"┴‫ج‬‫ا‬"‫ن‬ ‫م‬ ،"┴‫ء‬‫ب‬"‫ن‬ ‫م‬ ،"┴‫س‬ ‫ن‬"‫ن‬ ‫ﻓﻰ‬ ‫اﻟﺰاوﯾﺔ‬ ‫ﻗﺎﺋﻢ‬ ‫ن‬ ‫س‬ ‫م‬ ‫اﻟﻤﺜﻠﺚ‬ ‫ﯾﻜﻮن‬ ‫و‬ ،
‫اﻟﮭـــــــــﺮم‬
‫اﻟﻤﻨﺘﻈﻢ‬ ‫اﻟﮭﺮم‬

118. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
118
‫ﻧﻘﻄﺔ‬ ‫ھﻮ‬ ‫اﻟﻤﺮﺑﻊ‬ ‫ﻣﺮﻛﺰ‬ ‫و‬ .‫ﻣﺘﻮﺳﻄﺎﺗﮫ‬ ‫ﺗﻘﺎﻃﻊ‬ ‫ﻧﻘﻄﺔ‬ ‫ھﻮ‬ ‫اﻻﺿﻼع‬ ‫اﻟﻤﺘﺴﺎوى‬ ‫اﻟﻤﺜﻠﺚ‬ ‫:ﻣﺮﻛﺰ‬ ‫ﻣﻠﺤﻮﻇﺔ‬
‫ﻗﻄﺮﯾﮫ‬ ‫ﺗﻘﺎﻃﻊ‬.
*‫ا‬ ‫اﻟﮭﺮم‬‫ﻟﻘﺎﺋﻢ‬‫ﻣﻮﻗﻊ‬ ‫ﻛﺎن‬ ‫ﻓﻘﻂ‬ ‫و‬ ‫إذا‬ ‫ﻗﺎﺋﻤﺎ‬ ‫اﻟﮭﺮم‬ ‫ﯾﻜﻮن‬‫ﻋﻠﻰ‬ ‫اﻟﮭﺮم‬ ‫رأس‬ ‫ﻣﻦ‬ ‫اﻟﻤﺮﺳﻮم‬ ‫اﻟﻌﻤﻮد‬
‫اﻟﮭﻨﺪﺳﻲ‬ ‫ﺑﻤﺮﻛﺰھﺎ‬ ‫ﯾﻤﺮ‬ ‫ﻗﺎﻋﺪﺗﮫ‬.
‫ﻣﻼﺣﻈﺎت‬:
١-‫اﻟﮭﻨﺪﺳﻲ‬ ‫ﺑﻤﺮﻛﺰھﺎ‬ ‫ﯾﻤﺮ‬ ‫ﻗﺎﻋﺪﺗﮫ‬ ‫ﻋﻠﻰ‬ ‫رأﺳﮫ‬ ‫ﻣﻦ‬ ‫اﻟﻤﺮﺳﻮم‬ ‫اﻟﻌﻤﻮد‬ ‫ﻣﻮﻗﻊ‬ ‫ﻻن‬ ‫ﻗﺎﺋﻢ‬ ‫اﻟﻤﻨﺘﻈﻢ‬ ‫اﻟﮭﺮم‬
٢-‫ﻣﻀﻠﻊ‬ ‫أﺿﻼع‬ ‫ﻋﺪد‬ ‫ﺗﺰاﯾﺪ‬ ‫إذا‬ ‫و‬‫اﻟﻘﺎﻋﺪة‬ ‫ﺗﺼﺒﺢ‬ ‫ﻣﻨﺘﮫ‬ ‫ﻏﯿﺮ‬ ‫ﻋﺪد‬ ‫إﻟﻰ‬ ‫اﻗﺘﺮب‬ ‫و‬ ‫ﻣﻨﺘﻈﻢ‬ ‫ھﺮم‬ ‫ﻗﺎﻋﺪة‬
‫ﻗﺎﺋﻢ‬ ‫داﺋﺮى‬ ‫ﻣﺨﺮوط‬ ‫اﻟﻤﺠﺴﻢ‬ ‫ﯾﻜﻮن‬ ‫و‬ ‫ﻣﺨﺮوﻃﻰ‬ ‫اﻟﺠﺎﻧﺒﻲ‬ ‫اﻟﺴﻄﺢ‬ ‫ﯾﺼﺒﺢ‬ ‫و‬ ‫داﺋﺮة‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫م‬‫ء‬ ‫ج‬ ‫ب‬ ‫ا‬‫ﻗﺎﻋﺘﮫ‬ ‫ﺿﻠﻊ‬ ‫ﻃﻮل‬ ‫ﻣﻨﺘﻈﻢ‬ ‫رﺑﺎﻋﻰ‬ ‫ھﺮم‬‫ء‬‫ج‬‫ب‬‫ا‬‫ﯾﺴﺎوى‬١٠‫وارﺗﻔﺎﻋﮫ‬ ‫ﺳﻢ‬١٢‫ﺳﻢ‬
‫ﺷﺒﻜﺎﺗﮫ‬ ‫إﺣﺪى‬ ‫ارﺳﻢ‬ ‫و‬ ‫اﻟﺠﺎﻧﺒﻰ‬ ‫ارﺗﻔﺎﻋﮫ‬ ‫أوﺟﺪ‬.
‫اﻟﺤﻞ‬:
‫ن‬ ‫م‬=١٢، ‫اﻟﮭﺮم‬ ‫ارﺗﻔﺎع‬ ‫ﺳﻢ‬‫ب‬‫ا‬=١٠‫ﻗﺎﻋﺪﺗﮫ‬ ‫أﺿﻼع‬ ‫أﺣﺪ‬ ‫ﺳﻢ‬
‫ﻗﻄﺮى‬ ‫ﺗﻘﺎﻃﻊ‬ ‫ﻧﻘﻄﺔ‬ ‫ن‬ ،‫اﻟﻤﺮﺑﻊ‬‫ء‬‫ج‬‫ب‬‫ا‬
‫ﻣﻨﺘﻈﻢ‬ ‫رﺑﺎﻋﻰ‬ ‫اﻟﮭﺮم‬Ε‫ن‬ ‫م‬"n‫اﻟﻤﺴﺘﻮى‬‫ء‬‫ج‬‫ب‬‫ا‬ A
‫ﺟـ‬ ‫ب‬ ‫ﻣﻨﺘﺼﻒ‬ ‫س‬ ‫ﺑﻔﺮض‬"Ε‫س‬ ‫م‬"n‫ب‬"‫ﺟـ‬"
‫اﻟﻤﻨﺘﻈﻢ‬ ‫ﻟﻠﮭﺮم‬ ‫ﺟﺎﻧﺒﻰ‬ ‫ارﺗﻔﺎع‬ ‫س‬ ‫م‬ ‫ﯾﻜﻮن‬ ‫و‬.
‫ﻓﻰ‬Δ‫ج‬‫ب‬‫ء‬:‫ﻣﻨﺘﺼﻒ‬ ‫ن‬‫ب‬‫ء‬"‫ب‬ ‫ﻣﻨﺘﺼﻒ‬ ‫س‬ ،‫ج‬"
‫س‬ ‫ن‬=‫ج‬‫ء‬=×١٠=٥‫ﺳﻢ‬ Ε
e‫ن‬ ‫م‬"n‫اﻟﻤﺴﺘﻮى‬‫ء‬‫ج‬‫ب‬‫ا‬
ΕΔ‫س‬ ‫ن‬ ‫م‬‫ن‬ ‫ﻓﻰ‬ ‫اﻟﺰاوﯾﺔ‬ ‫ﻗﺎﺋﻢ‬
Ε)‫س‬ ‫م‬(٢
) =‫ن‬ ‫م‬(٢
) +‫س‬ ‫ن‬(٢
) =١٢(٢
) +٥(٢
=١٦٩
Ε‫ﻟﻠﮭﺮم‬ ‫اﻟﺠﺎﻧﺒﻰ‬ ‫اﻻرﺗﻔﺎع‬=١٣‫ﺳﻢ‬
‫اﻟﻤﻘﺎﺑ‬ ‫اﻟﺸﻜﻞ‬ ‫و‬‫م‬ ‫اﻟﮭﺮم‬ ‫ﺷﺒﻜﺎت‬ ‫إﺣﺪى‬ ‫ﯾﻮﺿﺢ‬ ‫ﻞ‬‫ء‬‫ج‬‫ب‬‫ا‬
١
٢
١
٢

119. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
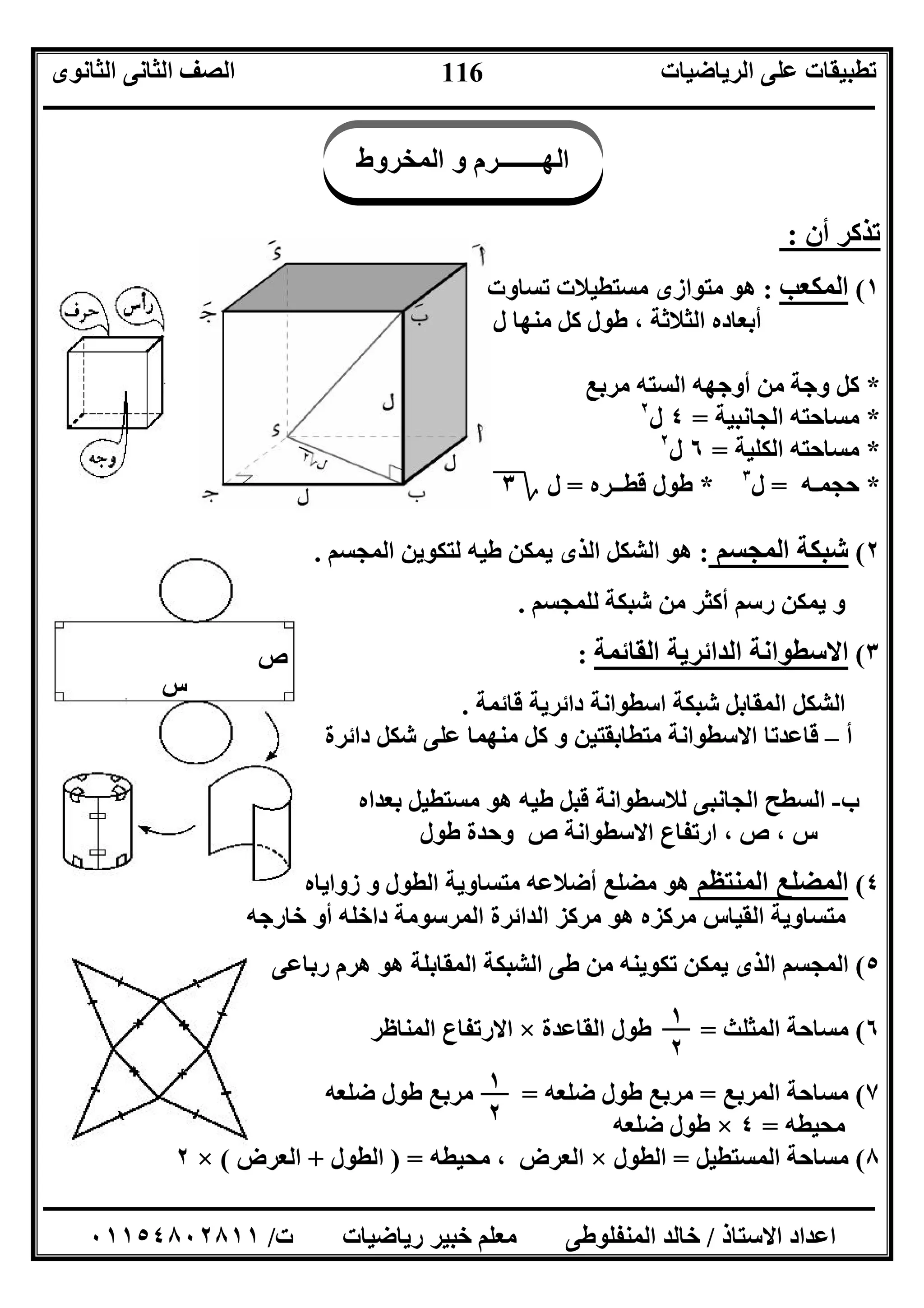
119
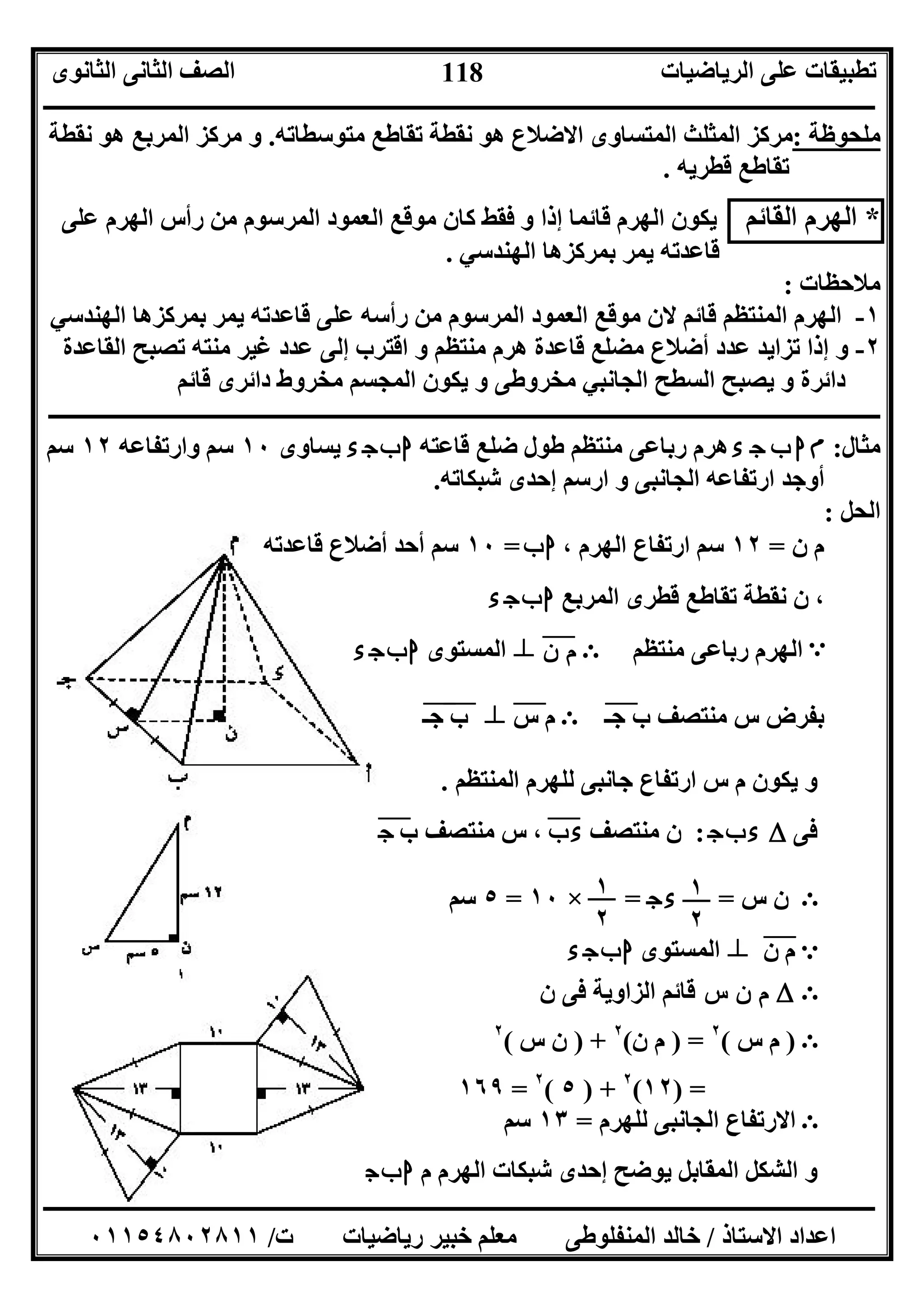
‫ﻣﺜﺎل‬:‫ء‬‫ج‬‫ب‬‫ا‬‫م‬‫ارﺗﻔﺎﻋﮫ‬ ‫ﻣﻨﺘﻈﻢ‬ ‫رﺑﺎﻋﻰ‬ ‫ھﺮم‬٢٠‫اﻟﺠﺎﻧﺒﻰ‬ ‫ارﺗﻔﺎﻋﮫ‬ ‫و‬ ، ‫ﺳﻢ‬٢٥‫ﺳﻢ‬
‫ﺷﺒﻜﺎﺗﮫ‬ ‫إﺣﺪى‬ ‫ﯾﻮﺿﺢ‬ ‫ﺷﻜﻼ‬ ‫ارﺳﻢ‬ ‫و‬ ، ‫اﻟﮭﺮم‬ ‫ﺿﻠﻊ‬ ‫ﻃﻮل‬ ‫أوﺟﺪ‬.
‫اﻟﺤﻞ‬:
‫ﺑﺎﻟﺤﻞ‬ ‫ﻧﻘﻮم‬ ‫اﻟﺴﺎﺑﻘﺔ‬ ‫اﻟﻄﺮﯾﻘﺔ‬ ‫ﺑﻨﻔﺲ‬
٢ + ‫اﻷﺣﺮف‬ ‫ﻋﺪد‬ = ‫اﻟﺮؤوس‬ ‫ﻋﺪد‬ + ‫اﻷوﺟﮫ‬ ‫ﻋﺪد‬ : ‫أوﯾﻠﺮ‬ ‫ﻗﺎﻋﺪة‬ *
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
. ‫اﻷﺿﻼع‬ ‫ﻣﺘﺴﺎوﯾﺔ‬ ‫ﻣﺜﻠﺜﺎت‬ ‫ﺳﻄﻮح‬ ‫اﻻرﺑﻌﺔ‬ ‫أوﺟﮭﮫ‬ ‫ﻗﺎﺋﻢ‬ ‫ھﺮم‬ ‫ھﻮ‬ : ‫اﻟﻤﻨﺘﻈﻢ‬ ‫اﻟﺜﻼﺛﻰ‬ ‫اﻟﮭﺮم‬ *
: ‫ﺧﻮاﺻﮫ‬ *
١-‫ﻗﺎﻋﺪة‬ ‫أوﺟﮭﮫ‬ ‫ﻣﻦ‬ ‫وﺟﮫ‬ ‫أى‬ ‫إﻋﺘﺒﺎر‬ ‫ﯾﻤﻜﻦ‬
٢-‫اﻟﻄﻮل‬ ‫ﻓﻰ‬ ‫ﻣﺘﺴﺎوﯾﺔ‬ ‫اﻟﺠﺎﻧﺒﯿﺔ‬ ‫اﻻرﺗﻔﺎﻋﺎت‬
٣-‫اﻟﻄﻮل‬ ‫ﻓﻰ‬ ‫ﻣﺘﺴﺎوﯾﺔ‬ ‫اﻟﺴﺘﺔ‬ ‫أﺣﺮﻓﮫ‬ ‫أﻃﻮال‬
‫اﻟﻤﻘﺎﺑﻞ‬ ‫اﻟﺸﻜﻞ‬ ‫ﻓﻰ‬:
‫ﻣﻨ‬ ‫ﺛﻼﺛﻰ‬ ‫ھﺮم‬‫ﺣﺮﻓﮫ‬ ‫ﻃﻮل‬ ‫ﺘﻈﻢ‬=‫ل‬‫ارﺗﻔﺎﻋﮫ‬ ،‫ع‬،‫ع‬/
‫اﻟﺠﺎﻧﺒﻰ‬ ‫ارﺗﻔﺎﻋﮫ‬
‫ﺟـ‬‫ء‬=‫ل‬،‫ن‬‫ء‬=‫ل‬،‫ن‬‫ج‬=‫ل‬،‫ء‬‫م‬=‫ل‬
‫ارﺗﻔﺎﻋﮫ‬ ،)‫ع‬= (‫ن‬ ‫م‬=‫ل‬‫اﻟﺠﺎﻧﺒﻰ‬ ‫ارﺗﻔﺎﻋﮫ‬ ،‫ع‬/
=‫ل‬
]Ε٣‫ع‬٢
=٢‫ل‬٢
،٤‫ع‬/٢
=٣‫ل‬٢
[
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫؟‬٣
٢
‫؟‬٣
٦
‫؟‬٣
٣
‫؟‬٦
٣
‫ع‬
‫م‬
‫ا‬
‫ب‬
‫ج‬
‫ء‬
‫ن‬
‫ء‬
‫ع‬/
‫؟‬٣
٢
‫؟‬٣
٢
‫اﻟﻤﺨـــﺮوط‬
‫ﺷﻜﻞ‬ ‫ﻋﻠﻰ‬ ‫واﺣﺪة‬ ‫ﻗﺎﻋﺪة‬ ‫ﻟﮫ‬ ‫ﻣﺠﺴﻢ‬ ‫ھﻮ‬
‫ﯾﺘﻜﻮن‬ ‫و‬ ‫واﺣﺪة‬ ‫رأس‬ ‫و‬ ‫ﻣﻐﻠﻖ‬ ‫ﻣﻨﺤﻨﻰ‬
‫اﻟﻘﻄﻊ‬ ‫ﻧﻘﻂ‬ ‫ﺟﻤﯿﻊ‬ ‫ﻣﻦ‬ ‫اﻟﺠﺎﻧﺒﻰ‬ ‫ﺳﻄﺤﮫ‬
‫إﻟﻰ‬ ‫رأﺳﮫ‬ ‫ﻣﻦ‬ ‫اﻟﻤﺮﺳﻮﻣﺔ‬ ‫اﻟﻤﺴﺘﻘﯿﻤﺔ‬
‫ﻣﻨﮭﺎ‬ ‫ﻛﻞ‬ ‫ﯾﻌﺮف‬ ‫اﻟﺘﻰ‬ ‫و‬ ‫ﻗﺎﻋﺪﺗﮫ‬ ‫ﻣﻨﺤﻨﻰ‬
‫اﻟﻤﺨﺮوط‬ ‫ﺑﺮاﺳﻢ‬.

120. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
120
: ‫اﻟﻘﺎﺋﻢ‬ ‫اﻟﺪاﺋﺮى‬ ‫اﻟﻤﺨﺮوط‬ ‫ﺧﻮاص‬ *
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﺑﺪﻻﻟﺔ‬ ‫أوﺟﺪ‬t‫ارﺗﻔﺎﻋﮫ‬ ‫ﻗﺎﺋﻢ‬ ‫داﺋﺮى‬ ‫ﻣﺨﺮوط‬ ‫ﻗﺎﻋﺪة‬ ‫ﻣﺴﺎﺣﺔ‬ ‫و‬ ‫ﻣﺤﯿﻂ‬٢٤‫راﺳﻤﮫ‬ ‫ﻃﻮل‬ ‫و‬ ‫ﺳﻢ‬
٢٦‫ﺳﻢ‬.
‫اﻟﺤﻞ‬:‫اﻟﺮاﺳﻢ‬ ‫ﻃﻮل‬ ‫ﺑﻔﺮض‬=‫اﻟﻤﺨﺮوط‬ ‫ارﺗﻔﺎع‬ ، ‫ل‬=، ‫ع‬
‫اﻟﻤﺨﺮوط‬ ‫داﺋﺮة‬ ‫ﻗﻄﺮ‬ ‫ﻧﺼﻒ‬ ‫ﻃﻮل‬=‫ﻧﻖ‬
e‫ﻧﻖ‬٢
=‫ل‬٢
–‫ع‬٢
Ε‫ﻧﻖ‬٢
) =٢٦(٢
–)٢٤(٢
=١٠٠
Ε‫ﻧﻖ‬=١٠‫ﺳﻢ‬
‫اﻟﻘﺎﺋﻢ‬ ‫اﻟﻤﺨﺮوط‬ ‫ﻗﺎﻋﺪة‬ ‫ﻣﺤﯿﻂ‬=٢t‫ﻧﻖ‬=٢t×١٠=٢٠t
‫اﻟﻘﺎﻋﺪة‬ ‫ﻣﺴﺎﺣﺔ‬=t‫ﻧﻖ‬٢
=t×)٢٤(٢
=٥٧٦t‫ﺳﻢ‬٢
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻛﺎﻣﻠﺔ‬ ‫دورة‬ ‫ﻧﺼﻒ‬ ‫ج‬‫ب‬‫ا‬ ‫اﻟﻤﺜﻠﺚ‬ ‫دار‬ ‫إذا‬ . "‫ـ‬‫ﺟ‬" ‫ب‬ ‫ﻣﻨﺘﺼﻒ‬‫ء‬ ، ‫ج‬‫ا‬=‫ب‬‫ا‬ ، ‫ﻣﺜﻠﺚ‬‫ج‬‫ب‬‫ا‬ : ‫ﻓﻜﺮ‬
‫ﺣﻮل‬‫ء‬‫ا‬‫ﯾﻨﺸﺄ‬ ‫ﻓﺈﻧﮫ‬ ‫ﻛﻤﺤﻮر‬‫ﻗﺎﺋﻢ‬ ‫داﺋﺮى‬ ‫ﻣﺨﺮوط‬‫ﻗﺎﻋﺪﺗﮫ‬‫ﻧﺼﻒ‬ ‫ﻃﻮل‬ ‫داﺋﺮة‬‫ب‬ ‫ﻗﻄﺮھﺎ‬‫ء‬"
‫ارﺗﻔﺎﻋﮫ‬‫ء‬‫ا‬"‫راﺳﻤﮫ‬ ‫ﻃﻮل‬ ،‫ب‬ ‫ا‬"
‫داﺋﺮﺗﮫ‬ ‫ﻗﻄﺮ‬ ‫ﻧﺼﻒ‬ ‫ﻧﻖ‬ ، ‫ﻗﻮﺳﮫ‬ ‫ﻃﻮل‬ ‫ل‬ ‫ﺣﯿﺚ‬ ‫ﻧﻖ‬ ‫ل‬ = ‫اﻟﺪاﺋﺮى‬ ‫اﻟﻘﻄﺎع‬ ‫ﻣﺴﺎﺣﺔ‬ : ‫أن‬ ‫ﺗﺬﻛﺮ‬
‫اﻟﻘﺎﺋﻢ‬ ‫اﻟﺪاﺋﺮى‬ ‫اﻟﻤﺨﺮوط‬
‫ﻗﺎﺋﻢ‬ ‫ﻣﺜﻠﺚ‬ ‫دوران‬ ‫ﻣﻦ‬ ‫ﯾﻨﺸﺄ‬ ‫اﻟﺬى‬ ‫اﻟﺠﺴﻢ‬ ‫ھﻮ‬‫ﻛﻤﺤﻮر‬ ‫اﻟﻘﺎﺋﻤﺔ‬ ‫ﺿﻠﻌﻰ‬ ‫أﺣﺪ‬ ‫ﺣﻮل‬ ‫ﻛﺎﻣﻠﺔ‬ ‫دورة‬ ‫اﻟﺰاوﯾﺔ‬
١
٢

121. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
121
: ‫اﻟﻘﺎﺋﻢ‬ ‫اﻟﻤﺨﺮوط‬ ‫ﺷﺒﻜﺔ‬ *
‫ﻋﺒﻮات‬ ‫ﻟﺘﻜﻮﯾﻦ‬ ‫اﻟﻘﺎﺋﻢ‬ ‫اﻟﻤﺨﺮوط‬ ‫ﺷﺒﻜﺔ‬ ‫ﻃﻰ‬ ‫ﯾﻤﻜﻦ‬
‫اﻟﺸﻜﻞ‬ ‫ﻣﺨﺮوﻃﯿﺔ‬.
‫اﻟﻤﻘﺎﺑﻞ‬ ‫اﻟﺸﻜﻞ‬ ‫ﻓﻰ‬:
١-‫ب‬‫ا‬=‫ج‬‫ا‬=‫ل‬)‫اﻟﻤﺨﺮوط‬ ‫راﺳﻢ‬ ‫ﻃﻮل‬(
٢-‫اﻟ‬‫ﻘﻄﺎع‬‫ج‬‫ب‬‫ا‬‫ﻟﻠﻤﺨﺮوط‬ ‫اﻟﺠﺎﻧﺒﻲ‬ ‫اﻟﺴﻄﺢ‬ ‫ﯾﻤﺜﻞ‬
‫ﻃﻮل‬ ،‫ج‬ ‫ب‬=٢t‫ﻧﻖ‬
‫اﻟﻤﺨﺮوط‬ ‫ﻗﺎﻋﺪة‬ ‫ﻗﻄﺮ‬ ‫ﻧﺼﻒ‬ ‫ﻃﻮل‬ ‫ﻧﻖ‬ ‫ﺣﯿﺚ‬
٣-‫اﻟﻤﺨﺮوط‬ ‫ارﺗﻔﺎع‬=‫ﻃﻮل‬‫ا‬‫ن‬"
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫اﻟﻤﻌﻄﺎه‬ ‫ﺑﺎﻟﺒﯿﺎﻧﺎت‬ ‫ﻣﺴﺘﻌﯿﻨﺎ‬ ‫ﻗﺎﺋﻢ‬ ‫ﻣﺨﺮوط‬ ‫ﺷﺒﻜﺔ‬ ‫ﯾﻮﺿﺢ‬ ‫اﻟﻤﻘﺎﺑﻞ‬ ‫اﻟﺸﻜﻞ‬.‫إرﺗﻔﺎﻋﮫ‬ ‫أوﺟﺪ‬.
‫اﻟﺤﻞ‬:
‫أن‬ ‫ﻧﻼﺣﻆ‬ ‫اﻟﻤﺨﺮوط‬ ‫ﺷﺒﻜﺔ‬ ‫ﻣﻦ‬:
‫اﻟﻤﺨﺮوط‬ ‫راﺳﻢ‬ ‫ﻃﻮل‬=‫م‬ ‫ﻃﻮل‬‫ا‬"=٢١‫ﺳﻢ‬
‫اﻟﻤﺨﺮوط‬ ‫ﻗﺎﻋﺪة‬ ‫ﻣﺤﯿﻂ‬=‫ﻃﻮل‬‫ب‬ ‫ا‬=٤٤‫ﺳﻢ‬
‫اﻟﻤﺨﺮوط‬ ‫ﻗﺎﻋﺪة‬ ‫ﻗﻄﺮ‬ ‫ﻧﺼﻒ‬ ‫ﻃﻮل‬=‫ن‬ ‫ﺟـ‬ ‫ﻃﻮل‬"=‫ﻧﻖ‬
‫اﻟﻤﻘﺎﺑﻞ‬ ‫اﻟﺸﻜﻞ‬ ‫ﻋﻠﻰ‬ ‫ﻧﺤﺼﻞ‬ ‫اﻟﻤﺨﺮوط‬ ‫ﺷﺒﻜﺔ‬ ‫ﻃﻰ‬ ‫ﻋﻨﺪ‬
‫ﻓﯿﻜﻮن‬‫اﻟﻤﺨﺮوط‬ ‫ارﺗﻔﺎع‬=‫ن‬ ‫م‬ ‫ﻃﻮل‬"=‫ع‬
e‫اﻟﻤﺨﺮوط‬ ‫ﻗﺎﻋﺪة‬ ‫ﻣﺤﯿﻂ‬=٤٤‫ﺳﻢ‬Ε٢t‫ﻧﻖ‬=٤٤
Ε٢× ×‫ﻧﻖ‬=٤٤Ε‫ﻧﻖ‬=٧‫ﺳﻢ‬
e‫ع‬٢
=‫ل‬٢
–‫ﻧﻖ‬٢
Ε‫ع‬٢
) =٢١(٢
–)٧(٢
=٣٩٢Ε‫ع‬=١٤‫؟‬٢‫ﺳﻢ‬
١٤‫؟‬٢‫ﺳﻢ‬ Ε‫اﻟﻘﺎﺋﻢ‬ ‫اﻟﺪاﺋﺮى‬ ‫اﻟﻤﺨﺮوط‬ ‫ارﺗﻔﺎع‬=
٢٢
٧

122. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
122
]١[
]٢[
]٣[
]٤[
]٥[
‫اﻟﻤﺨﺮوط‬ ‫و‬ ‫اﻟﮭﺮم‬ ‫ﻣﻔﮭﻮم‬ ‫ﻋﻠﻰ‬ ‫ﺗﻤﺎرﯾﻦ‬

123. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
123
: ‫اﻟﻘﺎﺋﻢ‬ ‫اﻟﻤﻨﺘﻈﻢ‬ ‫اﻟﮭﺮم‬ [١]
‫اﻟﺠﺎﻧﺒﯿﺔ‬ ‫اﻟﻤﺴﺎﺣﺔ‬‫ﻟﻠﮭﺮم‬‫اﻟﻘﺎﺋﻢ‬=‫اﻟﺠﺎﻧﺒﯿﺔ‬ ‫أوﺟﮭﮫ‬ ‫ﻣﺴﺎﺣﺎت‬ ‫ﻣﺠﻤﻮع‬
=‫ﻗﺎﻋﺪﺗﮫ‬ ‫ﻣﺤﯿﻂ‬×‫ارﺗﻔﺎﻋ‬‫اﻟﺠﺎﻧﺒﻰ‬ ‫ﮫ‬
‫ﻟﻠﮭﺮم‬ ‫اﻟﻜﻠﯿﺔ‬ ‫اﻟﻤﺴﺎﺣﺔ‬=‫ﻣﺴﺎﺣ‬‫اﻟﺠﺎﻧﺒﯿﺔ‬ ‫ﺘﮫ‬+‫ﻗﺎﻋﺪﺗﮫ‬ ‫ﻣﺴﺎﺣﺔ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫اﻟﻤﺠﺴﻢ‬ ‫ﺻﻒ‬ ‫أﻣﺎﻣﻚ‬ ‫اﻟﺘﻰ‬ ‫اﻟﺸﺒﻜﺔ‬ ‫ﺑﺎﺳﺘﺨﺪام‬
‫اﻟﻜﻠﯿﺔ‬ ‫ﻣﺴﺎﺣﺘﮫ‬ ‫أوﺟﺪ‬ ‫و‬.
‫اﻟﺤﻞ‬:
‫ﻟﻠﮭﺮم‬ ‫اﻟﻜﻠﯿﺔ‬ ‫و‬ ‫اﻟﺠﺎﻧﺒﯿﺔ‬ ‫اﻟﻤﺴﺎﺣﺔ‬
‫اﻟﺪاﺋﺮى‬ ‫اﻟﻤﺨﺮوط‬ ‫و‬ ‫اﻟﻘﺎﺋﻢ‬ ‫اﻟﻤﻨﺘﻈﻢ‬
١
٢

124. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
124
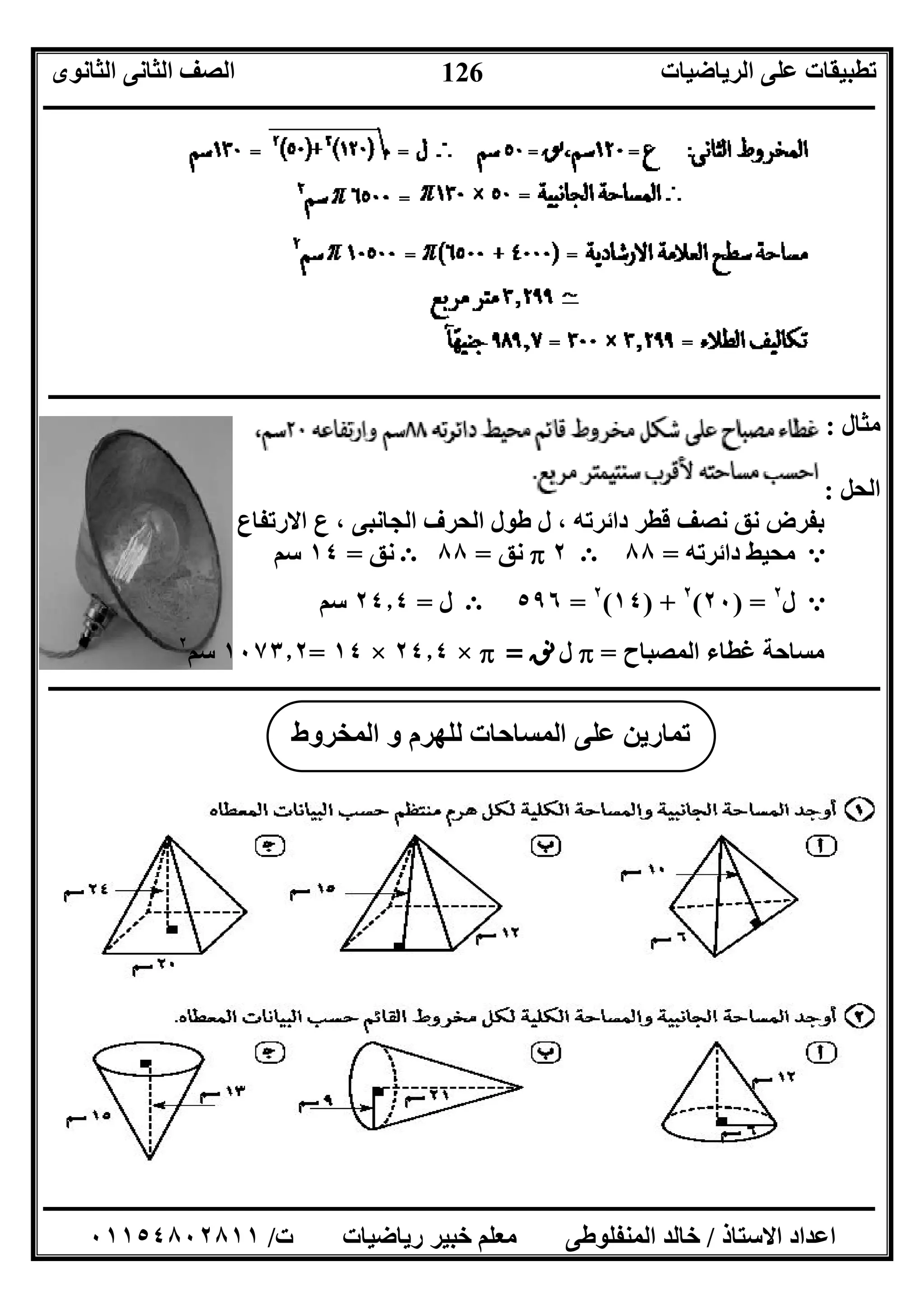
‫ﻣﺜﺎل‬:
‫اﻟﺤﻞ‬:
‫ﻗﺎﺋﻢ‬ ‫ﻣﻨﺘﻈﻢ‬ ‫ﺛﻼﺛﻰ‬ ‫ھﺮم‬ ‫اﻟﻤﺠﺴﻢ‬
‫ل‬ ‫ﺣﺮﻓﮫ‬ ‫ﻃﻮل‬=‫؟‬١٨٢
"–"٩"
٢
"=٩‫؟‬٣‫ﺳﻢ‬
‫اﻟﺠﺎﻧﺒﻰ‬ ‫ارﺗﻔﺎﻋﮫ‬=١٨‫ﺳﻢ‬
‫ﻗﺎﻋﺪﺗﮫ‬ ‫ﻣﺤﯿﻂ‬)‫اﻻﺿﻼع‬ ‫ﻣﺘﺴﺎوى‬ ‫ﻣﺜﻠﺚ‬= (٣×٩‫؟‬٣=٢٧‫؟‬٣‫ﺳﻢ‬
‫ﻗﺎﻋﺪﺗﮫ‬ ‫ﻣﺴﺎﺣﺔ‬=‫اﻟﻘﺎﻋﺪة‬×‫اﻻرﺗﻔﺎع‬=×٩‫؟‬٣×١٨=٨١‫؟‬٣‫ﺳﻢ‬٢
‫اﻟﺠﺎﻧﺒﯿﺔ‬ ‫اﻟﮭﺮم‬ ‫ﻣﺴﺎﺣﺔ‬=‫ﻗﺎﻋﺪﺗﮫ‬ ‫ﻣﺤﯿﻂ‬×‫اﻟﺠﺎﻧﺒﻲ‬ ‫اﻻرﺗﻔﺎع‬
=×٢٧‫؟‬٣×١٨=٤٢٠٫٩‫ﺳﻢ‬٢
‫اﻟﻜﻠﯿﺔ‬ ‫ﻣﺴﺎﺣﺘﮫ‬=‫اﻟﺠﺎﻧﺒﯿﺔ‬ ‫ﻣﺴﺎﺣﺘﮫ‬+‫ﻗﺎﻋﺪﺗﮫ‬ ‫ﻣﺴﺎﺣﺔ‬
=٤٢٠٫٩+٨١‫؟‬٣=٥٦١٫٢‫ﺳﻢ‬٢
‫ــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
: ‫اﻟﻤﺨﺮوط‬ [٢]
‫داﺋﺮﺗﮫ‬ ‫ﻗﻄﺮ‬ ‫ﻧﺼﻒ‬ ‫ﻃﻮل‬ ‫ﻧﻖ‬ ، ‫راﺳﻤﮫ‬ ‫ﻃﻮل‬ ‫ل‬ ‫ﺑﻔﺮض‬.
‫اﻟﻘﺎﺋﻢ‬ ‫ﻟﻠﻤﺨﺮوط‬ ‫اﻟﺠﺎﻧﺒﯿﺔ‬ ‫اﻟﻤﺴﺎﺣﺔ‬=t‫ل‬‫ﻧﻖ‬
t‫ل‬‫ﻧﻖ‬+t‫ﻧﻖ‬٢
‫اﻟ‬ ‫اﻟﻤﺴﺎﺣﺔ‬‫اﻟﻘﺎﺋﻢ‬ ‫ﻟﻠﻤﺨﺮوط‬ ‫ﻜﻠﯿﺔ‬=
=t‫ﻧﻖ‬)‫ل‬+‫ﻧﻖ‬(
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
=‫ء‬
‫ھـ‬ ‫اﻟﺪاﺋﺮى‬ ‫اﻟﻘﻄﺎع‬ ‫ﻓﻰ‬ : ‫أن‬ ‫ﺗﺬﻛﺮ‬
‫ھـ‬ ‫ﺣﯿﺚ‬‫ء‬
‫داﺋﺮﺗﮫ‬ ‫ﻗﻄﺮ‬ ‫ﻧﺼﻒ‬ ‫ﻃﻮل‬ ‫ﻧﻖ‬ ، ‫ﻗﻮﺳﮫ‬ ‫ﻃﻮل‬ ‫ل‬ ، ‫ﺑﺎﻟﺪاﺋﺮى‬ ‫اﻟﻘﻄﺎع‬ ‫زاوﯾﺔ‬
‫اﻟﻘﻄﺎع‬ ‫ﻣﺴﺎﺣﺔ‬=‫ل‬‫ﻧﻖ‬=‫ھـ‬‫ء‬
‫ﻧﻖ‬٢
‫اﻟﻘﻄﺎع‬ ‫ﻣﺤﯿﻂ‬=٢‫ﻧﻖ‬+‫ل‬
٩‫ﺳﻢ‬
١٨‫ﺳﻢ‬
٩‫ﺳﻢ‬
٩‫؟‬٣
١
٢
١
٢ ١
٢١
٢
‫ل‬
‫ﻧﻖ‬
١
٢
١
٢‫ﻧﻖ‬‫ﻧﻖ‬
‫ل‬
‫ھـ‬

125. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
125
١٧‫ﺳﻢ‬
١٥‫ﺳﻢ‬
‫ﺳﻢ‬ ‫ﻧﻖ‬
‫ﻣﺜﺎل‬:
‫ــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫راﺳﻤﮫ‬ ‫ﻃﻮل‬ ‫ﻗﺎﺋﻢ‬ ‫ﻟﻤﺨﺮوط‬ ‫اﻟﻜﻠﯿﺔ‬ ‫اﻟﻤﺴﺎﺣﺔ‬ ‫أوﺟﺪ‬١٧‫ارﺗﻔﺎﻋﮫ‬ ‫و‬ ‫ﺳﻢ‬١٥‫ﺳﻢ‬
‫اﻟﺤﻞ‬:
e‫ﻧﻖ‬٢
) =١٧(٢
–)١٥(٢
=٦٤Ε‫ﻧﻖ‬=٨‫ﺳﻢ‬
Ε‫اﻟﺠﺎﻧﺒﯿﺔ‬ ‫اﻟﻤﺴﺎﺣﺔ‬=t‫ل‬‫ﻧﻖ‬=t×١٧×٨=١٣٦t‫ﺳﻢ‬٢
Ε‫اﻟﻜﻠﯿﺔ‬ ‫اﻟﻤﺴﺎﺣﺔ‬=t‫ﻧﻖ‬)‫ل‬+‫ﻧﻖ‬= (٨t)١ ٧+٨(
‫ﺳﻢ‬٢
٨t×١ ٥=١٢٠t =
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:

126. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
126
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــ‬
‫ﻣﺜﺎل‬:
‫اﻟﺤﻞ‬:
‫اﻻرﺗﻔﺎع‬ ‫ع‬ ، ‫اﻟﺠﺎﻧﺒﻰ‬ ‫اﻟﺤﺮف‬ ‫ﻃﻮل‬ ‫ل‬ ، ‫داﺋﺮﺗﮫ‬ ‫ﻗﻄﺮ‬ ‫ﻧﺼﻒ‬ ‫ﻧﻖ‬ ‫ﺑﻔﺮض‬
e‫داﺋﺮﺗﮫ‬ ‫ﻣﺤﯿﻂ‬=٨٨Ε٢t‫ﻧﻖ‬=٨٨Ε‫ﻧﻖ‬=١٤‫ﺳﻢ‬
e‫ل‬٢
) =٢٠(٢
) +١٤(٢
=٥٩٦Ε‫ل‬=٢٤٫٤‫ﺳﻢ‬
‫اﻟﻤﺼﺒﺎح‬ ‫ﻏﻄﺎء‬ ‫ﻣﺴﺎﺣﺔ‬=t‫ل‬‫ﻧﻖ‬=t×٢٤٫٤×١٤=١٠٧٣٫٢‫ﺳﻢ‬٢
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻟﻤﺨﺮوط‬ ‫و‬ ‫ﻟﻠﮭﺮم‬ ‫اﻟﻤﺴﺎﺣﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻤﺎرﯾﻦ‬

127. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
127
‫ـــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻرﺗﻔﺎع‬ × ‫اﻟﻘﺎﻋﺪة‬ ‫ﻣﺴﺎﺣﺔ‬ = ‫اﻟﻤﻨﺸﻮراﻟﻘﺎﺋﻢ‬ ‫ﺣﺠﻢ‬ -١ : ‫أن‬ ‫ﺗﺬﻛﺮ‬
‫أو‬ ‫رﺑﺎﻋﻰ‬ ‫ﺷﻜﻞ‬ ‫أو‬ ‫ﻣﺮﺑﻊ‬ ‫أو‬ ‫ﻣﺜﻠﺚ‬ ‫ﻗﺎﻋﺪﺗﮫ‬٠٠٠٠٠
٢-‫اﻻﺳﻄ‬ ‫ﺣﺠﻢ‬‫اﻟﻘﺎﺋﻤﺔ‬ ‫ﻮاﻧﺔ‬=‫اﻟﻘﺎﻋﺪة‬ ‫ﻣﺴﺎﺣﺔ‬×‫اﻻرﺗﻔﺎع‬
‫ﻗﻄﺮھﺎ‬ ‫ﻧﺼﻒ‬ ‫ﻃﻮل‬ ‫داﺋﺮة‬ ‫ﻗﺎﻋﺪﺗﮭﺎ‬‫ﻧﻖ‬
٣-‫اﻟﻤﻨﺘﻈﻢ‬ ‫اﻟﻤﻀﻠﻊ‬ ‫ﺳﻄﺢ‬ ‫ﻣﺴﺎﺣﺔ‬=‫س‬٢
‫ﻇﺘﺎ‬
، ‫ﺿﻠﻌﮫ‬ ‫ﻃﻮل‬ ‫س‬ ، ‫اﺿﻼﻋﮫ‬ ‫ﻋﺪد‬ ‫ن‬ ‫ﺣﯿﺚ‬t=١٨٠٥
: ‫اﻻرﺗﻔﺎع‬ ‫و‬ ‫اﻟﻘﺎﻋﺪة‬ ‫ﻧﻔﺲ‬ ‫ﻓﻰ‬ ‫اﻟﻤﺸﺘﺮﻛﺘﺎن‬ ‫اﻟﻤﻨﺸﻮر‬ ‫و‬ ‫اﻟﮭﺮم‬ ‫ﺣﺠﻢ‬ ‫ﺑﯿﻦ‬ ‫اﻟﻌﻼﻗﺔ‬
‫اﻟﮭﺮم‬ ‫ﺣﺠﻢ‬=‫اﻟﻤﻨﺸﻮر‬ ‫ﺣﺠﻢ‬=‫ﻗﺎﻋﺪﺗﮫ‬ ‫ﻣﺴﺎﺣﺔ‬×‫ارﺗﻔﺎﻋﮫ‬
‫اﻟﻘﺎﺋﻢ‬ ‫واﻟﻤﺨﺮوط‬ ‫اﻟﮭﺮم‬ ‫ﺣﺠﻢ‬
١
٣
١
٣
t
‫ن‬
‫ن‬
٤

128. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
128
: ‫اﻟﮭــــﺮم‬ ‫ﺣﺠﻢ‬ *
‫اﻟﮭﺮم‬ ‫ﺣﺠﻢ‬=‫ﻗﺎﻋﺪﺗﮫ‬ ‫ﻣﺴﺎﺣﺔ‬ ‫ﺛﻠﺚ‬×‫ارﺗﻔﺎﻋﮫ‬=‫ق‬×‫ع‬
‫ﺣﯿﺚ‬)‫ق‬(، ‫اﻟﻘﺎﻋﺪة‬ ‫ﻣﺴﺎﺣﺔ‬)‫ع‬(‫اﻟﮭﺮم‬ ‫ارﺗﻔﺎع‬
‫ـــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:
‫اﻟﺤﻞ‬:‫اﻟﺸﻜﻞ‬ ‫ﻓﻰ‬)‫أ‬: (‫اﻟﻘﺎﻋﺪة‬ ‫ﻣﺴﺎﺣﺔ‬=١٠×١٠=١٠٠‫ﺳﻢ‬٢
‫اﻟﻤﻨﺘﻈﻢ‬ ‫اﻟﺮﺑﺎﻋﻰ‬ ‫اﻟﮭﺮم‬ ‫ﺣﺠﻢ‬=‫ق‬×‫ع‬=×١٠٠×٢١=٧٠٠‫ﺳﻢ‬٣
١
٣
١
٣
١
٣

129. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
129
‫س‬٢
‫ﻇﺘﺎ‬ ‫اﻟﺸﻜﻞ‬ ‫ﻓﻰ‬)‫ب‬: (‫اﻟﻘﺎﻋﺪة‬ ‫ﻣﺴﺎﺣﺔ‬)‫ﻣﻨﺘ‬ ‫ﺧﻤﺎﺳﻲ‬‫ﻈﻢ‬= (
=×)٨(٢
‫ﻇﺘﺎ‬=١١٠‫ﺳﻢ‬٢
‫اﻟﻤﻨﺘﻈﻢ‬ ‫اﻟﺨﻤﺎﺳﻲ‬ ‫اﻟﮭﺮم‬ ‫ﺣﺠﻢ‬=‫ق‬×‫ع‬=×١١٠×١٤=٥١٣٫٣‫ﺳﻢ‬٣
‫اﻟﺸﻜﻞ‬ ‫ﻓﻰ‬)‫ﺟـ‬: (‫س‬=‫؟‬)١٧"(٢
"–)"١٥"(٢
"=٨
‫اﻟﻘﺎﻋﺪة‬ ‫ﺿﻠﻊ‬ ‫ﻃﻮل‬=٢×٨=١٦‫ﺳﻢ‬
‫ع‬=‫؟‬)١٥"(٢
"–)"٨"(٢
"=‫؟‬١٦١"‫ﺳﻢ‬
‫اﻟﻘﺎﻋﺪة‬ ‫ﻣﺴﺎﺣﺔ‬=١٦×١٦=٢٥٦‫ﺳﻢ‬٢
‫اﻟﻤﻨﺘﻈﻢ‬ ‫اﻟﺮﺑﺎﻋﻰ‬ ‫اﻟﮭﺮم‬ ‫ﺣﺠﻢ‬=‫ق‬×‫ع‬=×٢٥٦×‫؟‬١٦١"=١٠٨٢٫٧‫ﺳﻢ‬٣
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
:‫ﻗﺎﺋﻤﺔ‬ ‫داﺋﺮﯾﺔ‬ ‫اﺳﻄﻮاﻧﺔ‬ ‫ﺣﺠﻢ‬ ‫و‬ ‫ﻗﺎﺋﻢ‬ ‫ﻣﺨﺮوط‬ ‫ﺣﺠﻢ‬ ‫ﺑﯿﻦ‬ ‫اﻟﻌﻼﻗﺔ‬ : ‫ﻓﻜﺮ‬
‫اﻟﻤﺨ‬ ‫ﺣﺠﻢ‬‫اﻟﻘﺎﺋﻢ‬ ‫ﺮوط‬=‫اﻟﻘﺎﺋﻤﺔ‬ ‫اﻟﺪاﺋﺮﯾﺔ‬ ‫اﻻﺳﻄﻮاﻧﺔ‬ ‫ﺣﺠﻢ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
: ‫اﻟﻘﺎﺋﻢ‬ ‫اﻟﻤﺨﺮوط‬ ‫ﺣﺠﻢ‬ *
‫اﻟﻤﺨﺮوط‬ ‫ﺣﺠﻢ‬=‫ﺿ‬ ‫ﺣﺎﺻﻞ‬ ‫ﺛﻠﺚ‬‫ارﺗﻔﺎﻋﮫ‬ ‫ﻓﻰ‬ ‫ﻗﺎﻋﺪﺗﮫ‬ ‫ﻣﺴﺎﺣﺔ‬ ‫ﺮب‬.
=t‫ﻧﻖ‬٢
‫ع‬
‫ﺣﯿﺚ‬)‫ﻧﻖ‬(، ‫اﻟﻤﺨﺮوط‬ ‫داﺋﺮة‬ ‫ﻗﻄﺮ‬ ‫ﻧﺼﻒ‬ ‫ﻃﻮل‬)‫ع‬(‫اﻟﻤﺨﺮوط‬ ‫ارﺗﻔﺎع‬
t
‫ن‬
‫ن‬
٤
٥
٤
t
٥
١
٣
١
٣
١٥‫ﺳﻢ‬ ١٧‫ﺳﻢ‬
‫س‬
‫ع‬ ١٥‫ﺳﻢ‬
٨‫ﺳﻢ‬
١
٣
١
٣
١
٣
١
٣

130. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
130
‫ﻣﺜﺎل‬:
‫اﻟﺤﻞ‬:
‫ﺳﻢ‬ ١٤ = ‫ع‬ ، ‫ﺳﻢ‬ ٩ = ‫ﻧﻖ‬ : ( ‫أ‬ ) ‫اﻟﺸﻜﻞ‬ ‫ﻓﻰ‬
Ε‫اﻟﻤﺨﺮوط‬ ‫ﺣﺠﻢ‬=t‫ﻧﻖ‬٢
‫ع‬=×t×)٩(٢
×١٤=١١٨٧٫٥‫ﺳﻢ‬٣
‫؟‬ = ‫ﻧﻖ‬ ، ‫ﺳﻢ‬ ٢٦ = ‫ل‬ ، ‫ﺳﻢ‬ ٢٤ = ‫ع‬ : (‫)ب‬ ‫اﻟﺸﻜﻞ‬ ‫ﻓﻰ‬
‫ﻧﻖ‬=‫؟‬)٢٦"(٢
"–")""""٢٤"(٢
"=١٠‫ﺳﻢ‬
Ε‫اﻟﻤﺨﺮوط‬ ‫ﺣﺠﻢ‬=t‫ﻧﻖ‬٢
‫ع‬=×t×)١٠(٢
×٢٤
=٢٥١٣٫٣‫ﺳﻢ‬٣
‫اﻟﺸﻜﻞ‬ ‫ﻓﻰ‬)‫ﺟـ‬: (‫ل‬=١٣‫ﻧﻖ‬ ، ‫ﺳﻢ‬=٥‫ع‬ ، ‫ﺳﻢ‬=‫؟‬
‫ع‬=‫؟‬)١٣"(٢
"–")٥"(٢
"=١٢‫ﺳﻢ‬
Ε‫اﻟﻤﺨﺮوط‬ ‫ﺣﺠﻢ‬=t‫ﻧﻖ‬٢
‫ع‬=×t×)٥(٢
×١٢
=٣١٤٫٢‫ﺳﻢ‬٣
‫ــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:
‫اﻟﺤﻞ‬:
١
٣
١
٣
‫ﻧﻖ‬
٢٤‫ﺳﻢ‬ ٢٦‫ﺳﻢ‬
١
٣
١
٣
٥
‫ع‬ ١٣‫ﺳﻢ‬
١
٣
١
٣

131. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
131
‫ﻣﺜﺎل‬:‫ﺣﺠﻤﮫ‬ ‫ﻗﺎﺋﻢ‬ ‫ﻣﺨﺮوط‬ ‫ھﯿﺌﺔ‬ ‫ﻋﻠﻰ‬ ‫اﻟﺸﯿﻜﻮﻻﺗﮫ‬ ‫ﻣﻦ‬ ‫ﻗﻄﻌﺔ‬٢٧t‫ﺳﻢ‬٣
‫ﻗﺎﻋﺪﺗﮫ‬ ‫ﻣﺤﯿﻂ‬ ‫و‬٦t‫ﺳﻢ‬
‫ارﺗﻔﺎﻋﮫ‬ ‫أوﺟﺪ‬.
‫اﻟﺤﻞ‬:
e‫ﻗﺎﻋﺪﺗ‬ ‫ﻣﺤﯿﻂ‬‫ﮫ‬=٦t‫ﺳﻢ‬Ε٢t‫ﻧﻖ‬=٦tΕ‫ﻧﻖ‬=٣‫ﺳﻢ‬
e‫اﻟﻤﺨﺮوط‬ ‫ﺣﺠﻢ‬=٢٧t‫ﺳﻢ‬٣
Εt‫ﻧﻖ‬٢
‫ع‬=٢٧t
Εt×)٣(٢
×‫ع‬=٢٧tΕ‫ع‬=٩‫ﻢ‬ ‫ﺳ‬Ε‫اﻻرﺗﻔﺎع‬=٩‫ﺳﻢ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:
‫اﻟﺤﻞ‬:
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــ‬
‫ﻧﻔﺲ‬ ‫ﺗﺴﺘﺨﺪم‬ ‫ﺳﻌﺘﮭﺎ‬ ‫وﻟﺤﺴﺎب‬ ، ‫ﺗﺤﺘﻮﯾﮫ‬ ‫اﻟﺬى‬ ‫اﻟﺴﺎﺋﻞ‬ ‫ﺑﺤﺠﻢ‬ ‫ﺗﻘﺪر‬ ‫ﺣﺎوﯾﺔ‬ ‫ﺳﻌﺔ‬ : ‫ھﺎﻣﺔ‬ ‫ﻣﻼﺣﻈﺔ‬
‫اﻟﻠﺘﺮ‬ ‫اﻟﺴﻌﺔ‬ ‫ﻗﯿﺎس‬ ‫ووﺣﺪة‬ ‫اﻟﺤﺠﻮم‬ ‫ﺣﺴﺎب‬ ‫ﻗﻮاﻧﯿﻦ‬
١‫ﻟﺘﺮ‬=١٠٠٠‫ﻣﻠﻠﯿﻤﺘﺮ‬=١٠٠٠‫ﺳﻢ‬٣
: ‫أن‬ ‫ﺗﺬﻛﺮ‬
‫أﺟﻮف‬ ‫ﺟﺴﻢ‬ ‫ﻷى‬ ‫اﻟﺪاﺧﻠﻰ‬ ‫اﻟﻔﺮاغ‬ ‫ﺣﺠﻢ‬ ‫ھﻰ‬ ‫اﻟﺴﻌﺔ‬ -١
٢-‫اﻟﻜﺮة‬ ‫ﺣﺠﻢ‬=t‫ﻧﻖ‬٣
‫اﻟﻜﺮة‬ ‫ﺳﻄﺢ‬ ‫ﻣﺴﺎﺣﺔ‬ ،=٤t‫ﻧﻖ‬٢
١
٣
١
٣
٤
٣

132. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
132
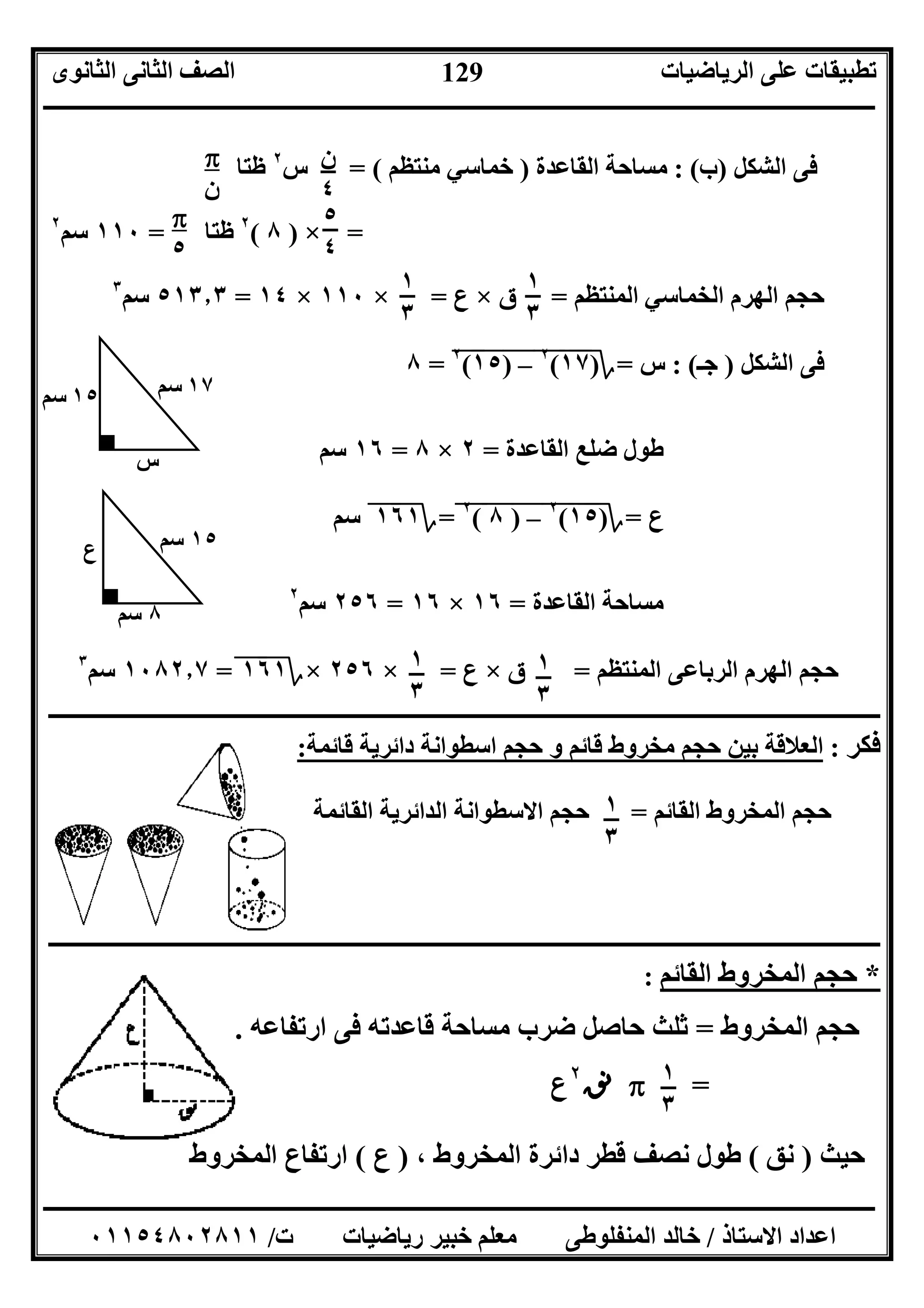
‫ﻣﺜﺎل‬:
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ا‬‫ﻟﻠﺸﺮاب‬ ‫ﻛﺄﺳﺎن‬ ‫ب‬ ،.‫ﺳﻌﺘﯿﮭﻤﺎ‬ ‫ﺑﯿﻦ‬ ‫اﻟﻔﺮق‬ ‫أوﺟﺪ‬ ‫؟‬ ‫أﻛﺒﺮ‬ ‫ﺳﻌﺘﮫ‬ ‫اﯾﮭﻤﺎ‬.
‫اﻟﺤﻞ‬:
‫اﻷول‬ ‫اﻟﻜﺄس‬:‫ﻧﻖ‬=٢٫٥‫ع‬ ، ‫ﺳﻢ‬=١١‫ﺳﻢ‬
‫اﻻول‬ ‫اﻟﻜﺄس‬ ‫ﺣﺠﻢ‬‫ا‬=t‫ﻧﻖ‬٢
‫ع‬
=t×)٢٫٥(٢
×١١=٧٢‫ﺳﻢ‬٣
‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﻜﺄس‬:‫ﻧﻖ‬=٥٫٥‫ع‬ ، ‫ﺳﻢ‬=٥‫ﺳﻢ‬
‫اﻟ‬ ‫ﺣﺠﻢ‬‫ب‬ ‫اﻟﺜﺎﻧﻰ‬ ‫ﻜﺄس‬=t‫ﻧﻖ‬٢
×‫ع‬=t×)٥٫٥(٢
×٥=٥٠٫٤‫ﺳﻢ‬٣
‫ﺳﻌﺘﯿﮭﻤﺎ‬ ‫ﺑﯿﻦ‬ ‫اﻟﻔﺮق‬=٧٢–٥٠٫٤=٢١٫٦‫ﺳﻢ‬٣
]‫أن‬ ‫ﺗﺬﻛﺮ‬:‫اﻟﺤﺠﻢ‬=‫اﻟﺴﻌﺔ‬[
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــ‬
١
٣
١
٣
١
٣
١
٣
‫اﻟﮭﺮم‬ ‫و‬ ‫اﻟﻤﺨﺮوط‬ ‫ﺣﺠﻢ‬ ‫ﻋﻠﻰ‬ ‫ﺗﻤﺎرﯾﻦ‬

133. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
133

134. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
134
: ‫أن‬ ‫ﺗﺬﻛﺮ‬ *
١-‫اﻟﺪاﺋﺮة‬:‫اﻟﺜﺎﺑﺖ‬ ‫اﻟﺒﻌﺪ‬ ‫ﻧﻔﺲ‬ ‫ﻋﻠﻰ‬ ‫ﺗﻜﻮن‬ ‫اﻟﺘﻰ‬ ‫اﻟﻤﺴﺘﻮى‬ ‫ﻧﻘﻂ‬ ‫ﻣﺠﻤﻮﻋﺔ‬ ‫ھﻰ‬
‫اﻟﻤﺴﺘﻮى‬ ‫ﻓﻰ‬ ‫ﺛﺎﺑﺘﺔ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻣﻦ‬.
‫اﻟﻨﻘﻄﺔ‬ ‫م‬ ‫ﺗﺴﻤﻰ‬ ‫ﺣﯿﺚ‬‫ﻧﻖ‬ ‫ﻗﻄﺮھﺎ‬ ‫ﻧﺼﻒ‬ ‫و‬ ‫اﻟﺪاﺋﺮة‬ ‫ﻣﺮﻛﺰ‬ ‫اﻟﺜﺎﺑﺘﺔ‬‫د‬ ‫ﺑـ‬ ‫ﻟﻠﺪاﺋﺮة‬ ‫ﻧﺮﻣﺰ‬ ‫و‬
٢-‫اﻟﻨﻘﻄﺘﯿﻦ‬ ‫ﺑﯿﻦ‬ ‫اﻟﺒﻌﺪ‬)‫س‬١‫ص‬ ،١(،)‫س‬٢‫ص‬ ،٢= (‫؟‬)‫س‬٢"–"‫س‬"١("+")"‫ص‬"٢"–"‫س‬"٢("
‫اﻟﺒﻌﺪ‬ ‫ﻣﺮﺑﻊ‬=)‫س‬٢–‫س‬١(٢
) +‫ص‬٢–‫ص‬١(٢
٣-‫اﻟﻨﻘﻄﺔ‬ ‫ﺻﻮرة‬)‫س‬١‫ص‬ ،١(‫ﺑﺎﻻﻧﺘﻘﺎل‬)‫ن‬ ، ‫م‬(‫اﻟﻨﻘﻄﺔ‬ ‫ھﻰ‬)‫س‬١+‫م‬‫ص‬ ،١+‫ن‬(
‫اﻟﻨﻘﻄﺔ‬ ‫ﺻﻮرة‬)-٢،٤(‫ﺑﺎﻻﻧﺘﻘﺎل‬)٤،١(‫اﻟﻨﻘﻄﺔ‬ ‫ھﻰ‬)٢،٥(
٤-‫اﻟﻨﻘﻄﺘﯿﻦ‬ ‫ﺑﯿﻦ‬ ‫اﻟﻤﺴﺎﻓﺔ‬ ‫ﻣﻨﺘﺼﻒ‬ ‫إﺣﺪاﺛﻰ‬)‫س‬١‫ص‬ ،١(،)‫س‬٢‫ص‬ ،٢(
) =،(
٥-‫ا‬ ‫ﻣﺴﺎﺣﺔ‬‫ﻣﻨﺘﻈﻢ‬ ‫ﻣﻀﻠﻊ‬ ‫ى‬=‫ﻧﻖ‬٢
‫ﺣﺎ‬
‫اﻟﻤﻀﻠﻊ‬ ‫أﺿﻼع‬ ‫ﻋﺪد‬ ‫ن‬ ، ‫ﺑﺮؤوﺳﮫ‬ ‫اﻟﻤﺎر‬ ‫اﻟﺪاﺋﺮة‬ ‫ﻗﻄﺮ‬ ‫ﻧﺼﻒ‬ ‫ﻧﻖ‬ ‫ﺣﯿﺚ‬.
٦-‫ﻧﻘﻄﺔ‬ ‫ﻣﻦ‬ ‫اﻟﻌﻤﻮد‬ ‫ﻃﻮل‬)‫س‬١‫ص‬ ،١(‫ﻟﻤﺴﺘﻘﯿﻢ‬ ‫ﺗﻨﺘﻤﻰ‬ ‫ﻻ‬‫س‬‫ا‬+‫ص‬‫ب‬+‫ج‬=٠
‫ل‬ ‫اﻟﻌﻤﻮد‬ ‫ﻃﻮل‬=
( ١‫ص‬ ، ١‫س‬ ) ‫اﻟﻨﻘﻄﺔ‬ ‫ﺑﯿﻦ‬ ‫اﻟﺒﻌﺪ‬ : ‫ﻣﻠﺤﻮﻇﺔ‬
‫اﻟ‬ ،‫س‬ ‫ﻤﺴﺘﻘﯿﻢ‬=٠)‫اﻟﺼﺎدات‬ ‫ﻣﺤﻮر‬= (|‫س‬١|
‫ﺑﯿﻦ‬ ‫اﻟﺒﻌﺪ‬ ،)‫س‬١‫ص‬ ،١(
‫ص‬ ‫اﻟﻤﺴﺘﻘﯿﻢ‬ ‫و‬=٠)‫ﻣﺤﻮراﻟﺴﯿﻨﺎت‬(=|‫ص‬١|
٧-‫ﻧﻖ‬ ‫ﻗﻄﺮﯾﮭﻤﺎ‬ ‫ﻧﺼﻔﻰ‬ ‫ﻃﻮﻻ‬ ‫ﺗﺴﺎوى‬ ‫إذا‬ ‫داﺋﺮﺗﺎن‬ ‫ﺗﺘﻄﺎﺑﻖ‬١=‫ﻧﻖ‬٢
‫اﻟﺪاﺋﺮة‬ ‫ﻣﻌﺎدﻟﺔ‬
٢‫ص‬ + ١‫ص‬
٢
٢‫س‬ + ١‫س‬
٢
٣٦٠
‫ن‬
‫ن‬
٢
|‫ا‬‫س‬١+‫ص‬ ‫ب‬١+‫ﺟـ‬|
‫ﰈ‬‫ا‬٢
+‫ﱂ‬‫ب‬٢
‫ﱂ‬
‫س‬‫ا‬+‫ص‬‫ب‬+‫ج‬=٠
×)‫س‬١‫ص‬ ،١(
‫ﺻﺲ‬
)‫س‬١‫،ص‬١(
‫ﺻﺺ‬
‫ص‬١
‫س‬١

135. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
135
)‫س‬–‫ء‬(٢
) +‫ص‬–‫ه‬(٢
=‫ﻧﻖ‬٢
‫م‬ ‫ﺣﯿﺚ‬)‫ء‬،‫ه‬(‫اﻟﺪاﺋﺮة‬ ‫ﻗﻄﺮ‬ ‫ﻧﺼﻒ‬ ‫ﻧﻖ‬ ، ‫اﻟﺪاﺋﺮة‬ ‫ﻣﺮﻛﺰ‬
‫ـــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫م‬ ‫ﻣﺮﻛﺰھﺎ‬ ‫ﻛﺎن‬ ‫إذا‬ ‫اﻟﺪاﺋﺮة‬ ‫ﻣﻌﺎدﻟﺔ‬ ‫اﻛﺘﺐ‬)٤،-٣(‫ﯾﺴﺎوى‬ ‫ﻗﻄﺮھﺎ‬ ‫ﻧﺼﻒ‬ ‫ﻃﻮل‬ ‫و‬٥‫وﺣﺪات‬
‫اﻟﺤﻞ‬:
‫اﻟﻨ‬ ‫أن‬ ‫ﺑﻔﺮض‬‫ر‬ ‫ﻘﻄﺔ‬)‫ص‬ ، ‫س‬(‫د‬ ‫اﻟﺪاﺋﺮة‬
e‫اﻟﺪاﺋﺮة‬ ‫ﻣﺮﻛﺰ‬)٤،-٣(‫اﻟﺪاﺋﺮة‬ ‫ﻗﻄﺮ‬ ‫ﻧﺼﻒ‬ ‫ﻃﻮل‬ ،=٥‫وﺣﺪات‬
Ε‫ء‬=٤،‫ه‬=-٣،‫ﻧﻖ‬=٥‫وﺣﺪات‬
Ε‫ھﻰ‬ ‫اﻟﻤﻌﺎدﻟﺔ‬ ‫ﺗﻜﻮن‬)‫س‬–٤(٢
) +‫ص‬+٣(٢
) =٥(٢
‫اى‬) :‫س‬–٤(٢
) +‫ص‬+٣(٢
=٢٥
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫م‬ ‫ﻣﺮﻛﺰھﺎ‬ ‫ﻛﺎن‬ ‫إذا‬ ‫اﻟﺪاﺋﺮة‬ ‫ﻣﻌﺎدﻟﺔ‬ ‫اﻛﺘﺐ‬)٢،٠(‫ﻗﻄﺮھﺎ‬ ‫ﻃﻮل‬ ‫و‬‫؟‬٢٨‫اﻟﻮﺣﺪات‬ ‫ﻓﻰ‬
‫اﻟﺤﻞ‬:‫م‬)٢،٠(‫ﻧﻖ‬ ،=‫وﺣﺪة‬
e)‫س‬–‫ء‬(٢
) +‫ص‬–‫ه‬(٢
=‫ﻧﻖ‬٢
Ε‫اﻟﻤﻌﺎدﻟﺔ‬)‫س‬–٢(٢
) +‫ص‬–٠(٢
( ) =٢
Ε‫ﻰ‬ ‫ﻫ‬ ‫ة‬ ‫ﺮ‬ ‫ﺋ‬ ‫ا‬ ‫ﺪ‬ ‫ﻟ‬ ‫ا‬ ‫ﺔ‬ ‫ﻟ‬ ‫د‬ ‫ﺎ‬ ‫ﻌ‬ ‫ﻣ‬)‫س‬–٢(٢
+‫ص‬٢
=٧
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﻣﺮﻛﺰھﺎ‬ ‫ﻛﺎن‬ ‫إذا‬ ‫اﻟﺪاﺋﺮة‬ ‫ﻣﻌﺎدﻟﺔ‬ ‫اﻛﺘﺐ‬)٠،-٥(‫ﺑﺎﻟﻨﻘﻄﺔ‬ ‫ﺗﻤﺮ‬ ‫و‬‫ا‬)-٢،-٩(
‫؟‬٢٨
٢
‫؟‬٢٨
٢

136. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
136
‫اﻟﺤﻞ‬:‫ﺑﯿﻦ‬ ‫اﻟﺒﻌﺪ‬ ‫ﻣﺮﺑﻊ‬‫ا‬‫م‬ ،) =‫م‬‫ا‬(٢
=
‫ﻧﻖ‬٢
) =-٢–٠(٢
) +-٩+٥(٢
=٢٠
‫م‬ ،)٠،-٥(‫اﻟﺪاﺋﺮة‬ ‫ﻣﺮﻛﺰ‬
Ε‫ھﻰ‬ ‫اﻟﺪاﺋﺮة‬ ‫ﻣﻌﺎدﻟﺔ‬)‫س‬–‫ء‬(٢
) +‫ص‬–‫ه‬(٢
=‫ﻧﻖ‬٢
Ε‫ھﻰ‬ ‫اﻟﻤﻌﺎدﻟﺔ‬)‫س‬–٠(٢
) +‫ص‬+٥(٢
=٢٠
‫اى‬:‫س‬٢
) +‫ص‬+٥(٢
=٢٠
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻟﻮﺣﺪات‬ ‫ﻣﻦ‬ ‫ﻧﻖ‬ ‫ﯾﺴﺎوى‬ ‫ﻗﻄﺮھﺎ‬ ‫ﻧﺼﻒ‬ ‫ﻃﻮل‬ ‫و‬ ‫اﻻﺻﻞ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻣﺮﻛﺰھﺎ‬ ‫ﻛﺎن‬ ‫إذا‬ ‫اﻟﺪاﺋﺮة‬ ‫ﻣﻌﺎدﻟﺔ‬ ‫اﻛﺘﺐ‬
‫اﻟﺤﻞ‬:
e‫م‬)٠،٠(‫اﻟﺪاﺋﺮة‬ ‫ﻗﻄﺮ‬ ‫ﻧﺼﻒ‬ ‫ﻃﻮل‬ ،=‫ﻧﻖ‬
Ε‫ھﻰ‬ ‫اﻟﺪاﺋﺮة‬ ‫ﻣﻌﺎدﻟﺔ‬)‫س‬–٠(٢
) +‫ص‬–٠(٢
=‫ﻧﻖ‬٢
‫وﺣﺪة‬ ‫ﻧﻖ‬ ‫ﻗﻄﺮھﺎ‬ ‫ﻧﺼﻒ‬ ‫و‬ ‫اﻻﺻﻞ‬ ‫ﻧﻘﻄﺔ‬ ‫ﻣﺮﻛﺰھﺎ‬ ‫اﻟﺘﻰ‬ ‫اﻟﺪاﺋﺮة‬ ‫ﻣﻌﺎدﻟﺔ‬ ‫اى‬
‫ھﻰ‬:‫س‬٢
+‫ص‬٢
=‫ﻧﻖ‬٢
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﻗﻄﺮھﺎ‬ ‫اﻟﺘﻰ‬ ‫اﻟﺪاﺋﺮة‬ ‫ﻣﻌﺎدﻟﺔ‬ ‫اﻛﺘﺐ‬‫ب‬‫ا‬"‫ﺣﯿﺚ‬‫ا‬)٢،-٧(‫ب‬ ،)٦،٥(
‫اﻟﺤﻞ‬:
‫م‬ ‫اﻟﻨﻘﻄﺔ‬ ‫ﺑﻔﺮض‬)‫ء‬‫ھـ‬ ،(‫ﻗﻄﺮھﺎ‬ ‫اﻟﺘﻰ‬ ‫ﻟﻠﺪاﺋﺮة‬ ‫ﻣﺮﻛﺰ‬‫ب‬‫ا‬"
‫ﻣﻨﺘﺼﻒ‬ ‫ھﻰ‬ ‫و‬‫ب‬‫ا‬"
Ε‫م‬)‫ء‬‫ھـ‬ ،) =(،() =٤،-١(
‫ﻧﻖ‬٢
) =‫م‬‫ا‬(٢
) =٢–٤(٢
) +-٧+١(٢
=٤+٣٦=٤٠
‫اﻟﺪاﺋﺮة‬ ‫ﻣﻌﺎدﻟﺔ‬ ‫ﺗﻜﻮن‬) :‫س‬–٤(٢
) +‫ص‬+١(٢
=٤٠
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــ‬
‫ﻣﻌﺎدﻟﺘﮭﺎ‬ ‫اﻟﺘﻰ‬ ‫د‬ ‫اﻟﺪاﺋﺮة‬ ‫ﻣﺴﺘﻮى‬ ‫ﻓﻰ‬ ( ١‫ص‬ ،١‫)س‬ ‫اﻟﻨﻘﻄﺔ‬ ‫ﺑﻔﺮض‬ : ‫ھﺎﻣﺔ‬ ‫ﻣﻼﺣﻈﺔ‬
)‫س‬–‫ء‬(٢
) +‫ص‬–‫ه‬(٢
=‫ﻧﻖ‬٢
‫ﻓﺈﻧﮫ‬:
١-‫ﻛﺎن‬ ‫إذا‬)‫س‬–‫ء‬(٢
) +‫ص‬–‫ه‬(٢
<‫ﻧﻖ‬٢
‫اﻟﺪاﺋﺮة‬ ‫ﺧﺎرج‬ ‫ﺗﻘﻊ‬ ‫اﻟﻨﻘﻄﺔ‬ ‫ﻓﺈن‬
٢-‫ﻛﺎن‬ ‫إذا‬)‫س‬–‫ء‬(٢
) +‫ص‬–‫ه‬(٢
>‫ﻧﻖ‬٢
‫اﻟﺪاﺋﺮة‬ ‫داﺧﻞ‬ ‫ﺗﻘﻊ‬ ‫اﻟﻨﻘﻄﺔ‬ ‫ﻓﺈن‬
٣-‫ﻛﺎن‬ ‫إذا‬)‫س‬–‫ء‬(٢
) +‫ص‬–‫ه‬(٢
=‫ﻧﻖ‬٢
‫اﻟﺪاﺋﺮة‬ ‫ﺗﻘﻊ‬ ‫اﻟﻨﻘﻄﺔ‬ ‫ﻓﺈن‬
‫ا‬
)-٢،-٩(
‫ﻧﻖ‬
‫م‬
)٠،-٥(
‫ا‬)٢،-٧(
‫م‬)‫ء‬‫،ھـ‬(
×‫ب‬)٦،٥(
٦ + ٢
٢
٥+ ٧-
٢

137. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
137
‫ﻣﺜﺎل‬:‫ﻣﻌﺎدﻟﺘﮭﺎ‬ ‫اﻟﺘﻰ‬ ‫د‬ ‫اﻟﺪاﺋﺮة‬ ‫اﻟﻰ‬ ‫ﺗﻨﺘﻤﻰ‬ ‫اﻟﺘﺎﻟﯿﺔ‬ ‫اﻟﻨﻘﻂ‬ ‫ﻣﻮﺿﻊ‬ ‫ﺣﺪد‬
)‫س‬–٦(٢
) +‫ص‬+١(٢
=٢٥‫اﻟﻨﻘﻂ‬ ‫ﺣﯿﺚ‬‫ا‬)٩،٣(‫ب‬ ،)٧،٥(‫ﺟـ‬ ،)٢،-٣(
‫اﻟﺤﻞ‬:‫ﻋﻦ‬ ‫ﺑﺎﻟﺘﻌﻮﯾﺾ‬‫ا‬‫ﻧﺠﺪ‬ ‫اﻟﻤﻌﻄﺎه‬ ‫اﻟﻤﻌﺎدﻟﺔ‬ ‫ﻓﻰ‬:
‫اﻻﯾﻤﻦ‬ ‫اﻟﻄﺮف‬) =٩–٦(٢
) +٣+١(٢
=٩+١٦=٢٥=‫اﻻﯾﺴﺮ‬ ‫اﻟﻄﺮف‬
Ε‫اﻟﻨﻘﻄﺔ‬‫ا‬)٩،٣(‫د‬ ‫اﻟﺪاﺋﺮة‬
‫ﻧﺠﺪ‬ ‫اﻟﻤﻌﻄﺎه‬ ‫اﻟﻤﻌﺎدﻟﺔ‬ ‫ﻓﻰ‬ ‫ب‬ ‫ﻋﻦ‬ ‫ﺑﺎﻟﺘﻌﻮﯾﺾ‬:
‫اﻻﯾﻤﻦ‬ ‫اﻟﻄﺮف‬) =٧–٦(٢
) +٥+١(٢
=١+٣٦=٣٧<‫اﻻﯾﺴﺮ‬ ‫اﻟﻄﺮف‬
Ε‫اﻟﺪاﺋﺮة‬ ‫ﺧﺎرج‬ ‫ﺗﻘﻊ‬ ‫ب‬ ‫اﻟﻨﻘﻄﺔ‬
‫اﻟﻤﻌﻄﺎه‬ ‫اﻟﻤﻌﺎدﻟﺔ‬ ‫ﻓﻰ‬ ‫ﺟـ‬ ‫ﻋﻦ‬ ‫ﺑﺎﻟﺘﻌﻮﯾﺾ‬:
‫اﻻﯾﻤﻦ‬ ‫اﻟﻄﺮف‬) =٢–٦(٢
) +-٣+١(٢
=١٤+٤=١٨>‫اﻻﯾﺴﺮ‬ ‫اﻟﻄﺮف‬
Ε‫اﻟﺪاﺋﺮة‬ ‫داﺧﻞ‬ ‫ﺗﻘﻊ‬ ‫ﺟـ‬ ‫اﻟﻨﻘﻄﺔ‬.
‫ـــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫د‬ ‫ﻓﯿﮫ‬ ‫اﻟﻤﻘﺎﺑﻞ‬ ‫اﻟﺸﻜﻞ‬١‫د‬ ،٢‫داﺋﺮﺗﺎن‬
‫ﻣﻨﮭﻤﺎ‬ ‫ﻛﻞ‬ ‫ﻣﻌﺎدﻟﺔ‬ ‫أوﺟﺪ‬ ‫ﺛﻢ‬ ‫ﻣﺘﻄﺎﺑﻘﺘﺎن‬ ‫اﻟﺪاﺋﺮﺗﺎن‬ ‫أن‬ ‫أﺛﺒﺖ‬
‫اﻟﺤﻞ‬:
‫ﻗﻄﺮﯾﮭﻤﺎ‬ ‫ﻧﺼﻔﻰ‬ ‫ﻃﻮﻻ‬ ‫ﺗﺴﺎوى‬ ‫إذا‬ ‫اﻟﺪاﺋﺮﺗﺎن‬ ‫ﺗﺘﻄﺎﺑﻖ‬
e‫ﻧﻖ‬١=‫ﻧﻖ‬٢=٢‫وﺣﺪة‬
‫ﻣﺘﻄﺎﺑﻘﺘﺎن‬ ‫اﻟﺪاﺋﺮﺗﺎن‬ Ε
e‫د‬ ‫اﻟﺪاﺋﺮة‬١:‫ﻣﺮﻛﺰھﺎ‬)٠،٠(‫ﻧﻖ‬ ،١=٢‫وﺣﺪة‬
Ε‫د‬ ‫اﻟﺪاﺋﺮة‬ ‫ﻣﻌﺎدﻟﺔ‬١:‫س‬٢
+‫ص‬٢
=٤
e‫د‬ ‫اﻟﺪاﺋﺮة‬٢:‫ﻣﺮﻛﺰھﺎ‬)٥،٢(‫ﻧﻖ‬ ،٢=٢‫وﺣﺪة‬
Ε‫د‬ ‫اﻟﺪاﺋﺮة‬ ‫ﻣﻌﺎدﻟﺔ‬٢) :‫س‬–٥(٢
) +‫ص‬–٢(٢
=٤
‫د‬ ‫اﻟﺪاﺋﺮة‬ ‫أن‬ ‫اﻟﺮﺳﻢ‬ ‫ﻣﻦ‬ ‫ﯾﻼﺣﻆ‬ ‫و‬٢‫د‬ ‫اﻟﺪاﺋﺮة‬ ‫ﺻﻮرة‬ ‫ھﻰ‬١‫ﺑﺎﻻﻧﺘﻘﺎل‬)٥،٢(
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﯾﺎﺗﻰ‬ ‫ﻣﺎ‬ ‫أﻛﻤـــﻞ‬:
‫د‬ ‫اﻟﺪاﺋﺮة‬ ‫ﻛﺎﻧﺖ‬ ‫إذا‬١:‫س‬٢
+‫ص‬٢
=٤‫د‬ ‫اﻟﺪاﺋﺮة‬ ،٢‫د‬ ‫اﻟﺪاﺋﺮة‬ ‫ﺻﻮرة‬ ‫ھﻰ‬١‫ﺑﺎﻻﻧﺘﻘﺎل‬)-٤،٣(
‫د‬ ‫اﻟﺪاﺋﺮة‬ ‫ﻣﻌﺎدﻟﺔ‬ ‫ﻓﺈن‬٢‫ھﻰ‬)‫س‬+٤(٢
) +‫ص‬–٣(٢
=٤

138. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
138
‫ﻣﺜﺎل‬:‫اﻟﻨﻘﻄﺔ‬ ‫ﻣﺮﻛﺰھﺎ‬ ‫اﻟﺘﻰ‬ ‫اﻟﺪاﺋﺮة‬ ‫ﻣﻌﺎدﻟﺔ‬ ‫اﻛﺘﺐ‬)٥،٤(‫س‬ ‫اﻟﻤﺴﺘﻘﯿﻢ‬ ‫ﺗﻤﺲ‬ ‫و‬=٢
‫اﻟﺤﻞ‬:
e‫اﻟﺪاﺋﺮة‬ ‫ﻣﺮﻛﺰ‬‫م‬)٥،٤(‫ﻗﻄﺮھﺎ‬ ‫ﻧﺼﻒ‬ ‫ﻃﻮل‬ ‫ﻧﻖ‬ ،
‫س‬ ‫اﻟﻤﺴﺘﻘﯿﻢ‬ ‫اﻟﻰ‬ ‫م‬ ‫ﻧﻘﻄﺔ‬ ‫ﻣﻦ‬ ‫اﻟﻌﻤﻮد‬ ‫ﻃﻮل‬ ‫ﻗﺎﻧﻮن‬ ‫ﻣﻦ‬ ‫و‬-٢=٠
‫ﺣﯿﺚ‬‫ا‬=١‫ب‬ ،=٠‫ﺟـ‬ ،=-٢
Ε‫ﻧﻖ‬=‫م‬‫ا‬==|٥–٢|=|٣|=٣
Ε‫ھﻰ‬ ‫اﻟﺪاﺋﺮة‬ ‫ﻣﻌﺎدﻟﺔ‬)‫س‬–‫ء‬(٢
) +‫ص‬–‫ه‬(٢
=‫ﻧﻖ‬٢
Ε‫ھﻰ‬ ‫اﻟﻤﻌﺎدﻟﺔ‬)‫س‬–٥(٢
) +‫ص‬–٤(٢
) =٣(٢
=٩
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
: ‫داﺋﺮة‬ ‫ﻣﻌﺎدﻟﺔ‬ ‫ﻣﻦ‬ ‫داﺋﺮة‬ ‫ﻗﻄﺮ‬ ‫ﻧﺼﻒ‬ ‫ﻃﻮل‬ ‫و‬ ‫ﻣﺮﻛﺰ‬ ‫اﯾﺠﺎد‬ *
‫ﻣﺜﺎل‬:‫اﻵﺗﯿﺔ‬ ‫اﻟﺪواﺋﺮ‬ ‫ﻣﻦ‬ ‫ﻛﻞ‬ ‫ﻗﻄﺮ‬ ‫ﻧﺼﻒ‬ ‫ﻃﻮل‬ ‫و‬ ‫اﻟﻤﺮﻛﺰ‬ ‫إﺣﺪاﺛﯿﺎ‬ ‫أوﺟﺪ‬:
)‫أ‬) (‫س‬–٢(٢
) +‫ص‬+٣(٢
=١٧)‫ب‬) (‫س‬+١(٢
=١٦‫ص‬ ‫ــ‬٢
‫اﻟﺤﻞ‬:
)‫أ‬(‫اﻟﻤﻌﺎدﻟﺔ‬ ‫ﻓﻰ‬ ‫ﻧﻈﯿﺮه‬ ‫و‬ ‫اﻟﻤﻌﻄﺎه‬ ‫اﻟﻤﻌﺎدﻟﺔ‬ ‫ﻓﻰ‬ ‫ﺟﺒﺮى‬ ‫ﻣﻘﺪار‬ ‫ﻛﻞ‬ ‫ﺑﻤﻘﺎرﻧﺔ‬
)‫س‬–‫ء‬(٢
) +‫ص‬–‫ھـ‬(٢
=‫ﻧﻖ‬٢
‫اﻟﻨﻘﻄﺔ‬ ‫ﺣﯿﺚ‬)‫ء‬‫ھـ‬ ،(‫ﻗﻄﺮھﺎ‬ ‫ﻧﺼﻒ‬ ‫ﻃﻮل‬ ‫ﻧﻖ‬ ، ‫اﻟﺪاﺋﺮة‬ ‫ﻣﺮﻛﺰ‬
Ε‫س‬–‫ء‬=‫س‬–٢Ε‫ء‬=٢
‫ص‬ ،–‫ھـ‬=‫ص‬+٣Ε‫ھـ‬=-٣
e‫ﻧﻖ‬٢
=١٧Ε‫ﻧﻖ‬=‫؟‬١٧
‫اﻟﻨﻘﻄﺔ‬ ‫اﻟﺪاﺋﺮة‬ ‫ﻣﺮﻛﺰ‬ ‫ﻓﯿﻜﻮن‬)٢،-٣(‫ﯾﺴﺎوى‬ ‫ﻗﻄﺮھﺎ‬ ‫ﻧﺼﻒ‬ ‫ﻃﻮل‬ ‫و‬‫؟‬١٧‫وﺣﺪة‬
)‫ب‬(‫ا‬ ‫ﻓﻰ‬ ‫اﻟﻤﻌﺎدﻟﺔ‬ ‫وﺿﻊ‬ ‫ﯾﺠﺐ‬‫ﺟﺒﺮى‬ ‫ﻣﻘﺪار‬ ‫ﻛﻞ‬ ‫ﺑﻤﻘﺎرﻧﺔ‬ ‫ﺛﻢ‬ ‫أوﻻ‬ ‫اﻻﺣﺪاﺛﯿﺔ‬ ‫ﻟﺼﻮرة‬
‫اﻟﻤﻌﻄﺎه‬ ‫اﻟﻤﻌﺎدﻟﺔ‬ ‫ﻓﻰ‬)‫س‬+١(٢
+‫ص‬٢
=١٦‫اﻟﻤﻌﺎدﻟﺔ‬ ‫ﻓﻰ‬ ‫ﻧﻈﯿﺮه‬ ‫و‬
)‫س‬–‫ء‬(٢
) +‫ص‬–‫ھـ‬(٢
=‫ﻧﻖ‬٢
‫اﻟﻨﻘﻄﺔ‬ ‫ﺣﯿﺚ‬)‫ء‬‫ھـ‬ ،(‫ﻧ‬ ‫ﻃﻮل‬ ‫ﻧﻖ‬ ، ‫اﻟﺪاﺋﺮة‬ ‫ﻣﺮﻛﺰ‬‫ﻗﻄﺮھﺎ‬ ‫ﺼﻒ‬
Ε‫س‬–‫ء‬=‫س‬+١Ε‫ء‬=-١
‫ص‬ ،–‫ھـ‬=‫ص‬Ε‫ھـ‬=‫ﺻﻔﺮ‬
e‫ﻧﻖ‬٢
=١٦Ε‫ﻧﻖ‬=٤
‫س‬=٢
‫م‬
‫ا‬ ‫ﻧﻖ‬
|‫ا‬‫س‬١+‫ص‬ ‫ب‬١+‫ﺟـ‬|
‫ﰈ‬‫ا‬٢
+‫ﱂ‬‫ب‬٢
‫ﱂ‬

139. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
139
‫اﻟﻨﻘﻄﺔ‬ ‫اﻟﺪاﺋﺮة‬ ‫ﻣﺮﻛﺰ‬ ‫ﻓﯿﻜﻮن‬)-١،٠(‫ﯾﺴﺎوى‬ ‫ﻗﻄﺮھﺎ‬ ‫ﻧﺼﻒ‬ ‫ﻃﻮل‬ ‫و‬٤‫وﺣﺪة‬
e‫ﻣ‬‫ﻣﺮﻛﺰھﺎ‬ ‫اﻟﺘﻰ‬ ‫اﻟﺪاﺋﺮة‬ ‫ﻌﺎدﻟﺔ‬)‫ء‬،‫ه‬(‫اﻟﻮﺣﺪات‬ ‫ﻣﻦ‬ ‫ﻧﻖ‬ ‫ﯾﺴﺎوى‬ ‫ﻗﻄﺮھﺎ‬ ‫ﻧﺼﻒ‬ ‫وﻃﻮل‬
‫ھﻰ‬)‫س‬–‫ء‬(٢
) +‫ص‬–‫ھـ‬(٢
=‫ﻧﻖ‬٢
‫اﻻﻗﻮاس‬ ‫ﺑﻔﻚ‬
Ε‫س‬٢
+‫ص‬٢
‫ــ‬٢‫ء‬‫ــ‬ ‫س‬٢‫ص‬ ‫ھـ‬+‫ء‬٢
+‫ھـ‬٢
‫ﻧﻖ‬ ‫ــ‬٢
=٠
e‫ء‬،‫ه‬‫ﻧﻖ‬ ،‫ﺛﻮاﺑﺖ‬Ε‫اﻟﻤﻘﺪار‬‫ء‬٢
+‫ھـ‬٢
‫ﻧﻖ‬ ‫ــ‬٢
=‫ﺛﺎ‬ ‫ﻣﻘﺪارا‬‫ﺑﺘﺎ‬
‫ل‬ ‫ﺑﻮﺿﻊ‬ ‫و‬=‫ــ‬‫ء‬‫ك‬ ،=‫ﺟـ‬ ، ‫ھـ‬ ‫ــ‬=‫ء‬٢
+‫ھـ‬٢
‫ﻧﻖ‬ ‫ــ‬٢
‫اﻟﺼﻮرة‬ ‫ﻋﻠﻰ‬ ‫اﻟﻤﻌﺎدﻟﺔ‬ ‫ﺗﺼﺒﺢ‬
‫اﻟﻌﺎﻣﺔ‬ ‫اﻟﺼﻮرة‬‫داﺋﺮة‬ ‫ﻟﻤﻌﺎدﻟﺔ‬:‫س‬٢
+‫ص‬٢
+٢‫س‬ ‫ل‬+٢‫ص‬ ‫ك‬+‫ﺟـ‬=٠
‫ﻣﺮﻛﺰھﺎ‬)‫ك‬ ‫ــ‬ ، ‫ل‬ ‫ــ‬(‫ﺣﯿﺚ‬ ‫ﻧﻖ‬ ‫ﯾﺴﺎوى‬ ‫ﻗﻄﺮھﺎ‬ ‫ﻧﺼﻒ‬ ‫ﻃﻮل‬ ‫و‬
‫ﻧﻖ‬=‫ﰈ‬‫ل‬٢
+‫ﱂ‬‫ك‬٢
‫ﱂ‬‫ــ‬‫ﱂ‬‫ﱂ‬‫ﺟـ‬‫ﱂ‬،‫ل‬٢
+‫ك‬٢
‫ﺟـ‬ ‫ــ‬<٠
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫م‬ ‫اﻟﻨﻘﻄﺔ‬ ‫ﻣﺮﻛﺰھﺎ‬ ‫ﻛﺎن‬ ‫إذا‬ ‫اﻟﺪاﺋﺮة‬ ‫ﻟﻤﻌﺎدﻟﺔ‬ ‫اﻟﻌﺎﻣﺔ‬ ‫اﻟﺼﻮرة‬ ‫اﻛﺘﺐ‬)٦،-٣(‫ﻧﺼ‬ ‫ﻃﻮل‬ ‫و‬‫ﻒ‬
‫ﻗﻄﺮھﺎ‬‫ﯾﺴﺎوى‬٥‫وﺣﺪات‬.
‫اﻟﺤﻞ‬:
e‫اﻟﺪ‬ ‫ﻣﺮﻛﺰ‬‫اﺋﺮة‬)-، ‫ل‬-‫ك‬(‫اﻟﻌﺎﻣﺔ‬ ‫اﻟﺼﻮرة‬ ‫ﻓﻰ‬‫ﻟﻤﻌﺎدﻟﺔ‬‫اﻟﺪاﺋﺮة‬
‫اﻟﺪاﺋﺮة‬ ‫ﻣﺮﻛﺰ‬ ،)٦،-٣(‫ﻣﻌﻄﻰ‬
Ε‫ل‬=-٦‫ك‬ ،=٣
e‫ﻧﻖ‬=٥‫ﺟـ‬ ،=‫ل‬٢
+‫ك‬٢
‫ﻧﻖ‬ ‫ــ‬٢
Ε‫ﺟـ‬) =-٦(٢
) +٣(٢
‫ــ‬)٥(٢
=٢٠
‫اﻟﺼﻮرة‬ ‫ﺗﻜﻮن‬ ‫و‬‫ھﻰ‬ ‫اﻟﺪاﺋﺮة‬ ‫ﻟﻤﻌﺎدﻟﺔ‬ ‫اﻟﻌﺎﻣﺔ‬:‫س‬٢
+‫ص‬٢
–١٢‫س‬+٦‫ص‬+٢٠=٠
: ‫ﻣﻠﺤﻮﻇﺔ‬
‫اﻟﺪاﺋﺮة‬ ‫ﻣﻌﺎدﻟﺔ‬ ‫ﺑﺎﺳﺘﺨﺪام‬ ‫اﻟﺤﻞ‬ ‫ﺻﺤﺔ‬ ‫ﻣﻦ‬ ‫اﻟﺘﺤﻘﻖ‬ ‫ﯾﻤﻜﻦ‬)‫س‬-٦(٢
) +‫ص‬+٣(٢
=٢٥‫ﺛﻢ‬
‫اﻟﻨﺘﺎﺋﺞ‬ ‫ﻣﻘﺎرﻧﺔ‬ ‫و‬ ‫ﺗﺒﺴﯿﻄﮭﺎ‬
‫ﻣﺜﻼ‬:‫اﻟﻤﻌﺎدﻟﺔ‬ ‫ﺑﺎﺧﺘﺼﺎر‬)‫س‬-٦(٢
) +‫ص‬+٣(٢
=٢٥‫ك‬ ‫ﻧﺠﺪ‬
‫س‬٢
‫ــ‬١٢‫س‬+٣٦+‫ص‬٢
+٦‫ص‬+٩–٢٥=٠
‫س‬٢
+‫ص‬٢
‫ــ‬١٢‫س‬+٦‫ص‬+٢٠=٠‫اﻟﻌﺎﻣﺔ‬ ‫اﻟﺼﻮرة‬ ‫ﻣﻌﺎدﻟﺔ‬ ‫ھﺬه‬ ‫و‬
‫اﻟﻌﺎ‬ ‫اﻟﺼﻮرة‬‫اﻟﺪاﺋﺮة‬ ‫ﻟﻤﻌﺎدﻟﺔ‬ ‫ﻣﺔ‬

140. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
140
‫ﻣﺜﺎل‬:‫ن‬ ‫اﻟﻨﻘﻄﺔ‬ ‫ﻣﺮﻛﺰھﺎ‬ ‫ﻛﺎن‬ ‫إذا‬ ‫اﻟﺪاﺋﺮة‬ ‫ﻟﻤﻌﺎدﻟﺔ‬ ‫اﻟﻌﺎﻣﺔ‬ ‫اﻟﺼﻮرة‬ ‫اﻛﺘﺐ‬)٥،-٣(‫ﺑﺎﻟﻨﻘﻄﺔ‬ ‫ﺗﻤﺮ‬ ‫و‬
‫ب‬)٢،١. (
‫اﻟﺤﻞ‬:
‫اﻟ‬ ‫ﻗﻄﺮ‬ ‫ﻧﺼﻒ‬ ‫ﻧﻖ‬ ‫ﻧﻔﺮض‬‫ن‬ ‫،ﻣﺮﻛﺰھﺎ‬ ‫اﻟﻤﻌﻄﺎه‬ ‫ﺪاﺋﺮة‬)٥،-٣(
‫ﻧﻖ‬) =‫ن‬ ‫ب‬= (‫؟‬)٢"–٥""(٢
"+")"١"+""٣"(٢
"=٥‫وﺣﺪة‬
Ε‫اﻟﺪاﺋﺮة‬ ‫ﻣﺮﻛﺰ‬)-، ‫ل‬-‫ك‬(‫اﻟﻌﺎﻣﺔ‬ ‫اﻟﺼﻮرة‬ ‫ﻓﻰ‬
Ε‫ل‬=-٥‫ك‬ ،=٣‫ﻧﻖ‬ ،=٥
Ε‫ﺟـ‬=‫ل‬٢
+‫ك‬٢
‫ﻧﻖ‬ ‫ــ‬٢
) =-٥(٢
) +٣(٢
‫ــ‬)٥(٢
=٩
‫اﻟﺪاﺋﺮة‬ ‫ﻟﻤﻌﺎدﻟﺔ‬ ‫اﻟﻌﺎﻣﺔ‬ ‫اﻟﺼﻮرة‬ ‫ﺗﻜﻮن‬ ‫و‬:‫س‬٢
+‫ص‬٢
+٢‫س‬ ‫ل‬+٢‫ص‬ ‫ك‬+‫ﺟـ‬=٠
Ε‫س‬٢
+‫ص‬٢
‫ــ‬١٠‫س‬+٦‫ص‬+٩=٠
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫اﻛﺘﺐ‬‫ﻟ‬ ‫اﻟﻌﺎﻣﺔ‬ ‫اﻟﺼﻮرة‬‫ﻗﻄﺮھﺎ‬ ‫اﻟﺘﻰ‬ ‫اﻟﺪاﺋﺮة‬ ‫ﻤﻌﺎدﻟﺔ‬‫ب‬‫ا‬"‫ﺣﯿﺚ‬‫ا‬)٢،-٧(‫ب‬ ،)٦،٥(
‫اﻟﺤﻞ‬:
‫م‬ ‫اﻟﻨﻘﻄﺔ‬ ‫ﺑﻔﺮض‬)‫ء‬‫ھـ‬ ،(‫ﻗﻄﺮھﺎ‬ ‫اﻟﺘﻰ‬ ‫ﻟﻠﺪاﺋﺮة‬ ‫ﻣﺮﻛﺰ‬‫ب‬‫ا‬"
‫ﻣﻨﺘﺼﻒ‬ ‫ھﻰ‬ ‫و‬‫ب‬‫ا‬"
Ε‫م‬)‫ء‬‫ھـ‬ ،) =(،) = (٤،-١(
Ε‫اﻟﺪاﺋﺮة‬ ‫ﻣﺮﻛﺰ‬)-، ‫ل‬-‫ك‬(‫اﻟﻌﺎﻣﺔ‬ ‫اﻟﺼﻮرة‬ ‫ﻓﻰ‬
B‫ل‬=-٤‫ك‬ ،=١
A‫ﻧﻖ‬٢
) =‫م‬‫ا‬(٢
) =٢–٤(٢
) +-٧+١(٢
=٤+٣٦=٤٠Ε‫ﻧﻖ‬=٢‫؟‬١٠
‫ﺟـ‬ ،=‫ل‬٢
+‫ك‬٢
‫ﻧﻖ‬ ‫ــ‬٢
) =-٤(٢
) +١(٢
–٤٠=-٢٣
‫اﻟﺪاﺋﺮة‬ ‫ﻟﻤﻌﺎدﻟﺔ‬ ‫اﻟﻌﺎﻣﺔ‬ ‫اﻟﺼﻮرة‬ ‫ﺗﻜﻮن‬ ‫و‬:‫س‬٢
+‫ص‬٢
+٢‫س‬ ‫ل‬+٢‫ص‬ ‫ك‬+‫ﺟـ‬=٠
‫س‬ ‫اى‬٢
+‫ص‬٢
–٨‫س‬+٢‫ص‬–٢٣=٠
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫اﻟﻨﻘﻂ‬ ‫ﻛﺎﻧﺖ‬ ‫إذا‬‫ا‬)٣،-٢(‫ب‬ ،)٣،٨(‫ﺟـ‬ ،)-١،٠(‫واﺣﺪة‬ ‫داﺋﺮة‬ ‫اﻟﻰ‬ ‫ﺗﻨﺘﻤﻰ‬
‫أن‬ ‫ﻓﺄﺛﺒﺖ‬‫ب‬ ‫ا‬"‫ﻟﻤﻌﺎدﻟﺘﮭﺎ‬ ‫اﻟﻌﺎﻣﺔ‬ ‫اﻟﺼﻮرة‬ ‫اﻛﺘﺐ‬ ‫ﺛﻢ‬ ‫ﻓﯿﮭﺎ‬ ‫ﻗﻄﺮ‬.
‫ب‬
)٢،١(
‫ﻧﻖ‬
‫ن‬
)٥،-٣(
٦ + ٢
٢
٥+ ٧-
٢
‫ا‬)٢،-٧(
‫م‬)‫ء‬‫،ھـ‬(
×‫ب‬)٦،٥(

141. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
141
‫اﻟﺤﻞ‬:)‫اﻻﺧﺮى‬ ‫اﻟﺤﻠﻮل‬ ‫ﯾﺮاﻋﻰ‬(
‫اﻟﺤﻞ‬:
= e‫ﻣﯿﻞ‬‫ج‬‫ا‬= =
‫ﺟـ‬ ‫ب‬ ‫ﻣﯿﻞ‬ ،= =٢
E‫ﻣﯿﻞ‬‫ج‬‫ا‬×‫ﺟـ‬ ‫ب‬ ‫ﻣﯿﻞ‬=×٢=-١
E‫ج‬ ‫ا‬n‫ج‬‫ـ‬‫ﺟ‬‫ب‬E‫ق‬)‫ﺟـ‬(‫ﻒ‬‫ﻓ‬=٩٠٥
‫داﺋﺮة‬ ‫ﻧﺼﻒ‬ ‫ﻓﻰ‬ ‫ﻣﺮﺳﻮﻣﺔ‬ ‫ﻣﺤﯿﻄﯿﺔ‬
E‫ب‬‫ا‬‫ﻓﻰ‬ ‫ﻗﻄﺮ‬‫اﻟﺪاﺋﺮة‬.
E‫م‬)-، ‫ل‬-‫ك‬(‫ﻣﻨﺘﺼﻒ‬ ‫اﻟﺪاﺋﺮة‬ ‫ﻣﺮﻛﺰ‬‫ب‬‫ا‬"‫اﻟﺪاﺋﺮة‬ ‫ﻗﻄﺮ‬
e‫م‬)-، ‫ل‬-‫ك‬) = (،) = (٣،٣(E‫ل‬=-٣‫ك‬ ،=-٣
‫ﻧﻖ‬ ،٢
=)‫ا‬‫م‬(٢
) =٣–٣(٢
) +-٢–٣(٢
=٠+٢٥=٢٥
‫ﺟـ‬ ،=‫ل‬٢
+‫ك‬٢
‫ﻧﻖ‬ ‫ــ‬٢
) =-٣(٢
) +-٣(٢
–٢٥=-٧
E‫اﻟﺪاﺋﺮة‬ ‫ﻟﻤﻌﺎدﻟﺔ‬ ‫اﻟﻌﺎﻣﺔ‬ ‫اﻟﺼﻮرة‬:‫س‬٢
+‫ص‬٢
+٢‫س‬ ‫ل‬+٢‫ص‬ ‫ك‬+‫ﺟـ‬=٠
‫س‬ ‫أى‬٢
+‫ص‬٢
–٦‫س‬–٦‫ص‬–٧=٠
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
: ‫اﻟﻌﺎﻣﺔ‬ ‫اﻟﺼﻮرة‬ ‫ﻓﻰ‬ ‫اﻟﺪاﺋﺮة‬ ‫ﻣﻌﺎدﻟﺔ‬ ‫ﻟﺘﺼﺒﺢ‬ ‫اﻟﻼزﻣﺔ‬ ‫اﻟﺸﺮوط‬ *
‫س‬٢
+‫ص‬٢
+٢‫س‬ ‫ل‬+٢‫ص‬ ‫ك‬+‫ﺟـ‬=٠‫ﻣﻌﺎ‬ ‫اﻷﺗﯿﺔ‬ ‫اﻟﺜﻼﺛﺔ‬ ‫اﻟﺸﺮوط‬ ‫ﺗﺤﻘﻖ‬ ‫ﯾﺠﺐ‬:
١-‫ص‬ ، ‫س‬ ‫ﻓﻰ‬ ‫اﻟﺜﺎﻧﯿﺔ‬ ‫اﻟﺪرﺟﺔ‬ ‫ﻣﻦ‬ ‫اﻟﻤﻌﺎدﻟﺔ‬
٢-‫ﻣﻌﺎﻣﻞ‬‫س‬٢
=‫ص‬ ‫ﻣﻌﺎﻣﻞ‬٢
=‫اﻟﻮﺣﺪة‬
٣-‫ص‬ ‫س‬ ‫ﻣﻌﺎﻣﻞ‬ ‫أى‬ ‫ص‬ ‫س‬ ‫ﯾﺤﺘﻮى‬ ‫اﻟﺬى‬ ‫اﻟﺤﺪ‬ ‫ﻣﻦ‬ ‫ﺧﺎﻟﯿﺔ‬=٠‫ل‬ ،٢
+‫ك‬٢
–‫ﺟـ‬<٠
‫ب‬)٣،٨( ‫ا‬)٣،-٢(
‫م‬)-‫ل‬،-‫ك‬(
×
‫ﺟـ‬)-١،٠(
١‫ص‬ – ٢‫ص‬
‫س‬٢–‫س‬١
٠ – ٢-
٣+١
١-
٢
٠ – ٨
٣+١
١-
٢
٣ + ٣
٢
٨ + ٢-
٢

142. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
142
‫ﻣﺜﺎل‬:‫داﺋﺮة‬ ‫ﻣﻌﺎدﻟﺔ‬ ‫ﻛﺎﻧﺖ‬ ‫وإذا‬ ‫داﺋﺮة‬ ‫ﺗﻤﺜﻞ‬ ‫اﻵﺗﯿﺔ‬ ‫اﻟﻤﻌﺎدﻻت‬ ‫أى‬.
‫ﻗﻄﺮھﺎ‬ ‫ﻧﺼﻒ‬ ‫ﻃﻮل‬ ‫و‬ ‫ﻣﺮﻛﺰھﺎ‬ ‫أوﺟﺪ‬:
١(‫س‬٢
+‫ص‬٢
–٦‫س‬+٤‫ص‬+١٧=٠٢(٤‫س‬٢
+٤‫ص‬٢
=٤٩
٣(‫س‬٢
+‫ص‬٢
+٤‫س‬–٢‫ص‬=٠٤(‫س‬٢
+‫ص‬٢
+٢‫ص‬ ‫س‬+٣=٠
٥(‫س‬٢
+‫ص‬٢
+٤‫س‬+٢٥=٠٦(٣‫س‬٢
+٢‫ص‬٢
+٦‫س‬–٨‫ص‬=٠
‫اﻟﺤﻞ‬:
١(‫س‬٢
+‫ص‬٢
–٦‫س‬+٤‫ص‬+١٧=٠٣(‫س‬٢
+‫ص‬٢
+٤‫س‬–٢‫ص‬=٠
‫س‬ ‫ﻣﻌﺎﻣﻞ‬٢
=‫ﻣ‬‫ص‬ ‫ﻌﺎﻣﻞ‬٢
=‫اﻟﻮﺣﺪة‬‫س‬ ‫ﻣﻌﺎﻣﻞ‬٢
=‫ص‬ ‫ﻣﻌﺎﻣﻞ‬٢
=‫اﻟﻮﺣﺪة‬
‫ص‬ ‫س‬ ‫ﻋﻠﻰ‬ ‫اﻟﻤﺤﺘﻮى‬ ‫اﻟﺤﺪ‬ ‫ﻣﻦ‬ ‫ﺧﺎﻟﯿﺔ‬ ،‫ص‬ ‫س‬ ‫ﻋﻠﻰ‬ ‫اﻟﻤﺤﺘﻮى‬ ‫اﻟﺤﺪ‬ ‫ﻣﻦ‬ ‫ﺧﺎﻟﯿﺔ‬ ‫اﻟﻤﻌﺎدﻟﺔ‬ ،
‫ل‬ ،=-٣‫ك‬ ،=٢‫ﺟـ‬ ،=١٧‫ل‬ ،=٢‫ك‬ ،=-١‫ﺟـ‬ ،=٠
e‫ل‬٢
+‫ك‬٢
–‫ﺟـ‬=٩+٤–١٧=-٤>٠‫ل‬ ،٢
+‫ك‬٢
–‫ﺟـ‬=٤+١–٠=٥<٠
‫داﺋﺮة‬ ‫ﻟﯿﺴﺖ‬ ‫اﻟﻤﻌﺎدﻟﺔ‬E‫ﻧﻖ‬=‫؟‬٥ E
‫ـــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــ‬‫ﻣﺮﻛﺰھﺎ‬ ‫داﺋﺮة‬ ‫ﺗﻤﺜﻞ‬ ‫اﻟﻤﻌﺎدﻟﺔ‬)-٢،١(
٢(٤‫س‬٢
+٤‫ص‬٢
=٤٩‫ﺑﺎﻟ‬‫ﻋﻠﻰ‬ ‫ﻘﺴﻤﺔ‬٤‫ﻗﻄﺮھﺎ‬ ‫ﻧﺼﻒ‬ ‫ﻃﻮل‬ ،=‫؟‬٥
E‫س‬٢
+‫ص‬٢
‫ــ‬=٠‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬ ‫ﻣﻌﺎﻣﻞ‬٢
=‫ص‬ ‫ﻣﻌﺎﻣﻞ‬٢
=‫اﻟﻮﺣﺪة‬٤(‫س‬٢
+‫ص‬٢
+٢‫ص‬ ‫س‬+٣=٠
‫ا‬ ‫ﻣﻦ‬ ‫ﺧﺎﻟﯿﺔ‬ ‫اﻟﻤﻌﺎدﻟﺔ‬ ،‫ص‬ ‫س‬ ‫ﻋﻠﻰ‬ ‫اﻟﻤﺤﺘﻮى‬ ‫ﻟﺤﺪ‬‫س‬ ‫ﻣﻌﺎﻣﻞ‬٢
=‫ص‬ ‫ﻣﻌﺎﻣﻞ‬٢
=‫اﻟﻮﺣﺪة‬
‫ل‬ ،=٠‫ك‬ ،=٠‫ﺟـ‬ ،=‫ــ‬‫ص‬ ‫س‬ ‫ﻋﻠﻰ‬ ‫ﻋﻠﻰ‬ ‫ﺗﺤﺘﻮى‬ ‫اﻟﻤﻌﺎدﻟﺔ‬ ‫و‬
‫ل‬ ،٢
+‫ك‬٢
–‫ﺟـ‬=٠+٠–)-(<٠E‫داﺋﺮة‬ ‫ﻟﯿﺴﺖ‬ ‫اﻟﻤﻌﺎدﻟﺔ‬
‫ﻧﻖ‬=‫ﻣﺮﻛﺰھﺎ‬ ‫داﺋﺮة‬ ‫اﻟﻤﻌﺎدﻟﺔ‬)٠،٠(
‫ﻟﻤﻌﺎدﻟﺘﮭﺎ‬ ‫اﻟﻌﺎﻣﺔ‬ ‫اﻟﺼﻮرة‬ ‫ﻣﻦ‬ ‫ﻗﻄﺮھﺎ‬ ‫ﻧﺼﻒ‬ ‫ﻃﻮل‬ ‫و‬ ‫داﺋﺮة‬ ‫ﻣﺮﻛﺰ‬ ‫إﺣﺪاﺛﻰ‬ ‫ﻟﺘﻌﯿﯿﻦ‬
١(‫ﺣﯿﺚ‬ ‫اﻟﻌﺎﻣﺔ‬ ‫اﻟﺼﻮرة‬ ‫ﻓﻰ‬ ‫اﻟﻤﻌﺎدﻟﺔ‬ ‫وﺿﻊ‬ ‫ﻣﻦ‬ ‫أوﻻ‬ ‫ﺗﺤﻘﻖ‬:‫س‬ ‫ﻣﻌﺎﻣﻞ‬٢
‫ص‬ ‫ﻣﻌﺎﻣﻞ‬٢
=١
٢(‫اﻟﻤﺮﻛﺰ‬ ‫إﺣﺪاﺛﯿﺎ‬)-، ‫ل‬-‫ك‬(‫أى‬)،(
٣(‫ﻧ‬ ‫ﻃﻮل‬‫اﻟﻌﻼﻗﺔ‬ ‫ﻣﻦ‬ ‫ﯾﺘﻌﯿﻦ‬ ‫اﻟﺪاﺋﺮة‬ ‫ﻗﻄﺮ‬ ‫ﺼﻒ‬:‫ﻧﻖ‬=‫؟‬‫ل‬٢
"+"‫ك‬٢
"‫ــ‬""‫ﺟـ‬"
‫ل‬ ‫ﺣﯿﺚ‬٢
+‫ك‬٢
‫ﺟـ‬ ‫ــ‬<٠
‫ص‬ ‫ﻣﻌﺎﻣﻞ‬ ‫ــ‬
٢
‫س‬ ‫ﻣﻌﺎﻣﻞ‬ ‫ــ‬
٢
٤٩
٤
٧
٢
٤٩
٤

143. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
143
٥(‫س‬٢
+‫ص‬٢
+٤‫س‬+٢٥=٠٦(٣‫س‬٢
+٢‫ص‬٢
+٦‫س‬–٨‫ص‬=٠
‫س‬ ‫ﻣﻌﺎﻣﻞ‬٢
=‫ص‬ ‫ﻣﻌﺎﻣﻞ‬٢
=١
‫ص‬ ‫س‬ ‫ﻋﻠﻰ‬ ‫اﻟﻤﺤﺘﻮى‬ ‫اﻟﺤﺪ‬ ‫ﻣﻦ‬ ‫ﺧﺎﻟﯿﺔ‬ ‫اﻟﻤﻌﺎدﻟﺔ‬ ،e‫س‬ ‫ﻞ‬ ‫ﻣ‬ ‫ﺎ‬ ‫ﻌ‬ ‫ﻣ‬٢
≠‫ص‬ ‫ﻞ‬ ‫ﻣ‬ ‫ﺎ‬ ‫ﻌ‬ ‫ﻣ‬٢
‫ل‬ ،=٢‫ك‬ ،=٠‫ﺟـ‬ ،=٢٥
‫ل‬ ،٢
+‫ك‬٢
–‫ﺟـ‬=٤+٠–٢٥=-٢٤>٠E‫داﺋﺮة‬ ‫ﻟﯿﺴﺖ‬ ‫اﻟﻤﻌﺎدﻟﺔ‬
E‫داﺋﺮة‬ ‫ﻟﯿﺴﺖ‬ ‫اﻟﻤﻌﺎدﻟﺔ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫د‬ ‫اﻟﺪاﺋﺮﺗﯿﻦ‬ ‫ھﻞ‬١:‫س‬٢
+‫ص‬٢
–١٠‫س‬–٨‫ص‬+١٦=٠
‫د‬ ،٢:‫س‬٢
+‫ص‬٢
+١٤‫س‬+١٠‫ص‬–٢٦=٠
‫إﺟﺎﺑﺘﻚ‬ ‫ﻓﺴﺮ‬ ‫؟‬ ‫اﻟﺨﺎرج‬ ‫ﻣﻦ‬ ‫ﻣﺘﻤﺎﺳﺘﺎن‬.
‫اﻟﺤﻞ‬:
‫ﻧﻖ‬ ‫ﺑﻔﺮض‬١‫ﻧﻖ‬ ،٢‫د‬ ‫ﻗﻄﺮي‬ ‫ﻧﺼﻔﻰ‬ ‫ﻃﻮﻻ‬١‫د‬ ،٢‫اﻟﺘﺮﺗﯿﺐ‬ ‫ﻋﻠﻰ‬.
‫م‬١)-‫ل‬١،-‫ك‬١(‫د‬ ‫اﻟﺪاﺋﺮة‬ ‫ﻣﺮﻛﺰ‬١‫م‬ ،٢)-‫ل‬٢،-‫ك‬٢(‫د‬ ‫اﻟﺪاﺋﺮة‬ ‫ﻣﺮﻛﺰ‬٢
e‫د‬١:‫س‬٢
+‫ص‬٢
–١٠‫س‬–٨‫ص‬+١٦=٠
E‫ل‬١=-٥‫ك‬ ،١=-٤‫ﺟـ‬ ،=١٦E‫ل‬١
٢
+‫ك‬١
٢
–‫ﺟـ‬=٢٥+١٦–١٦=٢٥
E‫ﻧﻖ‬=٥‫د‬ ‫اﻟﺪاﺋﺮة‬ ‫ﻣﺮﻛﺰ‬ ، ‫وﺣﺪة‬١‫م‬ ‫ھﻮ‬١)٥،٤] ............ (١[
e‫د‬٢:‫س‬٢
+‫ص‬٢
+١٤‫س‬+١٠‫ص‬–٢٦=٠
E‫ل‬٢=٧‫ك‬ ،٢=٥‫ﺟـ‬ ،=-٢٦E‫ل‬٢
٢
+‫ك‬٢
٢
–‫ﺟـ‬=٤٩+٢٥+٢٦=١٠٠<٠
E‫ﻧﻖ‬٢=١٠‫د‬ ‫اﻟﺪاﺋﺮة‬ ‫ﻣﺮﻛﺰ‬ ، ‫وﺣﺪة‬٢‫م‬ ‫ھﻮ‬٢)-٧،-٥] ....... (٢[
‫ﻣﻦ‬١،٢‫ﻧﺠﺪ‬:‫ﻧﻖ‬١+‫ﻧﻖ‬٢=٥+١٠=١٥
‫اﻟﻤﺮﻛﺰﯾﻦ‬ ‫ﺧﻂ‬ ‫ﻃﻮل‬=‫م‬١‫م‬٢=‫؟‬)-"٧"–٥"("
٢
"+")"-"٥""–"٤""(٢
"=١٥
e‫م‬١‫م‬٢=‫ﻧﻖ‬١+‫ﻧﻖ‬٢E‫اﻟﺨﺎرج‬ ‫ﻣﻦ‬ ‫ﻣﺘﻤﺎﺳﺘﺎن‬ ‫اﻟﺪاﺋﺮﺗﺎن‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــ‬
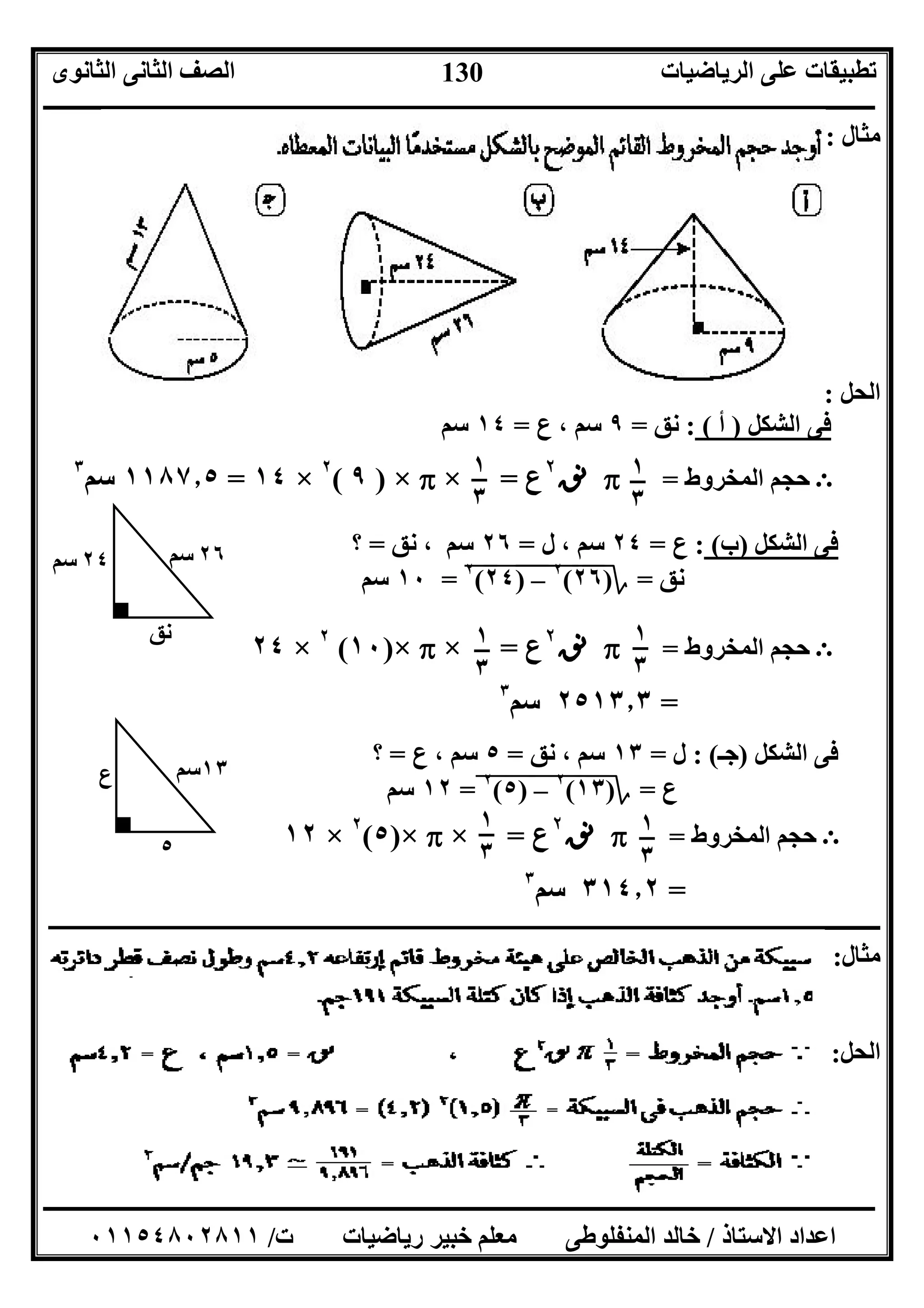
‫ﻣﺜﺎل‬:‫ﺑﻜﺮة‬ ‫اﻟﻤﻘﺎﺑﻞ‬ ‫اﻟﺸﻜﻞ‬ ‫ﯾﻮﺿﺢ‬‫ا‬‫ﯾﻤﺮ‬ ‫ﺳﯿﺮ‬ ‫ﺑﻮاﺳﻄﺔ‬ ‫ﺗﺪور‬ ‫اﻻﺣﺪاﺛﯿﺎت‬ ‫ﻣﺤﻮرى‬ ‫ﺗﻤﺲ‬ ‫آﻟﺔ‬ ‫ﻓﻰ‬
‫داﺋﺮﺗﮭﺎ‬ ‫ﻣﻌﺎدﻟﺔ‬ ‫ب‬ ‫ﺻﻐﯿﺮة‬ ‫ﺑﻜﺮة‬ ‫ﻋﻠﻰ‬:‫س‬٢
+‫ص‬٢
+١٤‫س‬+٤٥=٠
‫أوﺟﺪ‬:
)‫أ‬(‫اﻟﺒﻜﺮة‬ ‫داﺋﺮة‬ ‫ﻣﻌﺎدﻟﺔ‬‫ا‬‫ﻃﻮل‬ ‫ﻛﺎن‬ ‫إذا‬‫ﻧﺼﻒ‬
‫ﯾﺴﺎ‬ ‫ﻗﻄﺮھﺎ‬‫وى‬٥‫وﺣﺪات‬
)‫ب‬(‫ﻣﻦ‬ ‫وﺣﺪة‬ ‫ﻛﻞ‬ ‫ﻛﺎن‬ ‫إذا‬ ‫اﻟﺒﻜﺮﺗﯿﻦ‬ ‫ﻣﺮﻛﺰى‬ ‫ﺑﯿﻦ‬ ‫اﻟﺒﻌﺪ‬
‫ﺗﻤﺜﻞ‬ ‫اﻻﺣﺪاﺛﻰ‬ ‫اﻟﻤﺴﺘﻮى‬٦‫ﺳﻢ‬

144. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
144
‫اﻟﺤﻞ‬:
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫اﻟﺴﯿﺎرات‬ ‫ﻟﻤﺮور‬ ‫اﻟﺪاﺋﺮﯾﺔ‬ ‫اﻻﻧﻔﺎق‬ ‫أﺣﺪ‬ ‫ﻓﻰ‬ ‫رأﺳﯿﺎ‬ ‫ﻣﻘﻄﻌﺎ‬ ‫اﻟﻤﻘﺎﺑﻞ‬ ‫اﻟﺸﻜﻞ‬ ‫ﯾﻮﺿﺢ‬
‫داﺋﺮﺗﮫ‬ ‫ﻣﻌﺎدﻟﺔ‬:‫س‬٢
+‫ص‬٢
–٤‫س‬–٦‫ص‬–١٢=٠
،‫ب‬‫ا‬"‫ﻓﯿﮭﺎ‬ ‫ﻗﻄﺮ‬.‫ﻛﺎﻧﺖ‬ ‫إذا‬ ‫ﻟﻠﻨﻔﻖ‬ ‫ارﺗﻔﺎع‬ ‫أﻗﺼﻰ‬ ‫أوﺟﺪ‬
‫اﻟ‬ ‫ﻓﻰ‬ ‫اﻷﻃﻮال‬ ‫وﺣﺪة‬‫ﺗﻤﺜﻞ‬ ‫اﻻﺣﺪاﺛﻰ‬ ‫ﻤﺴﺘﻮى‬٧٠‫ﺳﻢ‬.
‫اﻟﺤﻞ‬:
e‫س‬ ‫اﻟﺪاﺋﺮة‬ ‫ﻣﻌﺎدﻟﺔ‬٢
+‫ص‬٢
–٤‫س‬–٦‫ص‬–١٢=٠
E‫ل‬=-٢‫ك‬ ،=-٣‫ﺟـ‬ ،=-١٢
E‫ل‬٢
+‫ك‬٢
–‫ﺟـ‬=٤+٩+١٢=٢٥<٠E‫ﻧﻖ‬=٥‫وﺣﺪة‬
E‫ﻟﻠﻨﻔﻖ‬ ‫ارﺗﻔﺎع‬ ‫أﻗﺼﻰ‬=‫ﻧﻖ‬=٥×٧٠=٣٥٠‫ﺳﻢ‬

145. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
145
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻟﺪاﺋﺮة‬ ‫ﻣﻌﺎدﻟﺔ‬ ‫ﻋﻠﻰ‬ ‫ﺗﻤﺎرﯾﻦ‬

146. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
146

147. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
147

148. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
148
‫ﻣﺼﻄﻠﺤﺎت‬ ‫و‬ ‫ﻣﻔﺎھﯿﻢ‬
: ‫اﻻﺣﺘﻤﺎل‬ ‫ﺣﺴﺎب‬ *
‫ﻡ‬‫ﺃﻭ‬ ‫ﺍﻟﻤﺼﻄﻠﺢ‬‫ﺍﻟﻤﻔﻬﻮﻡ‬‫ﺍﻟﺘﻌـــــــــــــــــــــــــــﺮﻳﻒ‬
١
‫ﺍﻟﺘﺠــــــــــــﺮﺑﺔ‬
‫ﺍﻟﻌﺸﻮﺍﺋﻴﺔ‬
‫ﺎ‬‫ﻟﮭ‬ ‫ﺔ‬‫اﻟﻤﻤﻜﻨ‬ ‫ﻮاﺗﺞ‬‫اﻟﻨ‬ ‫ﻊ‬‫ﺟﻤﯿ‬ ‫ﻧﺤﺪد‬ ‫أن‬ ‫ﻧﺴﺘﻄﯿﻊ‬ ‫ﺗﺠﺮﺑﺔ‬ ‫ھﻰ‬
‫ﻮاﺗﺞ‬‫اﻟﻨ‬ ‫ﺬه‬‫ھ‬ ‫أى‬ ‫ﺪ‬‫ﺗﺤﺪﯾ‬ ‫ﺴﺘﻄﯿﻊ‬‫ﻧ‬ ‫ﻻ‬ ‫ﻛﻨﺎ‬ ‫وإن‬ ‫إﺟﺮاﺋﮭﺎ‬ ‫ﻗﺒﻞ‬
‫اﺟﺮاﺋﮭﺎ‬ ‫ﻋﻨﺪ‬ ً‫ﻼ‬‫ﻓﻌ‬ ‫ﺳﯿﺘﺤﻘﻖ‬.
٢
‫ﻓﻀــــــــــــــــــــﺎﺀ‬
‫ﺍﻟﻌﻴﻨـــــــﺔ‬
‫ﺔ‬‫اﻟﺘﺠﺮﺑ‬ ‫ﺬه‬‫ﻟﮭ‬ ‫اﻟﺤﺪوث‬ ‫اﻟﻤﻤﻜﻨﺔ‬ ‫اﻟﻨﻮاﺗﺞ‬ ‫ﻛﻞ‬ ‫ﻣﺠﻤﻮﻋﺔ‬ ‫ھﻮ‬
‫ﺑﺎﻟﺮﻣﺰ‬ ‫ﻋﺎدة‬ ‫ﻟﮭﺎ‬ ‫وﯾﺮﻣﺰ‬)‫ف‬. (
٣
‫ﺍﻷ‬‫ﻋـــــــــــــــــــﺪﺍﺩ‬
‫ﺍﻷﻭﻟﻴﺔ‬
‫اﻟﻮاﺣﺪ‬ ‫ﻋﻠﻰ‬ ‫أو‬ ‫ﻧﻔﺴﮭﺎ‬ ‫ﻋﻠﻰ‬ ‫إﻻ‬ ‫اﻟﻘﺴﻤﺔ‬ ‫ﺗﻘﺒﻞ‬ ‫ﻻ‬ ‫أﻋﺪاد‬ ‫ھﻰ‬
‫ﻣﺜﻞ‬ ‫اﻟﺼﺤﯿﺢ‬) :٢،٣،٥،٧،. . .‫اﻟﺦ‬. (
*‫اﻟﻌﺸﻮاﺋﯿﺔ‬ ‫اﻟﺘﺠﺮﺑﺔ‬ ‫ﻋﻠﻰ‬ ‫أﻣﺜﻠﺔ‬:
١-‫إﻟﻘﺎء‬‫ﻗطﻌﺔ‬‫ﻧﻘود‬‫ﻣرﺗﯾن‬‫ﻣﺗﺗﺎﻟﯾﺗﯾن‬‫وﻣﻼﺣظﺔ‬‫ﺗﺗﺎﺑﻊ‬‫اﻟﺻور‬‫واﻟﻛﺗﺎﺑﺎت‬.
٢-‫ﺳﺣب‬‫ﺑطﺎﻗﺔ‬‫واﺣدة‬‫ﻣن‬‫ﺣﻘ‬‫ﯾﺑﺔ‬‫ﺑﮭﺎ‬٢٠‫ﺑطﺎﻗﺔ‬‫ﻣﺗﻣﺎﺛﻠﺔ‬‫ﻣرﻗﻣﺔ‬‫ﻣن‬١‫إﻟﻰ‬٢٠‫وﻣﻼﺣظﺔ‬‫اﻟﻌدد‬
‫اﻟذى‬‫ﯾظﮭر‬‫ﻋﻠﻰ‬‫اﻟﺑطﺎﻗﺔ‬‫اﻟﻣﺳﺣوﺑﺔ‬.
٣-‫إﻟﻘﺎء‬‫ﺣﺟر‬‫ﻧرد‬‫ﻣﻧﺗظم‬‫وﻣﻼﺣظﺔ‬‫اﻟﻌدد‬‫اﻟظﺎھر‬‫ﻋﻠﻰ‬‫اﻟوﺟﮫ‬‫اﻟﻌﻠوى‬.
٤-‫إﻟﻘﺎء‬‫ﻗطﻌﺔ‬‫ﻧﻘود‬‫ﻣﻌدﻧﯾﺔ‬‫وﻣﻼﺣظﺔ‬‫ﻣﺎ‬‫ﯾظﮭر‬‫ﻋﻠﻰ‬‫اﻟوﺟﮫ‬‫اﻟﻌﻠوى‬.
٥-‫ﺳﺣب‬‫ﻛرة‬‫ﻣن‬‫ﻛﯾس‬‫ﺑﮫ‬‫أرﺑﻊ‬‫ﻛرات‬‫ﻣﺗﻣﺎﺛﻠﺔ‬‫ﻓﻰ‬‫اﻟﺣﺟم‬،‫واﻟوزن‬‫اﻷوﻟﻰ‬‫ﺑﯾﺿﺎء‬،‫اﻟﺛﺎﻧﯾﺔ‬
،‫ﺳوداء‬‫اﻟﺛﺎﻟﺛﺔ‬،‫ﺣﻣراء‬‫اﻟراﺑﻌﺔ‬،‫ﺧﺿراء‬‫وﻣﻼﺣظﺔ‬‫ﻟون‬‫اﻟﻛرة‬
*‫اﻟﻌﯿﻨﺔ‬ ‫ﻓﻀﺎء‬ ‫ﻋﻠﻰ‬ ‫أﻣﺜﻠﺔ‬:
)١(‫اﻟﻈﺎھﺮ‬ ‫اﻟﻮﺟﮫ‬ ‫ﻣﻼﺣﻈﺔ‬ ‫و‬ ‫واﺣﺪة‬ ‫ﻣﺮة‬ ‫ﻧﻘﻮد‬ ‫ﻗﻄﻌﺔ‬ ‫إﻟﻘﺎء‬ ‫ﺗﺠﺮﺑﺔ‬:
‫ف‬=}، ‫ص‬‫ك‬{‫ﺣﯿﺚ‬:‫ن‬)‫ف‬= (۲
)۲(‫ﻗ‬ ‫إﻟﻘﺎء‬ ‫ﺗﺠﺮﺑﺔ‬‫ﻣﺘﺘﺎﻟﺘﯿﻦ‬ ‫ﻣﺮﺗﯿﻦ‬ ‫ﻧﻘﻮد‬ ‫ﻄﻌﺔ‬"‫واﺣﺪة‬ ‫ﻣﺮة‬ ‫ﻣﺘﻤﺎﯾﺰﺗﯿﻦ‬ ‫ﻧﻘﻮد‬ ‫ﻗﻄﻌﺘﻰ‬"
‫اﻟﻜﺘﺎﺑﺎت‬ ‫و‬ ‫اﻟﺼﻮر‬ ‫ﻇﮭﻮر‬ ‫ﺗﺘﺎﺑﻊ‬ ‫ﻣﻼﺣﻈﺔ‬ ‫و‬:
‫اﻟﺮاﺑﻌﺔ‬ ‫اﻟﻮﺣﺪة‬:‫اﻻﺣﺘﻤـﺎل‬

149. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
149
‫ف‬=})‫ص‬ ، ‫ص‬(،)، ‫ص‬‫ك‬(،)‫ك‬‫ص‬ ،(،)‫ك‬،‫ك‬({
‫ﺣﯿﺚ‬:‫ن‬)‫ف‬= (
۲
۲=٤
)٣(‫ﻣﺘﺘﺎﻟﯿﺔ‬ ‫ﻣﺮات‬ ‫ﺛﻼث‬ ‫ﻧﻘﻮد‬ ‫ﻗﻄﻌﺔ‬ ‫إﻟﻘﺎء‬ ‫ﺗﺠﺮﺑﺔ‬"‫ﻗﻄﻊ‬ ‫ﺛﻼث‬‫واﺣﺪة‬ ‫ﻣﺮة‬ ‫ﻧﻘﻮد‬ ‫ﻣﺘﻤﺎﯾﺰة‬"
‫اﻟﻜﺘﺎﺑﺎت‬ ‫و‬ ‫اﻟﺼﻮر‬ ‫ﻇﮭﻮر‬ ‫ﺗﺘﺎﺑﻊ‬ ‫ﻣﻼﺣﻈﺔ‬ ‫و‬:
‫ف‬=})‫ص‬ ، ‫ص‬ ، ‫ص‬(،)، ‫ص‬ ، ‫ص‬‫ك‬(،)، ‫ص‬‫ك‬‫ص‬ ،(،)، ‫ص‬‫ك‬،‫ك‬(
،)‫ك‬‫ص‬ ، ‫ص‬ ،(،)‫ك‬، ‫ص‬ ،‫ك‬(،)‫ك‬،‫ك‬‫ص‬ ،) (‫ك‬،‫ك‬،‫ك‬({
‫ﺣﯿﺚ‬:‫ن‬)‫ف‬= (
٣
۲=٨
)٤(‫اﻟﻌﻠﻮى‬ ‫اﻟﻮﺟﮫ‬ ‫ﻋﻠﻰ‬ ‫اﻟﻈﺎھﺮ‬ ‫اﻟﻌﺪد‬ ‫ﻣﻼﺣﻈﺔ‬ ‫و‬ ‫واﺣﺪة‬ ‫ﻣﺮة‬ ‫ﻧﺮد‬ ‫ﺣﺠﺮ‬ ‫إﻟﻘﺎء‬ ‫ﺗﺠﺮﺑﺔ‬:
‫ف‬=}١،۲،٣،٤،٥،٦{‫ﺣﯿﺚ‬:‫ن‬)‫ف‬= (٦
)٥(‫ﻣﺘﺘﺎﻟﺘﯿﻦ‬ ‫ﻣﺮﺗﯿﻦ‬ ‫ﻧﺮد‬ ‫ﺣﺠﺮ‬ ‫إﻟﻘﺎء‬ ‫ﺗﺠﺮﺑﺔ‬"‫واﺣﺪة‬ ‫ﻣﺮة‬ ‫ﻣﺘﻤﺎﯾﺰﯾﻦ‬ ‫ﻧﺮد‬ ‫ﺣﺠﺮى‬"
)‫اﻟﺤﺠﻢ‬ ‫أو‬ ‫اﻟﺸﻜﻞ‬ ‫ﻓﻰ‬ ‫ﻣﺨﺘﻠﻔﺘﺎن‬ ‫اى‬(‫ﻣﻼﺣﻈﺔ‬ ‫و‬‫اﻟﻌﻠﻮى‬ ‫اﻟﻮﺟﮫ‬ ‫ﻋﻠﻰ‬ ‫اﻟﻈﺎھﺮة‬ ‫اﻷﻋﺪاد‬:
‫ف‬=})١،١(،)١،۲(،٠٠٠٠،)٦،٦({‫ﺣﯿﺚ‬:‫ن‬)‫ف‬= (٦
۲
=٣٦
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــ‬
‫ﻑ‬ ‫ﻋﻠﻰ‬ ‫ﺍﻟﺤﺼﻮﻝ‬ ‫ﻃﺮﻳﻘﺔ‬
‫ﻣﺜﻼ‬:‫ﻣﺮﺗﻴﻦ‬ ‫ﻣﻨﺘﻈﻤﺔ‬ ‫ﻧﻘﻮﺩ‬ ‫ﻗﻄﻌﺔ‬ ‫ﺍﻟﻘﺎﺀ‬
‫ﺃﻭﻻ‬:‫ﺍﻟﺪﻳﻜﺎﺭﺗﻰ‬ ‫ﺍﻟﺤﺎﺻﻞ‬ ‫ﻃﺮﻳﻘﺔ‬:
‫ف‬=}‫ص‬،‫ك‬{×}‫ص‬،‫ك‬{=})‫ص‬،‫ص‬(،)‫ص‬،‫ك‬(،)‫ك‬،‫ك‬(،)‫ك‬،‫ص‬({
‫ﺛﺎﻧﻴﺎ‬:‫ﺍﻟﺠـــــــــــــــــــﺪﻭﻝ‬ ‫ﻃﺮﻳﻘــــــﺔ‬:
‫اﻟﺜﺎﻧﯿﺔ‬ ‫اﻟﺮﻣﯿﺔ‬
‫اﻟ‬‫اﻷوﻟﻰ‬ ‫ﺮﻣﯿﺔ‬
‫ص‬‫ك‬
‫ص‬)‫ص‬،‫ص‬()‫ص‬،‫ك‬(
‫ك‬)‫ك‬،‫ص‬()‫ك‬،‫ك‬(

150. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
150
‫ﺛﺎﻟﺜﺎ‬:‫ﺍﻟﺒﻴﺎﻧـــــــﻰ‬ ‫ﺍﻟﺘﻤﺜﻴﻞ‬ ‫ﻃﺮﻳﻘﺔ‬:
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــ‬
‫ﺭﺍﺑﻌﺎ‬:‫ﺍﻟﺒﻴﺎﻧﻴــــــﺔ‬ ‫ﺍﻟﺸﺠﺮﺓ‬ ‫ﻃﺮﻳﻘﺔ‬:
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﻧﻘﻮد‬ ‫ﻗﻄﻌﺔ‬ ‫إﻟﻘﺎء‬ ‫ﺗﺠﺮﺑﺔ‬ ‫ﻓﻰ‬٣‫ﻣﺘﺘﺎﻟﯿﺔ‬ ‫ﻣﺮات‬‫أو‬٣‫وﻣﻼﺣﻈﺔ‬ ‫واﺣﺪة‬ ‫ﻣﺮة‬ ‫ﻧﻘﻮد‬ ‫ﻗﻄﻊ‬
‫ﺑﯿﺎﻧﯿﺎ‬ ‫وﺗﻤﺜﯿﻠﮭﺎ‬ ‫اﻟﻨﻮاﺗﺞ‬.
‫اﻟﺤﻞ‬:
‫ف‬=})‫ص‬،‫ص‬،‫ص‬(،)‫ص‬،‫ص‬،‫ك‬(،)‫ص‬،‫ك‬،‫ص‬(،)‫ك‬،‫ص‬،‫ص‬(،
)‫ص‬،‫ك‬،‫ك‬(،)‫ك‬،‫ص‬،‫ك‬(،)‫ك‬ ‫و‬ ‫ك‬،‫ص‬(،)‫ك‬،‫ك‬،‫ك‬({
)‫ص‬،‫ص‬(
)‫ص‬،‫ك‬(
)‫ك‬،‫ص‬(
)‫ك‬،‫ك‬(
‫ك‬
‫ﺹ‬
‫ك‬
‫ﺹ‬
‫ك‬
‫ﺹ‬
‫ﻑ‬
‫ﻛﻞ‬ ‫أن‬ ‫اﻟﻤﺜﺎل‬ ‫ھﺬا‬ ‫ﻓﻰ‬ ‫ﻧﻼﺣﻆ‬
‫ﻓﻰ‬ ‫ﯾﻈﮭﺮ‬ ‫اﻟﻨﻮاﺗﺞ‬ ‫ﻣﻦ‬ ‫ﻧﺎﺗﺞ‬
‫ﻣﺮﺗﺐ‬ ‫زوج‬ ‫ﺷﻜﻞ‬:
)‫اﻷوﻟﻰ‬ ‫اﻟﺮﻣﯿﺔ‬،‫اﻟﺮﻣﯿﺔ‬
‫اﻟﺜﺎﻧﯿﺔ‬. (
)‫ك‬،‫ك‬(
)‫ك‬،‫ص‬(
)‫ص‬،‫ك‬(
)‫ص‬،‫ص‬(
‫ك‬
‫ﺹ‬
‫ك‬‫ﺹ‬

151. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
151
‫اﻟﺑﯾﺎ‬ ‫اﻟﺗﻣﺛﯾل‬‫ﻧﻰ‬:
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ھﺎﻣﺔ‬ ‫ﻣﻼﺣﻈﺎت‬:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
‫ك‬
‫ك‬
‫ص‬
‫ك‬
‫ص‬
‫ك‬
‫ص‬
‫ك‬
‫ص‬
‫ص‬
‫ص‬
‫ص‬
‫ك‬
‫ك‬
‫ﺔ‬ ‫ﻃﺮﯾﻘ‬ ‫ﻀﻞ‬ ‫أﻓ‬ ‫ﺔ‬ ‫اﻟﺒﯿﺎﻧﯿ‬ ‫ﺸﺠﺮة‬ ‫اﻟ‬
‫ﻰ‬ ‫ﻋﻠ‬ ‫ﺔ‬ ‫اﻟﻤﺤﺘﻮﯾ‬ ‫ﺔ‬ ‫اﻟﺘﺠﺮﺑ‬ ‫ﻞ‬ ‫ﻟﺘﻤﺜﯿ‬
‫اﻟﺸﺒﻜﺔ‬ ‫ﺑﻌﻜﺲ‬ ‫ﻋﻤﻠﯿﺘﯿﻦ‬ ‫ﻣﻦ‬ ‫أﻛﺜﺮ‬
‫ﺔ‬ ‫ﺣﺎﻟ‬ ‫ﻰ‬ ‫ﻓ‬ ‫ﻀﻞ‬ ‫ﺗﻔ‬ ‫ﺚ‬ ‫ﺣﯿ‬ ‫ﺔ‬ ‫اﻟﺒﯿﺎﻧﯿ‬
‫ﻋﻤﻠﯿﺘﯿﻦ‬ ‫ﻋﻠﻰ‬ ‫اﻟﻤﺤﺘﻮﯾﺔ‬ ‫اﻟﺘﺠﺮﺑﺔ‬
١(‫ﻣﺘﺘﺎﻟ‬ ‫ﻣﺮﺗﻴﻦ‬ ‫ﻧﻘﻮﺩ‬ ‫ﻗﻄﻌﺔ‬ ‫ﺇﻟﻘﺎﺀ‬ ‫ﻟﺘﺠﺮﺑﺔ‬ ‫ﺍﻟﻌﻴﻨﺔ‬ ‫ﻓﻀﺎﺀ‬‫ﻓﻀﺎﺀ‬ ‫ﻧﻔﺴﻬﺎ‬ ‫ﻫﻰ‬ ‫ﻴﺘﻴﻦ‬
‫ﻭﺍﺣﺪﺓ‬ ‫ﻣﺮﺓ‬ ‫ﻣﺘﻤﺎﻳﺰﺗﻴﻦ‬ ‫ﺍﻟﻨﻘﻮﺩ‬ ‫ﻣﻦ‬ ‫ﻗﻄﻌﺘﻴﻦ‬ ‫ﺭﻣﻰ‬ ‫ﻋﻨﺪ‬ ‫ﺍﻟﻨﻮﺍﺗﺞ‬)‫ﻣﻌﺎ‬(.
‫ﻋﻨﺎﺻﺮ‬ ‫ﻋﺪﺩ‬‫ﻑ‬‫ﺍﻟﺤﺎﻟﺔ‬ ‫ﻫﺬﻩ‬ ‫ﻓﻰ‬=‫ﻑ‬١×‫ﻑ‬٢
٣(‫ﺇﺟﺮﺍﺀ‬ ‫ﺣﺎﻟﺔ‬ ‫ﻓﻰ‬ ‫ﻑ‬ ‫ﻋﻨﺎﺻﺮ‬ ‫ﻋﺪﺩ‬٣‫ﻋﻤﻠﻴﺎﺕ‬=‫ﻑ‬١×‫ﻑ‬٢×‫ﻑ‬٣‫ﻭﻫﻜﺬﺍ‬.
٤(‫ﻭﺍﺣﺪﺓ‬ ‫ﻣﺮﺓ‬ ‫ﺣﺠﺮﻳﻦ‬ ‫ﺃﻭ‬ ‫ﻣﺘﺘﺎﻟﻴﺘﻴﻦ‬ ‫ﻣﺮﺗﻴﻦ‬ ‫ﻧﺮﺩ‬ ‫ﺣﺠﺮ‬ ‫ﺇﻟﻘﺎﺀ‬ ‫ﻋﻨﺪ‬‫ﻭﻣﻼﺣﻈﺔ‬
‫ﺃﻥ‬ ‫ﻧﺠﺪ‬ ‫ﺍﻟﻌﻠﻮﻯ‬ ‫ﺍﻟﻮﺟﻪ‬ ‫ﻋﻠﻰ‬ ‫ﺗﻈﻬﺮ‬ ‫ﺍﻟﺘﻰ‬ ‫ﺍﻷﻋﺪﺍﺩ‬:‫ﻑ‬=‫ﺍﻟﺮﻣﻴﺔ‬ ‫ﻋﻨﺎﺻﺮ‬ ‫ﻋﺪﺩ‬
‫ﺍﻷﻭﻟﻰ‬٦×‫ﺍﻟﺜﺎﻧﻴﺔ‬ ‫ﺍﻟﺮﻣﻴﺔ‬ ‫ﻋﻨﺎﺻﺮ‬ ‫ﻋﺪﺩ‬٦=٦٢
=٣٦‫ﻋﻨﺼﺮﺍ‬.
٥(‫ﻧﻘﻮﺩ‬ ‫ﻗﻄﻌﺔ‬ ‫ﺭﻣﻰ‬ ‫ﻋﻨﺪ‬‫م‬‫ﻥ‬ ‫ﻳﻜﻮﻥ‬ ‫ﺍﻟﻤﺘﺘﺎﻟﻴﺔ‬ ‫ﺍﻟﻤﺮﺍﺕ‬ ‫ﻣﻦ‬)‫ﻑ‬= (٢
‫م‬
،)‫ك‬ ، ‫ص‬(})‫ك‬،‫ص‬(
٦(‫ﺍﻟﻌﻴ‬ ‫ﻓﻀﺎﺀ‬ ‫ﻳﻜﻮﻥ‬‫ﻣﻨﺘﻬﻪ‬ ‫ﻏﻴﺮ‬ ‫ﺃﻭ‬ ‫ﹰ‬‫ﺍ‬‫ﻣﺤﺪﻭﺩ‬ ‫ﻋﻨﺎﺻﺮﻩ‬ ‫ﻋﺪﺩ‬ ‫ﻛﺎﻥ‬ ‫ﺇﺫﺍ‬ ‫ﻣﻨﻬﻴﺎ‬ ‫ﻨﺔ‬
‫ﻋﺪﺩ‬ ‫ﻛﺎﻥ‬ ‫ﺇﺫﺍ‬‫ﺍﻟﻤﻨﺘﻪ‬ ‫ﺍﻟﻨﻮﺍﺗﺞ‬ ‫ﻓﻀﺎﺀ‬ ‫ﻓﻘﻂ‬ ‫ﺳﻨﺪﺭﺱ‬ ‫ﻭ‬ ‫ﻣﺤﺪﻭﺩ‬ ‫ﻏﻴﺮ‬ ‫ﻋﻨﺎﺻﺮﻩ‬.
٧(‫ﺍﻟﻜﻴﺲ‬ ‫ﺍﻟﻰ‬ ‫ﺍﻟﻜﺮﺓ‬ ‫ﺇﻋﺎﺩﺓ‬ ‫ﻋﺪﻡ‬ ‫ﻳﻌﻨﻰ‬ ‫ﻓﻬﺬﺍ‬ ‫ﺇﺣﻼﻝ‬ ‫ﺩﻭﻥ‬ ‫ﺍﻟﻜﺮﺓ‬ ‫ﺳﺤﺒﺖ‬ ‫ﺇﺫﺍ‬
‫ﺍﻟﺜﺎﻧﻴﺔ‬ ‫ﺍﻟﺴﺤﺒﺔ‬ ‫ﻓﻰ‬ ‫ﻟﻈﻬﻮﺭﻫﺎ‬ ‫ﻓﺮﺹ‬ ‫ﻫﻨﺎﻙ‬ ‫ﻳﻜﻮﻥ‬ ‫ﻟﻦ‬ ‫ﺑﺬﻟﻚ‬ ‫ﻭ‬ ‫ﺳﺤﺒﻬﺎ‬ ‫ﺑﻌﺪ‬

152. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
152
‫ﻣﺜﺎل‬:‫ﻣﺘﻤﺎﺛﻠﺔ‬ ‫ﻛﺮات‬ ‫ﺛﻼث‬ ‫ﺑﮫ‬ ‫ﻛﯿﺲ‬‫ﺻﻔﺮاء‬ ‫واﻟﺜﺎﻟﺜﺔ‬ ‫ﺑﯿﻀﺎء‬ ‫واﻟﺜﺎﻧﯿﺔ‬ ‫ﺣﻤﺮاء‬ ‫اﻷوﻟﻰ‬.‫ﻓﻀﺎء‬ ‫اﻛﺘﺐ‬
‫اﻟﻜﺮة‬ ‫ﺳﺤﺐ‬ ‫ﻗﺒﻞ‬ ‫اﻟﻤﺴﺤﻮﺑﺔ‬ ‫اﻟﻜﺮة‬ ‫إﻋﺎدة‬ ‫ﻣﻊ‬ ‫اﻵﺧﺮى‬ ‫ﺑﻌﺪ‬ ‫اﻟﻮاﺣﺪة‬ ‫ﻛﺮﺗﺎن‬ ‫ﺳﺤﺒﺖ‬ ‫إذا‬ ‫اﻟﻌﯿﻨﺔ‬
‫اﻟﺜﺎﻧﯿﺔ‬)‫اﻹﺣﻼل‬ ‫ﻣﻊ‬(‫اﻷﻟﻮان‬ ‫ﺗﺘﺎﺑﻊ‬ ‫ﻣﻼﺣﻈﺔ‬ ‫و‬.
‫اﻟﺤﻞ‬:
‫اﻟﺤﻤﺮاء‬ ‫اﻟﻜﺮة‬ ‫اﻟﻰ‬ ‫ﻧﺮﻣﺰ‬)‫ح‬(‫اﻟﺒﯿﻀﺎء‬ ‫اﻟﻜﺮة‬ ‫و‬)‫ب‬(
‫اﻟﺼﻔﺮاء‬ ‫اﻟﻜﺮة‬ ‫و‬)‫ص‬. (
‫اﻟﻌﯿﻨﺔ‬ ‫ﻟﻔﻀﺎء‬ ‫اﻟﺒﯿﺎﻧﯿﺔ‬ ‫اﻟﺸﺠﺮة‬ ‫ﯾﻤﺜﻞ‬ ‫اﻟﻤﻘﺎﺑﻞ‬ ‫اﻟﺸﻜﻞ‬
‫ن‬ ‫ﺣﯿﺚ‬)‫ف‬= (٣٢
=٩
،)‫ح‬ ، ‫ب‬( ‫ف‬=})‫ح‬ ، ‫ح‬(،)‫ب‬ ، ‫ح‬(،)‫ص‬ ، ‫ح‬(
،)‫ب‬ ، ‫ب‬(،)‫ص‬ ، ‫ب‬(،)‫ح‬ ، ‫ص‬(،)‫ب‬ ، ‫ص‬(
،)‫ص‬ ، ‫ص‬({
‫ـــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﺻﻔﺮاء‬ ‫واﻟﺜﺎﻟﺜﺔ‬ ‫ﺑﯿﻀﺎء‬ ‫واﻟﺜﺎﻧﯿﺔ‬ ‫ﺣﻤﺮاء‬ ‫اﻷوﻟﻰ‬ ‫ﻣﺘﻤﺎﺛﻠﺔ‬ ‫ﻛﺮات‬ ‫ﺛﻼث‬ ‫ﺑﮫ‬ ‫ﻛﯿﺲ‬.‫ﻓﻀﺎء‬ ‫اﻛﺘﺐ‬
‫اﻟﻌﯿﻨﺔ‬‫ﻛﺮﺗﯿ‬ ‫ﺳﺤﺒﺖ‬ ‫إذا‬‫اﻵﺧﺮى‬ ‫ﺑﻌﺪ‬ ‫اﻟﻮاﺣﺪة‬ ‫ﻦ‬‫اﻷﻟﻮان‬ ‫ﺗﺘﺎﺑﻊ‬ ‫ﻣﻼﺣﻈﺔ‬ ‫و‬ ‫إﺣﻼل‬ ‫ﺑﺪون‬.
‫اﻟﺤﻞ‬:
‫ﻣﺜﺎل‬:‫ﻣﻦ‬ ‫ﻣﺮﻗﻤﺔ‬ ‫و‬ ‫ﻣﺘﻤﺎﺛﻠﺔ‬ ‫ﻛﺮات‬ ‫ﺛﻼث‬ ‫ﺑﮫ‬ ‫ﺻﻨﺪوق‬١‫إﻟﻰ‬٣‫اﻷﺧﺮى‬ ‫ﺑﻌﺪ‬ ‫اﻟﻮاﺣﺪة‬ ‫ﻛﺮﺗﺎن‬ ‫ﺳﺤﺒﺖ‬
‫اﻟﻜﺮة‬ ‫رﻗﻢ‬ ‫ﻣﻼﺣﻈﺔ‬ ‫و‬ ‫اﻹﺣﻼل‬ ‫ﻣﻊ‬.‫ﻋﻨﺎﺻﺮه‬ ‫ﻋﺪد‬ ‫ﺑﯿﻦ‬ ‫و‬ ‫اﻟﻌﯿﻨﺔ‬ ‫ﻓﻀﺎء‬ ‫اﻛﺘﺐ‬.

153. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
153
‫اﻷﺣﺪاث‬
‫ﻛﺎن‬ ‫ﻓﺈذا‬:‫ا‬‫ﻓﺈن‬ ‫ف‬ ‫ﻓﻰ‬ ‫ﺣﺪث‬:‫ا‬e‫ف‬
‫ھﻮ‬ ‫ﻋﻨﺎﺻﺮه‬ ‫ﻋﺪد‬ ‫و‬:‫ن‬)‫ا‬(‫اﻟﺤﺪث‬ ‫وﻗﻮع‬ ‫ﻓﺮص‬ ‫ﻋﺪد‬ ‫أى‬‫ا‬
‫ﻓ‬‫ﻤﺜﻼ‬:‫ﻛﺎن‬ ‫إذا‬‫ا‬‫رﻗﻢ‬ ‫ﻇﮭﻮر‬ ‫ﺣﺪث‬ ‫ھﻮ‬‫وﻣﻼﺣﻈﺔ‬ ‫واﺣﺪة‬ ‫ﻣﺮة‬ ‫ﻣﻨﺘﻈﻢ‬ ‫ﻧﺮد‬ ‫ﺣﺠﺮ‬ ‫إﻟﻘﺎء‬ ‫ﻋﻨﺪ‬ ‫زوﺟﻰ‬
‫ﻓﺈن‬ ‫اﻟﻌﻠﻮى‬ ‫اﻟﻮﺟﮫ‬ ‫ﻋﻠﻰ‬ ‫اﻟﻈﺎھﺮ‬ ‫اﻟﺮﻗﻢ‬:‫ا‬=}۲،٤،٦{
‫أن‬ ‫ﻻﺣﻆ‬:‫ا‬=}۲،٤،٦{g‫ف‬
*‫ﻣﻼﺣﻈﺔ‬‫ھﺎﻣﺔ‬:‫ﻣﺜﻨﻰ‬ ‫ﻣﺜﻨﻰ‬ ‫ﻣﺘﻨﺎﻓﯿﺔ‬ ‫ﺗﻜﻮن‬ ‫اﻟﻌﯿﻨﺔ‬ ‫ﻓﻀﺎء‬ ‫ﻓﻰ‬ ‫اﻟﺒﺴﯿﻄﺔ‬ ‫اﻷﺣﺪاث‬
‫ا‬‫ﻟﺤﺪث‬‫اﻟﻌﯿﻨﺔ‬ ‫ﻓﻀﺎء‬ ‫ﻣﻦ‬ ‫ﺟﺰﺋﯿﺔ‬ ‫ﻣﺠﻤﻮﻋﺔ‬ ‫ھﻮ‬
‫اﻟﺤﺪث‬
‫اﻟﻤﺴﺘﺤﯿﻞ‬
‫اﻟﺬى‬ ‫اﻟﺤﺪث‬ ‫ھﻮ‬‫وﻗﻮﻋﮫ‬ ‫ﯾﻤﻜﻦ‬ ‫ﻻ‬"Т"
‫ﻋﻨﺼﺮ‬ ‫أى‬ ‫ﻣﻦ‬ ‫اﻟﺨﺎﻟﻰ‬ ‫اﻟﺤﺪث‬ ‫ھﻮ‬
‫اﻟﻤﺆﻛﺪ‬ ‫اﻟﺤﺪث‬‫اﻟﻌﺸﻮاﺋﯿﺔ‬ ‫اﻟﺘﺠﺮﺑﺔ‬ ‫إﺟﺮاء‬ ‫ﻋﻨﺪ‬ ‫ﯾﻘﻊ‬ ‫أن‬ ‫ﻻﺑﺪ‬ ‫ﺣﺪث‬ ‫ھﻮ‬
‫ف‬ ‫اﻟﻌﯿﻨﺔ‬ ‫ﻓﻀﺎء‬ ‫ﻋﻨﺎﺻﺮ‬ ‫ھﻰ‬ ‫ﻋﻨﺎﺻﺮه‬ ‫اﻟﺬى‬ ‫اﻟﺤﺪث‬ ‫ھﻮ‬ ‫و‬
‫اﻟ‬ ‫اﻟﺤﺪث‬‫ﺒﺴﯿﻂ‬
)‫اﻵوﻟﻰ‬ ‫اﻟﺤﺪث‬(
‫ھﻮ‬‫ھﻮ‬‫ﺟﺰﺋﯿﺔ‬ ‫ﻣﺠﻤﻮﻋﺔ‬‫ﻋﻨﺼﺮ‬ ‫ﻋﻠﻰ‬ ‫ﺗﺤﺘﻮى‬ ‫ف‬ ‫اﻟﻌﯿﻨﺔ‬ ‫ﻓﻀﺎء‬ ‫ﻣﻦ‬
‫ﻓﻘﻂ‬ ‫واﺣﺪ‬.
‫اﻟ‬ ‫اﻟﺤﺪث‬‫ﻤﺮﻛﺐ‬‫ﺑﺴﯿﻂ‬ ‫ﻏﯿﺮ‬ ‫ﺣﺪث‬ ‫ﯾﺴﻤﻰ‬ ‫و‬ ‫ﻋﻨﺼﺮ‬ ‫ﻣﻦ‬ ‫أﻛﺜﺮ‬ ‫ﻣﻦ‬ ‫ﯾﺘﻜﻮن‬ ‫ﺣﺪث‬ ‫ھﻮ‬
‫اﻟﺤﺪﺛ‬‫اﻟﻤﺘﻨﺎﻓﯿﺎن‬ ‫ﺎن‬‫ﻻ‬ ‫ﺣﺪﺛﺎن‬ ‫ھﻤﺎ‬‫أن‬ ‫أى‬ ً‫ﺎ‬‫ﻣﻌ‬ ‫وﻗﻮﻋﮭﻤﺎ‬ ‫ﯾﻤﻜﻦ‬:‫ﺗﻘﺎﻃﻌﮭﻤﺎ‬ ‫ﺣﺪﺛﺎن‬ ‫ھﻤﺎ‬=Т

154. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
154
*‫ﻟﺤﺪﺛﯿﻦ‬ ‫ﯾﻘﺎل‬‫ا‬،‫ب‬‫ﻣﺘﻨﺎﻓﯿﺎن‬ ‫أﻧﮭﻤﺎ‬ ‫ف‬ ‫ﻋﯿﻨﺔ‬ ‫ﻓﻀﺎء‬ ‫ﻣﻦ‬
‫ﻛﺎن‬ ‫إذا‬‫ا‬∩‫ب‬=‫ﺻﺤﯿﺢ‬ ‫واﻟﻌﻜﺲ‬.
*‫ﯾ‬ ‫أن‬ ‫ﯾﻤﻜﻦ‬ ‫ﻻ‬ ‫اﻟﻤﺘﻨﺎﻓﯿﯿﻦ‬ ‫اﻟﺤﺪﺛﯿﻦ‬ ‫أن‬ ‫ﯾﻌﻨﻰ‬ ‫ھﺬا‬‫ﻓﻰ‬ ً‫ﺎ‬‫ﻣﻌ‬ ‫ﻘﻌﺎ‬
‫اﻵﺧﺮ‬ ‫وﻗﻮع‬ ‫ﯾﻨﻔﻰ‬ ‫أﺣﺪھﻤﺎ‬ ‫وﻗﻮع‬ ‫أن‬ ‫أى‬ ‫اﻟﻮﻗﺖ‬ ‫ﻧﻔﺲ‬.
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
*‫ھﺎﻣﺔ‬ ‫ﻣﻼﺣظﺎت‬:
‫ا‬ ‫اﻷﺣﺪاث‬ ‫ﺣﺎﻟﺔ‬ ‫ﻓﻰ‬‫ﺗﻘﺎﻃﻊ‬ ‫ﯾﻮﺟﺪ‬ ‫ﻻ‬ ‫ﻟﻤﺘﻨﺎﻓﯿﺔ‬) :‫ا‬∩‫ب‬=Т(
‫ﺑﻌﺪه‬ ‫واﻟﺬى‬ ‫ﻧﻔﺴﮫ‬ ‫اﻟﺤﺪث‬ ‫ﻣﻌﻨﺎھﺎ‬ ‫اﻷﻗﻞ‬ ‫ﻋﻠﻰ‬.
‫ﻗﺒﻠﮫ‬ ‫واﻟﺬى‬ ‫ﻧﻔﺴﮫ‬ ‫اﻟﺤﺪث‬ ‫ﻣﻌﻨﺎھﺎ‬ ‫اﻷﻛﺜﺮ‬ ‫ﻋﻠﻰ‬.
‫أﺣﺪاث‬ ‫ﻟﻌﺪة‬ ‫ﯾﻘﺎل‬‫ا‬،‫ب‬،‫ﺟ‬‫ﻣﺜﻨﻰ‬ ‫ﻣﺜﻨﻰ‬ ‫ﻣﺘﻨﺎﻓﯿﺔ‬ ‫ﻛﺎﻧﺖ‬ ‫إذا‬ ‫ﺣﺎﻟﺔ‬ ‫ﻓﻰ‬ ‫ﻓﻘﻂ‬ ‫ﻣﺘﻨﺎﻓﯿﺔ‬ ‫إﻧﮭﺎ‬ ‫ـ‬.
‫ﻓﺈن‬:‫ا‬‫ب‬=،‫ب‬‫ﺟـ‬=،‫ا‬‫ﺟـ‬=
‫اﻻﺗﺤﺎد‬‫ﻣﻌﻨﺎه‬)‫أو‬) (‫اﻷﻗﻞ‬ ‫ﻋﻠﻰ‬. (
‫اﻟﺘﻘﺎﻃﻊ‬‫ﻣﻌﻨﺎه‬)‫و‬) (‫اﻷﻛﺜﺮ‬ ‫ﻋﻠﻰ‬. (
‫ل‬)‫ف‬= (١.
‫ﺣﺪث‬ ‫أى‬‫ا‬‫ﻣﻜﻤﻠﮫ‬ ‫و‬‫ا‬/
‫ﺣﺪ‬ ‫ھﻤﺎ‬‫ﻣﺘﻨﺎﻓﯿﺎن‬ ‫ﺛﺎن‬.
‫اﻟﺒﺴﯿﻄﺔ‬ ‫اﻷﺣﺪاث‬)‫اﻷوﻟﯿﺔ‬(‫ﻣﺘﻨﺎﻓﯿﺔ‬ ‫ﺗﻜﻮن‬ ‫ﻋﺸﻮاﺋﯿﺔ‬ ‫ﺗﺠﺮﺑﺔ‬ ‫أة‬ ‫ﻓﻰ‬.
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:
‫اﻟﺤﻞ‬:‫ا‬ ‫ﻣﻦ‬‫أن‬ ‫ﻧﺠﺪ‬ ‫ﻟﺮﺳﻢ‬:
‫ف‬=}، ‫ص‬)‫ص‬ ، ‫ك‬(،)‫ص‬ ، ‫ك‬ ، ‫ك‬(،)‫ك‬ ، ‫ك‬ ، ‫ك‬({
‫ا‬=}، ‫ص‬)‫ص‬ ، ‫ك‬(،)‫ص‬ ، ‫ك‬ ، ‫ك‬(،)‫ك‬ ، ‫ك‬ ، ‫ك‬({=‫ف‬
‫ب‬=}، ‫ص‬)‫ص‬ ، ‫ك‬(،)‫ص‬ ، ‫ك‬ ، ‫ك‬({
‫ج‬=})‫ص‬ ، ‫ك‬ ، ‫ك‬(،)‫ك‬ ، ‫ك‬ ، ‫ك‬({‫د‬ ،={ }=Т‫اﻟﻤﺴﺘﺤﯿﻞ‬ ‫اﻟﺤﺪث‬
‫ا‬‫ب‬

155. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
155
‫اﻟﺤﺪث‬ً‫ﺎ‬‫ﻟﻔﻈﯿ‬ ‫ﻋﻨﮫ‬ ‫اﻟﺘﻌﺒﯿﺮ‬‫ﻓﻦ‬ ‫ﺑﺸﻜﻞ‬ ‫ﺗﻤﺜﯿﻠﮫ‬
‫اﻟﻌﻤﻠﯿﺎت‬‫اﻻﺣﺪاث‬ ‫ﻋﻠﻰ‬
‫اﻟﺘﻘﺎﻃﻊ‬ ‫ﻋﻤﻠﯿﺔ‬
‫ا‬∩‫ب‬‫أ‬ ‫وﻗوع‬ ‫ﺣدث‬،‫ﻣﻌﺎ‬ ‫ب‬ً
‫اﻻﺗﺤﺎد‬ ‫ﻋﻤﻠﯿﺔ‬‫وﻗوع‬ ‫ﺣدث‬‫ا‬‫ﻛﻠﯾﮭﻣﺎ‬ ‫أو‬ ‫ب‬ ‫أو‬
‫أو‬
‫ا‬‫ب‬‫اﻷﻗل‬ ‫ﻋﻠﻰ‬ ‫أﺣدھﻣﺎ‬ ‫وﻗوع‬ ‫ﺣدث‬
‫اﻻﻛﻣﺎل‬ ‫ﻋﻣﻠﯾﺔ‬‫اﻟﻣﻛ‬ ‫اﻟﺣدث‬‫ﻟﻠﺣدث‬ ‫ﻣل‬
‫أو‬
‫ا‬/
=‫ف‬-‫ا‬‫اﻟﺣدث‬ ‫وﻗوع‬ ‫ﻋدم‬ ‫ﺣدث‬‫ا‬
‫اﻟﻔرق‬ ‫ﻋﻣﻠﯾﺔ‬‫وﻗوع‬ ‫ﺣدث‬‫ا‬‫وﻗوع‬ ‫وﻋدم‬‫ب‬
‫ا‬–‫ب‬‫أو‬
=‫ا‬∩‫ب‬/
‫و‬ ‫ﺣدث‬‫ﻗوع‬‫ا‬‫ﻓﻘط‬
=‫ا‬–)‫ا‬∩‫ب‬(
‫ب‬–‫ا‬‫ﻓﻘﻂ‬ ‫ب‬ ‫اﻟﺤﺪث‬ ‫وﻗﻮع‬
=‫ب‬∩‫ا‬/
‫أو‬
=‫ب‬–)‫ا‬∩‫ب‬(‫وﻗﻮع‬‫وﻗﻮع‬ ‫وﻋﺪم‬ ‫ب‬‫ا‬

156. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
156
‫ﻓﻦ‬ ‫ﺑﺸﻜﻞ‬ ‫ﺗﻤﺜﯿﻠﮫ‬ ‫ﻟﻔﻈﯿﺎ‬ ‫ﻋﻨﮫ‬ ‫اﻟﺘﻌﺒﯿﺮ‬ ‫اﻟﺤﺪث‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــ‬
‫أن‬ ‫ﺗﺬﻛﺮ‬:‫ﻣﺠﻤﻮﻋﺘﯿﻦ‬ ‫ﻻى‬‫ا‬‫ﯾﻜﻮن‬ ‫ب‬ ،‫ا‬-‫ب‬=‫ا‬∩‫ب‬/
=‫ب‬/
-‫ا‬/
،‫ا‬‫ﺑﻶ‬‫ا‬/
=، ‫ف‬‫ا‬‫ﺑﻼ‬‫ا‬/
=
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻟﮭﺎ‬ ‫اﻟﻌﻠﻮﯾﯿﻦ‬ ‫اﻟﻮﺟﮭﯿﻦ‬ ‫ﻋﻠﻰ‬ ‫اﻟﻈﺎھﺮﯾﻦ‬ ‫اﻟﻌﺪدﯾﻦ‬ ‫ﻣﻼﺣﻈﺔ‬ ‫و‬ ‫ﻣﺘﻤﺎﯾﺰن‬ ‫ﻧﺮد‬ ‫ﺣﺠﺮى‬ ‫إﻟﻘﺎء‬ ‫ﺗﺠﺮﺑﺔ‬ ‫ﻓﻰ‬
١(‫اﻵﺗﯿﯿﻦ‬ ‫اﻟﺤﺪﺛﯿﻦ‬ ‫ﻣﻦ‬ ‫ﻛﻼ‬ ‫اﻛﺘﺐ‬ ‫و‬ ‫ھﻨﺪﺳﯿﺎ‬ ‫اﻟﻌﯿﻨﺔ‬ ‫ﻓﻀﺎء‬ ‫ﻣﺜﻞ‬.
٢(‫اﻟﺤﺪث‬‫ا‬"‫اﻟﻌﺪد‬ ‫ﻧﻔﺲ‬ ‫ﻇﮭﻮر‬‫اﻟﻮﺟﮭﯿﻦ‬ ‫ﻋﻠﻰ‬"
٣(‫ب‬ ‫اﻟﺤﺪث‬"‫ﻣﺠﻤﻮﻋﮭﻤﺎ‬ ‫ﻋﺪدﯾﻦ‬ ‫ﻇﮭﻮر‬٧"
٤(‫اﻟﺤﺪﺛﺎن‬ ‫ھﻞ‬‫ا‬‫إﺟﺎﺑﺘﻚ‬ ‫ﻓﺴﺮ‬ ‫؟‬ ‫ﻣﺘﻨﺎﻓﯿﺎن‬ ‫ب‬ ،.
)‫ا‬∩‫ب‬(/
=‫ا‬/
‫ب‬/
‫ﻣﻌﺎ‬ ‫اﻟﺤﺪﺛﯿﻦ‬ ‫وﻗﻮع‬ ‫ﻋﺪم‬ ‫ﺣﺪث‬
‫أو‬
‫اﻷﻛﺜﺮ‬ ‫ﻋﻠﻰ‬ ‫أﺣﺪھﻤﺎ‬ ‫وﻗﻮع‬
)‫ا‬‫ب‬(/
=‫ا‬/
∩‫ب‬/
‫اﻟﺤﺪﺛﯿﻦ‬ ‫ﻣﻦ‬ ‫أى‬ ‫وﻗﻮع‬ ‫ﻋﺪم‬ ‫ﺣﺪث‬
‫أو‬
‫وﻗﻮع‬ ‫ﻋﺪم‬‫ا‬‫ب‬ ‫وﻗﻮع‬ ‫وﻋﺪم‬
‫وﻗﻮع‬ ‫إﺣﺘﻤﺎل‬‫اﻟﺤﺪﺛﯿﻦ‬ ‫أﺣﺪ‬‫ﻓﻘﻂ‬
)‫ا‬–‫ب‬()‫ب‬–‫ا‬(=‫أو‬
)‫ا‬‫ب‬(‫ــ‬)‫ا‬∩‫ب‬(‫وﻗﻮع‬ ‫إﺣﺘﻤﺎل‬‫اﻟﺤﺪﺛﯿﻦ‬ ‫أﺣﺪ‬
‫دون‬‫اﻵﺧﺮ‬
‫ف‬
‫ب‬
‫ا‬
‫ف‬
‫ب‬
‫ا‬
‫ﻣﻮرﺟﺎن‬ ‫دى‬ ‫ﻗﺎﻧﻮﻧﺎ‬

157. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
157
‫اﻟﺤﻞ‬:
‫ن‬)‫ف‬= (٦٢
=٣٦
١(‫اﻟﮭﻨﺪﺳﻰ‬ ‫اﻟﺘﻤﺜﯿﻞ‬ ‫ھﻮ‬ ‫اﻟﻤﻘﺎﺑﻞ‬ ‫اﻟﺸﻜﻞ‬)‫اﻟﺒﯿﺎﻧﻰ‬(‫اﻟﻌﯿﻨﺔ‬ ‫ﻟﻔﻀﺎء‬
٢(‫ا‬=})١،١(،)٢،٢(،)٣،٣(،)٤،٤(
،)٥،٥(،)٦،٦({
٣(‫ب‬=})٦،١(،)٥،٢(،)٤،٣(،)٣،٤(
،)٢،٥(،)١،٦({
٤(‫ا‬∩‫ب‬=ТE‫ا‬‫ﻣﺘﻨﺎﻓﯿﺎن‬ ‫ﺣﺪﺛﺎن‬ ‫ب‬ ،.
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
*‫اﻻﺣﺘﻤﺎل‬ ‫ﺣﺴﺎب‬:‫ف‬ ‫اﻟﻌﯿﻨﺔ‬ ‫ﻓﻀﺎء‬ ‫ﻣﻦ‬ ‫ﺟﺰﺋﯿﺔ‬ ‫ﻣﺠﻤﻮﻋﺔ‬ ‫اﻟﺤﺪث‬
‫ﻛﺎن‬ ‫إذا‬‫ﺍ‬‫ﻓﺎن‬ ‫اﻻﻣﻜﺎﻧﺎت‬ ‫ﻣﺘﺴﺎو‬ ‫ﻓﻀﺎء‬ ‫ﻣﻦ‬ ‫ﺟﺰﺋﻰ‬ ‫ﺣﺪث‬:
‫ل‬)‫ا‬= (=
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﺑﮫ‬ ‫ﺻﻨﺪوق‬ ‫ﻣﻦ‬ ‫ﻋﺸﻮاﺋﯿﺎ‬ ‫ﻛﺮة‬ ‫ﺳﺤﺒﺖ‬١٠‫ﻣﻨﮭﺎ‬ ‫ﻣﺘﻤﺎﺛﻠﺔ‬ ‫ﻛﺮات‬٥‫ﻛﺮﺗﺎن‬ ، ‫ﺑﯿﻀﺎء‬ ‫ﻛﺮات‬
‫اﻵﺗﯿﺔ‬ ‫اﻷﺣﺪاث‬ ‫اﺣﺘﻤﺎل‬ ‫اﺣﺴﺐ‬ ، ‫اﻷﺧﻀﺮ‬ ‫ﺑﺎﻟﻠﻮن‬ ‫اﻟﺒﺎﻗﻰ‬ ، ‫أﺣﻤﺮ‬ ‫ﻟﻮﻧﮭﻤﺎ‬:
١(‫ا‬‫ﺣﻤﺮاء‬ ‫اﻟﻤﺴﺤﻮﺑﺔ‬ ‫اﻟﻜﺮة‬ ‫ﺗﻜﻮن‬ ‫أن‬ ‫ﺣﺪث‬.
٢(‫ب‬‫ﺧﻀﺮاء‬ ‫أو‬ ‫ﺣﻤﺮاء‬ ‫اﻟﻤﺴﺤﻮﺑﺔ‬ ‫اﻟﻜﺮة‬ ‫ﺗﻜﻮن‬ ‫أن‬ ‫ﺣﺪث‬
٣(‫ﺧﻀﺮاء‬ ‫ﻟﯿﺴﺖ‬ ‫اﻟﻤﺴﺤﻮﺑﺔ‬ ‫اﻟﻜﺮة‬ ‫ﺗﻜﻮن‬ ‫أن‬ ‫ﺣﺪث‬ ‫ج‬.
٤(‫ﺑﯿﻀﺎء‬ ‫أو‬ ‫ﺣﻤﺮاء‬ ‫اﻟﻤﺴﺤﻮﺑﺔ‬ ‫اﻟﻜﺮة‬ ‫ﺗﻜﻮن‬ ‫أن‬ ‫ﺣﺪث‬ ‫د‬
٥(‫ﺧﻀﺮاء‬ ‫أو‬ ‫ﺑﯿﻀﺎء‬ ‫أو‬ ‫ﺣﻤﺮاء‬ ‫اﻟﻤﺴﺤﻮﺑﺔ‬ ‫اﻟﻜﺮة‬ ‫ﺗﻜﻮن‬ ‫أن‬ ‫ﺣﺪث‬ ‫ھـ‬
‫اﻟﺤﻞ‬:
‫اﻟﻌﯿﻨﺔ‬ ‫ﻓﻀﺎء‬ ‫ﻋﻨﺎﺻﺮ‬ ‫ﻋﺪد‬:‫ن‬)‫ف‬= (١٠‫اﻟﺒﯿﻀﺎء‬ ‫اﻟﻜﺮات‬ ‫ﻋﺪد‬ ،=٥
‫اﻟﺤﻤﺮاء‬ ‫اﻟﻜﺮات‬ ‫ﻋﺪد‬ ،=٢‫اﻟﺨﻀﺮاء‬ ‫اﻟﻜﺮات‬ ‫ﻋﺪد‬ ،=٣
١(‫ﺣﻤﺮاء‬ ‫اﻟﻜﺮة‬ ‫ﺗﻜﻮن‬ ‫أن‬ ‫اﺣﺘﻤﺎل‬=‫ل‬)‫ا‬= (= ==٠٫٢
‫اﻟﺤﺪث‬ ‫ﻟﻮﻗﻮع‬ ‫ﺗﺆدى‬ ‫اﻟﺘﻰ‬ ‫اﻟﻨﻮاﺗﺞ‬ ‫ﻋﺪد‬)‫ا‬(
‫اﻟﻤﻤﻜﻨﺔ‬ ‫اﻟﻨﻮاﺗﺞ‬ ‫ﺟﻤﯿﻊ‬ ‫ﻋﺪد‬
‫ن‬)‫ا‬(
‫ن‬)‫ف‬(
‫ن‬)‫ا‬(
‫ن‬)‫ف‬(
٢
١٠
١
٥

158. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
158
٢(‫ﺧﻀﺮاء‬ ‫أو‬ ‫ﺣﻤﺮاء‬ ‫اﻟﻜﺮة‬ ‫ﺗﻜﻮن‬ ‫أن‬ ‫اﺣﺘﻤﺎل‬= = ==٠٫٥
٣(‫ﺧﻀﺮاء‬ ‫ﻟﯿﺴﺖ‬ ‫اﻟﻜﺮة‬ ‫ﺗﻜﻮن‬ ‫أن‬ ‫اﺣﺘﻤﺎل‬= =٠٫٧
‫آﺧﺮ‬ ‫ﺣﻞ‬:‫ﺧﻀﺮاء‬ ‫ﻟﯿﺴﺖ‬ ‫اﻟﻜﺮة‬ ‫ﺗﻜﻮن‬ ‫أن‬ ‫اﺣﺘﻤﺎل‬=١–‫ﺧﻀﺮاء‬ ‫اﻟﻜﺮة‬ ‫اﺣﺘﻤﺎل‬
=١‫ــ‬==٠٫٧
٤(‫ﺑﯿﻀﺎء‬ ‫أو‬ ‫ﺣﻤﺮاء‬ ‫اﻟﻜﺮة‬ ‫ﺗﻜﻮن‬ ‫أن‬ ‫اﺣﺘﻤﺎل‬= = =٠٫٧
٥(‫ﺧﻀﺮاء‬ ‫أو‬ ‫ﺑﯿﻀﺎء‬ ‫أو‬ ‫ﺣﻤﺮاء‬ ‫اﻟﻜﺮة‬ ‫ﺗﻜﻮن‬ ‫أن‬ ‫اﺣﺘﻤﺎل‬= = =١
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
*‫اﻻﺣﺘﻤﺎل‬ ‫ﻣﺴﻠﻤﺎت‬:
‫ﻛﺎن‬ ‫إذا‬:‫ا‬‫أى‬ ‫ﻣﺎ‬ ‫ﻋﺸﻮاﺋﯿﺔ‬ ‫ﻟﺘﺠﺮﺑﺔ‬ ‫اﻟﻌﯿﻨﺔ‬ ‫ﻓﻀﺎء‬ ‫أﺣﺪاث‬ ‫ﻣﻦ‬ ً‫ﺎ‬‫ﺣﺪﺛ‬‫ا‬e‫ف‬
‫ﻓﺈن‬:‫اﻟﺤﺪث‬ ‫إﺣﺘﻤﺎل‬‫ا‬"‫ل‬)‫ا‬" (‫ﯾﺄﺗﻰ‬ ‫ﻣﺎ‬ ‫ﯾﺤﻘﻖ‬ ‫ﺣﻘﯿﻘﻰ‬ ‫ﻋﺪد‬ ‫ھﻮ‬:
)١(‫ل‬)‫ا‬= (=
‫ﺣﯿﺚ‬:٠≥‫ل‬)‫ا‬(≥١‫أى‬:‫ل‬)‫ا‬(g]٠،١[
‫أن‬ ‫أى‬:‫اﻟ‬ ‫ﻋﻦ‬ ‫ﯾﺰﯾﺪ‬ ‫ﻻ‬ ‫ﻣﻮﺟﺐ‬ ‫ﺣﻘﯿﻘﻰ‬ ‫ﻋﺪد‬ ‫ھﻮ‬ ‫ﺣﺪث‬ ‫أى‬ ‫وﻗﻮع‬ ‫إﺣﺘﻤﺎل‬‫اﻟﺼﺤﯿﺢ‬ ‫ﻮاﺣﺪ‬
)۲(‫ل‬)‫ف‬= (١‫أن‬ ‫أى‬:‫اﻟﻤﺆﻛﺪ‬ ‫اﻟﺤﺚ‬ ‫إﺣﺘﻤﺎل‬=١
)٣(‫ل‬)Т= (‫أن‬ ‫أى‬ ‫ﺻﻔﺮ‬:‫اﻟﻤﺴﺘﺤﯿﻞ‬ ‫اﻟﺤﺪث‬ ‫إﺣﺘﻤﺎل‬=‫ﺻﻔﺮ‬
)٤(‫ﻛﺎن‬ ‫إذا‬:‫ا‬‫ﻓﺈن‬ ‫ﻋﯿﻨﺔ‬ ‫ﻓﻀﺎء‬ ‫ﻣﻦ‬ ‫ﻣﺘﻨﺎﻓﯿﻦ‬ ‫ﺣﺪﺛﯿﻦ‬ ‫ب‬ ،:
‫ل‬)‫ﺑﻼ‬ ‫ا‬‫ب‬= (‫ﺻﻔﺮ‬
،‫ل‬)‫ﺑﻶ‬ ‫ا‬‫ب‬= (‫ل‬)‫ا‬+ (‫ل‬)‫ب‬(
)٥(‫ﻛﺎن‬ ‫إذا‬:‫ف‬=}‫ا‬١،‫ا‬۲،‫ا‬٣،٠٠٠،‫ا‬‫ن‬
{
‫ﻓﺈن‬:‫ل‬)‫ا‬١+ (‫ل‬)‫ا‬۲+ (‫ل‬)‫ا‬٣+ (٠٠٠‫ل‬)‫ا‬‫ن‬= (١
‫ﻟﻸﺣﺪاث‬ ‫اﻻﺣﺘﻤﺎﻻت‬ ‫ﻣﺠﻤﻮع‬‫اﻵوﻟﯿﺔ‬=١
٢+٣
١٠
٥
١٠
١
٢
٧
١٠
٣
١٠
٧
١٠
٢+٥
١٠
٧
١٠
٢+٥+٣
١٠
١٠
١٠
‫ن‬)‫ف‬(
‫ن‬)‫ا‬(
‫ﻓﻀﺎء‬ ‫ﻋﻨﺎﺻﺮ‬ ‫ﻋﺪد‬
‫اﻟﺤﺪث‬ ‫ﻋﻨﺎﺻﺮ‬ ‫ﻋﺪد‬

159. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
159
)٦(‫ﻛﺎن‬ ‫إذا‬:‫ا‬، ‫ﻋﯿﻨﺔ‬ ‫ﻓﻀﺎء‬ ‫ﻣﻦ‬ ‫ﺣﺪﺛﯿﻦ‬ ‫ب‬ ،‫ا‬e‫ب‬
‫ﻓﺈن‬:‫ل‬)‫ﺑﻼ‬ ‫ا‬‫ب‬= (‫ل‬)‫ا‬(،‫ل‬)‫ﺑﻶ‬ ‫ا‬‫ب‬= (‫ل‬)‫ب‬(‫ل‬ ،)‫ا‬(Y‫ل‬)‫ب‬(
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
*‫ھﺎﻣﺔ‬ ‫ﻧﺘﺎﺋﺞ‬:
)١(‫ل‬)Т= (٠
)٢(‫ل‬)‫ا‬/
= (١–‫ل‬)‫ا‬(،‫ل‬)‫ا‬+ (‫ل‬)‫ا‬/
= (١
)٣(‫ل‬)‫ا‬-‫ب‬= (‫ل‬)‫ا‬(–‫ل‬)‫ا‬∩‫ب‬(
)٤(‫ل‬)‫ا‬‫ب‬=(‫ل‬)‫ا‬+ (‫ل‬)‫ب‬(–‫ل‬)‫ا‬∩‫ب‬(
‫ل‬)‫ا‬‫ﺑﻼ‬‫ب‬= (‫ل‬)‫ا‬+ (‫ل‬)‫ب‬(–‫ل‬)‫ا‬‫ﺑﻶ‬‫ب‬(
)٥(‫اﻟﺤﺪﺛﯿﻦ‬ ‫وﻗﻮع‬ ‫ﻋﺪم‬ ‫إﺣﺘﻤﺎل‬‫ا‬‫ب‬ ‫و‬ً‫ﺎ‬‫ﻣﻌ‬E‫ل‬)‫ا‬∩‫ب‬(
/
=١-‫ل‬)‫ا‬‫ﺑﻼ‬‫ب‬(
)٦(‫إﺣﺘﻤﺎل‬‫ﻋﺪم‬‫اﻟﺤﺪﺛﯿﻦ‬ ‫أﺣﺪ‬ ‫وﻗﻮع‬‫ا‬‫ب‬ ‫أو‬‫اﻷﻗﻞ‬ ‫ﻋﻠﻰ‬‫ﻋﺪم‬ ‫أو‬‫وﻗﻮع‬‫ﻛﻼھﻤﺎ‬
‫ل‬)‫ا‬‫ﺑﻶ‬‫ب‬(
/
=١-‫ل‬)‫ا‬‫ﺑﻶ‬‫ب‬= (‫ل‬)‫ا‬/
∩‫ب‬/
(
)٧(‫اﻻﻛﺛر‬ ‫ﻋﻠﻰ‬ ‫أﺣدھﻣﺎ‬ ‫وﻗوع‬ ‫اﺣﺗﻣﺎل‬) =‫ا‬∩‫ب‬(/
=١–‫ل‬)‫ا‬∩‫ب‬= (‫ل‬)‫ا‬/
‫ب‬/
(
)٨(‫ل‬)‫ا‬/
‫ب‬= (‫ل‬)‫ا‬∩‫ب‬/
(/
=١‫ل‬ ‫ــ‬)‫ا‬∩‫ب‬/
= (١‫ل‬ ‫ــ‬)‫ـ‬‫ـ‬‫ا‬‫ب‬ ‫ــ‬(
)٩(‫ﻣﻮرﺟﺎن‬ ‫دى‬ ‫ﻗﺎﻧﻮﻧﺎ‬:‫ل‬)‫ا‬/
∩‫ب‬/
(=‫ل‬)‫ا‬‫ب‬(/
‫ل‬ ،)‫ا‬/
‫ب‬/
= (‫ل‬)‫ا‬∩‫ب‬(/
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﻛﺎن‬ ‫إذا‬‫ا‬‫ﺣ‬ ‫ب‬ ،‫ﺣﯿﺚ‬ ‫ﻋﺸﻮاﺋﯿﺔ‬ ‫ﻋﯿﻨﺔ‬ ‫ﻓﻀﺎء‬ ‫ﻣﻦ‬ ‫ﺪﺛﯿﻦ‬:
‫ل‬)‫ا‬= (‫ل‬ ،)‫ب‬= (‫ل‬ ،)‫ا‬∩‫ب‬= (‫اﺣﺴﺐ‬:
١(‫ل‬)‫ا‬‫ب‬(٢(‫ل‬)‫ا‬/
(٣(‫ل‬)‫ا‬–‫ب‬(
٤(‫ل‬)‫ا‬/
∩‫ب‬/
(٥(‫ل‬)‫ا‬/
‫ب‬/
(٦(‫ل‬)‫ا‬‫ب‬(/
٣
٤
٣
٨
١
٤

160. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
160
‫اﻟﺤﻞ‬:١(‫ل‬)‫ا‬‫ب‬= (‫ل‬)‫ا‬+ (‫ل‬)‫ب‬(‫ل‬ ‫ــ‬)‫ا‬∩‫ب‬+ = (‫ــ‬=
٢(‫ل‬)‫ا‬/
= (١‫ل‬ ‫ــ‬)‫ا‬= (١‫ــ‬=
٣(‫ل‬)‫ا‬–‫ب‬= (‫ل‬)‫ا‬(‫ل‬ ‫ــ‬)‫ا‬∩‫ب‬= (‫ــ‬=
٤(‫ل‬)‫ا‬/
∩‫ب‬/
(=‫ل‬)‫ا‬‫ب‬(/
=١‫ــ‬‫ل‬)‫ا‬‫ب‬(=١‫ــ‬=
٥(‫ل‬)‫ا‬/
‫ب‬/
(=‫ل‬)‫ا‬∩‫ب‬(/
=١‫ل‬ ‫ــ‬)‫ا‬∩‫ب‬= (١‫ــ‬=
٦(‫ل‬)‫ا‬‫ب‬(/
=١‫ل‬ ‫ــ‬)‫ا‬‫ب‬(=١‫ــ‬=
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﻛﺎن‬ ‫إذا‬‫ا‬‫ل‬ ‫ﻛﺎن‬ ‫و‬ ‫ف‬ ‫ﻋﺸﻮاﺋﯿﺔ‬ ‫ﻟﺘﺠﺮﺑﺔ‬ ‫ﻋﯿﻨﺔ‬ ‫ﻓﻀﺎء‬ ‫ﻣﻦ‬ ‫ﺣﺪﺛﯿﻦ‬ ‫ب‬ ،)‫ا‬/
= (‫ل‬)‫ا‬(
‫ل‬ ،)‫ب‬= (‫ل‬ ،)‫ا‬/
‫ب‬/
= (‫ﻓﺄوﺟﺪ‬:
‫أ‬(‫اﻻﻗﻞ‬ ‫ﻋﻠﻰ‬ ‫اﻟﺤﺪﺛﯿﻦ‬ ‫أﺣﺪ‬ ‫وﻗﻮع‬ ‫اﺣﺘﻤﺎل‬‫ب‬(‫اﻷﻛﺜﺮ‬ ‫ﻋﻠﻰ‬ ‫اﻟﺤﺪﺛﯿﻦ‬ ‫أﺣﺪ‬ ‫وﻗﻮع‬ ‫اﺣﺘﻤﺎل‬
‫ﺟـ‬(‫د‬ ‫ﻓﻘﻂ‬ ‫ب‬ ‫اﻟﺤﺪث‬ ‫وﻗﻮع‬ ‫اﺣﺘﻤﺎل‬(‫ﻓﻘﻂ‬ ‫اﻟﺤﺪﺛﯿﻦ‬ ‫أﺣﺪ‬ ‫وﻗﻮع‬ ‫اﺣﺘﻤﺎل‬
‫اﻟﺤﻞ‬:e‫ل‬)‫ا‬/
‫ب‬/
= (E‫ل‬)‫ا‬∩‫ب‬(/
=١‫ل‬ ‫ــ‬)‫ا‬∩‫ب‬= (E‫ل‬)‫ا‬∩‫ب‬= (
e‫ل‬)‫ا‬/
= (‫ل‬)‫ا‬(E١‫ل‬ ‫ــ‬)‫ا‬= (‫ل‬)‫ا‬(E‫ل‬)‫ا‬= (١E‫ل‬)‫ا‬=(
‫أ‬(‫اﻷﻗﻞ‬ ‫ﻋﻠﻰ‬ ‫اﻟﺤﺪﺛﯿﻦ‬ ‫أﺣﺪ‬ ‫وﻗﻮع‬ ‫اﺣﺘﻤﺎل‬=‫ل‬)‫ا‬‫ب‬= (‫ل‬)‫ا‬+ (‫ل‬)‫ب‬(‫ل‬ ‫ــ‬)‫ا‬∩‫ب‬(
+ =‫ــ‬=
‫ب‬(‫اﻷ‬ ‫ﻋﻠﻰ‬ ‫أﺣﺪ‬ ‫وﻗﻮع‬ ‫اﺣﺘﻤﺎل‬‫ﻛﺜﺮ‬=‫ل‬)‫ا‬∩‫ب‬(/
=‫ل‬)‫ا‬/
‫ب‬/
= (
‫ﺟـ‬(‫ﻓﻘﻂ‬ ‫ب‬ ‫اﻟﺤﺪث‬ ‫وﻗﻮع‬ ‫اﺣﺘﻤﺎل‬=‫ل‬)‫ــ‬ ‫ب‬‫ا‬= (‫ل‬)‫ب‬(‫ل‬ ‫ــ‬)‫ا‬∩‫ب‬= (‫ــ‬=
‫د‬(‫ﻓﻘﻂ‬ ‫اﻟﺤﺪﺛﯿﻦ‬ ‫أﺣﺪ‬ ‫وﻗﻮع‬ ‫اﺣﺘﻤﺎل‬=‫ل‬)‫ا‬‫ب‬(‫ل‬ ‫ــ‬)‫ا‬∩‫ب‬(=‫ــ‬= =
٣
٨
٣
٤
١
٤
٧
٨
٣
٨
٥
٨
٣
٨
١
٤
١
٨
٧
٨
١
٨
١
٤
٣
٤
٧
٨
١
٨
١
٣ ١
٢
٥
٨
٥
٨
٥
٨
٣
٨
١
٣
١
٣
٤
٣
٣
٤
٣
٤
١
٢
٣
٨
٧
٨
٥
٨
٥
٨
١
٢
١
٨
٥
٨
٧
٨
٢
٨
١
٤

161. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
161
‫ﻣﺜﺎل‬:‫ﻛﺎن‬ ‫إذا‬‫ا‬‫ﻣ‬ ‫ﺣﺪﺛﯿﻦ‬ ‫ب‬ ،‫ل‬ ، ‫ف‬ ‫ﻦ‬)‫ا‬= (‫ل‬ ،)‫ﺑﻶ‬ ‫ا‬‫ب‬= (
‫ل‬ ‫أوﺟﺪ‬)‫ب‬(‫ﻛﺎن‬ ‫إذا‬:
]١[‫ا‬‫ﻣﺘﻨﺎﻓﯿﯿﻦ‬ ‫ﺣﺪﺛﯿﻦ‬ ‫ب‬ ،]۲[‫ا‬e‫ب‬
‫اﻟﺤﻞ‬:
]١[A‫ا‬‫ﻣﺘﻨﺎﻓﯿﯿﻦ‬ ‫ﺣﺪﺛﯿﻦ‬ ‫ب‬ ،
B‫ل‬)‫ا‬‫ﺑﻶ‬‫ب‬= (‫ل‬)‫ا‬+ (‫ل‬)‫ب‬(
B=+‫ل‬)‫ب‬(
B‫ل‬)‫ب‬= (–=
]۲[A‫ا‬e‫ب‬B‫ل‬)‫ﺑﻶ‬ ‫ا‬‫ب‬= (‫ل‬)‫ب‬(B‫ل‬)‫ب‬= (
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﻛﺎن‬ ‫إذا‬‫ا‬G‫ف‬،=‫ﻋﺸ‬ ‫ﻋﯿﻨﺔ‬ ‫ﻓﻀﺎء‬ ‫ف‬ ،‫ل‬ ‫أوﺟﺪ‬ ‫ﻮاﺋﯿﺔ‬)‫ا‬(
‫اﻟﺤﻞ‬:e=E‫ل‬)‫ا‬/
= (‫ل‬)‫ا‬(
e‫ل‬)‫ا‬/
+ (‫ل‬)‫ا‬= (١E‫ل‬)‫ا‬+ (‫ل‬)‫ا‬= (١E‫ل‬)‫ا‬= (١
E‫ل‬)‫ا‬= = (٠٫٧
‫ـــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﯾﺴﺎوى‬ ‫اﻟﻔﯿﺰﯾﺎء‬ ‫اﻣﺘﺤﺎن‬ ‫ﻓﻰ‬ ‫ﻃﺎﻟﺐ‬ ‫ﻧﺠﺎح‬ ‫اﺣﺘﻤﺎل‬ ‫ﻛﺎن‬ ‫إذا‬٠٫٨٥‫ﻓﻰ‬ ‫ﻧﺠﺎﺣﮫ‬ ‫اﺣﺘﻤﺎل‬ ‫و‬
ً‫ﺎ‬‫ﻣﻌ‬ ‫اﻻﻣﺘﺤﺎﻧﯿﻦ‬ ‫أﺣﺪ‬ ‫ﻓﻰ‬ ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫اﻣﺘﺤﺎن‬٠٫٨‫اﺣﺘﻤﺎل‬ ‫أوﺟﺪ‬:
‫أ‬(‫اﻷﻗﻞ‬ ‫ﻋﻠﻰ‬ ‫اﻻﻣﺘﺤﺎﻧﯿﻦ‬ ‫أﺣﺪ‬ ‫ﻓﻰ‬ ‫اﻟﻄﺎﻟﺐ‬ ‫ﻧﺠﺎح‬
‫ب‬(‫ﻓﻘﻂ‬ ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫اﻣﺘﺤﺎن‬ ‫ﻓﻰ‬ ‫اﻟﻄﺎﻟﺐ‬ ‫ﻧﺠﺎح‬
‫ﺟـ‬(‫ﻣﻌﺎ‬ ‫اﻻﻣﺘﺤﺎﻧﯿﻦ‬ ‫ﻓﻰ‬ ‫اﻟﻄﺎﻟﺐ‬ ‫ﻧﺠﺎح‬ ‫ﻋﺪم‬.
‫اﻟﺤﻞ‬:
٣
٤
٣
٥
٣
٤
٣
٥
٣
٢٠
٣
٤
٣
٥
٣
٤
‫ل‬)‫ا‬/
(
‫ل‬)‫ا‬(
٣
٧ ‫ل‬)‫ا‬/
(
‫ل‬)‫ا‬(
٣
٧
٣
٧
٣
٧
١٠
٧
٧
١٠

162. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
162
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﻣﺮة‬ ‫ﻛﻞ‬ ‫ﻓﻰ‬ ‫اﻟﻌﻠﻮى‬ ‫اﻟﻮﺟﺔ‬ ‫ﻋﻠﻰ‬ ‫اﻟﻈﺎھﺮ‬ ‫اﻟﻌﺪد‬ ‫ﻟﻮﺣﻆ‬ ‫و‬ ‫ﻣﺘﺘﺎﻟﯿﺘﯿﻦ‬ ‫ﻣﺮﺗﯿﻦ‬ ‫ﻣﻨﺘﻈﻢ‬ ‫ﻧﺮد‬ ‫ﺣﺠﺮ‬ ‫أﻟﻘﻰ‬
‫اﺣﺘﻤﺎل‬ ‫اﺣﺴﺐ‬:
١(‫ا‬‫ﯾﻜﻮن‬ ‫أن‬ ‫ﺣﺪث‬"‫ﯾﺴﺎوى‬ ‫أو‬ ‫ﻣﻦ‬ ‫أﻗﻞ‬ ‫اﻟﻈﺎھﺮﯾﻦ‬ ‫اﻟﻌﺪدﯾﻦ‬ ‫ﻣﺠﻤﻮع‬٤"
٢(‫ﯾﻜﻮن‬ ‫أن‬ ‫ﺣﺪث‬ ‫ب‬"‫اﻵﺧﺮ‬ ‫ﺿﻌﻒ‬ ‫اﻟﻌﺪدﯾﻦ‬ ‫أﺣﺪ‬"
٣(‫ﯾﻜﻮن‬ ‫أن‬ ‫ﺣﺪث‬ ‫ج‬"‫ﯾﺴﺎوى‬ ‫ﻟﻠﻌﺪدﯾﻦ‬ ‫اﻟﻤﻄﻠﻖ‬ ‫اﻟﻔﺮق‬٢"
٤(‫ﯾﻜﻮن‬ ‫أن‬ ‫ﺣﺪث‬ ‫د‬"‫ﻣﻦ‬ ‫أﻛﺒﺮ‬ ‫اﻟﻌﺪدﯾﻦ‬ ‫ﻣﺠﻤﻮع‬١٢"
٥(‫ﺣﺪث‬ ‫ھـ‬"‫ﻣﺘﺴﺎوﯾﺎن‬ ‫اﻟﻈﺎھﺮان‬ ‫اﻟﻌﺪدان‬"
٦(‫ﺣﺪث‬ ‫ط‬"‫اﻟ‬ ‫ﻓﻰ‬ ‫و‬ ‫ﻓﺮدى‬ ‫اﻷوﻟﻰ‬ ‫اﻟﺮﻣﯿﺔ‬ ‫ﻓﻰ‬ ‫اﻟﻌﺪد‬‫زوﺟﻰ‬ ‫اﻟﺜﺎﻧﯿﺔ‬ ‫ﺮﻣﯿﺔ‬:
‫اﻟﺤﻞ‬:‫ن‬)‫ف‬= (٦٢
=٣٦‫واﺣﺪة‬ ‫ﻟﺮﻣﯿﺔ‬ ‫ف‬ ،=}١،٢،٣،٤،٥،٦{
١(‫ا‬=})١،١(،)١،٢(،)١،٣(،)٢،١(،)٢،٢(،)٣،١({
‫ن‬)‫ا‬= (٦E‫ل‬)‫ا‬= = (
٢(‫ب‬=})١،٢(،)٢،١(،)٢،٤(،)٤،٢(،)٣،٦(،)٦،٣({
‫ن‬)‫ب‬= (٦E‫ل‬)‫ب‬= = (
٦
٣٦
١
٦
٦
٣٦
١
٦

163. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
163
٣(‫ج‬=})١،٣(،)٣،١(،)٢،٤(،)٤،٢(،)٣،٥(،)٥،٣(،
)٤،٦(،)٦،٤({
‫ن‬)‫ج‬= (٨E‫ل‬)‫ج‬= = (
٤(‫ﻣﻦ‬ ‫أﻛﺒﺮ‬ ‫ﻣﺠﻤﻮﻋﮭﻤﺎ‬ ‫ﻋﺪدان‬ ‫ﯾﻈﮭﺮ‬ ‫أن‬ ‫ﯾﻤﻜﻦ‬ ‫ﻻ‬ ‫اﻧﮫ‬ ‫ﺣﯿﺚ‬١٢E‫د‬=ТE‫ل‬)‫د‬= (٠
٥(‫ھـ‬=})١،١(،)٢،٢(،)٣،٣(،)٤،٤(،)٥،٥(،)٦،٦({
‫ن‬)‫ھـ‬= (٦E‫ل‬)‫ھـ‬= = (
٦(‫ط‬=})١،٢(،)١،٤(،)١،٦(،)٣،٢(،)٣،٤(،)٣،٦(،
)٥،٢(،)٥،٤(،)٥،٦({
‫ن‬)‫ط‬= (٩E‫ل‬)‫ط‬= = (
‫ــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫اﻻﺣﺪاث‬ ‫اﺣﺘﻤﺎﻻت‬ ‫اﺣﺴﺐ‬ ‫اﻟﻜﺘﺎﺑﺎت‬ ‫و‬ ‫اﻟﺼﻮر‬ ‫ﺗﺘﺎﺑﻊ‬ ‫ﻟﻮﺣﻆ‬ ‫و‬ ‫ﻣﺘﺘﺎﻟﯿﺔ‬ ‫ﻣﺮات‬ ‫ﺛﻼث‬ ‫ﻧﻘﻮد‬ ‫أﻟﻘﯿﺖ‬
‫اﻵﺗﯿﺔ‬:
١(‫ا‬‫ﻓﻘﻂ‬ ‫واﺣﺪة‬ ‫ﺻﻮرة‬ ‫ﻇﮭﻮر‬ ‫ﺣﺪث‬٢(‫ب‬‫اﻷﻗﻞ‬ ‫ﻋﻠﻰ‬ ‫ﺻﻮرﺗﯿﻦ‬ ‫ﻇﮭﻮر‬ ‫ﺣﺪث‬
٣(‫ﺑﺎﻟﻀﺒﻂ‬ ‫ﺻﻮرﺗﯿﻦ‬ ‫ﻇﮭﻮر‬ ‫ﺣﺪث‬ ‫ج‬٤(‫اﻟﺜﻼث‬ ‫اﻟﺮﻣﯿﺎت‬ ‫ﻓﻰ‬ ‫اﻟﻮﺟﺔ‬ ‫ﻧﻔﺲ‬ ‫ﻇﮭﻮر‬ ‫ﺣﺪث‬ ‫س‬
٥(‫اﻷﻛﺜﺮ‬ ‫ﻋﻠﻰ‬ ‫ﺻﻮرة‬ ‫ﻇﮭﻮر‬ ‫ﺣﺪث‬ ‫ص‬٦(‫اﻟﺼﻮر‬ ‫ﻣﻦ‬ ‫ﻓﺮدى‬ ‫ﻋﺪد‬ ‫ﻇﮭﻮر‬ ‫ﺣﺪث‬ ‫ع‬
٧(‫ﻣﻦ‬ ‫اﻟﻌﺪد‬ ‫ﻧﻔﺲ‬ ‫ﯾﺴﺎوى‬ ‫اﻟﺼﻮر‬ ‫ﻣﻦ‬ ‫ﻋﺪد‬ ‫ﻇﮭﻮر‬ ‫ﺣﺪث‬ ‫ھـ‬‫اﻟﻜﺘﺎﺑﺎت‬
٨(‫اﻷﻗﻞ‬ ‫ﻋﻠﻰ‬ ‫ﻛﺘﺎﺑﺔ‬ ‫ﻇﮭﻮر‬ ‫ﺣﺪث‬ ‫ط‬
‫اﻟﺤﻞ‬:‫ف‬=})‫ص‬ ، ‫ص‬ ، ‫ص‬(،)‫ك‬ ، ‫ص‬ ، ‫ص‬(،)‫ص‬ ، ‫ك‬ ، ‫ص‬(
،)‫ك‬ ، ‫ك‬ ، ‫ص‬(،)‫ص‬ ، ‫ص‬ ، ‫ك‬(،)‫ك‬ ، ‫ص‬ ، ‫ك‬(،
،)‫ص‬ ، ‫ك‬ ، ‫ك‬(،)‫ك‬ ، ‫ك‬ ، ‫ك‬({
‫ن‬)‫ف‬= (٨
١(‫ا‬=})‫ك‬ ، ‫ك‬ ، ‫ص‬(،)‫ك‬ ، ‫ص‬ ، ‫ك‬(،)‫ص‬ ، ‫ك‬ ، ‫ك‬({
‫ن‬)‫ا‬= (٣E‫ل‬)‫ا‬= (
٨
٣٦
٢
٩
٦
٣٦
١
٦
٩
٣٦
١
٤
٣
٨

164. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
164
٢(‫اﻻﻗﻞ‬ ‫ﻋﻠﻰ‬ ‫ﺻﻮرﺗﯿﻦ‬ ‫ﻇﮭﻮر‬ ‫ﺣﺪث‬ ‫ب‬)‫ﺻﻮر‬ ‫ﺛﻼث‬ ‫أو‬ ‫ﺻﻮرﺗﺎن‬ ‫إﻣﺎ‬ ‫أى‬(
‫ب‬=})‫ك‬ ، ‫ص‬ ، ‫ص‬(،)‫ص‬ ، ‫ك‬ ، ‫ص‬(،)‫ص‬ ، ‫ص‬ ، ‫ك‬(،)‫ص‬ ، ‫ص‬ ، ‫ص‬({
‫ن‬)‫ب‬= (٤E‫ل‬)‫ب‬= = (
٣(‫ج‬=})‫ك‬ ، ‫ص‬ ، ‫ص‬(،)‫ص‬ ، ‫ك‬ ، ‫ص‬(،)‫ص‬ ، ‫ص‬ ، ‫ك‬({
‫ن‬)‫ج‬= (٣E‫ل‬)‫ج‬= (
٥(‫اﻟﺜﻼث‬ ‫اﻟﺮﻣﯿﺎت‬ ‫ﻓﻰ‬ ‫اﻟﻮﺟﺔ‬ ‫ﻧﻔﺲ‬ ‫ﻇﮭﻮر‬ ‫ﺣﺪث‬ ‫س‬=})‫ص‬ ، ‫ص‬ ، ‫ص‬(،)‫ك‬ ، ‫ك‬ ، ‫ك‬({
‫ن‬)‫س‬= (٢E‫ل‬)‫س‬= = (
٦(‫اﻷﻛﺜﺮ‬ ‫ﻋﻠﻰ‬ ‫ﺻﻮرة‬ ‫ﻇﮭﻮر‬ ‫ﺣﺪث‬ ‫ص‬
‫ص‬=})‫ك‬ ، ‫ك‬ ، ‫ص‬(،)‫ص‬ ، ‫ص‬ ، ‫ك‬(،)‫ص‬ ، ‫ك‬ ، ‫ك‬(،)‫ك‬ ، ‫ك‬ ، ‫ك‬({
‫ن‬)‫ص‬= (٤E‫ل‬)‫ص‬= = (
٧(‫اﻟﻌﺪد‬ ‫ﻧﻔﺲ‬ ‫ﯾﺴﺎوى‬ ‫اﻟﺼﻮر‬ ‫ﻣﻦ‬ ‫ﻋﺪد‬ ‫ﻇﮭﻮر‬ ‫ﺣﺪث‬ ‫ھـ‬‫اﻟﻜﺘﺎﺑﺎت‬ ‫ﻣﻦ‬
‫ھـ‬=ТE‫ل‬)‫ھـ‬(=‫ﺻﻔﺮ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ﻣﺜﺎل‬:‫ﻛﺎن‬ ‫إذا‬‫ا‬‫اﻻﻣﻜﺎﻧﺎت‬ ‫ﻣﺘﺴﺎوﯾﺔ‬ ‫ﻧﻮاﺗﺠﮭﺎ‬ ‫ﺟﻤﯿﻊ‬ ‫ﻋﺸﻮاﺋﯿﺔ‬ ‫ﻟﺘﺠﺮﺑﺔ‬ ‫ﻋﯿﻨﺔ‬ ‫ﻓﻀﺎء‬ ‫ﻣﻦ‬ ‫ﺣﺪﺛﯿﻦ‬ ‫ب‬ ،
‫و‬‫ﻛﺎن‬‫ل‬)‫ا‬‫ب‬= (‫ل‬ ،)‫ب‬= (‫وﻗﻮع‬ ‫اﻟﻰ‬ ‫ﺗﺆدى‬ ‫اﻟﺘﻰ‬ ‫اﻟﻨﻮاﺗﺞ‬ ‫ﻋﺪد‬ ‫ﻛﺎن‬ ‫ﻓﺈذا‬
‫اﻟﺤﺪث‬‫ا‬‫ﯾﺴﺎوى‬١٣‫ﯾﺴﺎوى‬ ‫اﻟﻤﻤﻜﻨﺔ‬ ‫اﻟﻨﻮاﺗﺞ‬ ‫ﺟﻤﯿﻊ‬ ‫ﻋﺪد‬ ‫و‬٣٦‫ﻓﺄوﺟﺪ‬:
‫أوﻻ‬:‫وﻗﻮع‬ ‫اﺣﺘﻤﺎل‬‫ا‬‫ﻣﻌﺎ‬ ‫ب‬ ‫و‬‫ﺛﺎﻧﯿﺎ‬:‫وﻗﻮع‬ ‫اﺣﺘﻤﺎل‬‫ا‬‫ب‬ ‫وﻗﻮع‬ ‫ﻋﺪم‬ ‫و‬
‫اﻟﺤﻞ‬:
‫ن‬)‫ا‬= (١٣‫ن‬ ،)‫ف‬= (٣٦E‫ل‬)‫ا‬= = (
‫أوﻻ‬:‫وﻗﻮع‬ ‫اﺣﺘﻤﺎل‬‫ا‬‫ﻣﻌﺎ‬ ‫ب‬ ‫و‬E‫ل‬)‫ا‬∩‫ب‬= (‫ل‬)‫ا‬+ (‫ل‬)‫ب‬(–‫ل‬)‫ا‬‫ب‬(
+ =‫ــ‬=
‫ﺛﺎﻧﯿﺎ‬:‫وﻗﻮع‬ ‫اﺣﺘﻤﺎل‬‫ا‬‫ب‬ ‫وﻗﻮع‬ ‫وﻋﺪم‬E‫ل‬)‫ا‬∩‫ب‬/
= (‫ل‬)‫ا‬–‫ب‬(
=‫ل‬)‫ا‬(–‫ل‬)‫ا‬∩‫ب‬(
=‫ــ‬=
٤
٨
١
٢
٣
٨
٢
٨
١
٤
٤
٨
١
٢
٥
٦
٧
١٢
١٣
٣٦
١
٣
١
٣
٧
١٢
٥
٦
١
١٢
١
٣
١
١٢
١
٤

165. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
165
]١[
]٢[
]٣[
]٤[
]٥[
‫اﻻﺣﺘﻤﺎل‬ ‫ﻋﻠﻰ‬ ‫ﺗﻤﺎرﯾﻦ‬

166. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
166
]٦[
]٧[‫ﺑﯿﻦ‬ ‫ﻣﻦ‬ ‫اﻻﺧﺮى‬ ‫ﺑﻌﺪ‬ ‫اﻟﻮاﺣﺪة‬ ‫ﺑﻄﺎﻗﺘﺎن‬ ‫ﺳﺤﺒﺖ‬٨‫ﻣﻦ‬ ‫ﻣﺮﻗﻤﺔ‬ ‫و‬ ‫ﻣﺘﻤﺎﺛﻠﺔ‬ ‫ﺑﻄﺎﻗﺎت‬١‫اﻟﻰ‬٨‫ﻣﻊ‬
‫ﻛﺎن‬ ‫إذا‬ ‫و‬ ‫؟‬ ‫اﻟﻌﯿﻨﺔ‬ ‫ﻓﻀﺎء‬ ‫ﻋﻨﺎﺻﺮ‬ ‫ﻋﺪد‬ ‫ﻣﺎ‬ ، ‫اﻟﺜﺎﻧﯿﺔ‬ ‫اﻟﺒﻄﺎﻗﺔ‬ ‫ﻗﺒﻞ‬ ‫أوﻻ‬ ‫اﻟﺒﻄﺎﻗﺔ‬ ‫إﻋﺎدة‬:
‫ا‬‫ﺣﺪث‬"‫اﻷوﻟﻰ‬ ‫اﻟﺴﺤﺒﺔ‬ ‫ﻓﻰ‬ ‫اﻟﻌﺪد‬ ‫أﻣﺜﺎل‬ ‫ﺛﻼﺛﺔ‬ ‫اﻟﺜﺎﻧﯿﺔ‬ ‫اﻟﺴﺤﺒﺔ‬ ‫ﻓﻰ‬ ‫اﻟﻌﺪد‬"
‫ﺣﺪث‬ ‫ب‬"‫ﻣﻦ‬ ‫أﻛﺒﺮ‬ ‫اﻟﻌﺪدﯾﻦ‬ ‫ﻣﺠﻤﻮع‬١٣"
‫ﻣﻦ‬ ‫ﻛﻼ‬ ‫اﻛﺘﺐ‬‫ا‬‫ب‬ ،‫ھﻞ‬ ،‫ا‬‫ذﻟﻚ‬ ‫ﻓﺴﺮ‬ ‫؟‬ ‫ﻣﺘﻨﺎﻓﯿﺎن‬ ‫ﺣﺪﺛﺎن‬ ‫ب‬ ،.
]٨[‫اﻟﻜﺘﺎﺑﺎ‬ ‫و‬ ‫اﻟﺼﻮر‬ ‫ﺗﺘﺎﺑﻊ‬ ‫ﻣﻼﺣﻈﺔ‬ ‫و‬ ‫ﻣﺘﺘﺎﻟﯿﺔ‬ ‫ﻣﺮات‬ ‫ﺛﻼث‬ ‫ﻗﻄﻌﺔ‬ ‫إﻟﻘﺎء‬ ‫ﺗﺠﺮﺑﺔ‬ ‫ﻓﻰ‬‫ﻓﻀﺎء‬ ‫ﻣﺜﻞ‬ ‫ت‬
‫اﻵﺗﯿﺔ‬ ‫اﻷﺣﺪاث‬ ‫ﻋﯿﻦ‬ ‫ﺛﻢ‬ ، ‫ﺷﺠﺮى‬ ‫ﺑﺸﻜﻞ‬ ‫اﻟﻨﻮاﺗﺞ‬:
‫ا‬‫ﺣﺪث‬"‫اﻻﻗﻞ‬ ‫ﻋﻠﻰ‬ ‫ﻛﺘﺎﺑﺘﯿﻦ‬ ‫ﻇﮭﻮر‬"
‫ﺣﺪث‬ ‫ب‬"‫اﻷﻛﺜﺮ‬ ‫ﻋﻠﻰ‬ ‫ﻛﺘﺎﺑﺘﯿﻦ‬ ‫ﻇﮭﻮر‬
‫ﺣﺪث‬ ‫ج‬"‫اﻷوﻟﻰ‬ ‫اﻟﺮﻣﯿﺔ‬ ‫ﻓﻰ‬ ‫ﺻﻮرة‬ ‫ﻇﮭﻮر‬
‫ﺣﺪث‬ ‫د‬"‫اﻟﺜﻼث‬ ‫اﻟﺮﻣﯿﺎت‬ ‫ﻓﻰ‬ ‫ﺻﻮرة‬ ‫ﻇﮭﻮر‬ ‫ﻋﺪم‬"
]٩[‫ﻗﻄﻌﺔ‬ ‫أﻟﻘﯿﺖ‬‫ﻋﻠﻰ‬ ‫اﻟﻈﺎھﺮ‬ ‫اﻟﻌﺪد‬ ‫و‬ ‫اﻟﻨﻘﻮد‬ ‫ﻟﻘﻄﻌﺔ‬ ‫اﻟﻌﻠﻮى‬ ‫اﻟﻮﺟﮫ‬ ‫ﻣﻼﺣﻈﺔ‬ ‫و‬ ‫ﻧﺮد‬ ‫ﺣﺠﺮ‬ ‫ﺛﻢ‬ ‫ﻧﻘﻮد‬
‫اﻵﺗﯿﺔ‬ ‫أوﺟﺪ‬ ‫ﺛﻢ‬ ‫ﺷﺠﺮى‬ ‫ﺑﺸﻜﻞ‬ ‫اﻟﻌﯿﻨﺔ‬ ‫ﻓﻀﺎء‬ ‫ﻣﺜﻞ‬ ، ‫اﻟﻨﺮد‬ ‫ﻟﺤﺠﺮ‬ ‫اﻟﻌﻠﻮى‬ ‫اﻟﻮﺟﺔ‬:
‫ا‬‫ﺣﺪث‬"‫زوﺟﻰ‬ ‫ﻋﺪد‬ ‫و‬ ‫ﻛﺘﺎﺑﺔ‬ ‫ﻇﮭﻮر‬"‫ﺣﺪث‬ ‫ب‬"‫ﻓﺮدى‬ ‫ﻋﺪد‬ ‫و‬ ‫ﺻﻮرة‬ ‫ﻇﮭﻮر‬"
‫ﺣﺪث‬ ‫ج‬"‫وﻗﻮع‬ ‫ﻋﺪم‬‫ا‬‫أ‬‫ﺣﺪث‬ ‫د‬ ‫ب‬ ‫وﻗﻮع‬ ‫ﻋﺪم‬ ‫و‬"‫اﻟﺤﺪث‬ ‫وﻗﻮع‬‫ا‬‫ﻓﻘﻂ‬"
‫ﺣﺪث‬ ‫ھـ‬"‫اﻟﺤﺪث‬ ‫وﻗﻮع‬‫ا‬‫ب‬ ‫اﻟﺤﺪث‬ ‫وﻗﻮع‬ ‫و‬"
]١٠[‫اﻟﻤﻌﻄﺎة‬ ‫اﻹﺟﺎﺑﺎت‬ ‫ﻣﻦ‬ ‫اﻟﺼﺤﯿﺤﺔ‬ ‫اﻹﺟﺎﺑﺔ‬ ‫اﺧﺘﺮ‬:
١(‫ﻣﻦ‬ ‫أﻗﻞ‬ ‫ﻓﺮدى‬ ‫ﻋﺪد‬ ‫ﻋﻠﻰ‬ ‫اﻟﺤﺼﻮل‬ ‫اﺣﺘﻤﺎل‬ ‫ﻓﺈن‬ ‫واﺣﺪة‬ ‫ﻣﺮة‬ ‫ﻣﻨﺘﻈﻢ‬ ‫ﻧﺮد‬ ‫ﺣﺠﺮ‬ ‫أﻟﻘﻰ‬ ‫إذا‬٥:
]، ، ،[ ١
٦
٢
٥
١
٢
١
٣

167. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
167
٢(‫زوﺟﻰ‬ ‫ﻋﺪد‬ ‫ﻋﻠﻰ‬ ‫اﻟﺤﺼﻮل‬ ‫اﺣﺘﻤﺎل‬ ‫ﻓﺈن‬ ‫ﻣﺘﺘﺎﻟﯿﻦ‬ ‫ﻣﺮﺗﯿﻦ‬ ‫ﻣﻨﺘﻈﻢ‬ ‫ﻧﺮد‬ ‫ﺣﺠﺮ‬ ‫إﻟﻘﺎء‬ ‫ﺗﺠﺮﺑﺔ‬ ‫ﻓﻰ‬
‫ھﻮ‬ ‫اﻟﺜﺎﻧﯿﺔ‬ ‫اﻟﺮﻣﯿﺔ‬ ‫ﻓﻰ‬ ‫أوﻟﻰ‬ ‫ﻋﺪد‬ ‫و‬ ‫اﻷوﻟﻰ‬ ‫اﻟﺮﻣﯿﺔ‬ ‫ﻓﻰ‬:]، ، ،[
٣(‫ﺑﮫ‬ ‫ﺻﻨﺪوق‬ ‫ﻣﻦ‬ ‫ﻋﺸﻮاﺋﯿﺎ‬ ‫ﻛﺮة‬ ‫ﺳﺤﺒﺖ‬ ‫إذا‬٣، ‫ﺑﯿﻀﺎء‬ ‫ﻛﺮات‬٥، ‫ﺣﻤﺮاء‬ ‫ﻛﺮات‬٧‫ﻛﺮات‬
‫ھﻮ‬ ‫ﺧﻀﺮاء‬ ‫أو‬ ‫ﺑﯿﻀﺎء‬ ‫اﻟﻤﺴﺤﻮﺑﺔ‬ ‫اﻟﻜﺮة‬ ‫ﺗﻜﻮن‬ ‫أن‬ ‫اﺣﺘﻤﺎل‬ ‫ﻓﺈن‬ ‫ﺧﻀﺮاء‬:
]، ، ،[
٤(‫ﻣﻦ‬ ‫اﻷرﻗﺎم‬ ‫ﺗﺤﻤﻞ‬ ‫ﻣﺘﻤﺎﺛﻠﺔ‬ ‫ﺑﻄﺎﻗﺎت‬ ‫ﺗﺴﻊ‬ ‫ﻋﻠﻰ‬ ‫ﺻﻨﺪوق‬ ‫ﯾﺤﺘﻮى‬١‫إﻟﻰ‬٩‫ﺑﻄﺎﻗﺔ‬ ‫اﺧﺘﯿﺮت‬
‫اﻟﻌﺪد‬ ‫ﯾﻘﺴﻢ‬ ‫رﻗﻢ‬ ‫اﻟﻤﺴﺤﻮﺑﺔ‬ ‫اﻟﺒﻄﺎﻗﺔ‬ ‫ﺗﺤﻤﻞ‬ ‫أن‬ ‫اﺣﺘﻤﺎل‬ ‫ﻓﺈن‬ ‫ﻋﺸﻮاﺋﯿﺎ‬٩‫ھﻮ‬ ‫ﻓﺮدﯾﺎ‬ ‫رﻗﻤﺎ‬ ‫أو‬:
]، ، ،[
٥(‫ﻛﺎن‬ ‫إذا‬‫ا‬‫ب‬ ‫ﻛﺎن‬ ‫و‬ ‫ﻋﺸﻮاﺋﯿﺔ‬ ‫ﻟﺘﺠﺮﺑﺔ‬ ‫اﻟﻨﻮاﺗﺞ‬ ‫ﻓﻀﺎء‬ ‫ف‬ ‫ﻣﻦ‬ ‫ﺣﺪﺛﯿﻦ‬ ‫ب‬ ،G‫ا‬
‫ل‬ ،)‫ا‬= (٢‫ل‬)‫ب‬= (٠٫٦‫ل‬ ‫ﻓﺈن‬)‫ا‬-‫ب‬(‫ﯾﺴﺎوى‬:
]٠٫٦،٠٫٣،٠٫٤،٠٫٢[
]١١[‫اﻷﻋﺪاد‬ ‫أوﺟﮭﮫ‬ ‫ﻋﻠﻰ‬ ‫ﻛﺘﺐ‬ ‫ﻣﻨﺘﻈﻢ‬ ‫ﻧﺮد‬ ‫ﺣﺠﺮ‬ ‫أﻟﻘﻰ‬٨،٩،١٠،١١،١٢،١٣‫ﻟﻮﺣﻆ‬ ‫و‬
‫اﻟﻌﻠﻮى‬ ‫اﻟﻮﺟﮫ‬ ‫ﻋﻠﻰ‬ ‫اﻟﻌﺪد‬:
)‫أ‬(‫اﻟﺘﺎﻟ‬ ‫اﻷﺣﺪاث‬ ‫ﻣﻦ‬ ‫ﻛﻞ‬ ‫اﺣﺘﻤﺎل‬ ‫اﺣﺴﺐ‬‫ﯿﺔ‬:
*‫ا‬"‫ﻓﺮدى‬ ‫ﻋﺪد‬ ‫ﻇﮭﻮر‬ ‫ﺣﺪث‬* "‫ب‬"‫أوﻟﻰ‬ ‫ﻋﺪد‬ ‫ﻇﮭﻮر‬ ‫ﺣﺪث‬"
*‫ج‬"‫زوﺟﻰ‬ ‫ﻋﺪد‬ ‫ﻇﮭﻮر‬ ‫ﺣﺪث‬* "‫د‬"‫ﻣﻦ‬ ‫أﻛﺒﺮ‬ ‫ﻋﺪد‬ ‫ﻇﮭﻮر‬ ‫ﺣﺪث‬١٢"
*‫ھـ‬"‫رﻗﻤﯿﻦ‬ ‫ﻣﻦ‬ ‫ﻣﻜﻮن‬ ‫ﻋﺪد‬ ‫ﻇﮭﻮر‬ ‫ﺣﺪث‬"
*‫و‬"‫ﻣﻜﻮ‬ ‫ﻋﺪد‬ ‫ﻇﮭﻮر‬ ‫ﺣﺪث‬‫واﺣﺪ‬ ‫رﻗﻢ‬ ‫ﻣﻦ‬ ‫ن‬"
)‫ب‬(‫اﺣﺴﺐ‬:‫ل‬)‫ا‬‫ﺑﻶ‬‫ج‬(‫ل‬ ،)‫ھـ‬‫ﺑﻶ‬‫و‬(‫ل‬ ،)‫ب‬∩‫د‬(
]١٢[‫ف‬ ‫ﻛﺎن‬ ‫إذا‬=}‫ا‬‫د‬ ، ‫ج‬ ، ‫ب‬ ،{‫أوﺟﺪ‬ ‫ﻋﺸﻮاﺋﯿﺔ‬ ‫ﻟﺘﺠﺮﺑﺔ‬ ‫ﻋﯿﻨﺔ‬ ‫ﻓﻀﺎء‬:
‫ل‬)‫ا‬(‫ل‬ ،)‫ب‬(‫ل‬ ‫ﻛﺎن‬ ‫إذا‬ ،)‫ا‬= (٣‫ل‬)‫ب‬(‫ل‬ ،)‫ج‬= (‫ل‬)‫د‬= (
١
٤
١
٣
١
٦
١
٩
١
٥
٢
٣
١
٢
٧
١٥
٥
٩
١
٣
٧
٩
١
٢
٧
١٨

168. ‫اﻟﺮﯾﺎﺿﯿﺎت‬ ‫ﻋﻠﻰ‬ ‫ﺗﻄﺒﯿﻘﺎت‬‫اﻟﺜﺎﻧﻮى‬ ‫اﻟﺜﺎﻧﻰ‬ ‫اﻟﺼﻒ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫اﻻﺳﺘﺎذ‬ ‫اﻋﺪاد‬/‫ت‬ ‫رﯾﺎﺿﯿﺎت‬ ‫ﺧﺒﯿﺮ‬ ‫ﻣﻌﻠﻢ‬ ‫اﻟﻤﻨﻔﻠﻮﻃﻰ‬ ‫ﺧﺎﻟﺪ‬/٠١١٥٤٨٠٢٨١١
168
]١٣[‫ﻛﺎن‬ ‫إذا‬‫ا‬‫ﺣ‬ ‫ب‬ ،‫ﻛﺎن‬ ‫و‬ ‫ﻋﺸﻮاﺋﯿﺔ‬ ‫ﻟﺘﺠﺮﺑﺔ‬ ‫ﻋﯿﻨﺔ‬ ‫ﻓﻀﺎء‬ ‫ﻣﻦ‬ ‫ﻣﺘﻨﺎﻓﯿﻦ‬ ‫ﺪﺛﯿﻦ‬:
‫ل‬)‫ا‬‫ﺑﻶ‬‫ب‬=(٠٫٦‫ل‬ ،)‫ا‬–‫ب‬= (٠٫٢٥‫ل‬ ‫اﺣﺴﺐ‬)‫ا‬(‫ل‬ ،)‫ب‬(
]١٤[‫ﻛﺎن‬ ‫إذا‬‫ا‬‫ل‬ ‫ﻛﺎن‬ ‫و‬ ‫ﻋﺸﻮاﺋﯿﺔ‬ ‫ﻟﺘﺠﺮﺑﺔ‬ ‫ﻋﯿﻨﺔ‬ ‫ﻓﻀﺎء‬ ‫ﻣﻦ‬ ‫ﺣﺪﺛﯿﻦ‬ ‫ب‬ ،)‫ا‬= (‫ل‬ ،)‫ب‬= (
‫ل‬ ،)‫ا‬‫ﺑﻼ‬‫ب‬= (‫أوﺟﺪ‬:
‫أ‬(‫ل‬)‫ا‬/
(‫ب‬(‫ل‬)‫ا‬‫ﺑﻶ‬‫ب‬(‫ﺟـ‬(‫ل‬)‫ا‬–‫ب‬(‫د‬(‫ل‬)‫ا‬/
‫ﺑﻼ‬‫ب‬/
(
]١٥[‫ﻛﺎن‬ ‫إذا‬‫ا‬‫ل‬ ‫ﺣﯿﺚ‬ ، ‫ﻋﺸﻮاﺋﯿﺔ‬ ‫ﻟﺘﺠﺮﺑﺔ‬ ‫ﻋﯿﻨﺔ‬ ‫ﻓﻀﺎء‬ ‫ﻣﻦ‬ ‫ﺣﺪﺛﯿﻦ‬ ‫ب‬ ،)‫ا‬= (٠٫٤
‫ل‬ ،)‫ب‬/
= (٣‫ل‬)‫ب‬(‫ل‬ ،)‫ا‬‫ﺑﻼ‬‫ب‬= (٠٫٢‫اﺣﺘﻤﺎل‬ ‫اﺣﺴﺐ‬:
‫أ‬(‫وﻗﻮع‬‫ا‬‫ب‬ ‫ﻓﻘﻂ‬(‫وﻗﻮع‬‫ا‬‫ﺟـ‬ ‫ب‬ ‫أو‬(‫وﻗﻮع‬‫ا‬‫ب‬ ‫وﻗﻮع‬ ‫ﻋﺪم‬ ‫و‬
]١٦[‫ﻣﻨﮭﺎ‬ ‫ﻣﻠﻮﻧﮫ‬ ‫و‬ ‫ﻣﺘﻤﺎﺛﻠﺔ‬ ‫ﻛﺮات‬ ‫ﺑﮫ‬ ‫ﺻﻨﺪوق‬٤، ‫ﺣﻤﺮاء‬٦، ‫زرﻗﺎء‬٥‫ﻣﻨﮫ‬ ‫ﺳﺤﺒﺖ‬ ‫ﺻﻔﺮاء‬
‫ﻋﺸﻮاﺋﯿﺔ‬ ‫واﺣﺪة‬ ‫ﻛﺮة‬.‫اﻟﻤﺴﺤﻮﺑﺔ‬ ‫اﻟﻜﺮة‬ ‫ﺗﻜﻮن‬ ‫أن‬ ‫اﺣﺘﻤﺎل‬ ‫اﺣﺴﺐ‬:
‫أ‬(‫ب‬ ‫ﺣﻤﺮاء‬(‫ﺟـ‬ ‫ﺻﻔﺮاء‬ ‫أو‬ ‫زرﻗﺎء‬(‫د‬ ‫زرﻗﺎء‬ ‫ﻟﯿﺴﺖ‬(‫ﺻﻔﺮاء‬ ‫ﻻ‬ ‫و‬ ‫ﺣﻤﺮاء‬ ‫ﻟﯿﺴﺖ‬
]١٧[‫ﻣﻦ‬ ‫ﻣﺮﻗﻤﺔ‬ ‫و‬ ‫ﻣﺘﻤﺎﺛﻠﺔ‬ ‫ﺑﻄﺎﻗﺎت‬ ‫ﻣﺠﻤﻮﻋﺔ‬١‫إﻟﻰ‬٣٠‫ﻋﺸﻮاﺋﯿﺎ‬ ‫واﺣﺪة‬ ‫ﺑﻄﺎﻗﺔ‬ ‫ﻣﻨﮭﺎ‬ ‫ﺳﺤﺒﺖ‬
‫ﻋﻠﯿﮭﺎ‬ ‫اﻟﻤﺪون‬ ‫اﻟﻌﺪد‬ ‫ﻟﻮﺣﻆ‬ ‫و‬.‫ﺗﺤﻤﻞ‬ ‫اﻟﻤﺴﺤﻮﺑﺔ‬ ‫اﻟﺒﻄﺎﻗﺔ‬ ‫ﺗﻜﻮن‬ ‫أن‬ ‫اﺣﺘﻤﺎل‬ ‫اﺣﺴﺐ‬:
‫أ‬(‫ﻋﻠﻰ‬ ‫اﻟﻘﺴﻤﺔ‬ ‫ﯾﻘﺒﻞ‬ ‫ﻋﺪدا‬٣‫ب‬(‫ﯾﻘ‬ ‫ﻋﺪدا‬‫ﻋﻠﻰ‬ ‫اﻟﻘﺴﻤﺔ‬ ‫ﺒﻞ‬٥
‫ﺟـ‬(‫ﻋﻠﻰ‬ ‫اﻟﻘﺴﻤﺔ‬ ‫ﯾﻘﺒﻞ‬ ‫ﻋﺪدا‬٣‫و‬٥‫د‬(‫ﻋﻠﻰ‬ ‫اﻟﻘﺴﻤﺔ‬ ‫ﯾﻘﺒﻞ‬ ‫ﻋﺪدا‬٣‫أو‬٥
]١٨[
]١٩[‫ﻛﻞ‬ ‫ﻓﻰ‬ ‫اﻟﻌﻠﻮى‬ ‫اﻟﻮﺟﮫ‬ ‫ﻋﻠﻰ‬ ‫ﯾﻈﮭﺮ‬ ‫اﻟﺬى‬ ‫اﻟﻌﺪد‬ ‫ﻣﻼﺣﻈﺔ‬ ‫و‬ ‫ﻣﺮﺗﯿﻦ‬ ‫ﻧﺮد‬ ‫ﺣﺠﺮ‬ ‫إﻟﻘﺎء‬ ‫ﺗﺠﺮﺑﺔ‬ ‫ﻓﻰ‬
‫ﻣﺮة‬.‫اﻟﺘﺎﻟﯿﺔ‬ ‫اﻷﺣﺪاث‬ ‫ﻣﻦ‬ ‫ﻛﻞ‬ ‫اﺣﺘﻤﺎل‬ ‫اﺣﺴﺐ‬:
١(‫ﻇﮭﻮ‬ ‫ﺣﺪث‬‫اﻟﻌﺪد‬ ‫ر‬٤‫اﻷوﻟﻰ‬ ‫اﻟﺮﻣﯿﺔ‬ ‫ﻓﻰ‬
٢(‫ﯾﺴﺎوى‬ ‫اﻟﺮﻣﯿﺘﯿﻦ‬ ‫ﻓﻰ‬ ‫اﻟﻌﺪدﯾﻦ‬ ‫ﻣﺠﻤﻮع‬ ‫ﺣﺪث‬٨
٣(‫ﯾﺴﺎوى‬ ‫أو‬ ‫ﻣﻦ‬ ‫أﻗﻞ‬ ‫اﻟﺮﻣﯿﺘﯿﻦ‬ ‫ﻓﻰ‬ ‫اﻟﻌﺪدﯾﻦ‬ ‫ﻣﺠﻤﻮع‬ ‫ﺣﺪث‬٥
١
٨
١
٤
١
٣