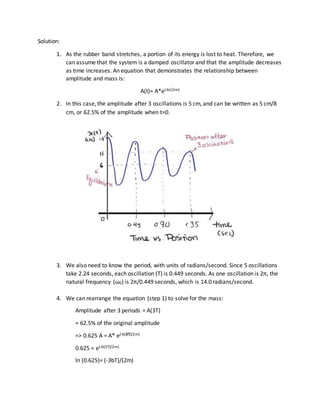
1. Goose wants to know the mass of his pencil box without a scale by using a rubber band, ruler, timer and laptop. He attaches the rubber band to a tree and pencil box, stretching it from 1-6 cm. After releasing it when stretched to 14 cm, it oscillates down to 11 cm over 3 oscillations. 2. The solution models the system as a damped oscillator. The equation relates amplitude to mass and drag constant. Using the measured 5 oscillations over 2.24 seconds, the natural frequency is calculated to be 14 radians/second. 3. The mass is then solved for using the damped oscillator equation, relating initial and measured amplitudes after 3 oscillations. The calculated mass

1. Learning Object 2: Damped Oscillations
Mass of a Pencil Box
Question:
Goose is packing for his annual
migration and wants to know how heavy his
pencil box is. Though he has no access to a
scale, he does have a ruler, a rubber band, a
timer and his laptop. He hooks one end of
the rubber band to a tree branch and the
other to his pencil box and finds that the
rubber band stretches from 1.0 to 6.0 cm.
After pulling the object down to 14.0 cm, he
lets go and finds that the top of the pencil
box is at 11.0 cm after counting 3
oscillations. He times the oscillating pencil
box and finds that 5 oscillations take around
2.24 seconds. What is the mass of the pencil
box if he finds online that the spring
constant for rubber band is 41.94 N/m and
the drag constant for rubber band is 0.149
kg/s?

2. Solution:
1. As the rubber band stretches, a portion of its energy is lost to heat. Therefore, we
can assume that the system is a damped oscillator and that the amplitude decreases
as time increases. An equation that demonstrates the relationship between
amplitude and mass is:
A(t)= A*e(-bt/2m)
2. In this case, the amplitude after 3 oscillations is 5 cm, and can be written as 5 cm/8
cm, or 62.5% of the amplitude when t=0.
3. We also need to know the period, with units of radians/second. Since 5 oscillations
take 2.24 seconds, each oscillation (T) is 0.449 seconds. As one oscillation is 2π, the
natural frequency (ω0) is 2π/0.449 seconds, which is 14.0 radians/second.
4. We can rearrange the equation (step 1) to solve for the mass:
Amplitude after 3 periods = A(3T)
= 62.5% of the original amplitude
=> 0.625 A = A* e(-b(3T)/2m)
0.625 = e(-b(3T)/2m)
ln (0.625)= (-3bT)/(2m)

3. -3bT/2*ln (0.625)= m
Since b= 0.1494 kg/s and T=14.0 rad/s,
-3 (0.1494)(0.449)/2* ln (0.625)
= 0.214 kg
Check:
We are assuming that the system to be an underdamped oscillator. If the answer is
reasonable, the natural frequency without the loss of energy should be greater than the drag
constant over two times the mass, according to the equation:
ω0> b/2m
Substituting the values give:
14.0> 0.1494/2*0.214= 14.0> 0.349