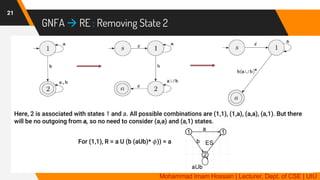
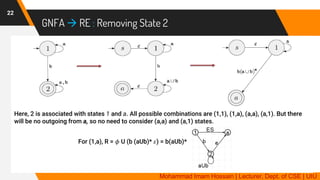
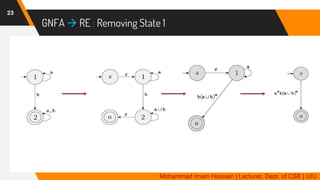
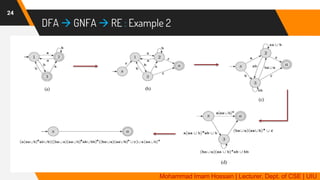
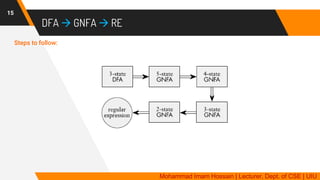
The document provides an overview of regular languages, their properties, and operations such as union, concatenation, and Kleene star, as well as their closure properties. It explains the definition and precedence of regular expressions, along with examples of constructing expressions that describe specific languages. Additionally, it covers topics such as generalized nondeterministic finite automata (GNFA) and their conversion to regular expressions.










![RE NFA : Practices
14
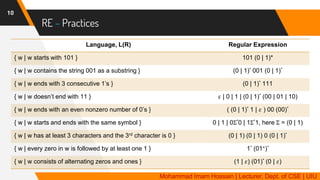
▸ ( a U b ) * a b a
▸ ( 0 U 1 ) * 0 0 0 ( 0 U 1 )* = Σ* 0 0 0 Σ* where Σ = 0, 1 = 0 U 1
▸ ( ( ( 0 0 )* ( 1 1 ) ) U 0 1 ) *
▸ ( 0 1 U 0 0 1 U 0 1 0 ) *
▸ a ( a b b ) * U b
▸ a+ U ( a b ) +
▸ ( a U b+ ) a+ b+ [ Hint: replace a+ with (a a*) ]
▸ 1* ( 0 1+)*
▸ ( Σ Σ Σ ) *
▸ 0 Σ* 0 U 1 Σ* 1 U 0 U 1
▸ 𝜙*
▸ ( 0 U 𝜀 ) 1*
Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU](https://image.slidesharecdn.com/regularexpressions-201125112656/85/TOC-5-Regular-Expressions-14-320.jpg)
![GNFA – Formal Definition
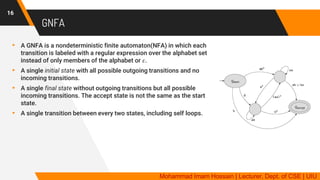
A generalized nondeterministic finite automaton is a 5 tuple,
(Q, Σ, 𝛿, qstart, qaccept ), where
▸ Q is the finite set of states
▸ Σ is the input alphabet
▸ 𝛿: ( Q - {qaccept} ) x ( Q - {qstart} ) ℛ is the transition function
[if you travel from state a 𝜖 ( Q - {qaccept} ) to state b 𝜖 ( Q - {qstart} ) then
this relation will generate ℛ regular expression ]
▸ qstart is the start state and
▸ qaccept is the accept state
17
Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU](https://image.slidesharecdn.com/regularexpressions-201125112656/85/TOC-5-Regular-Expressions-17-320.jpg)
![DFA GNFA : Steps to Follow
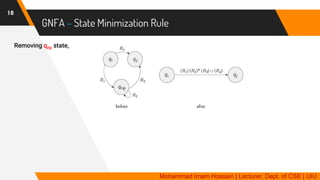
19
▸ Add a new start state with an 𝜀 arrow to the old start state
▸ Add a new accept state with 𝜀 arrows from the old accept states to this new accept state
▸ If any arrows have multiple labels, replace each with a single arrow whose label is the union of the
previous labels
▸ Add arrows labeled 𝜙 between states that had no arrows. [better no to show this in the diagram, for
simplicity]
Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU](https://image.slidesharecdn.com/regularexpressions-201125112656/85/TOC-5-Regular-Expressions-19-320.jpg)