Perhitungan Manual korelasi dan regresi
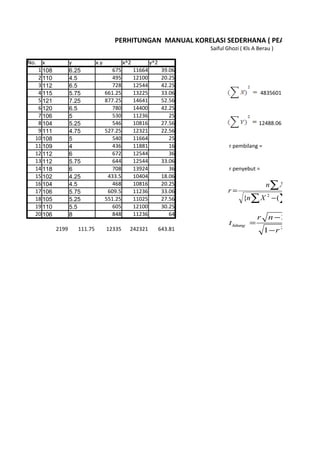
- 1. PERHITUNGAN MANUAL KORELASI SEDERHANA ( PEARSON PROD Saiful Ghozi ( Kls A Berau ) No. x y x.y x^2 y^2 1 108 6.25 675 11664 39.06 2 110 4.5 495 12100 20.25 3 112 6.5 728 12544 42.25 4 115 5.75 661.25 13225 33.06 4835601 5 121 7.25 877.25 14641 52.56 6 120 6.5 780 14400 42.25 7 106 5 530 11236 25 8 104 5.25 546 10816 27.56 12488.06 9 111 4.75 527.25 12321 22.56 10 108 5 540 11664 25 11 109 4 436 11881 16 r pembilang = 12 112 6 672 12544 36 13 112 5.75 644 12544 33.06 14 118 6 708 13924 36 r penyebut = 15 102 4.25 433.5 10404 18.06 16 104 4.5 468 10816 20.25 n∑ XY − (∑ X )(∑ 17 106 5.75 609.5 11236 33.06 r= 18 105 5.25 551.25 11025 27.56 {n∑ X 2 − (∑ X ) 2 }{n∑ 19 110 5.5 605 12100 30.25 20 106 8 848 11236 64 r n −2 t hitung = = 2199 111.75 12335 242321 643.81 1− r 2
- 2. ANA ( PEARSON PRODUCT MOMENT) Berau ) 12335 242321 643.81 961.75 Determinasi 2049.34 n∑ XY − (∑ X )(∑Y ) = 0.47 R2 = 0.22 ∑X 2 − (∑ X ) }{n∑Y − (∑Y ) } 2 2 2 r n −2 = = 2.25 1− r 2
- 3. PERHITUNGAN MANUAL KORELASI GANDA Saiful Ghozi ( Kls A Berau ) No X1 X2 Y X1^2 X2^2 Y^2 X1.Y X2.Y 1 108 80 6.25 11664 6400 39.06 675 500 2 110 78 4.5 12100 6084 20.25 495 351 3 112 79 6.5 12544 6241 42.25 728 513.5 4 115 80 5.75 13225 6400 33.06 661.25 460 5 121 90 7.25 14641 8100 52.56 877.25 652.5 6 120 89 6.5 14400 7921 42.25 780 578.5 7 106 77 5 11236 5929 25 530 385 8 104 76 5.25 10816 5776 27.56 546 399 9 111 78 4.75 12321 6084 22.56 527.25 370.5 10 108 77 5 11664 5929 25 540 385 11 109 78 4 11881 6084 16 436 312 12 112 79 6 12544 6241 36 672 474 13 112 78 5.75 12544 6084 33.06 644 448.5 14 118 80 6 13924 6400 36 708 480 15 102 70 4.25 10404 4900 18.06 433.5 297.5 16 104 67 4.5 10816 4489 20.25 468 301.5 17 106 65 5.75 11236 4225 33.06 609.5 373.75 18 105 65 5.25 11025 4225 27.56 551.25 341.25 19 110 78 5.5 12100 6084 30.25 605 429 20 106 77 5 11236 5929 25 530 385 ∑ 2199 1541 108.75 242321 119525 604.81 12017 8437.5 ∑X1 = 2199 ∑X2 = 1541 ∑Y= ∑X12 = 242321 ∑X22 = 119525 ∑Y2 = ∑X1Y= 12017 ∑X2Y = 8437.5 ∑X1X2 = (∑X1) 4835601 (∑X2)2 = 2374681 (∑Y)2 = Korelasi Ganda n∑ X 1Y − (∑ X 1 )(∑Y ) r n −2 ry1 = = 0.7 thitung = = {n∑ X 12 − (∑ X 1 ) 2 }{n∑Y 2 − (∑Y ) 2 } 1 −r 2 n∑ X 2Y − (∑ X 2 )(∑Y ) r n −2 ry 2 = = 0.56 t hitung = = {n∑ X 2 − (∑ X 2 ) 2 }{n∑Y 2 − (∑Y )2 } 2 1 −r 2 r n −2 thitung = = 1 −r 2
- 4. r n −2 n∑ X 1 X 2 − (∑ X 1 )(∑ X 2 ) thitung = = r12 = = 0.82 1 −r 2 {n∑ X 12 − (∑ X 1 )2 }{n∑ X 2 − (∑ X 2 )2 } 2 R pembilang = 0.16 R penyebut = 0.33 2 R x1 x 2 y 0.702024 ry21 + ry22 − 2ry1ry 2 r12 0.7 Fhitung = k = 2 Ry.12 = = (1 − R x1 x 2 y ) /( n − k −1) 1 − (0.702024 ) 2 2 1 − r12 2 2 Korelasi Parsial rx 2 y − rx1 y .rx1x 2 rx1( x 2 y ) = = -0.03 (1 − r )(1 − r 2 x1 y 2 x1 x 2 ) rx1 y − rx 2 y .rx1x 2 0,702 - (0,564).(0,820)) rx 2 ( x1 y ) = = = (1 − r 2 x2 y )(1 − r 2 x1 x 2 ) 2 (1 - (0,564) (1 - (0,820) ) 2
- 5. X1.X2 8640 8580 8848 9200 10890 10680 8162 7904 8658 8316 8502 8848 8736 9440 7140 6968 6890 6825 8580 8162 169969 169969 604.81 169969 28889460961 r n −2 hitung = = 4.18 1 −r 2 r n −2 t hitung = = 2.9 1 −r 2 r n −2 thitung = = 1 −r 2
- 6. r n −2 6.07 thitung = = 1 −r 2 2y 0.702024 = 2 = 8.26 ( n − k −1) 1 − (0.702024 ) 2 20 − 2 −1 r n −2 -0.11 thitung = = 1 −r 2 r n −2 0.51 thitung = = 2.49 1 −r 2
- 7. Perhitungan Persamaan Regresi Tabel Bantu Uji Per No X Y X.Y X^2 Y^2 X 1 108 6.25 675 11664 39.06 102 2 110 4.5 495 12100 20.25 104 3 112 6.5 728 12544 42.25 104 4 115 5.75 661.25 13225 33.06 105 5 121 7.25 877.25 14641 52.56 106 6 120 6.5 780 14400 42.25 106 7 106 5 530 11236 25 106 8 104 5.25 546 10816 27.56 108 9 111 4.75 527.25 12321 22.56 108 10 108 5 540 11664 25 109 11 109 4 436 11881 16 110 12 112 6 672 12544 36 110 13 112 5.75 644 12544 33.06 111 14 118 6 708 13924 36 112 15 102 4.25 433.5 10404 18.06 112 16 104 4.5 468 10816 20.25 112 17 106 5.75 609.5 11236 33.06 115 18 105 5.25 551.25 11025 27.56 118 19 110 5.5 605 12100 30.25 120 20 106 8 848 11236 64 121 2199 111.75 12335 242321 643.81 ∑X = 2199 ∑Y= 111.75 ∑XY= 12335 242321 ∑X2 = ∑Y2 = 643.81 (∑X )2 ### (∑Y)2 = 12488.06 109.95 (∑Yi )(∑ X i2 ) − (∑ X i )(∑ X i Yi ) -4.19 a= = n ∑ X − (∑ X i ) i 2 2 n∑ X i Yi − (∑ X i )(∑Yi ) 0.09 b= = n∑ X − (∑ X i ) i 2 2 Persamaan Regresinya : Y= -4.19 Plus 0.09 X
- 8. 102 4.25 104 5.25 104 4.5 105 5.25 106 5 106 5.75 106 8 108 6.25 108 5 109 4 110 4.5 110 5.5 111 4.75 112 6.5 112 6 112 5.75 115 5.75 118 6 120 6.5 121 7.25
- 9. Tabel Bantu Uji Persamaan Regresi Kelompok N Y JK(G) J (T ) = ∑Y K 2 = 643.81 1 1 4.25 0 2 2 4.5 0.28 5.25 0 (∑Y ) 2 624.4 3 1 5.25 0 JK ( A) = = n 4 35 4.88 5.75 (∑X )( ∑ ) Y 8 JK (b / a ) = b ∑XY − = 5 25 0.78 n 6.25 6 14 0 JK(S) = JK(T) – JK(a) – JK(a/b) = 15.13 7 2 4.5 0.5 5.5 8 1 4.75 0 (∑ ) 2 Y 4.252 2 9 3 6.5 0.29 JK (G ) = ∑∑ ni Y − 2 ni = 4.252 − + 4.5 + 5 1 6 5.75 10 2 5.75 0.03 11 6 0 JK(TC) = JK(S) – JK(G) = 8.37 12 2 6.5 0 13 7.25 0 6.76 Sumber variasi .dk JK KT Total 20 624.403.1 Reg (a) 1 624.4 Reg(b/a) 1 4.27 4.27 5.59 Residu/Sisa 20-2 =18 15.13 0.84 Tuna Cocok 13-2 = 11 8.37 0.93
- 11. (∑X )( ∑ ) Y = 4.27 n 4.252 2 ( 4.5 + 5.25) 2 = 4.252 − + 4.5 + 5.252 − +. .. = 6.76 1 2 S2TC = JK(TC)/k-2 = 0.93 S2G = JK(G)/n-k = 0.97 F sres2 = {∑(Yi - Ŷi)2}/n - 2 = 0.84 5.08 0.96
- 13. PERHITUNGAN MANUAL ANALISIS GANDA DUA PREDIKTOR Saiful Ghozi (kls A Berau) No X1 X2 Y X12 X22 X1 Y X2Y 1 108 90 6.25 11664 8100 675 562.5 2 110 50 4.5 12100 2500 495 225 3 112 85 6.5 12544 7225 728 552.5 4 115 80 5.75 13225 6400 661.25 460 5 121 98 7.25 14641 9604 877.25 710.5 6 120 90 6.5 14400 8100 780 585 7 106 60 5 11236 3600 530 300 8 104 64 5.25 10816 4096 546 336 9 111 56 4.75 12321 3136 527.25 266 10 108 60 5 11664 3600 540 300 11 109 50 4 11881 2500 436 200 12 112 80 6 12544 6400 672 480 13 112 78 5.75 12544 6084 644 448.5 14 118 80 6 13924 6400 708 480 15 102 58 4.25 10404 3364 433.5 246.5 16 104 56 4.5 10816 3136 468 252 17 106 82 5.75 11236 6724 609.5 471.5 18 105 78 5.25 11025 6084 551.25 409.5 19 110 80 5.5 12100 6400 605 440 20 106 90 8 11236 8100 848 720 ∑ 2199 1465 111.75 242321 111553 12335 8445.5 X1 X2 Y X12 X22 X1 Y X2Y ∑X1 2199 ∑X 1 2 242321 ∑X2 1465 ∑X2 2 111553 ∑X1X2 = 161858 ∑Y 111.75 ∑X1Y = 12335 ∑X2Y = 8445.5 nb0 + b1∑X1 + b2 ∑X2 = ∑Y 20 b0 + 2199b1 + 1465 b0∑X1 + b1∑X12 + b2 ∑X1X2 = ∑X1Y 2199b0+ 242321 b b0∑X2 + b1∑X1X2 + b2 ∑X22 = ∑X2Y 1465 b0 + 161858 b
- 14. 20 2199 1465 111 .75 2199 1465 det ( A) = 2199 242321 161858 det( A1 ) = 12335 242321 161858 1465 161858 111553 8445 .5 161858 111553 X1X2 9720 20 2199 1465 20 2199 5500 det (A) = 2199 242321 161858 2199 242321 9520 1465 161858 111553 1465 161858 9200 11858 10800 det (A) = 33684462 6360 6656 111.75 2199 1465 111.75 2199 6216 det (A1)= 12335 242321 161858 12335 242321 6480 8445.5 161858 111553 8445.5 161858 5450 8960 8736 9440 det (A1)= 35158709.25 5916 5824 8692 8190 det( A1 ) 1.04 det( A2 ) b0 = = b1 = = 8800 det( A) det( A) 9540 161858 r12 = 0.52 R2 = 0.27 X1X2 b1 ∑ X 1Y SEPX1 = ( R 2 .100% ) = 0.37 (b1 ∑ X 1Y ) + (b2 ∑ X 2Y ) b2 ∑ X 2 Y SEPX2 = ( R 2 .100% ) = 26.23 (b1 ∑ X 1Y ) + (b2 ∑ X 2Y ) 2199b1 + 1465b2 = 111.75 242321 b1+ 161858 b2 = 12335 + 161858 b1+ 111553 b2 = 8445.5
- 15. 1465 20 111 .75 1465 20 2199 111 .75 161858 det( A2 ) = 2199 12335 161858 det( A3 ) 2199 242321 12335 111553 1465 8445 .5 111553 1465 161858 8445 .5 20 111.75 1465 20 111.75 20 det(A2)= 2199 12335 161858 2199 12335 det(A3)= 2199 1465 8445.5 111553 1465 8445.5 1465 det(A2)= 19932.75 det(A3)= 2059544.25 det( A2 ) det( A3 ) = = 0 b2 = = 0.06 det( A) det( A)
- 16. 111 .75 12335 8445 .5 2199 111.75 20 2199 242321 12335 2199 242321 161858 8445.5 1465 161858
