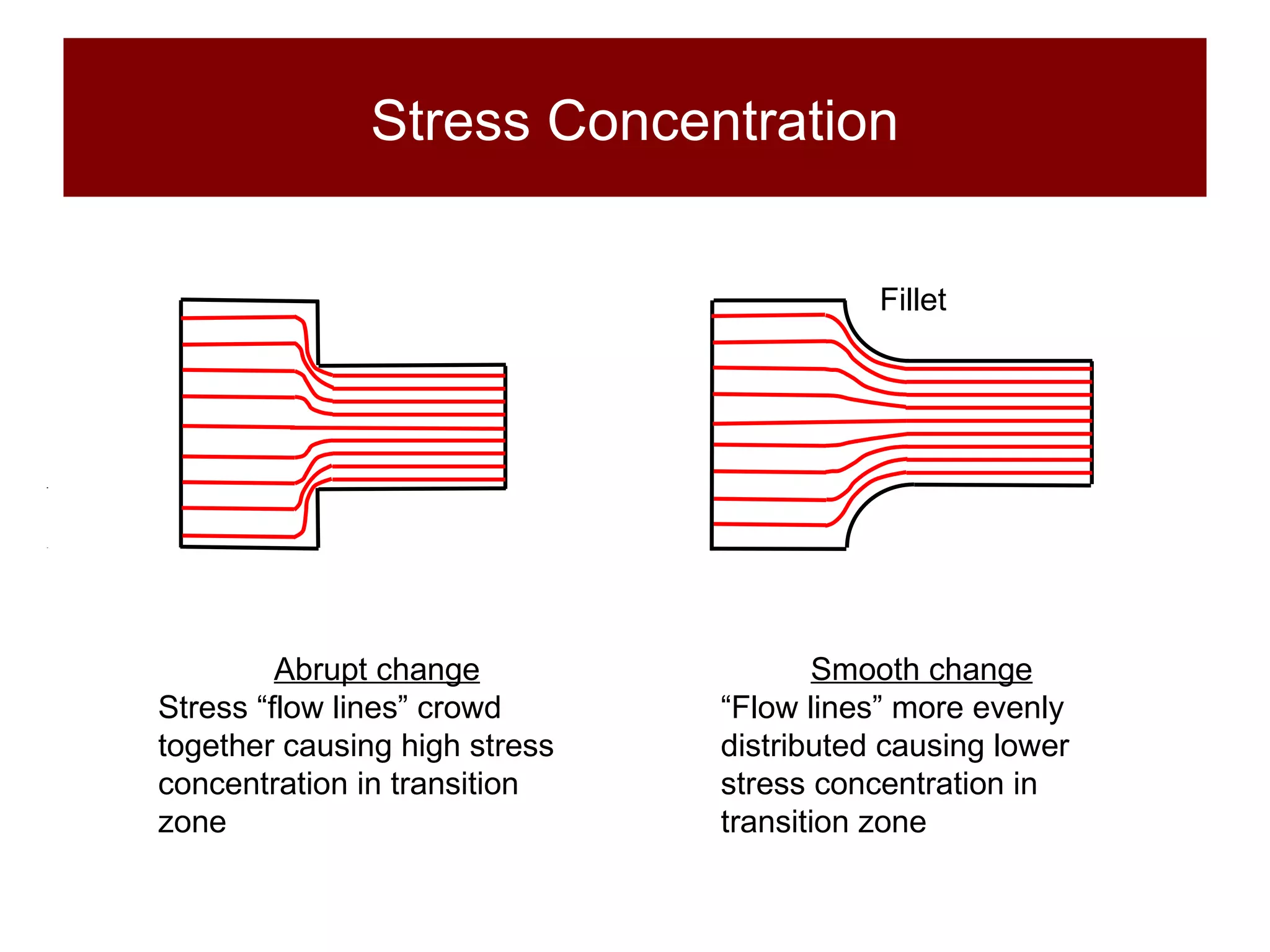
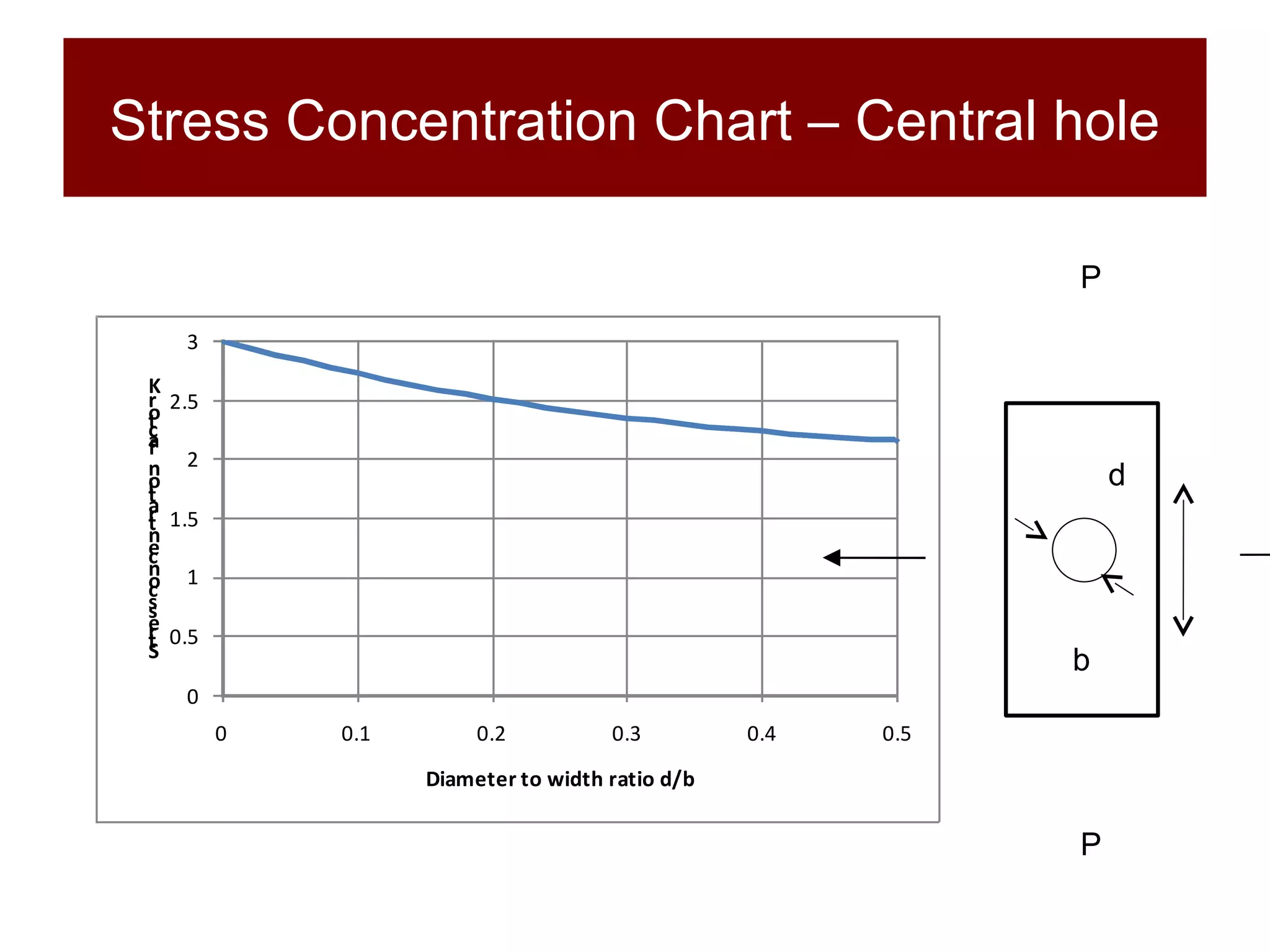
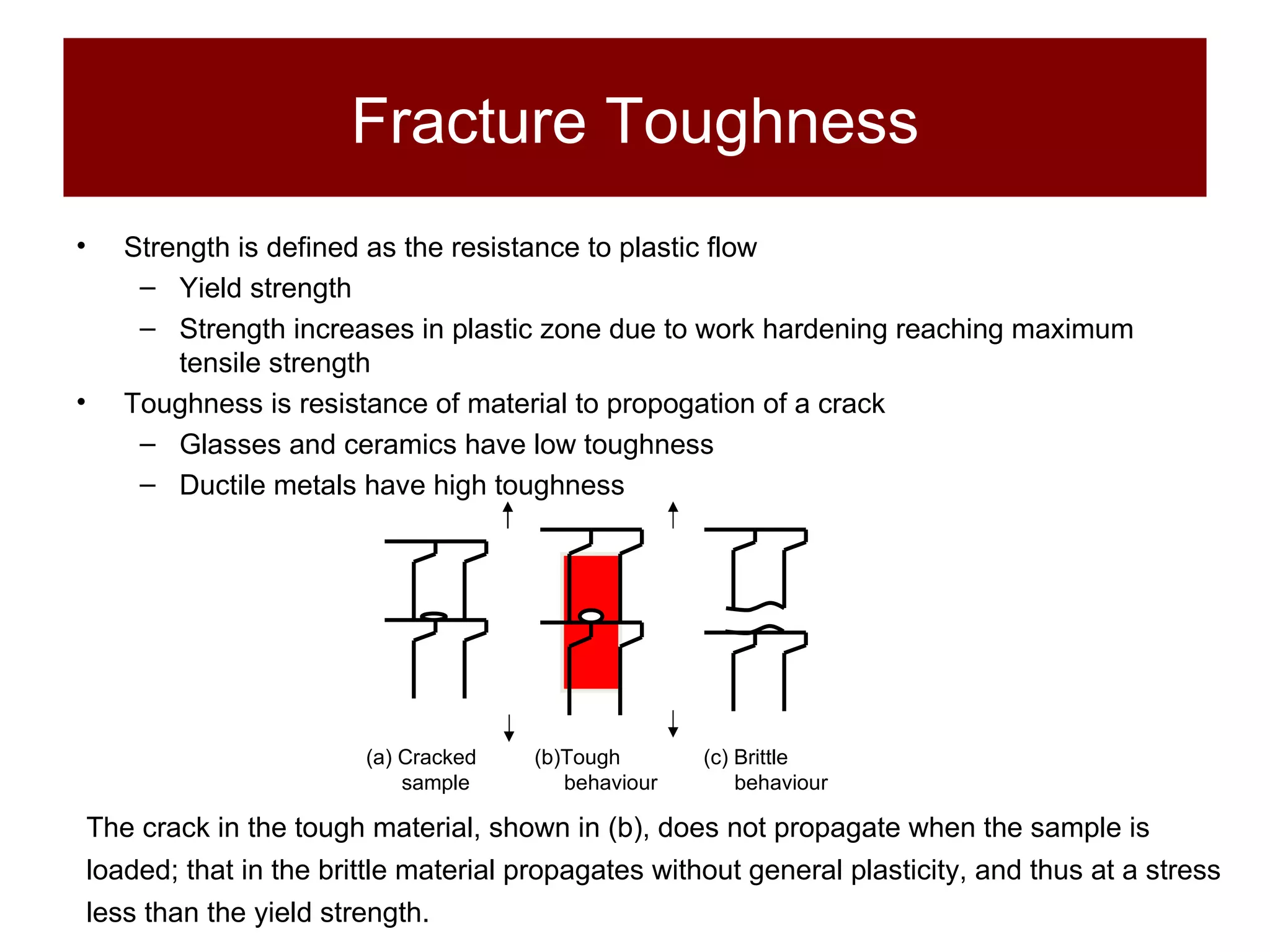
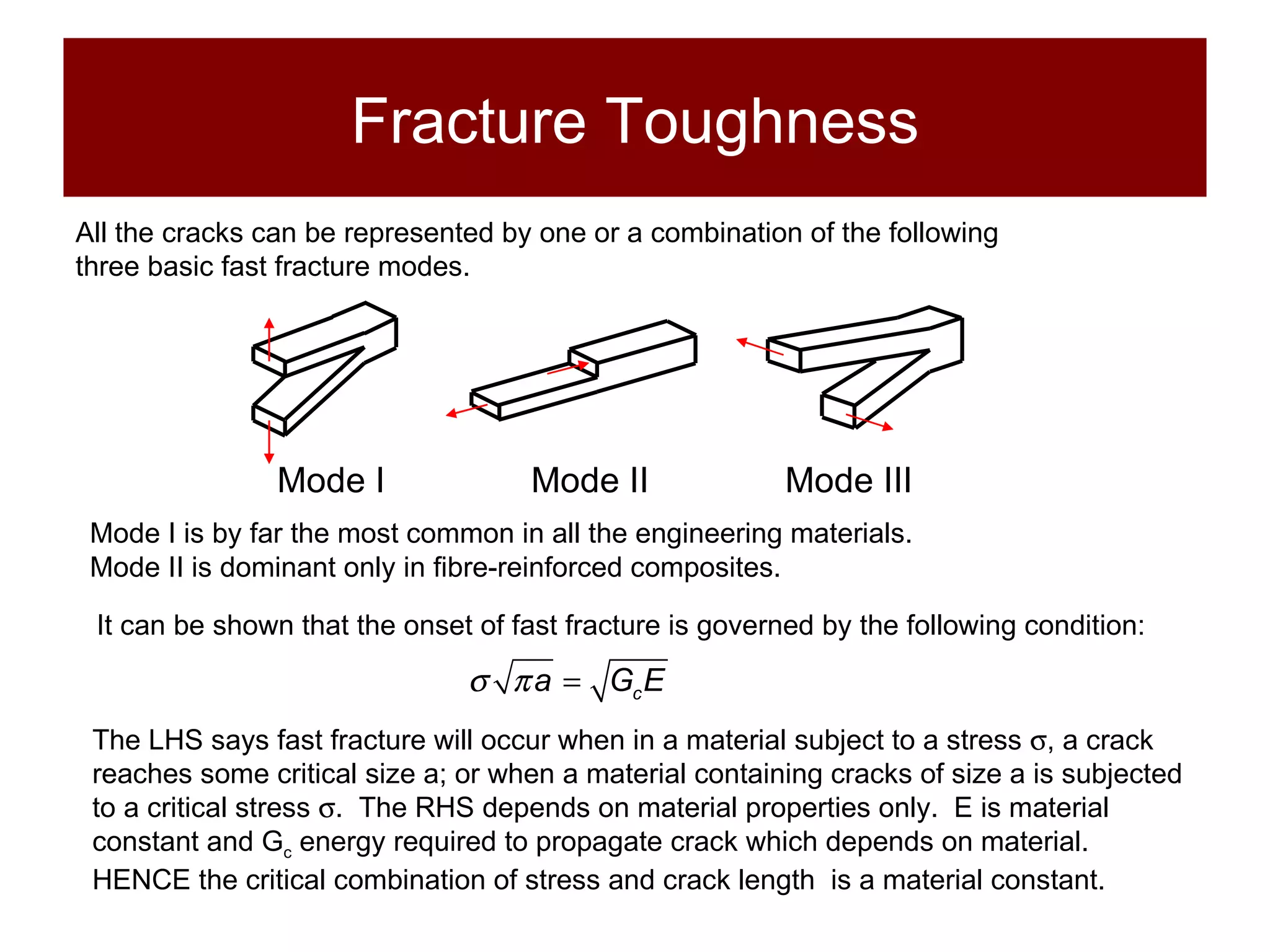
This document discusses stress concentrations in structural materials caused by discontinuities like holes, notches, and fillets, and introduces key concepts such as the stress concentration factor and fracture toughness. It emphasizes the importance of understanding local stresses, especially in brittle and ductile materials, along with examples illustrating how these factors affect material failure under repeated loading. The document also defines critical parameters for fracture toughness and provides experimental methods to determine material resilience against crack propagation.

1. Section 7 Stress Concentration Stress concentrations produced by discontinuities in structures such as holes, notches, and fillets will be introduced in this section. The stress concentration factor will be defined. The concept of fracture toughness will also be introduced. © Loughborough University 2010. This work is licensed under a Creative Commons Attribution 2.0 Licence .

2. Contents Stress Concentration Stress Concentration – Definition Stress Concentration chart – Central hole Stress Concentration Factor Formulae Basic Design Rule – Yield Limited Design Fatigue Fracture Toughness Example: Fracture Toughness Credits & Notices

3. Stress Concentration Engineering stress  = P/A or the far-field stress is invalid . In immediately vicinity where the external load is applied (St Venant) Around discontinuities such as: holes, notches, or fillets These irregularities (stress concentrations or stress raisers) cause a disruption to stress flow and stresses concentrations in localised regions. The change of section concentrates stress most strongly where the curvature of the surface is greatest. The far-field stresses are less useful as they underestimate the actual local stress. Hole Notch Fillet

4. Stress Concentration Abrupt change Stress “flow lines” crowd together causing high stress concentration in transition zone Smooth change “ Flow lines” more evenly distributed causing lower stress concentration in transition zone Fillet

5. Stress Concentration (Thickness h) P P b d

6. Stress Concentration - Definition Stress concentration factors are: Dependent on irregularity, dimensions of irregularity, overall dimensions, loading Obtained experimentally, analytically, etc Published in charts (e.g. Roark’s Formulas) Very important in brittle materials In ductile materials: Important in fatigue calculation. Important if safety is critical. Localized yielding hardens material (strain hardening). Redistributes stress concentration.

7. Stress Concentration Chart – Central hole P P d b

8. Stress Concentration Factor Formulae

9. Basic Design Rule – Yield Limited Design If limit load is reached we will get permanent deformation. Note that the holes, notches and fillets are being discussed in a structural sense. In reality we can get holes and notches through surface defects and manufacturing defects. These can become an issue in fatigue related issues. There are several examples of structural failure occurring relating to fatigue. P P b d

10. Example 1: Stress Concentration A stepped flat bar of 6 mm thick has a hole of 18 mm diameter. It has three widths of b 1 =40 mm, b 2 =50 mm and b 3 =36 mm. Stress concentration factors for the left fillet, hole and the right fillet are 1.24, 2.28 and 1.31, respectively. The allowable stress is 41 MPa. What is the permissible load P max ? b 1 d b 2 P P b 3

11. Example 1: Stress Concentration b 1 d b 2 P P b 3

12. Fatigue Fatigue is concerned with materials getting ‘tired’ due to repeated load cycles. The number of cycles is generally quite high. For instance the vibration of a aircraft wing during a long flight can result in tens of thousands of load cycles. During the lifetime of the aircraft the wing will see millions of load cycles. A con rod in a F1 car will see well over 1 million load cycles. If designed properly these structures will not fail if the stress is below the endurance stress limit. An increase in the required number of load cycles reduces the endurance limit. Generally fatigue problems are divided into high cycle and low cycle fatigue. (High and low refers to the number of load cycles). In the former the stress is not allowed to exceed yield in the latter the stress can exceed yield.

13. Example 2: Stress Concentration A round straight bar with a diameter of d 1 = 20 mm is being compared with a bar of the same diameter, which has an enlarged portion with a diameter of d 2 = 25 mm. The radius of the fillets is 2.5 mm and the associated stress concentration factor is 1.74. Does enlarging the bar in this manner make it stronger? Justify the answer by determining the maximum permissible load P 1 for the straight bar and the maximum permissible load P 2 for the enlarged bar if an allowable tensile stress of the material is 80 MPa. d 1 d 2 P 2 P 2 d 1 P 1 P 1 d 1

14. Example 2: Stress Concentration P 1 P 1 d 1 d 1 d 2 P 2 P 2 d 1

15. Fracture Toughness Structures which were properly designed to avoid large elastic deflections and plastic fail in a catastrophic way by fast fracture. Common to all such structures is the presence of cracks. Catastrophic failure is caused by the crack growing at the speed of sound in the material. This mechanism is called fast fracture. Two parameters are used to represent fracture toughness Critical stress intensity factor, K c Critical strain energy release rate, G c . G c is a measure of the material’s ability to yield and absorb strain energy released by crack propagation.

16. Fracture Toughness Strength is defined as the resistance to plastic flow Yield strength Strength increases in plastic zone due to work hardening reaching maximum tensile strength Toughness is resistance of material to propogation of a crack Glasses and ceramics have low toughness Ductile metals have high toughness The crack in the tough material, shown in (b), does not propagate when the sample is loaded; that in the brittle material propagates without general plasticity, and thus at a stress less than the yield strength. (a) Cracked (b)Tough (c) Brittle sample behaviour behaviour

17. Fracture Toughness Mode I is by far the most common in all the engineering materials. Mode II is dominant only in fibre-reinforced composites. All the cracks can be represented by one or a combination of the following three basic fast fracture modes. Mode I Mode II Mode III It can be shown that the onset of fast fracture is governed by the following condition: The LHS says fast fracture will occur when in a material subject to a stress  , a crack reaches some critical size a; or when a material containing cracks of size a is subjected to a critical stress  . The RHS depends on material properties only. E is material constant and G c energy required to propagate crack which depends on material. HENCE the critical combination of stress and crack length is a material constant.

18. Fracture Toughness The term  crops up quite frequently in fast fracture mechanics and is usually given the symbol K. The units of K are MN m -3/2 . It is called the stress intensity factory (!) G c : Toughness – strain energy release rate K c : Fracture toughness – critical stress intensity release factor If K<K c then crack is stable If K=K c then crack will propagate (at speed of sound in material 1 mile s -1 !!) K c is material property To measure K c , (Gc): experimental set up for mode I: (Caution: a is length of edge crack or a is half length of central crack)   a   2a

19. Example: Fracture Toughness A sheet of aluminium alloy has a 4mm central crack through the thickness. If a stress of 200 MPa is reached on the point of fast fracture, determine the fracture toughness of the sheet. If the Young’s Modulus is 70 GPa what is its toughness G C ?

20. Example: Fracture Toughness A sheet of aluminium alloy has a 4mm central crack through the thickness. If a stress of 200 MPa is reached on the point of fast fracture, determine the fracture toughness of the sheet. If the Youngs Modulus is 70 GPa what is its toughness G C ? Solution:

21. This resource was created by Loughborough University and released as an open educational resource through the Open Engineering Resources project of the HE Academy Engineering Subject Centre. The Open Engineering Resources project was funded by HEFCE and part of the JISC/HE Academy UKOER programme. © 2010 Loughborough University. Except where otherwise noted this work is licensed under a Creative Commons Attribution 2.0 Licence . The name of Loughborough University, and the Loughborough University logo are the name and registered marks of Loughborough University. To the fullest extent permitted by law Loughborough University reserves all its rights in its name and marks, which may not be used except with its written permission. The JISC logo is licensed under the terms of the Creative Commons Attribution-Non-Commercial-No Derivative Works 2.0 UK: England & Wales Licence. All reproductions must comply with the terms of that licence. The HEA logo is owned by the Higher Education Academy Limited may be freely distributed and copied for educational purposes only, provided that appropriate acknowledgement is given to the Higher Education Academy as the copyright holder and original publisher. Credits