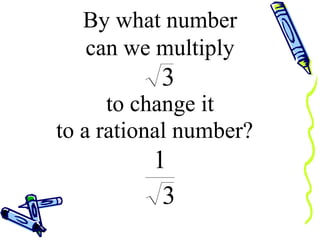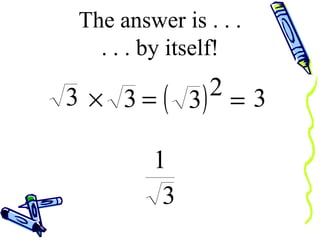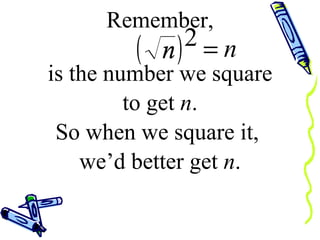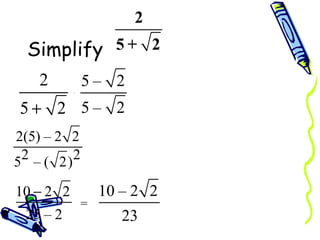Embed presentation
Downloaded 164 times






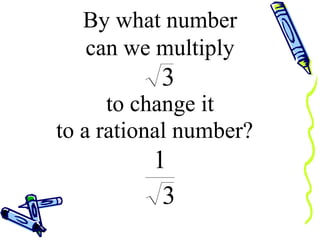
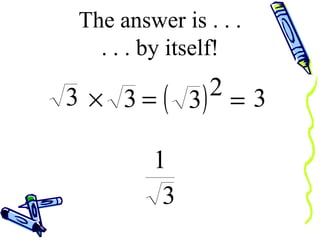
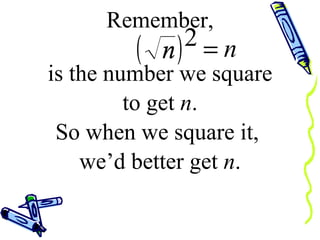






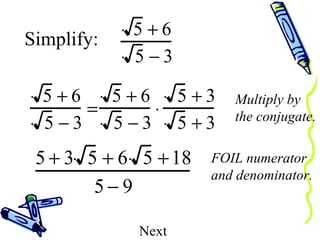
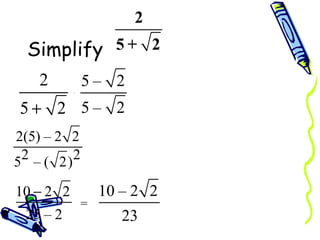
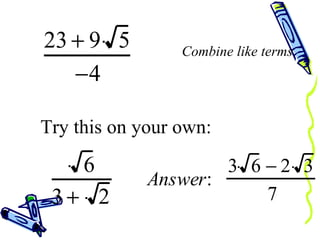

The document discusses how to rationalize the denominator of a fraction that contains a radical. It explains that to remove the radical from the denominator, one should multiply both the numerator and denominator by the radical term. This preserves the value of the fraction while removing the radical from the denominator, resulting in a rational number.