Recommended
PPTX
PDF
PDF
PDF
PDF
PDF
PDF
PDF
Cmdstanr入門とreduce_sum()解説
PDF
PDF
PDF
PDF
2 5 2.一般化線形モデル色々_ロジスティック回帰
PDF
PPTX
PDF
PPTX
PDF
状態空間モデルの考え方・使い方 - TokyoR #38
PDF
渡辺澄夫著「ベイズ統計の理論と方法」5.1 マルコフ連鎖モンテカルロ法
PDF
PDF
PPTX
StanとRでベイズ統計モデリングに関する読書会(Osaka.stan) 第四章
PDF
PDF
PDF
MCMCサンプルの使い方 ~見る・決める・探す・発生させる~
PDF
PDF
[PRML] パターン認識と機械学習(第2章:確率分布)
PPTX
【読書会資料】『StanとRでベイズ統計モデリング』Chapter12:時間や空間を扱うモデル
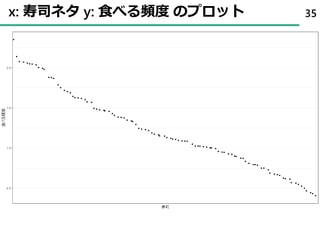
PDF
クラシックな機械学習入門:付録:よく使う線形代数の公式
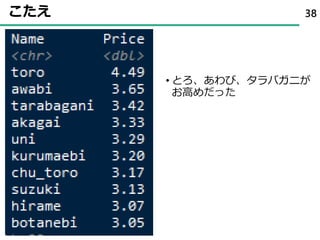
PDF
Rでベイズをやってみよう!(コワい本1章)@BCM勉強会
PDF
More Related Content
PPTX
PDF
PDF
PDF
PDF
PDF
PDF
PDF
Cmdstanr入門とreduce_sum()解説
What's hot
PDF
PDF
PDF
PDF
2 5 2.一般化線形モデル色々_ロジスティック回帰
PDF
PPTX
PDF
PPTX
PDF
状態空間モデルの考え方・使い方 - TokyoR #38
PDF
渡辺澄夫著「ベイズ統計の理論と方法」5.1 マルコフ連鎖モンテカルロ法
PDF
PDF
PPTX
StanとRでベイズ統計モデリングに関する読書会(Osaka.stan) 第四章
PDF
PDF
PDF
MCMCサンプルの使い方 ~見る・決める・探す・発生させる~
PDF
PDF
[PRML] パターン認識と機械学習(第2章:確率分布)
PPTX
【読書会資料】『StanとRでベイズ統計モデリング』Chapter12:時間や空間を扱うモデル
PDF
クラシックな機械学習入門:付録:よく使う線形代数の公式
Similar to Bayesian Sushistical Modeling
PDF
Rでベイズをやってみよう!(コワい本1章)@BCM勉強会
PDF
PPTX
NagoyaStat#7 StanとRでベイズ統計モデリング(アヒル本)4章の発表資料
PDF
StanとRでベイズ統計モデリング読書会 導入編(1章~3章)
PPTX
PDF
PDF
PDF
PPTX
PDF
Osaka.Stan #3 Chapter 5-2
PDF
PDF
認知心理学への実践:データ生成メカニズムのベイズモデリング【※Docswellにも同じものを上げています】
PPTX
PDF
PDF
PDF
Infer net wk77_110613-1523
PDF
PDF
[読会]Logistic regression models for aggregated data
PDF
rstanで情報仮説によるモデル評価してみる@Hjiyama.R
PDF
More from daiki hojo
PPTX
心理学におけるオープンサイエンス入門(OSF&PsyArXiv編)
PDF
心理学者のためのJASP入門(操作編)[説明文をよんでください]
PDF
GoogleCalenderをShinyを実装してみた(序) Tokyo.R #66 LT
PDF
MCMCしすぎて締め切り間近に焦っているあなたに贈る便利なgg可視化パッケージ
PDF
PDF
Bayesian Sushistical Modeling 1. Bayesian tistical Modeling
ベイズ塾 北條大樹(ほうじょう だいき)
: @dastatis
: https://dastatis.github.io/index.html
今日のコード(一時的) https://rstudio.cloud/project/40523
Tokyo.R #70
2018.06.09
2. 3. 自己紹介
• 名前:
• 北條大樹(ほうじょうだいき)
• 所属:
• 魁!!広島ベイズ塾
• 東京大学 教育学研究科 教育心理学コース D1
(*昨年までは専修大学にいました)
• 日本学術振興会
• 専門:
• 心理統計学 (IRT・認知モデリング)
• ベイズ統計学
• 連絡先:
dhojo@p.u-tokyo.ac.jp
@dastatis
3
4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. ˃sushi10 <- read_csv("sushi10.csv", col_names = TRUE) %>%
apply(1, order) %>%
t() %>%
data.frame() %>%
rename(えび=X1,穴子=X2,まぐろ=X3,いか=X4,うに=X5,
いくら=X6,玉子=X7,とろ=X8,鉄火巻=X9,かっぱ巻=X10)
˃sushi10 <- 11 - sushi10 #点数が高いと人気になるようにする
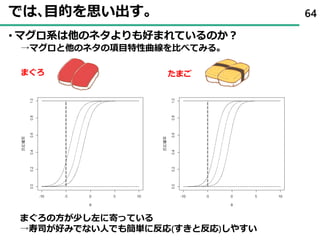
31まずは、sushi10から先ほどの図を出す
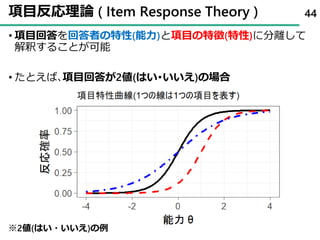
32. 33. 34. 35. 36. 37. 38. 39. 40. 41. 42. 43. 44. 項目反応理論 ( Item Response Theory )
• 項目回答を回答者の特性(能力)と項目の特徴(特性)に分離して
解釈することが可能
• たとえば、項目回答が2値(はい・いいえ)の場合
44
※2値(はい・いいえ)の例
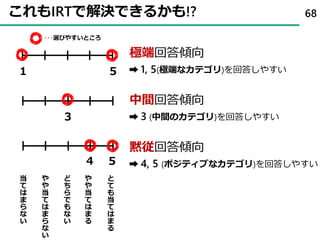
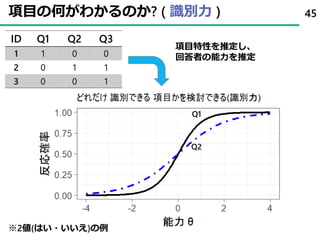
45. 項目の何がわかるのか? ( 識別力 )
ID Q1 Q2 Q3
1 1 0 0
2 0 1 1
3 0 0 1
45
Q1
Q2
項目特性を推定し、
回答者の能力を推定
※2値(はい・いいえ)の例
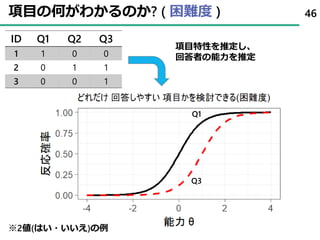
46. 項目の何がわかるのか? ( 困難度 )
ID Q1 Q2 Q3
1 1 0 0
2 0 1 1
3 0 0 1
46
Q1
項目特性を推定し、
回答者の能力を推定
※2値(はい・いいえ)の例
Q3
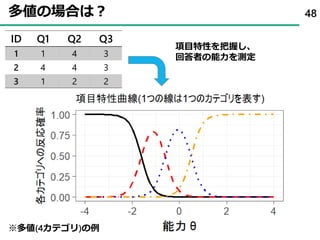
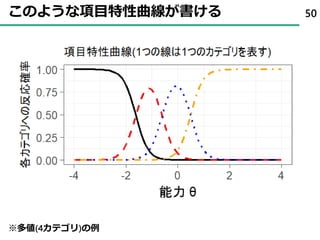
47. 48. 49. 50. 51. 部分得点モデル(Partial Credit model)
• カテゴリkと答えるか、k-1と答えるかの2つの確率を用いて、
前者を表現する。
𝑝 𝑦𝑖𝑗 = 𝑘 𝜃𝑖, 𝛽𝑗 =
exp σ 𝑘=1
𝐾
(𝜃𝑖 − 𝑏𝑗𝑘)
1 + σ 𝑚=1
𝐾
exp σ 𝑘=1
𝑚
(𝜃𝑖 − 𝑏𝑗𝑚)
*傾き𝑎𝑗𝑘をいれると、一般化部分得点モデルというモデルにな
ります。
• 今回は時間が無いので、
説明をいろいろ端折ってとりあえず推定します。
51
中間省略して,
最終的に...
52. 53. 54. 55. 56. 57. 段階反応モデル
• 項目反応がカテゴリk以上となる確率を考えるモデル
• 回答者𝑖が寿司𝑗を𝑘と回答する確率を
𝑝 𝑦𝑖𝑗 = 𝑘 𝜃𝑖, 𝛼𝑗, 𝛽𝑗𝑘 =
1
1 + exp −𝑎𝑗 𝜃𝑖 − 𝛽𝑗𝑘
−
1
1 + exp −𝑎𝑗 𝜃𝑖 − 𝛽𝑗𝑘+1
• カテゴリkで回答するということはk+1で回答するわけではな
いのでkまでの確率からk+1までの確率を引くことで、kの確率
を求めるモデル
• Stanで表すと…
𝑦𝑖𝑗 ~ ordered_logistic 𝑎𝑗𝑘 𝜃𝑖, 𝛽𝑗𝑘
𝛼𝑗𝑘~𝑛𝑜𝑟𝑚𝑎𝑙 0, 5 #識別力(お寿司が好まれやすいものか)
𝛽𝑗𝑘~𝑛𝑜𝑟𝑚𝑎𝑙(0, 5) #境界パラメータ(回答カテゴリ間の境界値)
𝜃𝑖~𝑛𝑜𝑟𝑚𝑎𝑙(0, 1) #特性(回答者がどれだけお寿司を好むか)
57
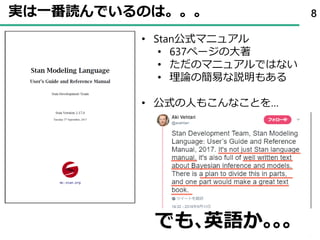
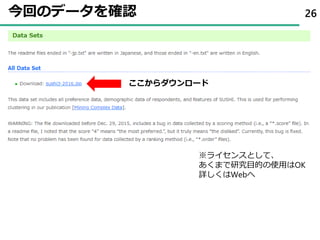
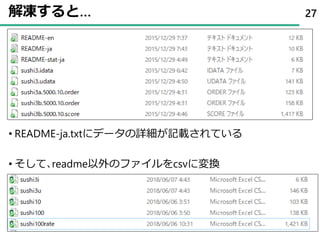
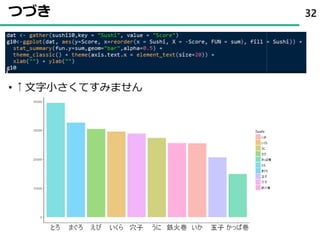
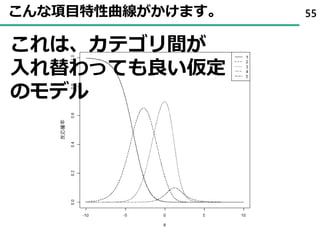
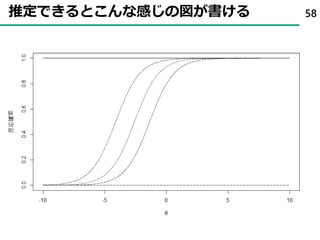
58. 59. 60. 60
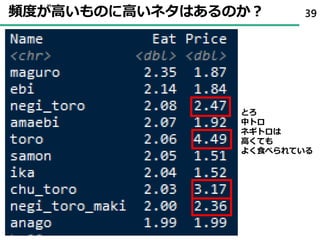
theta[9] theta[10]
theta[5] theta[6] theta[7] theta[8]
theta[1] theta[2] theta[3] theta[4]
0 250 500 7501000 0 250 500 7501000
0 250 500 7501000 0 250 500 7501000 0 250500 7501000 0 250 500 7501000
0 250 500 7501000 0 250 500 7501000 0 250500 7501000 0 250 500 7501000
-1
0
1
-1
0
1
-2
-1
0
-2
0
2
4
-1
0
1
2
-4
-3
-2
-1
0
1
-2
-1
0
1
2
-2
-1
0
1
2
3
-2
-1
0
1
2
-1
0
1
chain
1
2
3
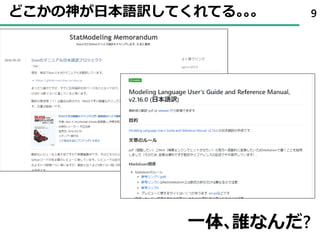
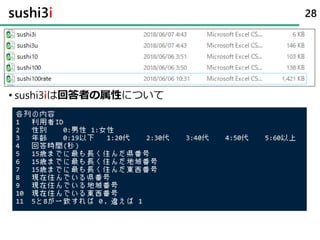
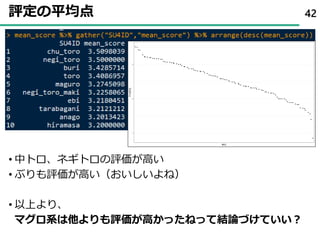
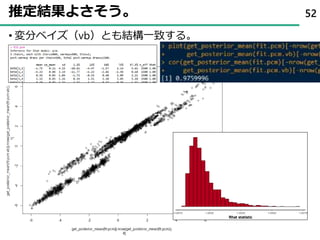
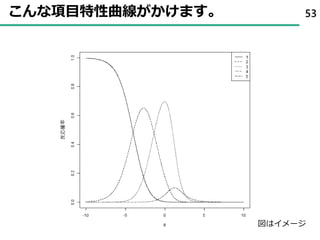
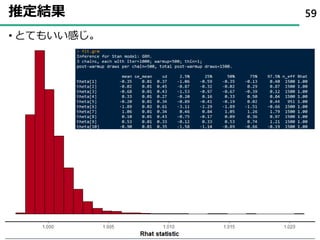
61. 62. 事後分布を確認する 62
theta[9] theta[10]
theta[5] theta[6] theta[7] theta[8]
theta[1] theta[2] theta[3] theta[4]
0 1 -2 -1 0
-1 0 1 -4 -3 -2 -1 0 0.0 0.5 1.0 1.5 2.0 2.5-1.5-1.0-0.5 0.0 0.5 1.0
-2 -1 0 1 -1 0 1 -2 -1 0 -0.5 0.0 0.5 1.0
63. 64. 65. 66. 67. 68. 69. 70. 参考文献
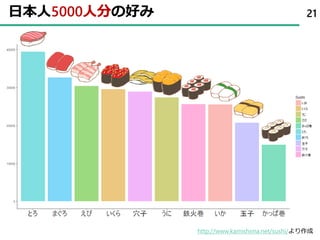
Data
• http://www.kamishima.net/sushi/
• T. Kamishima, "Nantonac Collaborative Filtering:
Recommendation Based on Order Responses", KDD2003,
pp.583-588 (2003)
Model
• Rによる項目反応理論
• https://www.amazon.co.jp/R%E3%81%AB%E3%82%88%E3%82
%8B%E9%A0%85%E7%9B%AE%E5%8F%8D%E5%BF%9C%E7%
90%86%E8%AB%96-%E5%8A%A0%E8%97%A4-
%E5%81%A5%E5%A4%AA%E9%83%8E/dp/4274050173
• Luo, Y., & Jiao, H. (2017). Using the Stan Program for
Bayesian Item Response Theory. Educational and
Psychological Measurement, 0013164417693666.
70






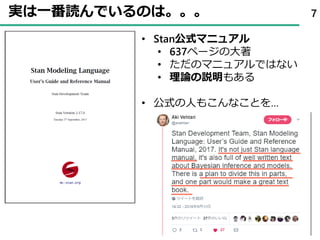






















![60
theta[9] theta[10]
theta[5] theta[6] theta[7] theta[8]
theta[1] theta[2] theta[3] theta[4]
0 250 500 7501000 0 250 500 7501000
0 250 500 7501000 0 250 500 7501000 0 250500 7501000 0 250 500 7501000
0 250 500 7501000 0 250 500 7501000 0 250500 7501000 0 250 500 7501000
-1
0
1
-1
0
1
-2
-1
0
-2
0
2
4
-1
0
1
2
-4
-3
-2
-1
0
1
-2
-1
0
1
2
-2
-1
0
1
2
3
-2
-1
0
1
2
-1
0
1
chain
1
2
3](https://image.slidesharecdn.com/tokyor-180610080458/85/Bayesian-Sushistical-Modeling-60-320.jpg)
![事後分布を確認する 62
theta[9] theta[10]
theta[5] theta[6] theta[7] theta[8]
theta[1] theta[2] theta[3] theta[4]
0 1 -2 -1 0
-1 0 1 -4 -3 -2 -1 0 0.0 0.5 1.0 1.5 2.0 2.5-1.5-1.0-0.5 0.0 0.5 1.0
-2 -1 0 1 -1 0 1 -2 -1 0 -0.5 0.0 0.5 1.0](https://image.slidesharecdn.com/tokyor-180610080458/85/Bayesian-Sushistical-Modeling-62-320.jpg)
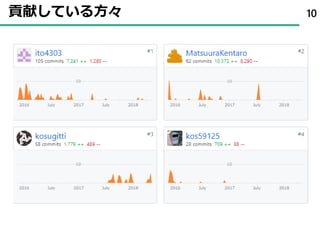
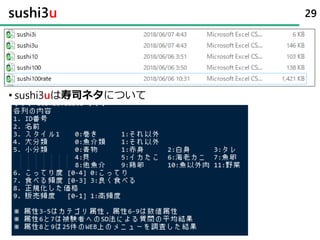
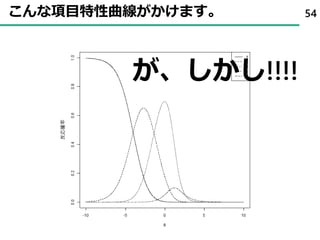
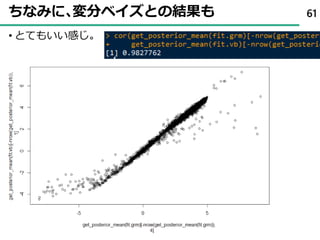
![寿司の好み軸のどこに回答者がいるか? 63
theta[1]
theta[2]
theta[3]
theta[4]
theta[5]
theta[6]
theta[7]
theta[8]
theta[9]
theta[10]
-4 -2 0 2
6番目の人は、普通の人(平均)よりすしが好きではない??](https://image.slidesharecdn.com/tokyor-180610080458/85/Bayesian-Sushistical-Modeling-63-320.jpg)