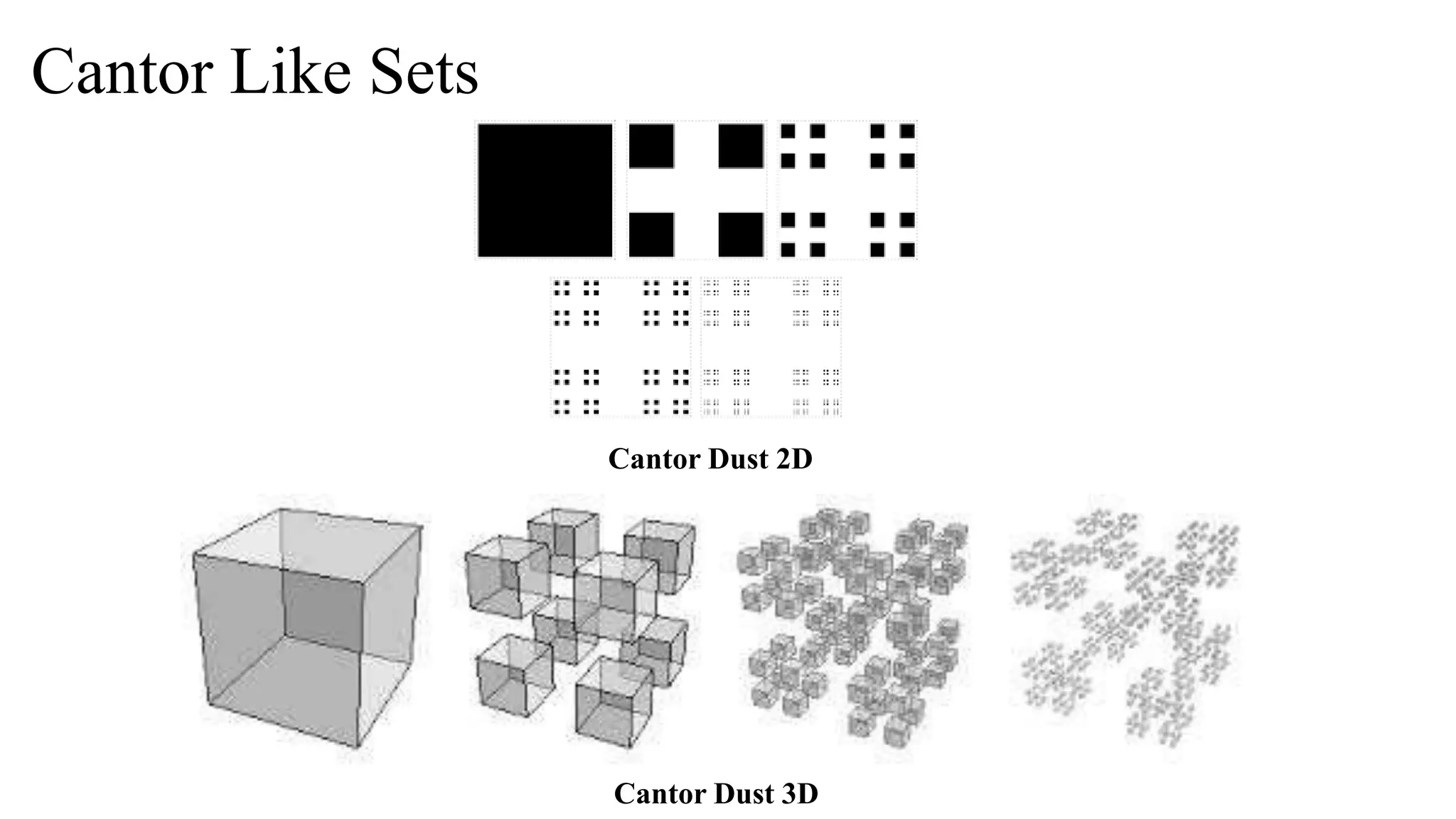
The Cantor set, first published by Georg Cantor in 1883, is a set of points with remarkable properties such as being uncountable, having zero measure, and being compact and totally disconnected. It is constructed by repeatedly removing the middle third of a line segment, leading to an infinite number of remaining points, although they are uncountable. Various mathematical properties associated with the Cantor set, including its perfect and nowhere dense characteristics, are outlined.

1. Georg Cantor

2. Let me Introduce…
CANTOR SET

3. History
• The Cantor Set was first published
in 1883.
• It is named after the German
Mathematician Georg Cantor.
• probably the most important
early mathematical set.

4. Properties of CANTOR SET
 Uncountably many elements
 Zero measure
 Compact
 Nowhere dense
 Perfect
 Totally disconnected
 Self similar

5. Before that..
What is Cantor Set…?
Google says….
In mathematics, the Cantor set is a set of points lying on a
single line segment that has a number of remarkable and
deep properties.

6. How to construct a CANTOR SET…?
Consider a real closed interval [0,1]

7. Have you got anything…
On continuing

8. We got…
Step 1
Step 2
Step 3
Step 4
Step 5
Step 6
Step 7

9. Consider a line segment of unit length (one).

Remove the middle third of the line segment.
Remove the middle thirds of the remaining pieces.
Repeat the process an infinite number of times.
(I have redrawn the remaining pieces.)
How much did we remove?
1
0
1 2 4 8 2
...
3 9 27 81 3
n
n
n



     
Since this is an infinite, convergent
geometric series, the sum is:
1
3 1
2
1
3


1 2
,
3 3
 
 
 
1 2 7 8
, ,
9 9 9 9
   
   
   
(open
interval)

10. 
We started with a length of one, and we removed one unit,
so how many points are left?
1 1 0  Are there zero points left? Are you sure?
Since the middle third of each remaining segment is
removed, the end points of each segment remain.
There are an infinite number of little segments remaining,
so are there an infinite number of points remaining?
NO. i.e. CANTOR SET is of Zero measure

11. The set of remaining points is called the Cantor Set.
The set was discovered in 1875
by Irish mathematician Henry
John Stephen Smith.
However as we have seen in
other cases, mathematical
concepts are not always named
after the first discoverer.


12. 
The set of remaining points is called the Cantor Set.
The set was further studied (and
published) by German mathematician
Georg Cantor in 1883.
The Cantor set has some remarkable
properties.

13. 2. Uncountable
It has a one – one correspondence with binary [0,1]. So. Cantor set is Uncountable with same as earlier

14. Next
3. Compact
What is compactness…
From
compact if for every open cover of SET there exist a finite subcover of SET
Heine-Borel Theorem states that a subset of R is compact iff it is closed and bounded,
it can be shown rather easily that C 3 is COMPACT.

15. a set is perfect if the set is closed and all the points of the set are
limit points of the set
I.e., for each non endpoint in the set there will always exist another point in the set
in same radius
within a deleted neighborhood of some radius "> 0 on both sides of that point
there exist a point
4. Perfect
It is Perfect

16. 5. Totally disconnected
A space said to be disconnected if the connected points are the single ton sets.
Since the cantor set does not contain any interval of non zero length. All elements are singleton set.
i.e. Cantor Set Is Totally Disconnected
6. Nowhere dense
a set is nowhere dense if the interior of the closure of the set is empty. The closure of a set
is the union of the set with the set of its limit points, so since every point in the set is a limit point of
the set the closure is simply the set itself. Now, the interior of the set must be empty since no two
points in the set are adjacent to each other.
Therefore Our Set Is Nowhere Dense

17. CANTOR SET IS of
1. Zero Measure
2. Uncountable
3. Compact
4. Perfect
5. Totally Disconnected
6. Nowhere Dense

18. Graph Of Cantor Function
Also called The Devil’s Staircase

19. Column capital with pattern like Cantor set.

20. Cantor Like Sets
Cantor Dust 2D
Cantor Dust 3D

21. References
1. Diary Of Mathematics Circles 2014-2015, Berchmans Mathematics Association
2. An Exploration of the Cantor Set, Christopher Shaver, Rockhurst University, 2009
3. The Elements of Cantor Sets_ With Applications-Robert W. Vallin(auth.)--Wiley (2013)
4. Wikipedia
5. Mathworld Wolfram
6. Platonic Realms