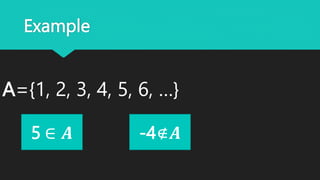
Georg Cantor founded set theory in the late 19th century and made notable contributions to mathematics. He demonstrated that transfinite numbers, which include infinite cardinal and ordinal numbers, are larger than finite numbers but not absolutely infinite. Cantor defined a set as a collection of definite objects that can be determined as members or non-members. He established the intuitive principle of extension stating that two sets are equal if they have the same members. Cantor also defined inclusion and the empty set, which contains no elements.

1. SET THEORY AND LOGIC
CHAPTER 1
Rejoyce C. Rubia-MEd Mathematics

2. GEORG CANTOR
• Georg Ferdinand Ludwig Philipp Cantor
shortly “Georg Cantor” was born on March
3, 1845 in St. Petersburg, Russian Empire.
• During his time he made a notable
accomplishments in the field of
Mathematics which are widely used and
studied today.

3. GEORG CANTOR’S CONTRIBUTIONS in the
FIELD OF MATHEMATICS
• SET THEORY. In the late 19th century, he founded and started
to developed the mathematical theory of sets, which aims to
investigate a well-defined collection of objects.
• TRANSFINITE NUMBERS. He demonstrated that these numbers
are infinite and are larger than all finite numbers, yet they are
not necessarily absolutely infinite.
• TRANSFINITE ORDINALS. These numbers are used to provide
an ordering of infinite sets.
• TRANSFINITE CARDINALS. These numbers are used to quantify
the size of infinite sets.

4. GEORG CANTOR’S CONCEPT OF A SET
A set S is any collection of definite, distinguishable objects of our intuition or
of our intellect to be conceived as a whole.
The attribute “definite” is interpreted as meaning that if given a set and an
object, it is possible to determine whether the object is, or is not, a member
of the set.
The implication is that a set is completely determined by its members.

5. Which is an example of a set?
A={counting numbers
or natural numbers}
B={the best musicians
in the world}

6. A set is represented by a capital letter.
The objects are called the elements or
members of S.

7. Example
A={counting numbers or natural numbers}
A={1, 2, 3, 4, 5, 6, …}

8. THE BASIS of INTUITIVE SET THEORY
According to Cantor, a set is made up of objects called members or
elements. The assumption that if presented with a specific object
and a specific set, one can determine whether or not that object is
a member of that set. Thus, the notion of membership is a relation
between objects and sets. We shall symbolize this relation by ∈ and
write
𝑥 ∈ 𝐴
If the object 𝑥 is a member of the set 𝐴. If 𝑥 is not a member we shall
write
𝑥 ∈ 𝐴

9. Example
A={1, 2, 3, 4, 5, 6, …}
5 ∈ 𝑨 -4∉𝑨

10. THE INTUITIVE PRINCIPLE OF EXTENSION
 Two sets are equal if and only if they have the same members.
The equality of two sets 𝑋 𝑎𝑛𝑑 𝑌 will be denoted by
𝑋 = 𝑌,
and the inequality of two sets 𝑋 𝑎𝑛𝑑 𝑌 will be denoted by
𝑋 = 𝑌,
Among the basic properties of this relation are
𝑋 = 𝑋
𝑋 = 𝑌 implies 𝑌 = 𝑋
𝑋 = 𝑌 and 𝑌 = 𝑍 imply 𝑋 = 𝑍,
For all the sets 𝑋, 𝑌, 𝑍.

11. EXAMPLE
A={2, 4, 6}
B= {2, 6, 4}
Thus, A=B
X={counting
numbers}
Y= {integers}
Thus, X≠ 𝒀

12. INCLUSION
If A and B are sets, then A is included in B, symbolized by
A⊆B,
If and only if each member of A is a member of B. In this
event one also says that A is a subset of B.
Example:
{9,14,28} ⊆ {9,14,28}
Set A is a subset of B. Set A is included in set B.

13. The principle of extension implies that there can
be only one set with no elements. We call this set
the empty set and symbolized it by
∅
EMPTY SET

14. THANK YOU FOR
LISTENING!!!