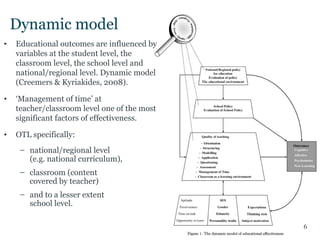
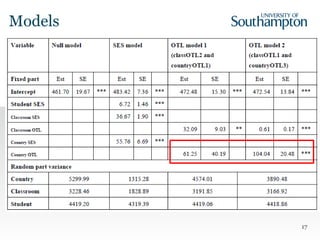
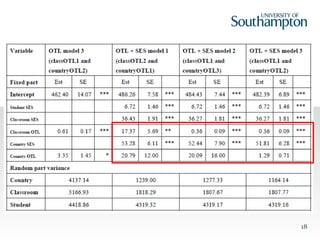
This document summarizes a study examining the relationship between students' socioeconomic status (SES), opportunity to learn (OTL) mathematics content, and achievement on the 2011 Trends in International Mathematics and Science Study (TIMSS) assessment. The study used multilevel modeling of TIMSS data from over 280,000 8th grade students in over 11,000 classrooms across 50 countries. Results showed that both SES and two measures of classroom-level OTL positively predicted student achievement, while country-level OTL measures showed mixed effects depending on the operationalization of OTL. Controlling for SES, classroom OTL remained a significant positive predictor of achievement but country-level OTL did not.

1. OPPORTUNITY TO LEARN
SECONDARY MATHS:
A CURRICULUM APPROACH
WITH TIMSS 2011 DATA
Dr. Christian Bokhove
Southampton Education School
ICME-13, TSG-39
July 2016

2. Rationale
• enGasia project, studying geometry education in
international perspective
• Differences in curriculum
• Existing international comparisons like TIMSS and PISA
• Recently published paper ‘Opportunity to Learn’ (Schmidt,
Burroughs, Zoido, & Houang, 2015)
• Also plays large role in recent OECD report on maths:
“Equations and Inequalities - Making Mathematics
Accessible to All”

3. Opportunity to Learn
• ‘Content covered’
• Relationship Socioeconomic status and achievement (e.g.
Sirin, 2005; Chudgar & Luschei, 2009)
• One factor: role of curriculum, exposure to curriculum
content.
• Opportunity to learn (OTL; Carroll, 1963), content coverage

4. Schmidt, Burroughs, Zoido & Houang (2015)
• Role of schooling in perpetuating
educational inequality
• PISA 2012 data
• Opportunity to Learn
• “instructional content as a
mediator for socioeconomic
inequality”
• Student level indicators?
• Key question what is involved in
OTL? Surely the
teacher/classroom level is
important?

5. 5

6. Dynamic model
• Educational outcomes are influenced by
variables at the student level, the
classroom level, the school level and
national/regional level. Dynamic model
(Creemers & Kyriakides, 2008).
• ‘Management of time’ at
teacher/classroom level one of the most
significant factors of effectiveness.
• OTL specifically:
– national/regional level
(e.g. national curriculum),
– classroom (content
covered by teacher)
– and to a lesser extent
school level.
6

7. So a curriculum approach
• Do students know best what contents is covered?
• And if they do, then isn’t that more a proxy for achievement?
• With content covered, teachers perhaps know best?
• TIMSS more curriculum oriented than PISA (Rindermann &
Baumeister, 2015)
• TIMSS samples classrooms
7

8. TIMSS 2011
“TIMSS 2011 is the fifth in IEA’s series of international
assessments of student achievement dedicated to
improving teaching and learning in mathematics and
science. First conducted in 1995, TIMSS reports every
four years on the achievement of fourth and eighth grade
students.“
http://timssandpirls.bc.edu/timss2011/

9. Curriculum model
• TIMSS’ curriculum model (Mullis, Martin, Ruddock,
O’Sullivan, & Preuschoff, 2009)
– intended curriculum (the educational system's aims and
goals)
– implemented curriculum (the actual strategies,
practices, and activities found in classrooms)
– attained curriculum (student learning)
9
Multilevel: students in classrooms in countriesMultilevel: students in classrooms in countries

10. Methodology: analytical approach
• Secondary data analysis of TIMSS 2011 data
• Use multilevel models
• Take into account complex sampling design of TIMSS 2011
– Different probabilities of units being selected
(classrooms, students) → sampling weights
– Rotated-booklet design → Plausible Values combined by
Rubin’s rules (Rubin, 1987).
– No jackknife for correct SE measurement → multilevel
approach should cater for this
10

11. Methodology: analytical approach
• IDB analyser used to create datasets for three levels
• HLM 6.08 used to build four models
– A null model
– A model with SES variables
– A model with OTL variables
– A model with both SES and OTL variables
• Further assumptions
– Group-centered variables at student and classroom levels
– Grand mean centered at country level
– Full Maximum Likelihood
– Missing data imputed with EM algorithm 11

12. Dataset
• TIMSS 2011 grade 8 data
• Data at three levels
– achievement and background data of students,
– classroom level data from the teacher questionnaire,
and
– curriculum data at the country level.
• After data preparation: 287395 students in 11688
classrooms in 50 countries.
• Choice of variables

13. Dependent variable
• Five plausible values for maths achievement, BSMMAT01
to BSMMAT05
13

14. Independent variables: student level
• ‘Home Economic Resources’
– Proxy for SES (and related to prior knowledge)
– Numbers of books at home, highest level education of
either parent, number of home study support
– One scale through IRT scaling (Rasch partial credit
model)
• No OTL measure at student level for reasons explained
previously.
14

15. Independent variables: class level
• Mean SES in a class → Classroom SES
• Two newly created OTL measures → Classroom OTL
– classOTL1: Percentage of the content domain covered
with students
– classOTL2: Percentage+ Maths
instruction time, expressed in
variable between 0
and 2 of content
coverage
15

16. Independent variables: country level
• Mean SES in a country → Country SES
• 3 newly created OTL measures → Country OTL
– countryOTL1: combination of
• Is there a national curriculum?
• Does curriculum prescribe goals and objectives?
• Curriculum coverage (content domains: number,
algebra, geometry and data and chance)
• Variable between 0 and 3 content coverage
– countryOTL2: mean of all classOTL1
– countryOTL3: only curriculum coverage
16

17. Models
17

18. 18

19. Conclusions
• SES variables reduce classroom and country variance, OTL
variables too, but less
• SES variables significant positive predictors
• OTL significant positive predictors at classroom level, at
country level depends on operationalisation of OTL
• But after controlling for SES all models classroom OTL
significantly positive predictor, country OTL not.
• Contradicts
Why?
19

20. Discussion/further analyses
• Content domains: number, algebra, geometry and data and
chance.
• Sampling classrooms
• Different correlations between the different
operationalisations of OTL, for example:

21. Thank you
• Questions/comments?
• More information:
Twitter: @cbokhove
C.Bokhove@soton.ac.uk
21

22. Selected references
Carroll, J.B. (1963). A model of school learning. Teachers College Record, 64(8), 723-733.
Chudgar, A. & Luschei, T.F. (2009). National income, income inequality, and the importance of schools: A hierarchical cross-
national comparison. American Educational Research Journal, 46(3), 626-658.
Creemers, B.P.M. & Kyriakides, L. (2008). The dynamics of educational effectiveness: a contribution to policy, practice and
theory in contemporary schools. London: Routledge.
Mullis, I.V.S., Martin, M.O., Ruddock, G.J., O’Sullivan, C.Y., & Preuschoff, C. (2009). TIMSS 2011 Assessment frameworks.
Lynch School of Education, Boston College.
Mullis, I.V.S., Martin, M.O., Foy, P., & Arora, A. (2012). TIMSS 2011 International results in mathematics. Lynch School of
Education, Boston College.
Rindermannm H, & Baumeister, A.E.E. (2015). Validating the interpretations of PISA and TIMSS tasks: A rating study.
International Journal of Testing, 15(1), 1-22.
Rubin, D. (1987). Multiple imputation for nonresponse in sample surveys. New York: John Wiley.
Rutkowski, L., Gonzalez, E., Joncas, M., & von Davier, M. (2010). International large-scale assessment data: Issues in
secondary analysis and reporting. Educational Researcher, 39(2), 142-151.
Schmidt, W.H., Zoido, P., & Cogan, L.S. (2013). Schooling matters: Opportunity to learn in PISA 2012 (OECD Education
Working Papers No. 95). Paris, France: Organisation for Economic Co-operation and Development.
Schmidt, W.H., Burroughs, N.A., Zoido, P., & Houang, R.T. (2015). Educational Researcher, 44(7), 371-386.
Sirin, S. R. (2005). Socioeconomic status and academic achievement: A meta-analytic review of research. Review of
Educational Research, 75(3), 417–453. 22