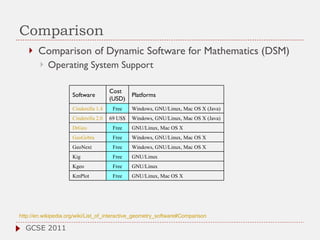
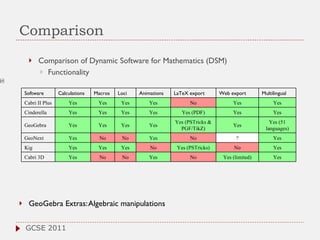
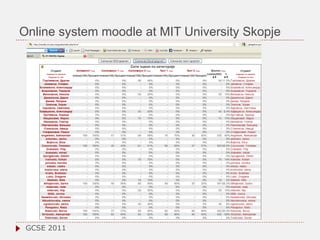
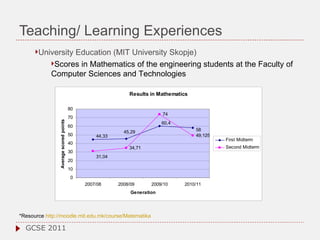
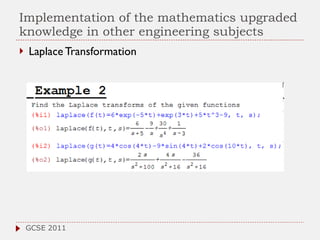
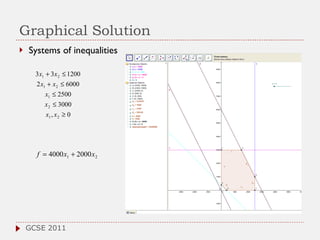
The document discusses the role of computer algebra systems (CAS) in teaching linear algebra, comparing several CAS such as Maple, Mathematica, and Maxima regarding their functionalities and costs. It emphasizes the need for university students to be familiar with CAS to enhance their mathematical understanding and provides examples of their applications in education. Additionally, the document highlights teaching experiences and solutions to mathematical problems using CAS, particularly in high school and university settings.

1. Computer Algebra Systems Supporting Teaching/ Learning Linear Algebra Ana Donevska Todorova International GeoGebra Conference for Southeast Europe January 2011, Novi Sad, Serbia

2. Overview Introduction Comparison Computer Algebra Systems Dynamic Software for Mathematics Teaching/ Learning Experiences University Education CAS Maxima and the online system moodle at the MIT University Secondary Education Some examples GCSE 2011

3. Introduction Faculties of engineering and informatics at the universities implement CAS: Mathematica Matlab during the contemporary lab classes in mathematics. First year students at universities are usually not familiar with any of the CAS or DGS and show lack of computer supported mathematics. Some possibilities to help the upper secondary school students in overcoming this problem and prepare them for university mathematics into lab. GCSE 2011

4. Comparison Comparison of Computer Algebra Systems (CAS) General Information GCSE 2011 http://en.wikipedia.org/wiki/Comparison_of_computer_algebra_systems System Creator Development started First public release Latest stable version Cost ( USD ) Open source Maple Maplesoft 1980 1984 14 (April 2010) $1,895 (Commercial), $1,795 (Government), $995 (Academic), $239 (Personal Edition), $99 (Student), $79 (Student, 12-Month term) No Mathema ica Wolfram Research 1986 1988 8.0 /November 2010 $2,495 (Professional), $1095 (Education), $140 (Student), $69.95 (Student annual license) $295 (Personal) No Maxima MIT Project MAC and Bill Schelter et al. 1967 1998 5.22 (2010) Free Yes

5. Comparison Comparison of Computer Algebra Systems (CAS) Functionality http://en.wikipedia.org/wiki/Comparison_of_computer_algebra_systems GCSE 2011 System Formula editor Calculus Solvers Graph theory Number theory Boolean algebra Integra tion Integral Transfor ms Equations Inequal ities Differential equations Recurrence relations Maple Yes Yes Yes Yes Yes Yes Yes Yes Yes No Mathem atica Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes Maxima No Yes Yes Yes Yes Yes No Yes Yes No

6. Comparison http://en.wikipedia.org/wiki/Comparison_of_computer_algebra_systems Comparison of Computer Algebra Systems (CAS) Operating System Support GCSE 2011 System Windows Linux Solaris Maple Yes Yes Yes Mathematica Yes Yes No Maxima Yes Yes Yes MuPAD Yes Yes No

7. Comparison Comparison of Dynamic Software for Mathematics (DSM) Operating System Support http://en.wikipedia.org/wiki/List_of_interactive_geometry_software#Comparison GCSE 2011 Software Cost (USD) Platforms Cinderella 1.4 Free Windows, GNU/Linux, Mac OS X (Java) Cinderella 2.0 69 US$ Windows, GNU/Linux, Mac OS X (Java) DrGeo Free GNU/Linux, Mac OS X GeoGebra Free Windows, GNU/Linux, Mac OS X GeoNext Free Windows, GNU/Linux, Mac OS X Kig Free GNU/Linux Kgeo Free GNU/Linux KmPlot Free GNU/Linux, Mac OS X

8. Comparison Comparison of Dynamic Software for Mathematics (DSM) Functionality GeoGebra Extras: Algebraic manipulations GCSE 2011 Software Calculations Macros Loci Animations LaTeX export Web export Multilingual Cabri II Plus Yes Yes Yes Yes No Yes Yes Cinderella Yes Yes Yes Yes Yes (PDF) Yes Yes GeoGebra Yes Yes Yes Yes Yes (PSTricks & PGF/TikZ) Yes Yes (51 languages) GeoNext Yes No No Yes No ? Yes Kig Yes Yes Yes No Yes (PSTricks) No Yes Cabri 3D Yes No No Yes No Yes (limited) Yes

9. Online system moodle at MIT University Skopje GCSE 2011

10. Teaching/ Learning Experiences *Resource http://moodle.mit.edu.mk/course/Matematika University Education (MIT University Skopje) Scores in Mathematics of the engineering students at the Faculty of Computer Sciences and Technologies GCSE 2011

11. Implementation of the mathematics upgraded knowledge in other engineering subjects Quantitive linear models for optimization Example 1: A company produces three types of products in three different facilities (machines). For each product in each in each facility the required processing time is given in the following table: How many peaces of each of the products can be produced if the first facility has a capacity of 3200 working hours per month, the second facility 1700 and the third one 1300 working hours per month? Solution (using wxMaxima) GCSE 2011 Facilities Product 1 Product 2 Product 3 1 2 3 4 2 1 2 1 3 1 1 2

12. Implementation of the mathematics upgraded knowledge in other engineering subjects Laplace Transformation GCSE 2011

13. Teaching/ Learning Experiences Secondary Education Properties of Determinants Calculate the values of the following determinants: Using CAS Maxima calculate the values of the determinants given in the previous assignment. Compare the obtained results and the given determinants; and explain what you noticed. Write the conclusion in your own words. Write the property using mathematical symbols. GCSE 2011

14. Teaching/ Learning Experiences Secondary Education Properties of Determinants Using CAS Maxima c alculate the values of the following determinants: Compare the obtained results and the given determinants; and explain what you noticed. Write the conclusion in your own words. Write the property using mathematical symbols. Generalize the property for n-dimension determinant. GCSE 2011

15. Teaching/ Learning Experiences Linear programming in GeoGebra Example: Two different types of products A and B can be produced on the machines M 1 and M 2 . The capacity of M 1 is 12000 working hours and the capacity of M 2 is 6000 w. h. Required time for producing one product of type A on the machine is M 1 is 3w. h. and on the machine M 2 is 2 w. h. Required time for producing one product of type B on the machine is M 1 is 3w. h. and on the machine M 2 is 1 w. h. The needs of the market are 2500 products of type A and 3000 products of type B. The profit of the company is 4000 euros per one product A and 2000 euros per one product B. The management of the company has to create the optimal plan for producing the products A and B in order to achieve the best profit. GCSE 2011

16. Graphical Solution Systems of inequalities GCSE 2011

17. References Literature D. Todorova A.: The transition from secondary to teriary level mathematics emphasized in the course of linear algebra, International conference dedicated to prof. d-r. Gorgi Cupona, Ohrid, 2010. Donevska-Todorova, A. (2010): Difficulties in Mathematics for the Students in the First Year at Higher Education; Zbornik na MIT Universitet, Skopje, Macedonia, p. 177-184 . Trencevski K.; Krsteska B.; Trencevski G.; Zdraveska S.; Linear algebra and analytic geometry for third year reformed gymnasium educatiom, Prosvetno delo, Skopje 2004. Roegner K. (2008) Linear Algebra as a Bridge Course for First-year Engineering students, Department of Mathematics, Technische Universität Berlin, Berlin Germany. Internet Recourses http://wxmaxima.sourceforge.net/wiki/index.php/Main_Page http://www.geogebra.org/cms/ http://moodle.mit.edu.mk/course/Matematika http://en.wikipedia.org/wiki/Comparison_of_computer_algebra_systems http://en.wikipedia.org/wiki/List_of_interactive_geometry_software#Comparison GCSE 2011