More Related Content
PDF
ベイジアンモデリングによるマーケティングサイエンス〜状態空間モデルを用いたモデリング PDF
PPTX
マルコフ連鎖モンテカルロ法 (2/3はベイズ推定の話) PDF
PPTX
【読書会資料】『StanとRでベイズ統計モデリング』Chapter12:時間や空間を扱うモデル PDF
PDF
PPTX
StanとRでベイズ統計モデリングに関する読書会(Osaka.stan) 第四章 What's hot
ZIP
PDF
PDF
PDF
PDF
PDF
最近のKaggleに学ぶテーブルデータの特徴量エンジニアリング PDF
Rによるやさしい統計学第20章「検定力分析によるサンプルサイズの決定」 PDF
PDF
PDF
PDF
PPTX
PPTX
ベイズ深層学習5章 ニューラルネットワークのベイズ推論 Bayesian deep learning PDF
Cmdstanr入門とreduce_sum()解説 PDF
PDF
MCMCサンプルの使い方 ~見る・決める・探す・発生させる~ PDF
PDF
PPTX
PDF
Viewers also liked
PDF
PDF
PDF
第2回 R言語で始めよう、データサイエンス(ハンズオン勉強会) 〜相関分析による需要予測編〜 PDF
PDF
PDF
セグメンテーションの考え方・使い方 - TokyoR #44 PDF
PDF
PPTX
PDF
時系列解析の使い方 - TokyoWebMining #17 PDF
状態空間モデルの考え方・使い方 - TokyoR #38 PDF
分析のビジネス展開を考える―状態空間モデルを例に @TokyoWebMining #47 PDF
PPTX
PDF
ロジスティック回帰の考え方・使い方 - TokyoR #33 PDF
Similar to 『予測にいかす統計モデリングの基本』の売上データの分析をトレースしてみた
PPTX
未来を予測せよ 〜あるエンジニアが挑んだKaggleコンペの軌跡〜 PDF
PDF
PPTX
Tori lab 輪読会 WWW 2014 - Modeling and predicting the growth and death PDF
PDF
ビジネス活用事例で学ぶデータサイエンス入門 #2 PDF
PDF
Tokyor60 r data_science_part1 PPTX
NagoyaStat#7 StanとRでベイズ統計モデリング(アヒル本)4章の発表資料 PDF
分析のリアルがここに!現場で使えるデータ分析 PDF
PDF
PDF
『手を動かしながら学ぶ ビジネスに活かすデータマイニング』で目指したもの・学んでもらいたいもの PDF
PPTX
Kaggle M5 Forecasting (日本語) PDF
GDPナウキャスティングアプリ「Nowcaster of the seven keys」をリリースしました PPTX
HiRoshima.R#6 by imuyaoti PDF
分析のリアルがここに!現場で使えるデータ分析(1限目) 先生:吉永 恵一 PDF
PPTX
「ビジネス活用事例で学ぶ データサイエンス入門」輪読会#7資料 More from . .
PDF
PDF
統計モデリングで癌の5年生存率データから良い病院を探す PDF
Stanの紹介と応用事例(age heapingの統計モデル) PDF
PDF
PDF
PDF
データ解析で割安賃貸物件を探せ!(山手線沿線編) LT PDF
PDF
とある病んだ院生の体内時計(サーカディアンリズム) PDF
『予測にいかす統計モデリングの基本』の売上データの分析をトレースしてみた
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
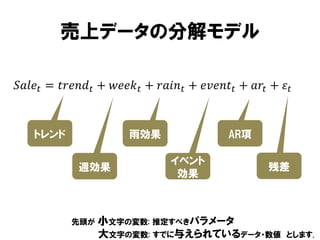
売上データの分解モデル
𝑆𝑎𝑙𝑒 𝑡 =𝑡𝑟𝑒𝑛𝑑 𝑡 + 𝑤𝑒𝑒𝑘 𝑡 + 𝑟𝑎𝑖𝑛 𝑡 + 𝑒𝑣𝑒𝑛𝑡 𝑡 + 𝑎𝑟 𝑡 + 𝜀 𝑡
トレンド
雨効果
週効果
先頭が
AR項
イベント
効果
残差
小文字の変数: 推定すべきパラメータ
大文字の変数: すでに与えられているデータ・数値
とします.
- 10.
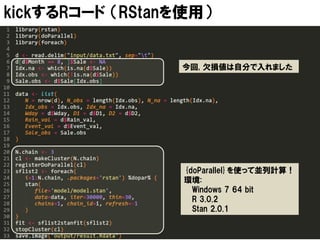
モデル | トレンド
長期的変動を表す.二次トレンドモデルを使う.
𝑡𝑟𝑒𝑛𝑑 𝑡 − 𝑡𝑟𝑒𝑛𝑑 𝑡−1 ≈ 𝑡𝑟𝑒𝑛𝑑 𝑡−1 − 𝑡𝑟𝑒𝑛𝑑 𝑡−2
𝑡𝑟𝑒𝑛𝑑 𝑡 = 2𝑡𝑟𝑒𝑛𝑑 𝑡−1 − 𝑡𝑟𝑒𝑛𝑑 𝑡−2 + 𝜀1 𝑡
𝜀1 𝑡 ~𝒩 0, 𝜎 𝑡𝑟𝑒𝑛𝑑
- 11.
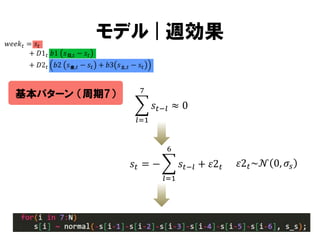
モデル | 週効果
𝑤𝑒𝑒𝑘𝑡 = 𝑠 𝑡
+ 𝐷1 𝑡 𝑏1 𝑠 日,𝑡 − 𝑠 𝑡
+ 𝐷2 𝑡 𝑏2 𝑠 金,𝑡 − 𝑠 𝑡 + 𝑏3 𝑠 土,𝑡 − 𝑠 𝑡
値=1
値=0
𝐷1 𝑡
月~金の祝日
それ以外
𝐷2 𝑡
祝日でない月~木
かつ翌日が祝日
それ以外
- 12.
- 13.
- 14.
- 15.
モデル | イベント効果
経験で変換:参加人数数値
推定する係数 [千円]
𝑒𝑣𝑒𝑛𝑡 𝑡 = 𝑐_𝑒𝑣𝑒𝑛𝑡 𝑡 ∗ 𝐸𝑣𝑒𝑛𝑡_𝑣𝑎𝑙
Event_val
イベントの参加人数
[万人]
𝑐_𝑒𝑣𝑒𝑛𝑡 𝑡 = 𝑐_𝑒𝑣𝑒𝑛𝑡 𝑡−1 + 𝜀3 𝑡
𝜀3 𝑡 ~𝒩 0, 𝜎 𝑒𝑣𝑒𝑛𝑡
𝑡
- 16.
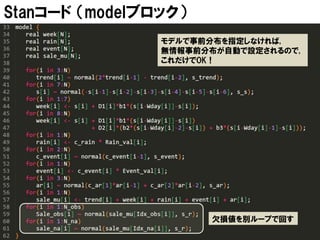
モデル | AR項
𝑎𝑟𝑡 は 𝑡𝑟𝑒𝑛𝑑 𝑡 よりは短く 𝑤𝑒𝑒𝑘 𝑡 よりは長い時間スケール、
具体的には1ヶ月程度の周期を担う成分
このような他の項では説明できない時間スケール変動を表す
項をあらかじめ入れておくことが, モデリングに基づくデータ分
析の秘訣である.
[書籍より]
2
𝑎𝑟 𝑡 =
𝑐_𝑎𝑟𝑙 𝑎𝑟 𝑡−𝑙 + 𝜀4 𝑡
𝑙=1
𝜀4 𝑡 ~𝒩 0, 𝜎 𝑎𝑟
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
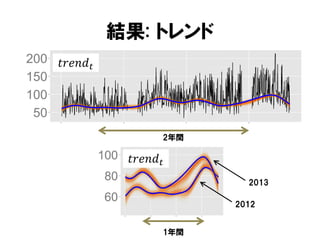
結果: 週効果 |基本パターン
𝑠𝑡
売上
[千円]
真の値
MCMCサンプルの中央値
週末に売上が減る.
ビジネス街の影響.
- 24.
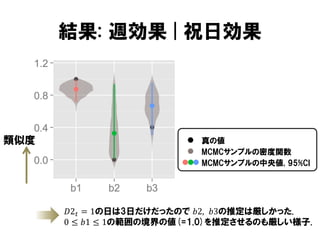
結果: 週効果 |祝日効果
類似度
真の値
MCMCサンプルの密度関数
MCMCサンプルの中央値, 95%CI
𝐷2 𝑡 = 1の日は3日だけだったので 𝑏2, 𝑏3の推定は厳しかった.
0 ≤ 𝑏1 ≤ 1の範囲の境界の値(=1.0)を推定させるのも厳しい様子.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
Web上の情報(予定含む)
• Small DataScientist Memorandum
– http://heartruptcy.blog.fc2.com/blog-entry-90.html
– R Advent Calendar 2013の26日目の記事になります.
• 書籍の元となった研究はこちら.
– 状態空間モデルを用いた飲食店売上の要因分解
• http://ci.nii.ac.jp/naid/110001183787
– 状態空間モデルによる 時系列データ解析 樋口知之 - 統計数理研究所
• http://tswww.ism.ac.jp/higuchi/index_e/papers/Kouza-TSA-Higuchi.pdf



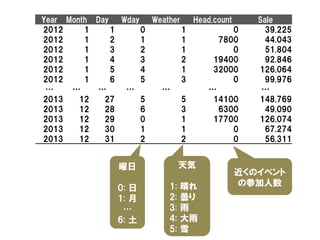
![仮想売上データ
オフィス街の近くのレストラン
• 2012/1/1~2013/12/31
• 繁忙期(8月)は欠損
売上
[千円]
day](https://image.slidesharecdn.com/random-131221040422-phpapp02/85/slide-4-320.jpg)
![売上
[千円]
イベントの参加人数
lm(formula = d$Sale ~ Sun + Mon + Tue + Wed + Thu + Fri + Sat
+ d$Weather + d$Head.count)
?](https://image.slidesharecdn.com/random-131221040422-phpapp02/85/slide-6-320.jpg)





![モデル | 雨効果
『悪天候になればなるほど・・・』
経験で変換: 天気数値
推定する係数 [千円]
Rain_val
𝑟𝑎𝑖𝑛 𝑡 = 𝑐_𝑟𝑎𝑖𝑛 ∗ 𝑅𝑎𝑖𝑛_𝑣𝑎𝑙
𝑡](https://image.slidesharecdn.com/random-131221040422-phpapp02/85/slide-14-320.jpg)
![モデル | イベント効果
経験で変換: 参加人数数値
推定する係数 [千円]
𝑒𝑣𝑒𝑛𝑡 𝑡 = 𝑐_𝑒𝑣𝑒𝑛𝑡 𝑡 ∗ 𝐸𝑣𝑒𝑛𝑡_𝑣𝑎𝑙
Event_val
イベントの参加人数
[万人]
𝑐_𝑒𝑣𝑒𝑛𝑡 𝑡 = 𝑐_𝑒𝑣𝑒𝑛𝑡 𝑡−1 + 𝜀3 𝑡
𝜀3 𝑡 ~𝒩 0, 𝜎 𝑒𝑣𝑒𝑛𝑡
𝑡](https://image.slidesharecdn.com/random-131221040422-phpapp02/85/slide-15-320.jpg)
![モデル | AR項
𝑎𝑟 𝑡 は 𝑡𝑟𝑒𝑛𝑑 𝑡 よりは短く 𝑤𝑒𝑒𝑘 𝑡 よりは長い時間スケール、
具体的には1ヶ月程度の周期を担う成分
このような他の項では説明できない時間スケール変動を表す
項をあらかじめ入れておくことが, モデリングに基づくデータ分
析の秘訣である.
[書籍より]
2
𝑎𝑟 𝑡 =
𝑐_𝑎𝑟𝑙 𝑎𝑟 𝑡−𝑙 + 𝜀4 𝑡
𝑙=1
𝜀4 𝑡 ~𝒩 0, 𝜎 𝑎𝑟](https://image.slidesharecdn.com/random-131221040422-phpapp02/85/slide-16-320.jpg)


![分解の結果
売上データ, トレンド
週
雨
イベント
AR
売上
[千円]
残差
day
真の値
MCMCサンプル (n=1500)
MCMCサンプルの中央値](https://image.slidesharecdn.com/random-131221040422-phpapp02/85/slide-21-320.jpg)
![結果: 週効果 | 基本パターン
𝑠𝑡
売上
[千円]
真の値
MCMCサンプルの中央値
週末に売上が減る.
ビジネス街の影響.](https://image.slidesharecdn.com/random-131221040422-phpapp02/85/slide-23-320.jpg)
![結果: 雨効果
係数
[千円]
真の値
MCMCサンプルの密度関数
MCMCサンプルの中央値, 95%CI
悪天候になると売上が伸びる.
ビジネス街の影響.](https://image.slidesharecdn.com/random-131221040422-phpapp02/85/slide-25-320.jpg)
![結果: イベント効果
𝑒𝑣𝑒𝑛𝑡 𝑡
𝑐_𝑒𝑣𝑒𝑛𝑡 𝑡
売上
[千円]
day
真の値
MCMCサンプル (n=1500)
MCMCサンプルの中央値](https://image.slidesharecdn.com/random-131221040422-phpapp02/85/slide-26-320.jpg)
![結果: AR項, 残差
𝑎𝑟 𝑡
欠損値のあるところ
𝜀𝑡
売上
[千円]
day](https://image.slidesharecdn.com/random-131221040422-phpapp02/85/slide-27-320.jpg)


