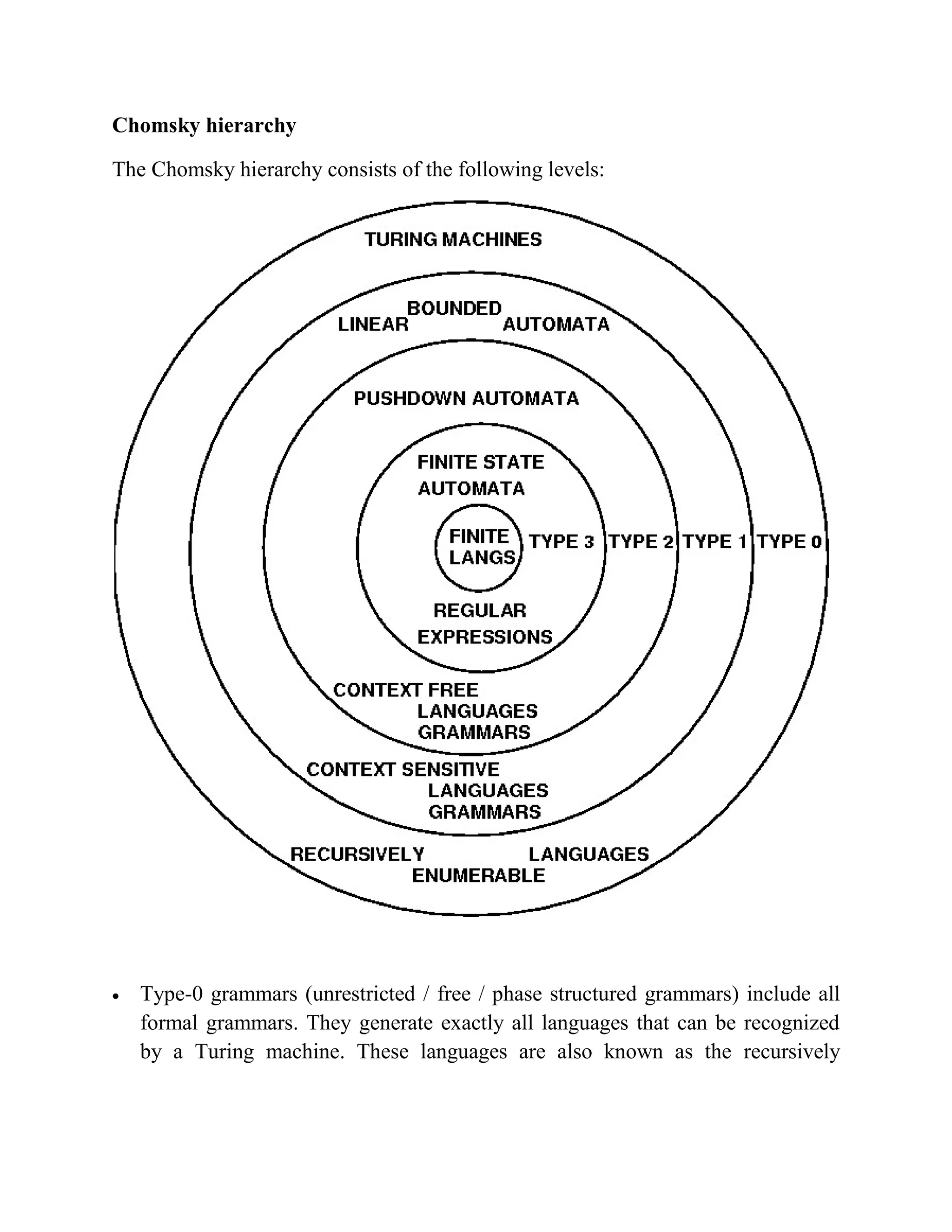
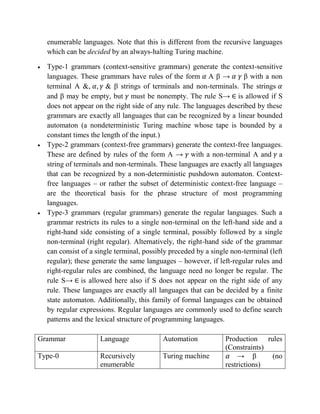
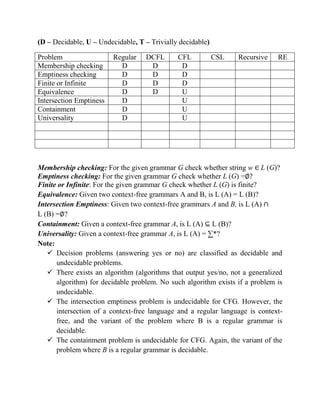
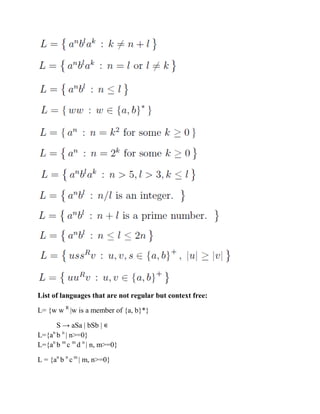The Chomsky hierarchy classifies formal grammars into four types: type-0 (recursively enumerable languages recognized by Turing machines), type-1 (context-sensitive languages recognized by linear bounded automata), type-2 (context-free languages recognized by pushdown automata), and type-3 (regular languages recognized by finite state automata). Each type has specific production rules and language recognition capabilities, with context-free grammars being significant for programming languages and deterministic context-free languages allowing for efficient parsing. Key concepts such as the pumping lemma, a method to demonstrate language properties, and Chomsky normal form, a standardized format for context-free grammars, are also discussed.