Embed presentation
Downloaded 29 times


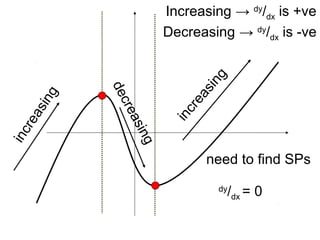

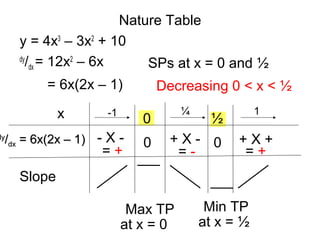





The document discusses increasing and decreasing functions. It defines an increasing function as one where the gradient (dy/dx) is always positive, and a decreasing function as one where the gradient is always negative. To determine if a function is increasing or decreasing, you find where the derivative (dy/dx) is equal to 0 to find critical points, and use a nature table to analyze the sign of the derivative on each interval. The derivative also needs to be analyzed to determine if a function is always increasing or decreasing.









