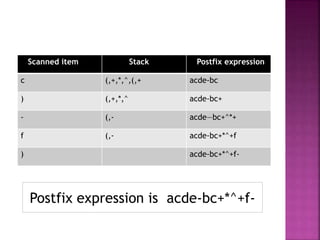
The document discusses converting infix expressions to postfix expressions using a stack. It defines infix and postfix expressions, provides examples of each, and presents an algorithm that uses a stack to scan an infix expression from left to right and output an equivalent postfix expression. Key steps include pushing operators to the stack based on precedence and popping operators to the output when encountering operands and parentheses.

2.  Introduction
 What is expression ?
 Infix Expression
 Postfix Expression
 Priority table
 Algorithm for conversion
 Reference

3. • In this presentation we are going to read
about how to convert infix expression to
postfix expression with the help of STACK.
• A Stack is a linear data structure in which
item may be inserted and deleted at one
end called TOP.
• The operational meaning of stack is LIFO
i.e. Last In Fast Out.
• This means the last element is inserted to
the stack is the first element to be
deleted.

4. An expression is any legal combination of
operators and operands that represents a
value.
Operands are values and Operators are
symbols that represent particular actions.
Ex:-a+b,p*q etc.

5. • This expression is common expression for
writing arithmetic expression.
• In infix expression the binary operator
symbol is placed between its two operands.
Ex:-A+B,P*Q,(X+Y)/Z

6. • In postfix expression the binary operator
symbol placed after its two operands.
• This expression is also called ‘Reverse polish
expression’.
• It doesn’t require parenthesis to determine
the order of precedence.
Ex:-AB+,PQ*,XY+Z/

7. Priority level Operators
1. Unary +,Unary -,NOT
2. ^
3. /,*
4. +,-
5. <,>,<=,>=
6. ==,!=
7. &&
8. ||

8. POSTFIX(Q,P):Here Q is an infix expression.This
algorithm finds the equivalent postfix expression P.
Step 1:Take an empty stack ‘S’.
Step 2:Push ‘(’ to stack ‘S’ and add ‘)’ to given infix
expression.
Step 3:Scan infix expression for left to right & repeat
step 4-7 for each element of infix expression until
stack is empty

9. Step 4:If an OPERAND is encountered, add it
to postfix expression.
Step 5:If LEFT PARENTHESIS is encountered
push it into stack .

10. Step 6:If an OPERATOR is encountered, then
a. Repeatedly POP from stack and add
to postfix expression, each operator which
has same or as higher precedence then the
scanned operator.
b.Push the scanned operator to stack
[End of step 6 if structure]

11. Step 7:If a RIGHT PARENTHESIS is encountered
then:
a.Repeatedly POP from stack and add to
postfix expression,until a left parethesis is
encountered.
b.Remove the left parethesis from stack.
[End of step 7 if structure]
[End of step 3 loop]
Step 8:Exit

12. Q:-a+c*(d-e)^(b+c)-f)
Scanned item Stack Postfix expression
(
a ( a
+ (,+ a
c (,+ ac
* (,+,* ac
( (,+,*,( ac
d (,+,*,( acd
- (,+,*,(,- acd
e (,+,*,(,- acde
) (,+,* acde-
^ (,+,*,^ acde-
( (,+,*,^,( acde-
b (,+,*,^,( acde-b
+ (,+,*,^,(,+ acde-b

13. Scanned item Stack Postfix expression
c (,+,*,^,(,+ acde-bc
) (,+,*,^ acde-bc+
- (,- acde—bc+^*+
f (,- acde-bc+*^+f
) acde-bc+*^+f-
Postfix expression is acde-bc+*^+f-