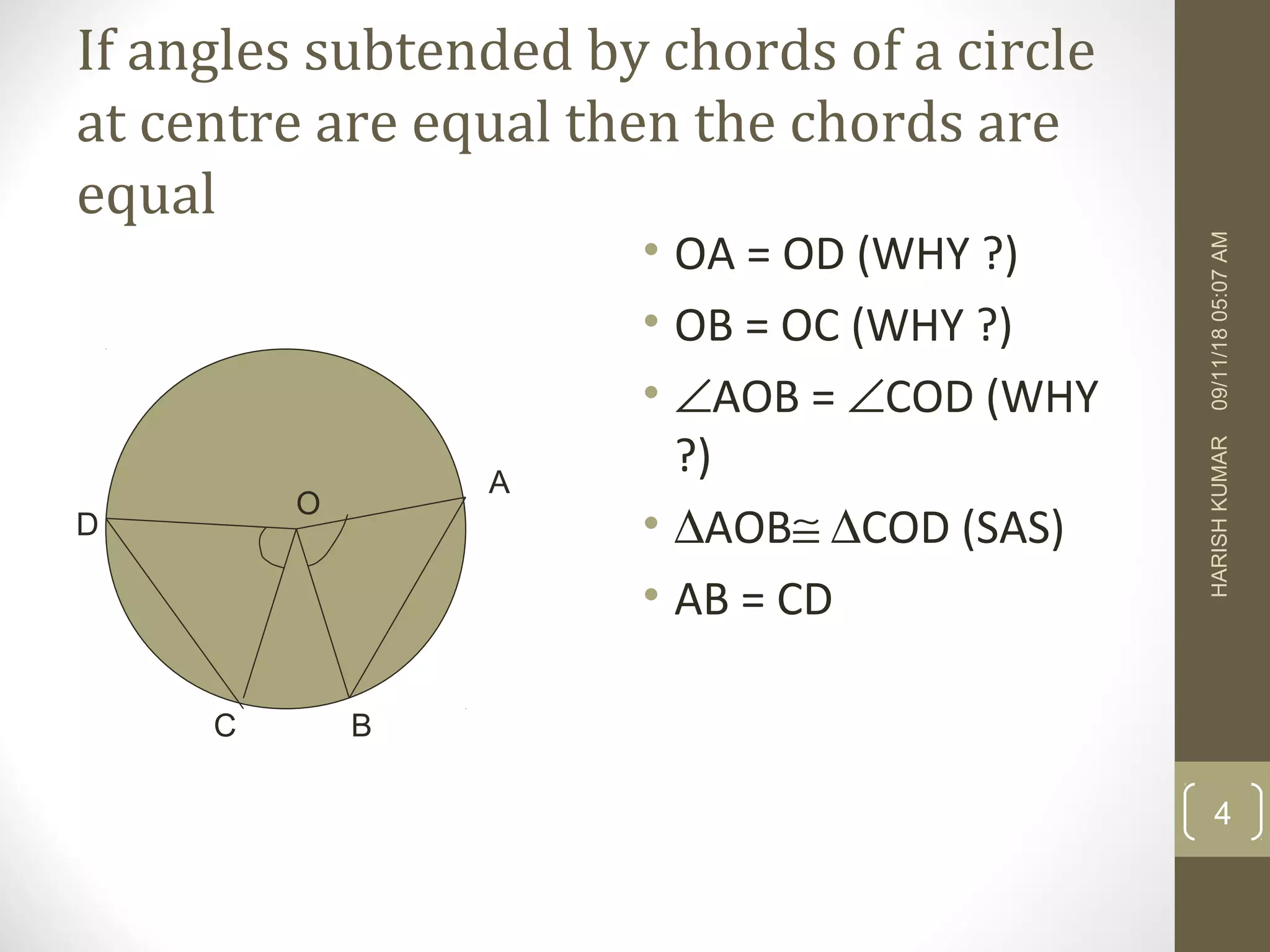
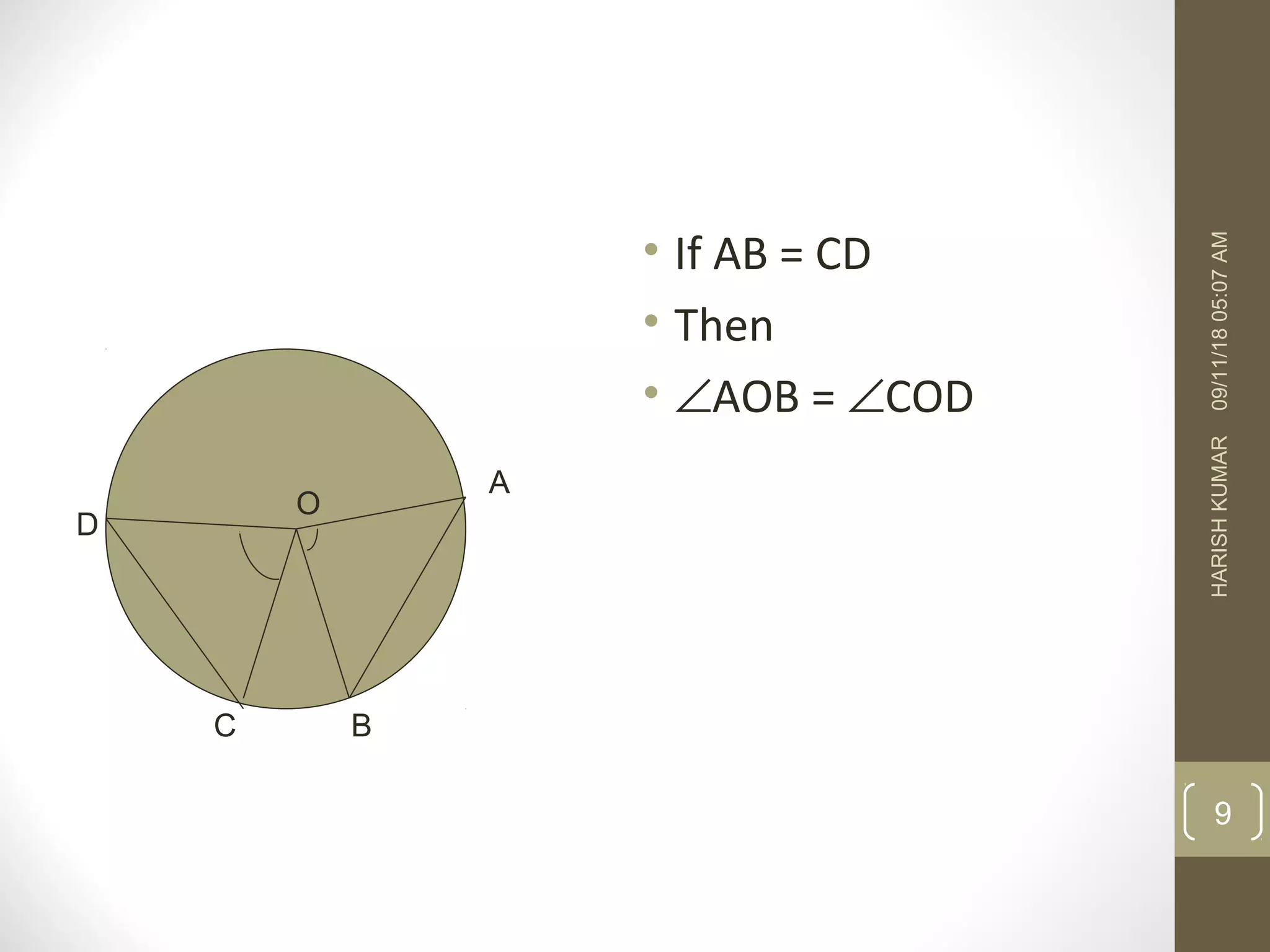
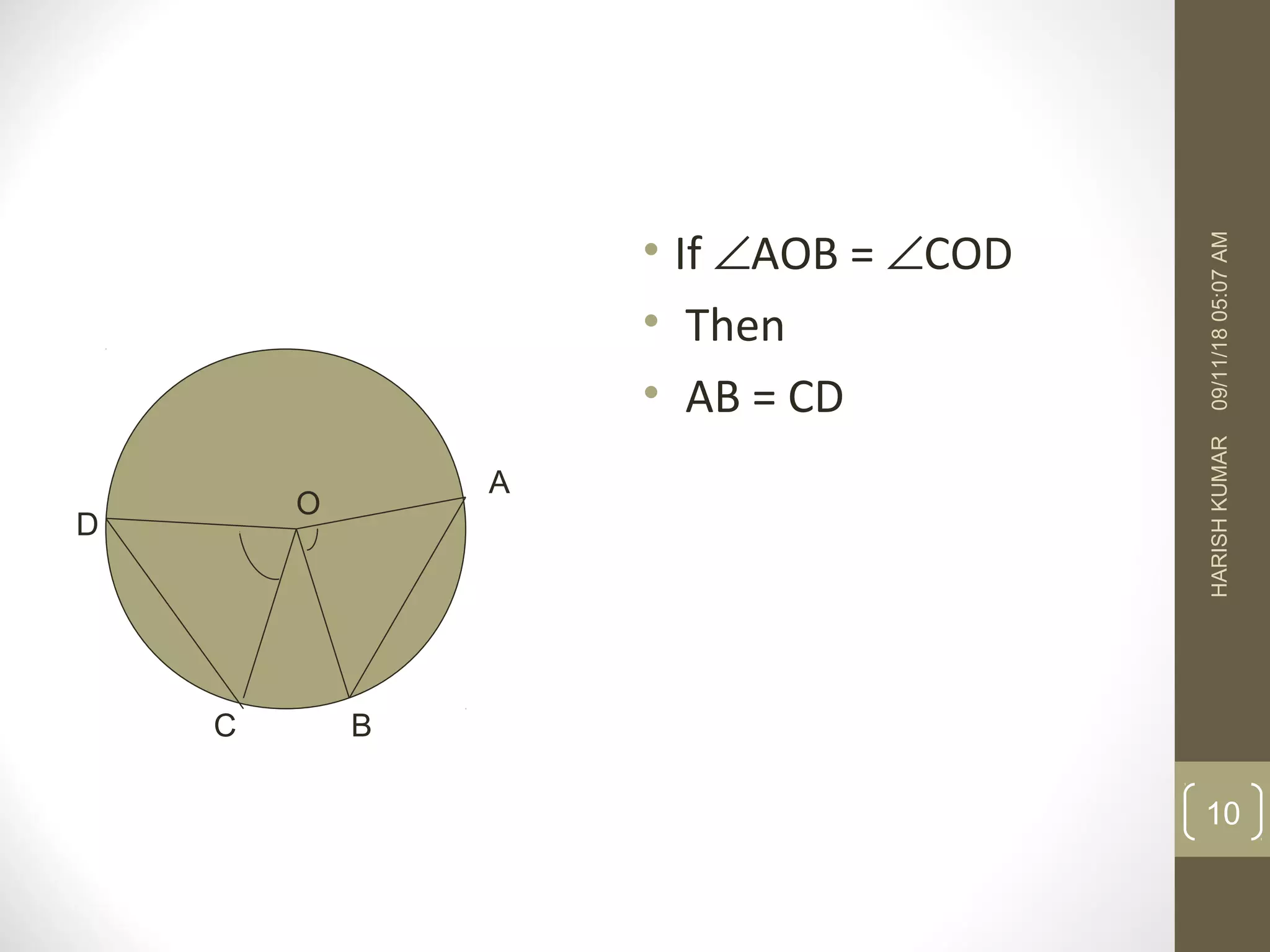
This document discusses properties of circles. It states that equal chords of a circle subtend equal angles at the center. It also notes that if angles subtended by chords at the center are equal, then the chords are equal. Additionally, it mentions that the perpendicular from the center of a circle to a chord bisects the chord, and that the line segment joining the center to the midpoint of a chord is perpendicular to the chord. Finally, it acknowledges that a circle can be drawn through any three non-collinear points.

1. Subject Mathematics
Class IX
•TOPIC
CIRCLES
09/11/1805:07AMHARISHKUMAR
1

2. Angle subtended by a chord at centre of
a circle
09/11/1805:07AMHARISHKUMAR
2

3. Equal chords of a circle subtends equal
angle at centre
• OA = OD (WHY ?)
• OB = OC (WHY ?)
• AB = CD (WHY ?)
• ∆AOB ≅ ∆COD (SSS)
• ∠AOB = ∠COD
09/11/1805:07AMHARISHKUMAR
3
O
BC
D
A

4. If angles subtended by chords of a circle
at centre are equal then the chords are
equal
• OA = OD (WHY ?)
• OB = OC (WHY ?)
• ∠AOB = ∠COD (WHY
?)
• ∆AOB≅ ∆COD (SAS)
• AB = CD
09/11/1805:07AMHARISHKUMAR
4
O
BC
D
A

5. The perpendicular from centre of a
circle to a chord bisects the chord
• OA=OB (WHY ?)
• ∠ OCA=∠OCB
(WHY ?)
• OC=OC (WHY ?)
• ∆ OAC ∆ ≅OBC
(WHY ?)
• AC=BC
09/11/1805:07AMHARISHKUMAR
5
O
A
B
C

6. Line segment joining centre to mid
point of a chord is perpendicular to the
chord
• OA=OB (WHY ?)
• AC=BC (WHY ?)
• OC=OC (WHY ?)
• ∆OAC≅ ∆OBC
(WHY ?)
• ∠ACO= ∠BCO=90
09/11/1805:07AMHARISHKUMAR
6
O
A
B
C

7. Circle through three points
• OA=OB
• OB=OC
• OA=OB=OC
09/11/1805:07AMHARISHKUMAR
7
A
B
C
O

8. SUMMARY
• Equal chords subtend equal angle at centre
• If angle subtended by chords at centre are equal
then chords are equal
• Perpendicular from centre bisects the chord
• Line segment joining mid point of a chord and
centre of circle is perpendicular to the chord
• A circle can be drawn through any three Non
collinear points
09/11/1805:07AMHARISHKUMAR
8

9. • If AB = CD
• Then
• ∠AOB = ∠COD
09/11/1805:07AMHARISHKUMAR
9
O
BC
D
A

10. • If ∠AOB = ∠COD
• Then
• AB = CD
09/11/1805:07AMHARISHKUMAR
10
O
BC
D
A

11. • If OC ⊥ AB
• Then
• AC=BC
09/11/1805:07AMHARISHKUMAR
11
O
A
B
C

12. • IF AC=BC
• THEN
• OC ⊥ AB
09/11/1805:07AMHARISHKUMAR
12
O
A
B
C

13. • Q. From an externl
point P, a tangent PT
and a line segment
PAB is drawn to a
circle with centre O.
ON is perpendicular
on the chord AB.
• Prove that :
• PA.PB = PT2
13
HARISHKUMAR09/11/1805:07AM

14. • Q. If a circle touches
the side BC of a
triangle ABC at P and
extended sides AB
and AC at Q and
R.Prove that
• AQ = ½(BC+CA+AB)
14
HARISHKUMAR09/11/1805:07AM

15. • Q. If a,b,c are the
sides of a right
triangle where c is
the hypotenuse
prove that the radius
r of the circle which
touches the sides of
the triangle is given
by r = (a+b-c)/2
15
HARISHKUMAR09/11/1805:07AM

16. • Q. Angle in alternate
segment.
16
HARISHKUMAR09/11/1805:07AM

17. • Q. AB is a diameter of a circle and chord CD = radius OC. If AC
and BD when produced meet at P prove that angle APB = 60
17
HARISHKUMAR09/11/1805:07AM

18. • Q. Prove that altitudes of a triangle are concurrent.
18
HARISHKUMAR09/11/1805:07AM