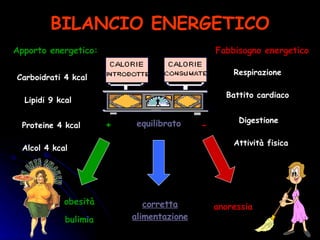
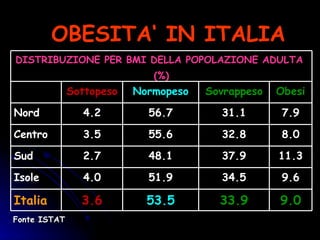
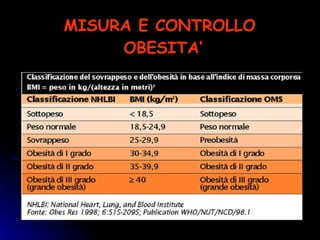
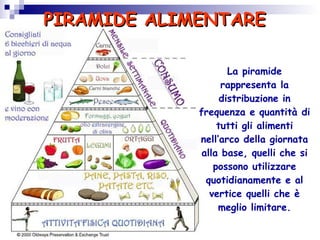
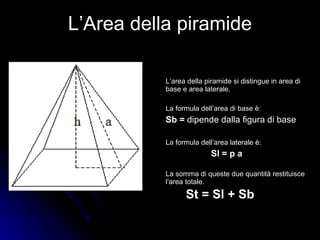
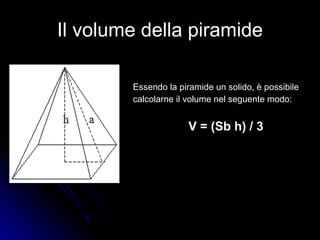
Il documento esplora la piramide alimentare e la sua importanza per una corretta alimentazione, evidenziando la funzione dei vari nutrienti. Discute anche la geometria della piramide, spiegando le sue caratteristiche e formula per il calcolo dell'area e del volume. Infine, presenta un esercizio pratico legato alla costruzione di una piramide con palle di cannone, dimostrando l'applicazione della geometria in situazioni reali.

1. PIRAMIDE: LA GEOMETRIA CHE NUTRE

2. I “MATTONI” DELLA NOSTRA ALIMENTAZIONE: I NUTRIENTI

3. I NUTRIENTI Principi nutritivi più semplici contenuti nei prodotti alimentari PROTEINE O PROTIDI GRASSI O LIPIDI CARBOIDRATI O GLUCIDI O ZUCCHERI VITAMINE SALI MINERALI ACQUA FIBRA ALIMENTARE

4. FUNZIONE NUTRIENTI PROTEINE = funzione plastica GRASSI = funzione energetica CARBOIDRATI = funzione energetica VITAMINE = funzione regolatrice SALI MINERALI = funzione regolatrice ACQUA = funzione idratante FIBRA ALIMENTARE = funzione digestiva

5. IL CORPO UMANO: UNA MACCHINA METABOLICA nutrienti, energia, acqua, anidride carbonica, calore ingestione digestione scissione

6. BILANCIO ENERGETICO Fabbisogno energetico Apporto energetico: Carboidrati 4 kcal Lipidi 9 kcal Proteine 4 kcal Alcol 4 kcal Respirazione Battito cardiaco Digestione Attività fisica equilibrato - + corretta alimentazione obesità bulimia anoressia

7. Fonte ISTAT OBESITA‘ IN ITALIA DISTRIBUZIONE PER BMI DELLA POPOLAZIONE ADULTA (%) Sottopeso Normopeso Sovrappeso Obesi Nord 4.2 56.7 31.1 7.9 Centro 3.5 55.6 32.8 8.0 Sud 2.7 48.1 37.9 11.3 Isole 4.0 51.9 34.5 9.6 Italia 3.6 53.5 33.9 9.0

8. MISURA E CONTROLLO OBESITA‘

9. La piramide rappresenta la distribuzione in frequenza e quantità di tutti gli alimenti nell’arco della giornata alla base, quelli che si possono utilizzare quotidianamente e al vertice quelli che è meglio limitare. PIRAMIDE ALIMENTARE

10. plastici energetici regolatori I gruppo II gruppo III gruppo IV gruppo V gruppo VI gruppo VII gruppo LATTE E DERIVATI Sono ricchi di proteine e di grassi; forniscono anche molti sali minerali, in particolare di calcio. CARNI, PESCI E UOVA Ricchi di proteine ad alto valore biologico, sono i cibi più importanti per la costruzione dei tessuti dell’organismo. Contengono anche molti composti del ferro. LEGUMI SECCHI Hanno caratteri simili al II gruppo, ma sono meno costosi. GRASSI ANIMALI E VEGETALI Forniscono soprattutto carboidrati e sono la fonte principale di energia. Forniscono anche proteine e vitamine del tipo B. CEREALI E DERIVATI Sono alimenti altamente energetici.Sono indispensabili fonti di vitamine tra le quali la A e la K. ORTAGGI E FRUTTA Forniscono vitamine in abbondanza. Ricchi di Sali minerali contengono anche moderate quantità di proteine e glucidi. POMODORI,AGRUMI E FRAGOLE Hanno le stesse caratteristiche del VI gruppo, dal quale si differiscono soprattutto per l’abbondanza di vitamina C.

11. Chiunque pensi che la piramide serva a nutrire solo la pancia, si sbaglia. La piramide è anche un ottimo nutriente per il cervello, infatti…..

12. La piramide in geometria: che cos’è? In geometria si definisce piramide un poliedro individuato da una faccia poligonale chiamata base e da un vertice che non giace sul piano della base e che talora viene chiamato apice della piramide. Sono suoi spigoli i lati del poligono di base e i segmenti delimitati dall'apice e da ciascuno dei vertici della base. Sono facce della piramide la sua base e le facce triangolari che hanno come vertice il suo apice (chiamate facce laterali).

13. La piramide in geometria: che cos’è? Una piramide avente come base un poligono di n lati (n = 3, 4, ...) si dice piramide n-gonale ed ha n+1 facce, 2n spigoli ed n+1 vertici. Una piramide è convessa se e solo se il poligono di base è convesso. Si dice altezza di una piramide il segmento che ha una estremità nell'apice e cade ortogonalmente sul piano contenente la base. Talora viene chiamata piramide obliqua una piramide la cui altezza cade al di fuori del poligono di base (o della sua chiusura convessa). Si dice apotema di una piramide retta con base rettangolare ogni segmento che congiunge il suo apice al punto medio di un suo lato di base, ovvero la loro lunghezza comune.

14. L’Area della piramide St = Sl + Sb L’area della piramide si distingue in area di base e area laterale. La formula dell’area di base è: Sb = dipende dalla figura di base La formula dell’area laterale è: Sl = p a La somma di queste due quantità restituisce l’area totale.

15. Il volume della piramide Essendo la piramide un solido, è possibile calcolarne il volume nel seguente modo: V = (Sb h) / 3

16. Formule inverse Dalle formule viste fin’ora è possibile ricavare quelle inverse. p = Sl / a a = Sl / p Sb = 3V / h h = 3V / Sb

17. La piramide dell’armiere Abbiamo visto la piramide egizia, quella alimentare e quella geometrica ….. Sapevate dell’esistenza della piramide dell’armiere?

18. La piramide dell’armiere In un deposito di munizioni sono ammucchiate alla rinfusa numerose palle di cannone il cui diametro misura 25 centimetri. Il capitano, amante dell’ordine e della geometria, ritiene che con esse si possano formare piramidi a base quadrata, accostando le sfere l’una all’altra e appoggiando quelle degli strati superiori negli interstizi creati da quelle sottostanti. Sebbene ogni palla sia molto pesante e debba essere sollevata con entrambe le mani, l’incarico viene affidato ad un unico armiere. Prima di accingersi all’ingrato compito l’armiere misura le dimensioni dell’arsenale: l’altezza utile dal pavimento al soffitto è pari a 220 centimetri. Quante palle potranno essere, realmente, collocate in ogni piramide?

19. La piramide dell’armiere: soluzione Se si devono formare piramidi a base quadrata, accostando le sfere l’una all’altra e appoggiando quelle degli strati superiori negli interstizi creati da quelle sottostanti, la disposizione è rappresentata in figura.

20. La piramide dell’armiere: soluzione Tale piramide sarebbe alta 219,45437 cm quindi rientrerebbe come altezza in un soffitto alto 220, ci sarebbe però una difficoltà di costruzione perche' per appoggiare l'ultima palla (sempre che il soldato sia abbastanza alto e dotato di braccia lunghe e possenti!) si dovrebbe scavalcare il piano inferiore. Nel momento dello scavalcamento i centri dell'ultima palla con quelle inferiori posti sullo stesso piano verticale formano un triangolo equilatero di lato 25 e altezza 25xsqrt(3)/2 = 21.65 cm, quasi 4 cm in più della posizione finale mentre il soffitto permette una tolleranza di poco superiore al mezzo cm. I piani possibili sarebbero allora 11 e formati da 506 palle.

21. GRAZIE PER L’ATTENZIONE!!