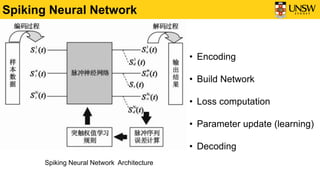
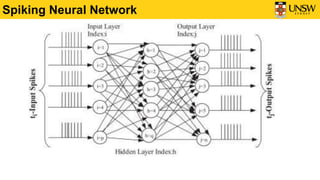
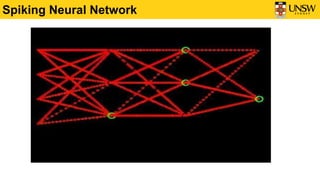
1) The document discusses Spiking Neural Networks (SNNs), which are a type of neural network that more closely mimic biological neural behavior.
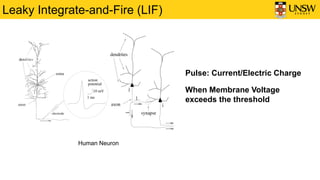
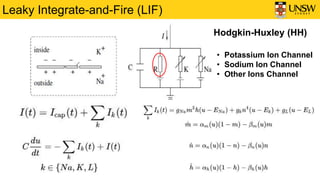
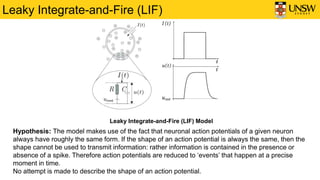
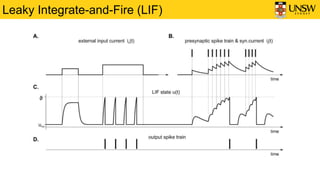
2) It describes the Leaky Integrate-and-Fire (LIF) neuron model, which is commonly used in SNNs. The LIF model integrates inputs over time and generates spikes when the voltage exceeds a threshold.
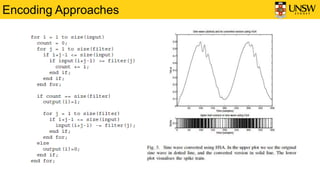
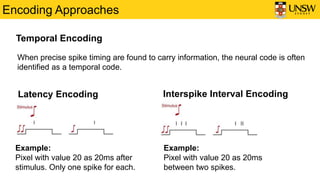
3) Different encoding approaches are discussed for representing input data as spike trains, including rate coding, temporal coding, population coding, and the Hough Spiker Algorithm. These approaches transform real-valued inputs into spike timings.











![Encoding Approaches
Rate Encoding
The rate coding model of neuronal firing communication states that as the intensity
of a stimulus increases, the frequency or rate of action potentials, or "spike firing",
increases.
Example:
Figures with 28x28 size, greyscale ([0 255]).
Pixel value as stimuli frequency
Present for 500ms
Pixel with value 20 as 20Hz generates 10 spikes during present duration.](https://image.slidesharecdn.com/spikingneuralnetworkanintroductioni-180710050240/85/Spiking-neural-network-an-introduction-I-20-320.jpg)

![Encoding Approaches
Population Encoding
Encode an input variable using multiple overlapping Gaussian Receptive Fields
(RF). Gaussian RF are used to generate firing times from real values. For a range
[IMax..IMin] of a variable, which is also called the coding interval, a set of m Gaussian
RF neurons are used.
The center Ci and the width σi of each RF neuron i are determined by the
following equations:
Where m is number of receptive fields in each population and γ is a constant
variable usually 1.5.](https://image.slidesharecdn.com/spikingneuralnetworkanintroductioni-180710050240/85/Spiking-neural-network-an-introduction-I-23-320.jpg)