1.
Seminar Series on
Linear Algebra for Machine Learning
Part 3: Factorization and Linear Transformations
Dr. Ceni Babaoglu
Data Science Laboratory
Ryerson University
cenibabaoglu.com
Dr. Ceni Babaoglu cenibabaoglu.com
Linear Algebra for Machine Learning: Factorization and Linear Transformations

2.
Overview
1 Row and Column Spaces
2 Rank of a Matrix
3 Rank and Singularity
4 Inner Product Spaces
5 Gram-Schmidt Process
6 Factorization
7 Linear Transformation
8 Linear Transformation and Singularity
9 Similar Matrices
10 References
Dr. Ceni Babaoglu cenibabaoglu.com
Linear Algebra for Machine Learning: Factorization and Linear Transformations

3.
Row and Column Spaces
Let
A =





a11 a12 a13 . . . a1n
a21 a22 a23 . . . a2n
...
...
...
...
...
am1 am2 am3 . . . amn





be an m × n matrix.
The rows of A, considered as vectors in Rn, span a subspace
of Rn called the row space of A.
Similarly, the columns of A, considered as vectors in Rm, span
a subspace of Rm called the column space of A.
If A and B are two m × n row (column) equivalent matrices,
then the row (column) spaces of A and B are equal.
Dr. Ceni Babaoglu cenibabaoglu.com
Linear Algebra for Machine Learning: Factorization and Linear Transformations

4.
Rank of a Matrix
The dimension of the row (column) space of A is called the
row (column) rank of A.
The row rank and column rank of the m × n matrix A = [aij ]
are equal.
Dr. Ceni Babaoglu cenibabaoglu.com
Linear Algebra for Machine Learning: Factorization and Linear Transformations

5.
Rank and Singularity
A is nonsingular.
Ax = 0 has only the trivial solution.
A is row (column) equivalent to In.
For every vector b in Rn, the system Ax = b has a unique
solution.
det(A) = 0.
The rank of A is n.
The rows of A form a linearly independent set of vectors in Rn.
The columns of A form a linearly independent set of vectors in
Rn.
Dr. Ceni Babaoglu cenibabaoglu.com
Linear Algebra for Machine Learning: Factorization and Linear Transformations

6.
Example
Let A =


1 −1 2 0 −3
0 1 0 4 0
2 −1 4 4 −6

. Find the following:
(i) A basis for the column space of A and its dimension.
(ii) A basis for the row space of A and its dimension.
Dr. Ceni Babaoglu cenibabaoglu.com
Linear Algebra for Machine Learning: Factorization and Linear Transformations

7.
Example


1 −1 2 0 −3
0 1 0 4 0
2 −1 4 4 −6

 S3−2S1→S3
−−−−−−−→


1 −1 2 0 −3
0 1 0 4 0
0 1 0 4 0


S1+S2→S1
S3−S2→S3
−−−−−−→


1 0 2 4 −3
0 1 0 4 0
0 0 0 0 0


(i) The column space of A is spanned by the vectors (1, 0, 2)T
and
(−1, 1, −1)T
. These vectors are linearly independent.
{(1, 0, 2)T
, (−1, 1, −1)T
} is a basis for this space and its dimension is 2.
(ii) The row space of A is spanned by the vectors (1, 0, 2, 4, −3) and
(0, 1, 0, 4, 0). These vectors are linearly independent.
{(1, 0, 2, 4, −3), (0, 1, 0, 4, 0)} is a basis for this space and its
dimension is 2.
Dr. Ceni Babaoglu cenibabaoglu.com
Linear Algebra for Machine Learning: Factorization and Linear Transformations

8.
Inner Product Spaces
Let V be a real vector space. An inner product on V is a function
that assigns to each ordered pair of vectors u, v in V real number
(u, v) satisfying the following properties:
(u, u) ≥ 0, (u, u) = 0 if and only if u = 0v
(v, u) = (u, v) for any u, v in V
(u + v, w) = (u, w) + (v, w) for any u, v, w in V
(cu, v) = c(u, v) for u, v in V and c, a real scalar
A real vector space that has an inner product defined on it is
called an inner product space. If the space is finite
dimensional it is called a Euclidean space.
In an inner product space we define the length of
a vector u by u = (u, u).
Dr. Ceni Babaoglu cenibabaoglu.com
Linear Algebra for Machine Learning: Factorization and Linear Transformations

9.
Gram-Schmidt Process
Let V be an inner product space and W = {0} an m-dimensional
subspace of V . Then there exists an orthonormal basis
T = {w1, w2, · · · , wm} for W .
Let S = {u1, u2, · · · , um} be any basis for W . Construct an
orthogonal basis T∗ = {v1, v2, · · · , vm} for W. Select any one of
the vectors in S, say u1 and call it v1. Look for a vector v2 in the
subspace W1 of W spanned by {u1, u2} that is orthogonal to v1.
v2 = u2 −
(u2, v1)
(v1, v1)
v1
Dr. Ceni Babaoglu cenibabaoglu.com
Linear Algebra for Machine Learning: Factorization and Linear Transformations

10.
Gram-Schmidt Process
Next, we look for a vector v3 in the subspace W2 of W spanned by
{u1, u2, u3} that is orthogonal to both v1 and v2.
v2 = u2 −
(u2, v1)
(v1, v1)
v1
v3 = u3 −
(u3, v1)
(v1, v1)
v1 −
(u3, v2)
(v2, v2)
v2
Dr. Ceni Babaoglu cenibabaoglu.com
Linear Algebra for Machine Learning: Factorization and Linear Transformations

11.
Example
Let’s use the Gram-Schmidt process to find an orthonormal basis
for the subspace of R4 with basis u1 = (1, 1, 1, 0)T ,
u2 = (−1, 0, −1, 1)T and u3 = (−1, 0, 0, −1)T . First let v1 = u1,
v2 = u2 −
(u2, v1)
(v1, v1)
v1 =




−1
0
−1
1



 − (−
2
3
)




1
1
1
1



 =




−1/3
2/3
−1/3
1




Multiplying v2 by 3 to clear fractions, we get




−1
2
−1
3




Dr. Ceni Babaoglu cenibabaoglu.com
Linear Algebra for Machine Learning: Factorization and Linear Transformations

12.
Example
v3 = u3 −
(u3, v1)
(v1, v1)
v1 −
(u3, v2)
(v2, v2)
v2 =




−4/5
3/5
1/5
−3/5




Multiplying v3 by 5 to clear fractions, we get (−4, 3, 1, −3)T . An
orthogonal basis:
{v1, v2, v3} =




1
1
1
0



 ,




−1
2
−1
3



 ,




−4
3
1
−3




An orthonormal basis:
{w1, w2, w3} =




1/
√
3
1/
√
3
1/
√
3
0



 ,




−1/
√
15
2/
√
15
−1/
√
15
3/
√
15



 ,




−4/
√
35
3/
√
35
1/
√
35
−3/
√
35




Dr. Ceni Babaoglu cenibabaoglu.com
Linear Algebra for Machine Learning: Factorization and Linear Transformations

13.
Factorization
If A is an m × n matrix with linearly independent columns, then A
can be factored as
A = QR,
Q: an m × n matrix whose columns form an orthonormal basis for
the column space of A,
R: an n × n nonsingular upper triangular matrix.
Dr. Ceni Babaoglu cenibabaoglu.com
Linear Algebra for Machine Learning: Factorization and Linear Transformations

14.
Example
Let’s find the factorization of




1 −1 −1
1 0 0
1 −1 0
0 1 −1



 .
Let’s define the columns of A as the vectors u1, u2, u3.
The orthonormal basis for the column space of A is
w1 =




1/
√
3
1/
√
3
1/
√
3
0



 , w2 =




−1/
√
15
2/
√
15
−1/
√
15
3/
√
15



 , w3 =




−4/
√
35
3/
√
35
1/
√
35
−3/
√
35



 .
Dr. Ceni Babaoglu cenibabaoglu.com
Linear Algebra for Machine Learning: Factorization and Linear Transformations

15.
Example
Q =




1/
√
3 −1/
√
15 −4/
√
35
1/
√
3 2/
√
15 3/
√
35
1/
√
3 −1/
√
15 1/
√
35
0 3/
√
15 −3/
√
35




R =


r11 r12 r13
0 r22 r23
0 0 r33


where rji = (ui , wj ).
R =


3/
√
3 −2/
√
3 −1/
√
3
0 5/
√
15 −2/
√
15
0 0 7/
√
35


A = QR
Dr. Ceni Babaoglu cenibabaoglu.com
Linear Algebra for Machine Learning: Factorization and Linear Transformations

16.
Linear Transformation
A mapping L : V −→ W is said to be a linear transformation or a
linear operator if
L(αv1 + βv2) = αL(v1) + βL(v2)
OR
L(v1 + v2) = L(v1) + L(v2), (α = β = 1)
L(αv) = αL(v) (v = v1, β = 0)
Dr. Ceni Babaoglu cenibabaoglu.com
Linear Algebra for Machine Learning: Factorization and Linear Transformations

17.
Example
L(x) = 3x, x ∈ R2
.
L(x + y) = 3(x + y) = L(x + y)
L(αx) = 3(αx) = αL(x)
L is a linear transformation.
α : positive scalar
F(x) = αx can be thought of as a stretching or shrinking by a
factor of α.
Dr. Ceni Babaoglu cenibabaoglu.com
Linear Algebra for Machine Learning: Factorization and Linear Transformations

18.
Example
L(x) = x1e1, x ∈ R2
.
If x = (x1, x2)T
, then L(x) = (x, 0)T
If y = (y1, y2)T
, then αx + βy =
αx1 + βy1
αx2 + βy2
L(αx + βy) = (αx1 + βy1)e1 = α(x1e1) + β(y1e1) = αL(x) + βL(y)
L is a linear transformation, a projection onto the x1 axis.
Dr. Ceni Babaoglu cenibabaoglu.com
Linear Algebra for Machine Learning: Factorization and Linear Transformations

19.
Example
L(x) = (−x2, x1)T , x = (x1, x2)T ∈ R2.
L(αx + βy) =
−(αx2 + βy2)
αx1 + βy1
= α
−x2
x1
+ β
−y2
y1
= αL(x) + βL(y)
L is a linear transformation. It has the effect of rotating each vector in R2
by
90◦
in the counterclockwise direction.
Dr. Ceni Babaoglu cenibabaoglu.com
Linear Algebra for Machine Learning: Factorization and Linear Transformations

20.
Example
M(x) = (x2
1 + x2
2 )1/2, M : R2 −→ R.
M(αx) = (α2
x2
1 + α2
x2
2 )1/2
=| α | M(x),
αM(x) = M(αx), α < 0, x = 0.
M is not a linear transformation.
Dr. Ceni Babaoglu cenibabaoglu.com
Linear Algebra for Machine Learning: Factorization and Linear Transformations

21.
Linear One-to-one Transformations
A linear transformation L : V → W is called one-to-one if it is
a one-to-one function; that is, if v1 = v2 implies that
L(v1) = L(v2).
An equivalent statement is that L is one-to-one if
L(v1) = L(v2) implies that v1 = v2.
Dr. Ceni Babaoglu cenibabaoglu.com
Linear Algebra for Machine Learning: Factorization and Linear Transformations

22.
Linear Onto Transformations
If L : V → W is a linear transformation of a vector space V
into a vector space W , then the range of L or image of V
under L, denoted by range L , consists of all those vectors in
W that are images under L of vectors in V .
Thus w is in range L if there exists some vector v in V such
that L(v) = w. The linear transformation L is called onto if
range L = W .
Dr. Ceni Babaoglu cenibabaoglu.com
Linear Algebra for Machine Learning: Factorization and Linear Transformations

23.
Linear Transformation and Singularity
A is nonsingular.
Ax = 0 has only the trivial solution.
A is row (column) equivalent to In.
For every vector b in Rn, the system Ax = b has a unique
solution.
det(A) = 0.
The rank of A is n.
The rows of A form a linearly independent set of vectors in Rn.
The columns of A form a linearly independent set of vectors in
Rn.
The linear transformation L : Rn −→ Rn defined by
L(x) = A(x), for x in Rn, is one-to-one and onto.
Dr. Ceni Babaoglu cenibabaoglu.com
Linear Algebra for Machine Learning: Factorization and Linear Transformations

24.
Similar Matrices
If A and B are n × n matrices, we say that B is similar to A if
there is a nonsingular matrix P such that B = P−1AP.
Let V be any n−dimensional vector space and let A and B be
any n × n matrices. Then A and B are similar if and only if A
and B represent the same linear transformation L : V → V
with respect to two ordered bases for V .
If A and B are similar n × n matrices, then rank A = rank B.
Dr. Ceni Babaoglu cenibabaoglu.com
Linear Algebra for Machine Learning: Factorization and Linear Transformations

25.
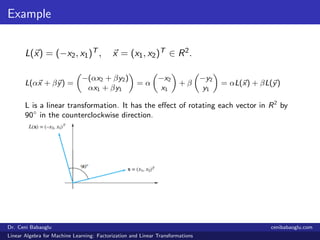
Example
Let L : R3 → R3 be defined by
L([ u1 u2 u3 ]) = [ 2u1 − u3 u1 + u2 − u3 u3 ]
and S = {[1 0 0], [0 1 0], [0 0 1]} be the natural basis
for R3. The representation of L with respect of S is
A =


2 0 −1
1 1 −1
0 0 1

 .
Considering S = {[1 0 1], [0 1 0], [1 1 0]} as ordered
bases for R3, the transition matrix P from S to S is
P =


1 0 1
0 1 1
1 0 0

 P−1
=


0 0 1
−1 1 1
1 0 −1

 .
Dr. Ceni Babaoglu cenibabaoglu.com
Linear Algebra for Machine Learning: Factorization and Linear Transformations

26.
Example
Then the representation of L with respect to S is
B = P−1
AP =


1 0 0
0 1 0
0 0 2


The matrices
A =


2 0 −1
1 1 −1
0 0 1

 and B =


1 0 0
0 1 0
0 0 2


are similar.
Dr. Ceni Babaoglu cenibabaoglu.com
Linear Algebra for Machine Learning: Factorization and Linear Transformations

27.
References
Linear Algebra With Applications, 7th Edition
by Steven J. Leon.
Elementary Linear Algebra with Applications, 9th Edition
by Bernard Kolman and David Hill.
Dr. Ceni Babaoglu cenibabaoglu.com
Linear Algebra for Machine Learning: Factorization and Linear Transformations