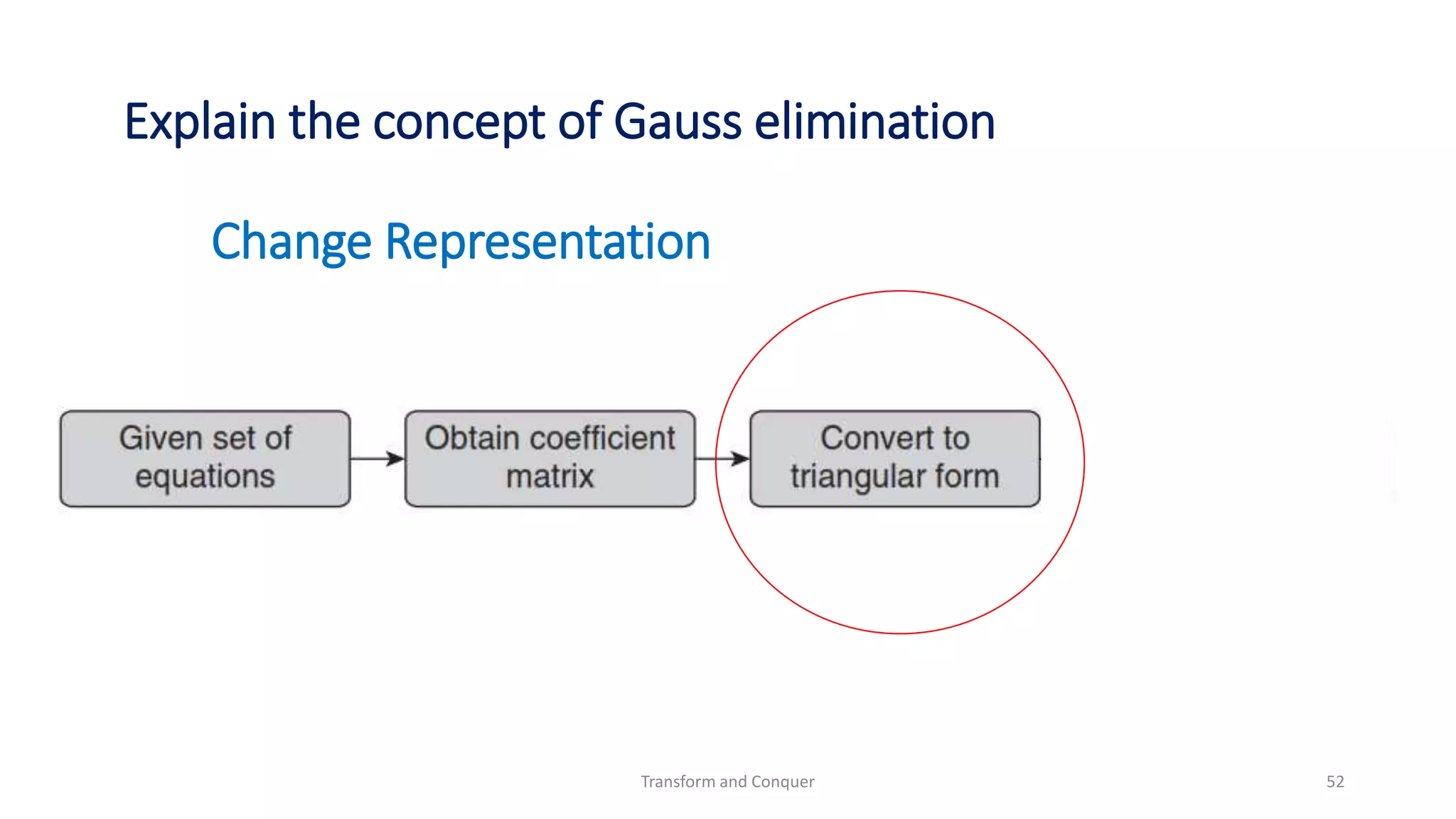
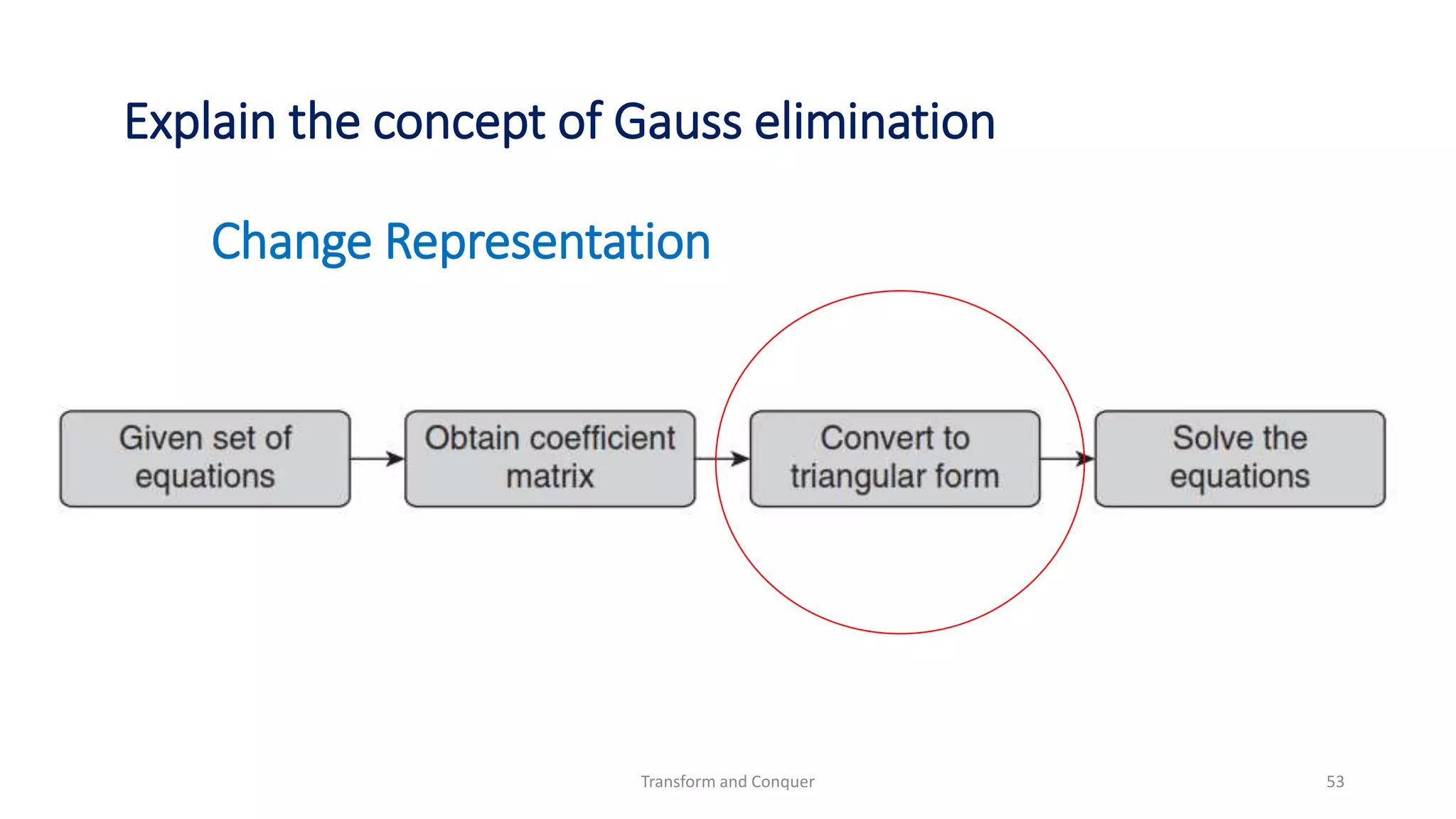
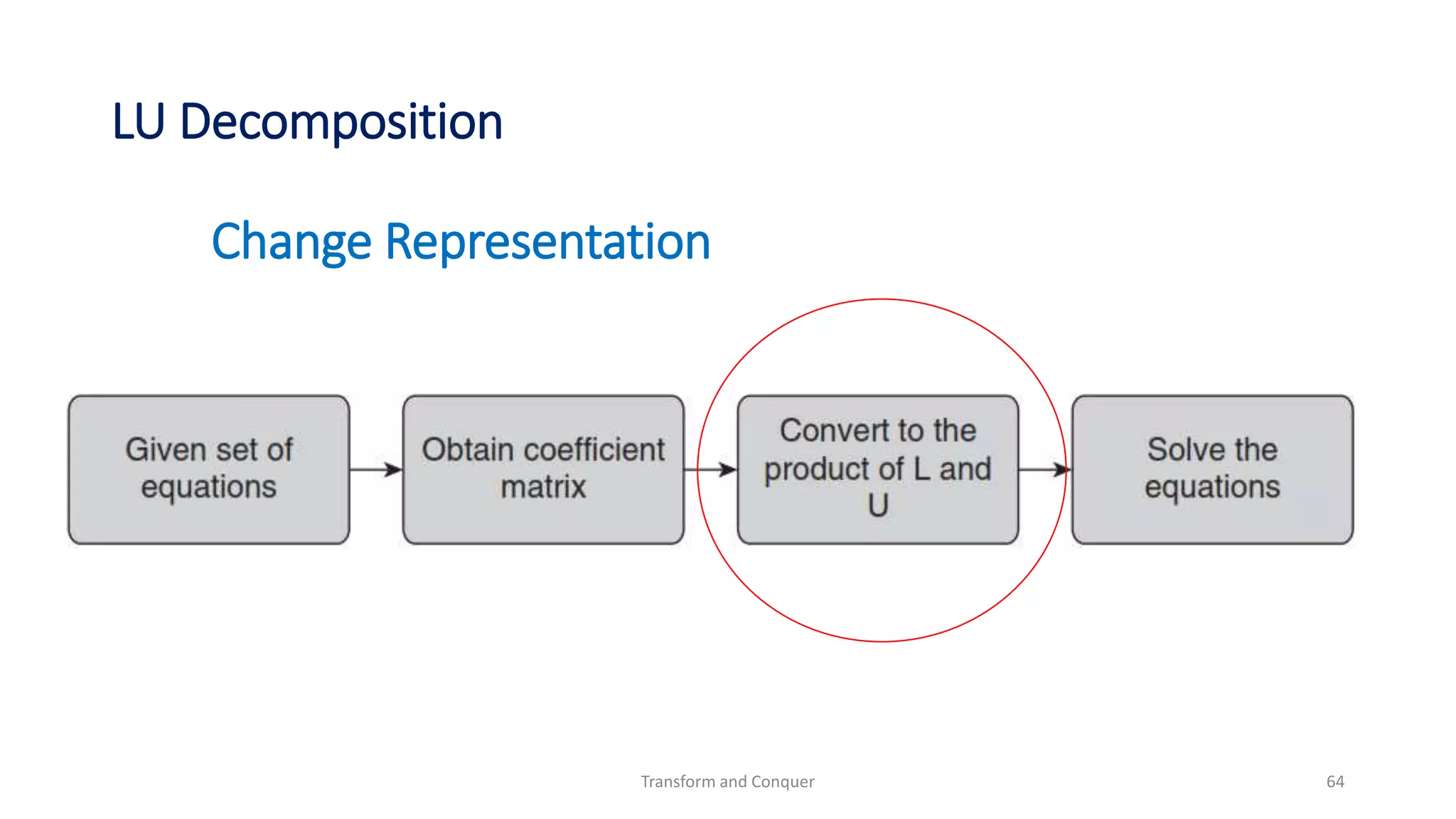
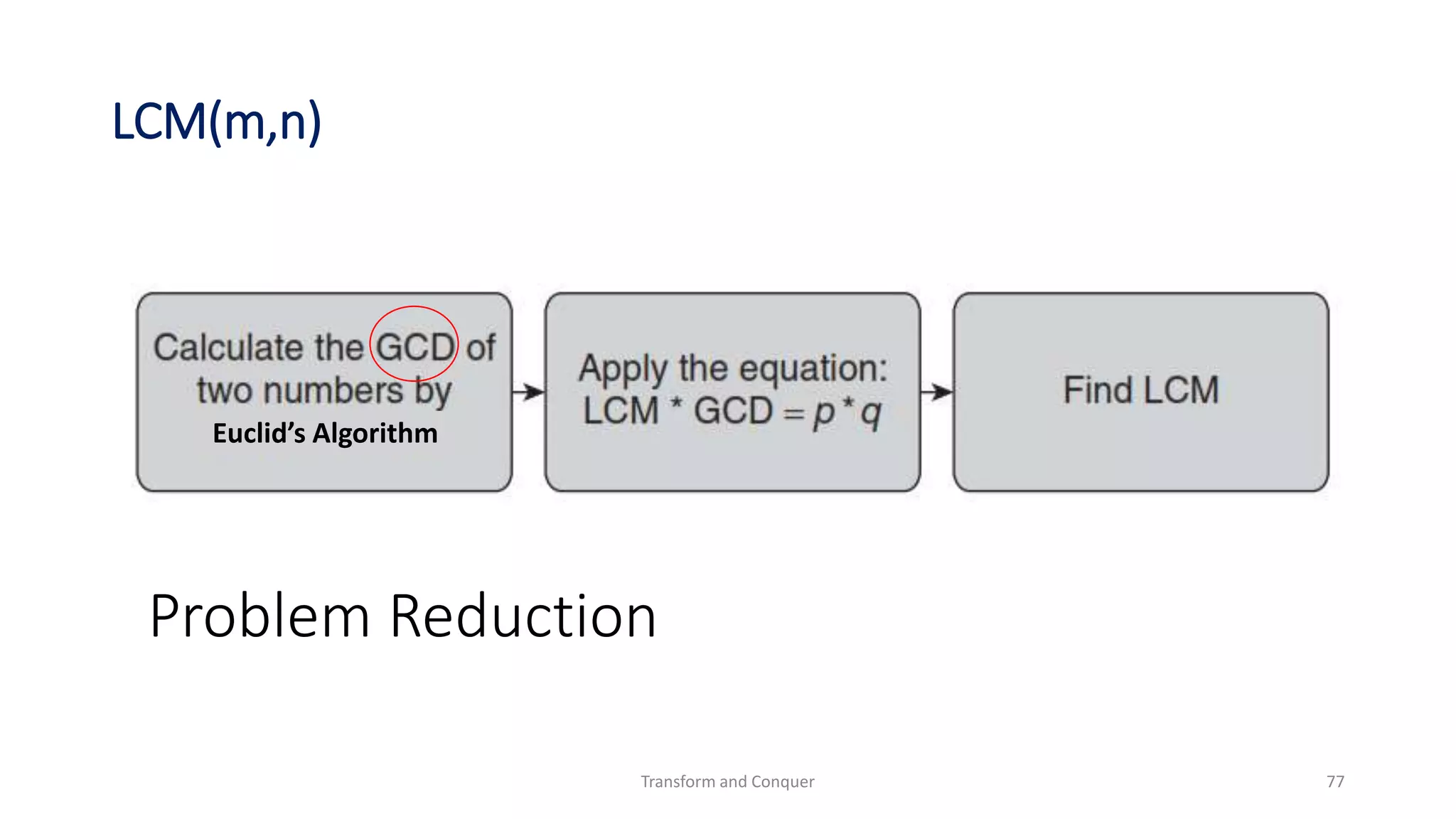
The document discusses the concept of 'transform and conquer' in algorithm design, detailing applications such as presorting, Gaussian elimination, Horner's rule for polynomial evaluation, and finding the least common multiple. It outlines methods for simplifying instances, changing representations, and problem reduction while analyzing the computational complexity of various algorithms. Numerous algorithms and examples are presented to illustrate these concepts and their applications.

1. By: Abdulrazak Zakieh
1Transform and Conquer

2. • Understand the concept of transform and conquer
• List the applications of presorting
• Explain the concept of Gauss elimination
• Use Horner’s rule for evaluating polynomials
• Find the lowest common multiple of two numbers
2Transform and Conquer

3. • Understand the concept of transform and conquer
• List the applications of presorting
• Explain the concept of Gauss elimination
• Use Horner’s rule for evaluating polynomials
• Find the lowest common multiple of two numbers
3Transform and Conquer

4. Understand the concept of transform and conquer
4Transform and Conquer

5. Understand the concept of transform and conquer
5Transform and Conquer

6. Understand the concept of transform and conquer
6
Minimize Complication
Transform and Conquer

7. Understand the concept of transform and conquer
7
•Instance Simplification
•Change Representation
•Problem Reduction
Transform and Conquer

8. • Understand the concept of transform and conquer
• List the applications of presorting
• Explain the concept of Gauss elimination
• Use Horner’s rule for evaluating polynomials
• Find the lowest common multiple of two numbers
8Transform and Conquer

9. 9
Presorting
Instance Simplification
Input Sorted Input Find Solution
Transform and Conquer

10. 10
Presorting
• Find if there is any repeated member
• Search
• Find mode
• Find frequencies
• Find the median
• …
Transform and Conquer

11. Presorting
11
15 3 4 -12 2
Find if there is any repeated member:
Transform and Conquer

12. Presorting
12
15 0 4 -12 2
Find if there is any repeated member:
Transform and Conquer

13. Presorting
13
15 0 4 -12 2
Find if there is any repeated member:
Transform and Conquer

14. Presorting
14
15 0 4 -12 2
Find if there is any repeated member:
Transform and Conquer

15. Presorting
15
15 0 4 -12 2
Find if there is any repeated member:
Transform and Conquer

16. Presorting
16
15 0 4 -12 2
Find if there is any repeated member:
Transform and Conquer

17. Presorting
17
15 3 4 -12 2
Find if there is any repeated member:
Transform and Conquer

18. Presorting
18
15 3 4 -12 2
Find if there is any repeated member:
Transform and Conquer

19. Presorting
19
15 3 4 -12 2
Find if there is any repeated member:
Transform and Conquer

20. Presorting
20
15 3 4 -12 2
Find if there is any repeated member:
Transform and Conquer

21. Presorting
21
15 3 4 -12 2
Find if there is any repeated member:
Transform and Conquer

22. Presorting
22
15 3 4 -12 2
Find if there is any repeated member:
Transform and Conquer

23. Presorting
23
15 3 4 -12 2
Find if there is any repeated member:
Transform and Conquer

24. Presorting
24
15 3 4 -12 2
Find if there is any repeated member:
Transform and Conquer

25. Presorting
25
15 3 4 -12 2
Find if there is any repeated member:
Transform and Conquer

26. Presorting
26
Find if there is any repeated member:
Algorithm:
Compare each pair and stop when finding repetition or
when all pairs are checked
Complication:
O(n2)
Transform and Conquer

27. Presorting
27
-12 2 3 4 15
Find if there is any repeated member:
1. Sort the list
Transform and Conquer

28. Presorting
28
-12 2 3 4 15
Find if there is any repeated member:
1. Linear scan for repeated members (Consequent)
Transform and Conquer

29. Presorting
29
-12 2 3 4 15
Find if there is any repeated member:
1. Linear search for repeated members (Consequent)
Transform and Conquer

30. Presorting
30
-12 2 3 4 15
Find if there is any repeated member:
1. Linear search for repeated members (Consequent)
Transform and Conquer

31. Presorting
31
-12 2 3 4 15
Find if there is any repeated member:
1. Linear search for repeated members (Consequent)
Transform and Conquer

32. Presorting
32
-12 2 3 4 15
Find if there is any repeated member:
1. Linear search for repeated members (Consequent)
Transform and Conquer

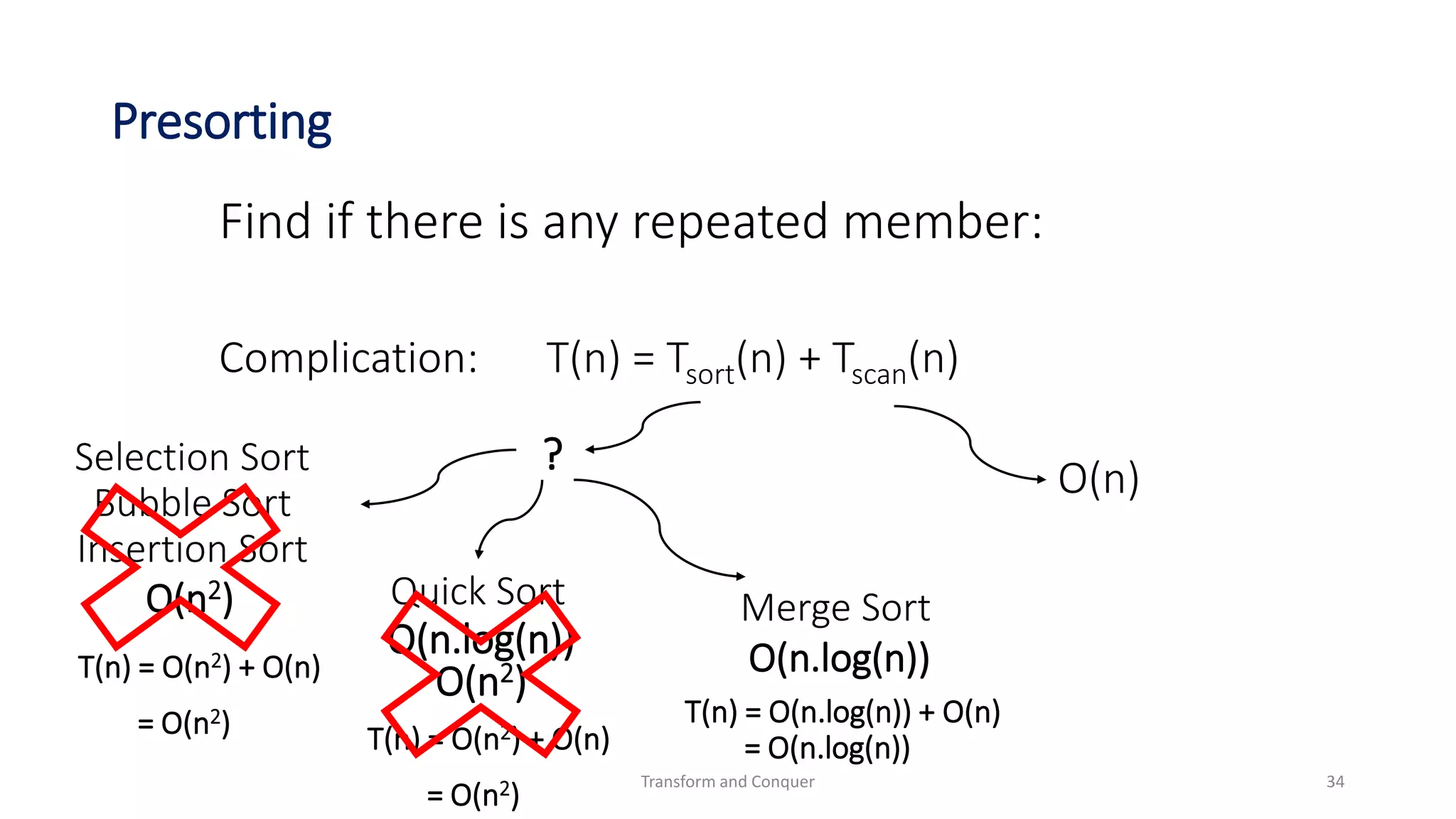
33. Presorting
33
Find if there is any repeated member:
Algorithm:
1. Sort the list
2. For i = 0 to n – 2:
2.1 if a[i] = a[i + 1] then return false
3. return true
Complication:
T(n) = Tsort(n) + Tscan(n)
Transform and Conquer

34. Presorting
34
Find if there is any repeated member:
Complication: T(n) = Tsort(n) + Tscan(n)
O(n)
?Selection Sort
Bubble Sort
Insertion Sort
O(n2) Merge Sort
O(n.log(n))
Quick Sort
O(n.log(n))
O(n2)T(n) = O(n2) + O(n)
= O(n2) T(n) = O(n.log(n)) + O(n)
= O(n.log(n))T(n) = O(n2) + O(n)
= O(n2)
Transform and Conquer

35. Presorting
35
15 3 4 -12 2
Searching: find 6
Transform and Conquer

36. Presorting
36
15 3 4 -12 2
Searching: find 6
Transform and Conquer

37. Presorting
37
15 3 4 -12 2
Searching: find 6
Transform and Conquer

38. Presorting
38
15 3 4 -12 2
Searching: find 6
Transform and Conquer

39. Presorting
39
15 3 4 -12 2
Searching: find 6
Transform and Conquer

40. Presorting
40
15 3 4 -12 2
Searching: find 6
Transform and Conquer

41. Presorting
41
Searching
Algorithm:
Linear search
Complication:
O(n)
Transform and Conquer

42. Presorting
42
-12 2 3 4 15
Searching
1. Sort the list
Transform and Conquer

43. Presorting
43
-12 2 3 4 15
Searching
2. Use binary search
Transform and Conquer

44. Presorting
44
Searching
Algorithm:
1. Sort the list
2. Binary Search
Complication:
T(n) = Tsort(n) + TBinarySearch(n)
Transform and Conquer

45. Presorting
45
Searching
Algorithm:
1. Sort the list
2. Binary Search
Complication:
T(n) = O(n.log(n)) + O(log(n))
Transform and Conquer

46. Presorting
46
Searching
Algorithm:
1. Sort the list
2. Binary Search
Complication:
T(n) = O(n.log(n))
Transform and Conquer

47. Presorting
47
Searching
Algorithm:
1. Sort the list
2. Binary Search
Complication:
T(n) = O(n.log(n))
Transform and Conquer

48. Presorting
48
Searching
Search 100 times in array with 1000 members:
With out presorting With presorting
100 * O(n) O(n.log(n)) + 100. O(log(n))
100,000 1000 * 3 + 100 * 3 = 3300
Transform and Conquer

49. • Understand the concept of transform and conquer
• List the applications of presorting
• Explain the concept of Gauss elimination
• Use Horner’s rule for evaluating polynomials
• Find the lowest common multiple of two numbers
49Transform and Conquer

50. Explain the concept of Gauss elimination
50
Change Representation
Transform and Conquer

51. Explain the concept of Gauss elimination
51
Change Representation
Transform and Conquer

52. Explain the concept of Gauss elimination
52
Change Representation
Transform and Conquer

53. Explain the concept of Gauss elimination
53
Change Representation
Transform and Conquer

54. Explain the concept of Gauss elimination
54Transform and Conquer

55. Explain the concept of Gauss elimination
55Transform and Conquer

56. Explain the concept of Gauss elimination
56Transform and Conquer

57. Explain the concept of Gauss elimination
57
Augmented
Array
2 3 4 9
3 2 1 6
1 2 1 4
Transform and Conquer

58. Explain the concept of Gauss elimination
58
2 3 4 9
0 5 10 15
0 1 -2 -1
Transform and Conquer

59. Explain the concept of Gauss elimination
59
2 3 4 9
0 5 10 15
0 0 -20 -20
Transform and Conquer

60. Explain the concept of Gauss elimination
60
2 3 4 9
0 5 10 15
0 0 -20 -20
Solve By back
substitution
Transform and Conquer

61. Explain the concept of Gauss elimination
61
2 3 4 9
0 5 10 15
0 0 -20 -20
Solve By back
substitution
Z = 1
Y = 1
X = 1
Transform and Conquer

62. Gauss elimination
62
Algorithm:
Transform and Conquer

63. Gauss elimination
63
Algorithm:
Complication
T(n) = O(n3)
Transform and Conquer

64. LU Decomposition
64
Change Representation
Transform and Conquer

65. • Understand the concept of transform and conquer
• List the applications of presorting
• Explain the concept of Gauss elimination
• Use Horner’s rule for evaluating polynomials
• Find the lowest common multiple of two numbers
65Transform and Conquer

66. Horner’s Rule
66
Used for Evaluating Polynomials.
Change Representation
Transform and Conquer

67. Horner’s Rule
67
Multiply by coefficients
Complication:
O(n2)
Transform and Conquer

68. Horner’s Rule
68Transform and Conquer

69. Horner’s Rule
69Transform and Conquer

70. 70
Algorithm:
Complication: T(n) = O(n)
0
i+1
i + 1
i < n
Horner’s Rule
Transform and Conquer

71. • Understand the concept of transform and conquer
• List the applications of presorting
• Explain the concept of Gauss elimination
• Use Horner’s rule for evaluating polynomials
• Find the lowest common multiple of two numbers
71Transform and Conquer

72. LCM(m,n)
72Transform and Conquer
The smallest integer that is divisible by both m and n

73. LCM(m,n)
73Transform and Conquer

74. LCM(m,n)
74Transform and Conquer

75. LCM(m,n)
75Transform and Conquer
Calculate GCD using Euclid’s Algorithm

76. LCM(m,n)
76Transform and Conquer

77. LCM(m,n)
77Transform and Conquer
Euclid’s Algorithm
Problem Reduction

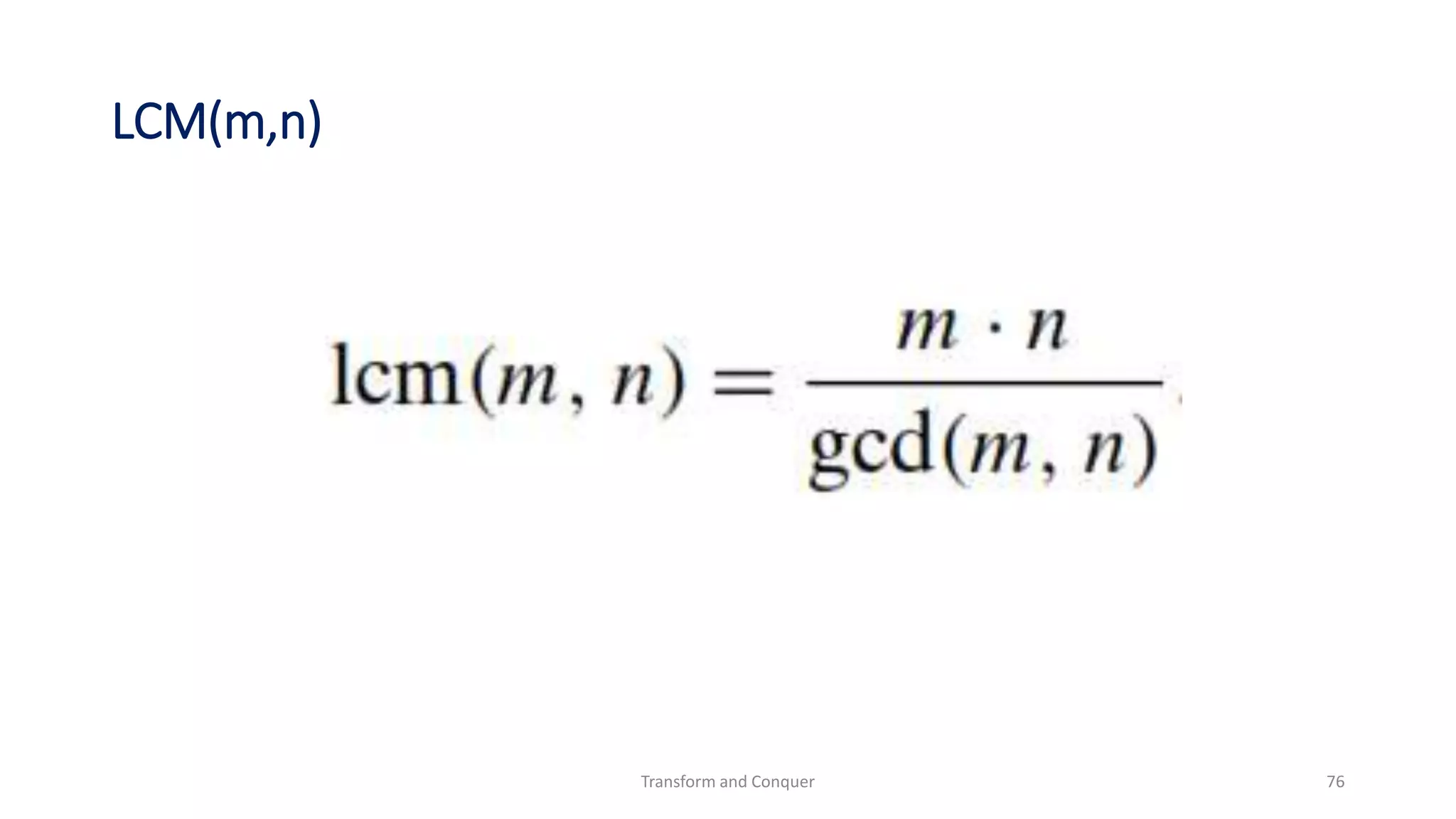
78. Resources
78Transform and Conquer
Algorithms_design and analysis [Harsh Bhasin] chapter 15.
Levitin A.-Introduction to the design and analysis of
algorithms-AW (2011) [Anany Levitin] chapter 6.

79. Transform and Conquer 79
Thanks for your listening