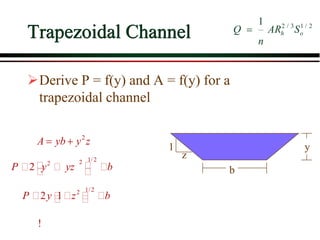
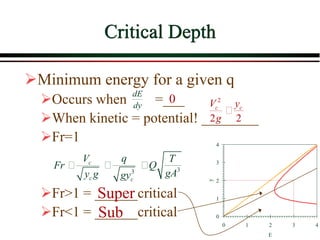
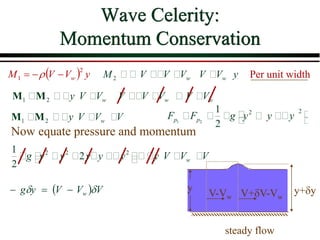
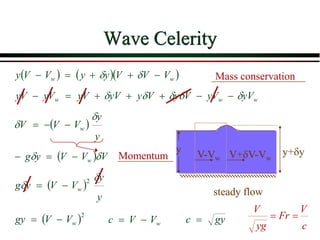
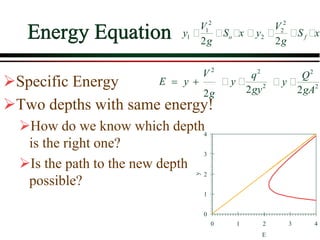
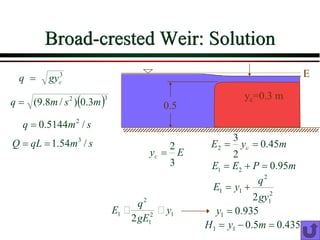
This document discusses open channel flow, including: 1) Key parameters like hydraulic radius, channel roughness, and types of flow profiles. 2) Empirical equations for open channel flow including Chezy and Manning's equations. 3) Concepts of critical flow including critical depth, specific energy, and the importance of the Froude number. 4) Measurement techniques for discharge like weirs and sluice gates. 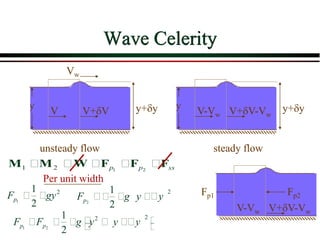5) Gradually and rapidly varied flow, water surface profiles, and hydraulic jumps.

1. Monroe L. Weber-Shirk
School of Civil and
Environmental Engineering
Open Channel Flow

2.  Liquid (water) flow with a (interface between water
and air)
relevant for:
natural channels: rivers, streams
engineered channels: canals, sewer
lines or culverts (partially full), storm drains
Open Channel Flow
Geometric Parameters :
1) Hydraulic Radius (Rh)
2) Channel Length (l)
3) Roughness (e)
P
A
Rh 

3. Steady and Unsteady:
Steady: velocity at a given point does not change with
time
Uniform, Gradually Varied, and Rapidly Varied
Uniform: velocity at a given time does
Gradually varied: gradual changes in velocity with
distance
Laminar and Turbulent
Laminar: No mixing of layers.
Turbulent: Mixing of layers
TYPES OF FLOWS

4. Chezy Equation (1768)
Introduced by the French engineer Antoine
Chezy in 1768 while designing a canal for
the water-supply system of Paris
h fV C R S
where C = Chezy coefficient
4 hd R
For a pipe
C=(8g/f)^(1/2)

5. Robert –Manning improved Work
Upon Chezy’s Equation and gave:
V(m/s)=1/n[Rh]^(2/3) S^(1/2)
V(ft/s)=1.486/n [Rh]^(2/3) S^(1/2)
These are emprical formulas
Where “n” is manning co-efficent

6. Values of Manning “n”
Lined Canals n
Cement plaster 0.011
Untreated gunite 0.016
Wood, planed 0.012
Wood, unplaned 0.013
Concrete, trowled 0.012
Concrete, wood forms, unfinished 0.015
Rubble in cement 0.020
Asphalt, smooth 0.013
Asphalt, rough 0.016
Natural Channels
Gravel beds, straight 0.025
Gravel beds plus large boulders 0.040
Earth, straight, with some grass 0.026
Earth, winding, no vegetation 0.030
Earth , winding with vegetation 0.050
n = f(surface roughness,
channel irregularity,
stage...)
6/1
031.0 dn 
6/1
038.0 dn 
d in ft
d in m
d = median size of bed material

7. Trapezoidal Channel
Derive P = f(y) and A = f(y) for a
trapezoidal channel
z
1
b
y
2/13/2
1
oh SAR
n
Q 
!
zyybA 2

1/ 222
2P y yz b
1/ 22
2 1P y z b

8. m
.
Flow in Round Conduits





 

r
yr
arccos
  cossin2
 rA
sin2rT 

y
T
A
r
rP 2
radians
Maximum discharge
when y = ______0.938d
sin cosr r

9. Critical Flow:
Rectangular channel
yc
T
Ac
3
2
1
c
c
gA
TQ

qTQ  TyA cc 
3
2
33
32
1
cc gy
q
Tgy
Tq

3/1
2









g
q
yc
3
cgyq 
Only for rectangular channels!
cTT 
Given the depth we can find the flow!

10. Critical Flow Relationships:
Rectangular Channels
3/1
2









g
q
yc cc yVq 









g
yV
y
cc
c
22
3
g
V
y
c
c
2

1
gy
V
c
c
Froude number
velocity head =
because
g
Vy cc
22
2

2
c
c
y
yE  Eyc
3
2

forcegravity
forceinertial
0.5 (depth)
g
V
yE
2
2

Kinetic energy
Potential energy

11. Critical Depth
Minimum energy for a given q
Occurs when =___
When kinetic = potential! ________
Fr=1
Fr>1 = ______critical
Fr<1 = ______critical
dE
dy
0
1
2
3
4
0 1 2 3 4
E
y
2
2 2
c cV y
g
3
T
Q
gA3
c
q
gy
c
c
V
Fr
y g
0
Super
Sub

12. Critical Flow
 Characteristics
Unstable surface
Series of standing waves
 Occurrence
Broad crested weir (and other weirs)
Channel Controls (rapid changes in cross-section)
Over falls
Changes in channel slope from mild to steep
 Used for flow measurements
___________________________________________Unique relationship between depth and discharge
Difficult to measure depth
0
1
2
3
4
0 1 2 3 4
E
y
0
dy
dE

13. Water Surface Profiles:
Putting It All Together
2 m
10 cm
Sluice gatereservoir
1 km downstream from gate there is a broad crested
weir with P = 1 m. Draw the water surface profile.

14. Wave Celerity
1
21
2pF gy 2
21
2pF g y y
1 2
221
2p pF F g y y y
Fp1
y+yV+VV
Vw
unsteady flow
y y y+yV+V-VwV-Vw
steady flow
V+V-VwV-Vw
Fp2
1 21 2 p p ssM M W F F F
Per unit width

15. Wave Celerity:
Momentum Conservation
1 2 w w wy V V V V V V VM M
1 2 wy V V VM M
  VVVyg w   y y+yV+V-VwV-Vw
steady flow
  yVVM w
2
1   Per unit width2 w wM V V V V V y
Now equate pressure and momentum
1 2
221
2p pF F g y y y
2 2 21
2
2 wg y y y y y y V V V

16. Wave Celerity
    ww VVVyyVVy  
www yVyVVyVyyVyVyVyV  
 
y
y
VVV w

 
  VVVyg w  
 
y
y
VVyg w

 2

 2
wVVgy  wVVc  gyc 
Mass conservation
y y+yV+V-VwV-Vw
steady flow
Momentum
c
V
Fr
yg
V


17. Wave Propagation
 Supercritical flow
c<V
waves only propagate downstream
water doesn’t “know” what is happening downstream
_________ control
 Critical flow
c=V
 Subcritical flow
c>V
waves propagate both upstream and downstream
upstream

18. Discharge Measurements
Sharp-Crested Weir
V-Notch Weir
Broad-Crested Weir
Sluice Gate
5/ 28
2 tan
15 2
dQ C g H
 
  
 
3/ 2
2
3
dQ C b g H
 
  
 
3/ 22
2
3
dQ C b gH
12d gQ C by gy
Explain the exponents of H! 2V gH

19. Summary (1)
All the complications of pipe flow plus
additional parameter... _________________
Various descriptions of energy loss
Chezy, Manning, Darcy-Weisbach
Importance of Froude Number
Fr>1 decrease in E gives increase in y
Fr<1 decrease in E gives decrease in y
Fr=1 standing waves (also min E given Q)
free surface location
0
1
2
3
4
0 1 2 3 4
E
y

20. Summary (2)
Methods of calculating location of free
surface (Gradually varying)
Direct step (prismatic channel)
Standard step (iterative)
Differential equation
Rapidly varying
Hydraulic jump
2
1 Fr
SS
dx
dy fo




21. Broad-crested Weir: Solution
0.5
yc
E
Broad-crested
weir
yc=0.3 m
3
cgyq 
 32
3.0)/8.9( msmq 
smq /5144.0 2

smqLQ /54.1 3

Eyc
3
2

myE c 45.0
2
3
2 
1 2 0.95E E P m  
2
1
2
11
2gy
q
yE 
435.05.011  myH
935.01 y
2
1 12
12
q
E y
gE

22. Summary/Overview
Energy losses
Dimensional Analysis
Empirical
8
f h
g
V S R
f
1/2
o
2/3
h SR
1
n
V 

23. Energy Equation
Specific Energy
Two depths with same energy!
How do we know which depth
is the right one?
Is the path to the new depth
possible?
2 2
1 2
1 2
2 2o f
V V
y S x y S x
g g
2
2
2
q
y
gyg
V
yE
2
2

2
2
2
Q
y
gA
0
1
2
3
4
0 1 2 3 4
E
y

24. What next?
Water surface profiles
Rapidly varied flow
A way to move from supercritical to subcritical flow
(Hydraulic Jump)
Gradually varied flow equations
Surface profiles
Direct step
Standard step

25. Mild Slope
If the slope is mild, the depth is less than the
critical depth, and a hydraulic jump occurs,
what happens next?
Rapidly varied flow!
When dy/dx is large
 then V isn’t normal to cs
Hydraulic jump! Check conjugate depths
0
0
0
0
0
0
0
0510152025303540
distance upstream (m)
bottom
surface
yc
yn

26. Hydraulic Jump!

27. Open Channel Reflections
 Why isn’t Froude number important for describing
the relationship between channel slope, discharge,
and depth for uniform flow?
 Under what conditions are the energy and
hydraulic grade lines parallel in open channel
flow?
 Give two examples of how the specific energy
could increase in the direction of flow.