Downloaded 36 times
Uploaded byCS, NcState
945 views
Lecture 7: Definite Clause Grammars
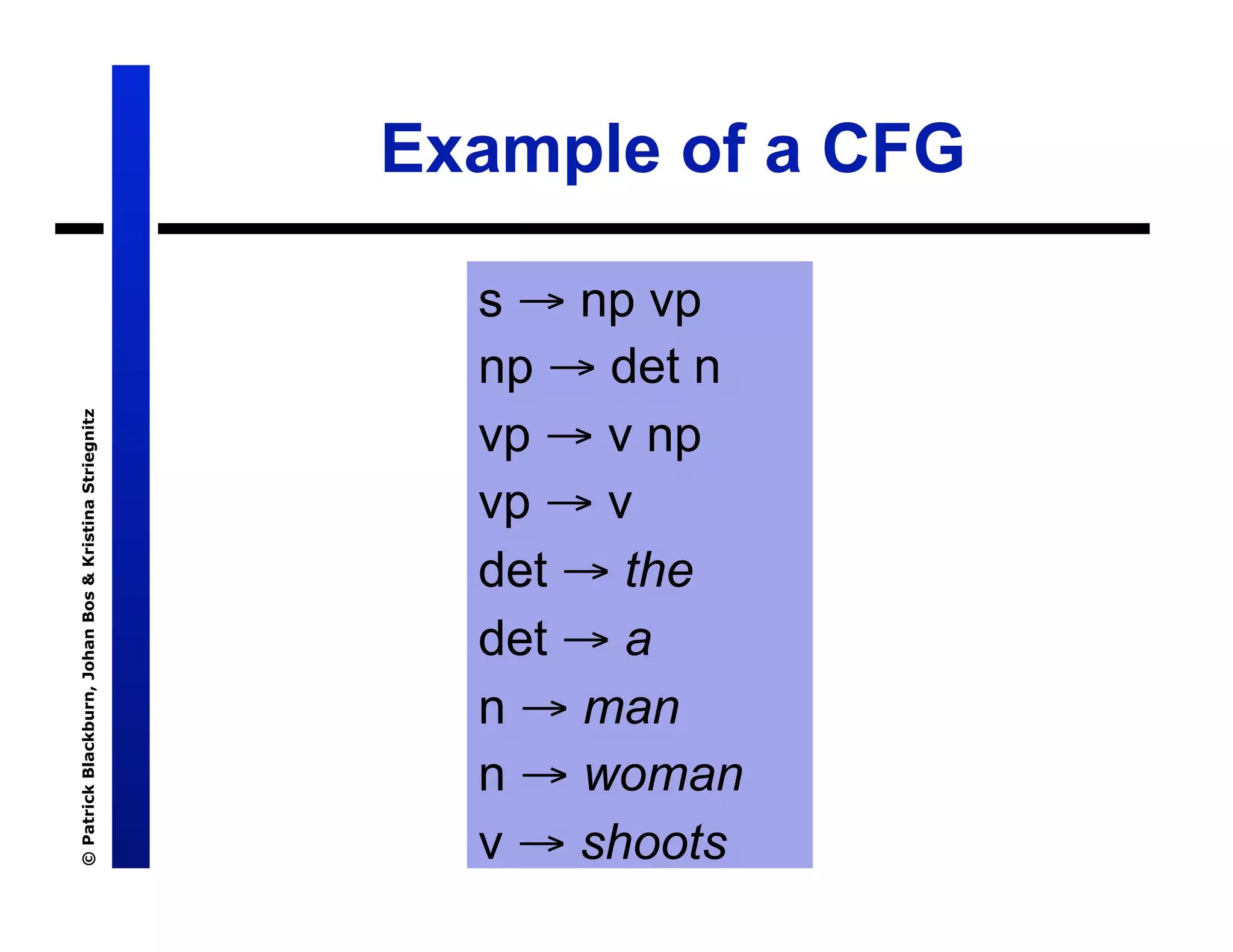
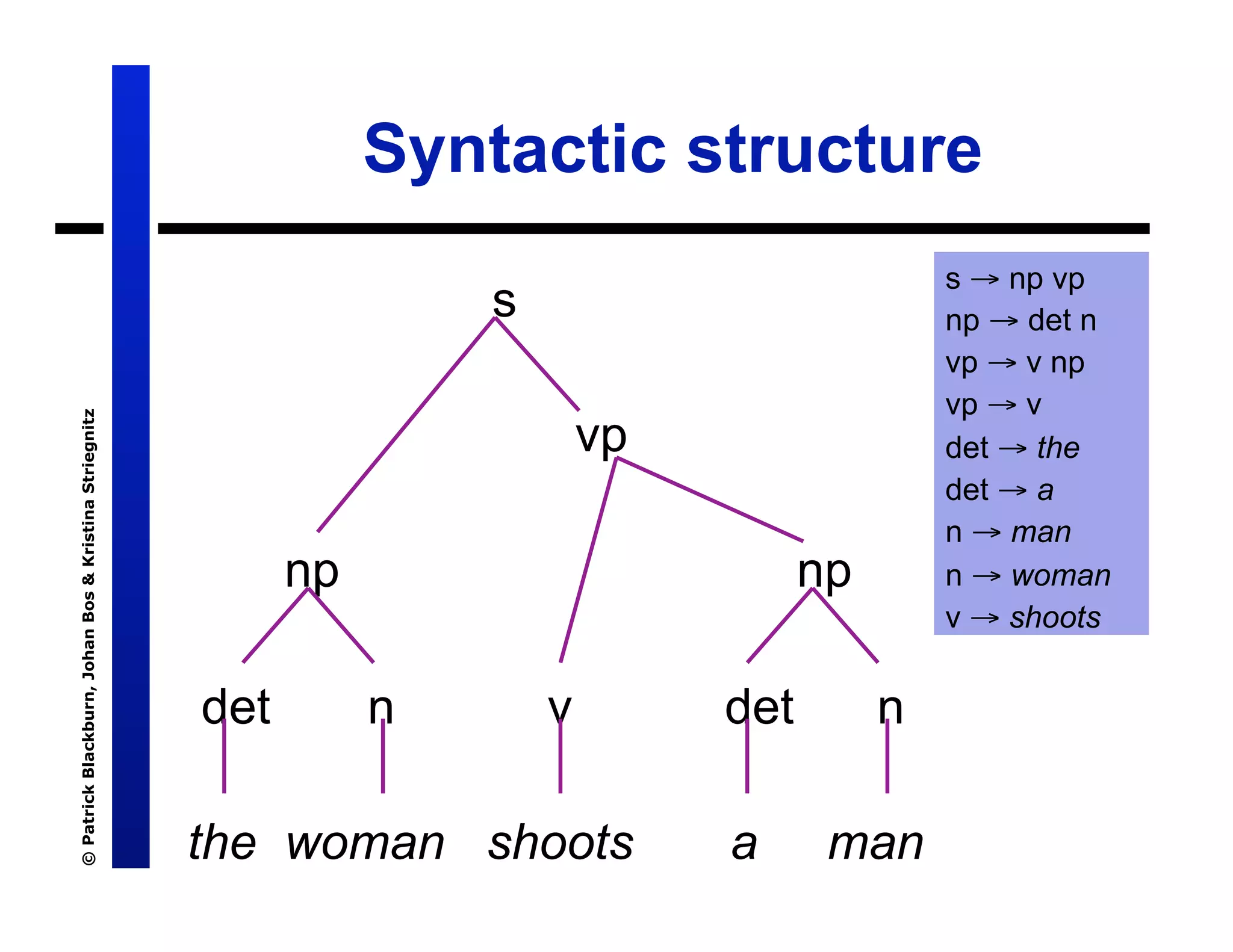
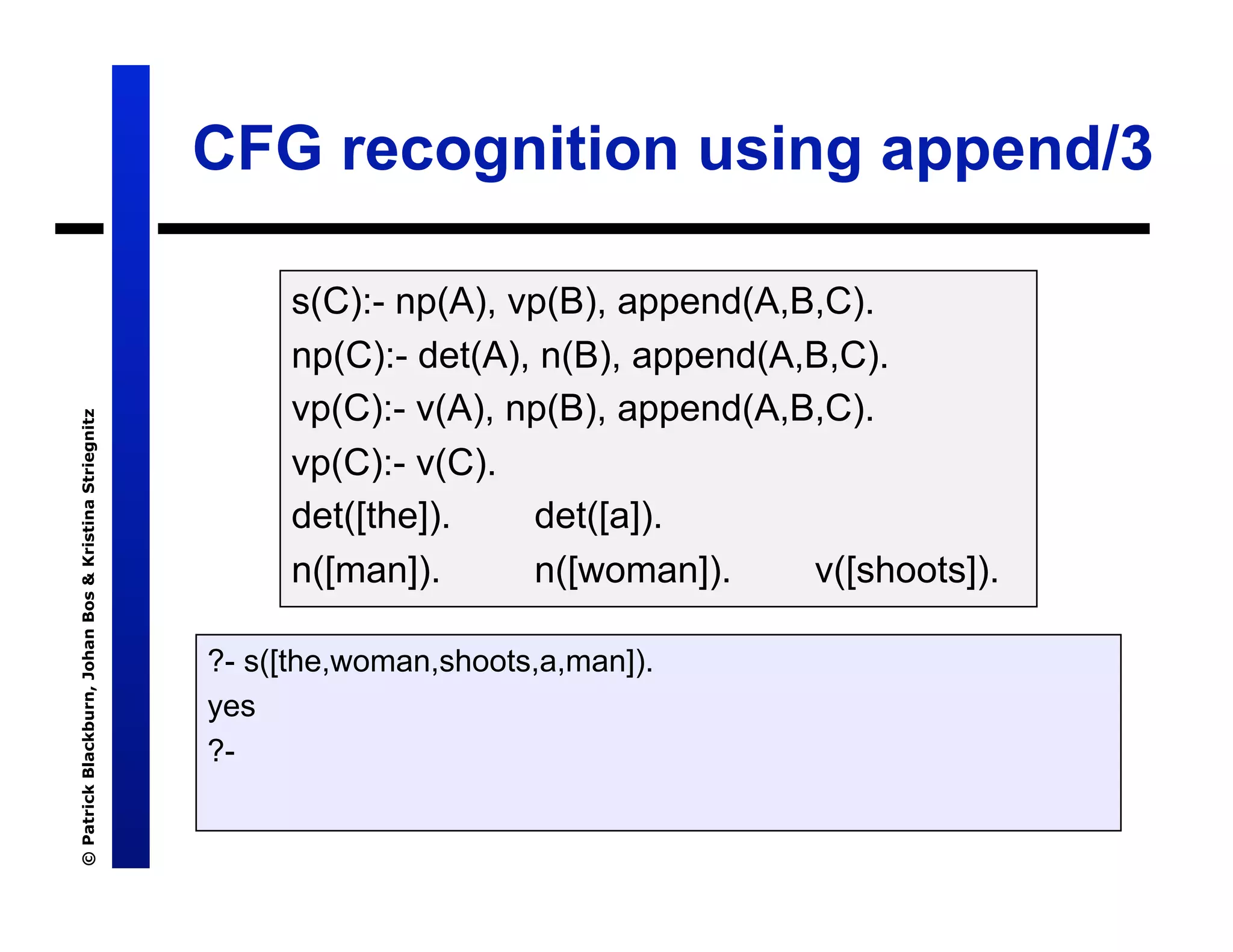
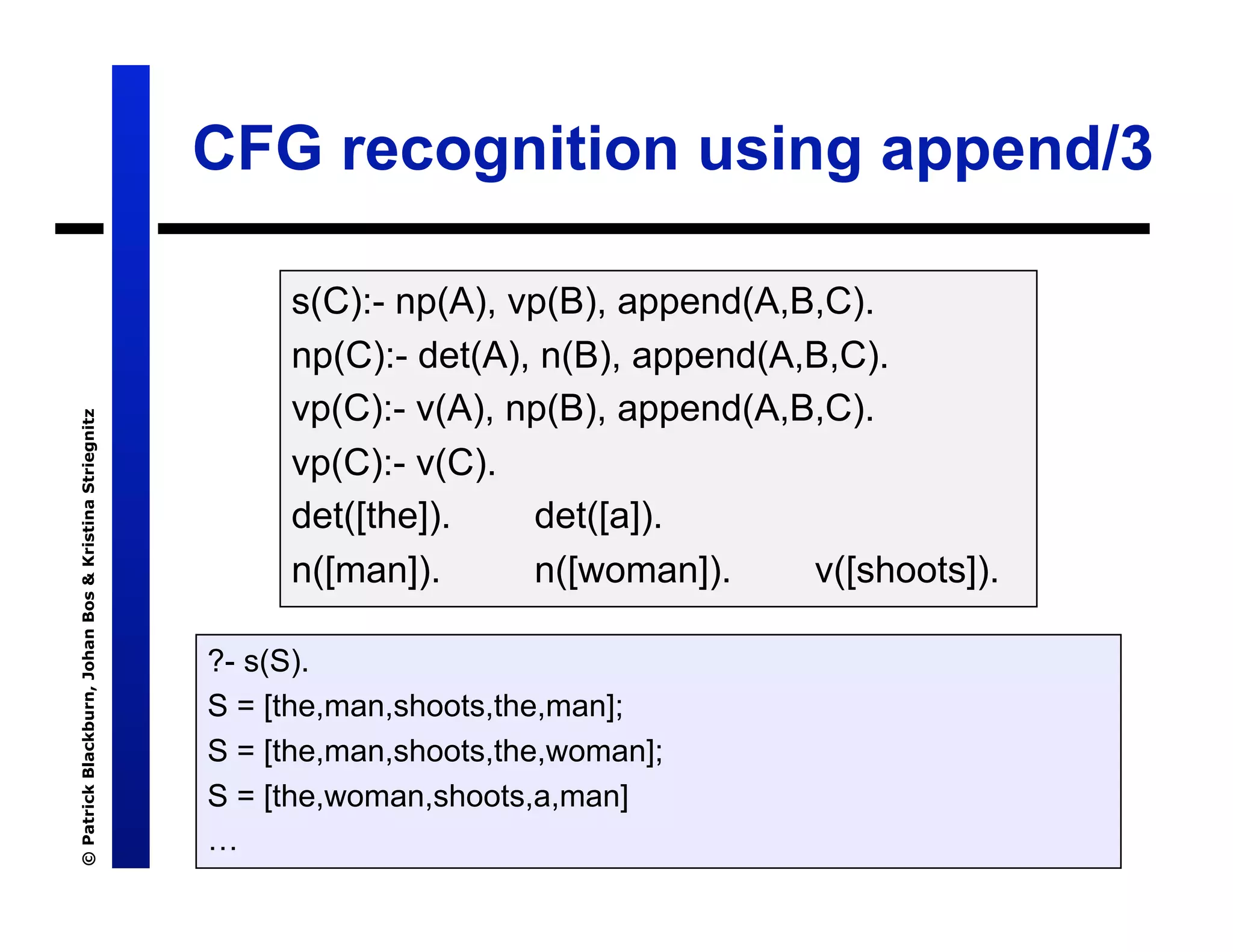
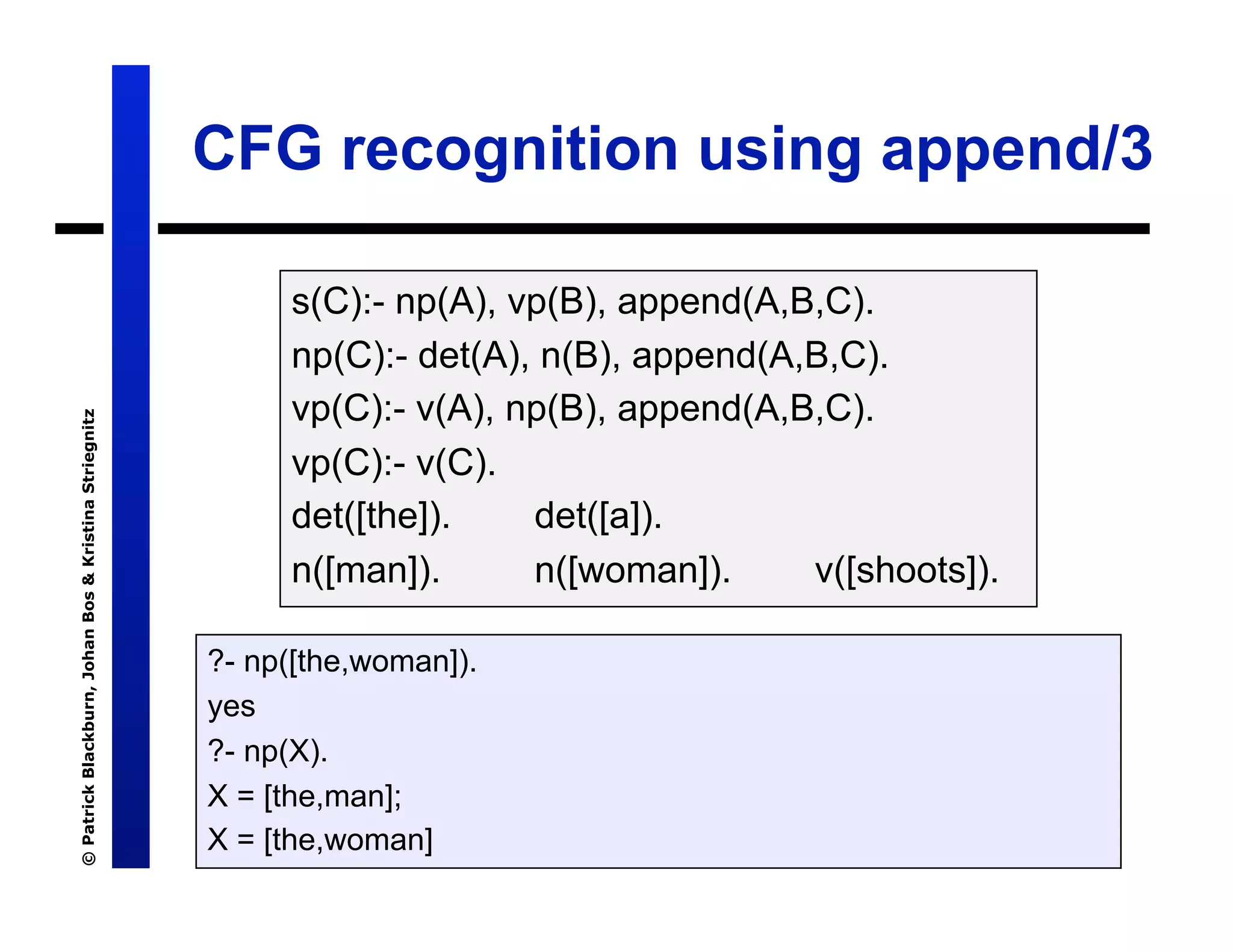
The document discusses Definite Clause Grammars (DCGs), a Prolog-based system for working with Context-Free Grammars (CFGs) which are essential for understanding the syntactic structure of natural languages. It explains the components of grammars, the concept of parse trees, and the distinction between recognizers and parsers. The text also compares traditional grammar recognition methods using append with more efficient techniques like difference lists, ultimately advocating for DCGs as an effective and user-friendly approach.
