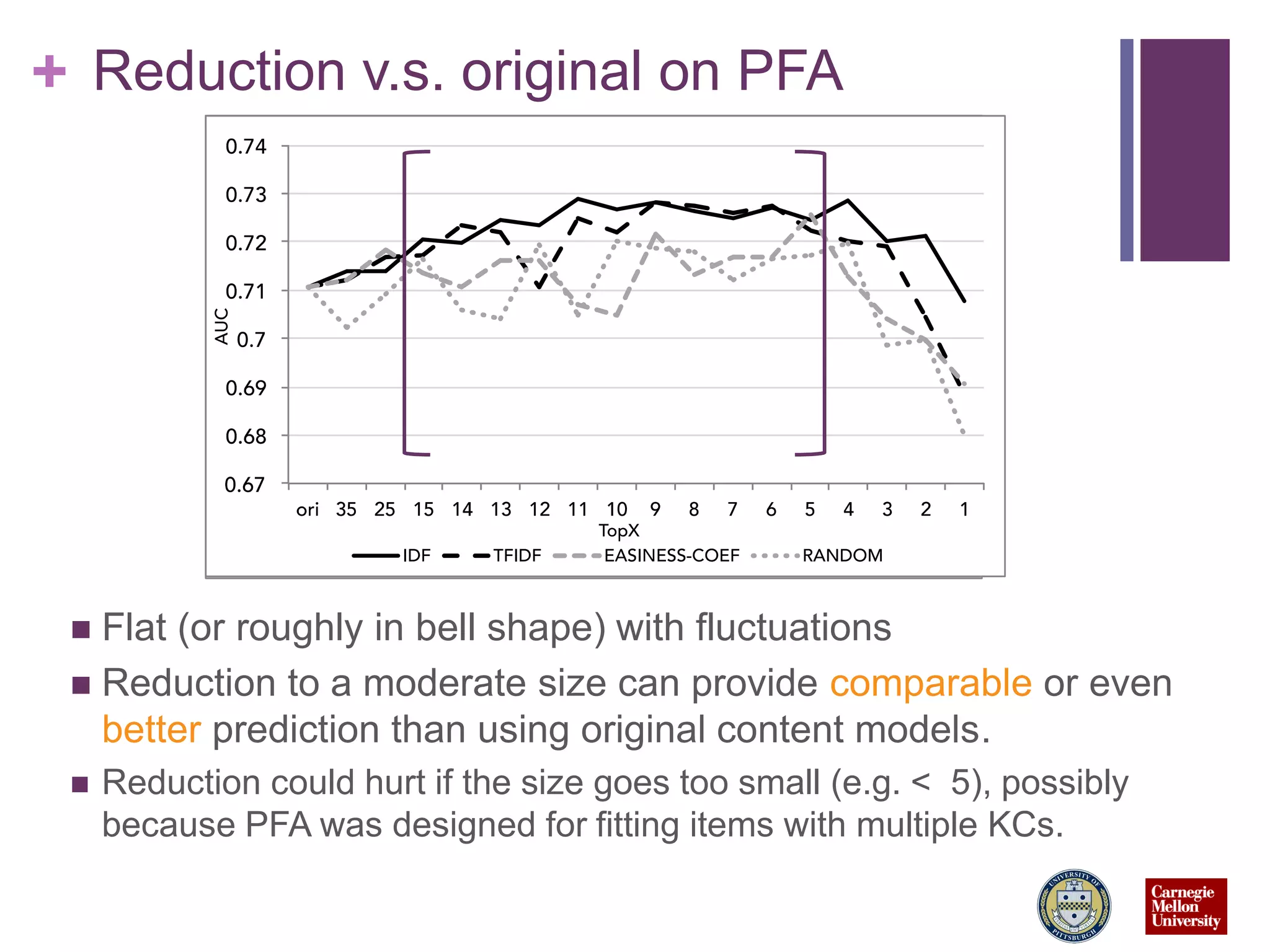
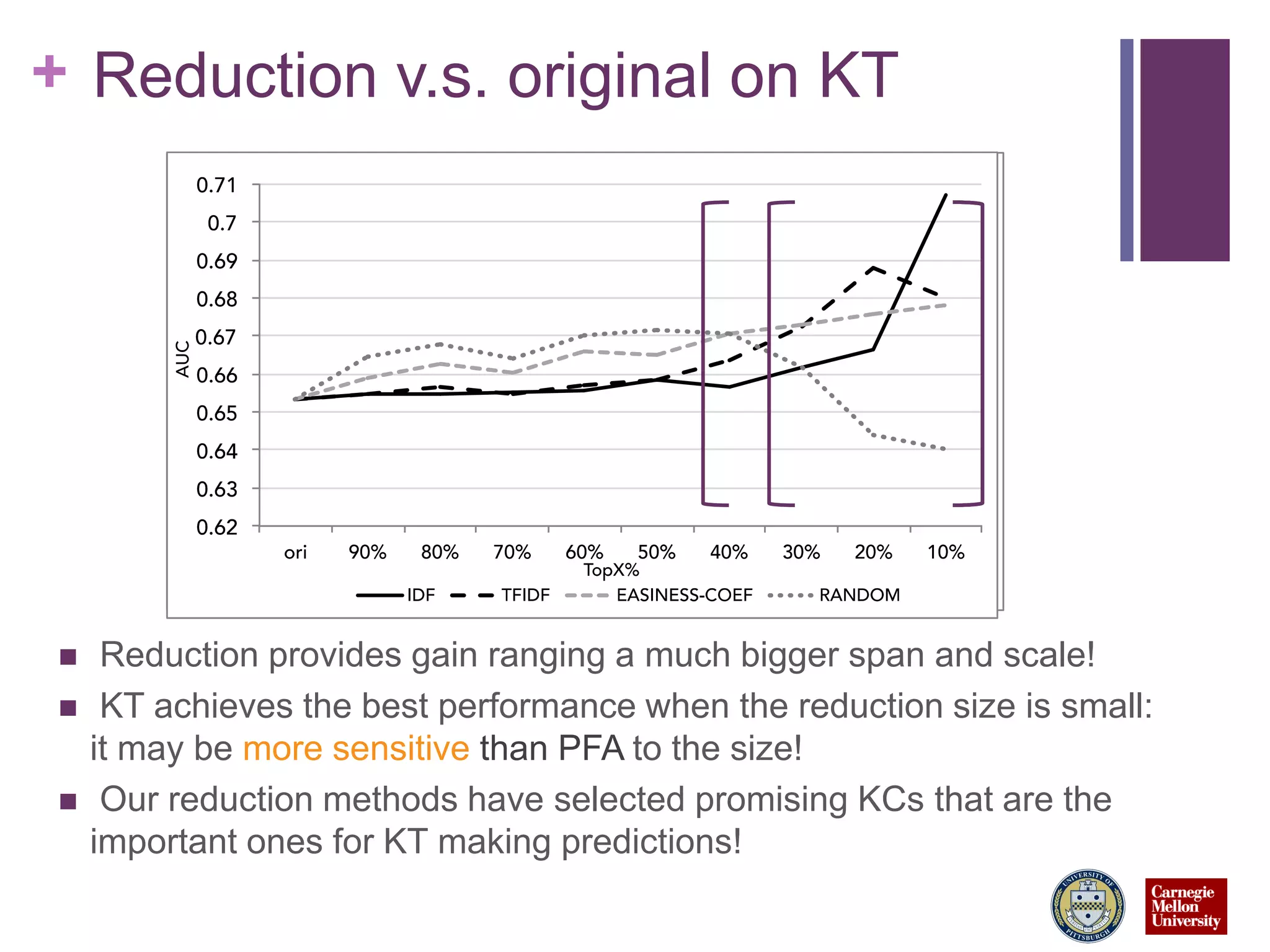
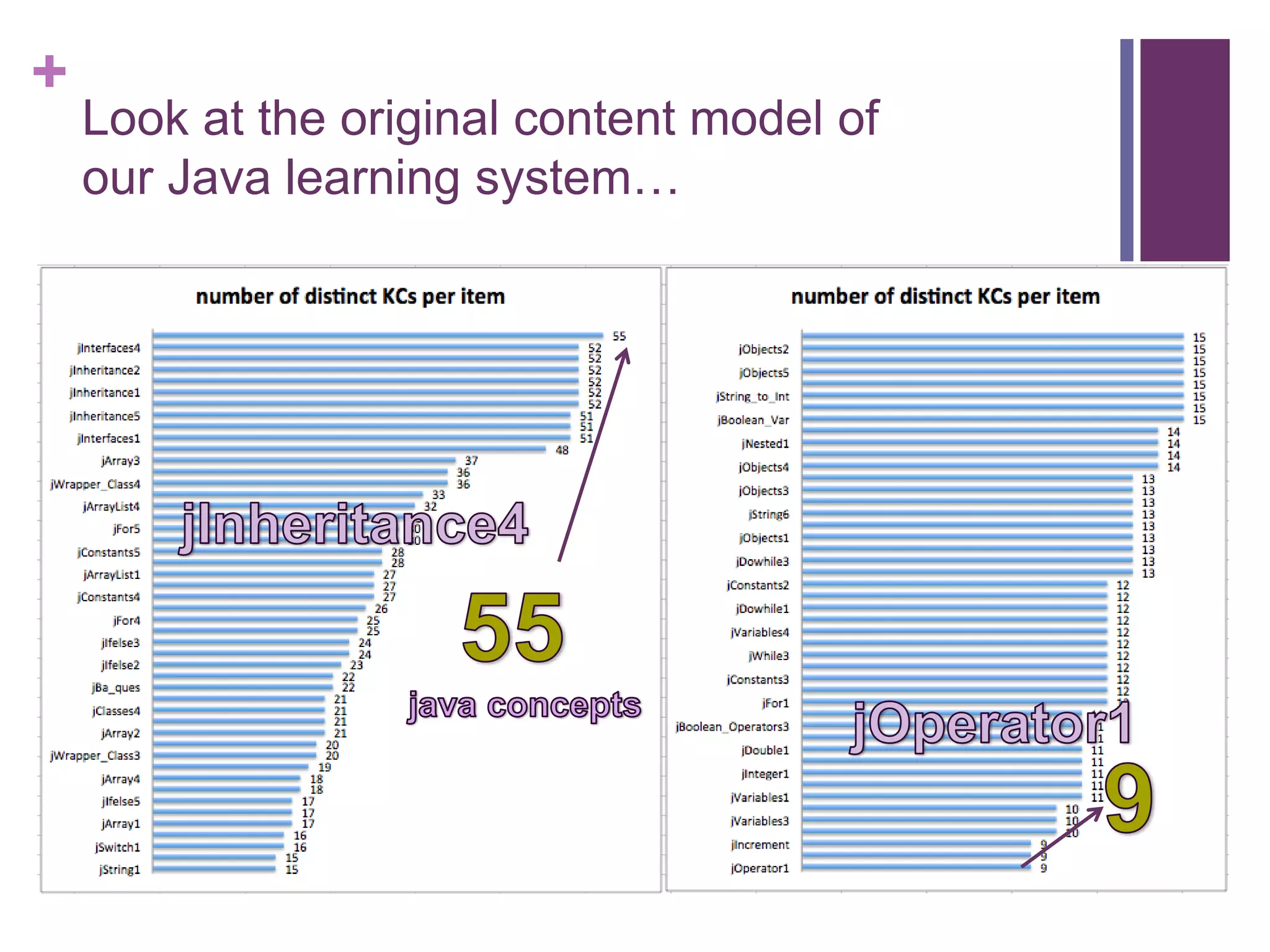
This talk discusses reducing the content models used for student modeling and performance prediction while maintaining or improving prediction accuracy. The researchers tested reducing the number of concepts (knowledge components or KCs) used to represent problems in a Java tutoring system. Their novel framework reduced the KCs for problems to 10-20% of the original numbers. When evaluated using two popular student modeling techniques, the reduced models either maintained or improved prediction performance compared to the original full models, with improvements up to 8% higher AUC. Different reduction methods and sizes worked best depending on the modeling technique used. The simple reduction approach enabled more effective student modeling with lower complexity models.

1. +
Doing More with Less :
Student Modeling and Performance
Prediction with Reduced Content
Models
Yun Huang, University of Pittsburgh
Yanbo Xu, Carnegie Mellon University
Peter Brusilovsky, University of Pittsburgh

2. +
This talk…
 What? More effective student modeling and
performance prediction
 How? A simple novel framework reducing
content model without loss of quality
 Why? Better and cheaper
 Reduced to 10%~20% while maintaining or
improving performance (up to 8% better AUC)
 Beat expert based reduction

3. +
Outline
 Motivation
 Content Model Reduction
 Experiments and Results
 Conclusion and Future Work

4. +
Motivation
 In some domains and some types of learning
content, each content problem (item) is related to
large number of domain concepts (Knowledge
Component, KCs)
 It complicates modeling due to increasing noise and
decreasing efficiency
 We argue that we only need a subset of the most
important KCs!

5. +
Content model
 The focus of this study: Java
 Each problem involves a complete program and
relates to many concepts
 Original content model
 Each problem is indexed by a set of Java
concepts from ontology
 In our context of study, number of concepts per
problem can range from 9 to 55!

6. +
An example of original content model
1. class definition
2. static method
3. public class
4. public method
5. void method
6. String array
7. int type variable
declaration
8. int type variable
initialization
9. for statement
10. assignment
11. increment
12. multiplication
13. less or equal
14. nested loop

7. +
Challenges
 Select best concepts to model problems
 Traditional feature selection focuses on
selecting a subset of features for all datapoints
(a domain).
item level not domain level

8. + Our intuitions of reduction methods
 Three types of methods from different information sources and
intuitions:
Intuition 1
“for statement” appears 2 times in
this problem -- it should be
important for this problem!
“assignment” appears in a lot of
problems -- it should be trivial for
this problem!
Intuition 2: When “nested loops” appears, students
always get it wrong -- it should be important for this
problem!
Intuition 3: Expert labeled “assignment”, “less than”
as prerequisite concepts, while “nested loops”, “for
statement” as outcome concepts --- outcome
concepts should be the important ones for current
problem!

9. +
Reduction Methods
 Content-based methods
 A problem = a document, a KC = a word
 Use IDF and TFIDF keyword weighting approach to
compute KC importance score.
 Response-based Method
 Train a logistic regression (PFA) to predict student
response
 Use the coefficient representing the initial easiness
(EASINESS-COEF) of a KC.
 Expert-based Method Use only the OUTCOME concepts
as the KCs for an item.

10. +
Item-level ranking of KC importance
 For each method, we define SCORE function
assigning a score to a KC in an item
 The higher the score, the more important a KC is in
an item.
 Then, we do item-level ranking: a KC's
importance can be differentiated
 by different score values, or/and
 by its different ranking positions in different items

11. +
Reduction Sizes
 What is the best number of KCs each
method should reduce to?
 Reducing non-adaptively to items (TopX)
 Reducing adaptively to items (TopX%)

12. +
Evaluating Reduction on PFA and KT
 We evaluate by the prediction performance of two
popular student modeling and performance prediction
models
 Performance Factor Analysis (PFA): logistic
regression model predicting student response
 Knowledge Tracing (KT): Hidden Markov Models
predicting student response and inferring student
knowledge level
*We select a variant that can handle multiple KCs.

13. +
Outline
 Motivation
 Content Model Reduction
 Experiments and Results
 Conclusion and Future Work

14. +
Tutoring System
Collected from JavaGuide, a tutor for learning Java programming.
Each question is generated from a template,
and students can try multiple attempts
Students give values for a variable or the
output
Java code

15. +
Experimental Setup
 Dataset
 19, 809 observations, about 69.3% correct
 132 students on 94 question templates (items)
 A problem is indexed into 9 ~ 55 KCs, 124 KCs in total
 Classification metric: Area Under Curve (AUC)
 1: perfect classifier, 0.5: random classifier
 Cross-validation: Two runs of 5-fold CV where in each run
80% of the users are in train, and the remaining are in test.
 We list the mean AUC on test sets across the 10 runs, and
use Wilcoxon Signed Ranks Test (alpha = 0.05) to test
AUC comparison significance.

16. + Reduction v.s. original on PFA
 Flat (or roughly in bell shape) with fluctuations
 Reduction to a moderate size can provide comparable or even
better prediction than using original content models.
 Reduction could hurt if the size goes too small (e.g. < 5), possibly
because PFA was designed for fitting items with multiple KCs.

17. + Reduction v.s. original on KT
 Reduction provides gain ranging a much bigger span and scale!
 KT achieves the best performance when the reduction size is small:
it may be more sensitive than PFA to the size!
 Our reduction methods have selected promising KCs that are the
important ones for KT making predictions!

18. + Automatic v.s. expert-based (OUTCOME)
reduction method
 IDF and TFIDF can be comparable to or outperform
OUTCOME method!
 E-COEF provides much gain on KT than PFA, suggesting
PFA coefficients can provide useful extra information for
reducing the KT content models.
(+/−: signicantly better/worse than OUTCOME,  : the optimal mean AUC)

19. +
Outline
 Motivation
 Content Model Reduction
 Experiments and Results
 Conclusion and Future Work

20. +
“Everything should be
made as simple as
possible, but not simpler.”
-- Albert Einstein

21. +
Conclusion
 “Content model should be made as simple as
possible, but not simpler.”
 Given the proper reduction size, reduction enables
prediction performance better!
 Different model reacts to reduction differently!
 KT is more sensitive to reduction than PFA
 Different models achieve the best balance between
model complexity and model fit in different ranges
 We are the first to explore reduction extensively!
 More ideas for selecting important KCs?
 Larger datasets?
 Other domains?

22. +
Acknowledgement
 Advanced Distributed Learning Initiative
(http://www.adlnet.gov/).
 LearnLab 2013 Summer School at CMU (Dr.
Kenneth R. Koedinger, Dr. Jose P. Gonzalez-Brenes, Dr.
Zachary A. Pardos for advising and initiating the project)

23. +
Thank you for listening !

24. +
Look at the original content model of
our Java learning system…

25. + Why RANDOM can occasionally be good?
 When remaining size is relatively large (e.g. > 4 or > 20%),
RANDOM can by chance target one or a subset of the important
KCs, and then
 it takes advantage of PFA’s logistic regression to adjust the
coefficients of other non-important KCs, or
 it take advantage of KT to pick out the most important one in the set
by computing the “weakest” KC.
 When remaining size of KCs is relatively small, proposed
methods becomes better than RANDOM more significantly.
 Our proposed method is not perfect…
(+/−: signicantly better/worse than RANDOM,  : the optimal mean AUC)