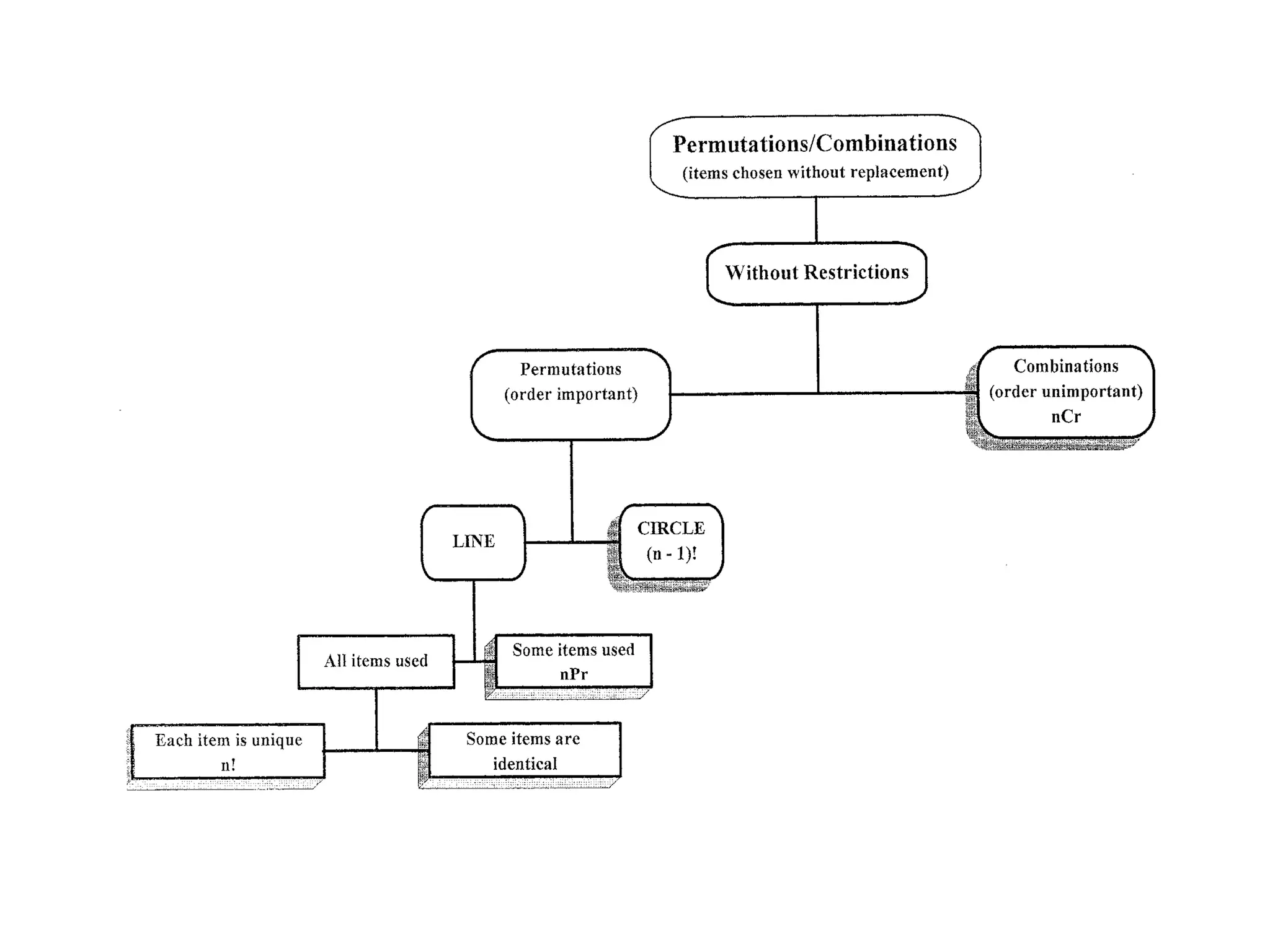
The document discusses the difference between arranging objects in a line versus in a circle. When objects are arranged in a line, there is a definite start and end point, so the first object can be placed in any of n positions. However, in a circular arrangement there is no definite start or end, so the number of arrangements is n! rather than n times the factorial of the remaining objects. Examples are provided to illustrate calculating the number of possible arrangements in different circular seating scenarios.

1. Permutations
Case 4: Ordered Sets of n Objects, Arranged in a Circle
What is the difference between placing objects in a line and placing
objects in a circle?

2. Permutations
Case 4: Ordered Sets of n Objects, Arranged in a Circle
What is the difference between placing objects in a line and placing
objects in a circle?
The difference is the number of ways the first object can be placed.

3. Permutations
Case 4: Ordered Sets of n Objects, Arranged in a Circle
What is the difference between placing objects in a line and placing
objects in a circle?
The difference is the number of ways the first object can be placed.
Line

4. Permutations
Case 4: Ordered Sets of n Objects, Arranged in a Circle
What is the difference between placing objects in a line and placing
objects in a circle?
The difference is the number of ways the first object can be placed.
Line

5. Permutations
Case 4: Ordered Sets of n Objects, Arranged in a Circle
What is the difference between placing objects in a line and placing
objects in a circle?
The difference is the number of ways the first object can be placed.
Line
In a line there is a definite start and finish of the line.

6. Permutations
Case 4: Ordered Sets of n Objects, Arranged in a Circle
What is the difference between placing objects in a line and placing
objects in a circle?
The difference is the number of ways the first object can be placed.
Line
In a line there is a definite start and finish of the line.
The first object has a choice of 6 positions

7. Permutations
Case 4: Ordered Sets of n Objects, Arranged in a Circle
What is the difference between placing objects in a line and placing
objects in a circle?
The difference is the number of ways the first object can be placed.
Line
In a line there is a definite start and finish of the line.
The first object has a choice of 6 positions
Circle

8. Permutations
Case 4: Ordered Sets of n Objects, Arranged in a Circle
What is the difference between placing objects in a line and placing
objects in a circle?
The difference is the number of ways the first object can be placed.
Line
In a line there is a definite start and finish of the line.
The first object has a choice of 6 positions
Circle

9. Permutations
Case 4: Ordered Sets of n Objects, Arranged in a Circle
What is the difference between placing objects in a line and placing
objects in a circle?
The difference is the number of ways the first object can be placed.
Line
In a line there is a definite start and finish of the line.
The first object has a choice of 6 positions
Circle
In a circle there is no definite start or
finish of the circle.

10. Permutations
Case 4: Ordered Sets of n Objects, Arranged in a Circle
What is the difference between placing objects in a line and placing
objects in a circle?
The difference is the number of ways the first object can be placed.
Line
In a line there is a definite start and finish of the line.
The first object has a choice of 6 positions
Circle
In a circle there is no definite start or
finish of the circle.
It is not until the first object chooses its
position that positions are defined.

11. Line
Circle

12. Line
possibilities
for object 1
Number of Arrangements  n
Circle
possibilities
for object 1
Number of Arrangements  1

13. Line possibilities
possibilities for object 2
for object 1
Number of Arrangements  n  n  1
Circle possibilities
possibilities for object 2
for object 1
Number of Arrangements  1  n  1

14. Line possibilities
possibilities for object 2 possibilities
for object 1 for object 3
Number of Arrangements  n  n  1  n  2 
Circle possibilities
possibilities for object 2 possibilities
for object 1 for object 3
Number of Arrangements  1  n  1  n  2 

15. Line possibilities
possibilities for object 2 possibilities possibilities
for object 1 for object 3
for last object
Number of Arrangements  n  n  1  n  2    1
Circle possibilities
possibilities for object 2 possibilities possibilities
for object 1 for object 3
for last object
Number of Arrangements  1  n  1  n  2    1

16. Line possibilities
possibilities for object 2 possibilities possibilities
for object 1 for object 3
for last object
Number of Arrangements  n  n  1  n  2    1
Circle possibilities
possibilities for object 2 possibilities possibilities
for object 1 for object 3
for last object
Number of Arrangements  1  n  1  n  2    1
n!
Number of Arrangements in a circle 
n

17. Line possibilities
possibilities for object 2 possibilities possibilities
for object 1 for object 3
for last object
Number of Arrangements  n  n  1  n  2    1
Circle possibilities
possibilities for object 2 possibilities possibilities
for object 1 for object 3
for last object
Number of Arrangements  1  n  1  n  2    1
n!
Number of Arrangements in a circle 
n
 n  1!

18. e.g. A meeting room contains a round table surrounded by ten
chairs.
(i) A committee of ten people includes three teenagers. How
many arrangements are there in which all three sit
together?

19. e.g. A meeting room contains a round table surrounded by ten
chairs.
(i) A committee of ten people includes three teenagers. How
many arrangements are there in which all three sit
together?
the number of ways the
three teenagers can be
arranged
Arrangements  3!

20. e.g. A meeting room contains a round table surrounded by ten
chairs.
(i) A committee of ten people includes three teenagers. How
many arrangements are there in which all three sit
together?
the number of ways the
three teenagers can be number of ways of arranging
arranged 8 objects in a circle
(3 teenagers)  7 others
Arrangements  3!  7!

21. e.g. A meeting room contains a round table surrounded by ten
chairs.
(i) A committee of ten people includes three teenagers. How
many arrangements are there in which all three sit
together?
the number of ways the
three teenagers can be number of ways of arranging
arranged 8 objects in a circle
(3 teenagers)  7 others
Arrangements  3!  7!
 30240

22. (ii) Elections are held for Chairperson and Secretary.
What is the probability that they are seated directly opposite each
other?

23. (ii) Elections are held for Chairperson and Secretary.
What is the probability that they are seated directly opposite each
other?
Ways (no restrictions)  9!

24. (ii) Elections are held for Chairperson and Secretary.
What is the probability that they are seated directly opposite each
other?
Ways (no restrictions)  9!
President can
sit anywhere
as they are 1st
in the circle
Ways (restrictions)  1

25. (ii) Elections are held for Chairperson and Secretary.
What is the probability that they are seated directly opposite each
other?
Ways (no restrictions)  9!
Secretary must
President can
sit opposite
sit anywhere
President
as they are 1st
in the circle
Ways (restrictions)  1 1

26. (ii) Elections are held for Chairperson and Secretary.
What is the probability that they are seated directly opposite each
other?
Ways (no restrictions)  9!
Secretary must
President can
sit opposite
sit anywhere
President
as they are 1st
Ways remaining
in the circle
people can go
Ways (restrictions)  1 1  8!

27. (ii) Elections are held for Chairperson and Secretary.
What is the probability that they are seated directly opposite each
other?
Ways (no restrictions)  9!
Secretary must
President can
sit opposite
sit anywhere
President
as they are 1st
Ways remaining
in the circle
people can go
Ways (restrictions)  1 1  8!
11 8!
PP & S opposite  
9!

28. (ii) Elections are held for Chairperson and Secretary.
What is the probability that they are seated directly opposite each
other?
Ways (no restrictions)  9!
Secretary must
President can
sit opposite
sit anywhere
President
as they are 1st
Ways remaining
in the circle
people can go
Ways (restrictions)  1 1  8!
11 8!
PP & S opposite  
9!
1

9

29. (ii) Elections are held for Chairperson and Secretary.
What is the probability that they are seated directly opposite each
other?
Ways (no restrictions)  9!
Secretary must
President can
sit opposite
sit anywhere
President
as they are 1st
Ways remaining
in the circle
people can go
Note: of 9 seats only
Ways (restrictions)  1 1  8!
1 is opposite the
President
11 8!  Popposite  
1
PP & S opposite  
9! 9
1 Sometimes simple
 logic is quicker!!!!
9

30. 2002 Extension 1 HSC Q3a)
Seven people are to be seated at a round table
(i) How many seating arrangements are possible?

31. 2002 Extension 1 HSC Q3a)
Seven people are to be seated at a round table
(i) How many seating arrangements are possible?
Arrangements  6!

32. 2002 Extension 1 HSC Q3a)
Seven people are to be seated at a round table
(i) How many seating arrangements are possible?
Arrangements  6!
 720

33. 2002 Extension 1 HSC Q3a)
Seven people are to be seated at a round table
(i) How many seating arrangements are possible?
Arrangements  6!
 720
(ii) Two people, Kevin and Jill, refuse to sit next to each other. How
many seating arrangements are then possible?

34. 2002 Extension 1 HSC Q3a)
Seven people are to be seated at a round table
(i) How many seating arrangements are possible?
Arrangements  6!
 720
(ii) Two people, Kevin and Jill, refuse to sit next to each other. How
many seating arrangements are then possible?
Note: it is easier to work out the number of ways Kevin and Jill are
together and subtract from total number of arrangements.

35. 2002 Extension 1 HSC Q3a)
Seven people are to be seated at a round table
(i) How many seating arrangements are possible?
Arrangements  6!
 720
(ii) Two people, Kevin and Jill, refuse to sit next to each other. How
many seating arrangements are then possible?
Note: it is easier to work out the number of ways Kevin and Jill are
together and subtract from total number of arrangements.
the number of ways
Kevin & Jill are together
Arrangements  2!

36. 2002 Extension 1 HSC Q3a)
Seven people are to be seated at a round table
(i) How many seating arrangements are possible?
Arrangements  6!
 720
(ii) Two people, Kevin and Jill, refuse to sit next to each other. How
many seating arrangements are then possible?
Note: it is easier to work out the number of ways Kevin and Jill are
together and subtract from total number of arrangements.
the number of ways number of ways of arranging
Kevin & Jill are together 6 objects in a circle
(Kevin & Jill)  5 others
Arrangements  2!  5!

37. 2002 Extension 1 HSC Q3a)
Seven people are to be seated at a round table
(i) How many seating arrangements are possible?
Arrangements  6!
 720
(ii) Two people, Kevin and Jill, refuse to sit next to each other. How
many seating arrangements are then possible?
Note: it is easier to work out the number of ways Kevin and Jill are
together and subtract from total number of arrangements.
the number of ways number of ways of arranging
Kevin & Jill are together 6 objects in a circle
(Kevin & Jill)  5 others
Arrangements  2!  5!
 240

38. 2002 Extension 1 HSC Q3a)
Seven people are to be seated at a round table
(i) How many seating arrangements are possible?
Arrangements  6!
 720
(ii) Two people, Kevin and Jill, refuse to sit next to each other. How
many seating arrangements are then possible?
Note: it is easier to work out the number of ways Kevin and Jill are
together and subtract from total number of arrangements.
the number of ways number of ways of arranging
Kevin & Jill are together 6 objects in a circle
(Kevin & Jill)  5 others
Arrangements  2!  5!
 240 Arrangements  720  240
 480

39. 2002 Extension 1 HSC Q3a)
Seven people are to be seated at a round table
(i) How many seating arrangements are possible?
Arrangements  6!
 720
(ii) Two people, Kevin and Jill, refuse to sit next to each other. How
many seating arrangements are then possible?
Note: it is easier to work out the number of ways Kevin and Jill are
together and subtract from total number of arrangements.
the number of ways number of ways of arranging
Kevin & Jill are together 6 objects in a circle
(Kevin & Jill)  5 others
Arrangements  2!  5!
 240 Arrangements  720  240
 480

41. 1995 Extension 1 HSC Q3a)
A B C D E F G H
A security lock has 8 buttons labelled as shown. Each person using
the lock is given a 3 letter code.
(i) How many different codes are possible if letters can be repeated
and their order is important?

42. 1995 Extension 1 HSC Q3a)
A B C D E F G H
A security lock has 8 buttons labelled as shown. Each person using
the lock is given a 3 letter code.
(i) How many different codes are possible if letters can be repeated
and their order is important?
With replacement
Use Basic Counting Principle

43. 1995 Extension 1 HSC Q3a)
A B C D E F G H
A security lock has 8 buttons labelled as shown. Each person using
the lock is given a 3 letter code.
(i) How many different codes are possible if letters can be repeated
and their order is important?
Codes  8  8  8 With replacement
Use Basic Counting Principle

44. 1995 Extension 1 HSC Q3a)
A B C D E F G H
A security lock has 8 buttons labelled as shown. Each person using
the lock is given a 3 letter code.
(i) How many different codes are possible if letters can be repeated
and their order is important?
Codes  8  8  8 With replacement
 512 Use Basic Counting Principle

45. 1995 Extension 1 HSC Q3a)
A B C D E F G H
A security lock has 8 buttons labelled as shown. Each person using
the lock is given a 3 letter code.
(i) How many different codes are possible if letters can be repeated
and their order is important?
Codes  8  8  8 With replacement
 512 Use Basic Counting Principle
(ii) How many different codes are possible if letters cannot be
repeated and their order is important?

46. 1995 Extension 1 HSC Q3a)
A B C D E F G H
A security lock has 8 buttons labelled as shown. Each person using
the lock is given a 3 letter code.
(i) How many different codes are possible if letters can be repeated
and their order is important?
Codes  8  8  8 With replacement
 512 Use Basic Counting Principle
(ii) How many different codes are possible if letters cannot be
repeated and their order is important?
Without replacement
Order is important
Permutation

47. 1995 Extension 1 HSC Q3a)
A B C D E F G H
A security lock has 8 buttons labelled as shown. Each person using
the lock is given a 3 letter code.
(i) How many different codes are possible if letters can be repeated
and their order is important?
Codes  8  8  8 With replacement
 512 Use Basic Counting Principle
(ii) How many different codes are possible if letters cannot be
repeated and their order is important?
Codes 8P3 Without replacement
Order is important
Permutation

48. 1995 Extension 1 HSC Q3a)
A B C D E F G H
A security lock has 8 buttons labelled as shown. Each person using
the lock is given a 3 letter code.
(i) How many different codes are possible if letters can be repeated
and their order is important?
Codes  8  8  8 With replacement
 512 Use Basic Counting Principle
(ii) How many different codes are possible if letters cannot be
repeated and their order is important?
Codes 8P3 Without replacement
 336 Order is important
Permutation

49. (iii) Now suppose that the lock operates by holding 3 buttons down
together, so that the order is NOT important.
How many different codes are possible?

50. (iii) Now suppose that the lock operates by holding 3 buttons down
together, so that the order is NOT important.
How many different codes are possible?
Without replacement
Order is not important
Combination

51. (iii) Now suppose that the lock operates by holding 3 buttons down
together, so that the order is NOT important.
How many different codes are possible?
Codes 8C3 Without replacement
Order is not important
Combination

52. (iii) Now suppose that the lock operates by holding 3 buttons down
together, so that the order is NOT important.
How many different codes are possible?
Codes 8C3 Without replacement
Order is not important
 56
Combination

53. (iii) Now suppose that the lock operates by holding 3 buttons down
together, so that the order is NOT important.
How many different codes are possible?
Codes 8C3 Without replacement
Order is not important
 56
Combination
Exercise 10I; odds