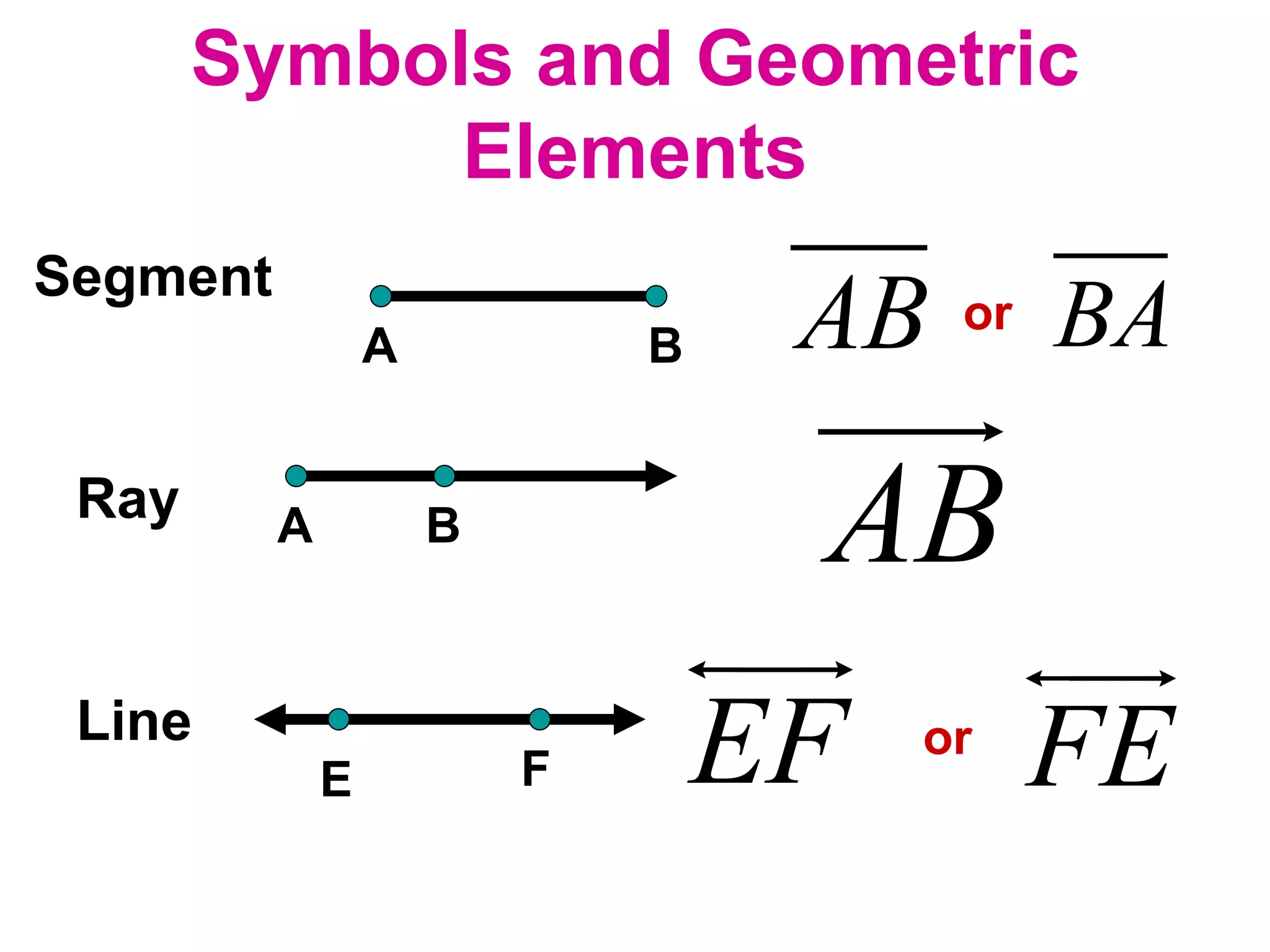
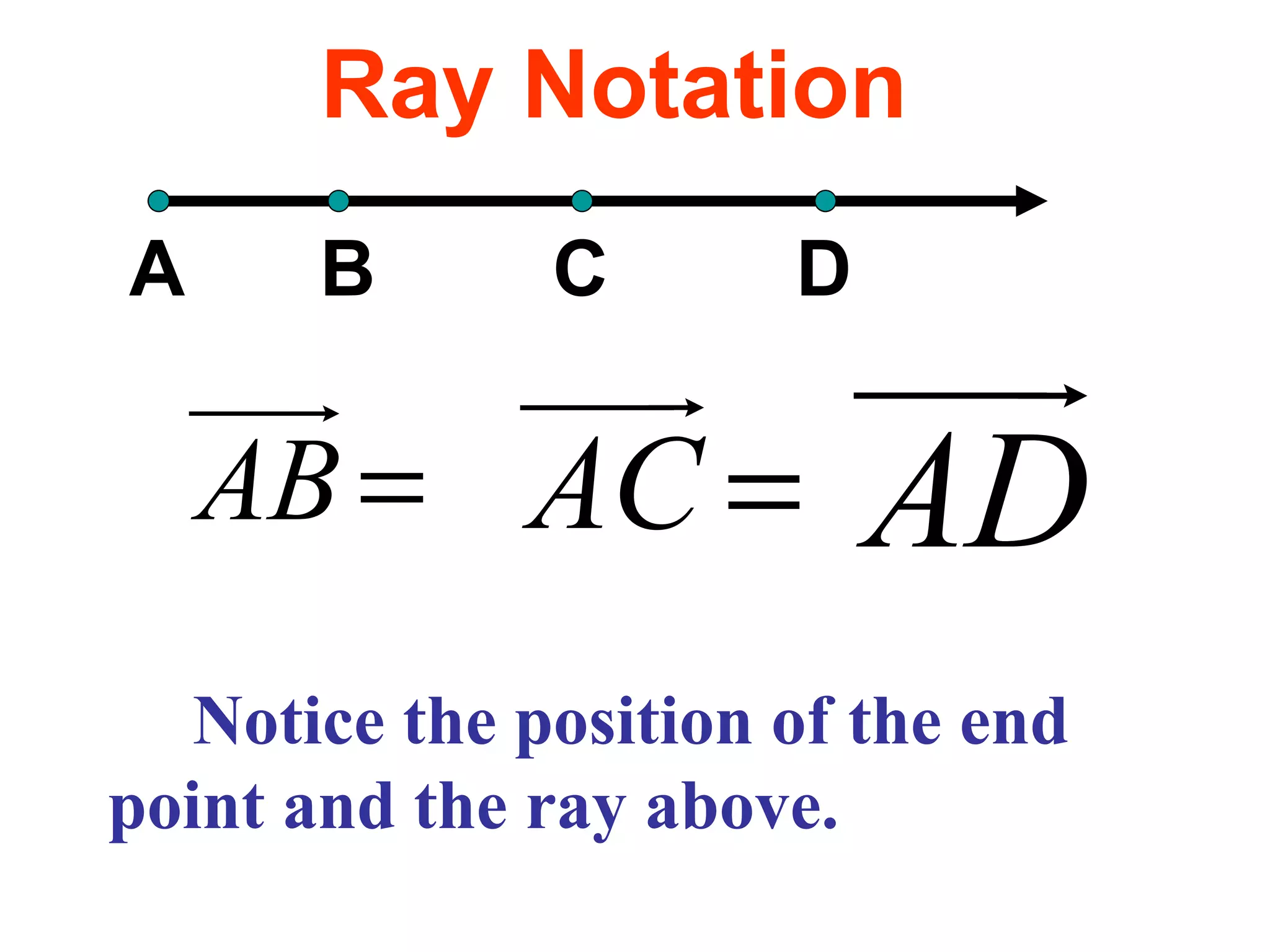
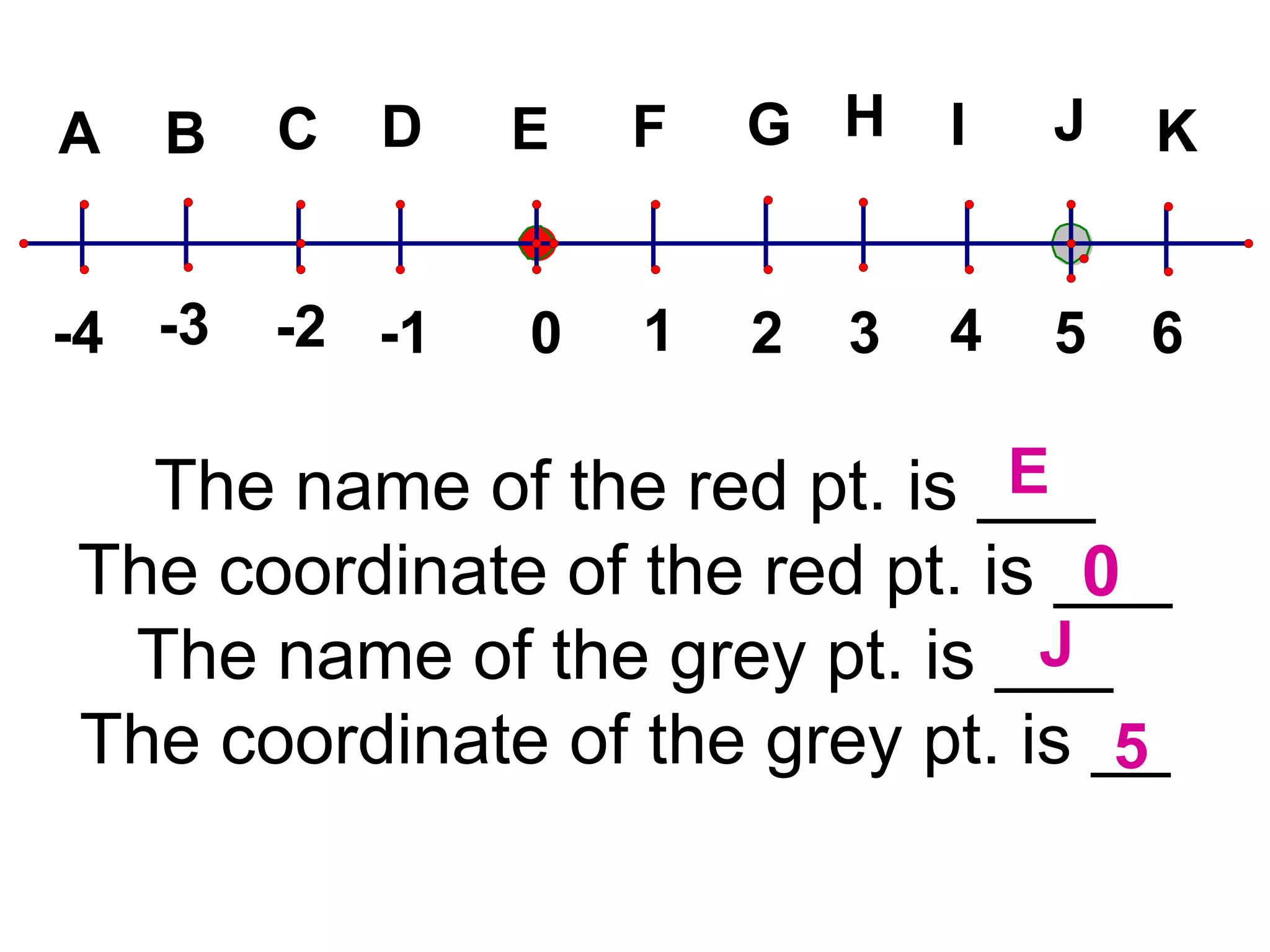
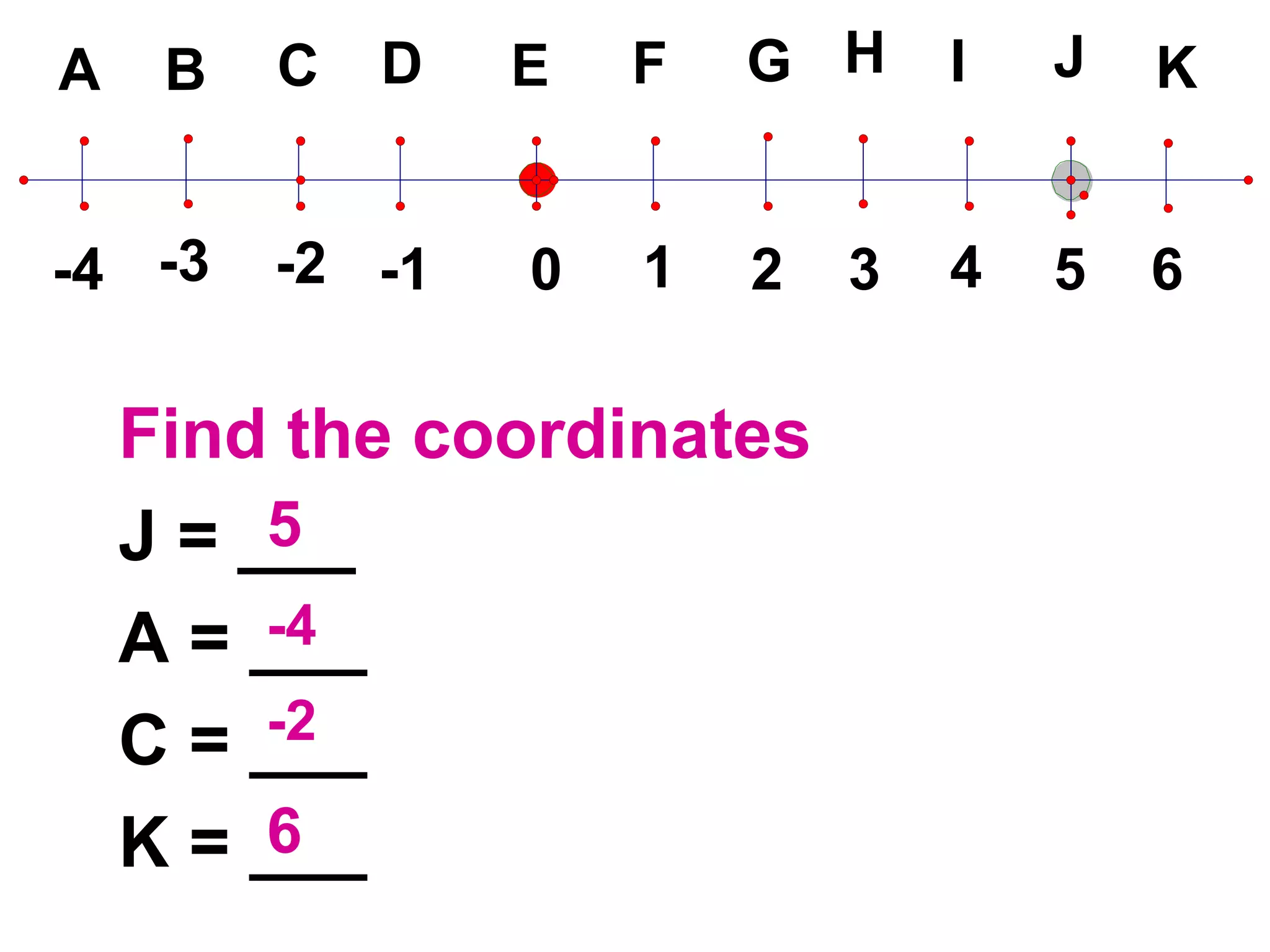
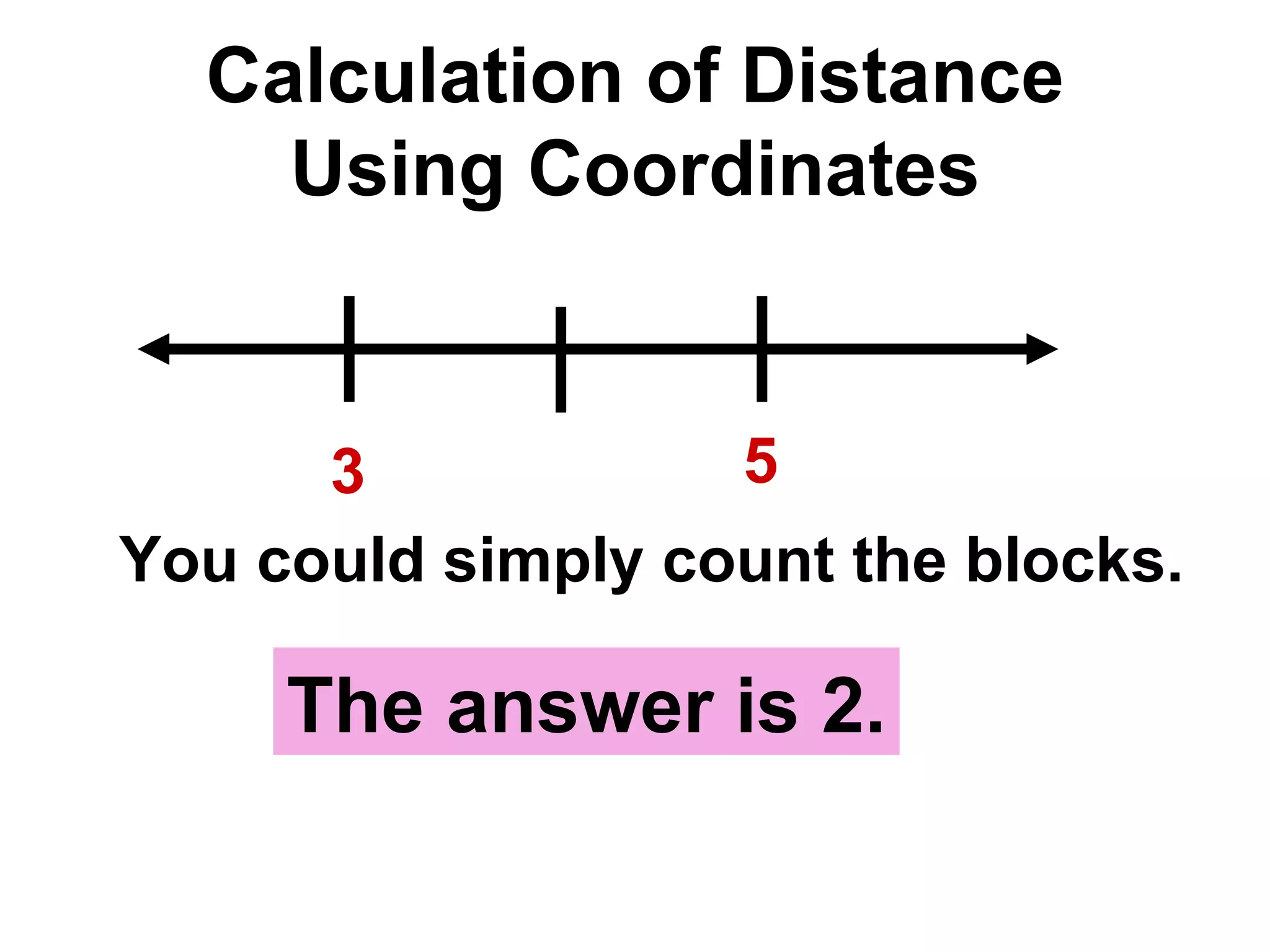
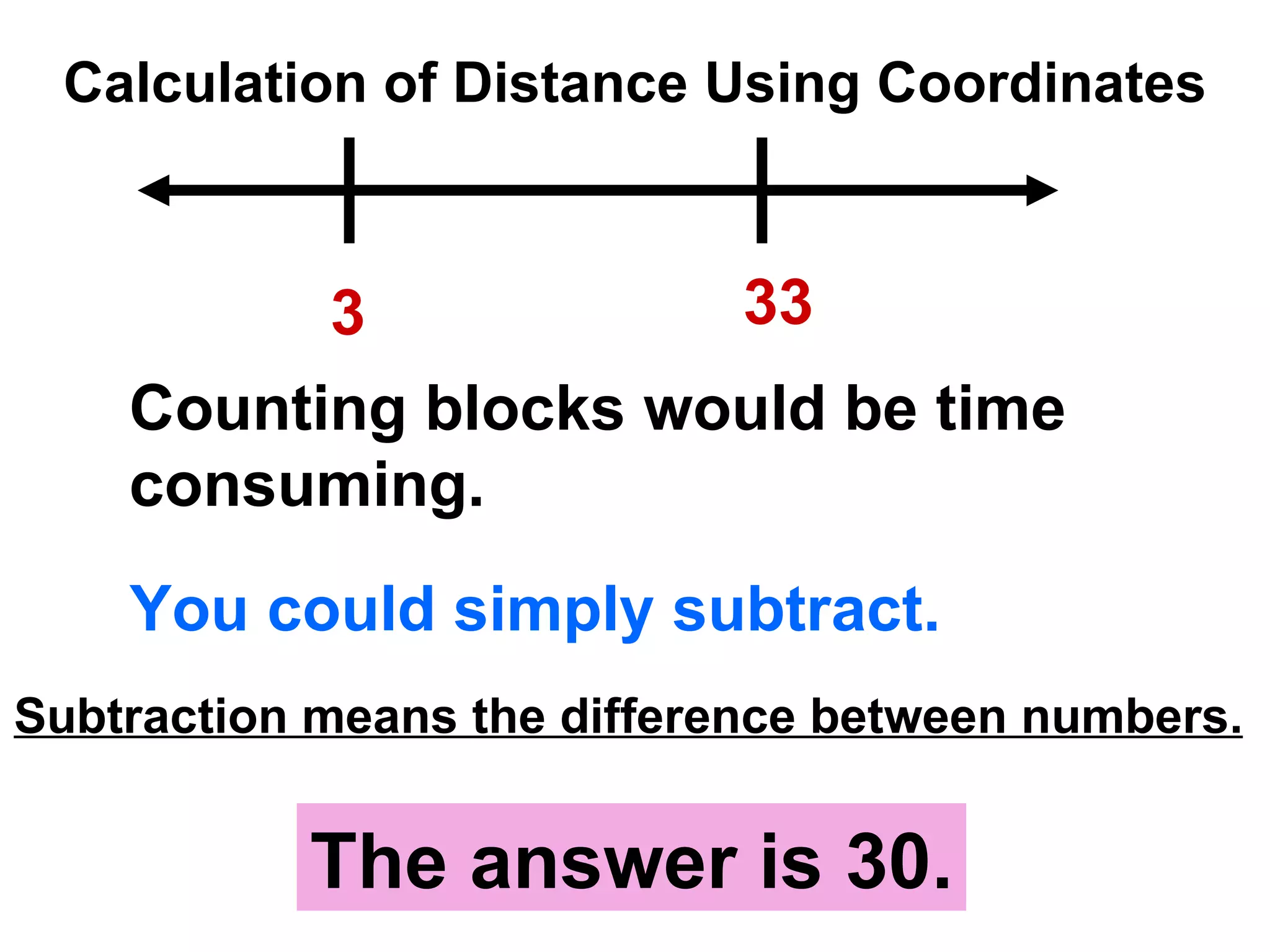
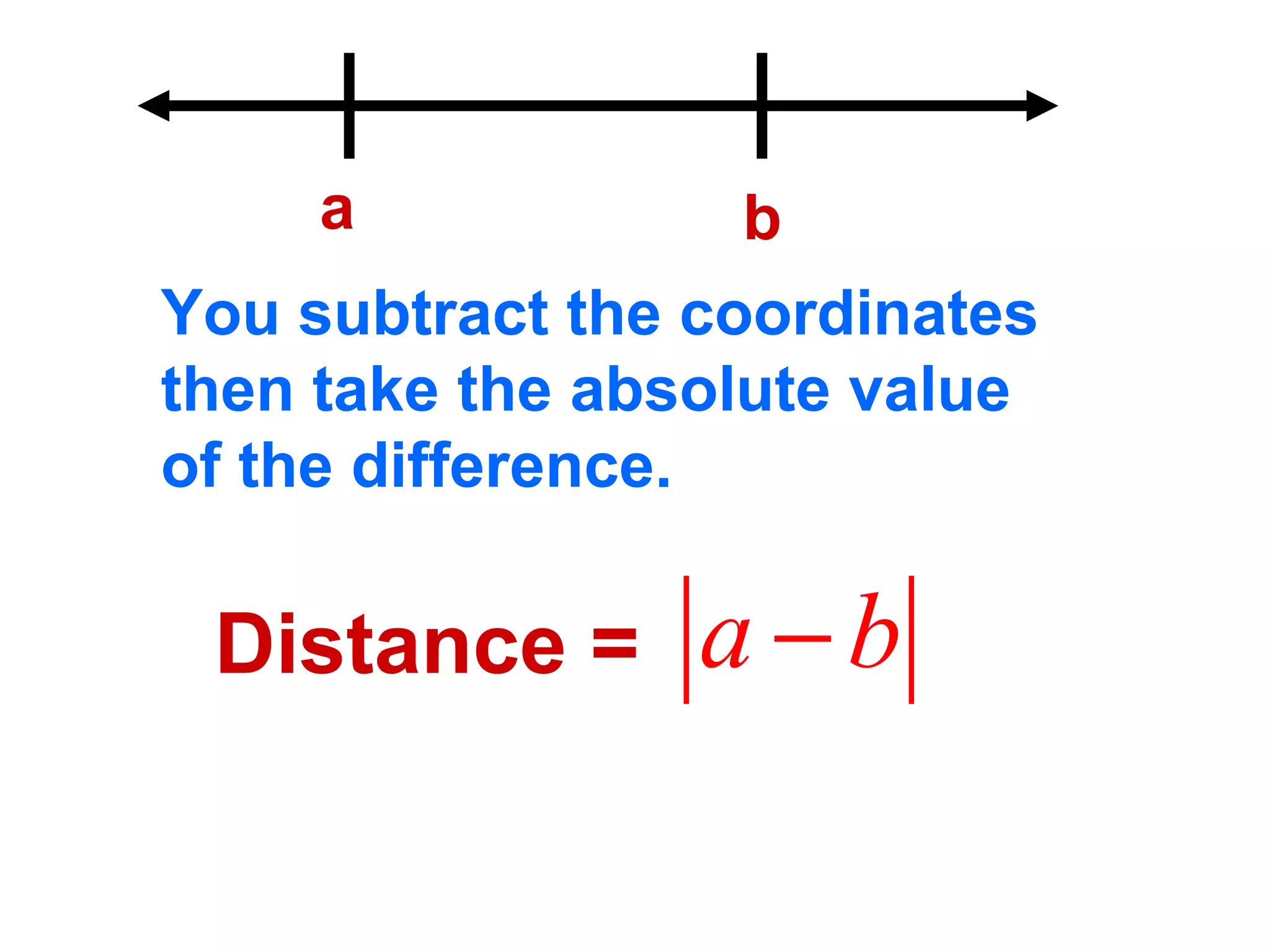
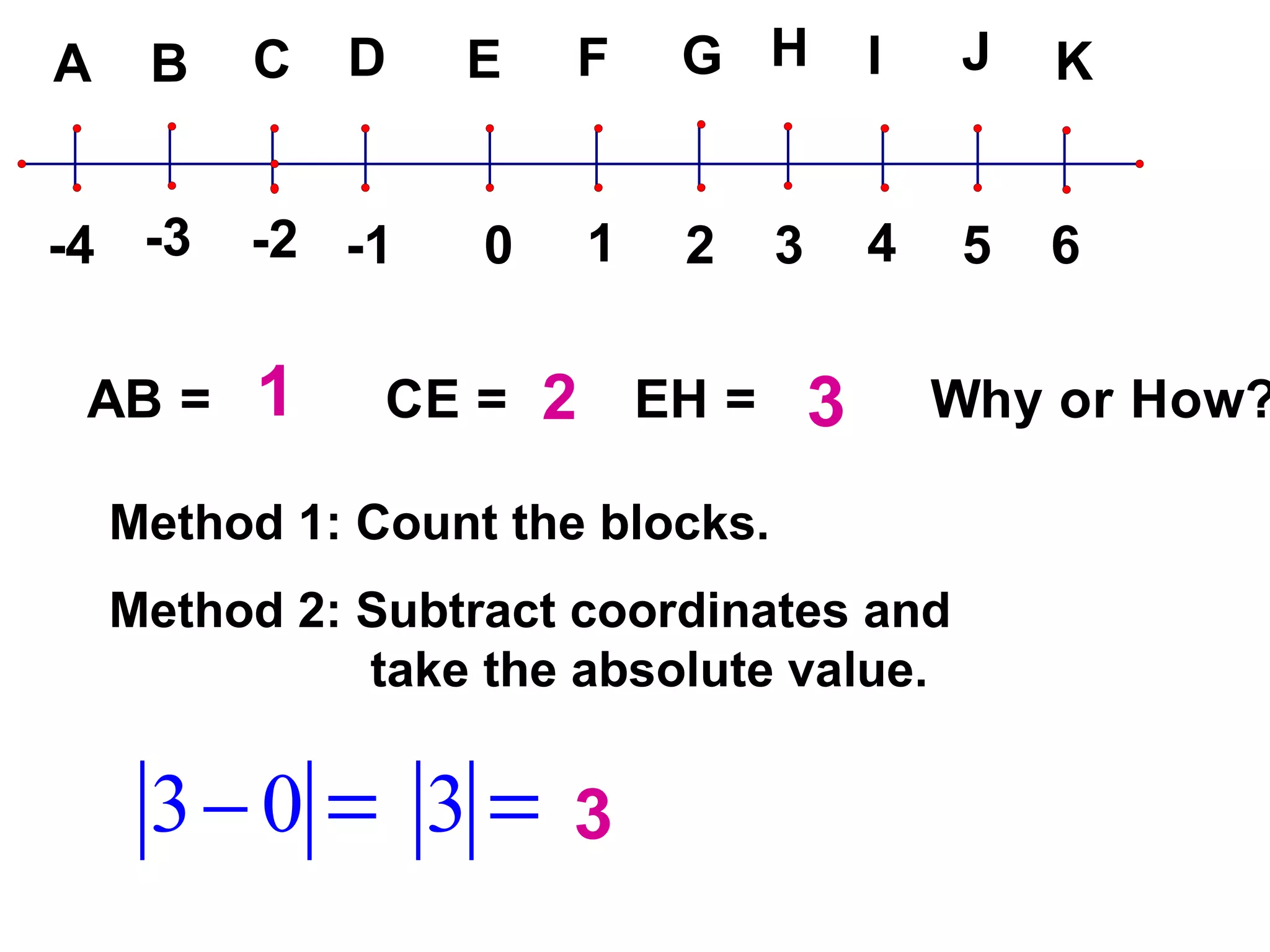
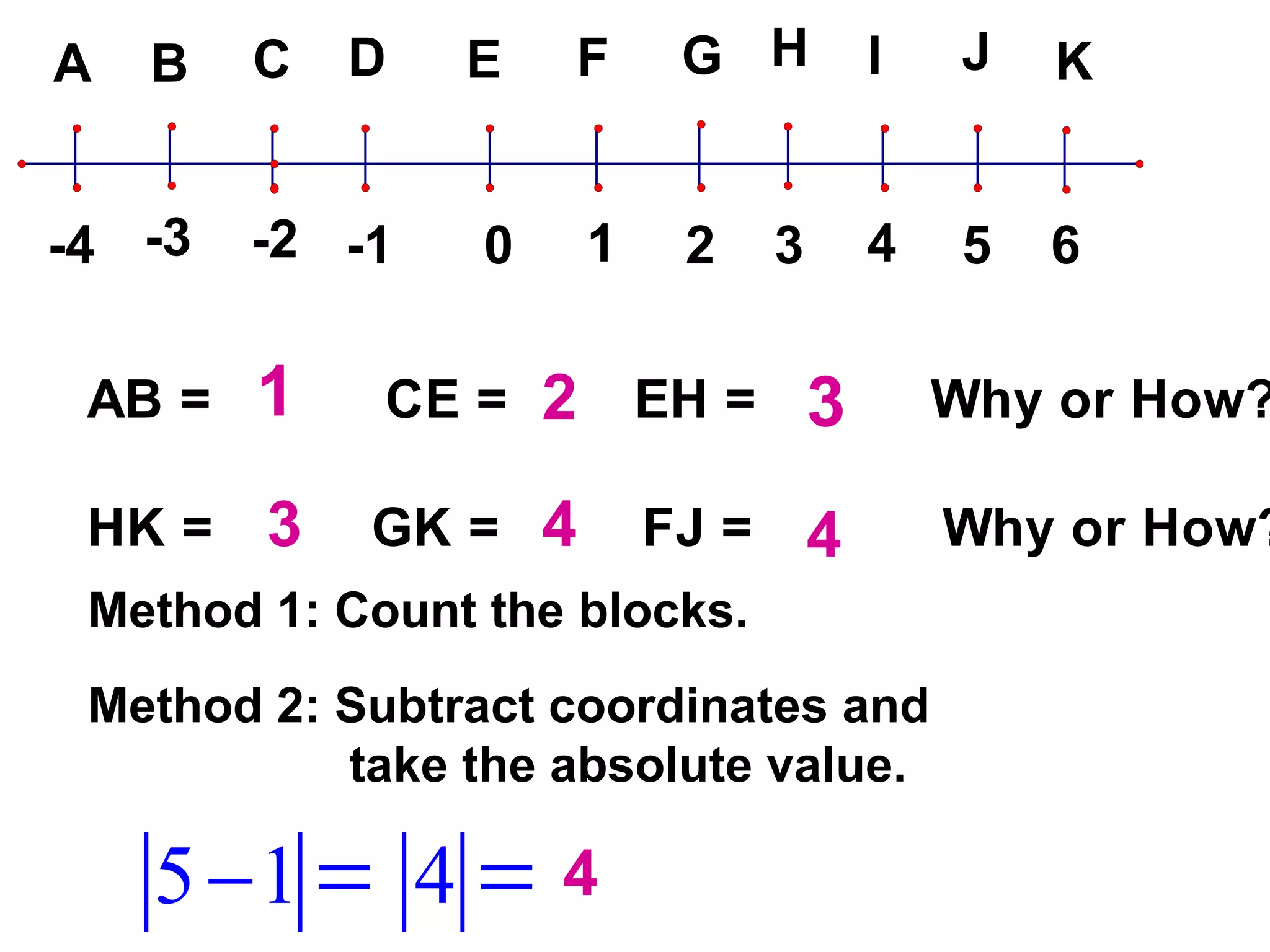
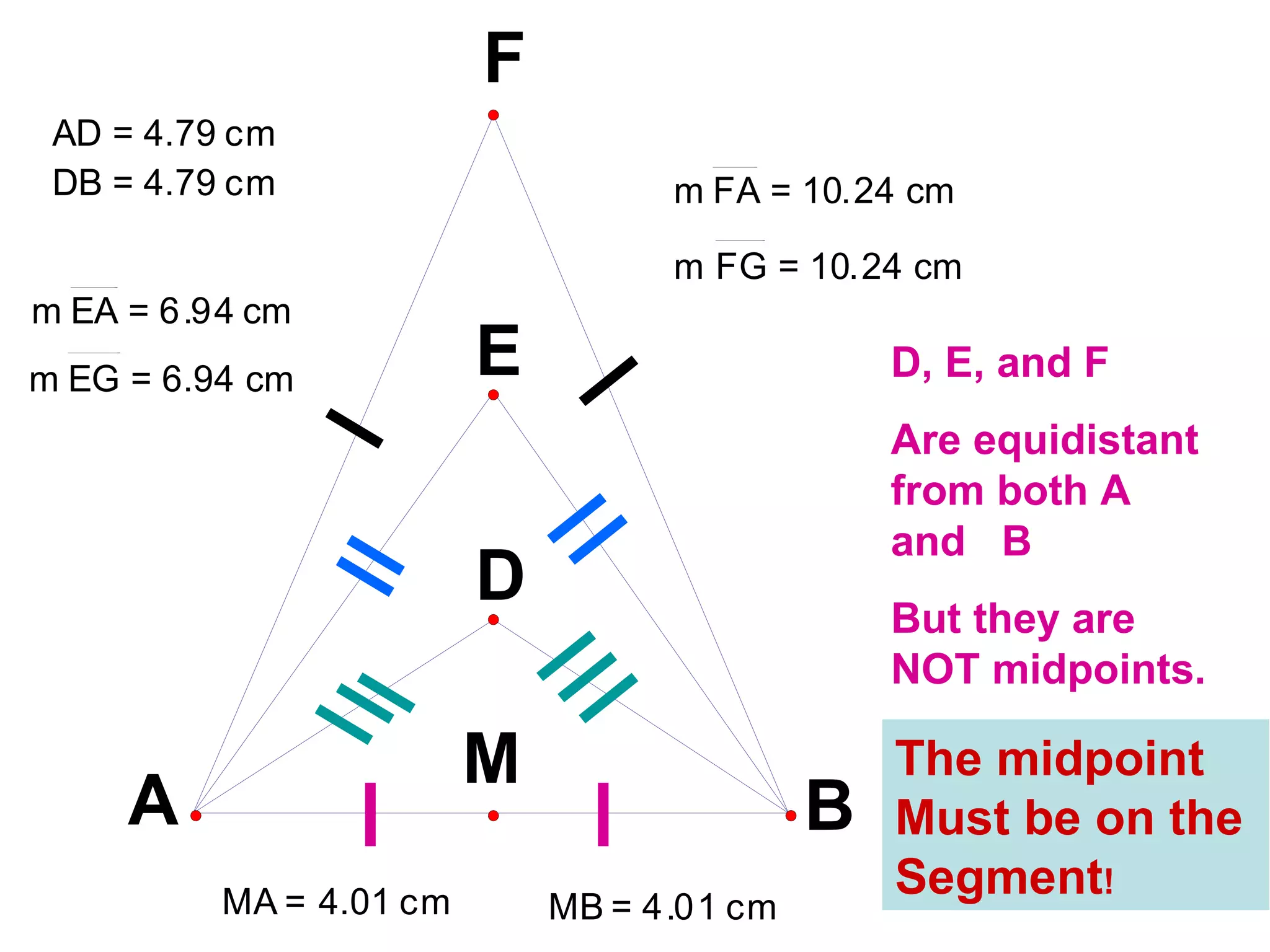
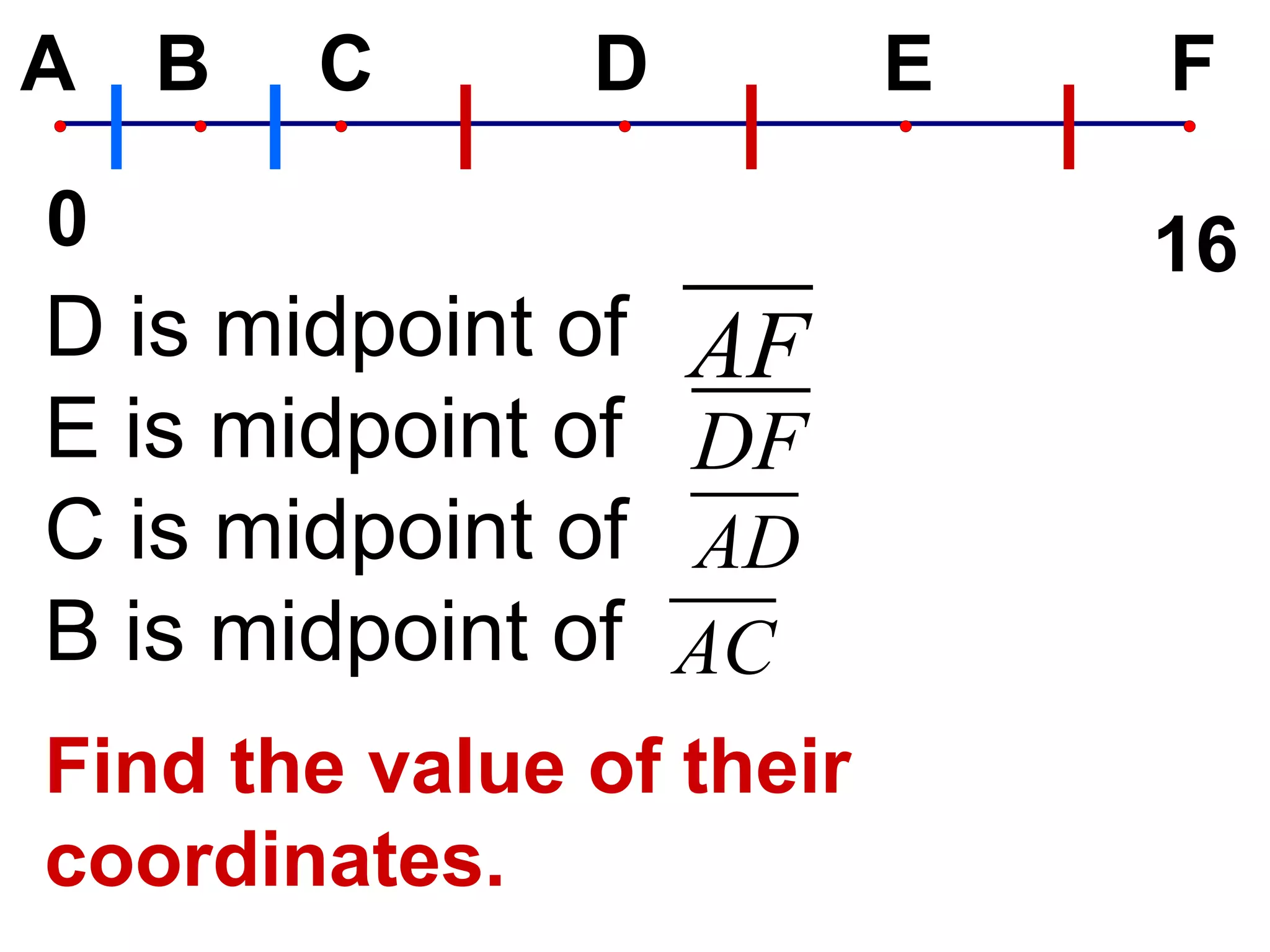
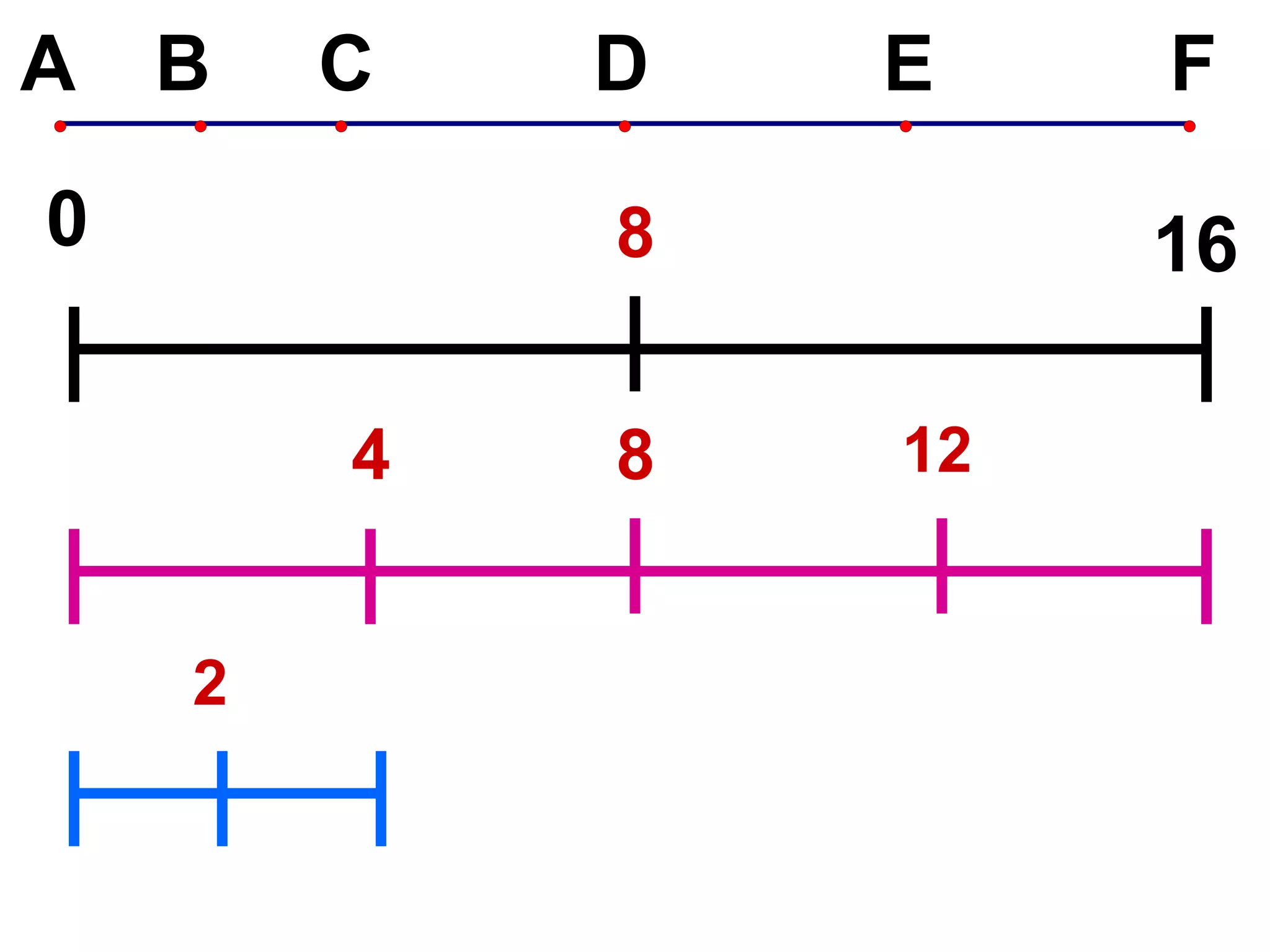
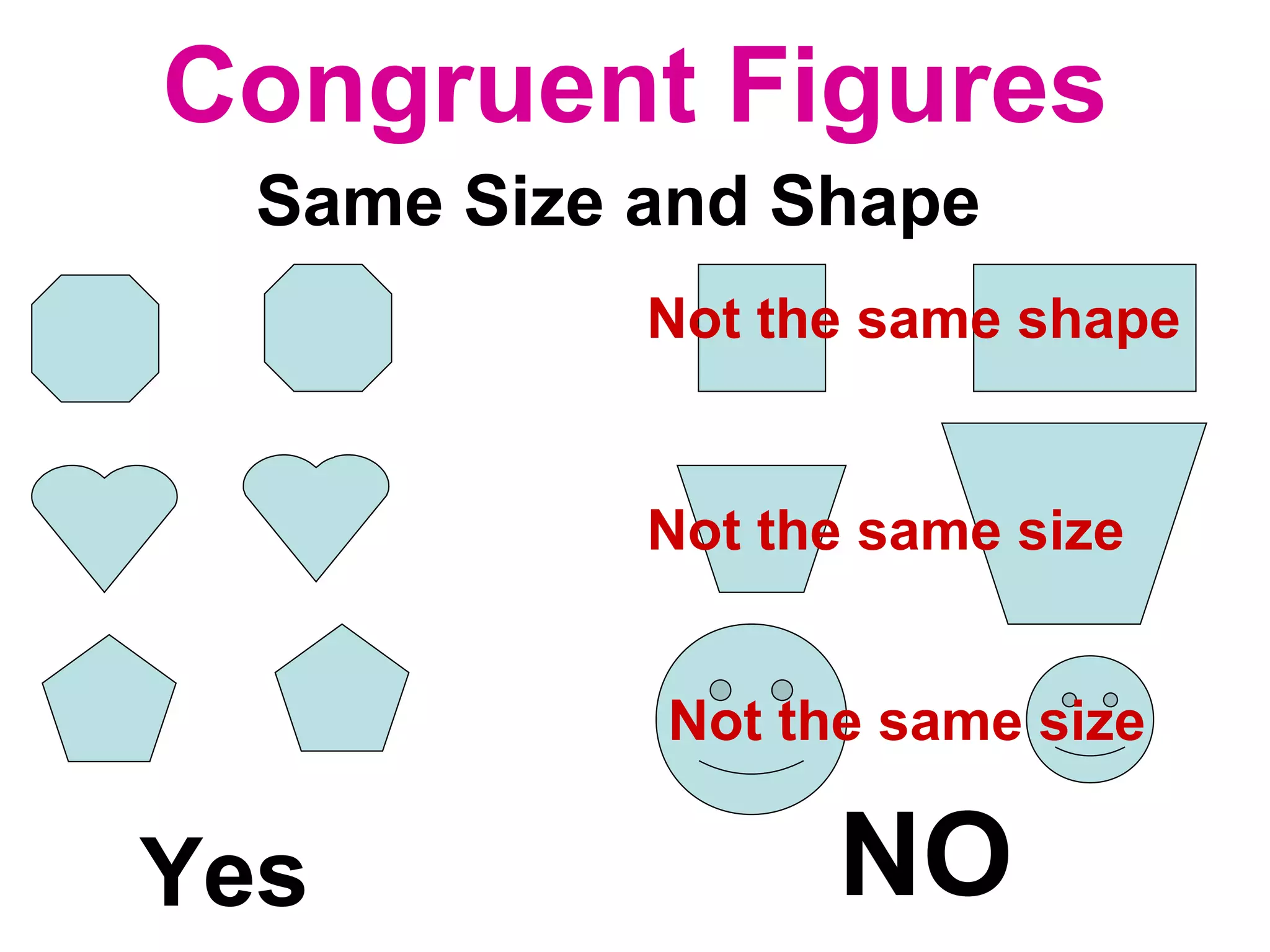
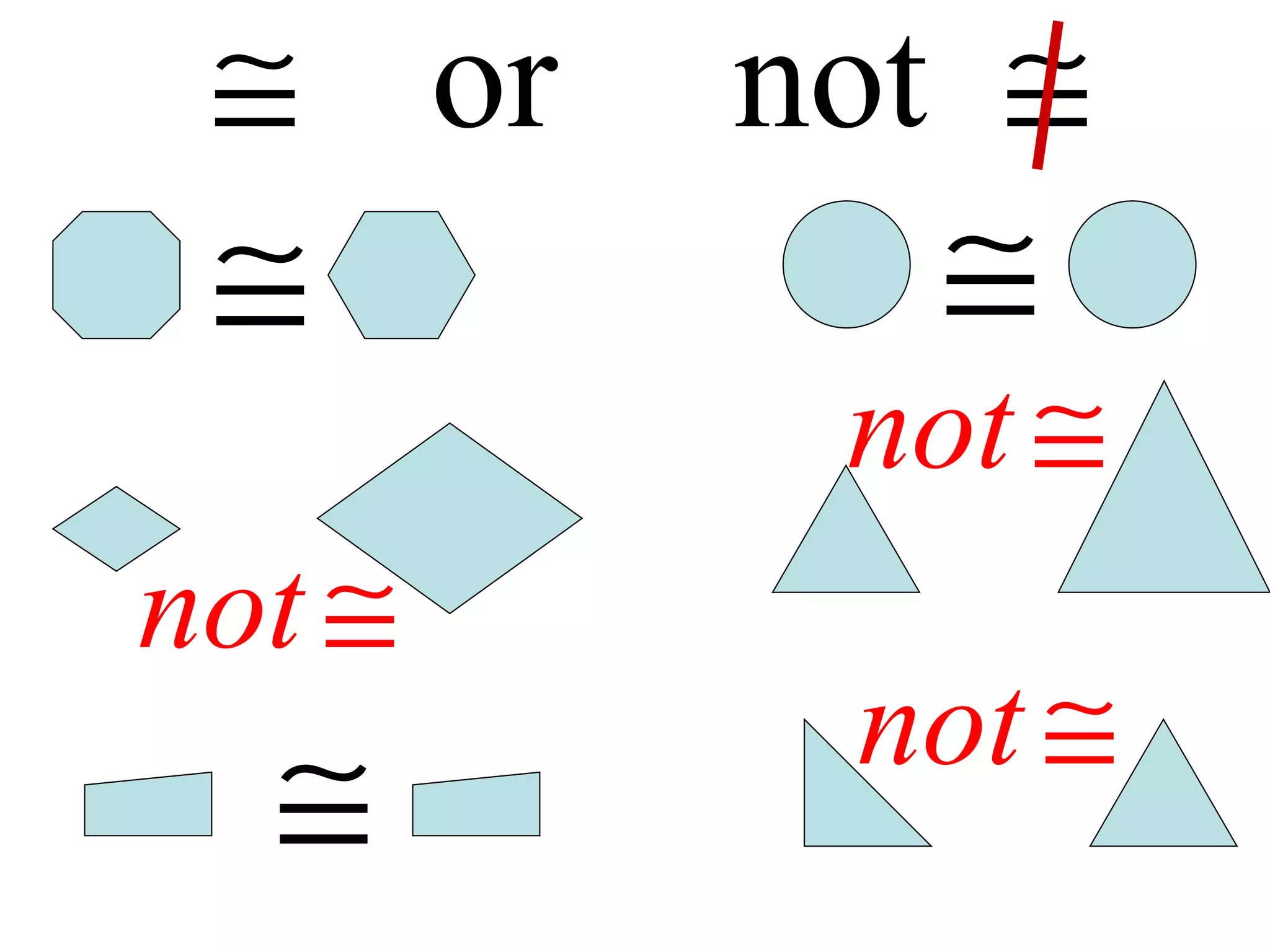
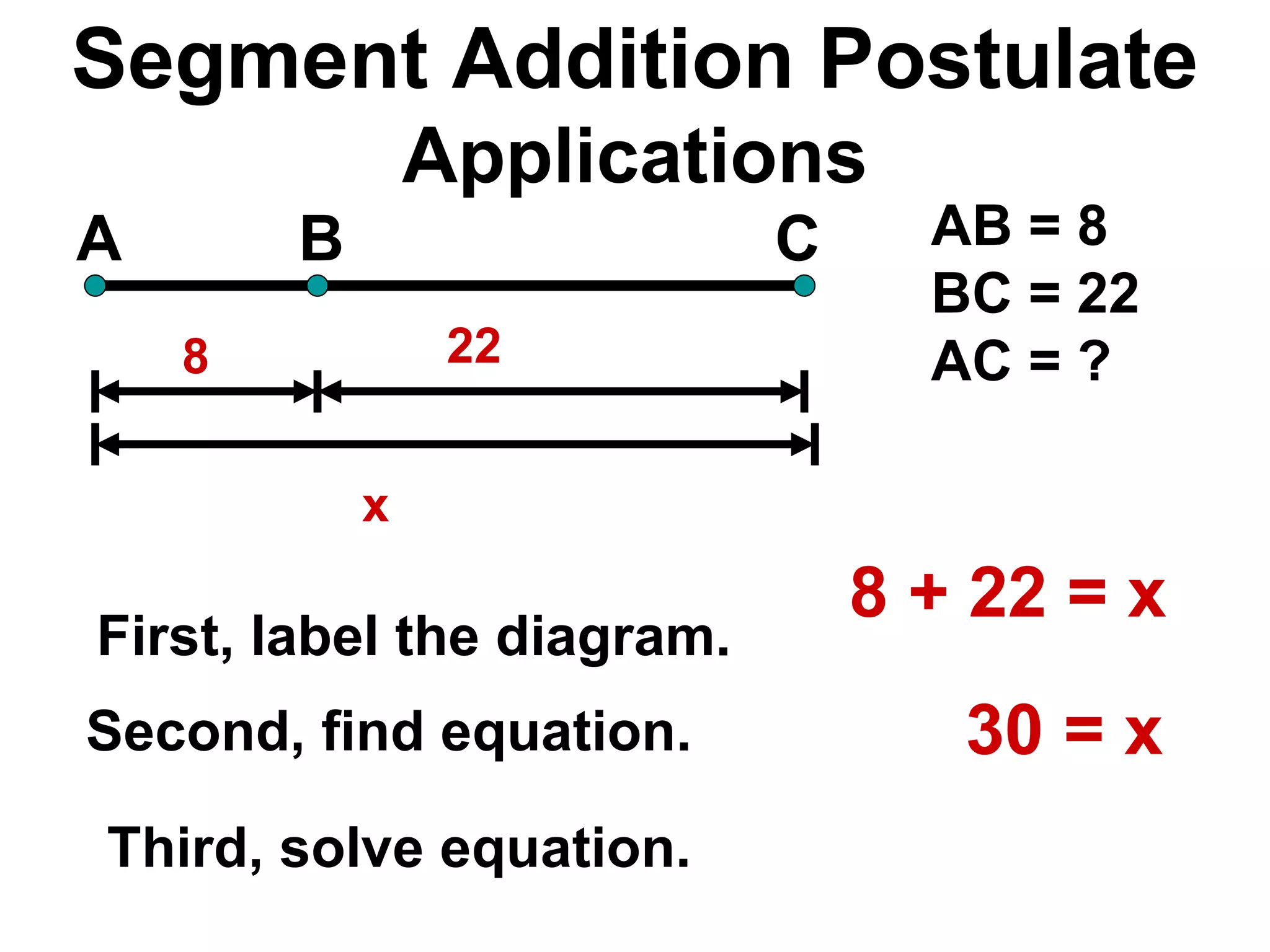
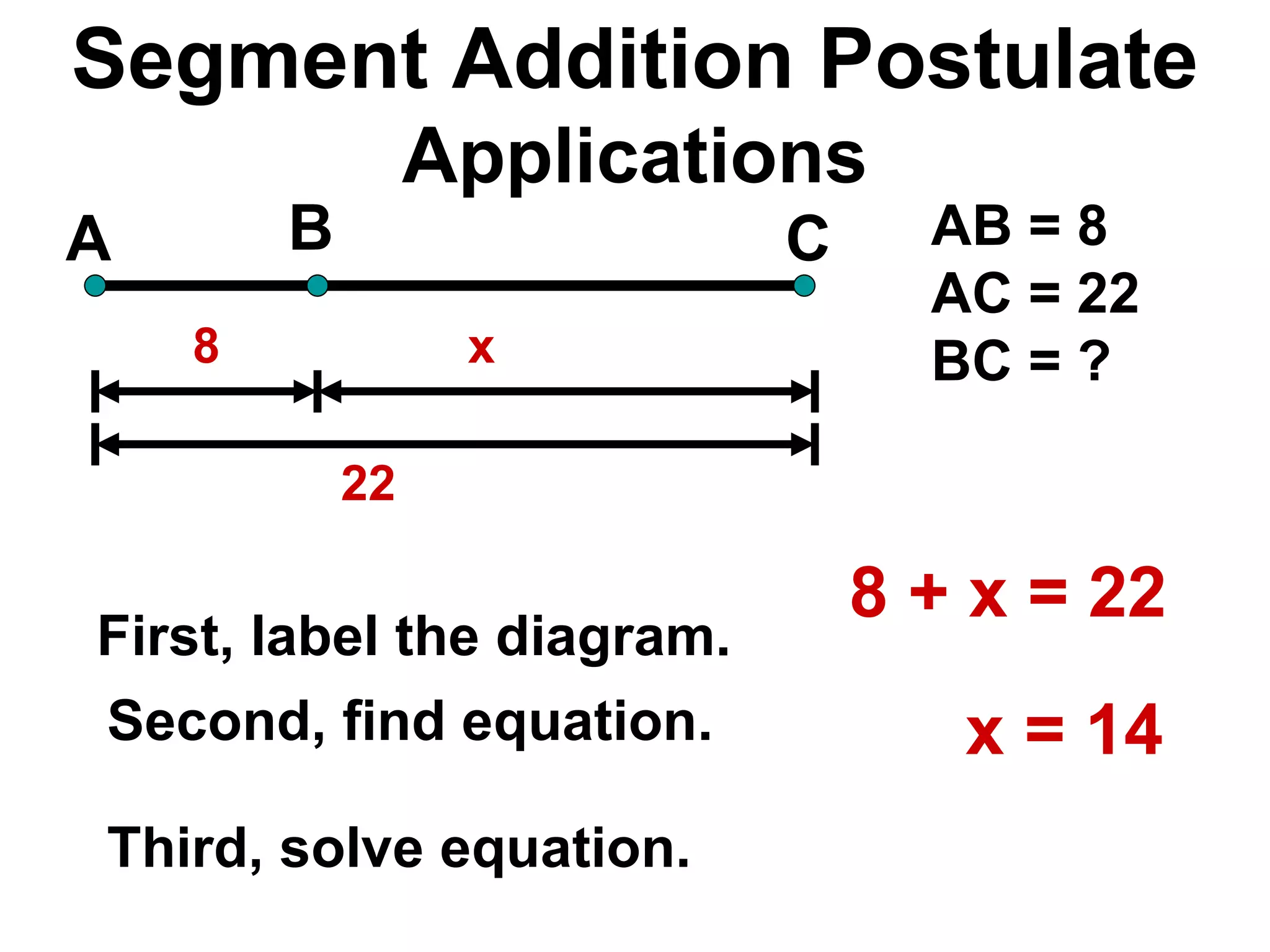
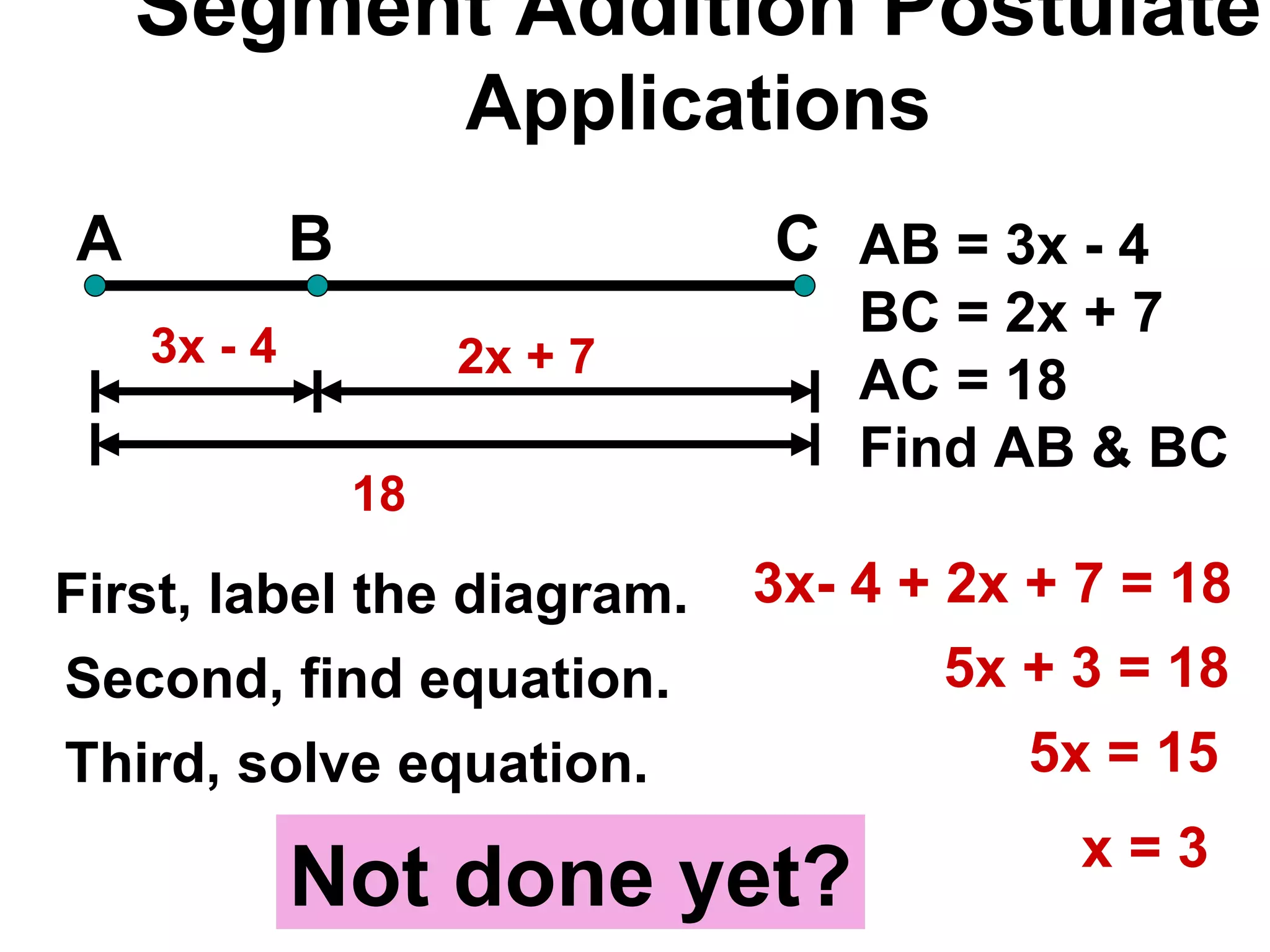
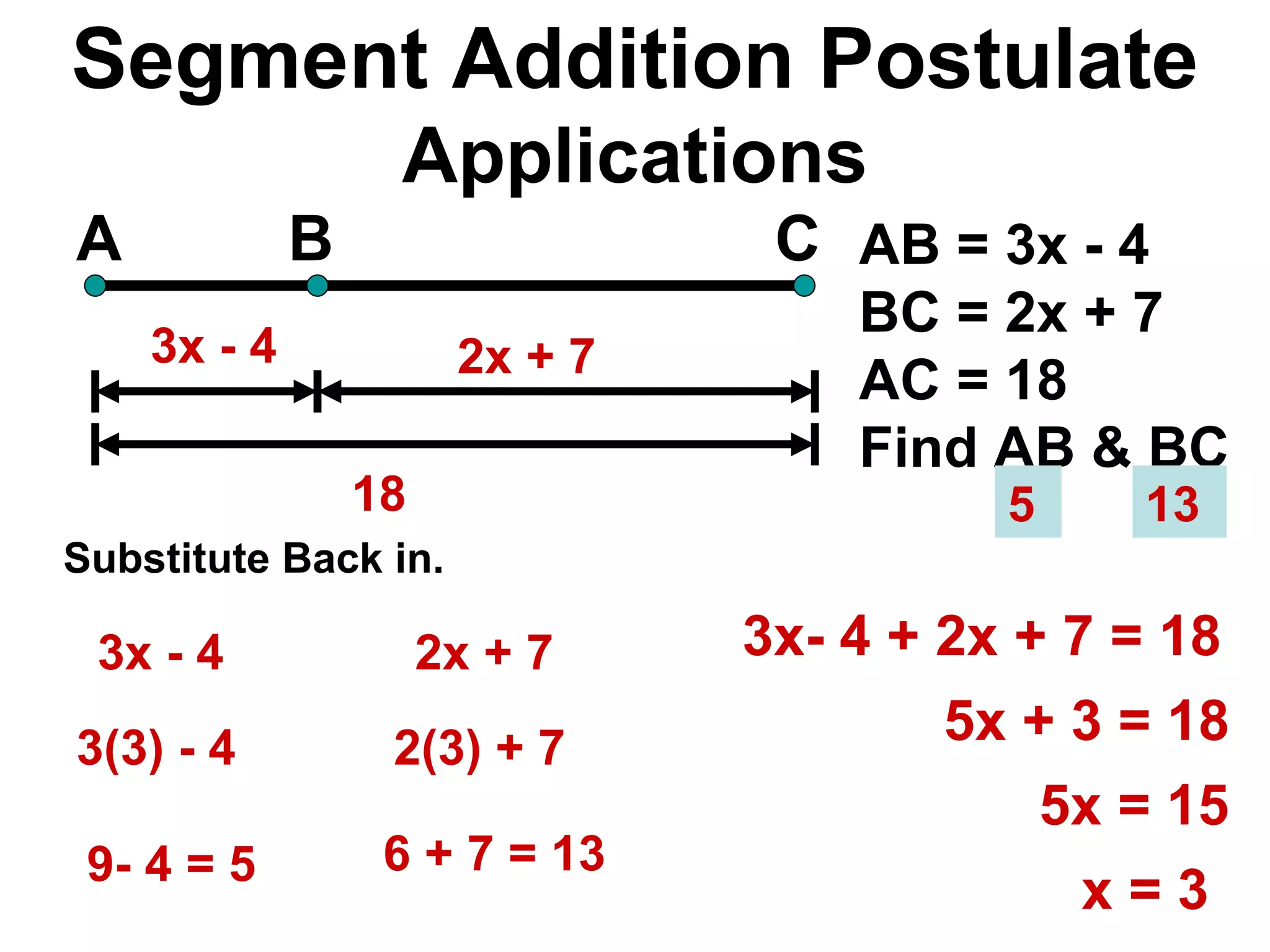
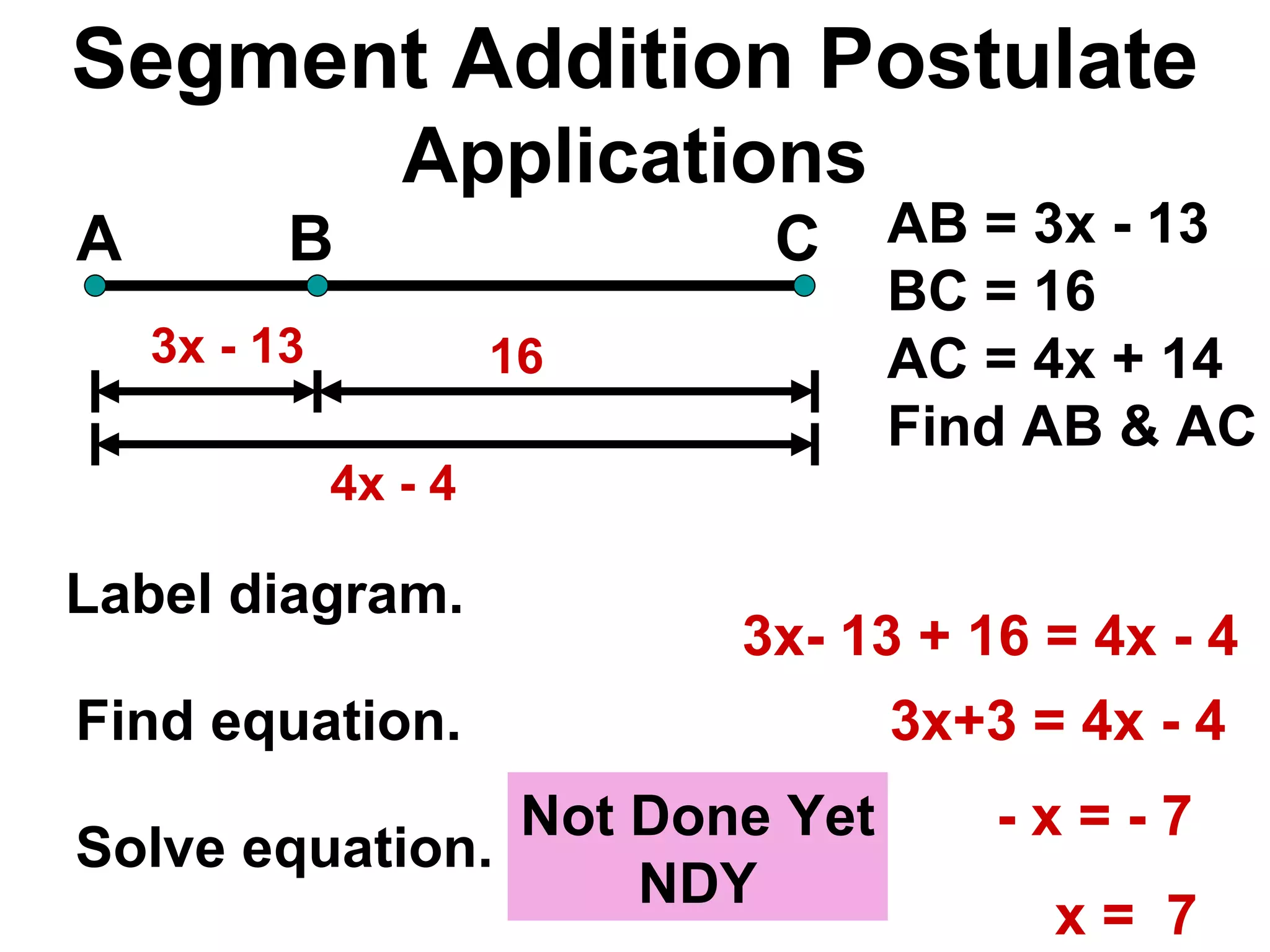
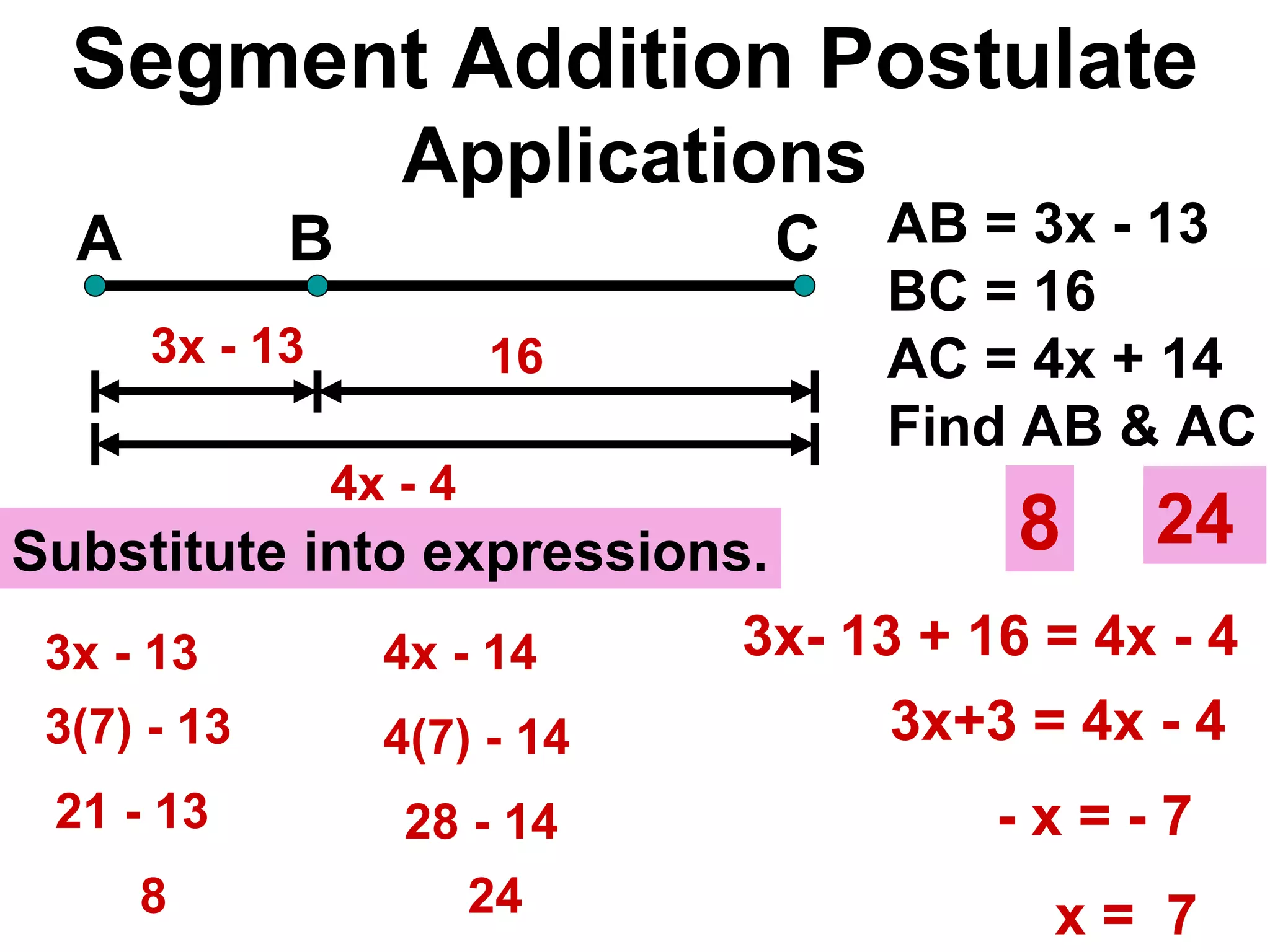
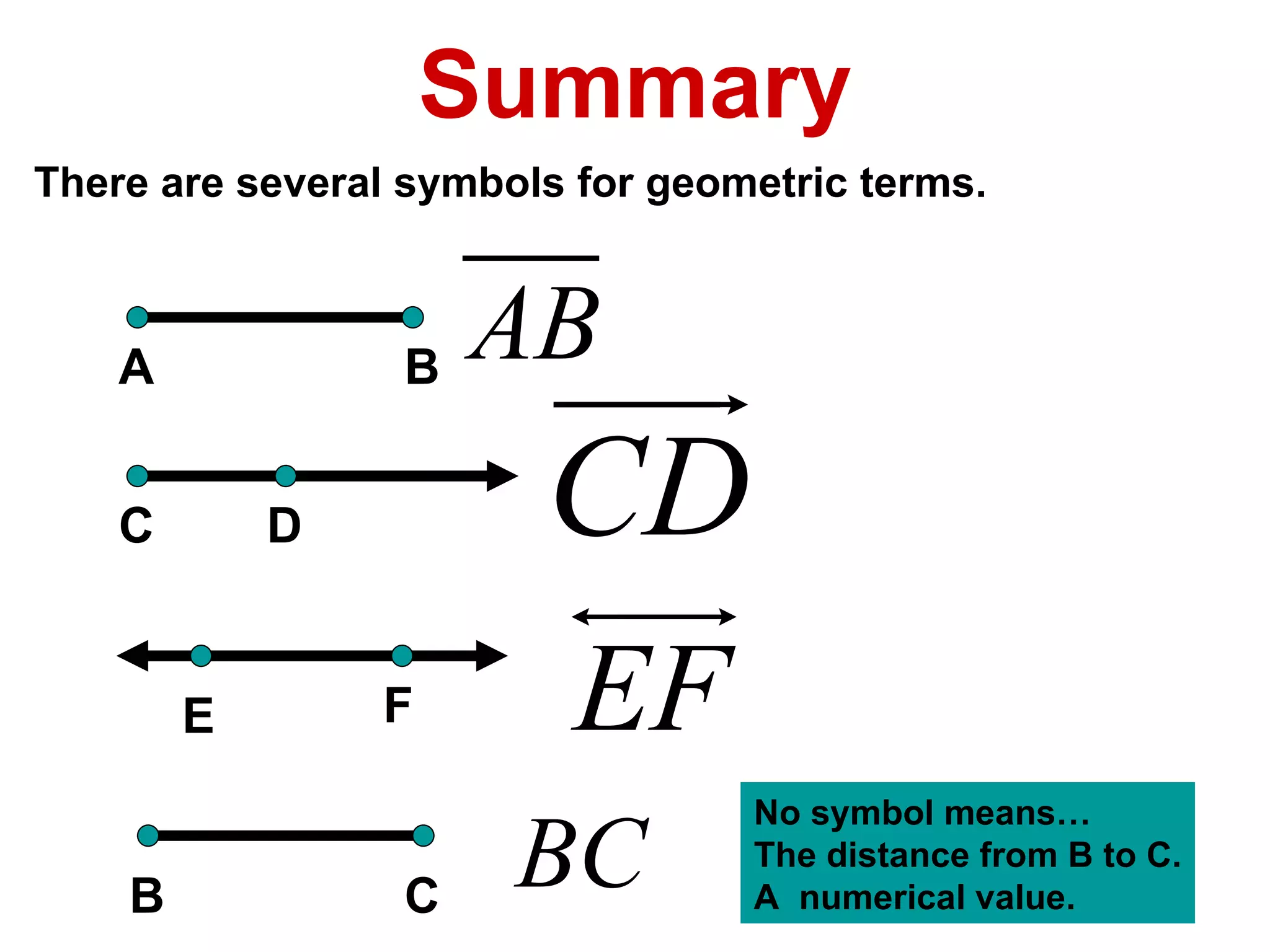
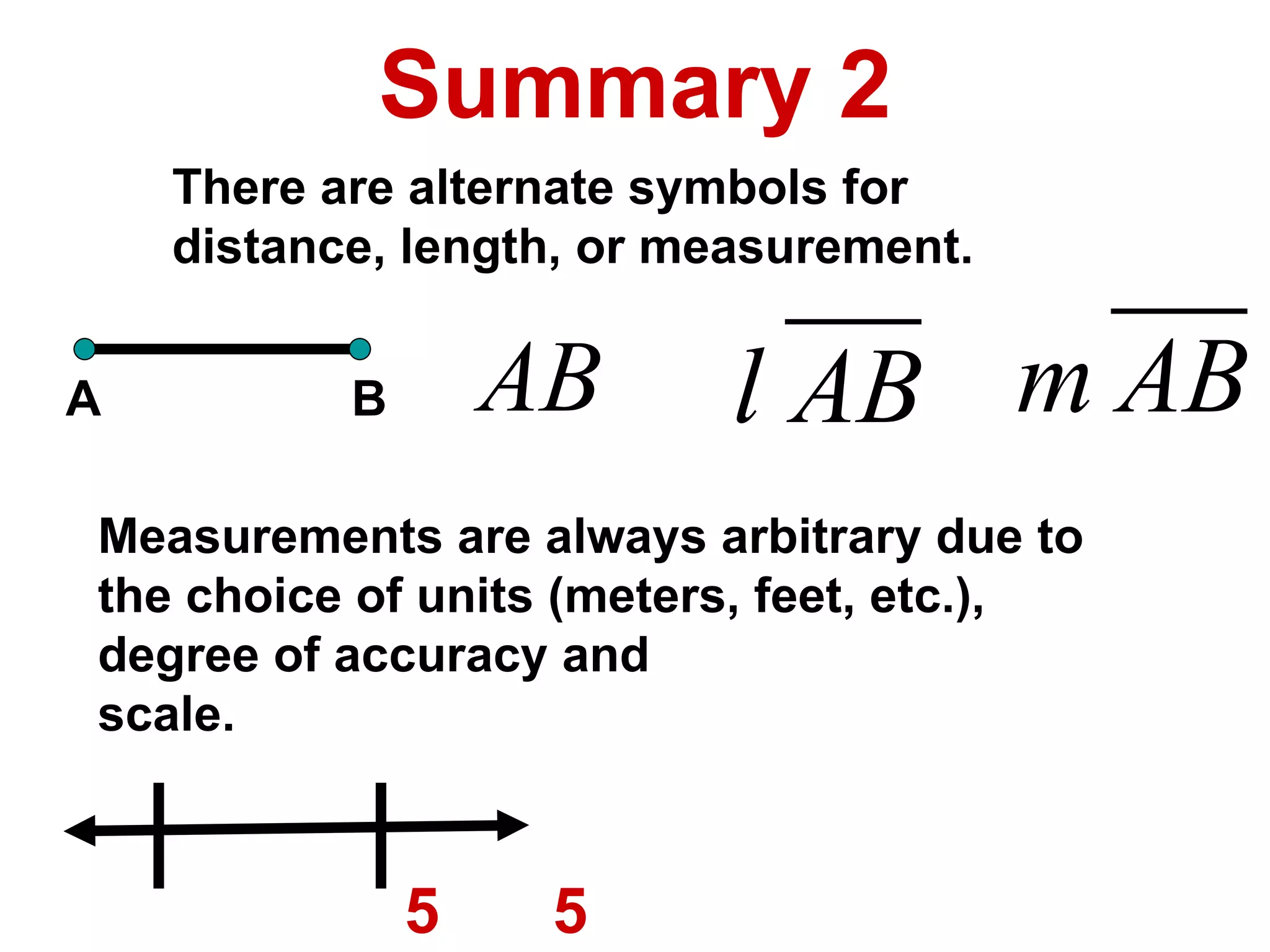
The document discusses various geometric symbols and concepts. Key symbols represent points, lines, segments, rays, and distance. Measurements are arbitrary due to choice of units and accuracy. Coordinates assign numbers to points on a number line to indicate position. The ruler postulate allows computing distance as the absolute value of coordinate differences. The segment addition postulate states the distance along a line equals the sum of its parts. Solving algebraic problems using these concepts is emphasized.

1. Symbols and Geometric Elements Segment A B or Ray A B Line F E or

2. Ray Notation Notice the position of the end point and the ray above. A B C D

3. Line Variations A B C D E or Any two letters can be used to name the line. Therefore, there can be multiple correct answers and confusion.

4. More Symbols Mathematical Shorthand B A Segments Set of Points Length or Measurement Or Distance A Number NOT a set of points

5. Inches , centimeters, feet , meters, etc. If a coordinate system is used on a line, then ALGEBRA comes into play. Just use a ruler. Measurements are arbitrary because the units of measurements are arbitrary. Measurements

6. Measure the Lines Below

7. Tolerance Measurements are never exact. They are always open to interpretation. Answers are sometimes rounded up. Answers are sometimes rounded down. Some visual interpretations are different. There may be a scale. The degree of accuracy depends on the accuracy of the equipment. The degree of accuracy depends on the accuracy of measurer.

8. Coordinate Systems Coordinate are numbers. Points are letters

9. The name of the red pt. is ___ The coordinate of the red pt. is ___ The name of the grey pt. is ___ The coordinate of the grey pt. is __ E 0 J 5

10. Find the coordinates J = ___ A = ___ C = ___ K = ___ 5 -4 -2 6

11. Calculation of Distance Using Coordinates 3 5 You could simply count the blocks. The answer is 2.

12. Calculation of Distance Using Coordinates 3 33 Counting blocks would be time consuming. The answer is 30. You could simply subtract. Subtraction means the difference between numbers.

13. Calculation of Distance Using Coordinates -8 33 The answer is 41. You could simply subtract. 33 – (-8) = 33 + 8 = 41 Note that negative numbers requires using algebra.

14. -8 -5 You could simply subtract. -5 – (-8) = -5 + 8 = 3 However if we subtract the numbers in reverse, then... -8 – (-5) = -8 + 5 = - 3 Therefore to avoid negative numbers, we take the absolute value of the differences.

15. a b You subtract the coordinates then take the absolute value of the difference. Distance =

16. 1 3 4 4 1 5 9 Method 1: Count the blocks. Method 2: Subtract coordinates and take the absolute value. 1

17. 1 2 3 4 4 1 5 9 Method 1: Count the blocks. Method 2: Subtract coordinates and take the absolute value. 2

18. 1 2 3 3 4 4 1 5 9 Method 1: Count the blocks. Method 2: Subtract coordinates and take the absolute value. 3

19. 1 2 3 3 1 5 9 Method 1: Count the blocks. Method 2: Subtract coordinates and take the absolute value. 3

20. 1 2 3 4 4 1 5 9 Method 1: Count the blocks. Method 2: Subtract coordinates and take the absolute value. 3

21. 1 2 3 4 4 4 1 5 9 Method 1: Count the blocks. Method 2: Subtract coordinates and take the absolute value. 3

22. 1 2 3 3 4 4 1 5 Method 1: Count the blocks. Method 2: Subtract coordinates and take the absolute value. 5

23. 1 2 3 3 4 4 1 5 9 Method 1: Count the blocks. Method 2: Subtract coordinates and take the absolute value. 9

24. Ruler Postulate The points on a line can be paired up with real numbers in such a way that any two points can have coordinates of 0 or 1. Once the coordinates have been chosen in this way, the distance between the any two points is the absolute value of the difference of their coordinates. The measuring scale is arbitrary .

25. If M is on the segment and M is a midpoint of It is necessary for both conditions. Let’s see why?

26. D, E, and F Are equidistant from both A and B But they are NOT midpoints. The midpoint Must be on the Segment !

27. Bisectors Bisectors can be any segment, ray, line, or plane if they go thru the midpoint of a segment.

28. D is midpoint of E is midpoint of C is midpoint of B is midpoint of Find the value of their coordinates.

29. 8 8 4 12 2

30. Symbol Scramble Segment Length of Segment Line Ray length of Segment Measure of Segment

31. Congruent Figures Same Size and Shape Yes NO Not the same shape Not the same size Not the same size

33. Distance Between Coordinates 4 12 12 8 -5 7 0 12 0 -12 -2 12 -12 -8 -5 7 0 18 0 -15 -12 12

34. Sometime, Always & Never The length of a segment is ______ negative. If point S is between points A and B, then S _____ lies on the segment. A coordinate can ______ be paired with a point on a number line. A bisector of a segment is __________ a line. A ray ______ has a midpoint. Always Never Always Never Sometimes

35. Sometime, Always & Never A ray _____ has an endpoint. Congruent segments ______ have equal lengths. and _____ denote the same rays. A line _____ has one midpoint. A ____ has many midpoints. Why? Always Always Never Never Always

36. Segment Addition Postulate A B C If B is between A and C, then…. AB + BC = AC Note: Between means that A, B, and C are collinear. B must be on the segment AC.

37. Segment Addition Postulate Applications A B C 22 AB = 8 BC = 22 AC = ? 8 First, label the diagram. x Second, find equation. Third, solve equation. 8 + 22 = x 30 = x

38. Segment Addition Postulate Applications A B C 22 AB = 8 AC = 22 BC = ? 8 First, label the diagram. x Second, find equation. Third, solve equation. 8 + x = 22 x = 14

39. Segment Addition Postulate Applications A B C 18 AB = 3x - 4 BC = 2x + 7 AC = 18 Find AB & BC 3x - 4 First, label the diagram. 2x + 7 Second, find equation. Third, solve equation. 3x- 4 + 2x + 7 = 18 5x + 3 = 18 5x = 15 x = 3 Not done yet?

40. Segment Addition Postulate Applications A B C 18 AB = 3x - 4 BC = 2x + 7 AC = 18 Find AB & BC 3x - 4 2x + 7 3x- 4 + 2x + 7 = 18 5x + 3 = 18 5x = 15 x = 3 Substitute Back in. 3x - 4 3(3) - 4 9- 4 = 5 2x + 7 2(3) + 7 6 + 7 = 13 13 5

41. Segment Addition Postulate Applications A B C 16 AB = 3x - 13 BC = 16 AC = 4x + 14 Find AB & AC 3x - 13 4x - 4 3x- 13 + 16 = 4x - 4 - x = - 7 Label diagram. Find equation. Solve equation. 3x+3 = 4x - 4 x = 7 Not Done Yet NDY

42. Segment Addition Postulate Applications A B C 16 AB = 3x - 13 BC = 16 AC = 4x + 14 Find AB & AC 3x - 13 4x - 4 3x- 13 + 16 = 4x - 4 - x = - 7 Substitute into expressions. 3x+3 = 4x - 4 x = 7 3x - 13 3(7) - 13 21 - 13 8 8 4(7) - 14 4x - 14 28 - 14 24 24

43. You must be able to do these complex algebraic problems. They will be in the chapter test and the marking period exam (QPA)

44. Summary A B There are several symbols for geometric terms. C D F E B C No symbol means… The distance from B to C. A numerical value.

45. Summary 2 A B There are alternate symbols for distance, length, or measurement. 5 5 Measurements are always arbitrary due to the choice of units (meters, feet, etc.), degree of accuracy and scale.

46. Summary 3 The letters are the names of the points. The numbers are the coordinates that indicate the relative position of each point.

47. Summary 4 The ruler postulate allows us to… 1. Build number lines at any scale. 2. Compute distance by taking the absolute value of the difference of the coordinates.

48. Summary 5 The segment addition postulate allows us to conclude… The distance on a line is the sum of its parts. A B C AB + BC = AC

49. Summary 6 A B C 18 AB = 3x - 4 BC = 2x + 7 AC = 18 Find AB & BC 3x - 4 2x + 7 You must be able to do these algebraic problems.

50. C’est fini. Good day and good luck.