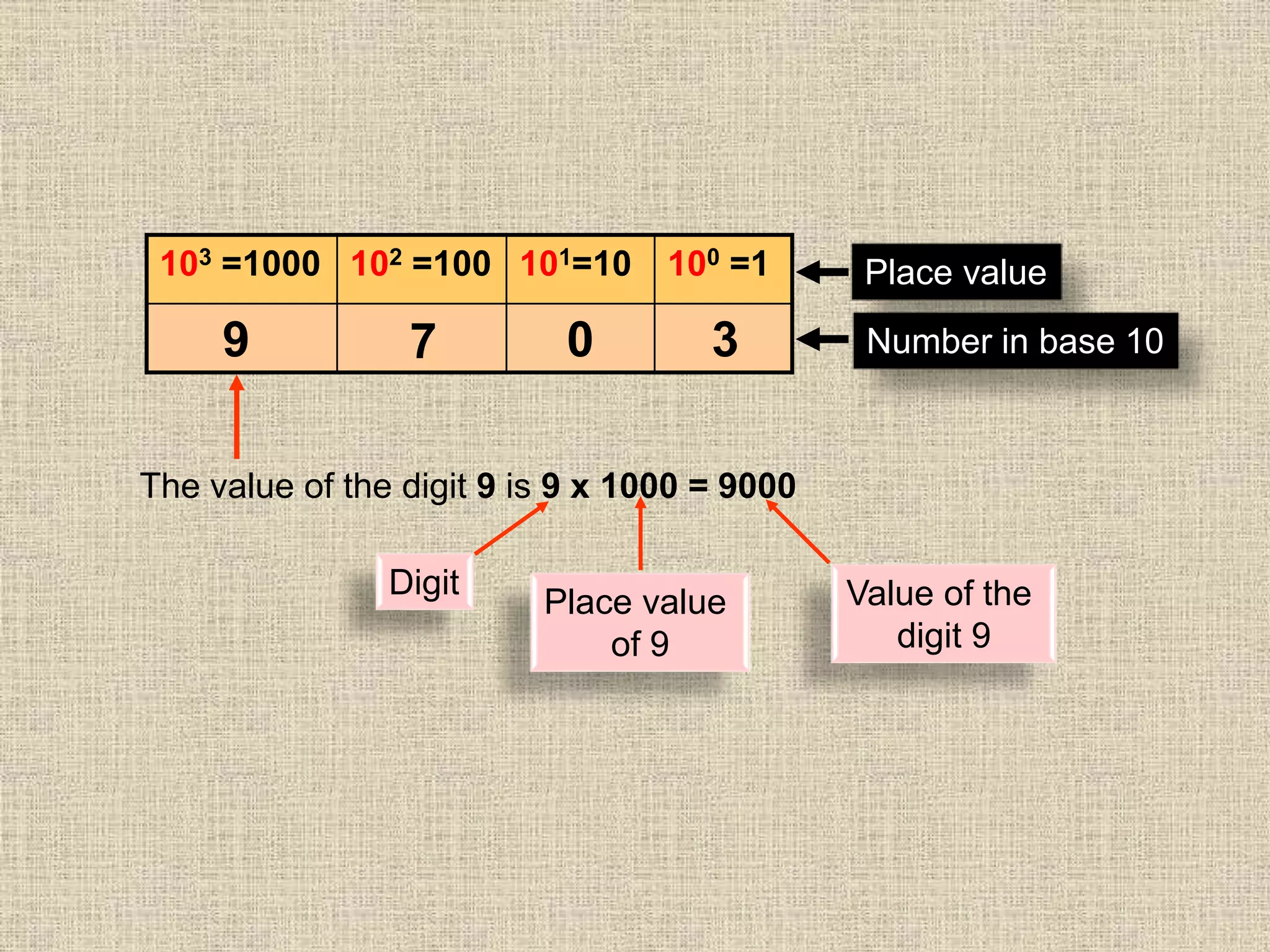
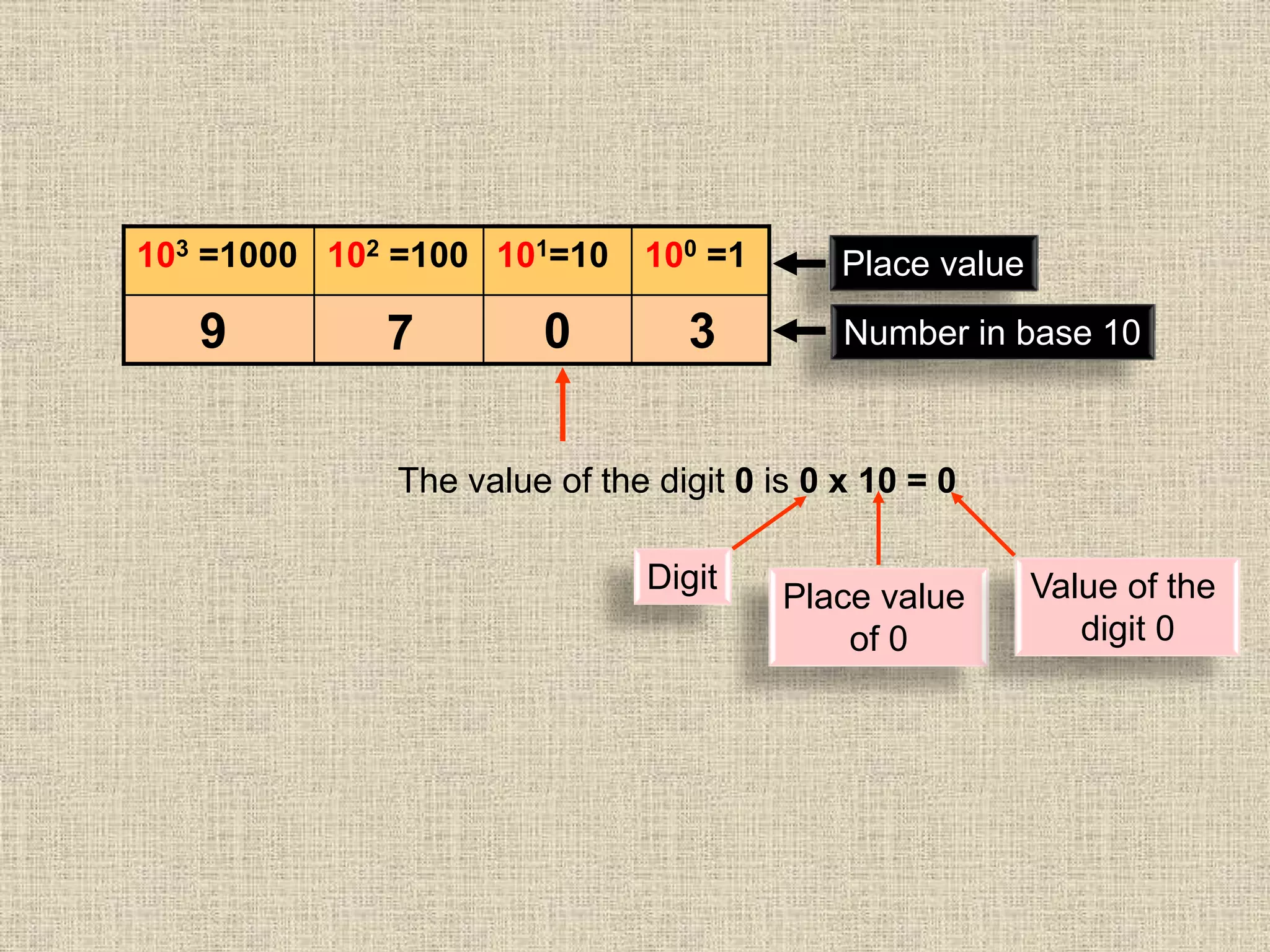
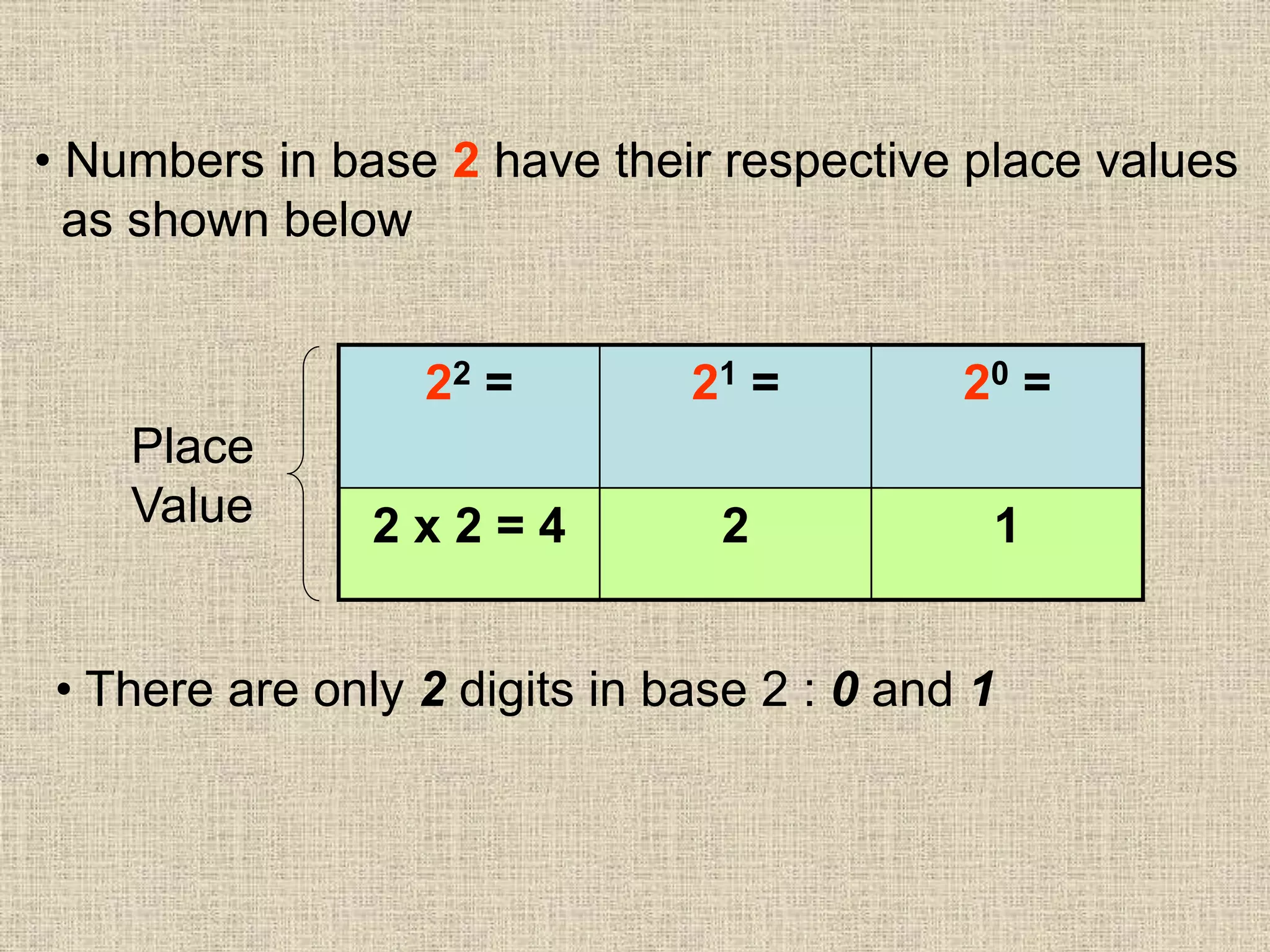
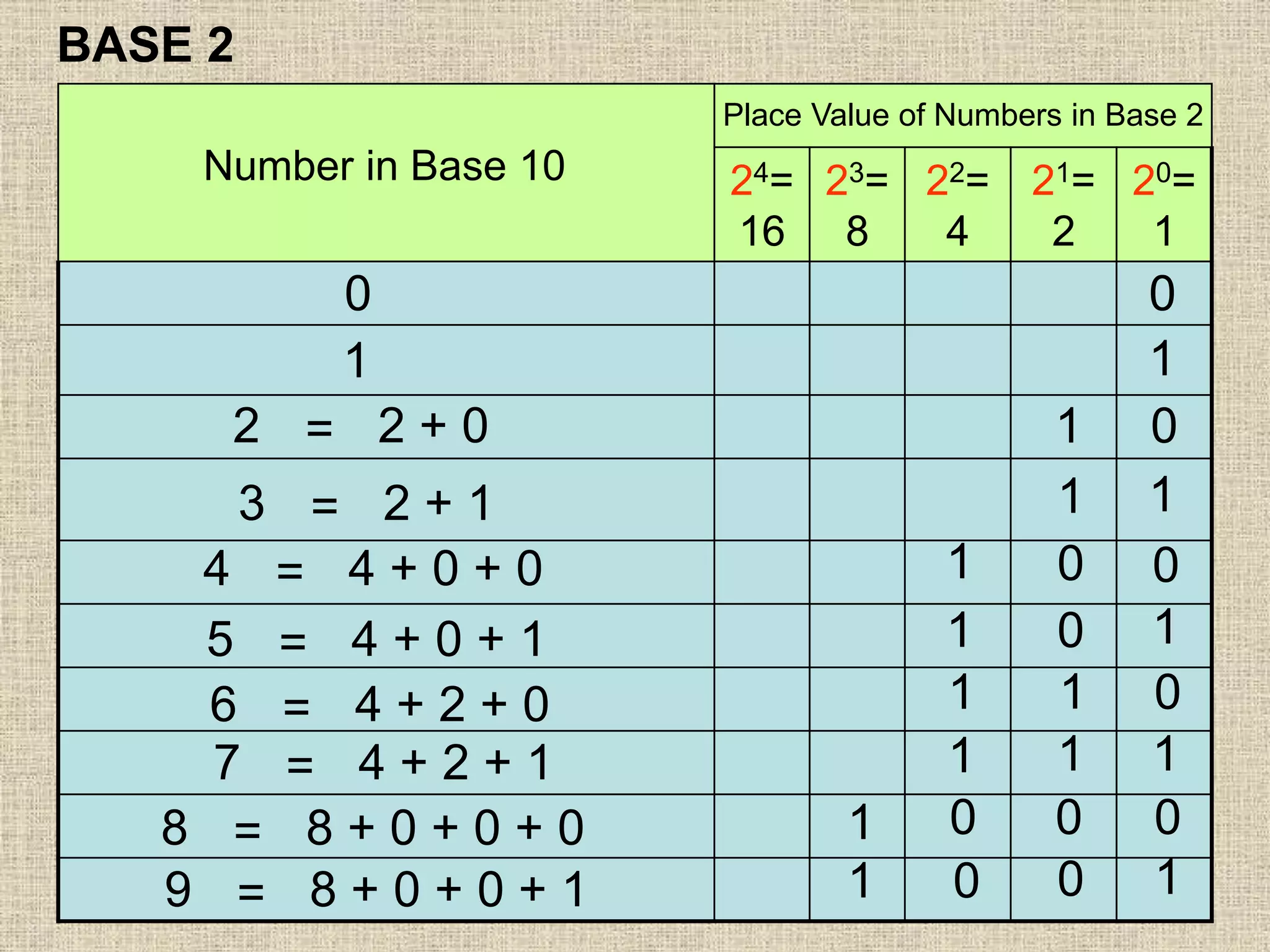
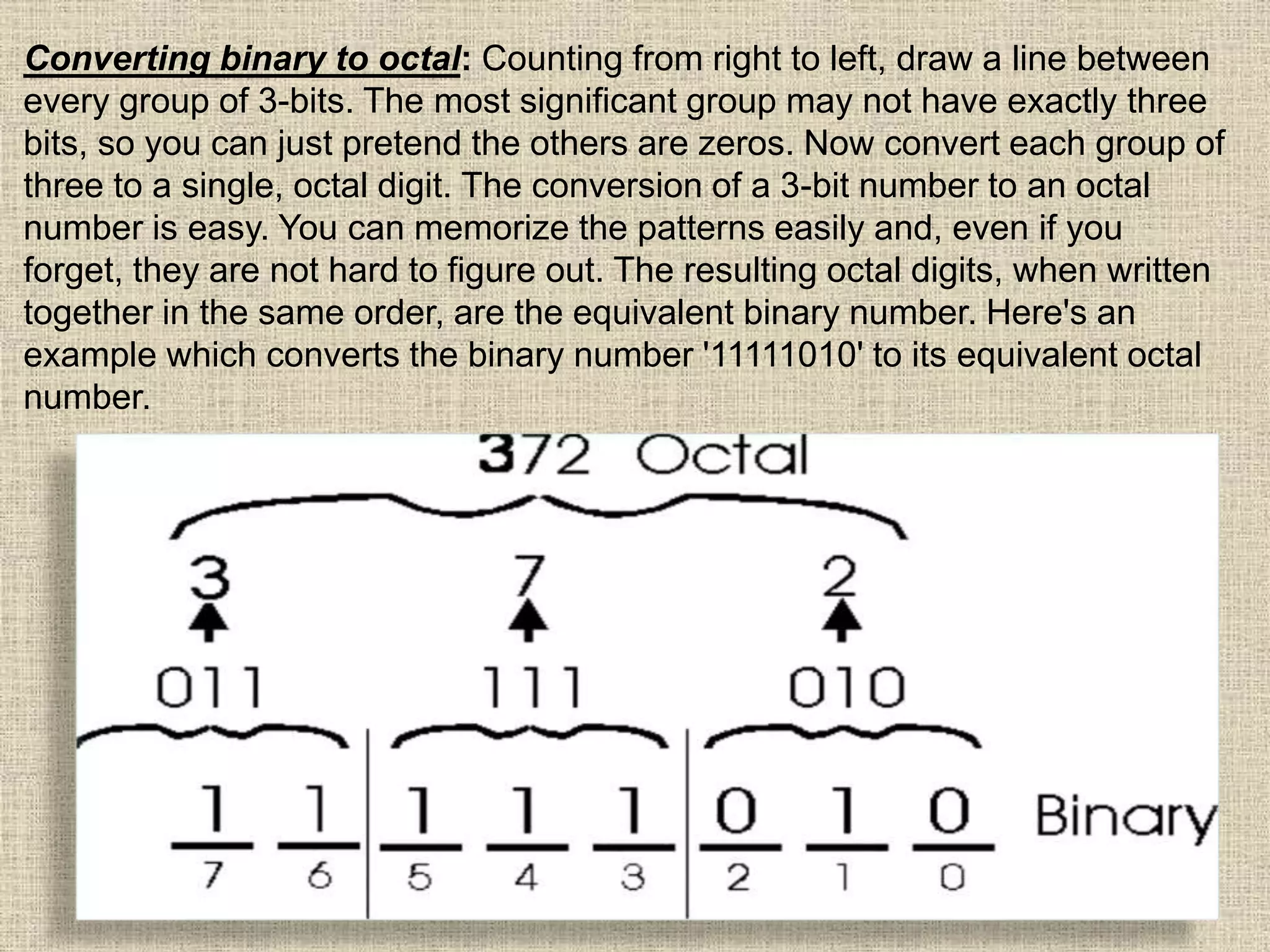
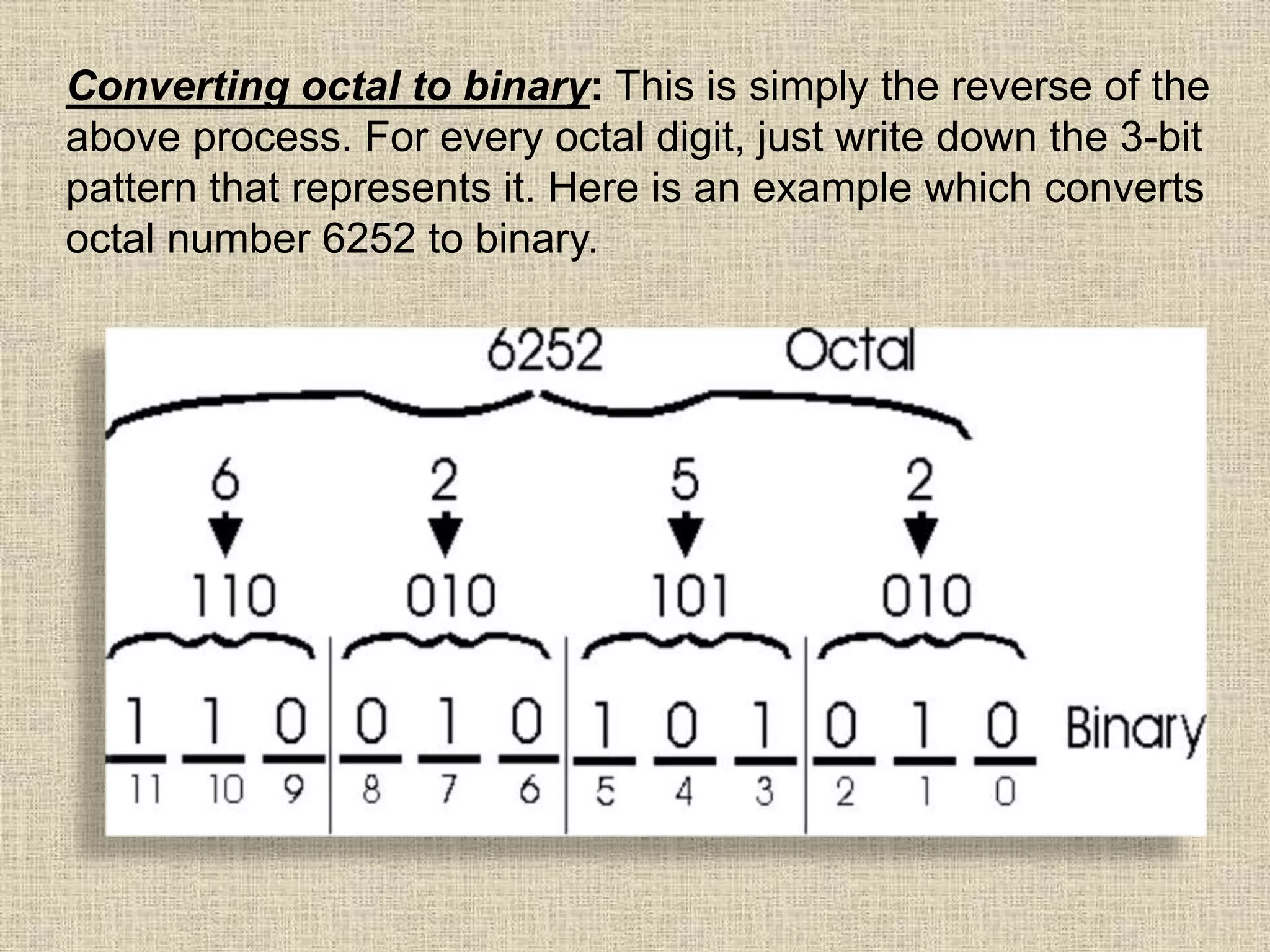
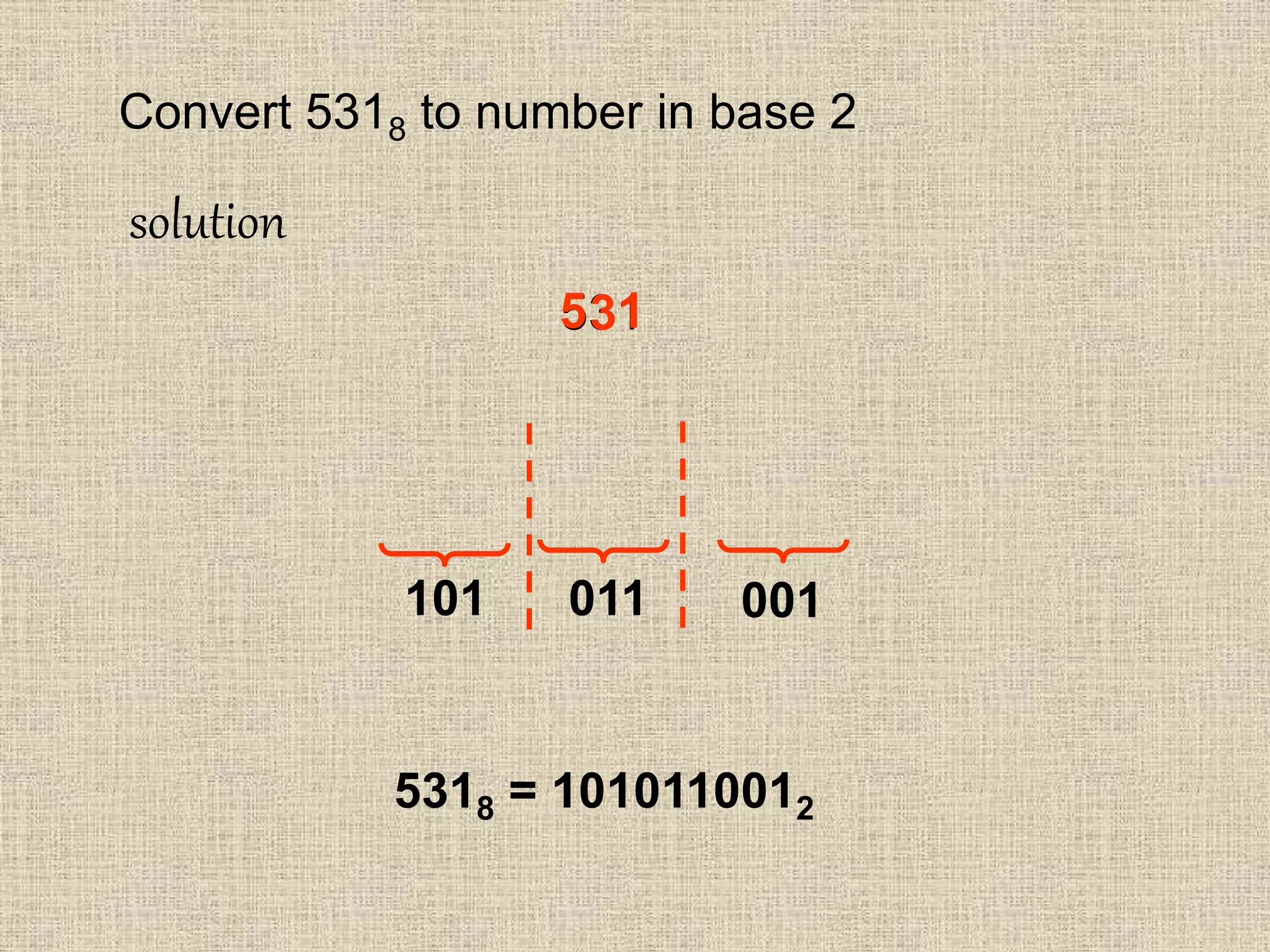
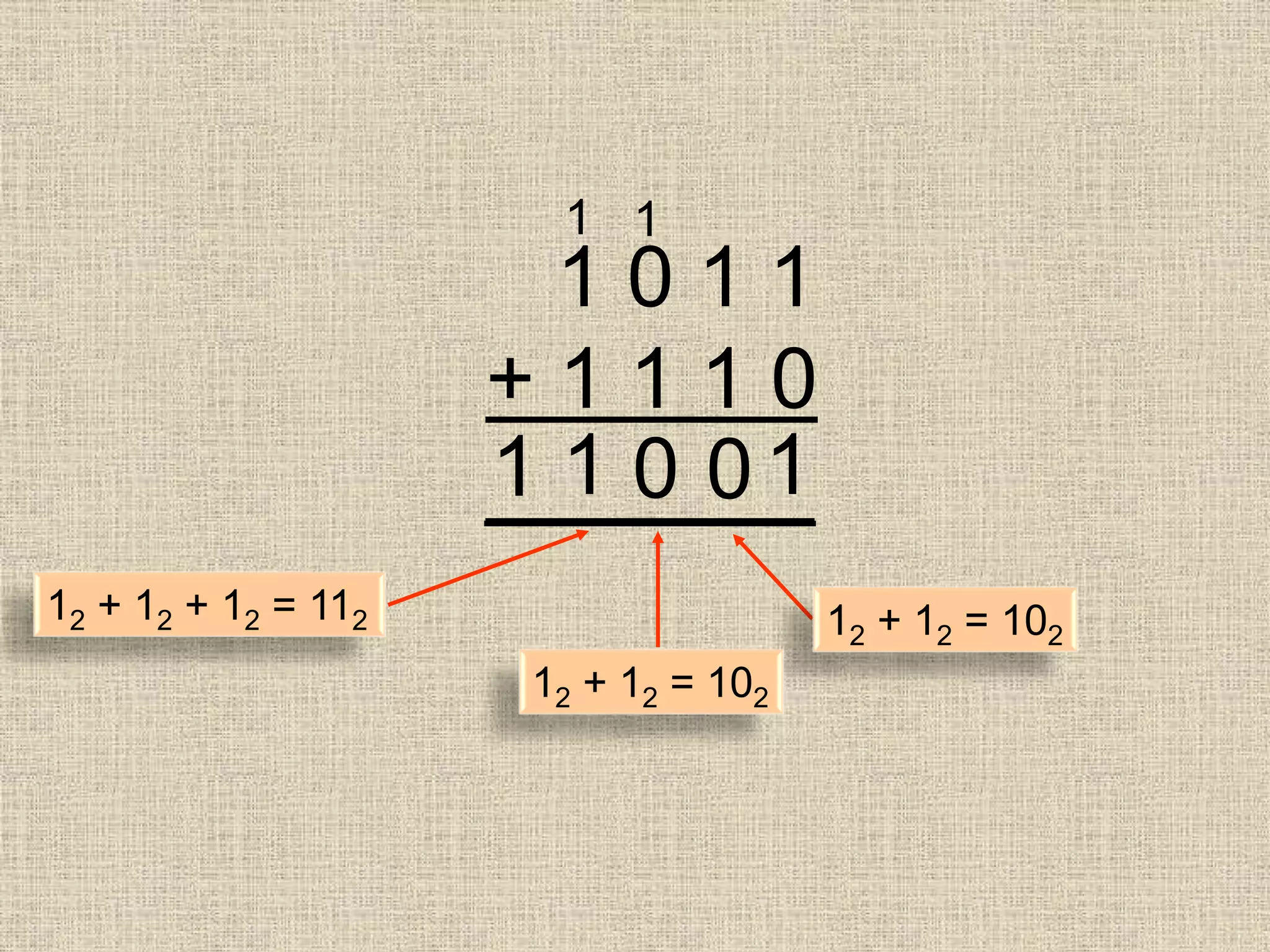
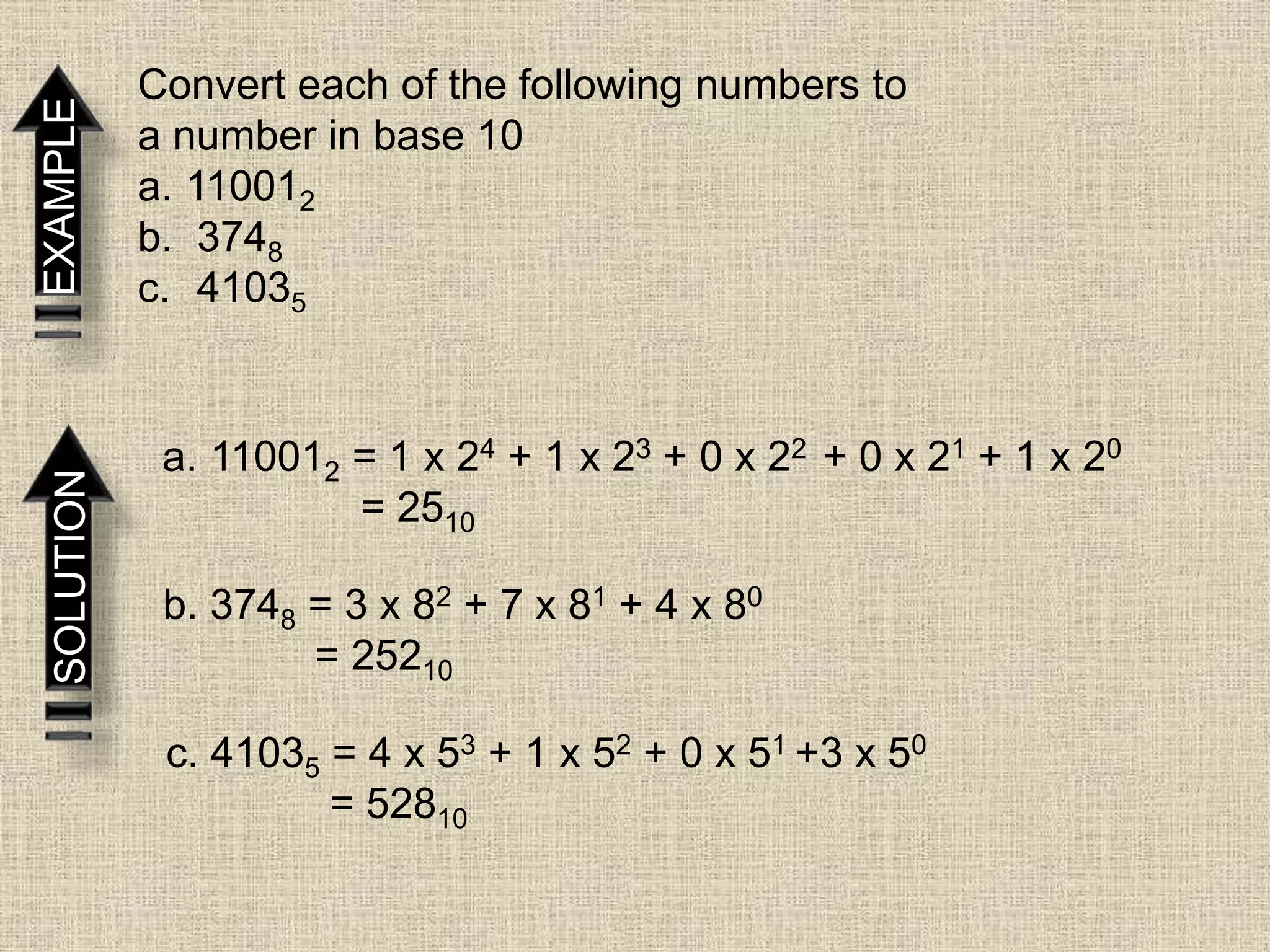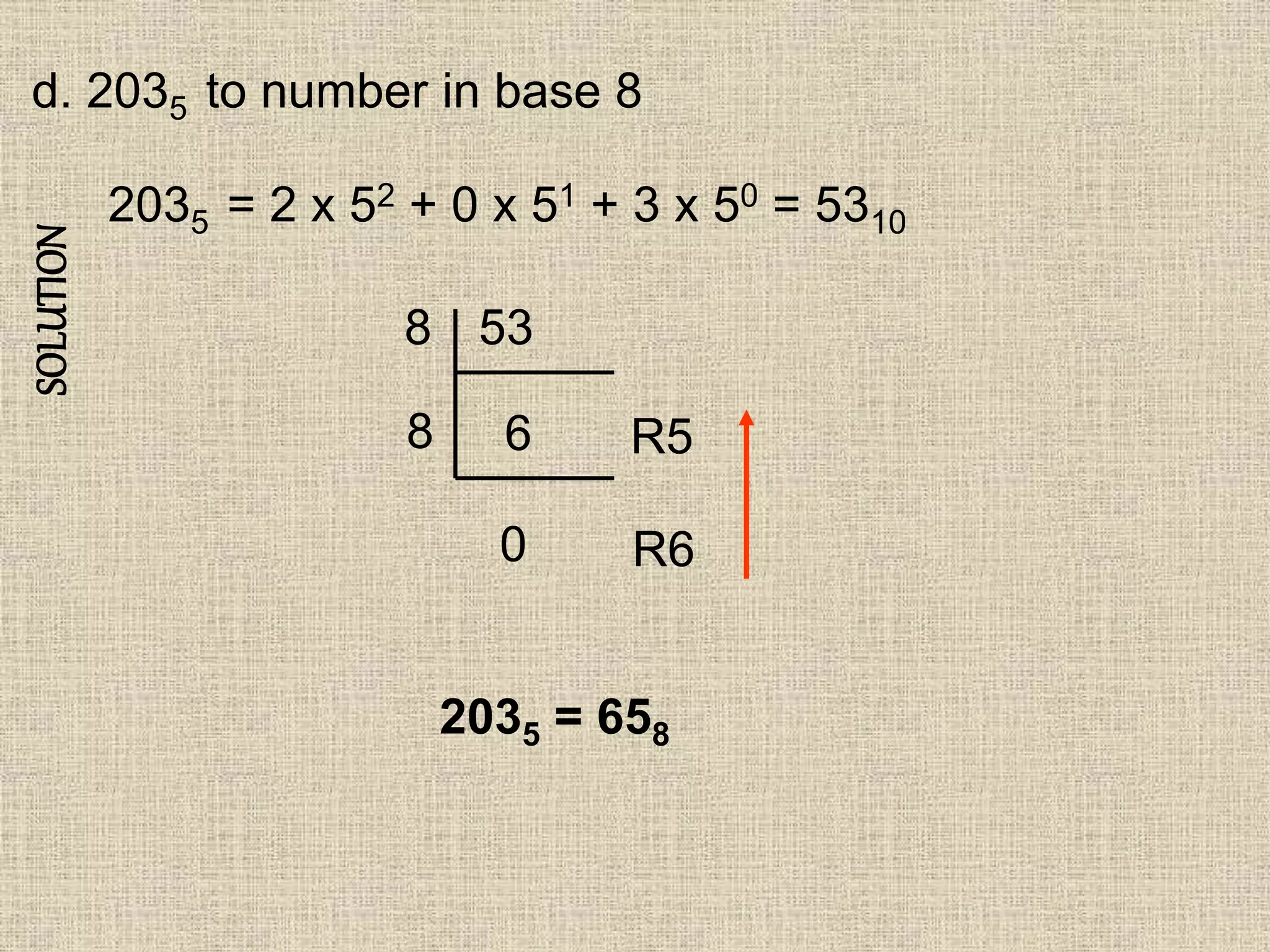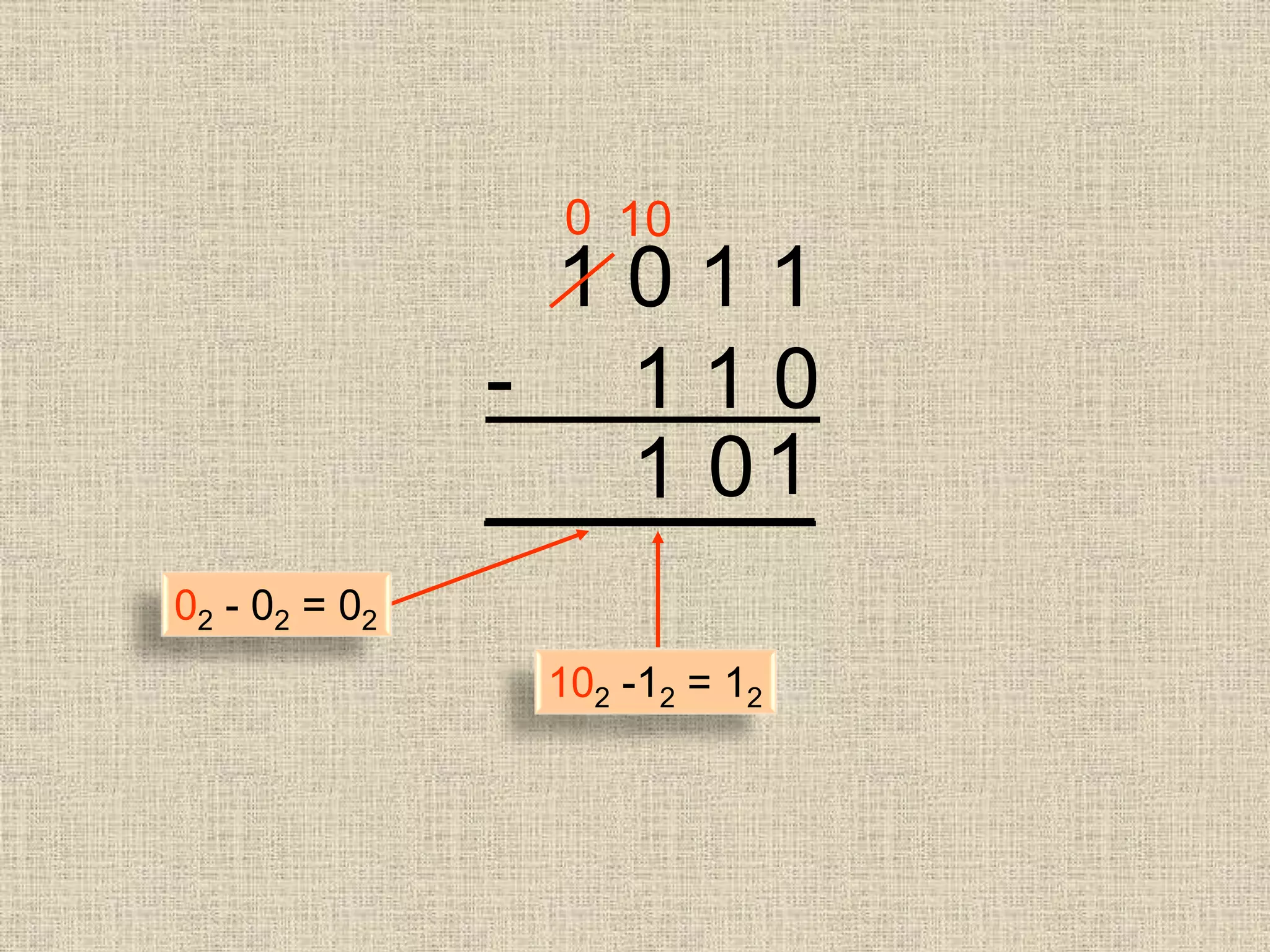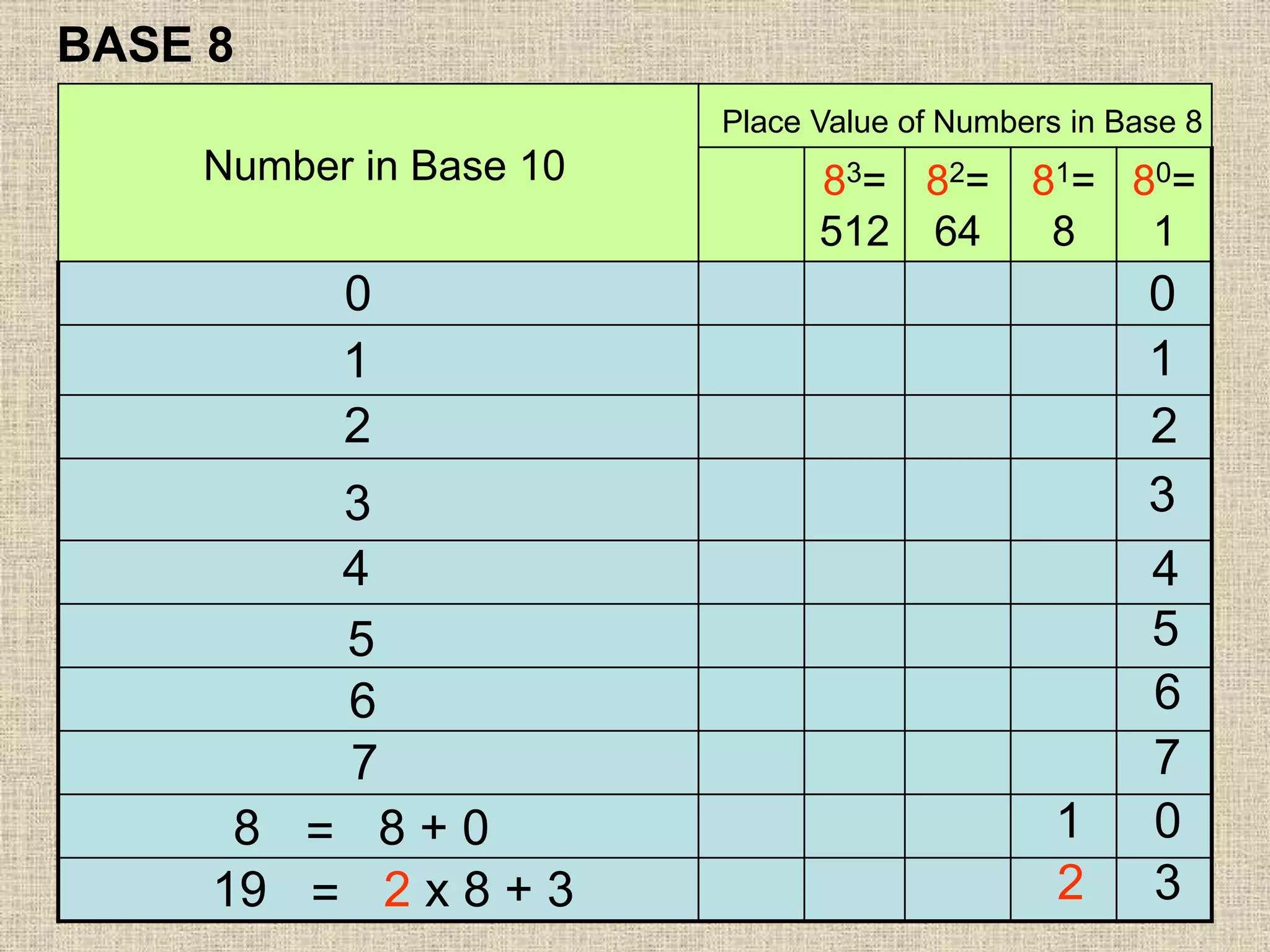
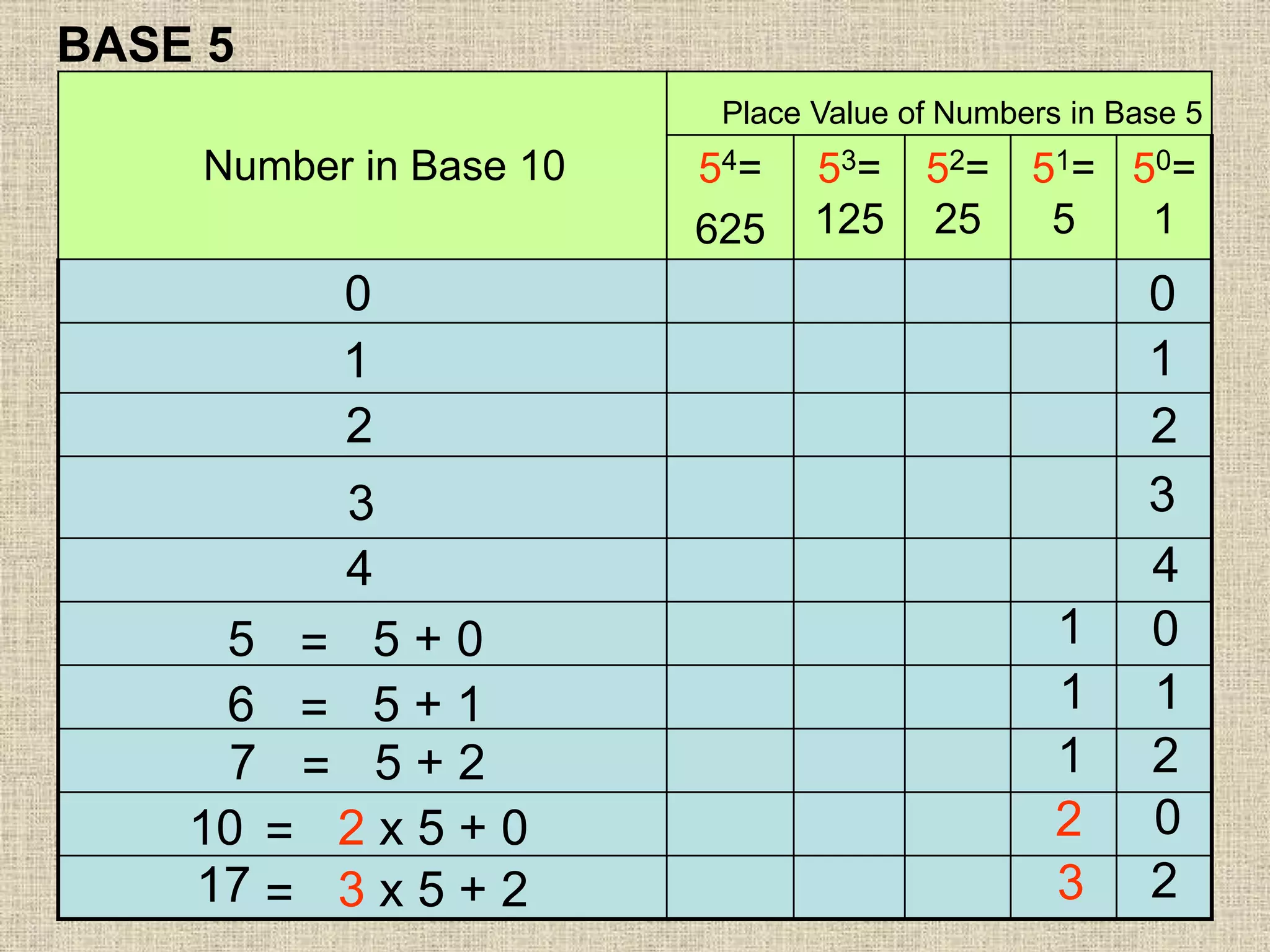
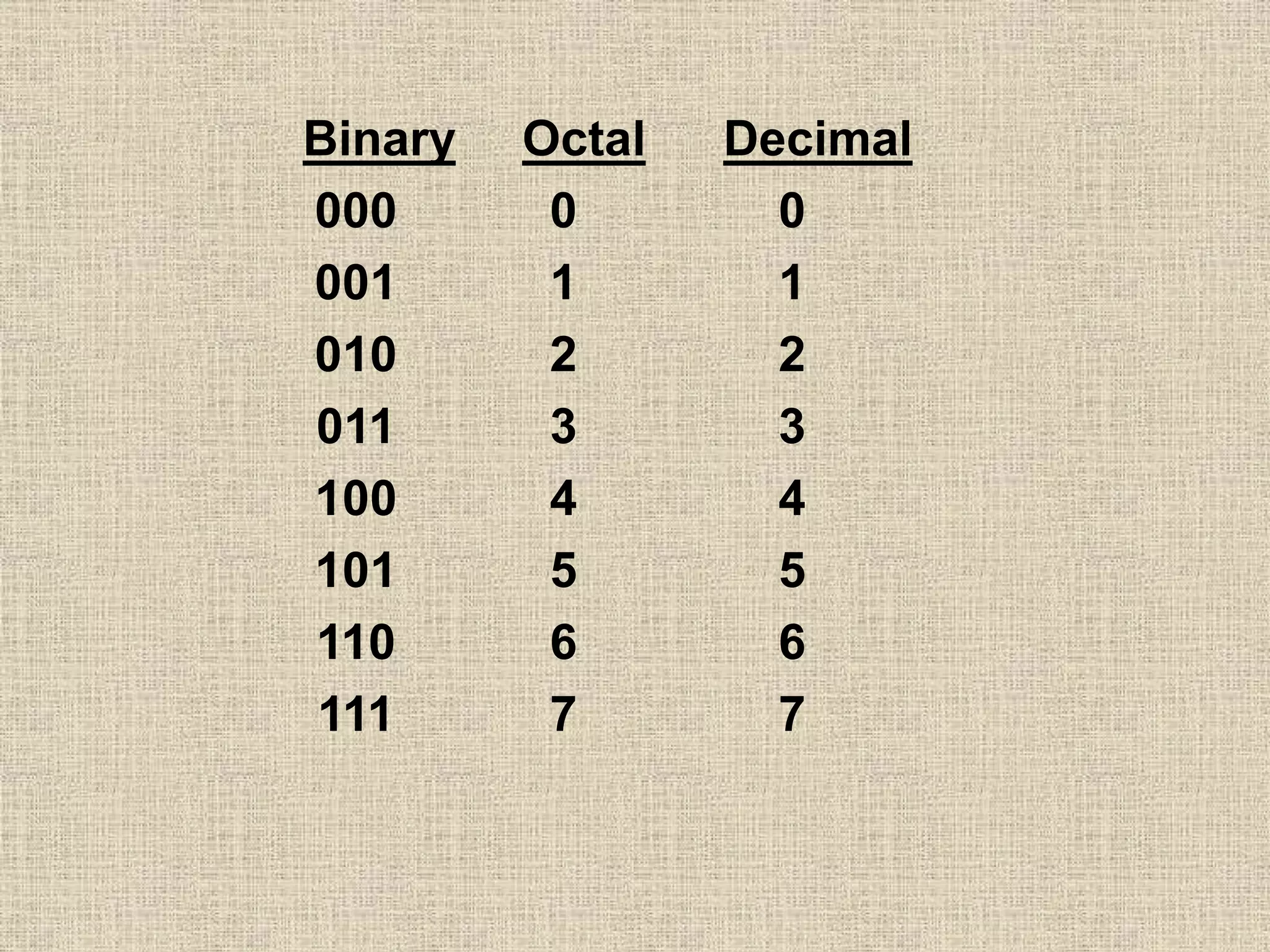
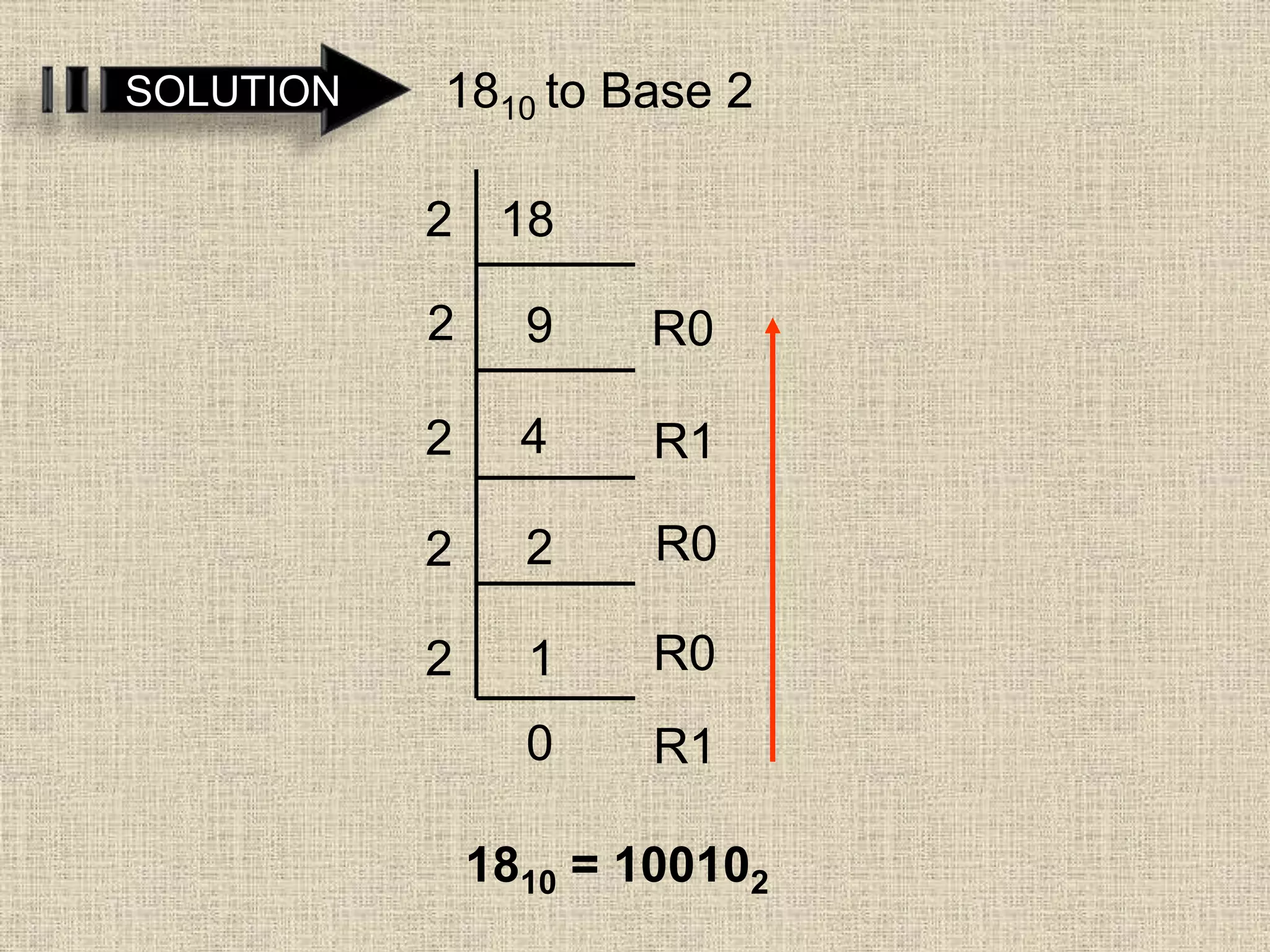
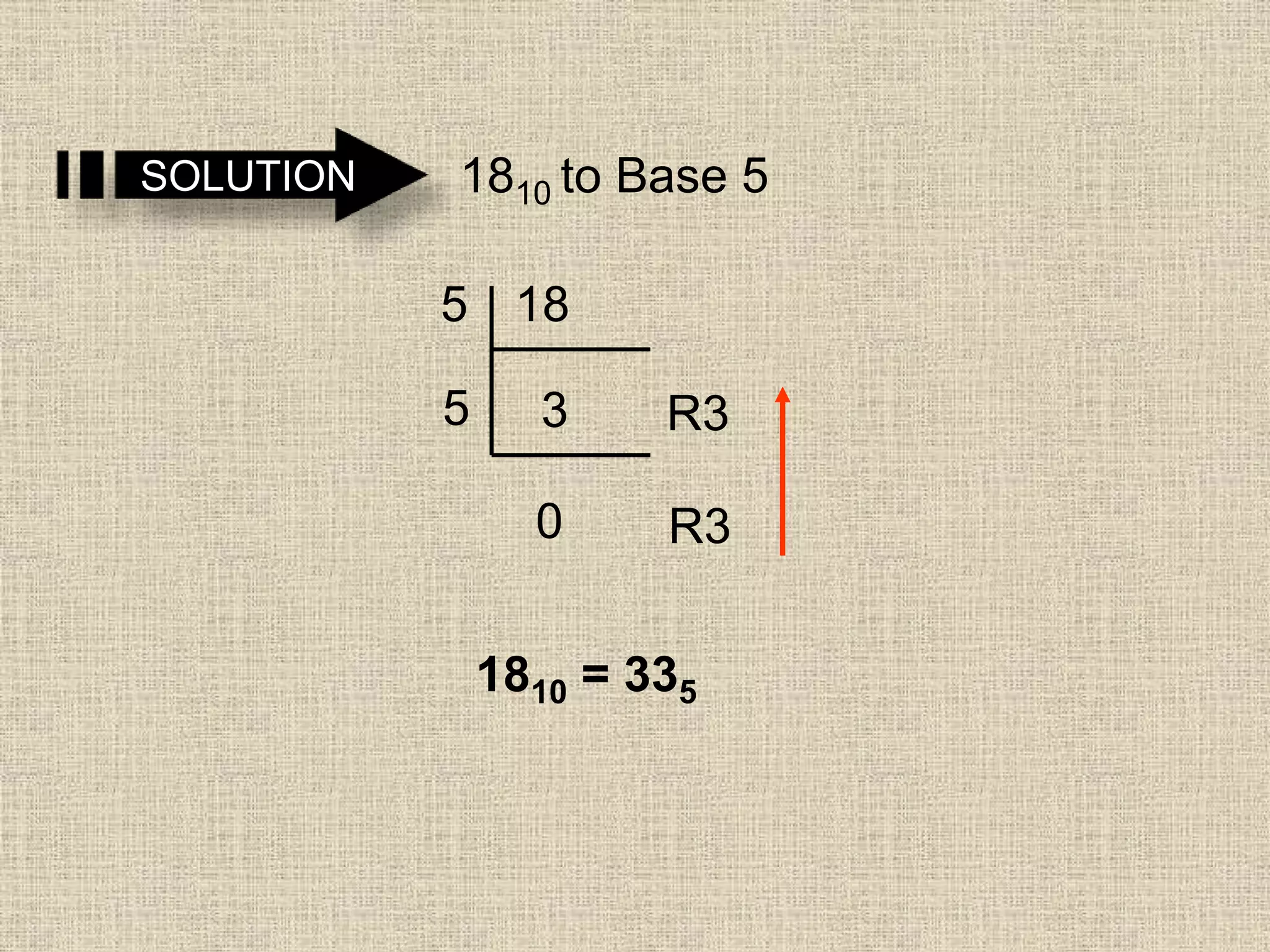
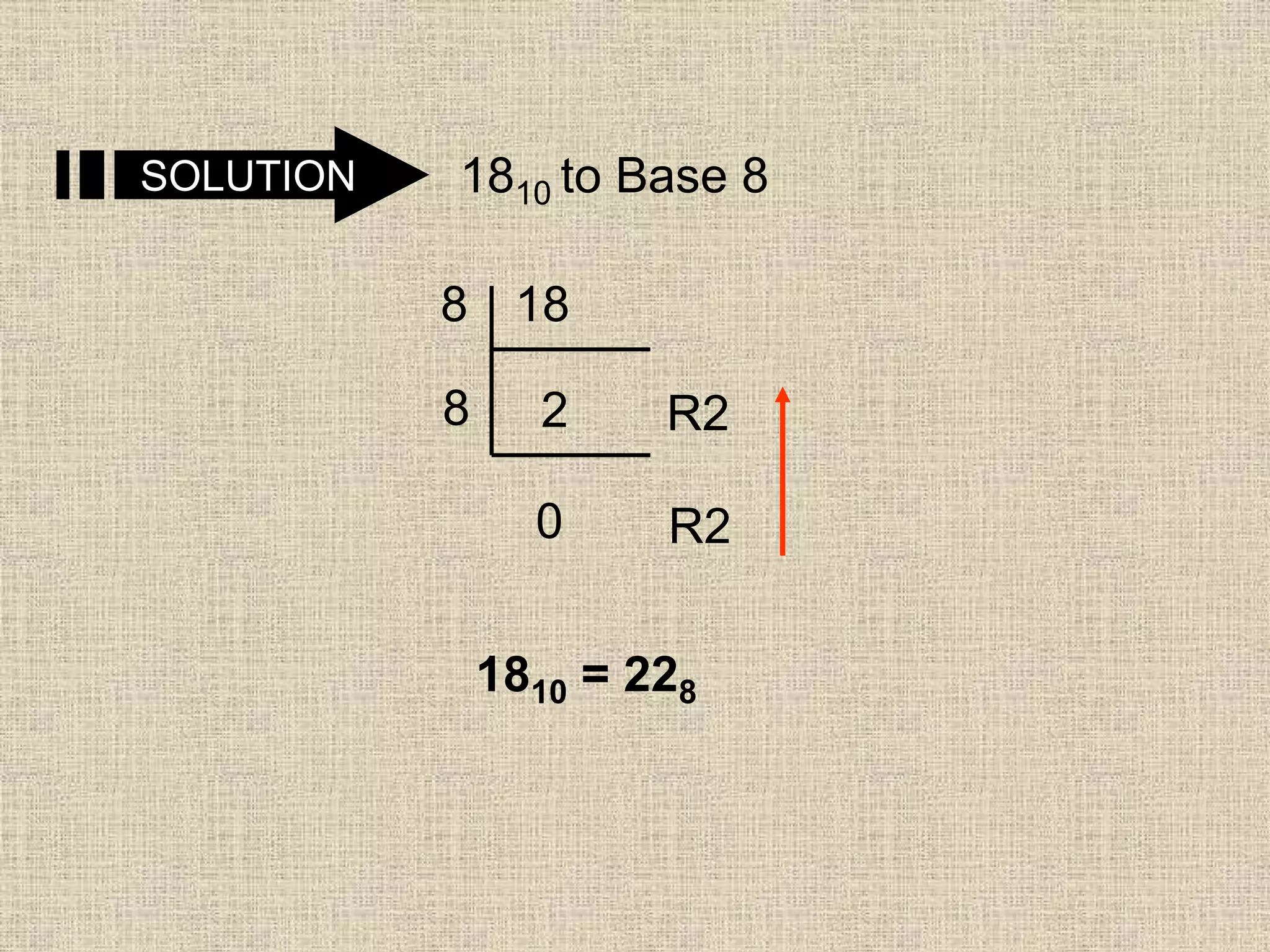
This document discusses number bases and converting between different number bases. It covers: - Place value and value of digits in base 2, 8, and 10 - Writing numbers in expanded notation in different bases - Converting numbers between bases 2, 8, 10 and vice versa - Addition and subtraction in base 2

1. Chapter 1 : Number Bases
• 1.1 a : Stating Numbers in Base Two, Eight and Five
• 1.1 b : Value of a Digit of a Number in Base 2, 8 and 5
• 1.1 c : Writing Numbers in Base 2, 8 and 5 in Expanded
Notation
• 1.1 d : Converting Numbers in Base 2, 8 and 5 to Base
10 and Vice Versa
• 1.I e : Converting from One Base to Another
• 1.1 f : Addition and Subtraction in Base Two

2. Chapter 1 Number Bases
Number in Base Two, Eight and Five1 1 a
1.1 Stating Numbers in Base Two, Eight and Five
• The numbers we use daily are in base 10. The place value of numbers in
base 10 are as shown below.
103 =1000 102 =100 101=10 100 =1 Place value
Number in base 10
9 7 0 39 7 0 3

3. 103 =1000 102 =100 101=10 100 =1 Place value
Number in base 109 7 0 3
The place value of the digit 7 in the
number 9703 is 100
• The place value of any digit of a number is a fixed value and does not
change with the value of the digit.
• There is no place value equal to zero.
• The smallest place value of all number bases is “ones”.
• The place value of 3 in the number 9703 is 1.

4. 103 =1000 102 =100 101=10 100 =1 Place value
Number in base 109 7 0 3
• There are 10 digits that can be written in any place value column
for numbers in base 10.
• The digits are 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9
• The digit value or value of digit varies with the place value and the
digit

5. 103 =1000 102 =100 101=10 100 =1 Place value
Number in base 109 7 0 3
The value of the digit 9 is 9 x 1000 = 9000
Digit
Place value
of 9
Value of the
digit 9

6. 103 =1000 102 =100 101=10 100 =1 Place value
Number in base 109 7 0 3
The value of the digit 0 is 0 x 10 = 0
Digit
Place value
of 0
Value of the
digit 0

7. • Numbers in base 2 have their respective place values
as shown below
22 = 21 = 20 =
2 x 2 = 4 2 1
Place
Value
• There are only 2 digits in base 2 : 0 and 1

8. • Numbers in base 8 have their respective place values
as shown below
82 = 81 = 80 =
8 x 8 = 64 8 1
Place
Value
• There are only 8 digits in base 8 : 0, 1, 2, 3, 4, 5, 6
and 7

9. • Numbers in base 5 have their respective place values
as shown below
52 = 51 = 50 =
5 x 5 = 25 5 1
Place
Value
• There are only 5 digits in base 5 : 0, 1, 2, 3 and 4

10. 24=
16
23=
8
22=
4
21=
2
20=
1
BASE 2
Place Value of Numbers in Base 2
Number in Base 10
0 0
2 = 2 + 0
1 1
01
11
1 0 0
0
0
000
00
1
11
111
11
3 = 2 + 1
4 = 4 + 0 + 0
5 = 4 + 0 + 1
6 = 4 + 2 + 0
7 = 4 + 2 + 1
8 = 8 + 0 + 0 + 0
9 = 8 + 0 + 0 + 1
1
1

11. 83=
512
82=
64
81=
8
80=
1
BASE 8
Place Value of Numbers in Base 8
Number in Base 10
0 0
2
1 1
2
3
4
6
01
2
5
7
3
3
4
5
6
7
8 = 8 + 0
19 = 2 x 8 + 3

12. 54=
625
53=
125
52=
25
51=
5
50=
1
BASE 5
Place Value of Numbers in Base 5
Number in Base 10
0 0
2
1 1
2
3
4
1
1
02
3
0
1
21
2
3
4
5 = 5 + 0
6 = 5 + 1
7 = 5 + 2
10 = 2 x 5 + 0
17 = 3 x 5 + 2

13. 910 = 8 + 0 + 0 + 1
=10012 Read as “one zero zero one base 2”
910 = 8 + 1
= 118 Read as “one one base 8”
910 = 5 + 4
=145 Read as “one four base 5”
• Numbers in base 2 are also known as binary numbers
• Numbers in base 8 are also known as octal numbers
• Numbers in base ten are also known as denary numbers

14. State two numbers in base two after 11102EXAMPLE
24=16 23=8 22=4 21=2 20=1 Base
10
1 1 1 0 8+4+2+
0 = 14
SOLUTION
8+4+2+
1=15
1 1 1 1
16+0+0+
0=16
0 0 0 01
11112 and 100002

15. State a number before and after 218 in base 8EXAMPLE
SOLUTION
81=8 80=1 Base 10
2 1 2 x 8 + 1 = 17
Before 2 x 8 + 0 = 162 0
After 2 x 8 + 2 = 182 2
208 and 228

16. State two numbers after 435 in base 5EXAMPLE
SOLUTION
52=25 51=5 50=1 Base 10
4 3 4 x 5 + 3 = 23
4 x 5 + 4 = 244 4
1 x 25 + 0 + 0 = 251 0 0
445 and 1005

17. 1.1 b Value of A Digit of A Number in Base Two, Eight and Five
Value of a digit = The digit x Place value of a digit
State the value of the underlined digit in each
of the following numbers
(a)11012
(b) 40328
(c)12435
EXAMPLE

18. SOLUTION
Place
Value
23=8 22=4 21=2 20=1
Number 1 1 0 1
Value of
Digit
1 x 4 = 4
The value of the digit “1” in 11012 is 4

19. SOLUTION
Place
Value
83=512 82=64 81=8 80=1
Number 4 0 3 2
Value of
Digit
0 x 64 = 0
The value of the digit “0” in 40328 is 0

20. SOLUTION
Place
Value
53=125 52=25 51=5 50=1
Number 1 2 4 3
Value of
Digit
4 x 5 = 20
The value of the digit “4” in 12435 is 20

21. 1.1 c Writing Numbers in Base Two, Eight and Five
in Expanded Notation
• A number written in expanded notation refers to
the sum of the value of the digits that make up
the number .
• Let us write 42510 in expanded notation
Place Value 102 101 100
Number
425
Therefore, 42510 written in expanded notation is as follows
42510 = 4 x 102 + 2 x 101 + 5 x 100

22. 1.1 c Writing Numbers in Base Two, Eight and Five
in Expanded Notation
• Let us write 3748 in expanded notation
Place Value 82 81 80
Number 3 7 4
Therefore, 3748 written in expanded notation is as follows
3748 = 3 x 82 + 7 x 81 + 4 x 80

23. 1.1 c Writing Numbers in Base Two, Eight and Five
in Expanded Notation
• Let us write 110012 in expanded notation
Place Value 24 23 22 21 20
Number
Therefore, 110012 written in expanded notation is as follows
110012 = 1 x 24 + 1 x 23 + 0 x 22 + 0 x 21 + 1 x 20
1 1 00 1

24. 1.1 c Writing Numbers in Base Two, Eight and Five
in Expanded Notation
• Let us write 41035 in expanded notation
Place Value 53 52 51 50
Number
Therefore, 41035 written in expanded notation is as follows
41035 = 4 x 53 + 1 x 52 + 0 x 51 +3 x 50
4 1 0 3

25. 1.1 d Converting Numbers in Base Two, Eight and Five to
Base 10 and Vice Versa
Steps to convert numbers in base 2, 8 and 5 to base 10 are as follows
1. Write the number in expanded notation
2. Simplify the expanded notation into a single number
EXAMPLE
Convert each of the following numbers to a number in base 10
a. 110012
b. 3748
c. 41035

26. EXAMPLE
Convert each of the following numbers to
a number in base 10
a. 110012
b. 3748
c. 41035
SOLUTION
a. 110012 = 1 x 24 + 1 x 23 + 0 x 22 + 0 x 21 + 1 x 20
= 2510
b. 3748 = 3 x 82 + 7 x 81 + 4 x 80
= 25210
c. 41035 = 4 x 53 + 1 x 52 + 0 x 51 +3 x 50
= 52810

27. 1.1 d Converting Numbers in Base Two, Eight and Five to
Base 10 and Vice Versa
Steps to convert numbers in base 10 to base 2, 8 or 5 are as follows
1. Perform repeated division until the quotient is 0
2. Write the number in the new base by referring to the remainders
from bottom to the top
EXAMPLE Convert 1810 to numbers in base two, eight and five

28. SOLUTION 1810 to Base 2
18
9
4
2
1
0
2
2
2
2
2
R1
R0
R0
R1
R0
1810 = 100102

29. SOLUTION 1810 to Base 5
18
3
0
5
5
R3
R3
1810 = 335

30. SOLUTION 1810 to Base 8
18
2
0
8
8
R2
R2
1810 = 228

31. 1.1 e Converting Numbers from One Base to Another
The following steps are used to convert from one base to another
1. Convert the number to a number in base 10
2. Use repeated division to convert the number in base 10 to the
respective bases
EXAMPLE Convert
a. 1102 to number in base 5
b. 325 to number in base 2
c. 1278 to number in base 5
d. 2035 to number in base 8

32. SOLUTION
a.1102 to number in base 5
1102 = 1 x 22 + 1 x 21 + 0 x 20 = 610
6
1
0
5
5
R1
R1
1102 = 115

33. SOLUTION
b. 325 to number in base 2
325 = 3 x 51 + 2 x 50 = 1710
17
8
4
2
1
0
2
2
2
2
2
R1
R0
R0
R0
R1
325 = 100012

34. SOLUTION
c. 1278 to number in base 5
1278 = 1 x 82 + 2 x 81 + 7 x 80 = 8710
87
17
3
5
5
R2
R2
1278 = 3225
5
0 R3

35. SOLUTION
d. 2035 to number in base 8
2035 = 2 x 52 + 0 x 51 + 3 x 50 = 5310
53
6
0
8
8
R6
R5
2035 = 658

36. Binary Octal Decimal
000 0 0
001 1 1
010 2 2
011 3 3
100 4 4
101 5 5
110 6 6
111 7 7

37. Converting binary to octal: Counting from right to left, draw a line between
every group of 3-bits. The most significant group may not have exactly three
bits, so you can just pretend the others are zeros. Now convert each group of
three to a single, octal digit. The conversion of a 3-bit number to an octal
number is easy. You can memorize the patterns easily and, even if you
forget, they are not hard to figure out. The resulting octal digits, when written
together in the same order, are the equivalent binary number. Here's an
example which converts the binary number '11111010' to its equivalent octal
number.

38. Converting octal to binary: This is simply the reverse of the
above process. For every octal digit, just write down the 3-bit
pattern that represents it. Here is an example which converts
octal number 6252 to binary.

39. Convert 1000111012 to number in base 8
solution
101011100 101011100
534
1000111012 = 4358

40. Convert 5318 to number in base 2
solution
5318 = 1010110012
531135
001011101

41. 1.1f Addition and Subtraction in Base Two
• To add two numbers in base two, the following addition
rules are important

42. 1 0 1 1
+ 1 1 1 0
_______10
1
0
1
11
12 + 12 = 102
12 + 12 = 102
12 + 12 + 12 = 112

43. 1.1f Addition and Subtraction in Base Two
• To subtract two numbers in base two, the following
subtraction rules are important
02 - 02 =
12 - 02 =
12 - 12 =
102 - 12 =
02
12
02
12

44. 1 0 1 1
- 1 1 0
_______10
10
1
0
102 -12 = 12
02 - 02 = 02

45. BASE

46. BASE
Binary BIN (b)
Octal OCT (o)
Denary DEC (d)

47. Example 1
MODE BASE
3 3
4 6 2 =
ln
OCT
8181 x2
DEC
2x
o
d
Convert 14628 to a number in base
10

48.  To clear the Base-n specification
MODE
COMP
1 1Press
1X
 To continue the Base-n specification
Press
ON

49. Convert 11012 to a number in base 8
Example 2
MODE BASE
3 3
1 0 1 =
log
BIN
151 ln
OCT
2x
b
o

50.  To clear the Base-n specification
MODE
COMP
1 1Press
1X
 To continue the Base-n specification
Press
ON

51. Example 3
Convert 146210 to a number in
base 8
MODE BASE
3 3
4 6 2 =
x2
DEC
26661 ln
OCT
2x
d
o

52. Example 4
Calculate 10012 + 1112, stating your answer
as a number in base 2
MODE BASE
3 3
0 0 1 +
log
BIN
1
2x
b
1 1
= 10000
1
b

53.  To clear the Base-n specification
MODE
COMP
1 1Press
1X
 To continue the Base-n specification
Press
ON