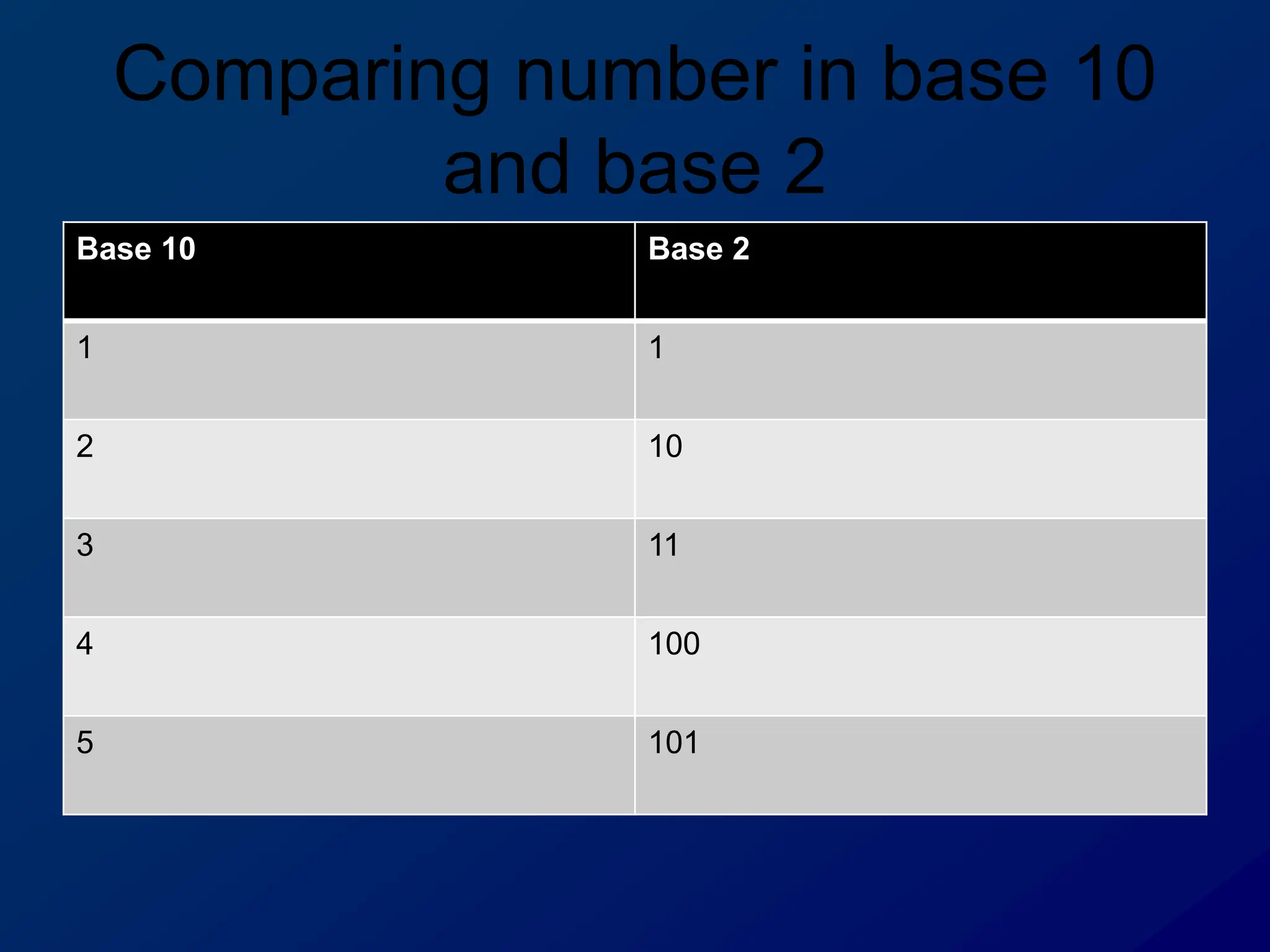
The document discusses number bases and converting between bases. It describes that number bases are systems for writing numbers, with different bases using different digits. Common number bases include base 2, base 8, and base 10. The document provides examples of converting numbers between base 10 and base 2. It also explains that to convert a binary number to its decimal equivalent, you sum the place value of each 1 digit.

2. Starter
• Think about it

3. Objectives
• Describe Number Bases
• Convert from base 2 to base 10
• Convert from base 10 to other
bases

4. • If DOVE = 415225,
What is: BROWN =
Hint: Decode the pattern

5. ANSWER
BROWN = 218152314
We make use of:
A B C D E F G H I J
1 2 3 4 5 6 7 8 9 10
K L M N O P Q R S T
11 12 13 14 15 16 17 18 19 20
U V W X Y Z
21 22 23 24 25 26

6. BRAIN STORM
• If DOVE = 46,
What is: BROWN =

7. Answer
• BROWN = 72

8. What are number bases?
They are simply a
system or way of
writing numbers

9. The same number written in
different form
Base 10 Base 2 Base 3 Base 4
45 101101 1200 231

10. Types of number bases
Number bases digit
Base 2 0,1
Base 3 0,1,2
Base 4 0,1,2,3
Base 5 0,1,2,3,4
Base 6 0,1,2,,3,4,5
Base 7 0,1,2,3,4,5,6
Base 8 0,1,2,3,4,5,6,7
Base 9 0,1,2,3,4,5,6,7,8
Base 10 0,1,2,3,4,5,6,7,8,9

11. Comparing number in base 10
and base 2
Base 10 Base 2
1 1
2 10
3 11
4 100
5 101

12. If you are to write 72 in
binary, will you have to start
from one to 72?
•No, you simply learn
the conversion from
base 10 to base 2

14. Try this
•What is 17 in base 2?
•Answer 10001

15. Converting from binary to denary
• Q.1: Convert the binary number 1001
to a decimal number.
• Solution: Given, binary number = 10012
• Hence, using the binary to decimal
conversion formula, we have:
• 10012 = (1 × 2³) + (0 × 2²) + (0 × 2¹) + (1
× 2⁰)
• = 8 + 0 + 0 + 1
• = (9)₁₀

16. Try this
•Convert 11010012 into
an equivalent decimal
number.

17. Solution
• (1101001)₂ = (1 × 2⁶) + (1 × 2⁵) + (0 × 2⁴)
+ (1 × 2³) + (0 × 2²) + (0 × 2¹) + (1 × 2⁰)
= 64 + 32 + 0 + 8 + 0 + 0 + 1
= (105)₁₀