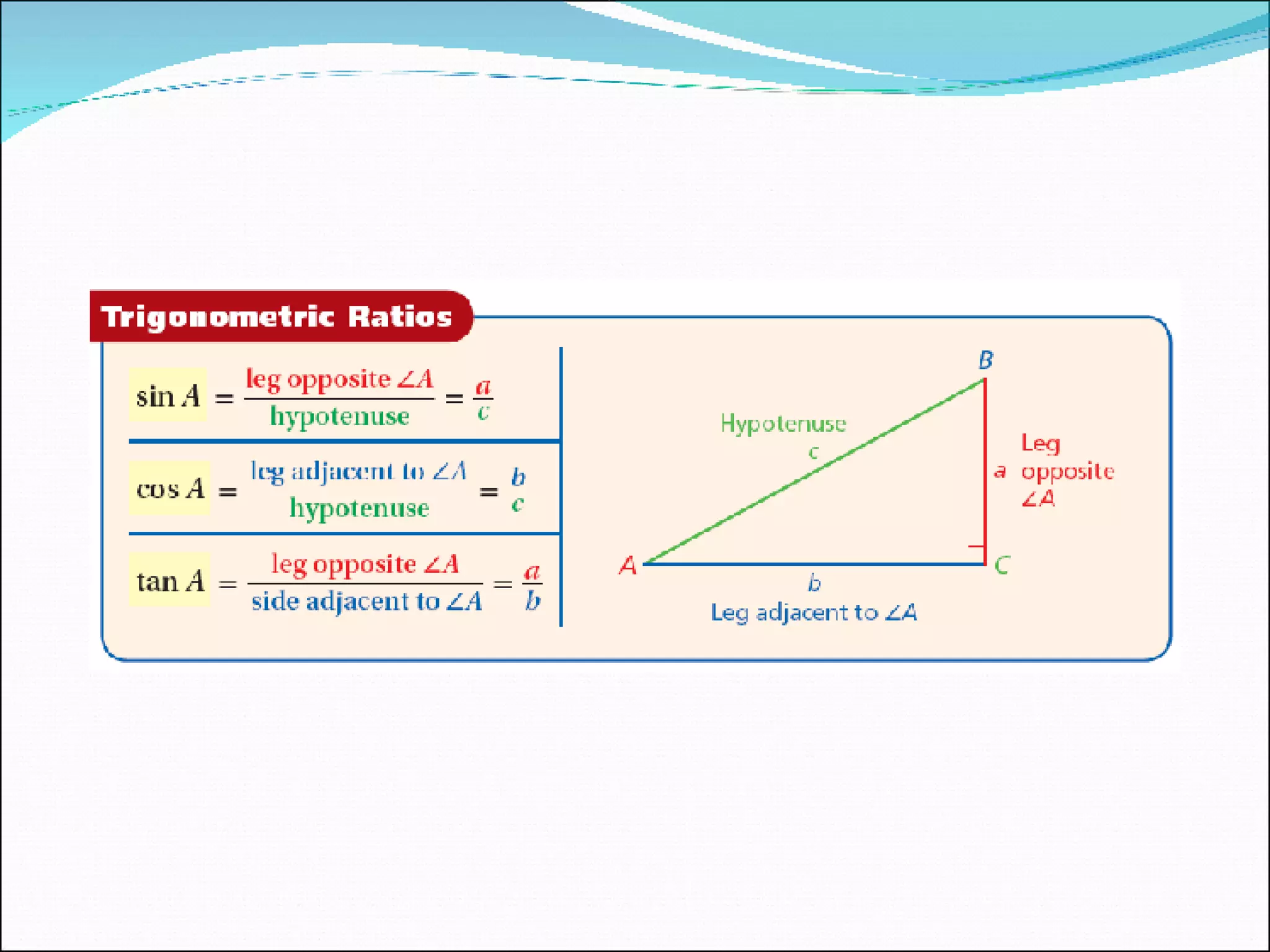
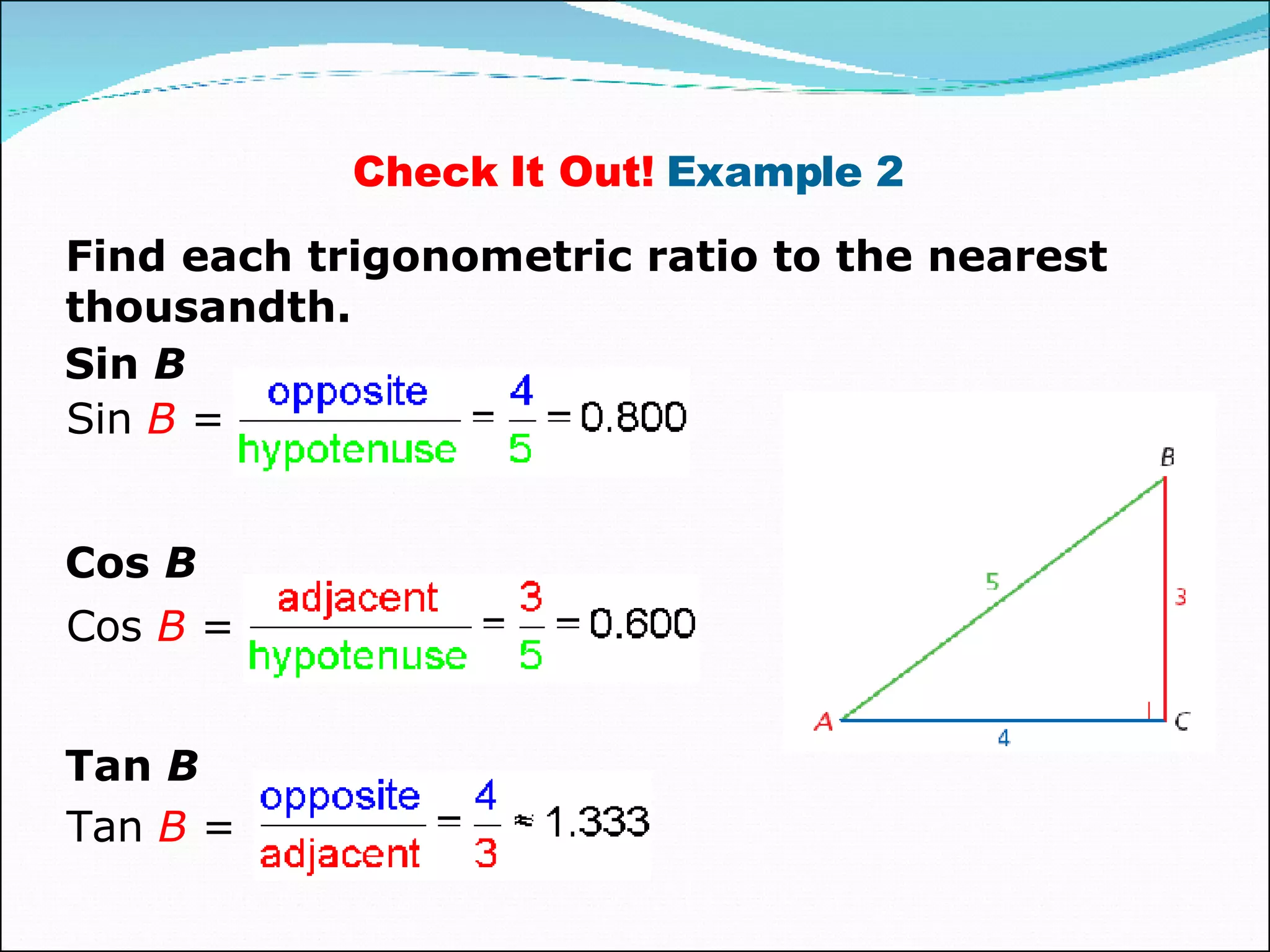
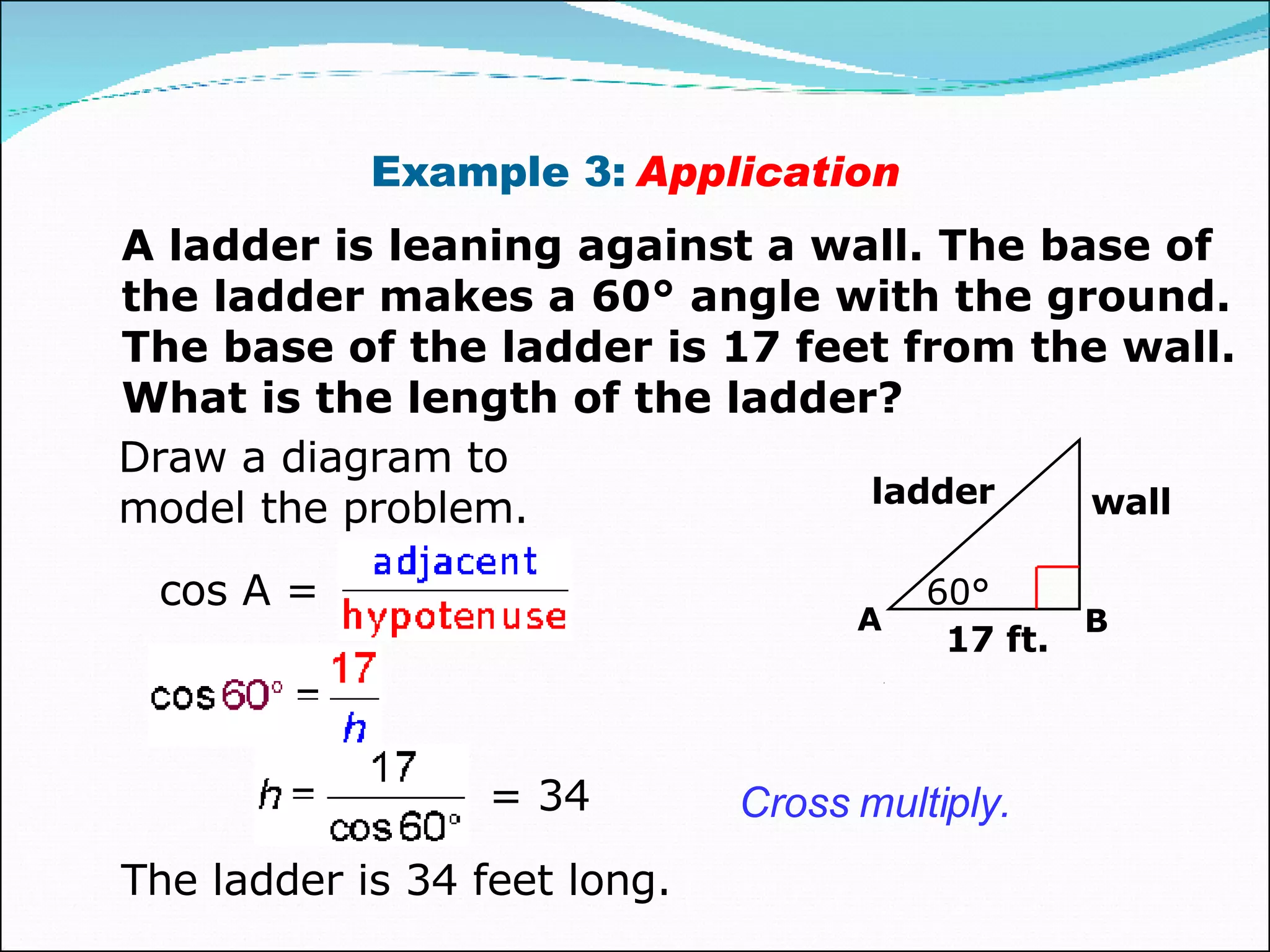
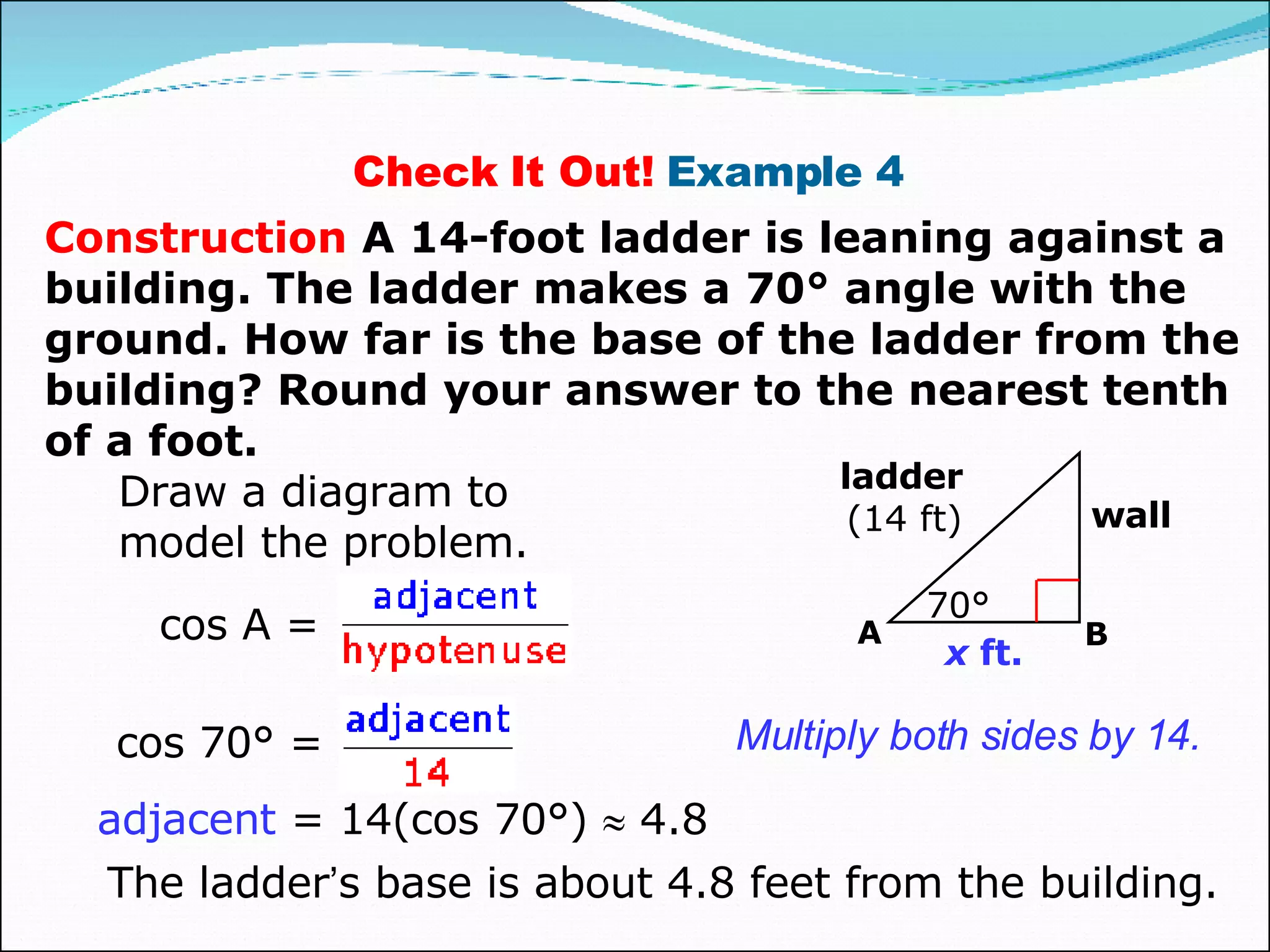
This document provides an overview of trigonometric ratios and how to use them to solve problems involving right triangles. It defines the sine, cosine, and tangent ratios and provides the mnemonic device SOH CAH TOA to remember them. Examples are given of calculating trig ratios in right triangles and using them to solve application problems like finding the length of a ladder leaning against a wall.

2. Find the three basic trigonometric ratios in a right triangle. Use trigonometric ratios to find missing lengths. Objectives

3. trigonometric ratios sine cosine tangent Vocabulary

4. A trigonometric ratio is a ratio of the lengths of two sides in a right triangle. Three basic trigonometric ratios are sine, cosine, and tangent, abbreviated sin, cos, and tan, respectively .

6. Confused? Here’s an acronym to help you remember the ratios S ine = O pposite divided by H ypotenuse C osine = A djacent divided by H ypotenuse T angent = O pposite divided by A djacent SOH CAH TOA

7. Example 1: Finding the Value of a Trigonometric Ratio Find sin A, cos A and tan A . Sin A Sin A Cos A Cos A Tan A Tan A A B C 17 15 8

8. Students tend to make simple mistakes by mislabeling the adjacent and opposite sides To overcome this mistake first determine the Hypotenuse (should be easy right?) Then determine the opposite side (across from the angle referred to.) The remaining side is the adjacent side. COMMON ERROR ALERT

9. Find each trigonometric ratio to the nearest thousandth. Check It Out! Example 2 Sin B Sin B = Cos B Cos B = Tan B Tan B =

10. To find trigonometric ratios on a graphing calculator, press and then the value of the degree. Be sure your calculator is in degrees. Helpful Hint

11. Example 3: Application A ladder is leaning against a wall. The base of the ladder makes a 60° angle with the ground. The base of the ladder is 17 feet from the wall. What is the length of the ladder? Draw a diagram to model the problem. Cross multiply. The ladder is 34 feet long. = 34 17 ft. 60° wall ladder A A B cos A =

12. Check It Out! Example 4 Construction A 14-foot ladder is leaning against a building. The ladder makes a 70° angle with the ground. How far is the base of the ladder from the building? Round your answer to the nearest tenth of a foot. Draw a diagram to model the problem. adjacent = 14(cos 70°)  4.8 The ladder ’ s base is about 4.8 feet from the building. Multiply both sides by 14. cos A = x ft. 70° wall ladder (14 ft) A B cos 70° =

13. Take out a piece of paper. Write your name at the top. Find each trigonometric ratio to the nearest thousandth. Sin B Cos B Tan B A C B 25 24 7