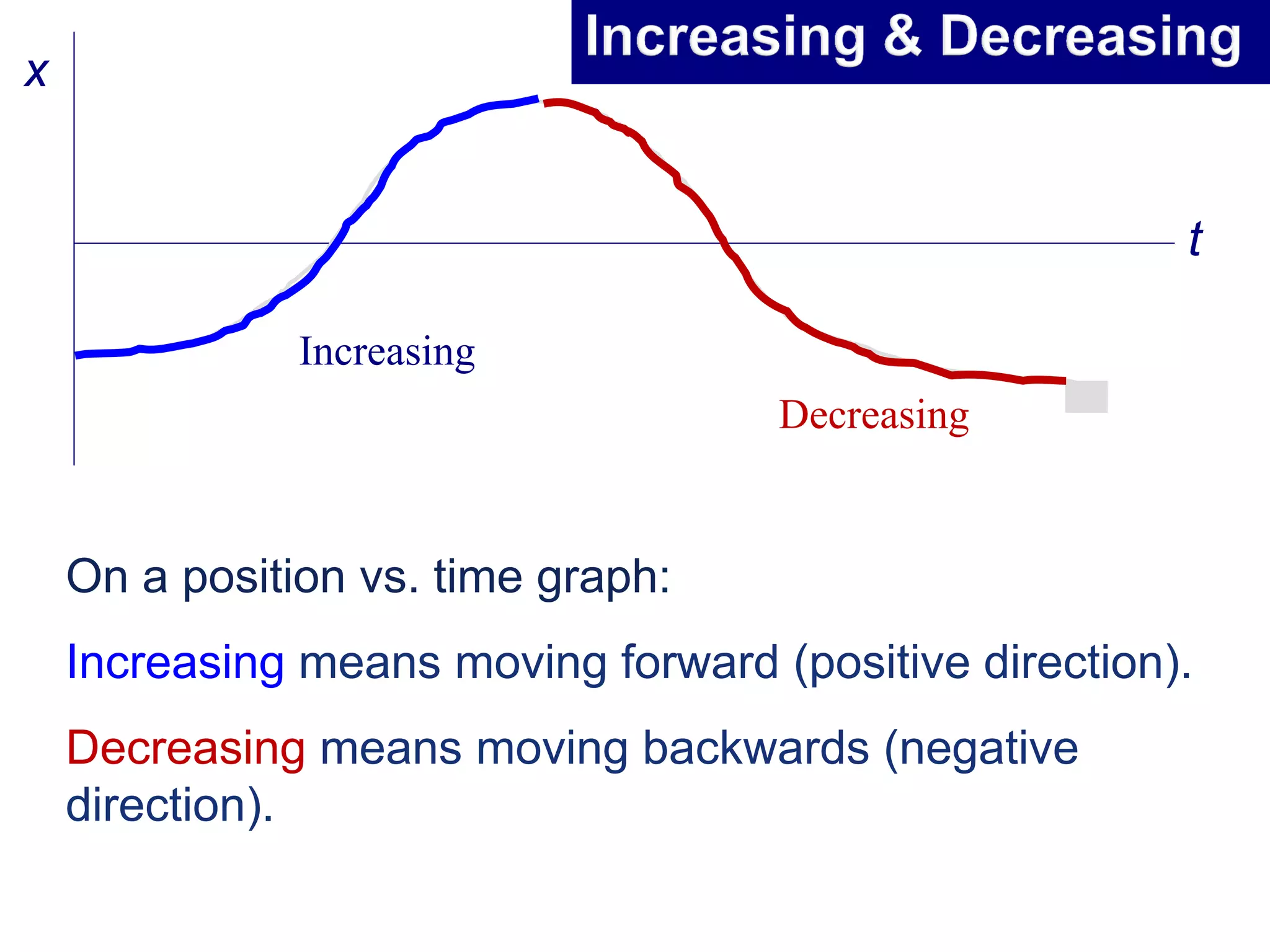
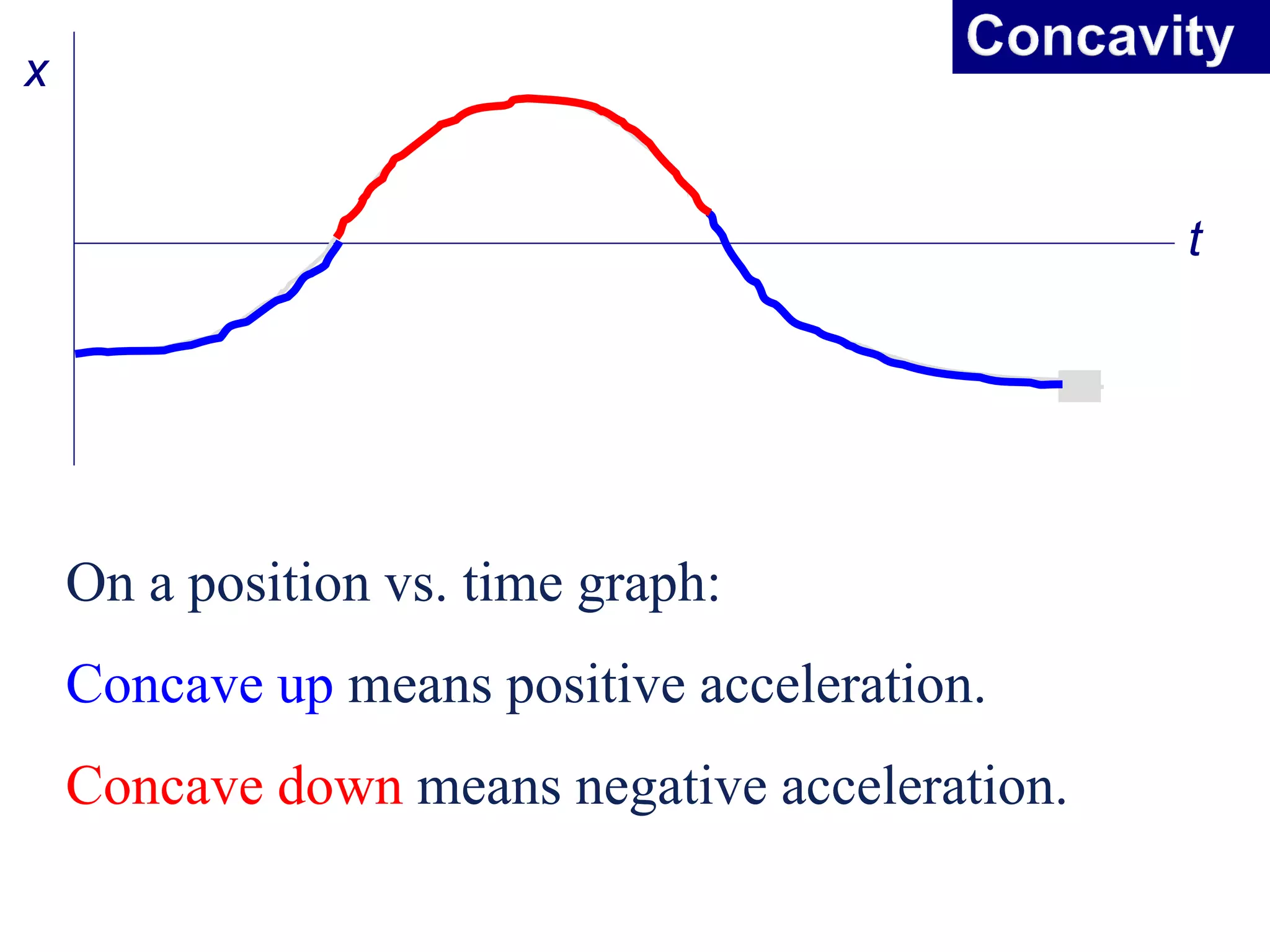
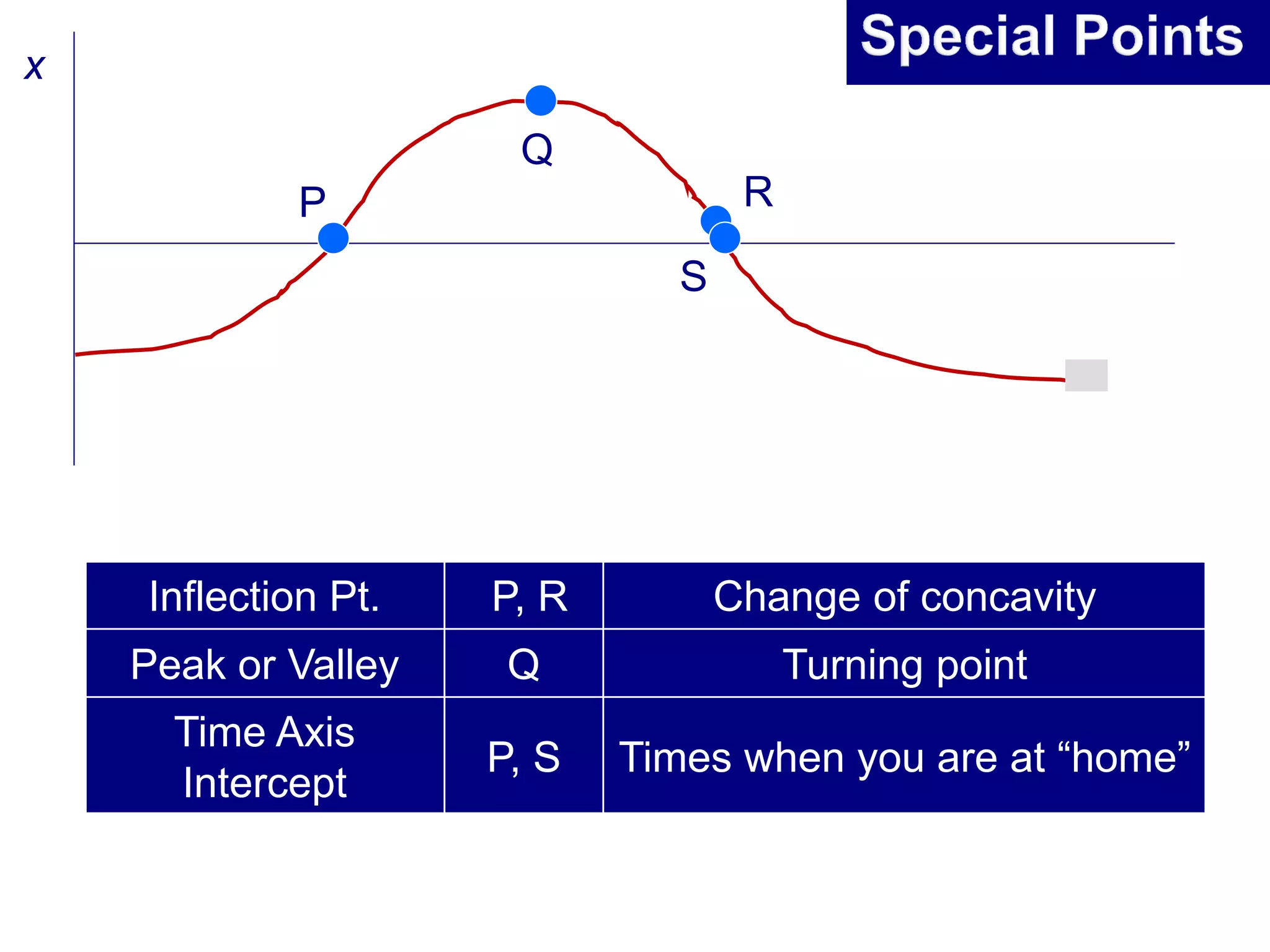
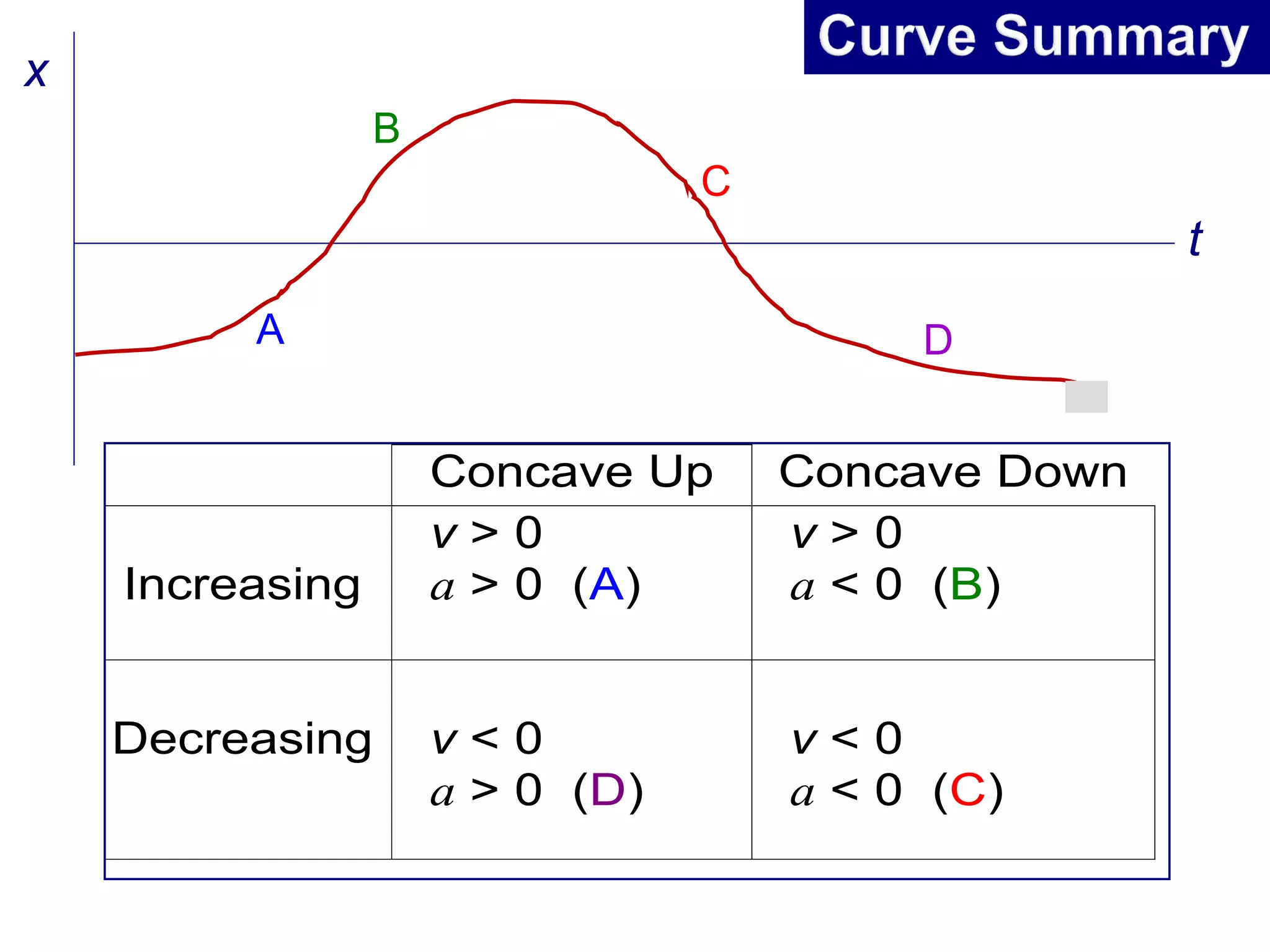
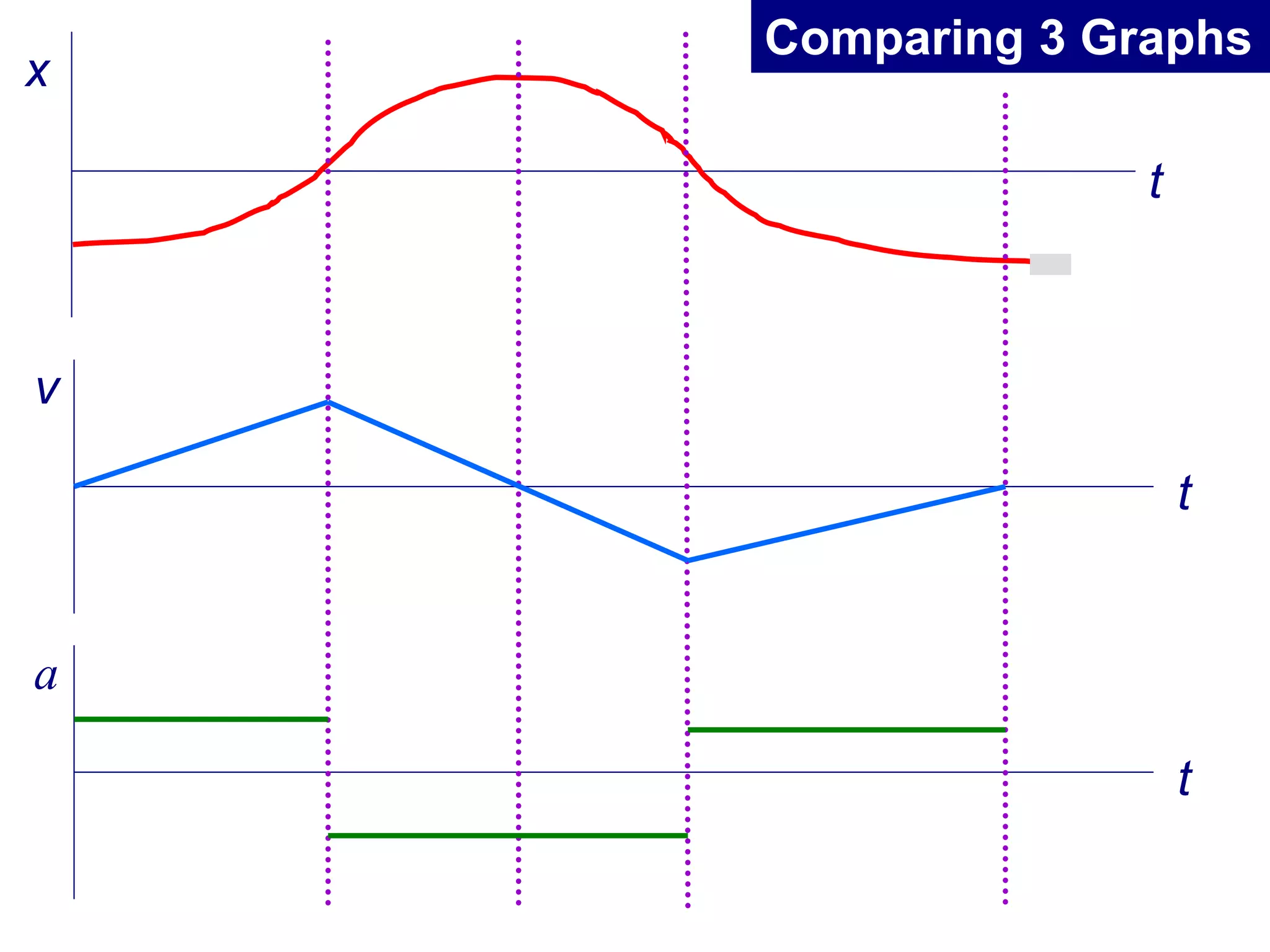
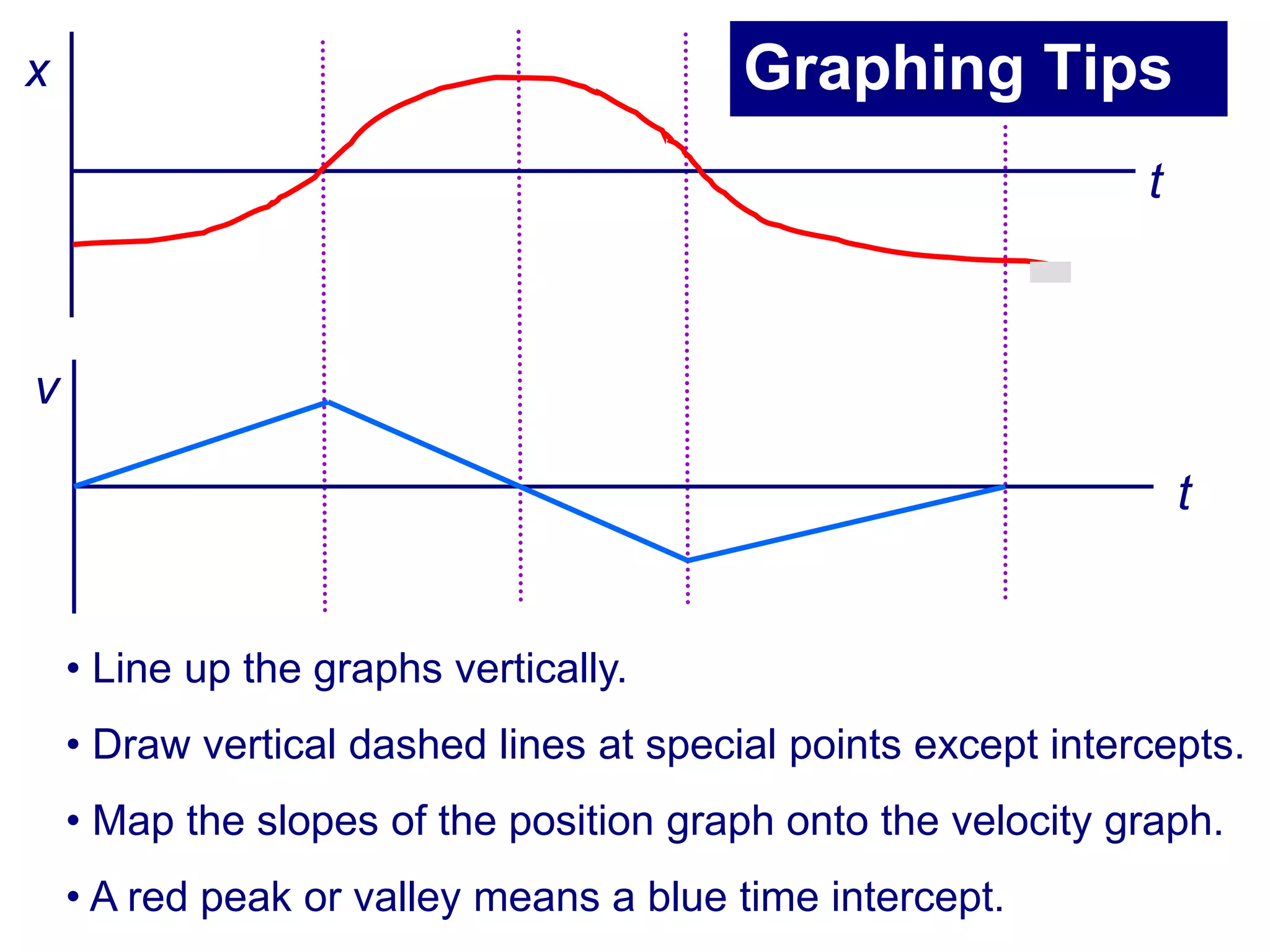
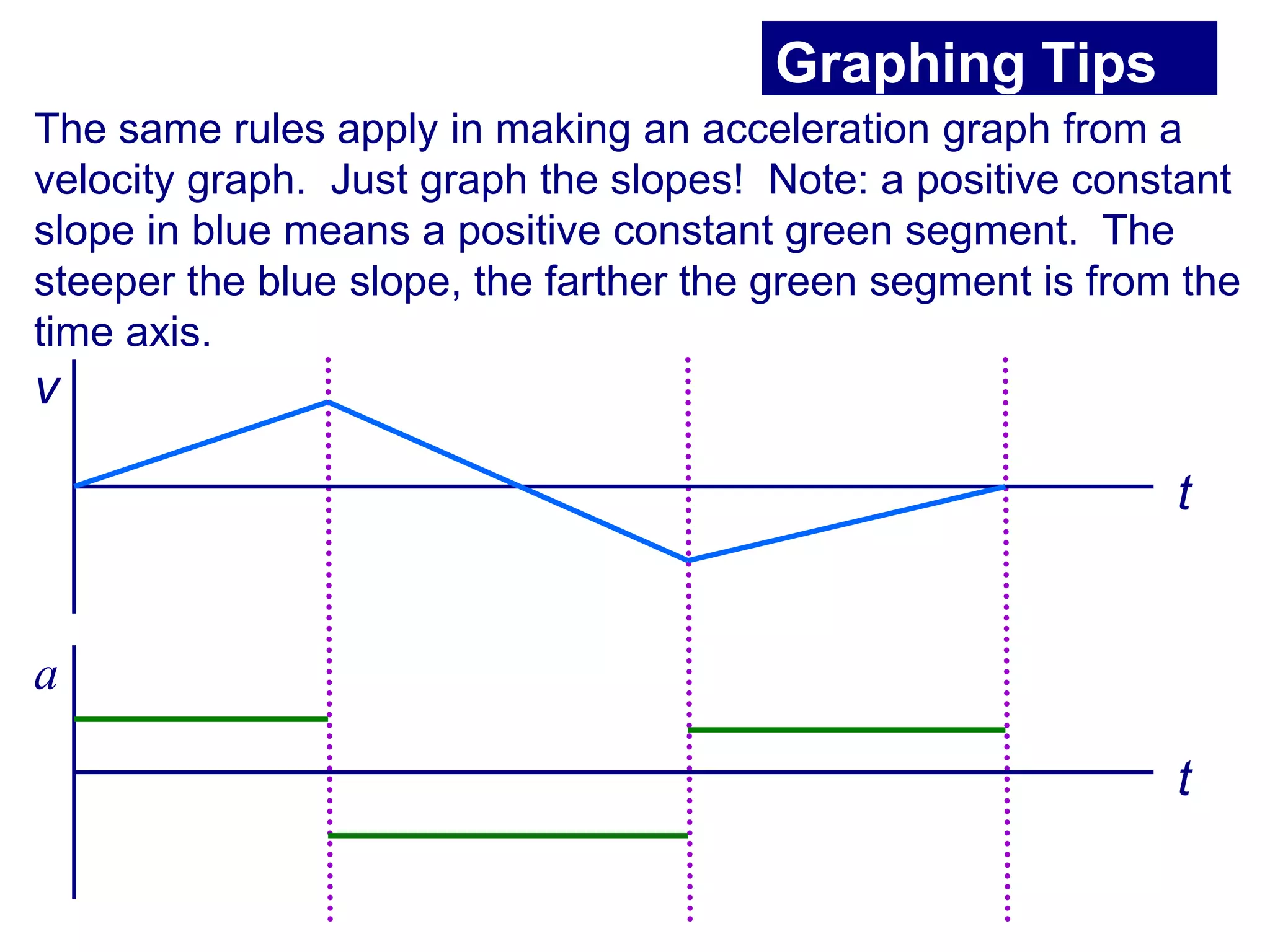
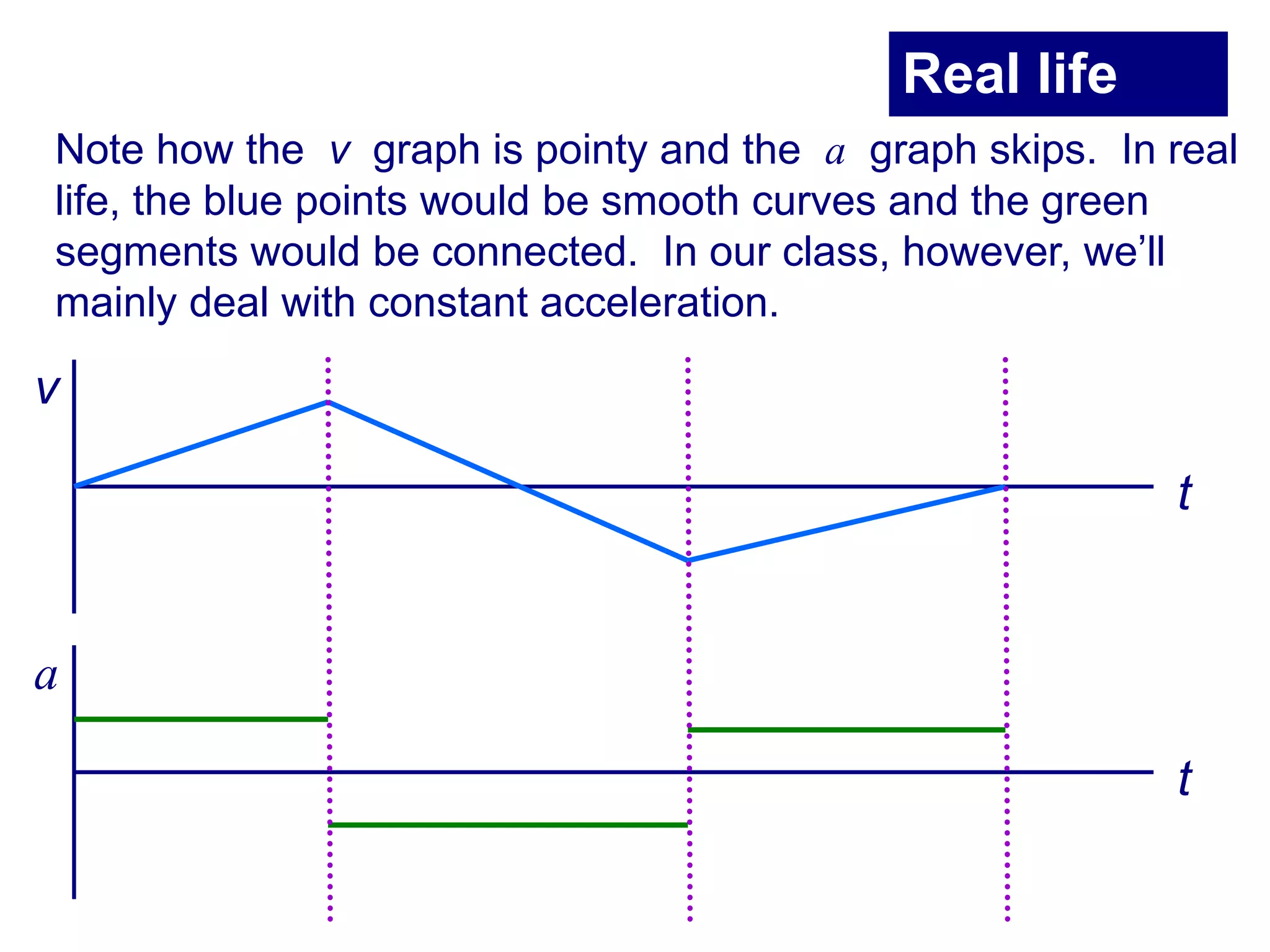
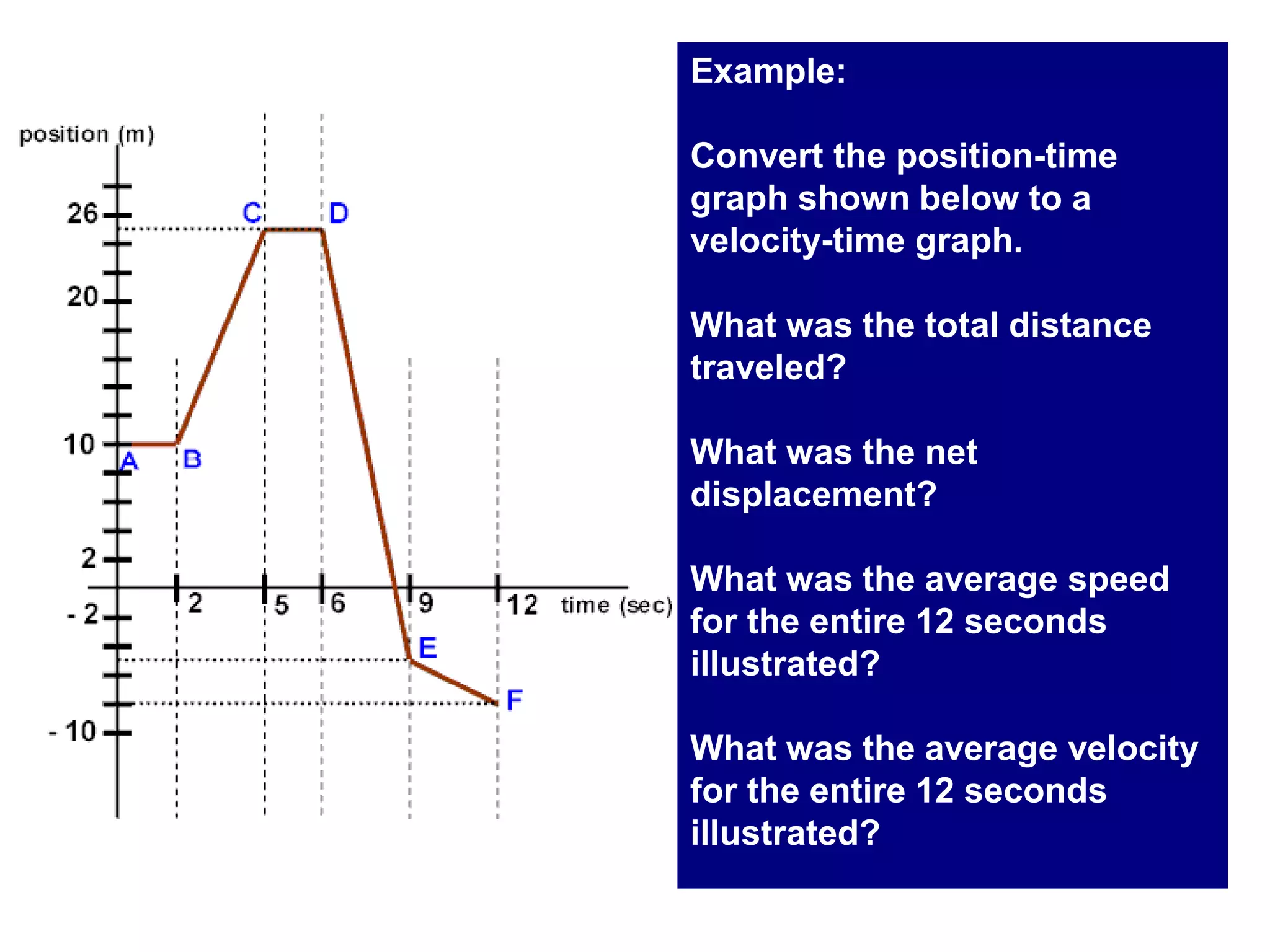
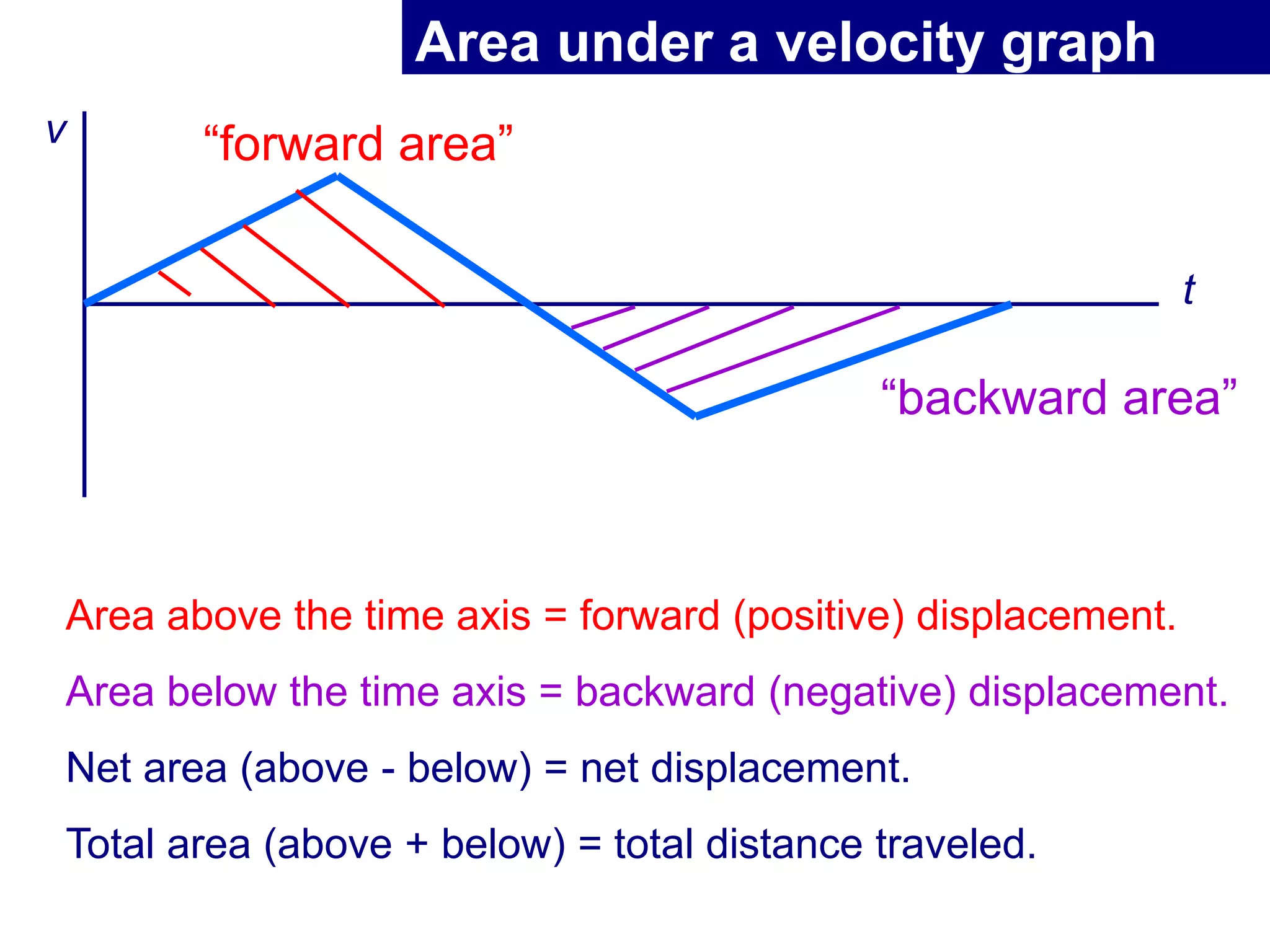
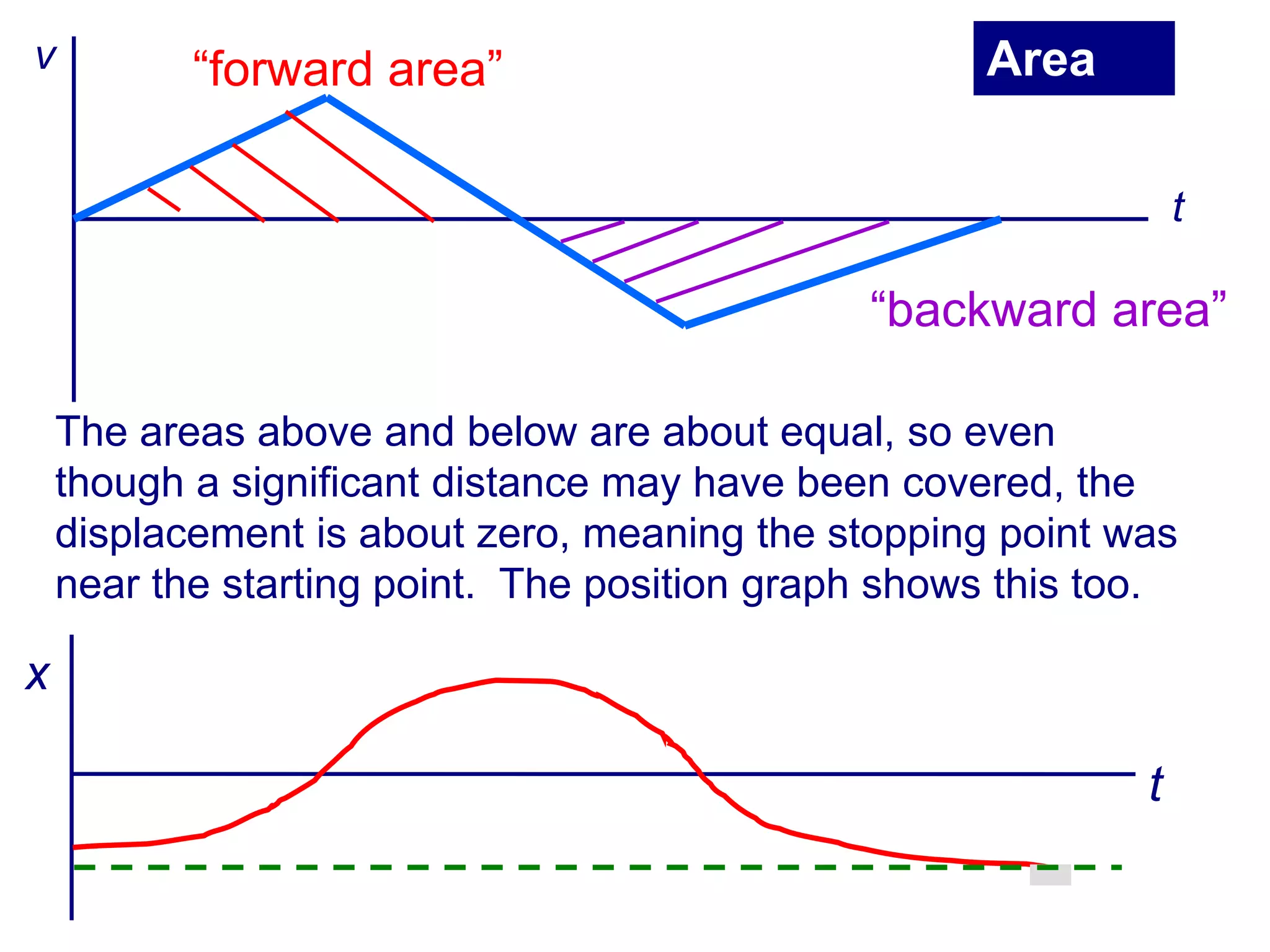
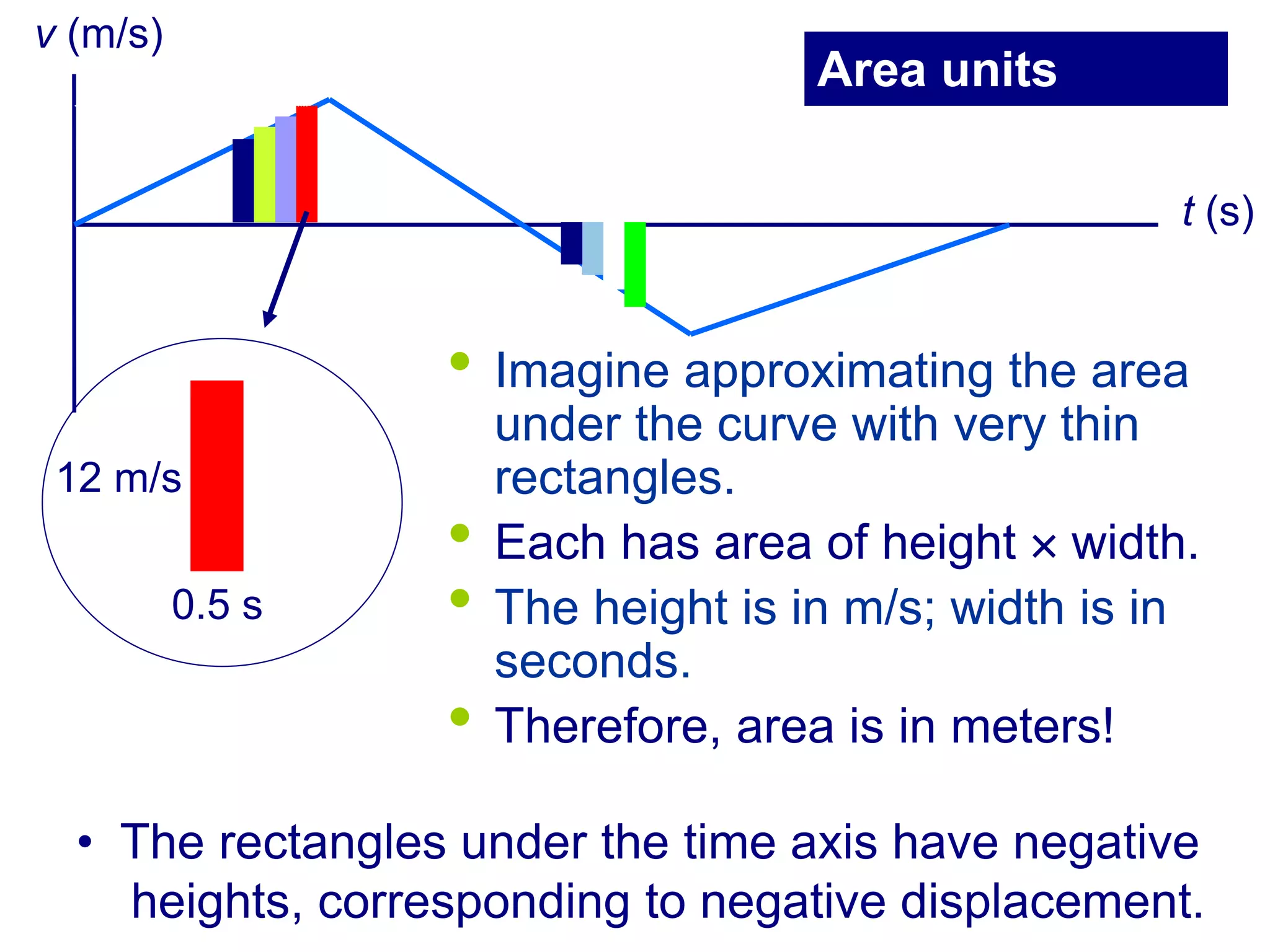
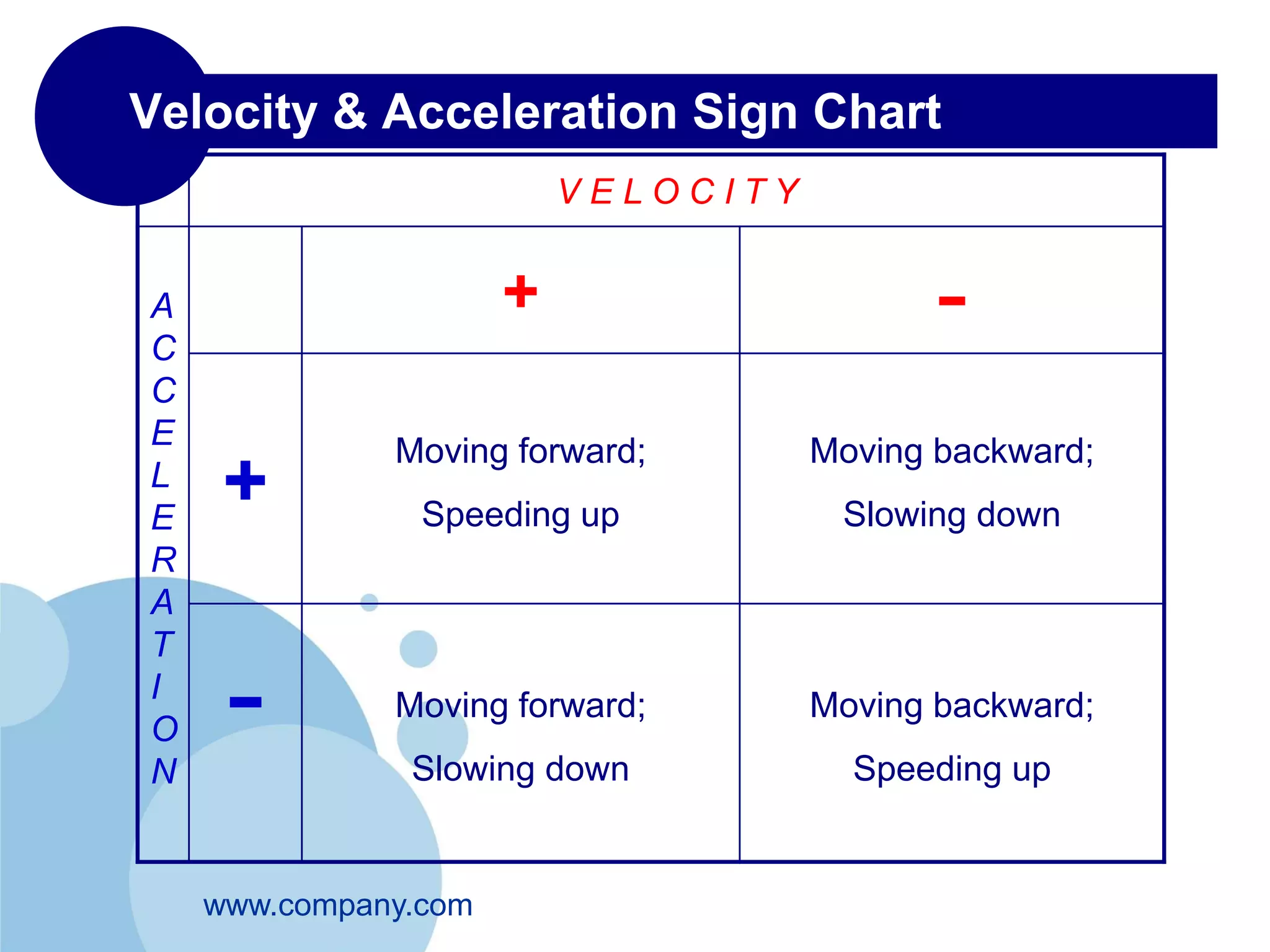
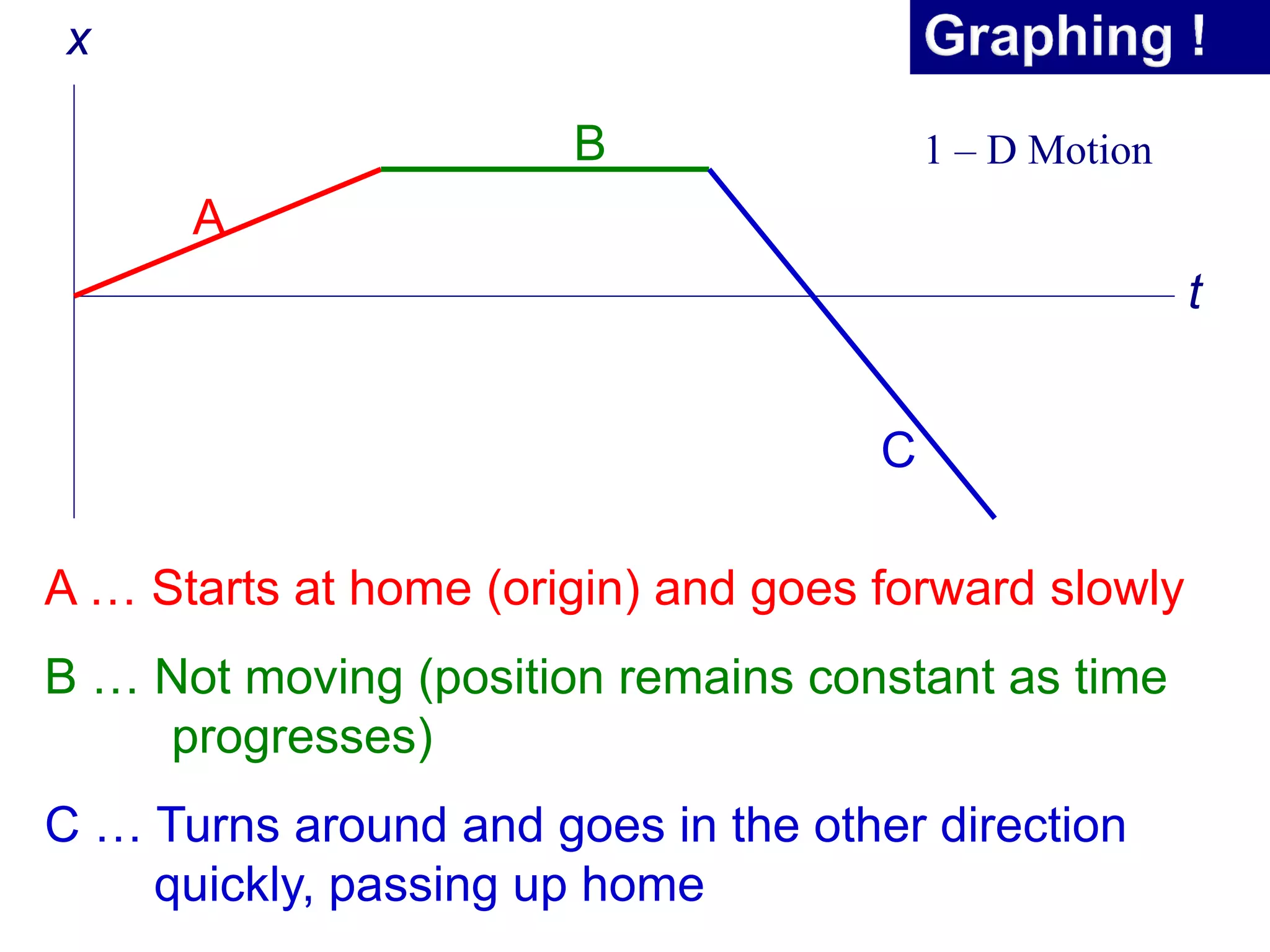
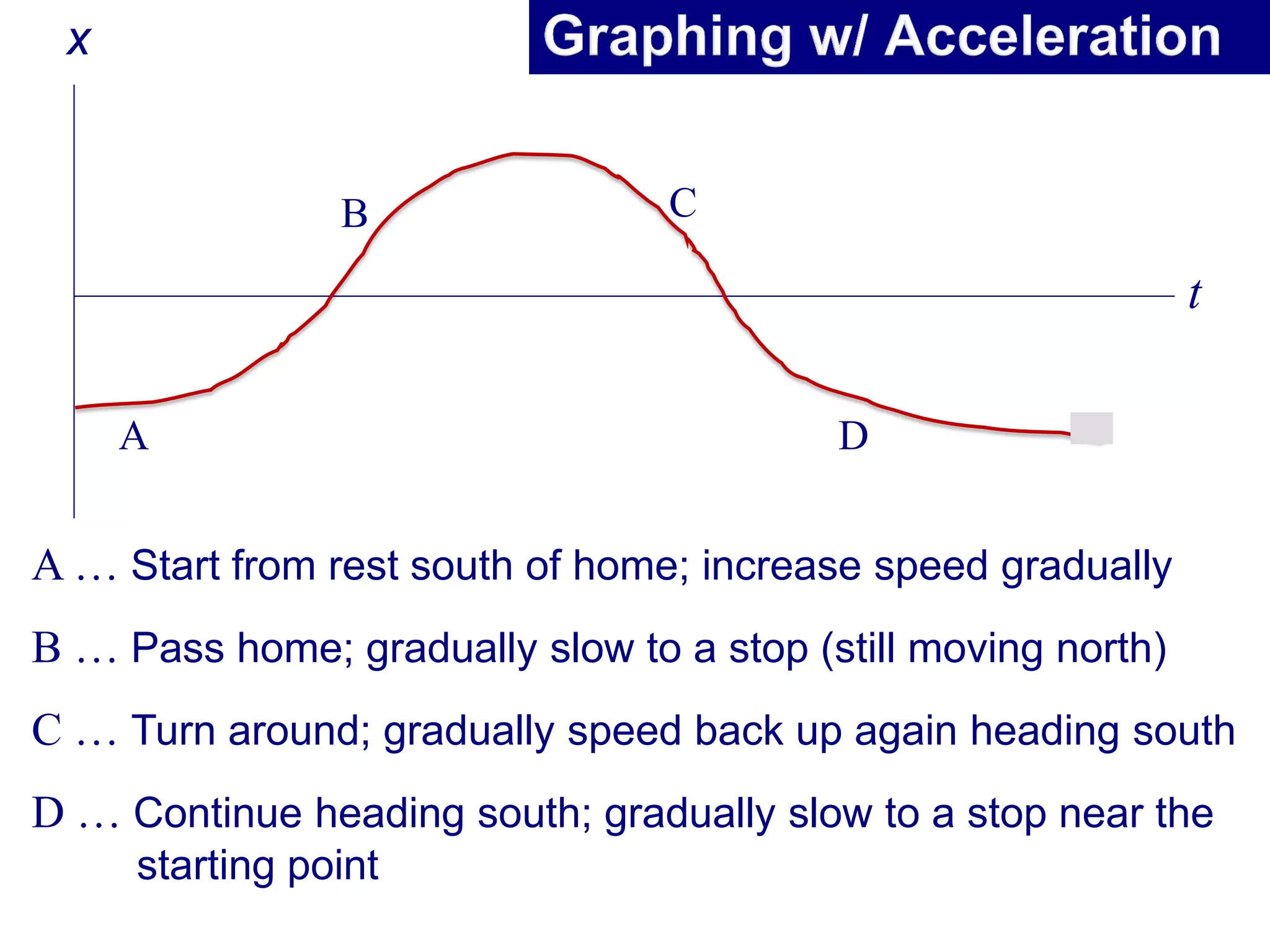
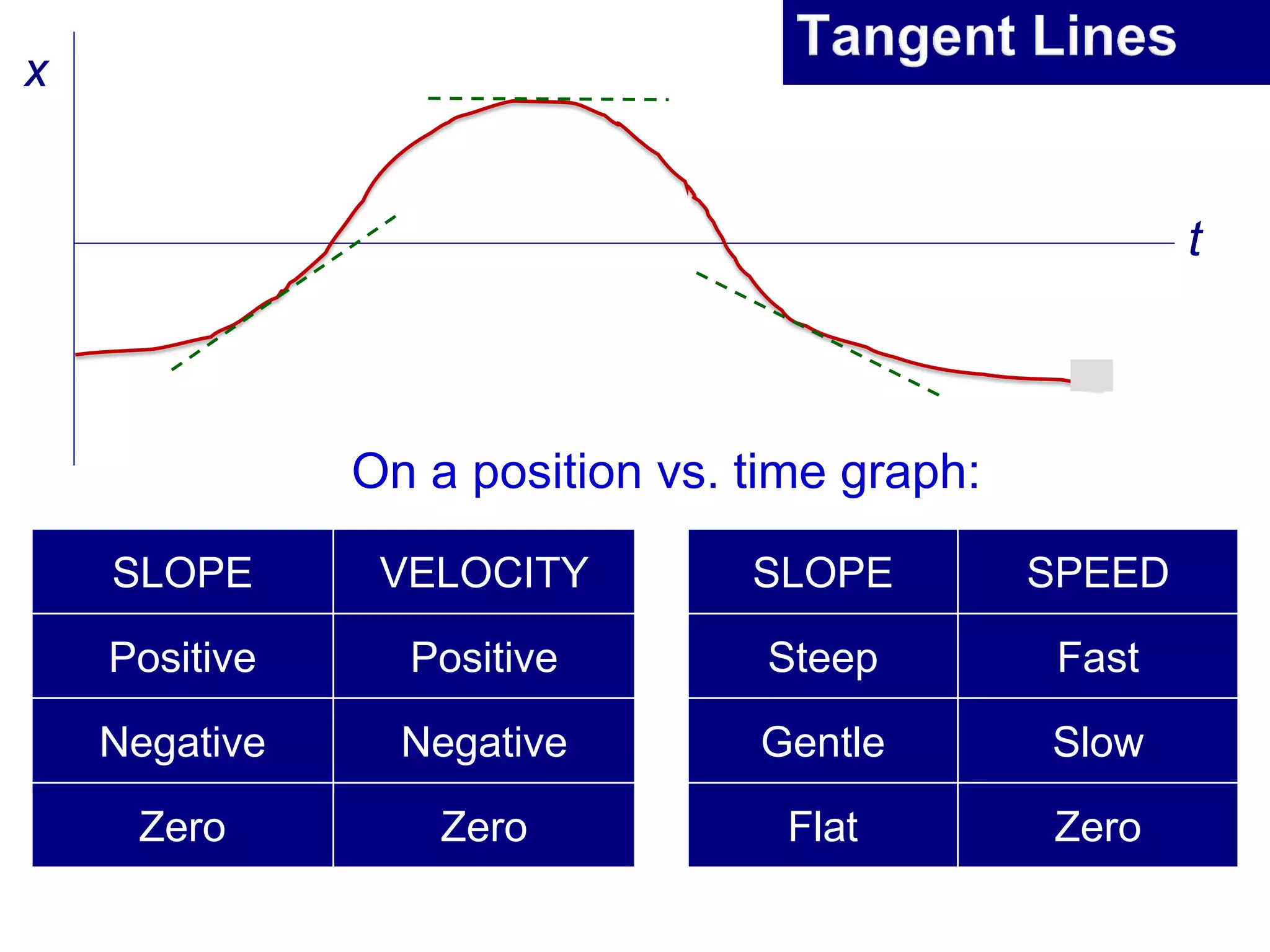
This document summarizes key concepts in kinematics including: - Scalars represent physical quantities with units while vectors have both magnitude and direction. - Vectors are defined by their components in a coordinate system and can be added by combining their x and y components or by graphical methods. - Displacement, velocity and acceleration are all described as vectors since they have both magnitude and direction.

1. Chapter 2 : Kinematics
• Objectives :
2-1 Scalars versus Vectors
2-2 Components of a Vector
2-3 Adding and Subtracting Vectors
2-4 Unit vectors
2-5 Position, Displacement, Velocity and Acceleration Vectors

2. 2-1 Scalars versus Vectors
• A scalar is a number with units. A vector on the other hand is
a mathematical quantity with both a direction and a
magnitude
• A vector is indicated with a boldface or written with a small
arrow above it. N
E
푟
푟
푟
Displacement vector

3. 2-2 Components of a Vector
• To find the components of a vector we need to set up a
coordinate system.
• In 2d we choose an origin, O and a positive direction for both
the x and y axes. (If 3d system we would also indicate a z axis)
• A vector is defined by its magnitude (indicated by the length
of the arrow representing the vector)
and its direction.
• The quantities of 푟푥 and 푟푦 are referred
to as the x and y scalar components
of the vector 푟
y
x
푟
푟 푥
푟 푦

4. 2-2 Components of a Vector
• We can find the components of a vector by using standard
trigonometric relations, as summarized below.
y
x
퐴
퐴 푥
퐴 푦
휃
퐴푥 = 퐴 cos 휃
퐴푦 = 퐴 sin 휃
2 + 퐴푦
퐴 = 퐴푥
2
휃 = 푡푎푛−1
퐴푦
퐴푥
푥 푠푐푎푙푎푟 푐표푚푝. 표푓 푉푒푐푡표푟퐴
y 푠푐푎푙푎푟 푐표푚푝. 표푓 푉푒푐푡표푟퐴
푚푎푔푛푖푡푢푑푒 표푓 푉푒푐푡표푟퐴
푑푖푟푒푐푡푖표푛 표푓 푉푒푐푡표푟퐴

5. 2-2 Components of a Vector
• How do you determine the correct signs for the x and y
components of a vector?
• To determine the signs of a vector’s components, it is only
necessary to observe the direction in which they point.
• For ex. In the case of a vector in the 2nd quadrant of
the coordinate system, the x component
points in the negative direction; hence
퐴푥 < 0 and the y component points
in the positive direction hence 퐴푥 < 0.
Here the direction is 180° − 휃
y
x
퐴
퐴 푥
퐴 푦
휃
퐴
퐴 푥
퐴 푦
휃
퐴
퐴 푦
휃
퐴
퐴 푦
휃

6. 2-3 Adding and Subtracting Vectors
In this section we begin by defining vector addition graphically,
and then show how the same addition can be performed more
concisely using and accurately using components.
2 Ways to do vector addition:
• Adding vectors graphically
• Adding vectors using components

7. 2-3 Adding and Subtracting Vectors
2.3.1 Adding vectors graphically
• It can be done using either
- Triangle method ( for 2 vectors)
- Parallelogram method (for 2 vectors)
- Vector polygon method (for >2 vectors)
• Vector 퐶 is the vector sum of 퐴 and 퐵
• To add the vectors, place the tail of 퐵 at the head
퐶 = 퐴 + 퐵
푦
퐴
of 퐴 . The sum, 퐶 = 퐴 + 퐵, is the vector extending from the
tail of 퐴 to the head of 퐵
퐵
퐶
• It’s fine to move the arrows, as long as you don’t change their
length or their direction. After all, a vector is defined by its length
and direction, if these are unchanged, so is the vector.
푥

8. 2-3 Adding and Subtracting Vectors
2.3.2 Adding vectors using components
• The graphical way of adding vectors yields approximate
results, limited by the accuracy with which the vectors can be
drawn and measured.
• In contrast, exact results can be obtained by adding the
vectors in terms of their components.
퐴
퐵
푦
푥
퐶 = 퐴 + 퐵
퐴
푦 퐵
퐵푦
푥
퐶
퐴 푥
퐴 푦
퐵푥
퐶푥 = 퐴푥+ 퐵푥
퐶푦 = 퐴푦+ 퐵푦
퐶 = 퐶푥
2 + 퐶푦
2
휃 = 푡푎푛−1
퐶푦
퐶푥
푦

9. 2-3 Adding and Subtracting Vectors
2.3.3 Subtracting vectors
• The negative of a vector is
represented by an arrow of the
same length as the original vector,
but pointing in the opposite direction.
• That is, multiplying a vector by minus one reverses its
direction
퐶 = 퐴 − 퐵
퐴
퐵
퐵
퐶
퐶 = 퐴 + (−퐵)
푦
푥

10. 2-4 Unit Vectors
• The unit vectors of an x-y coordinate system, 푥 푎푛푑 푦 , are
defined to be dimensionless vectors of unit magnitude 1,
pointing in the positive x and y directions.
• It is used to provide a convenient way of expressing an
arbitrary vector in terms of its components
y
푥 x
푦

11. 2-4 Unit Vectors
Multiplying Unit Vectors by Scalars
• This will increase its magnitude by a factor of x, but does not
change its direction. For example magnitude x = 3
• Now we can write a vector 퐴 in terms of its x and y vector
components
퐴 = 퐴푥푥 + 퐴푦푦
y
x
퐴 3퐴
−3퐴

12. 2-4 Unit Vectors
Multiplying Unit Vectors by Scalars
• Now we can write a vector 퐴 in terms of its x and y vector
components
퐴 = 퐴푥푥 + 퐴푦푦
• We see that the vector components are the projection of a
vector onto the x and y axes.
• The sign of the vector components is positive if they point in
the positive x or y direction and vice versa.
y
퐴 퐴푦푦
x
퐴푥푥

13. 2-5 Position, Displacement, Velocity
and Acceleration Vectors
• Position vectors
• Velocity vectors
• Acceleration Vectors