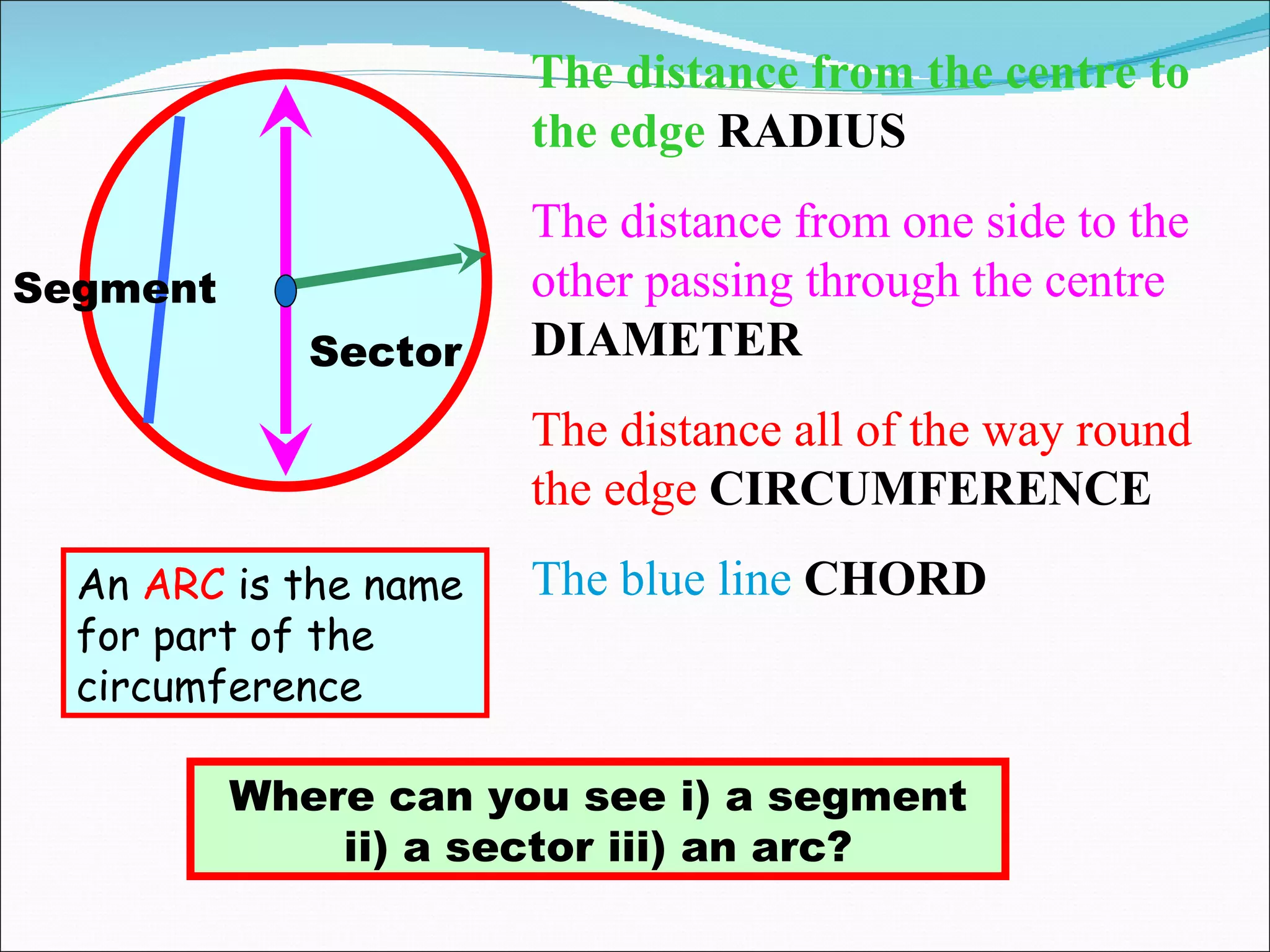
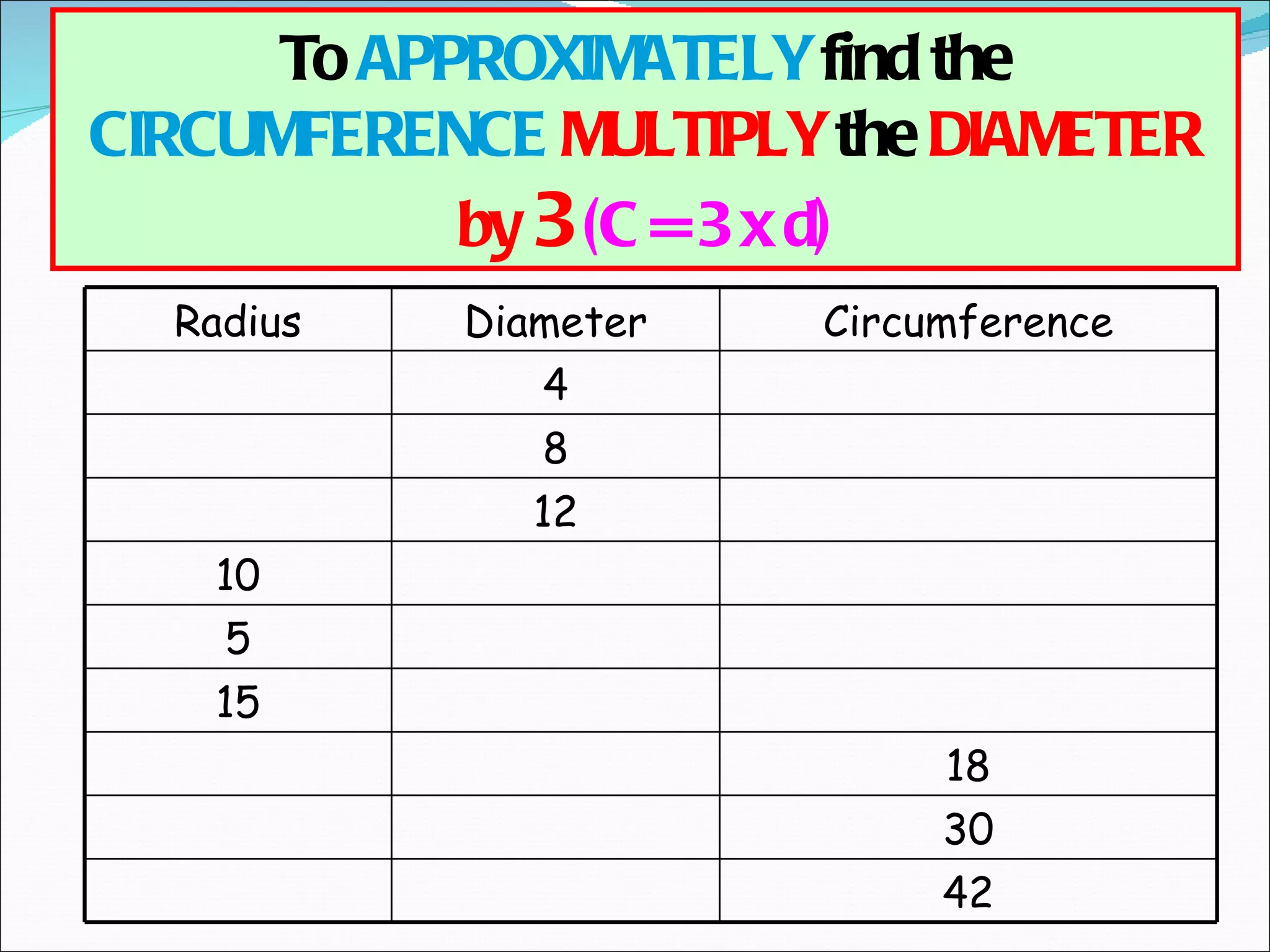
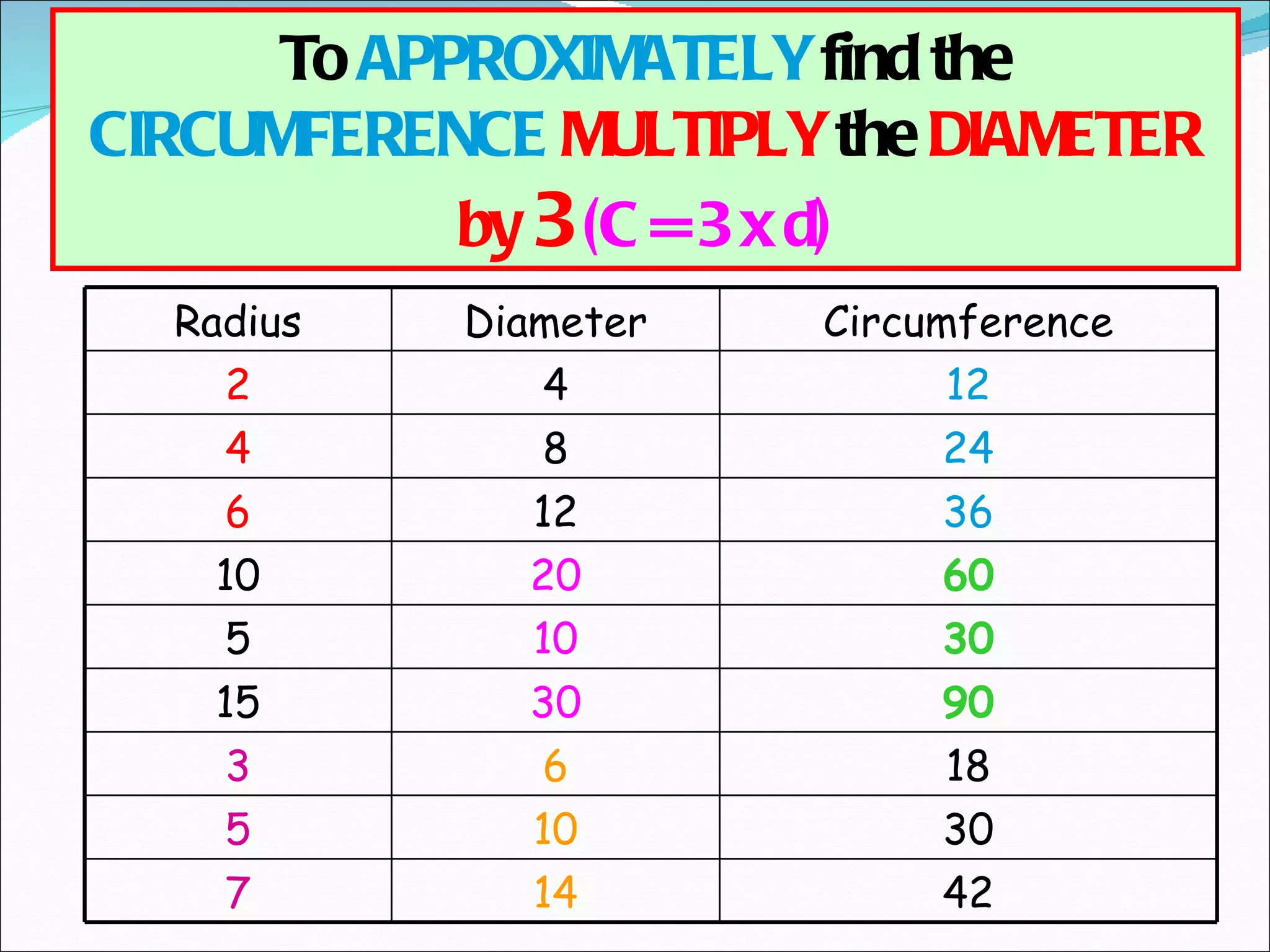
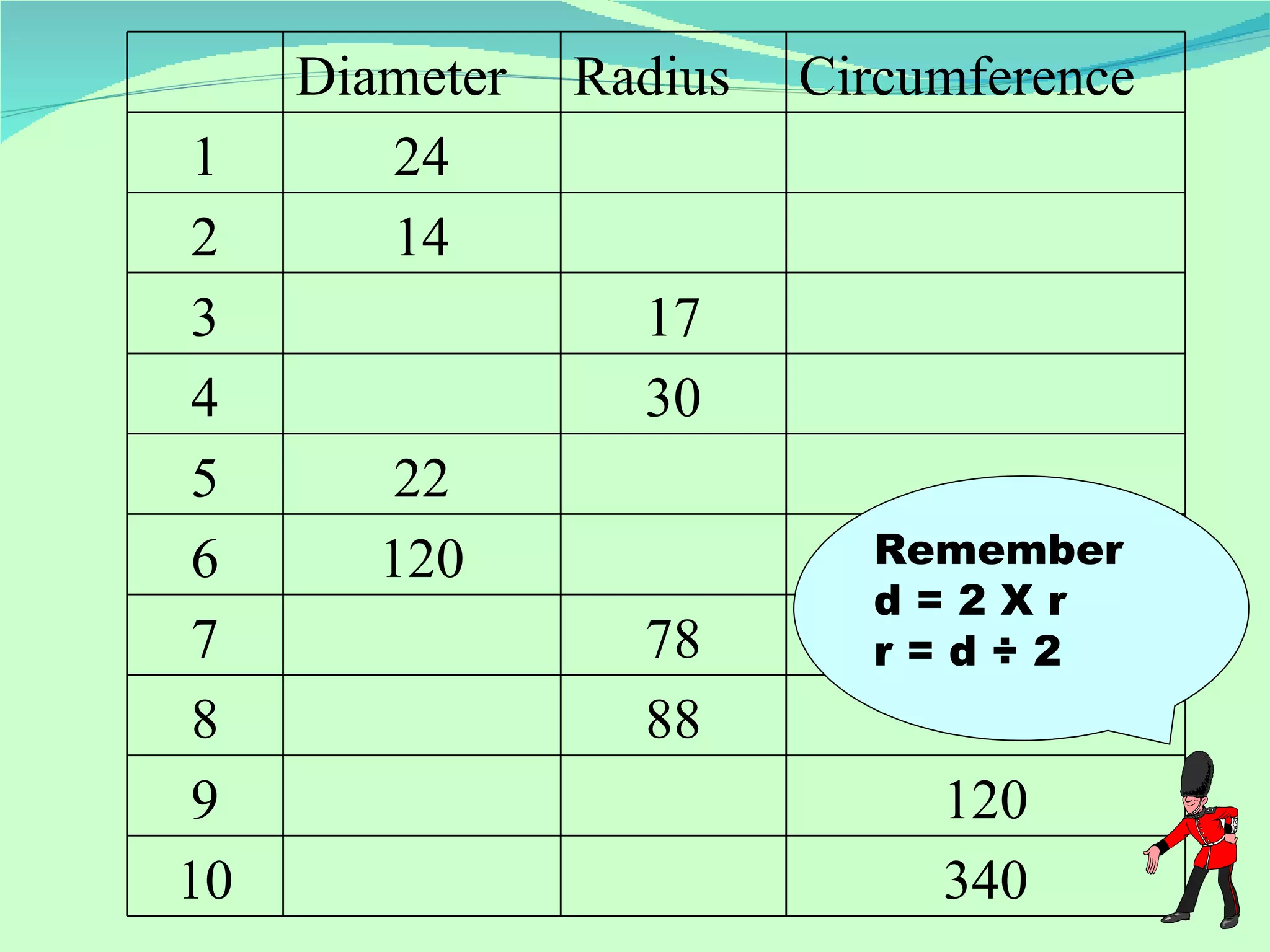
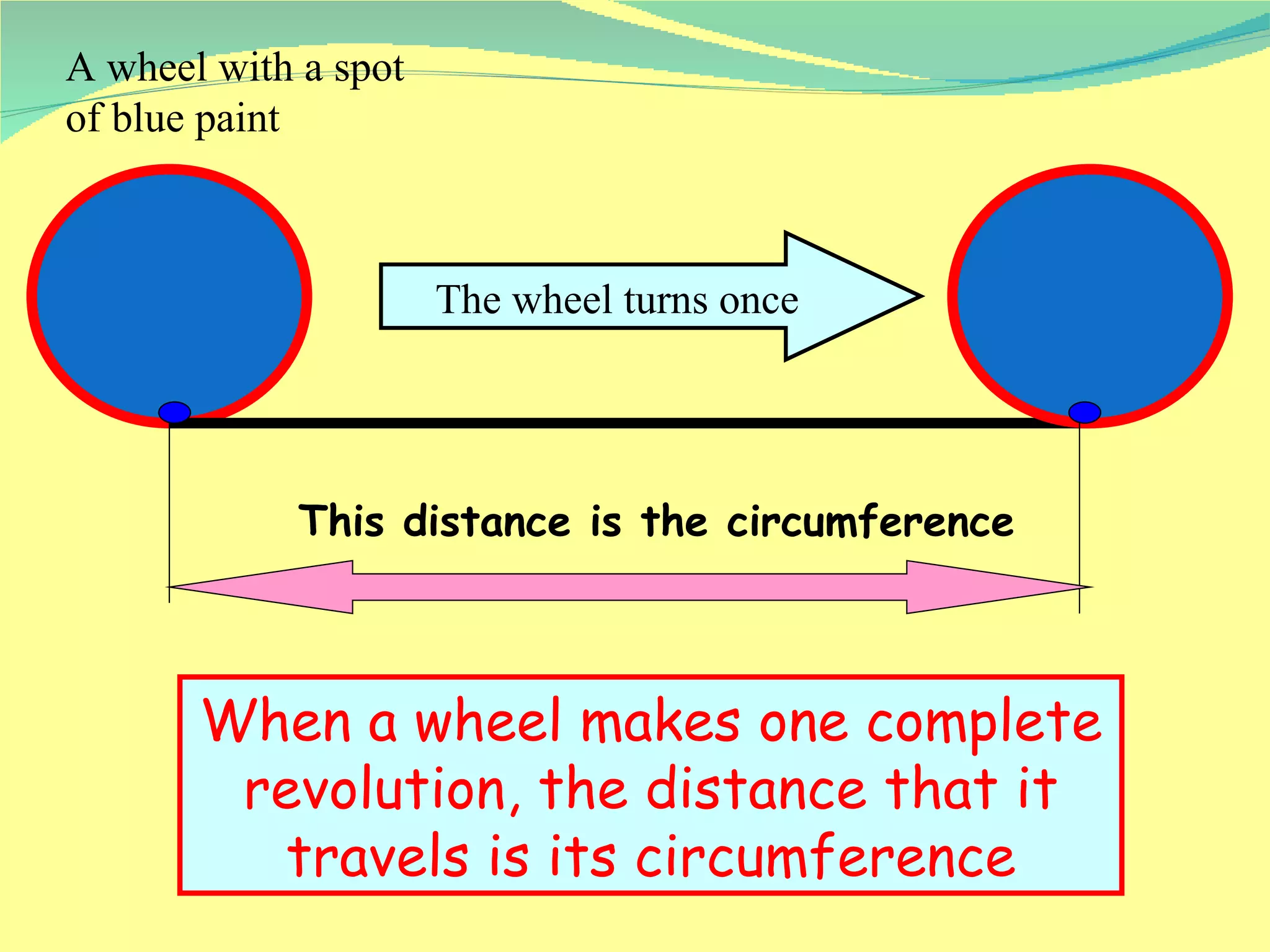
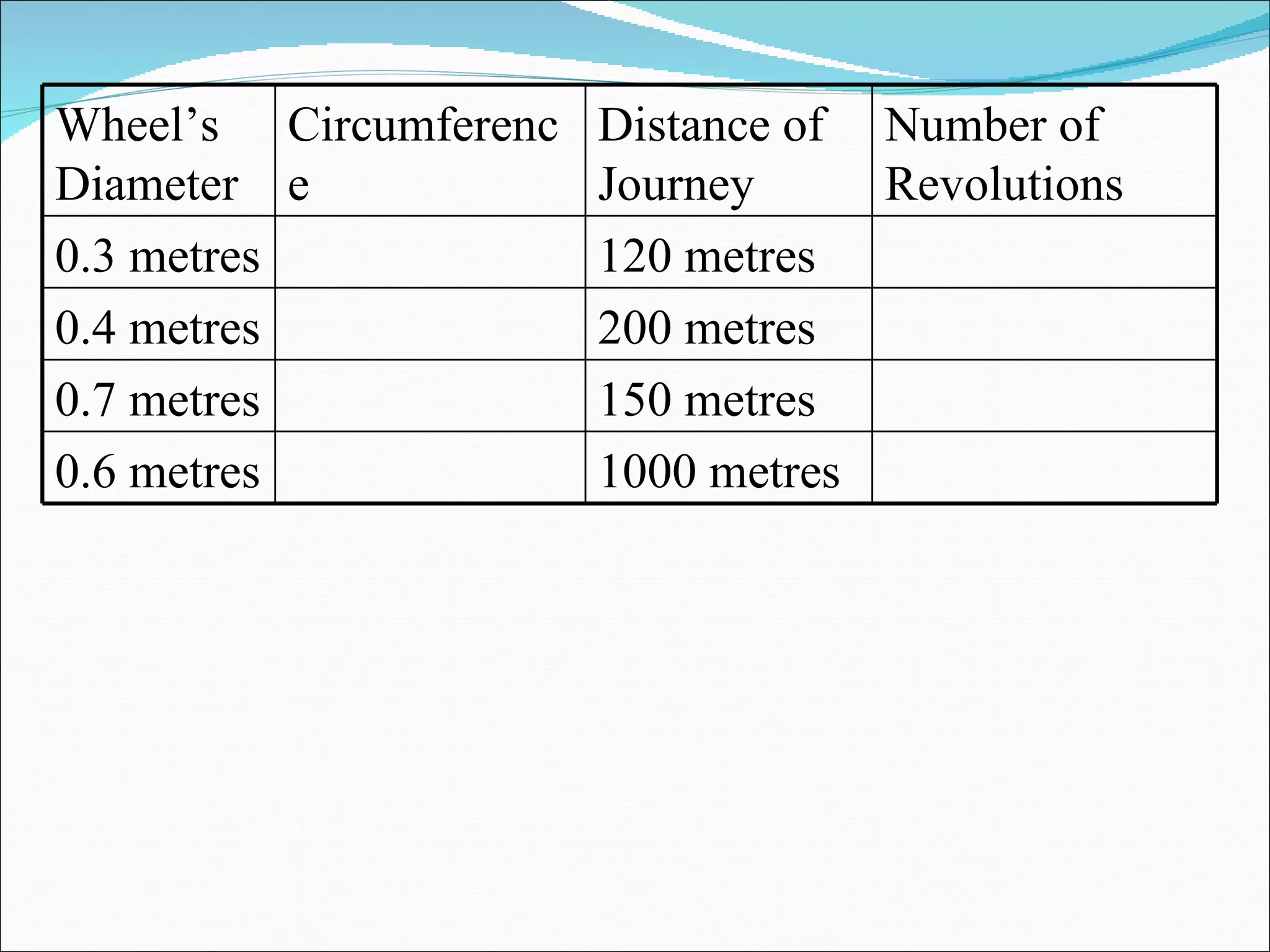
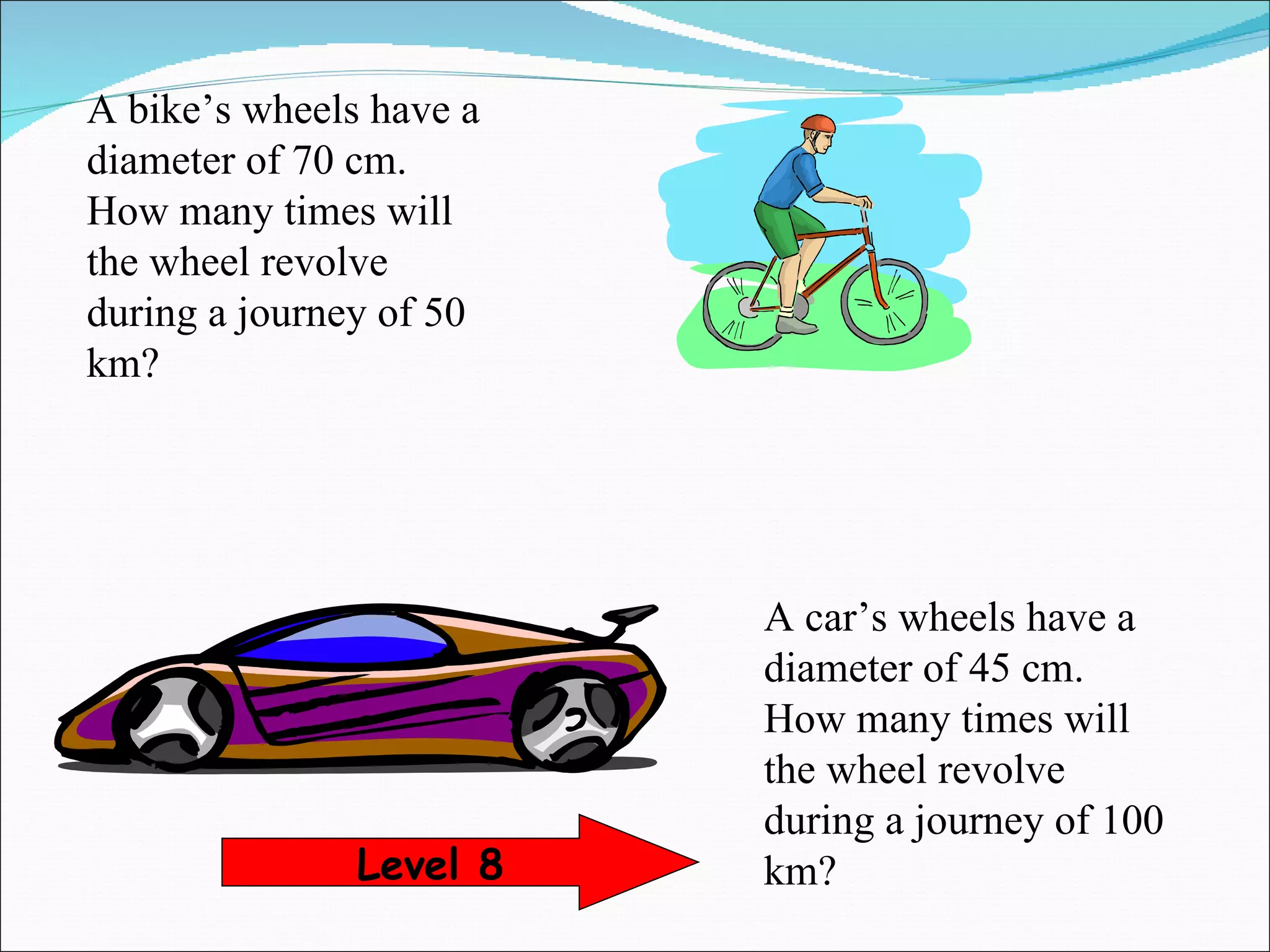
The document discusses calculating features of circles such as circumference, arc length, and number of revolutions of a wheel on a journey. It provides formulas for circumference (C=πd), arc length (Arc=Angle/360 x Circumference), and number of revolutions (Revolutions=Journey Distance/Circumference). Examples of using the formulas to calculate circumference, arc length, and number of revolutions are given for circles with different diameters and journey distances.

1. Know the names of a circle’s features Calculate the circumference Calculate an arc length Deal with the revolution of wheels and journey problem Levels 5  8 Saturday 29 October 2011 Why am I doing this? A wheel is a circle! Circles in design – Mickey Mouse is made from circles A real favourite SAT and GCSE question OK - What have I got to do?

2. Circle Starter Level 5

3. Name these Features The distance from the centre to the edge The distance from one side to the other passing through the centre The distance all of the way round the edge The blue line Area Circumference Rotation Radius Degree Chord Sector Segment Diameter Sphere Concentric Arc

4. The distance from the centre to the edge RADIUS The distance from one side to the other passing through the centre DIAMETER The distance all of the way round the edge CIRCUMFERENCE The blue line CHORD Where can you see i) a segment ii) a sector iii) an arc? Sector Segment An ARC is the name for part of the circumference

5. APPROXIMATELY FINDING THE CIRCUMFERENCE Level 5

6. APPROXIMATELY what is the relationship (connection) between a circle’s diameter and its circumference?

7. To APPROXIMATELY find the CIRCUMFERENCE MULTIPLY the DIAMETER by 3 (C = 3 x d) Radius Diameter Circumference 4 8 12 10 5 15 18 30 42

8. To APPROXIMATELY find the CIRCUMFERENCE MULTIPLY the DIAMETER by 3 (C = 3 x d) Radius Diameter Circumference 2 4 12 4 8 24 6 12 36 10 20 60 5 10 30 15 30 90 3 6 18 5 10 30 7 14 42

9. SAT Aural Question ( Answer a question in 10 seconds) A circle has a diameter of 10 cm. APPROXIMATELY (ROUGHLY), what is its circumference? A circle has a circumference of 18 cm. Approximately, what is its diameter? 30 cm 6 cm

10. Calculate the Circumference Using the Correct Formula Level 6

11. Diameter = 12 cm C = d C = 3.14 X 12 C = 37.68 How to calculate the circumference The symbol is the Greek letter pi. It stands for a number that can never be found exactly. It is approximately 3.14 Evaluate the CIRCUMFERENCE Always, write the formula (rule )

12. Diameter = ?cm C = d d = C ÷ d = C ÷ 3.14 d = 40 ÷ 3.14 d = 12.73 How to calculate the diameter from the circumference If the circumference is 40 cm. evaluate the DIAMETER Always, write the formula (rule )

13. Remember d = 2 X r r = d ÷ 2 Diameter Radius Circumference 1 24 2 14 3 17 4 30 5 22 6 120 7 78 8 88 9 120 10 340

14. Diameter Radius Circumference 1 24 12 75.36 2 14 7 43.96 3 34 17 106.76 4 60 30 188.4 5 22 11 69.08 6 120 60 376.8 7 156 78 489.84 8 176 88 552.64 9 38.22 19.11 120 10 108.28 54.14 340

15. Calculate an Arc Length Level 7

16. 72 0 A B How to Calculate an Arc Length Calculate the arc length AB for a circle with a diameter of 12 cm . Circumference C = 3.14 x 12 C = 37.6 cm But we only want the arc length AB. This is 72 0 of the circle and because there are 360 0 in a circle, this is 72 ÷ 360 = 0.2 as a decimal fraction of the circumference AB = 0.2 x C AB = 0.2 x 37.6 AB = 5.52

17. x 0 A B The FORMULA for an Arc Length Calculate the arc length AB for a circle with a diameter of d AB = x/360( d) AB = (x ÷ 360) x 3.14 x d Divide the arc length’s angle by 360 then multiply this by the circumference

18. x 0 A B Using the FORMULA for an Arc Calculate the arc length AB for these circles AB = x/360( d) AB = (x ÷ 360) x 3.14 x d X 0 Diam Arc AB X 0 Diam Arc AB 1. 144 12 4. 270 60 2. 48 40 5. 24 36 3. 180 25 6. 70 40

19. x 0 A B Using the FORMULA for an Arc Calculate the arc length AB for these circles AB = x/360( d) AB = (x ÷ 360) x 3.14 x d X 0 Diam Arc AB X 0 Diam Arc AB 1. 144 12 15.07 4. 270 60 141.3 2. 48 40 20.10 5. 24 36 7.54 3. 180 25 39.25 6. 70 40 24.42

20. Finding the Number of Revolutions (turns) of a Wheel on a Journey Level 8

21. A wheel with a spot of blue paint The wheel turns once This distance is the circumference When a wheel makes one complete revolution, the distance that it travels is its circumference

22. 1.57 When a wheel makes one complete revolution, the distance that it travels is its circumference How many times will a wheel with a diameter of 0.5 metre rotate when it travels distance of 100 metres? Find the circumference of the wheel C = 3.14 x 0.5 C = 1.57 2. Divide this into 100 to find the number of revolutions Revs = 100 ÷ 1.57 Revs = 63.7 times 100 metres

23. Find the circumference of the wheel C = 3.14 x d 2. Divide this into the journey to find the number of revolutions Revs = Journey Distance ÷ C Wheel’s Diameter Circumference Distance of Journey Number of Revolutions 0.3 metres 120 metres 0.4 metres 200 metres 0.7 metres 150 metres 0.6 metres 1000 metres

24. Wheel’s Diameter Circumference Distance of Journey Number of Revolutions 0.3 metres 120 metres 0.4 metres 200 metres 0.7 metres 150 metres 0.6 metres 1000 metres

25. A car’s wheels have a diameter of 45 cm. How many times will the wheel revolve during a journey of 100 km? Level 8 A bike’s wheels have a diameter of 70 cm. How many times will the wheel revolve during a journey of 50 km?