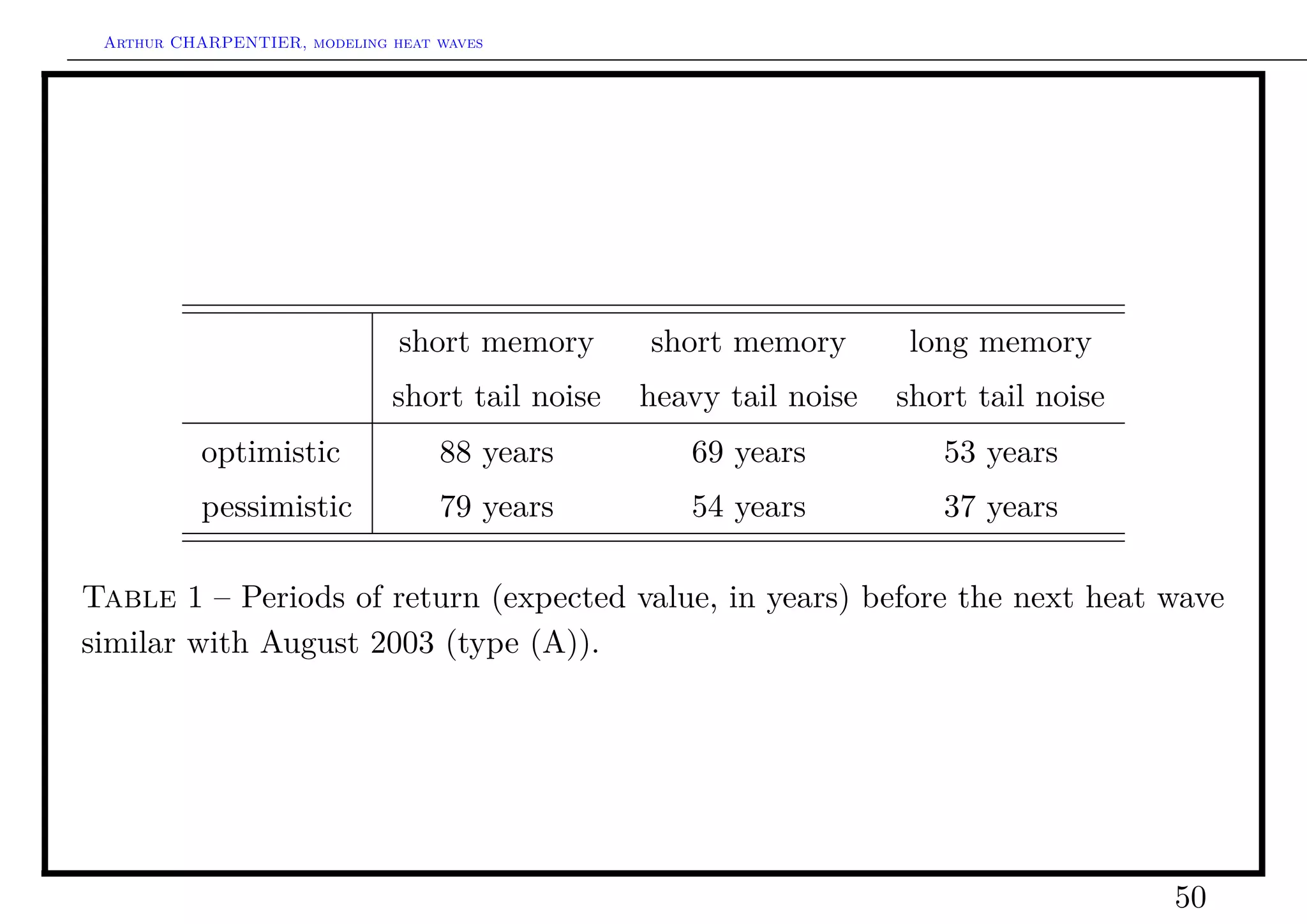
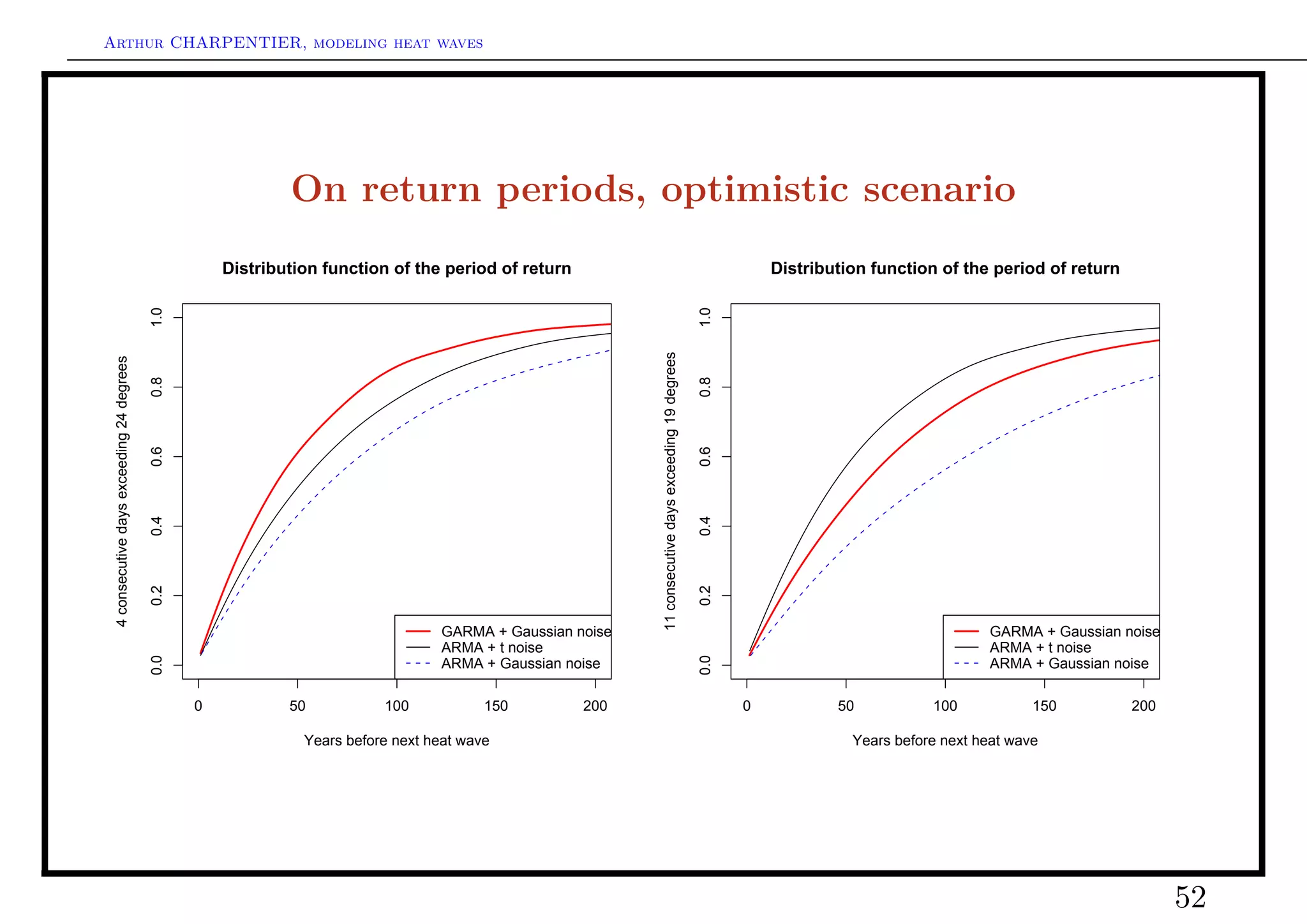
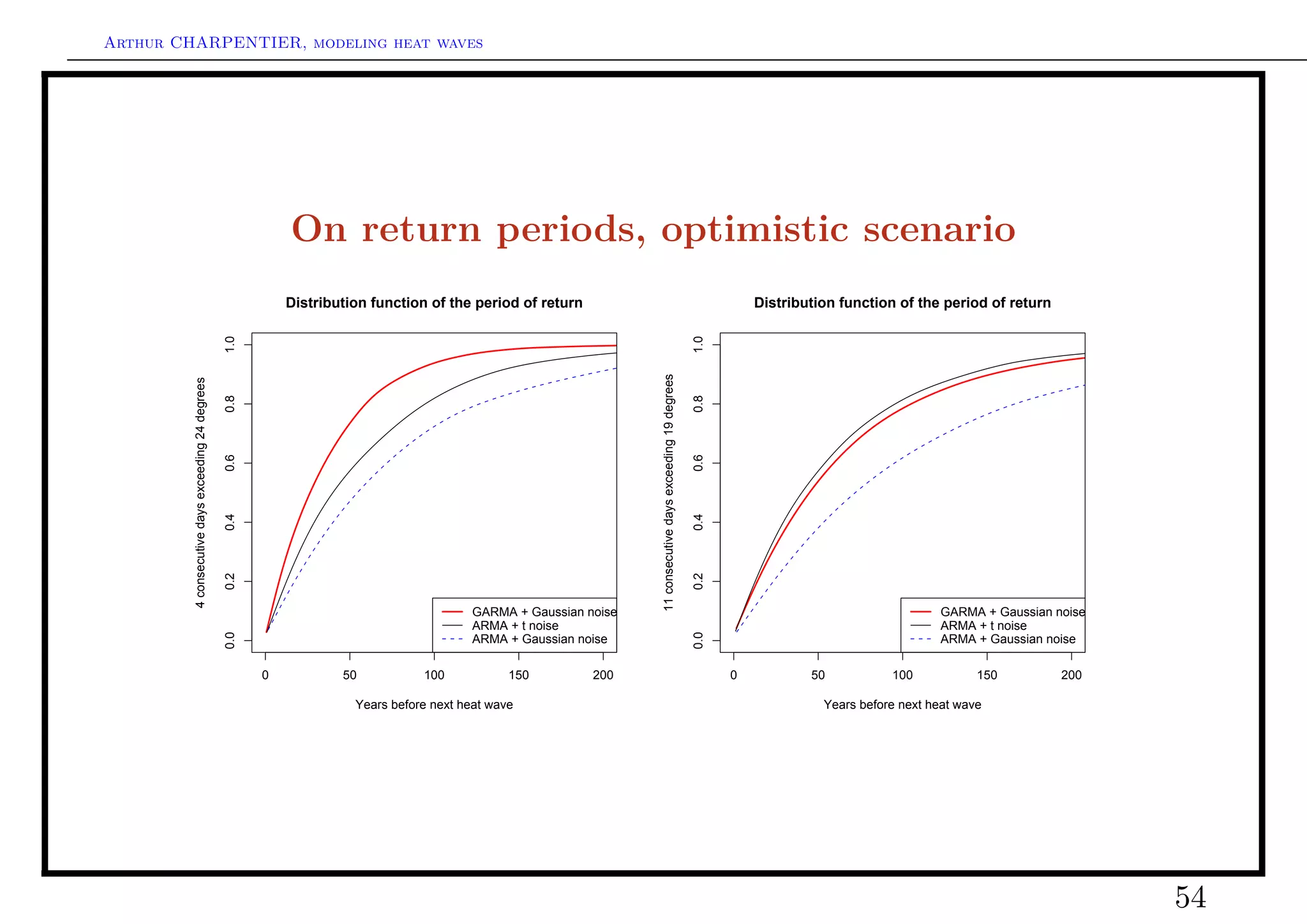
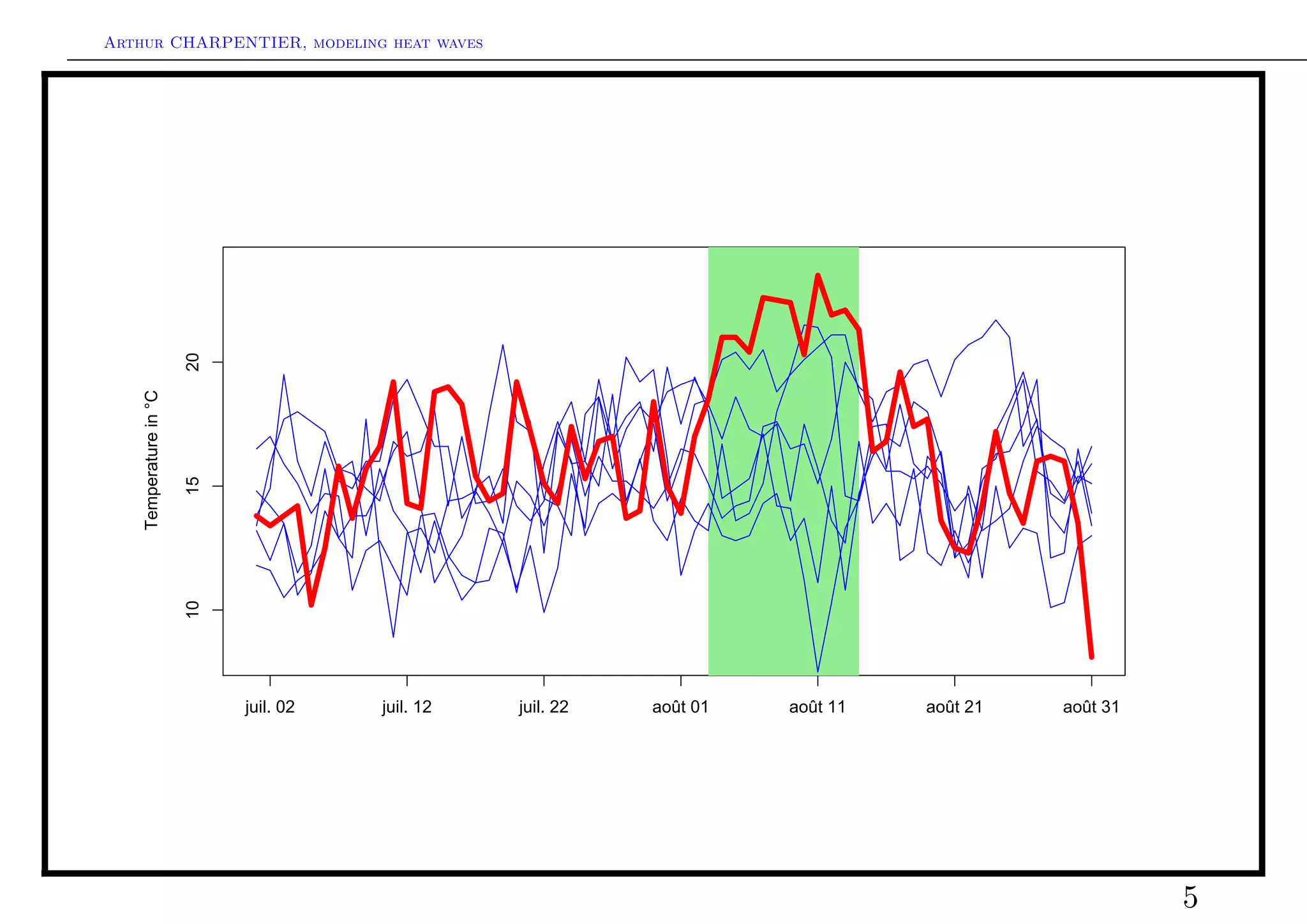
This document summarizes Arthur Charpentier's presentation on modeling heat waves under climate change. It discusses how heat waves are becoming more frequent and intense due to global warming. It also examines different approaches to modeling temperature data, including quantile regression to analyze extremes, modeling the trend, seasonal, and residual components of temperature, and the potential for spatial modeling of residuals between locations. Tail dependence indices are also introduced as a way to quantify dependence in temperature extremes between locations.


![Arthur CHARPENTIER, modeling heat waves
Motivation
“there is no longer any doubt that the Earth’s climate is changing [...] globally,
nine of the past 10 years have been the warmest since records began in 1861”,
February 2005, opening the conference Climate change : a global, national and
regional challenge, Dennis Tirpak.
source : Meehklet al. (2009).
3](https://image.slidesharecdn.com/slides-lyon-3-111114191033-phpapp02/75/Slides-lyon-2011-3-2048.jpg)






![Arthur CHARPENTIER, modeling heat waves
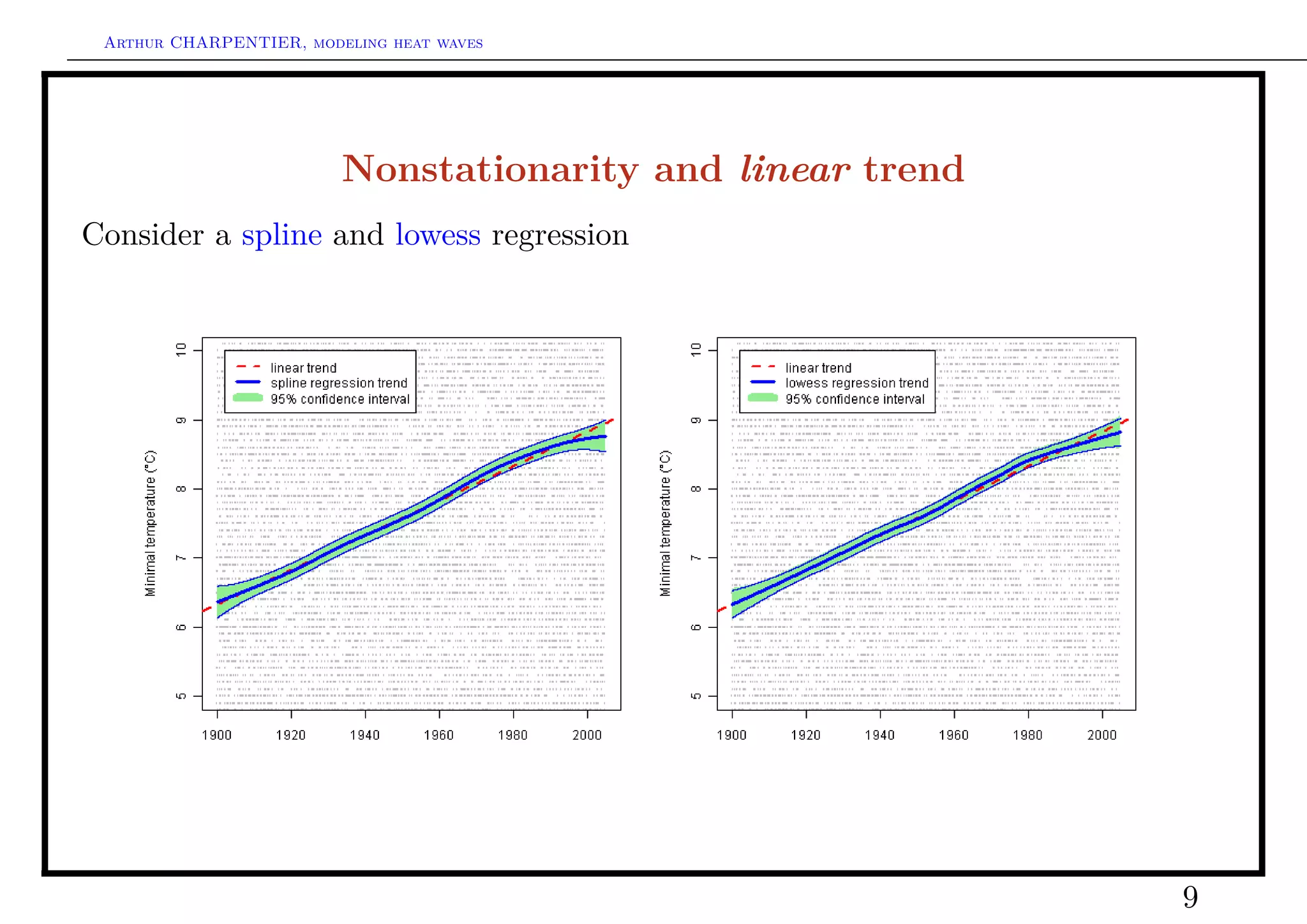
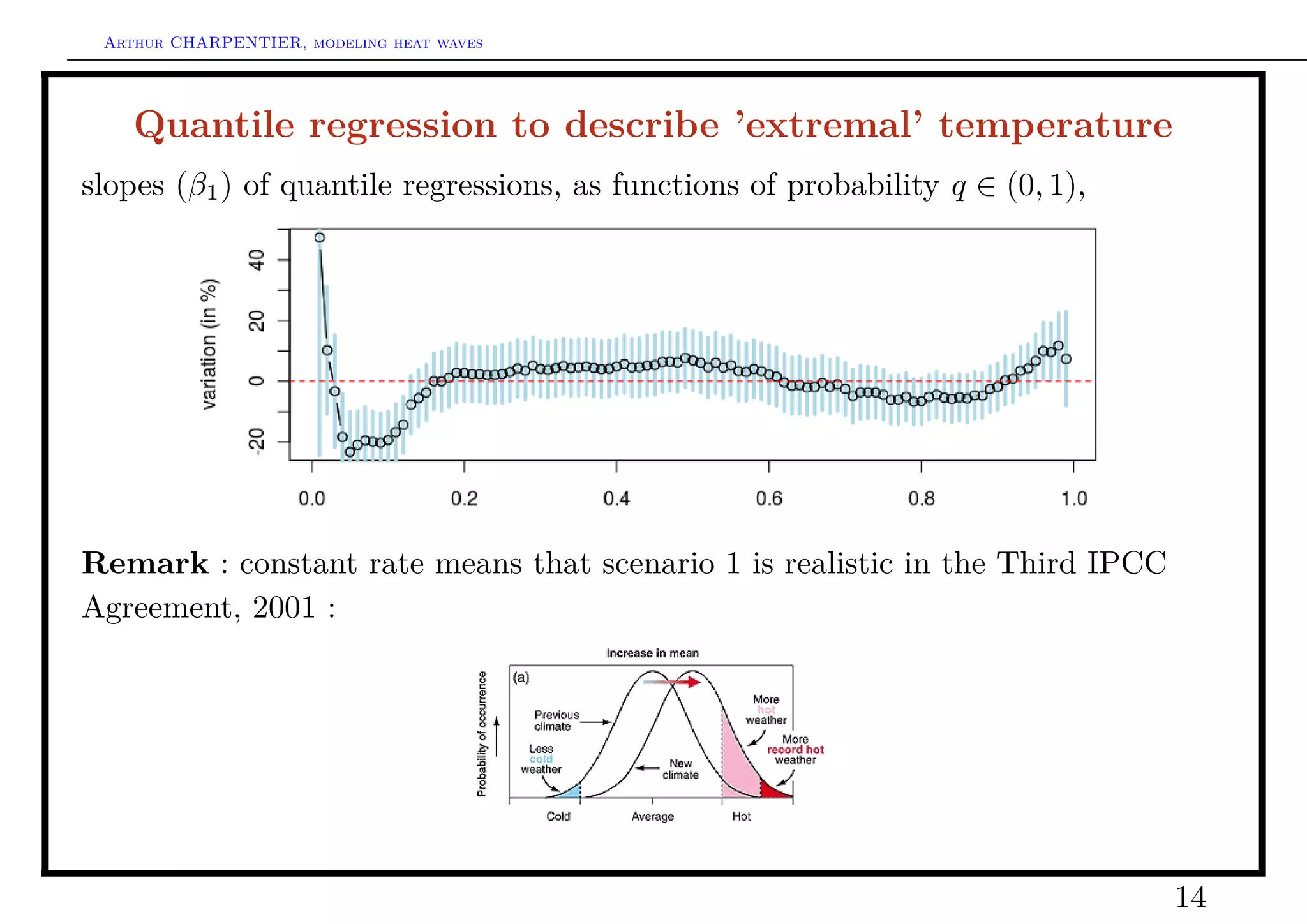
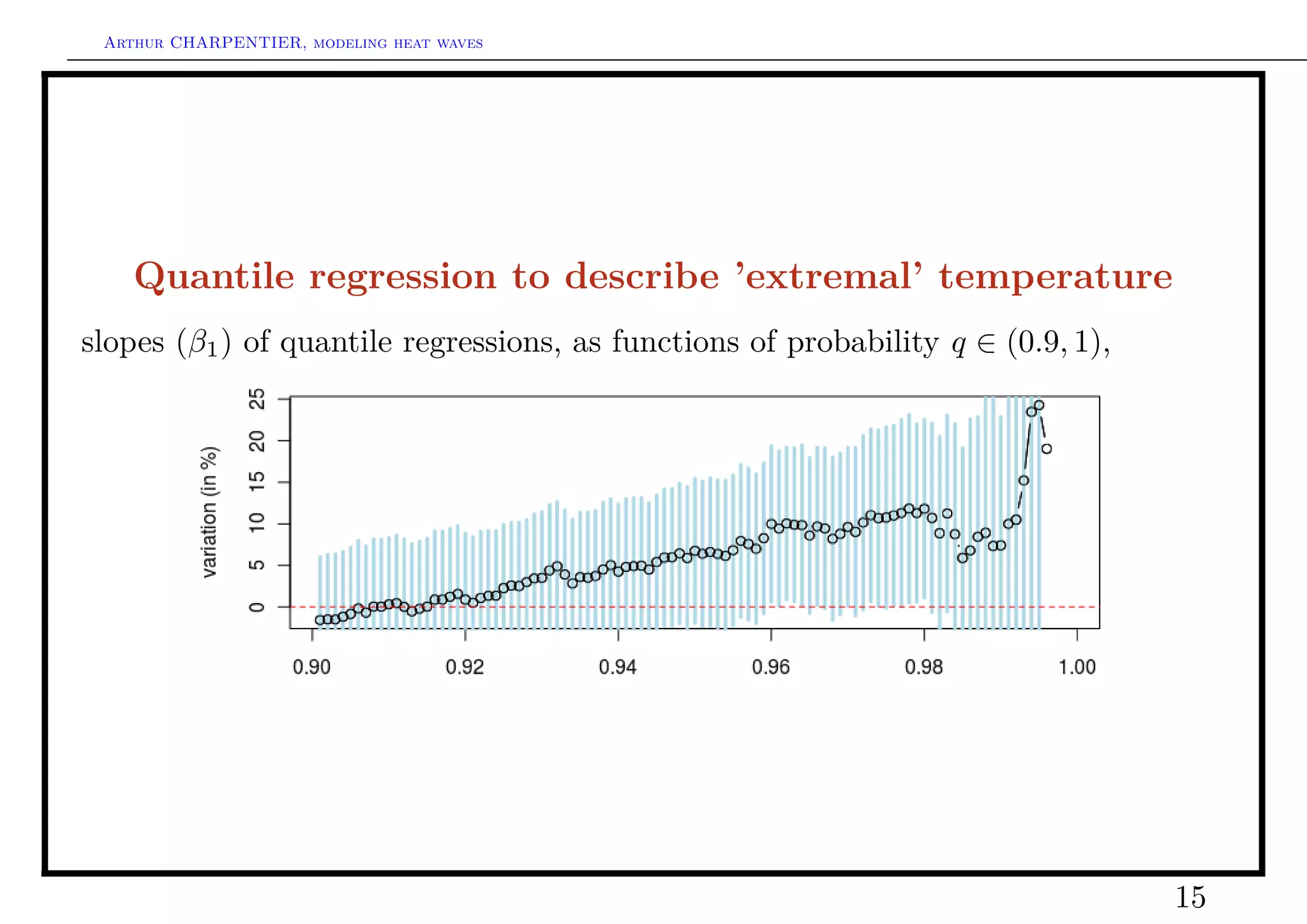
Quantile regression to describe ’extremal’ temperature
See Yan (2002), Meehl & Tebaldi (2004), or Alexanderet al. (2006).
Least square used to estimate a linear model for E(Yt ),
T T
min (Yt − [β0 + β1 t])2 = min R(Yt − [β0 + β1 t])
β0 ,β1 β0 ,β1
t=1 t=1
where R(x) = x2 .
Quantile regression can be used, let p ∈ (0, 1), and consider
T
min R(Yt − [β0 + β1 t])
β0 ,β1
t=1
where
x · (p − 1) if x < 0
Rp (x) = x · (p − 1(x < 0)) =
x · p if x > 0
12](https://image.slidesharecdn.com/slides-lyon-3-111114191033-phpapp02/75/Slides-lyon-2011-12-2048.jpg)
![Arthur CHARPENTIER, modeling heat waves
Remark :
E(Y ) = argmin E (Y − γ)2 = argmin (Y − γ)2 dF (y)
while
γ +∞
Qp (Y ) = argmin [p − 1] · [γ − x]dF (x) + p · [x − γ]dF (x) .
−∞ γ
5%, 25%, 75%, and 95% quantile regressions,
13](https://image.slidesharecdn.com/slides-lyon-3-111114191033-phpapp02/75/Slides-lyon-2011-13-2048.jpg)



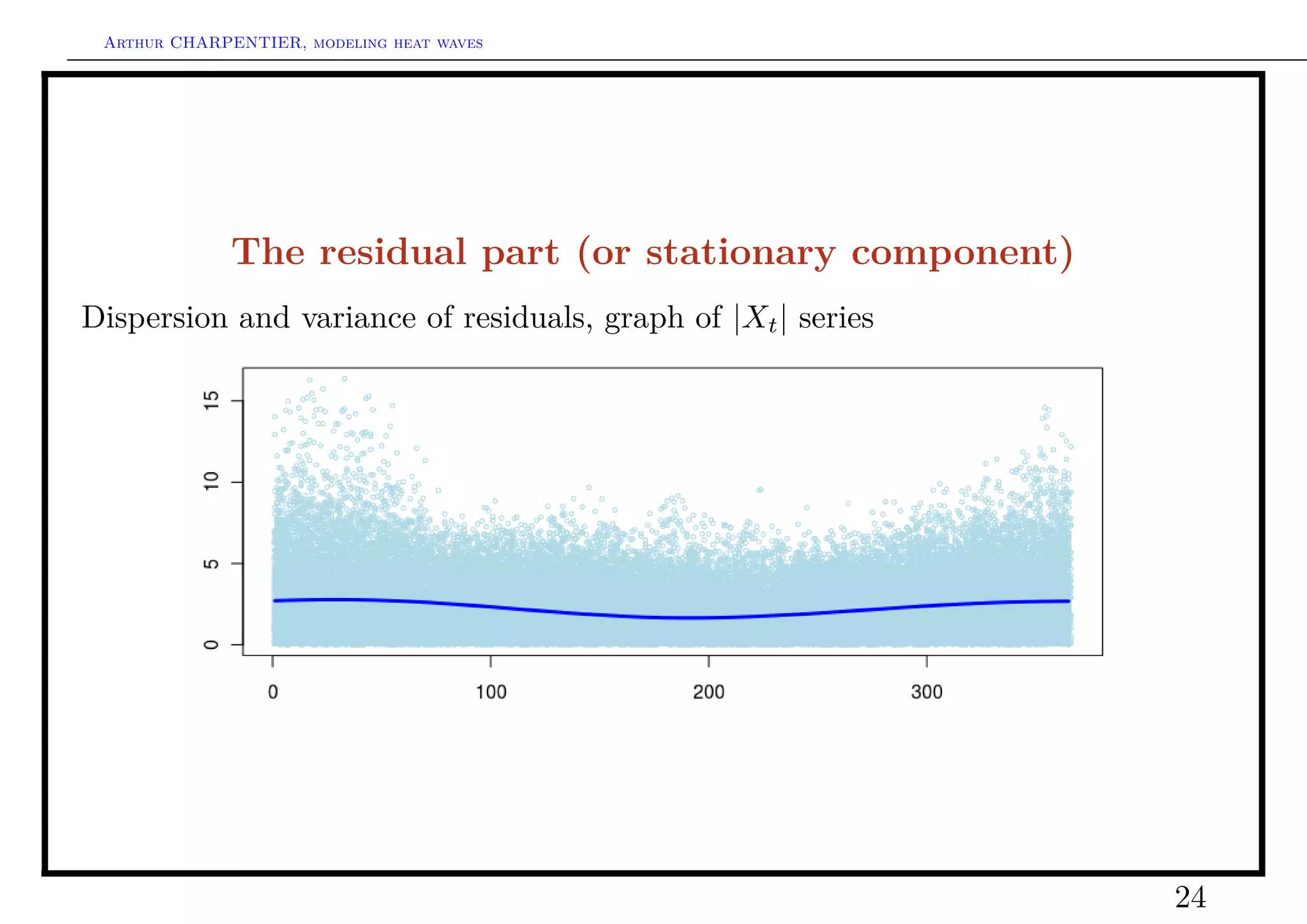
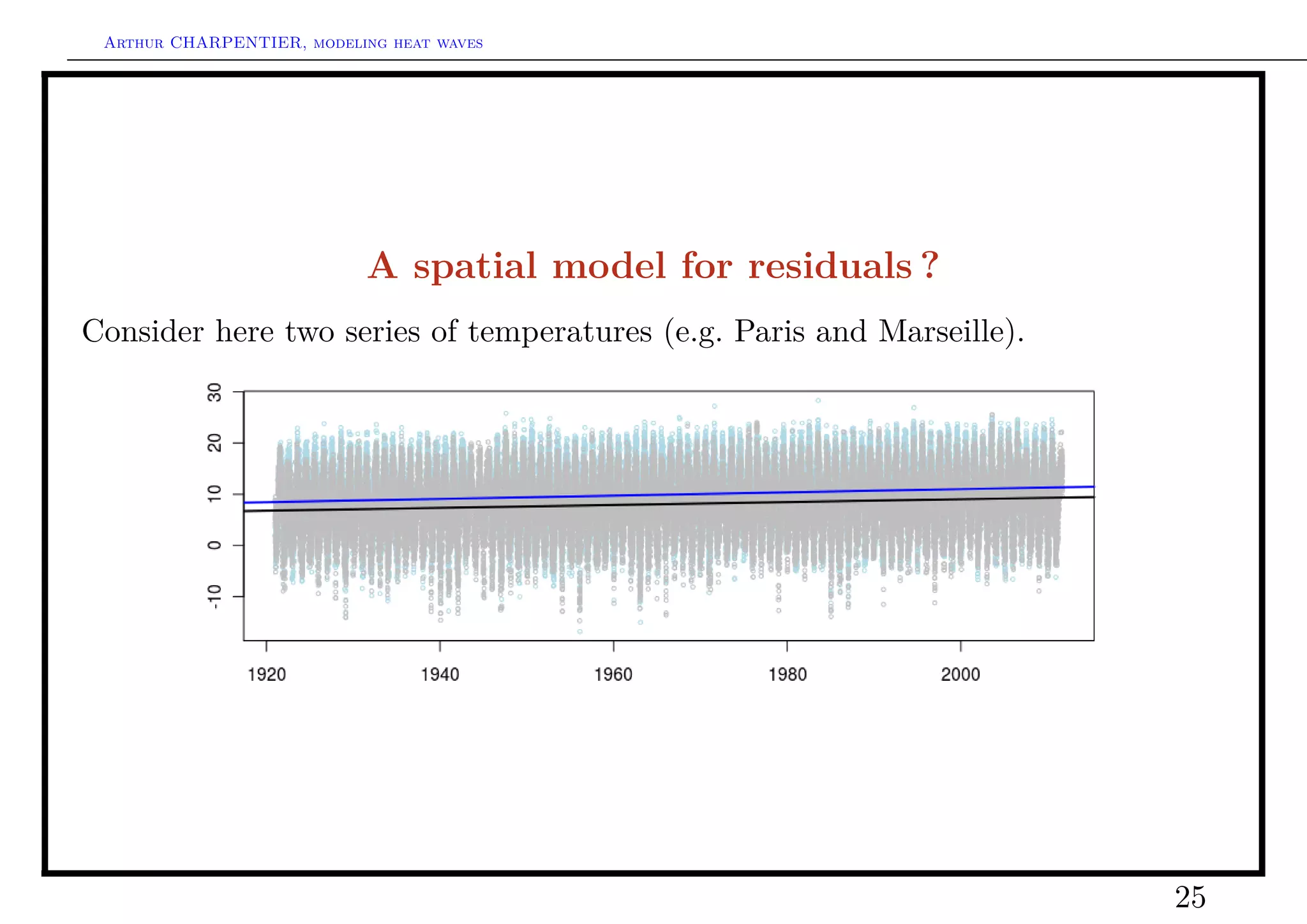
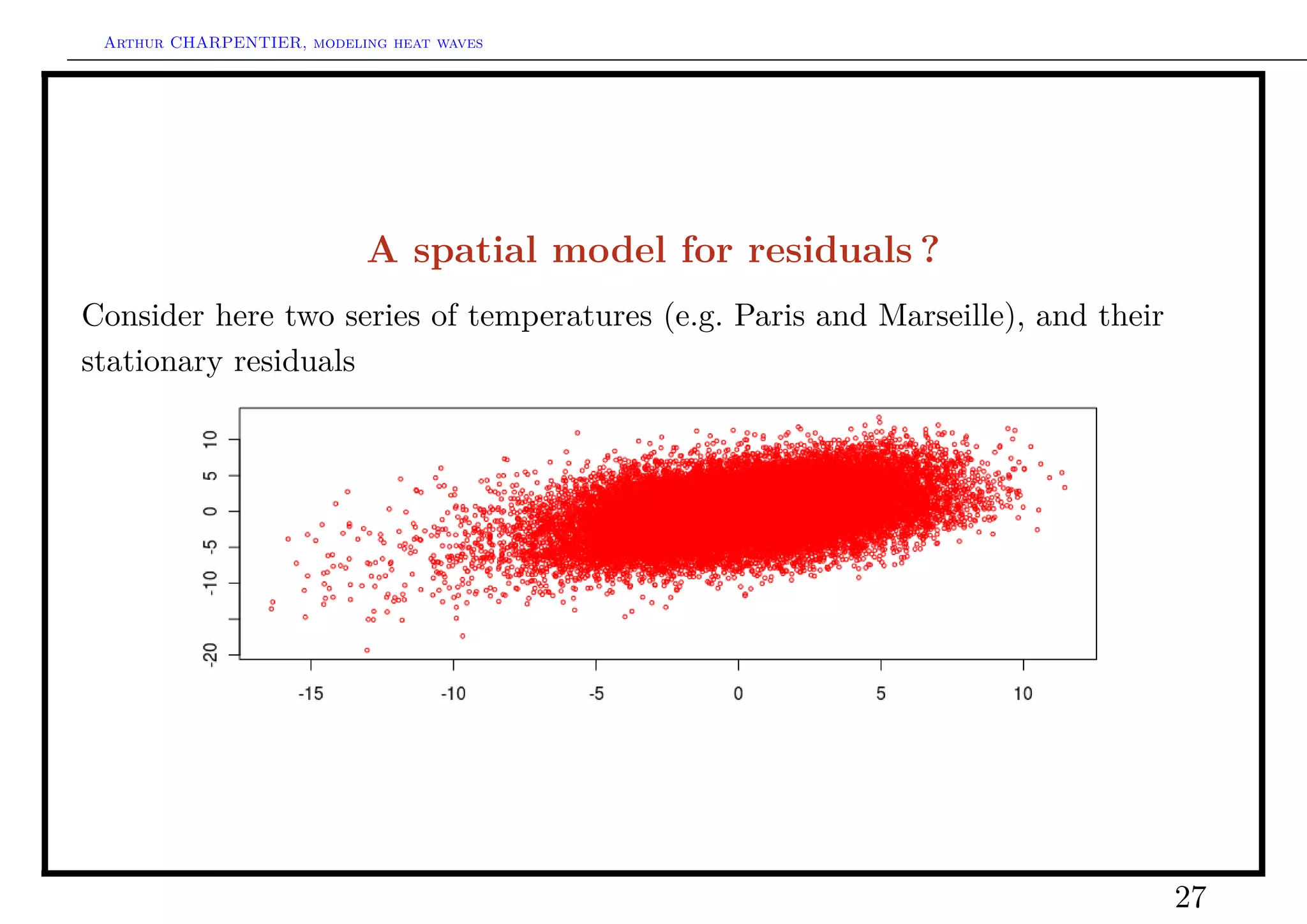

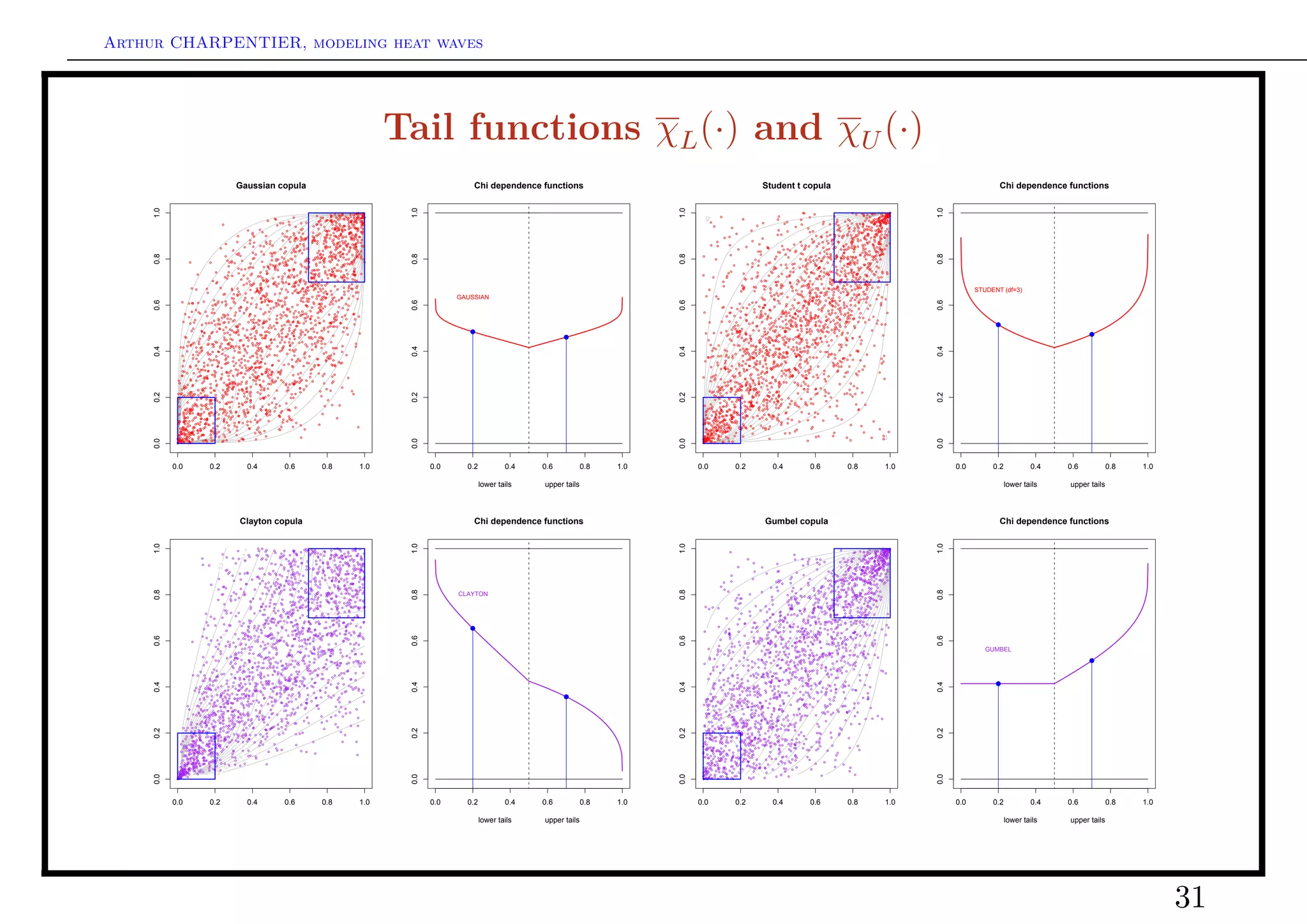
![Arthur CHARPENTIER, modeling heat waves
Tail dependence indices
Ledford & Tawn (1996) suggested the following alternative approach,
• for independent random variables,
P(X > t, Y > t) = P(X > t) × P(Y > t) = P(X > t)2 ,
• for comonotonic random variables, P(X > t, Y > t) = P(X > t) = P(X > t)1 ,
Assume that P(X > t, Y > t) ∼ P(X > t)1/η as t → ∞, where η ∈ (0, 1] will be a
tail index.
Define
2 log(1 − z) 2 log(1 − z)
χU (z) = − 1 and χL (z) = −1
log C (z, z) log C(z, z)
with ηU = (1 + limz→0 χU (z))/2 and ηL = (1 + limz→0 χL (z))/2 sont appelés
indices de queue supérieure et inférieure, respectivement.
29](https://image.slidesharecdn.com/slides-lyon-3-111114191033-phpapp02/75/Slides-lyon-2011-29-2048.jpg)








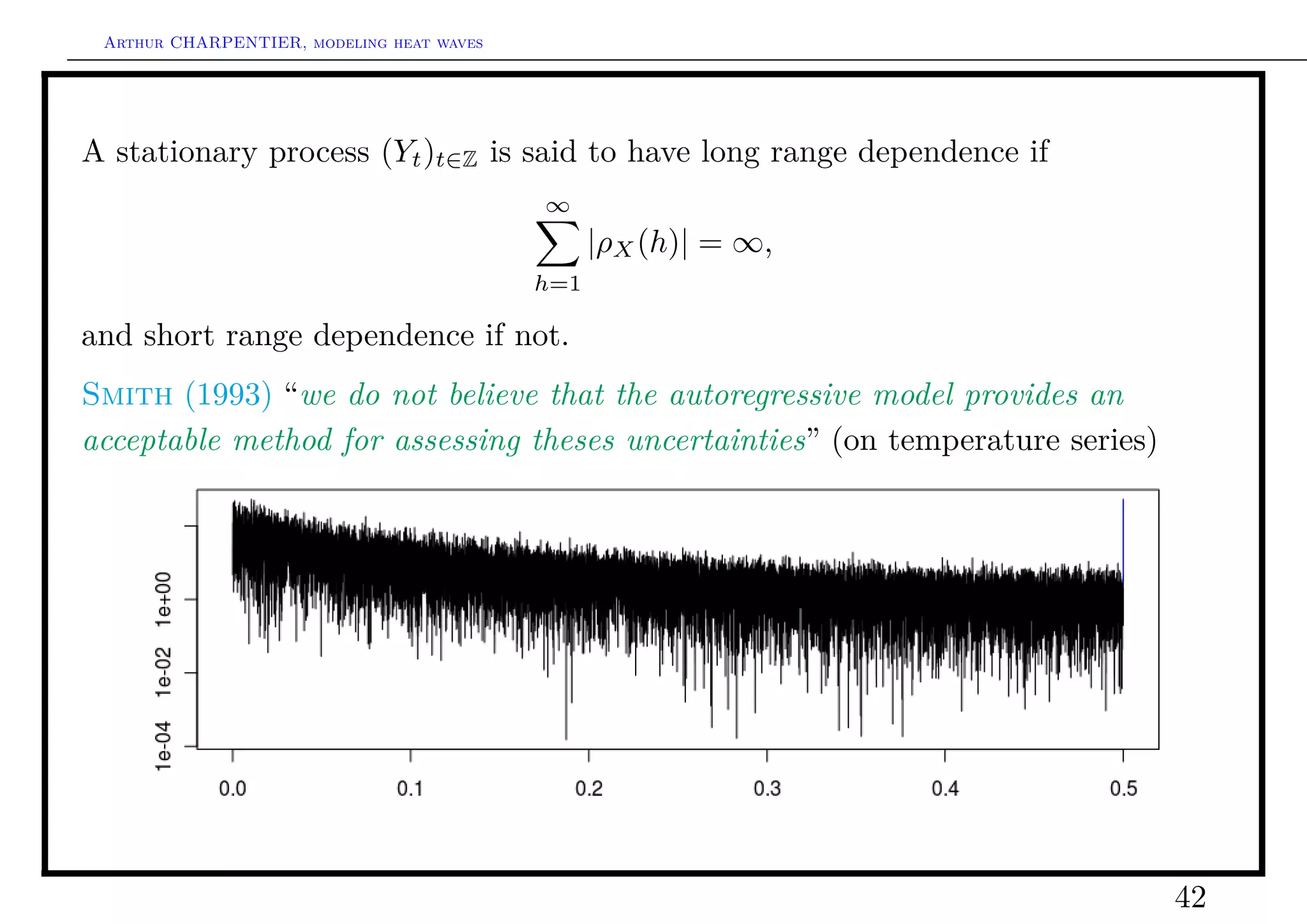
![Arthur CHARPENTIER, modeling heat waves
Long range dependence and regression
Gray, Zhang & Woodward (1989) proposed an extension to model persistent
seasonal series, using Gegenbauer’s polynomial Gd (·), defined as
n
(−2)n Γ(n + d)Γ(n + 2d) 2 −α+1/2 d
n
Gd (x)
n = (1 − x ) (1 − x2 )n+d−1/2 .
n! Γ(d)Γ(2n + 2d) dxn
and such that Gd (·) is the unique polynomial of degree n such that
n
∞
(1 − 2uZ + Z 2 )d = Gd (u) · Z n .
n
n=0
If d ∈ (0, 1/2), and |u| < 1 then
ρ(h) ∼ h2d−1 sin([π − arccos(u)]h) as h → ∞.
43](https://image.slidesharecdn.com/slides-lyon-3-111114191033-phpapp02/75/Slides-lyon-2011-43-2048.jpg)