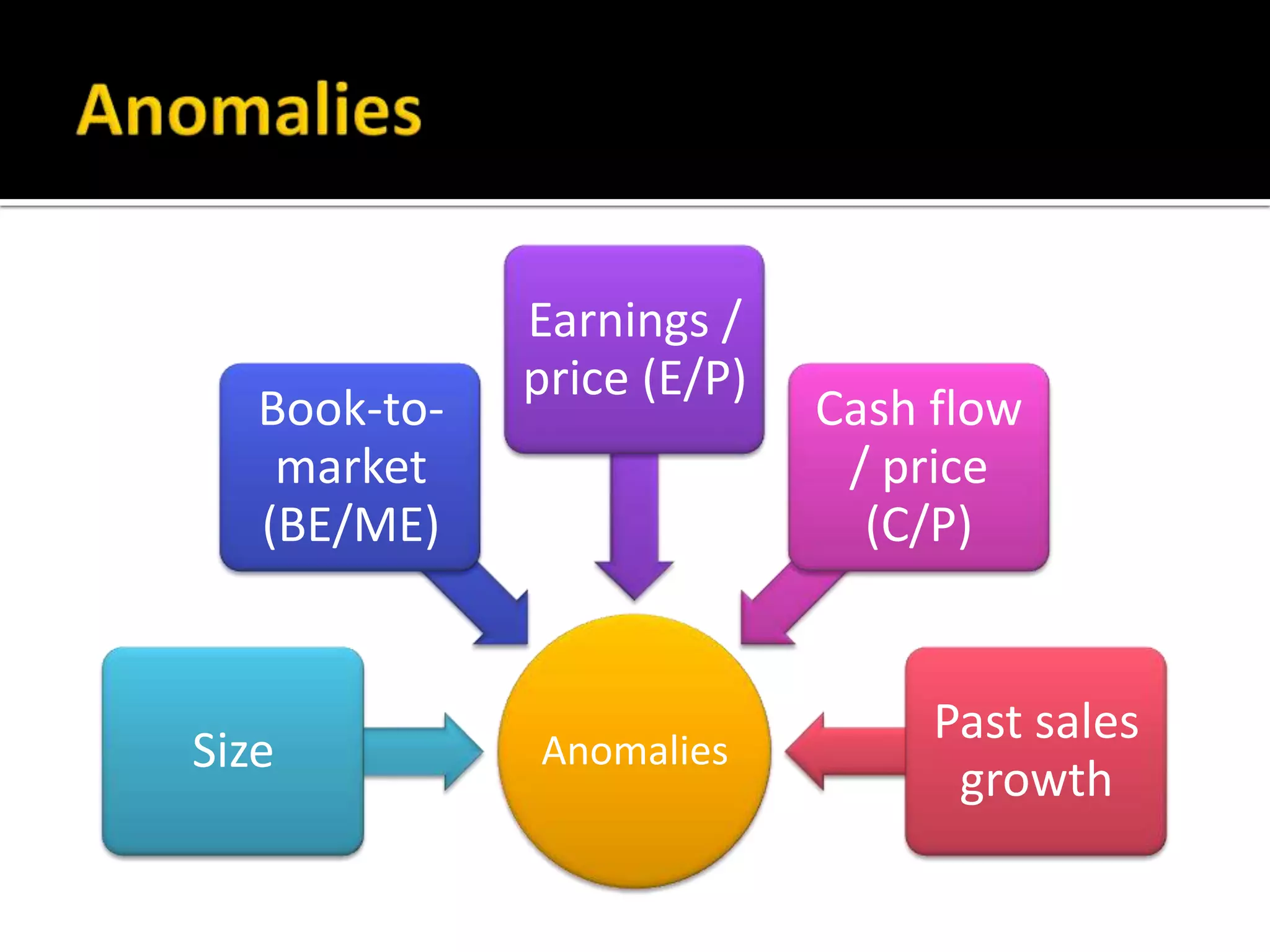
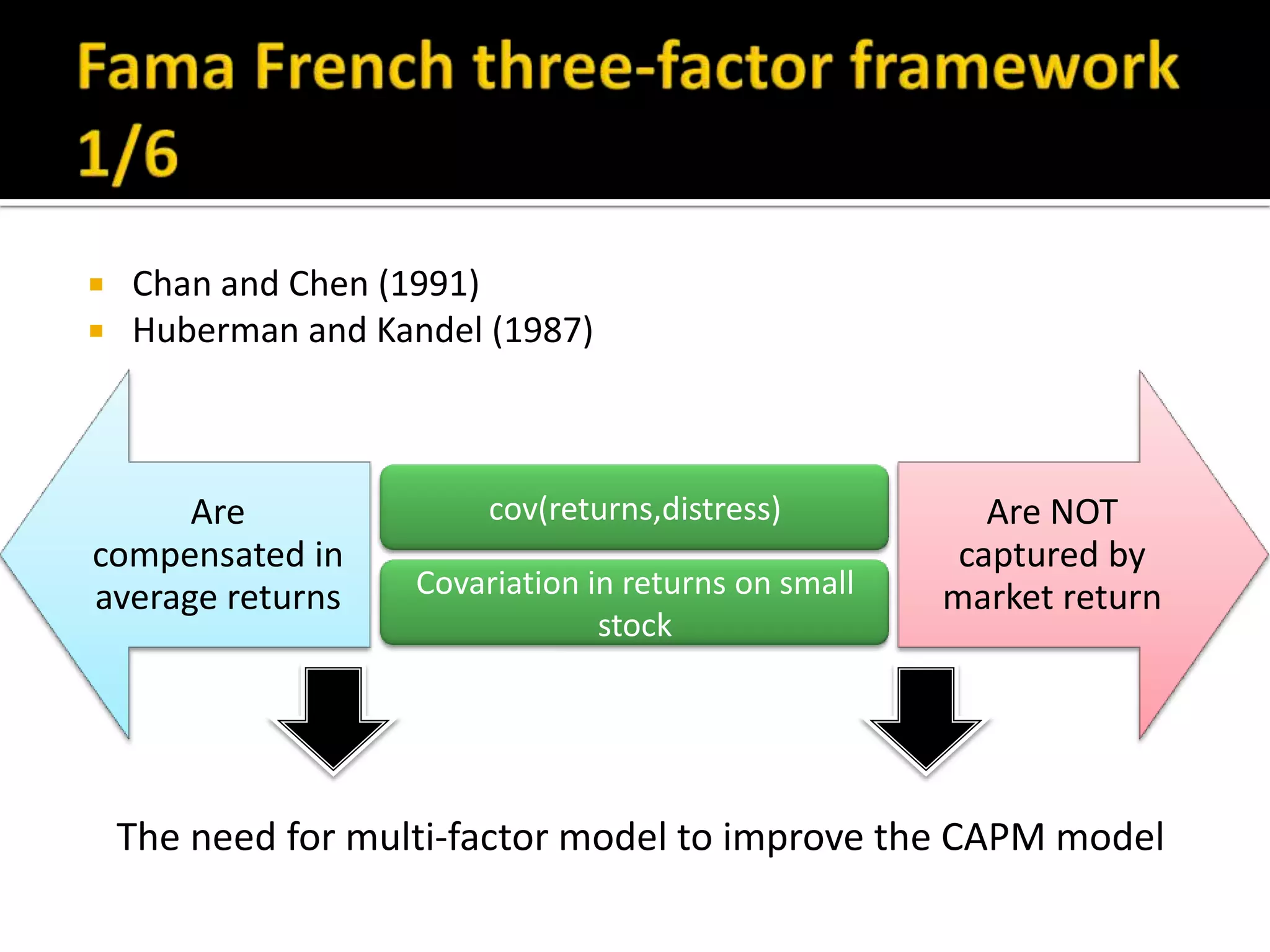
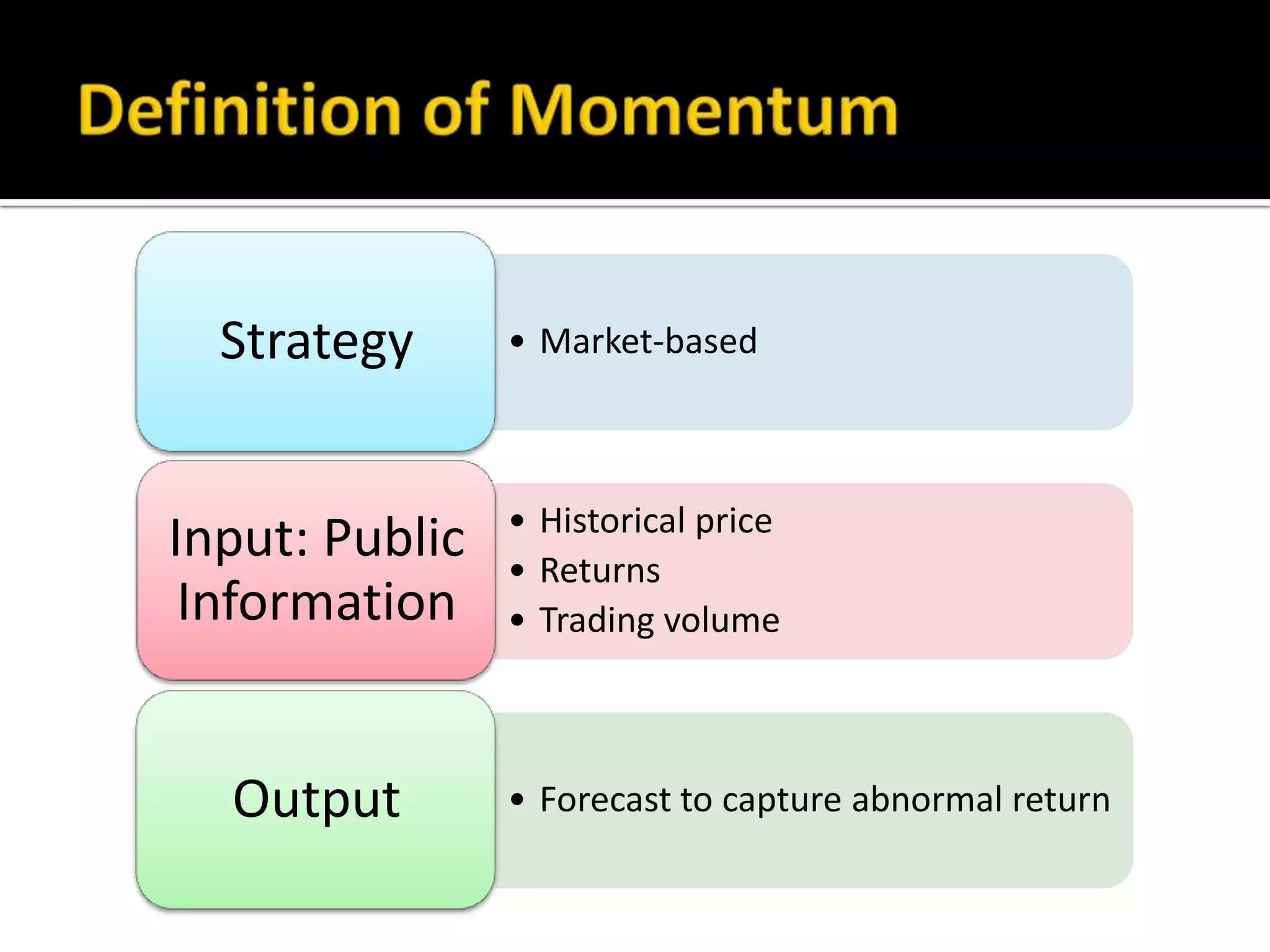
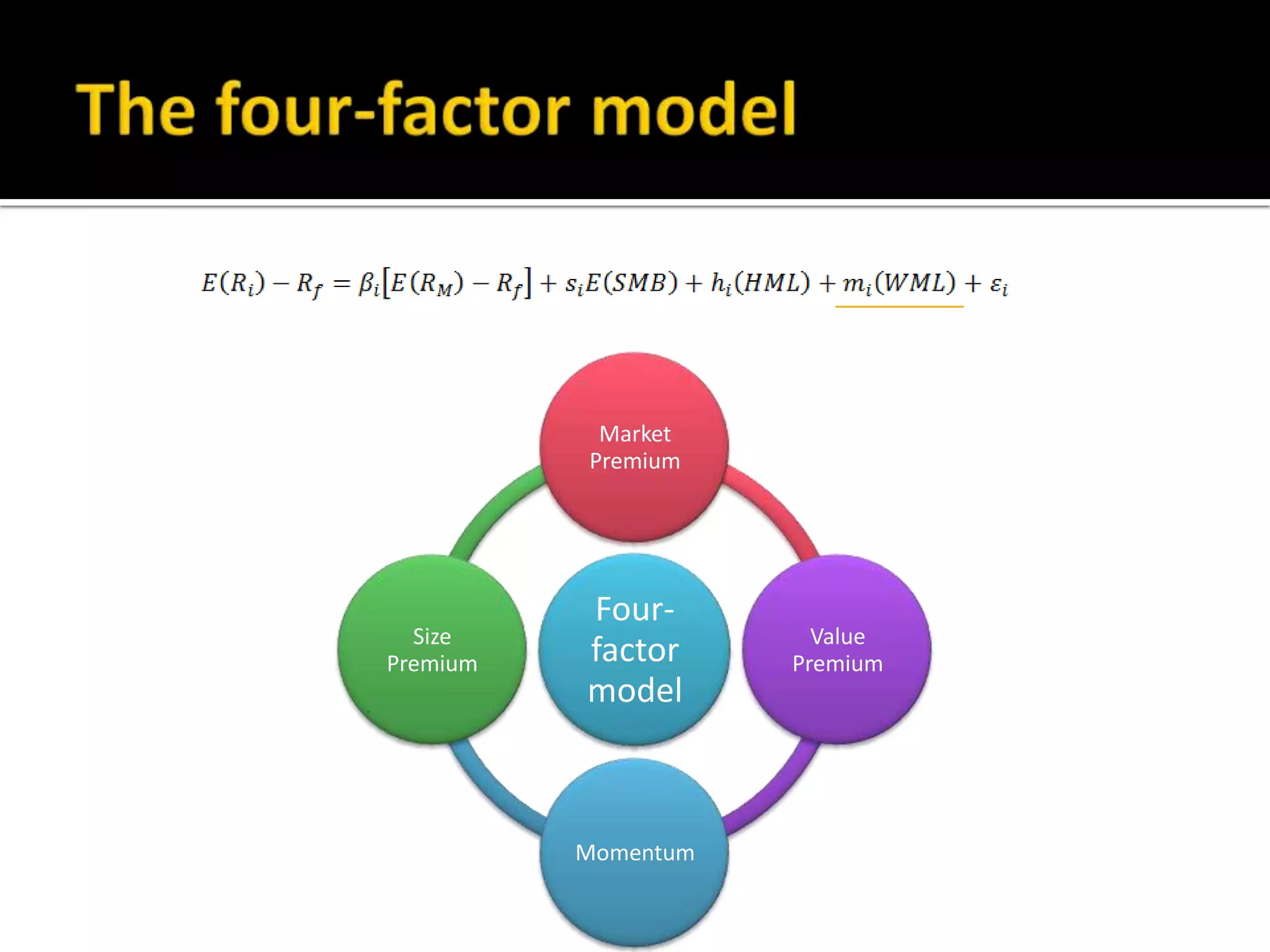
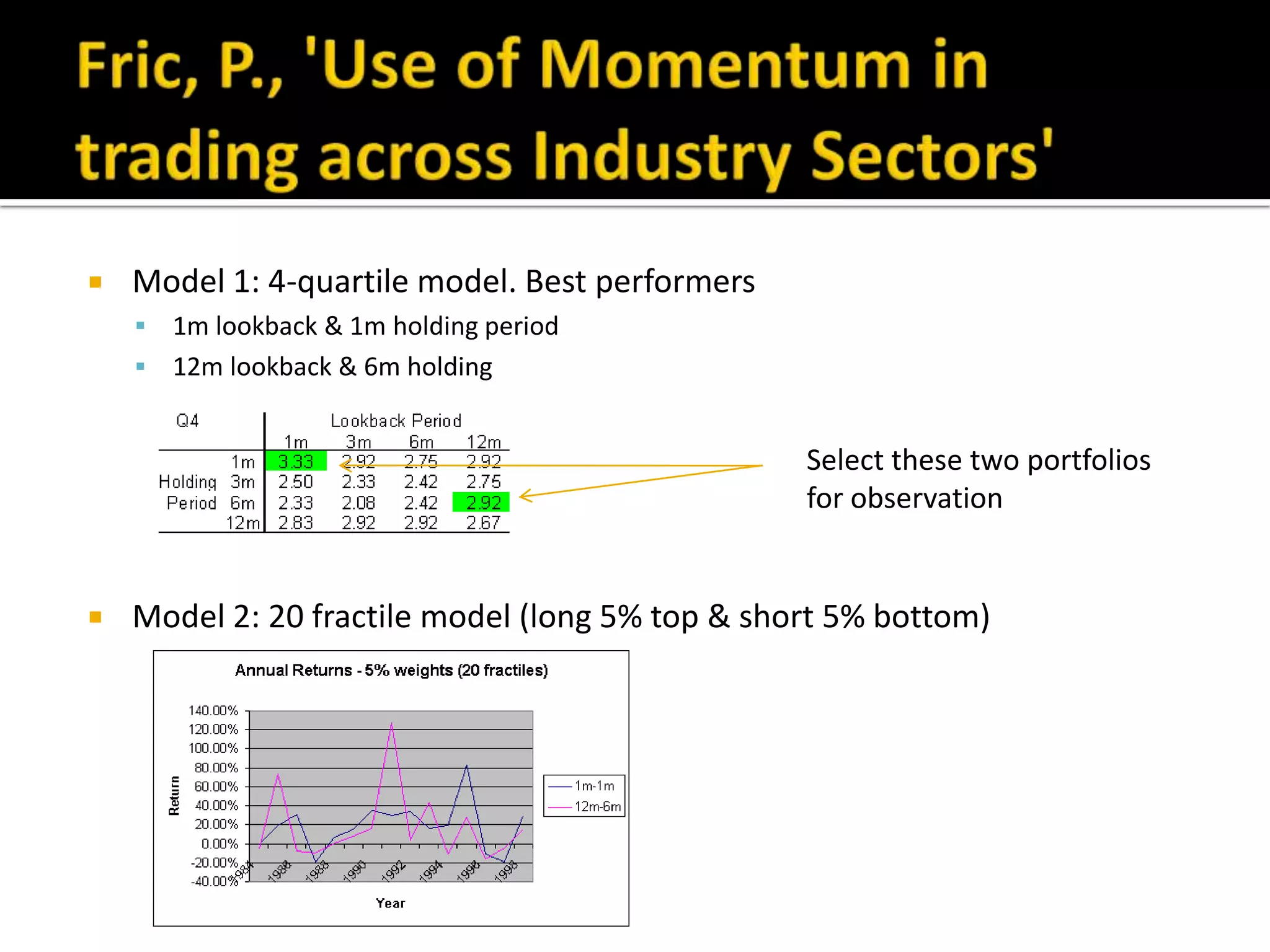
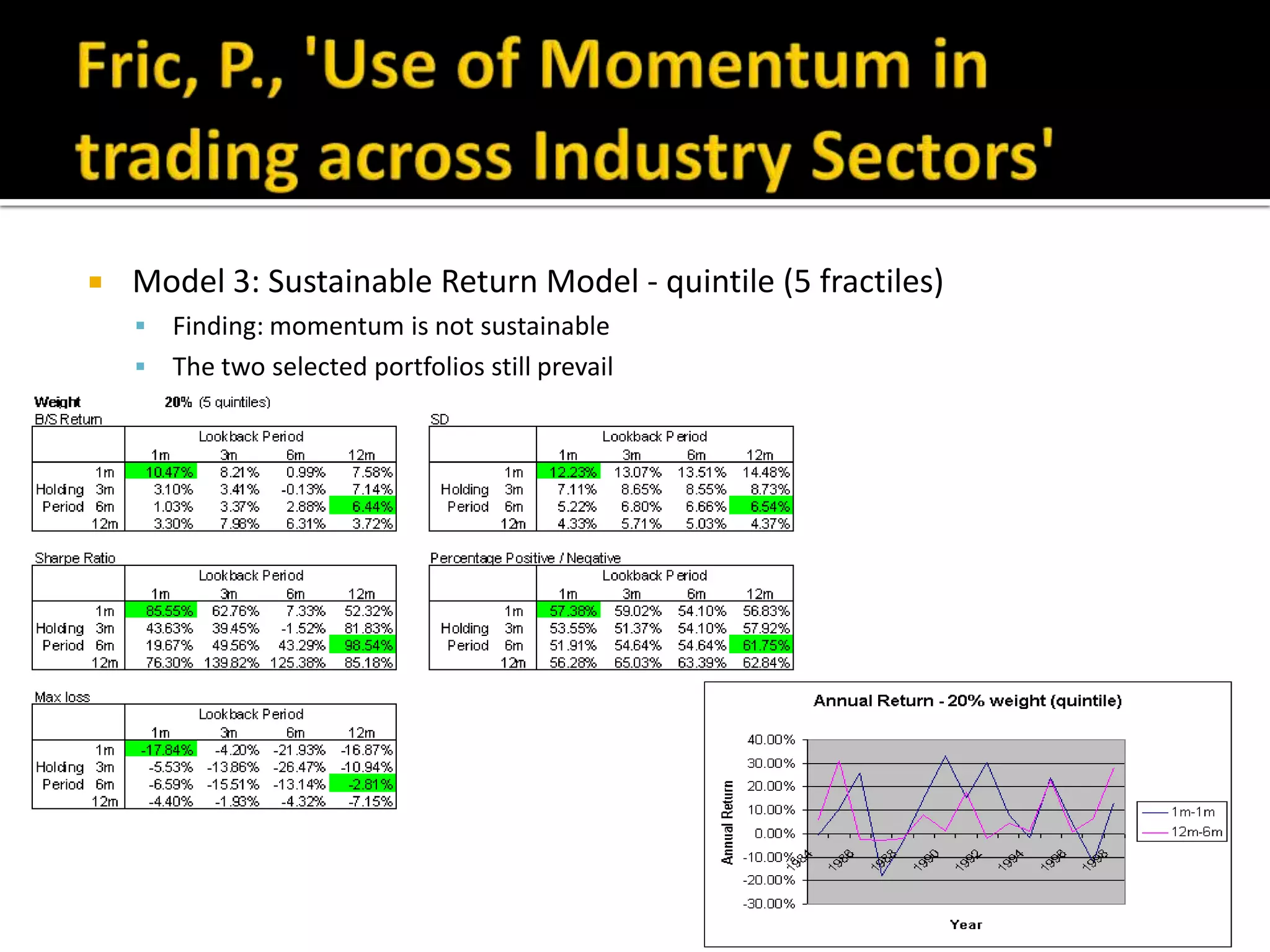
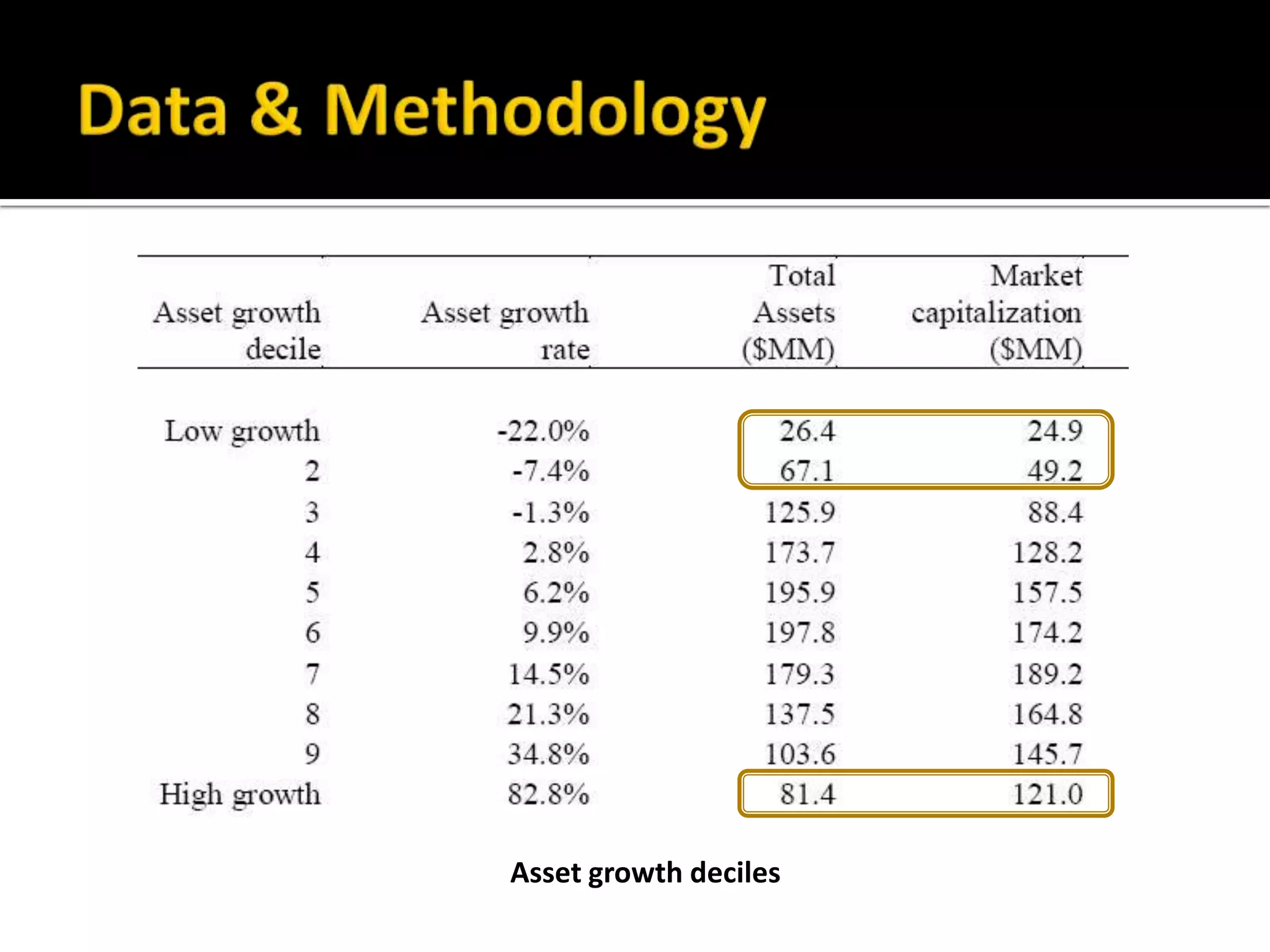
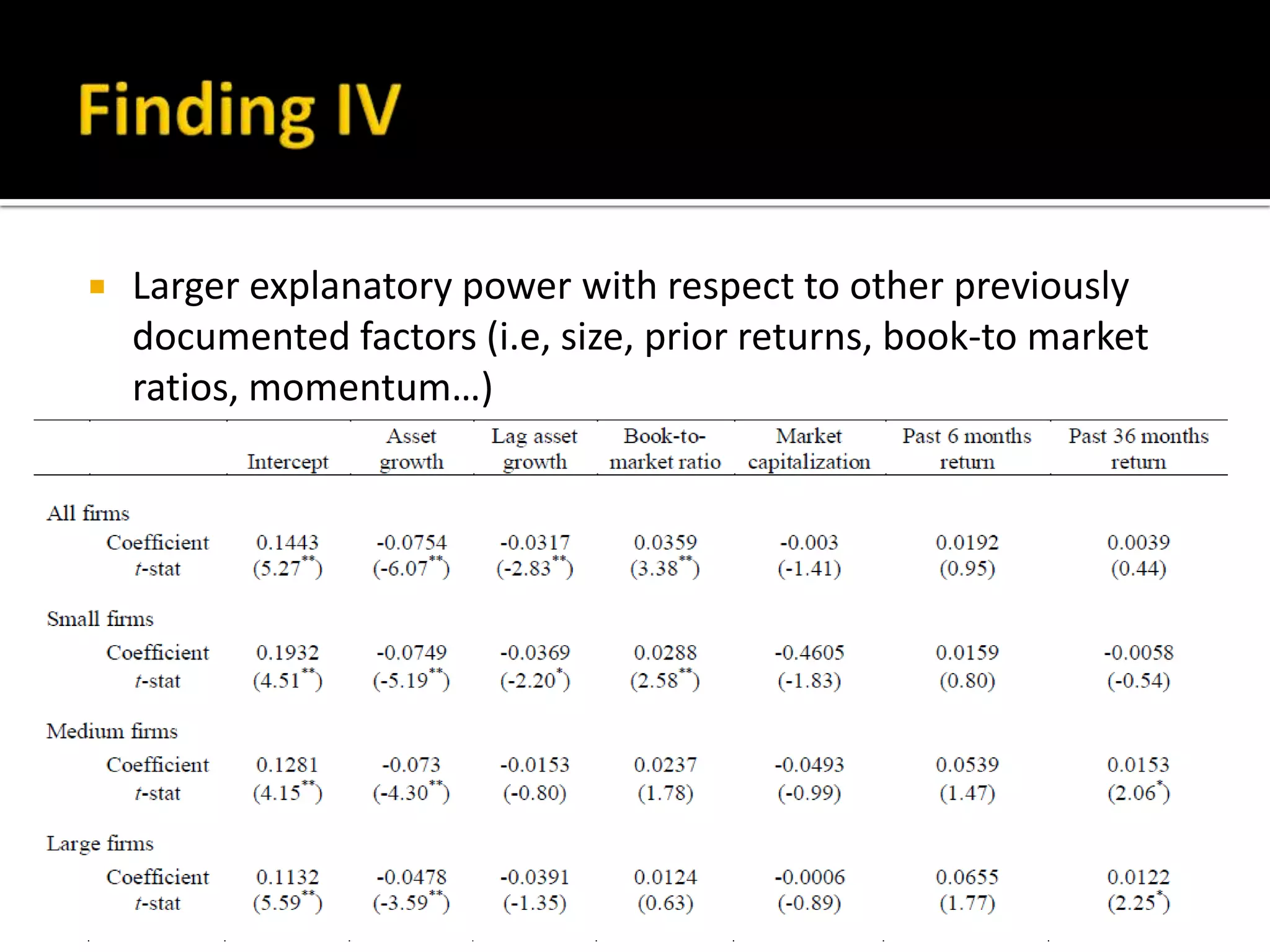
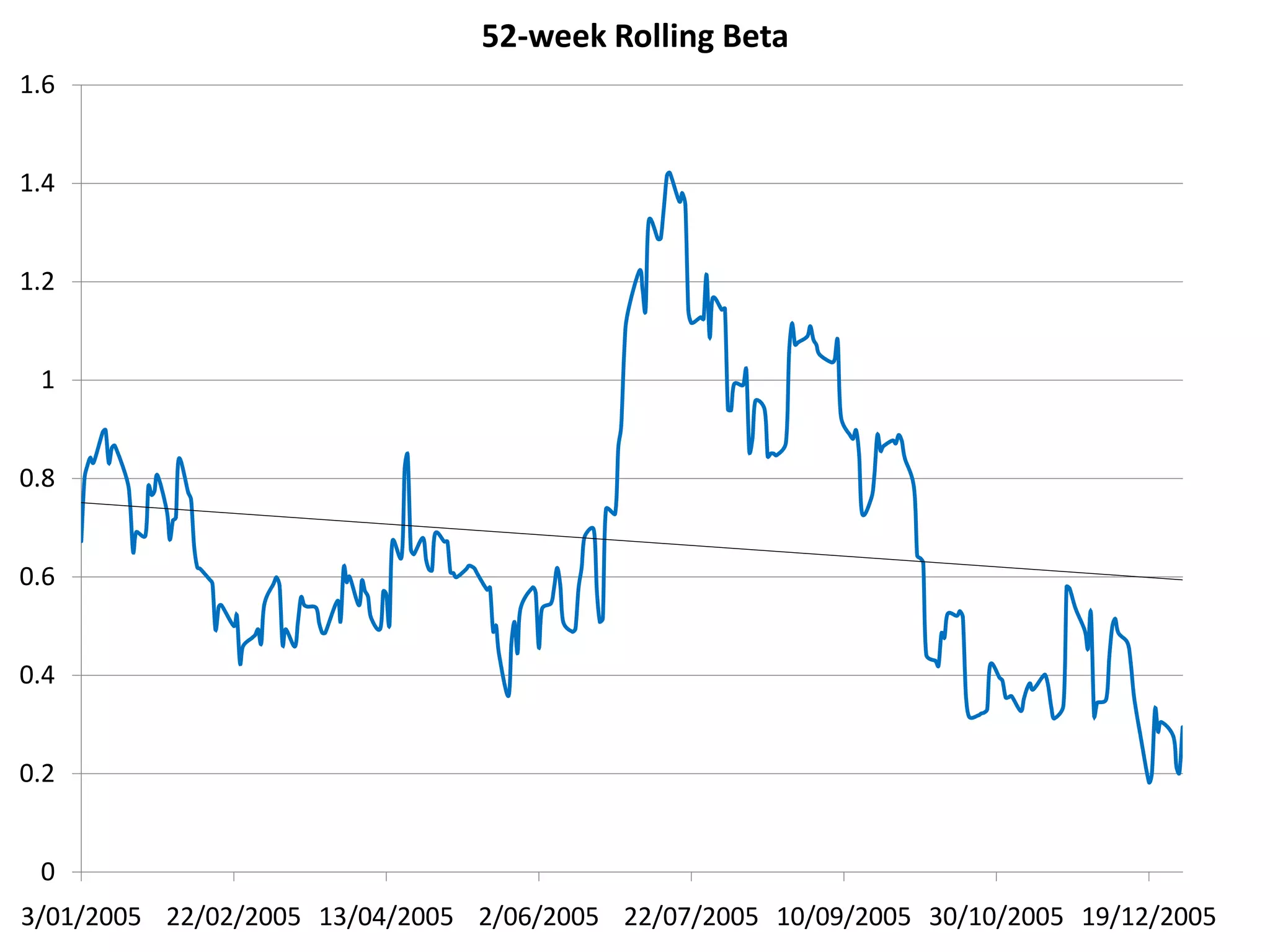
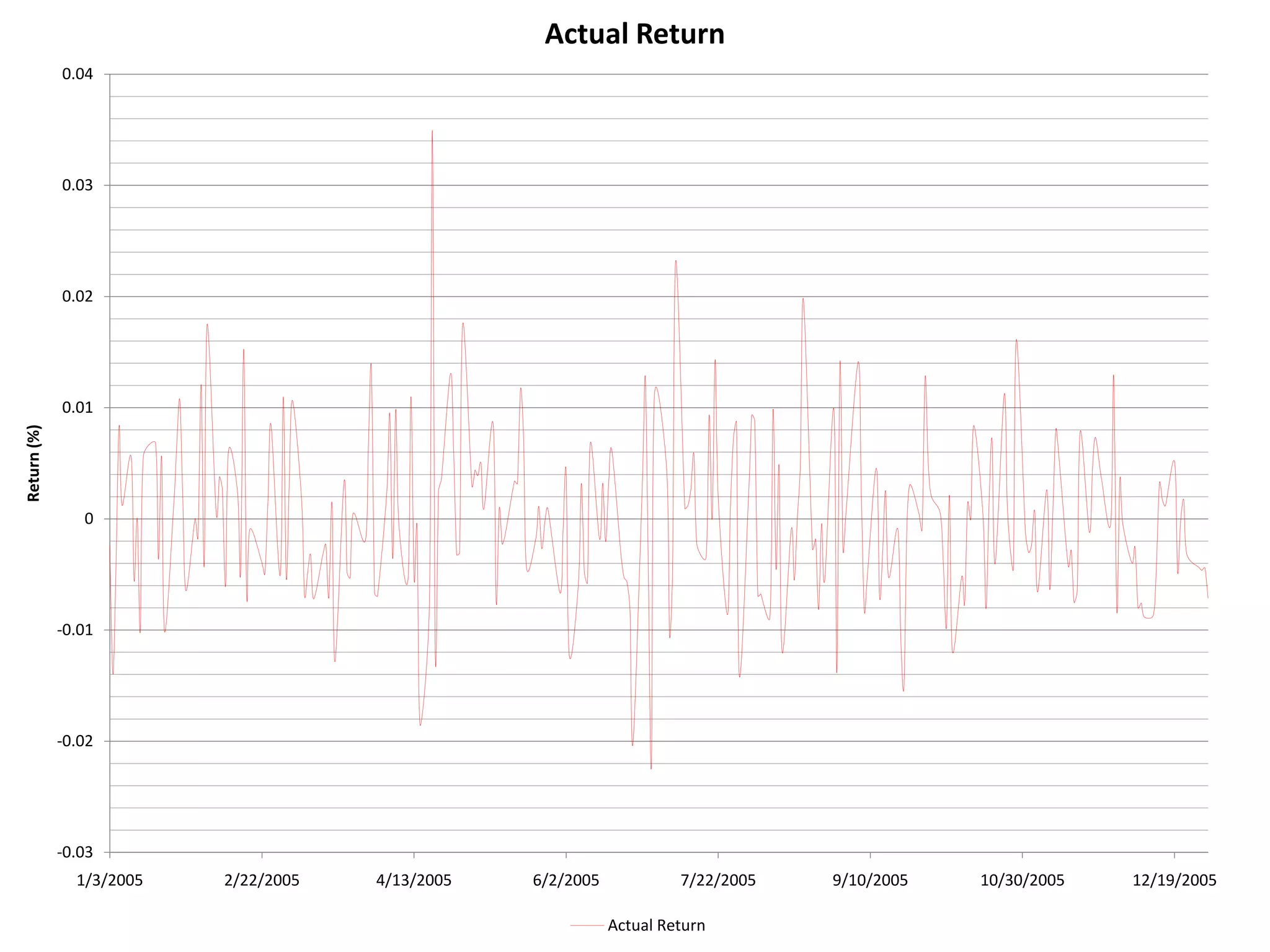
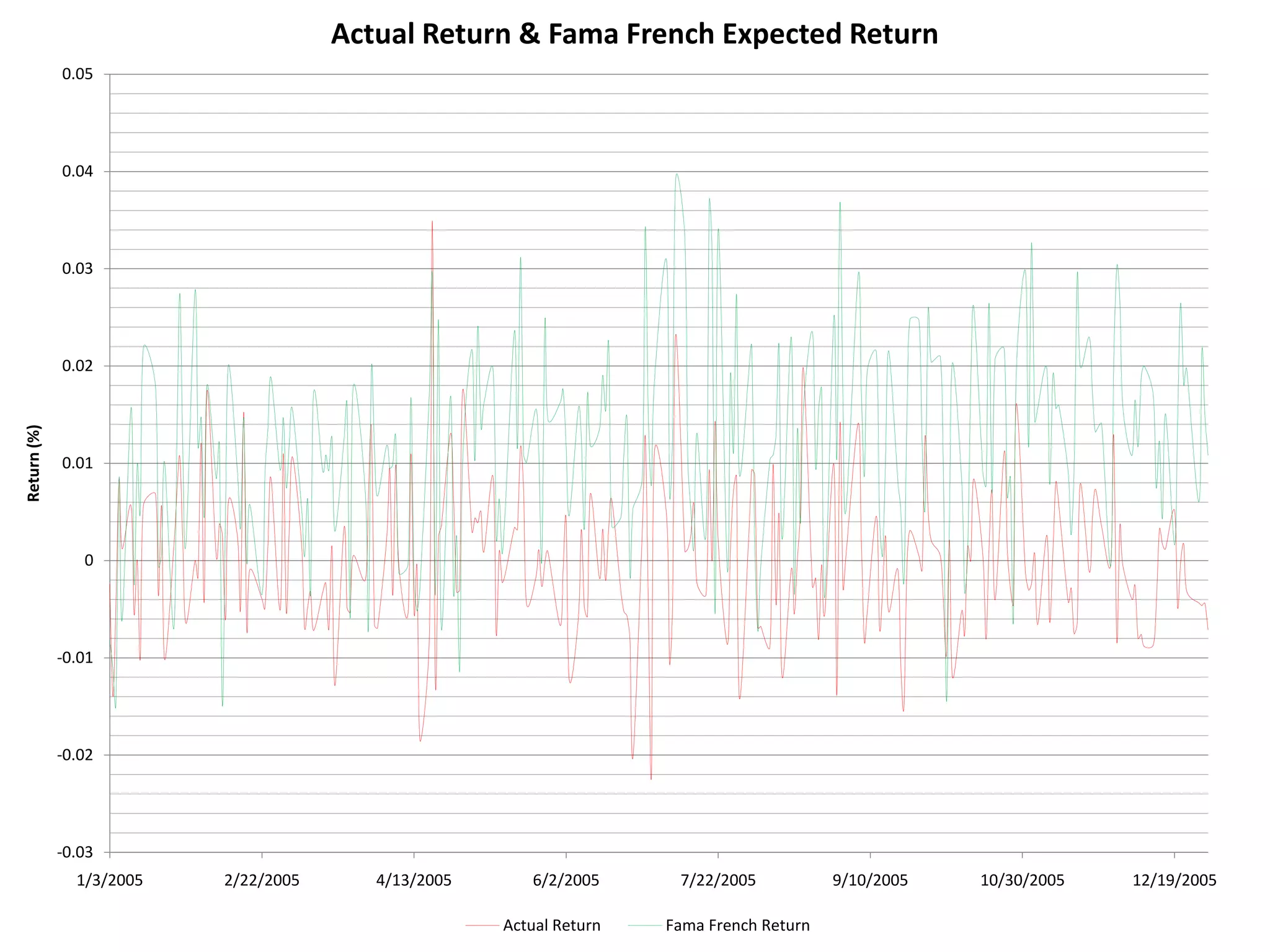
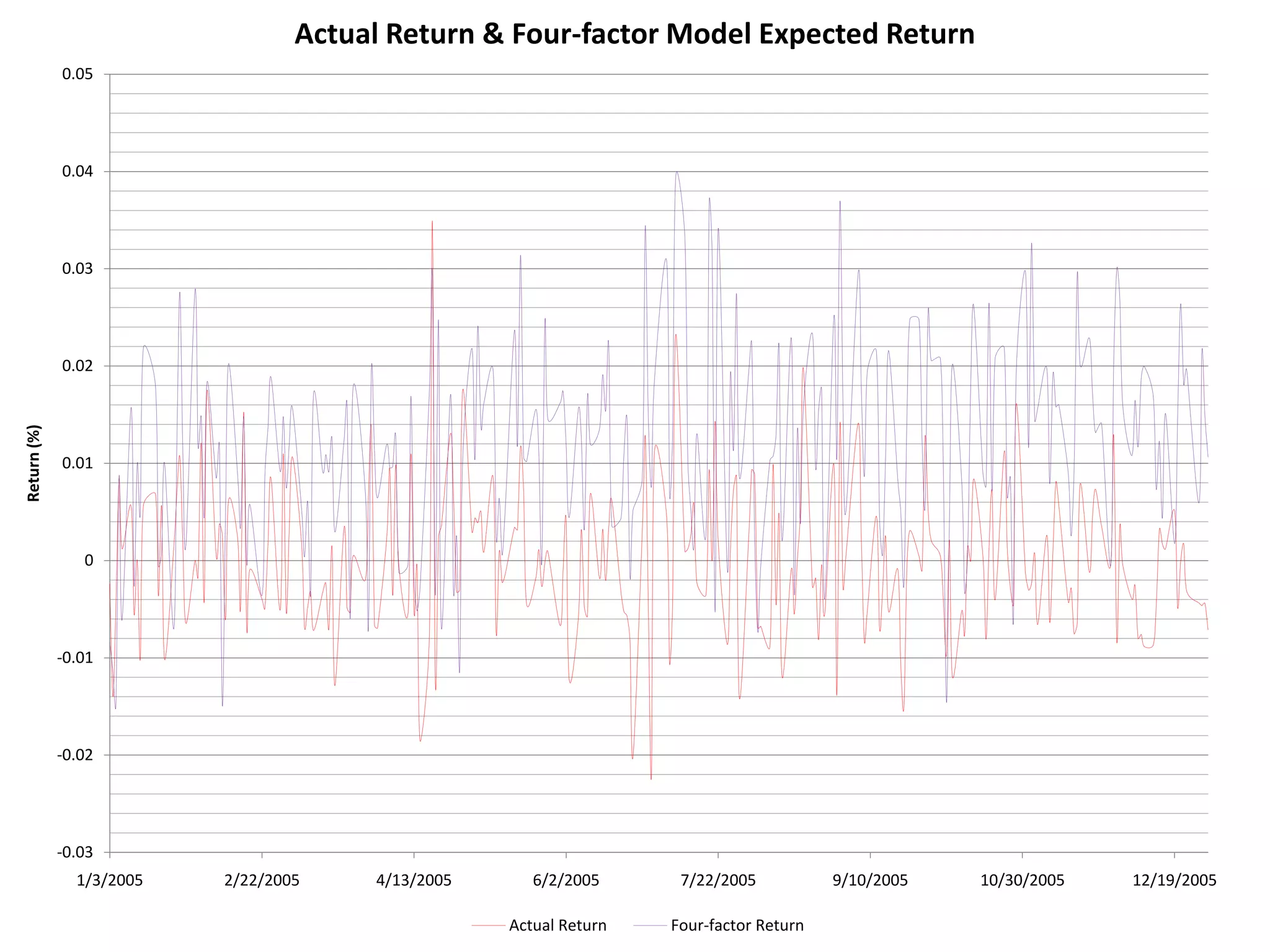
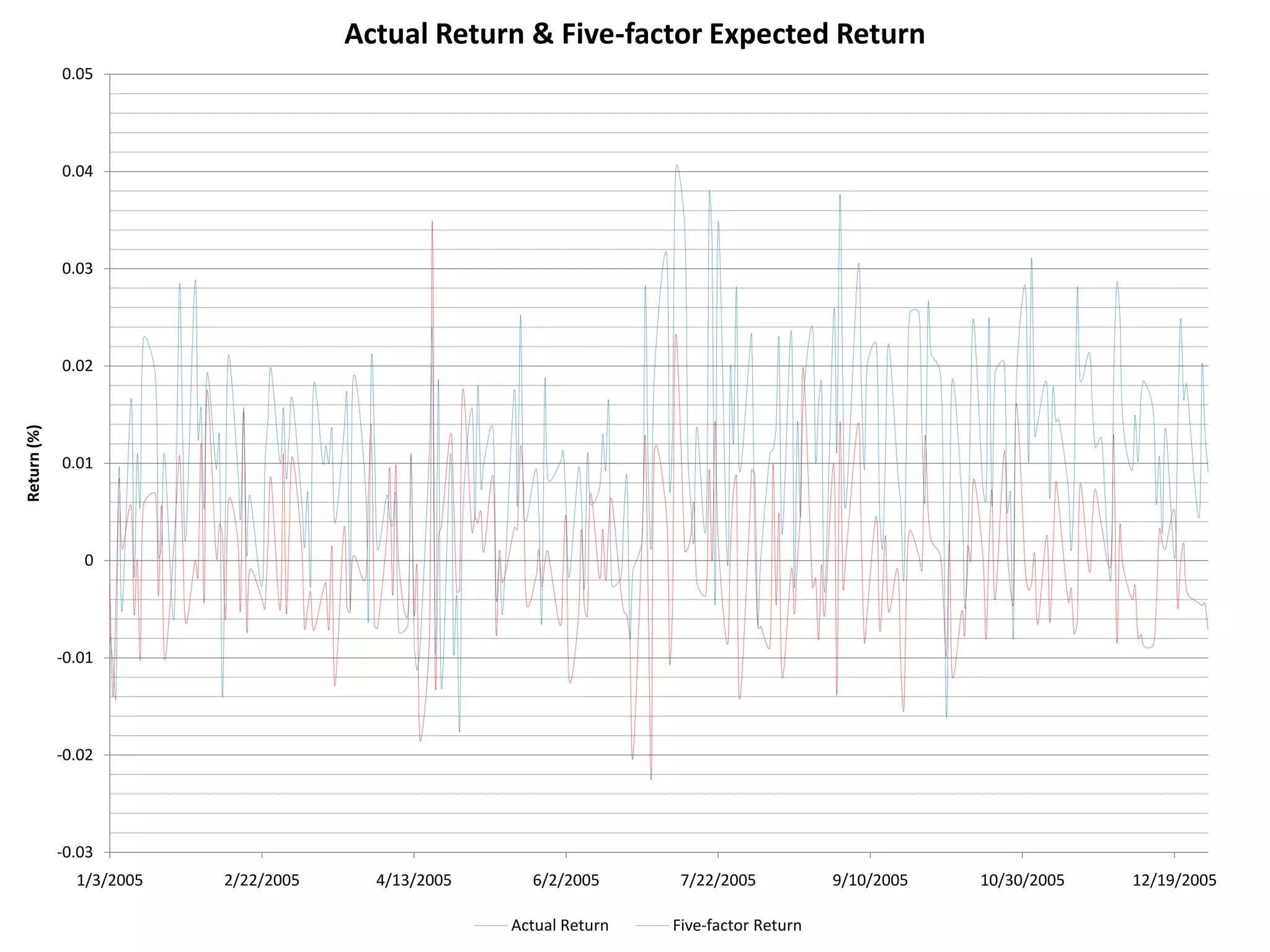
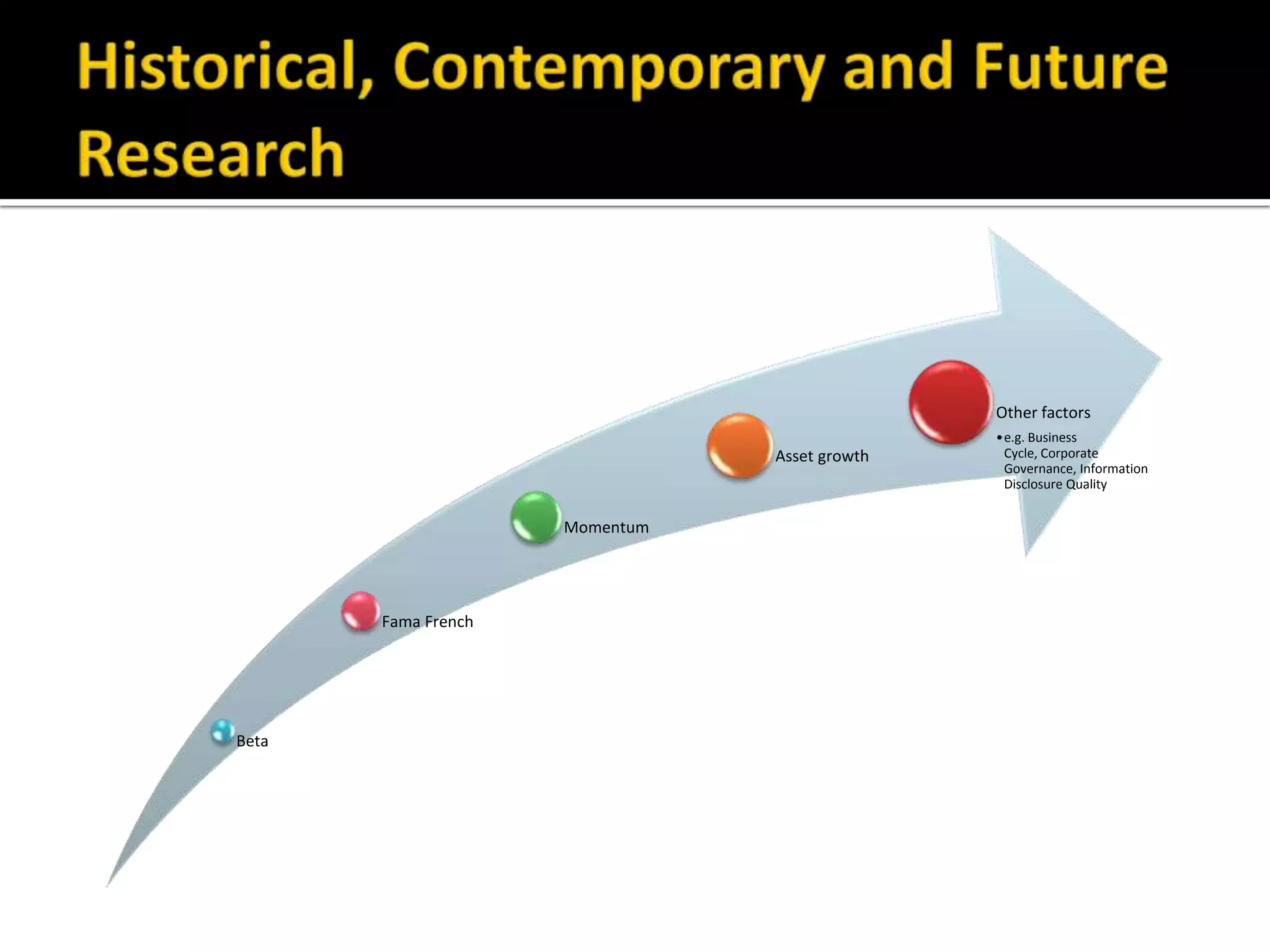
The document discusses several models for stock return forecasting including CAPM, the Fama-French three-factor model, a four-factor model with momentum, and a five-factor model including asset growth. Empirical evidence is presented analyzing daily returns of Coca-Cola stock in 2005, finding that momentum is highly significant in predicting returns, while beta is less so. Multi-factor models, particularly the four and five-factor models, provide improved forecasting over CAPM alone, though with increasing complexity. Limitations include selection bias and issues with beta estimation.