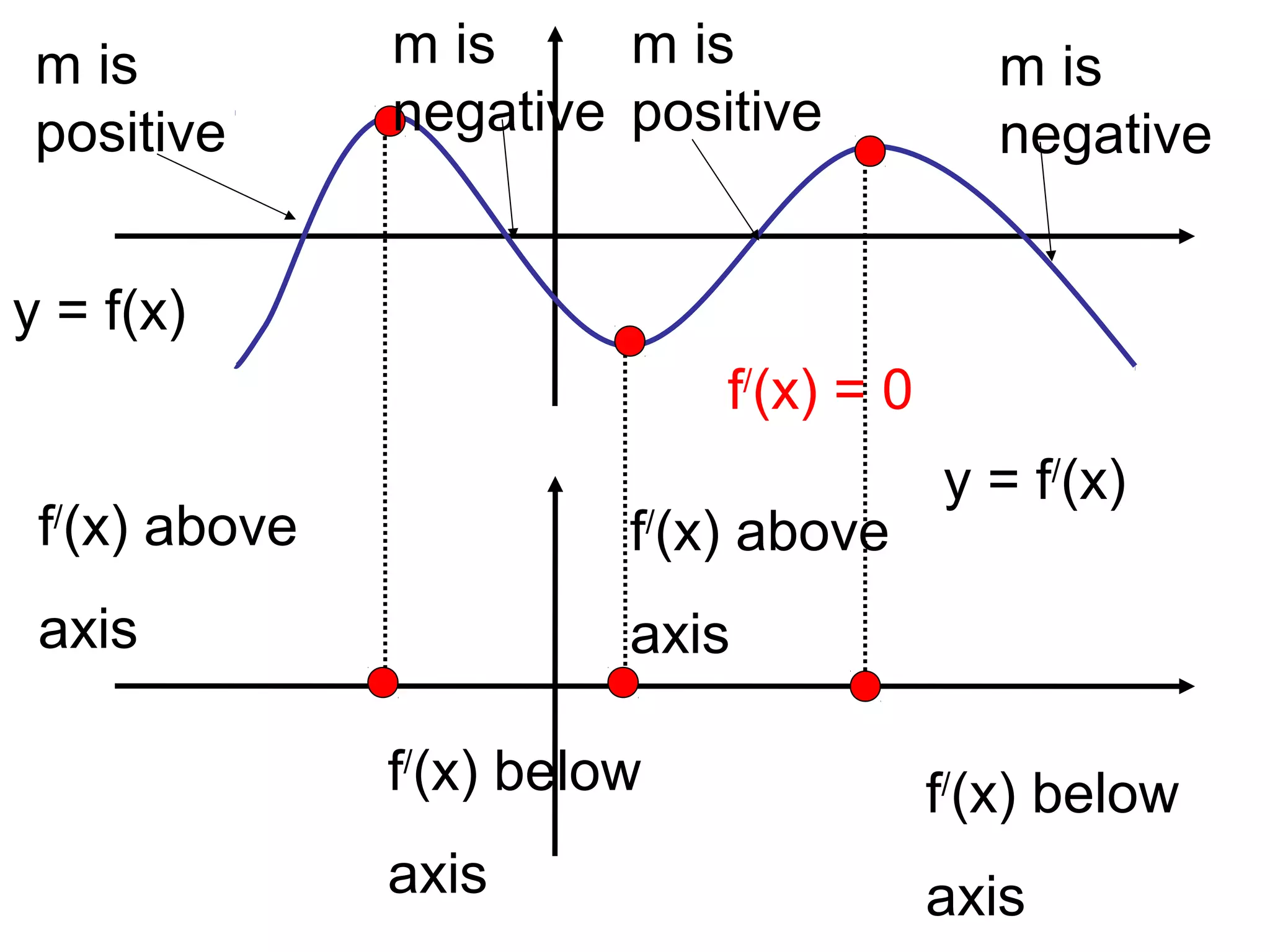
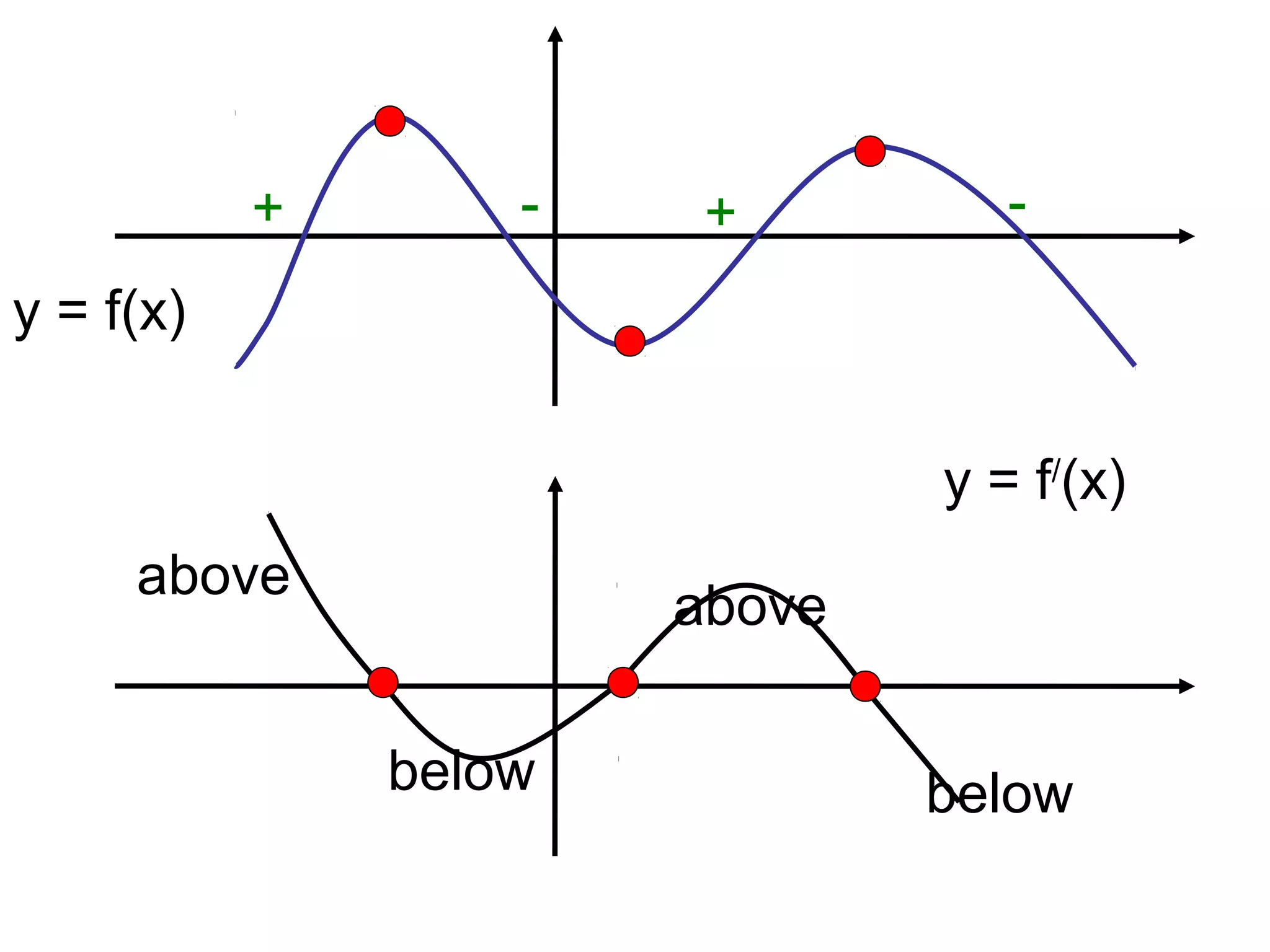
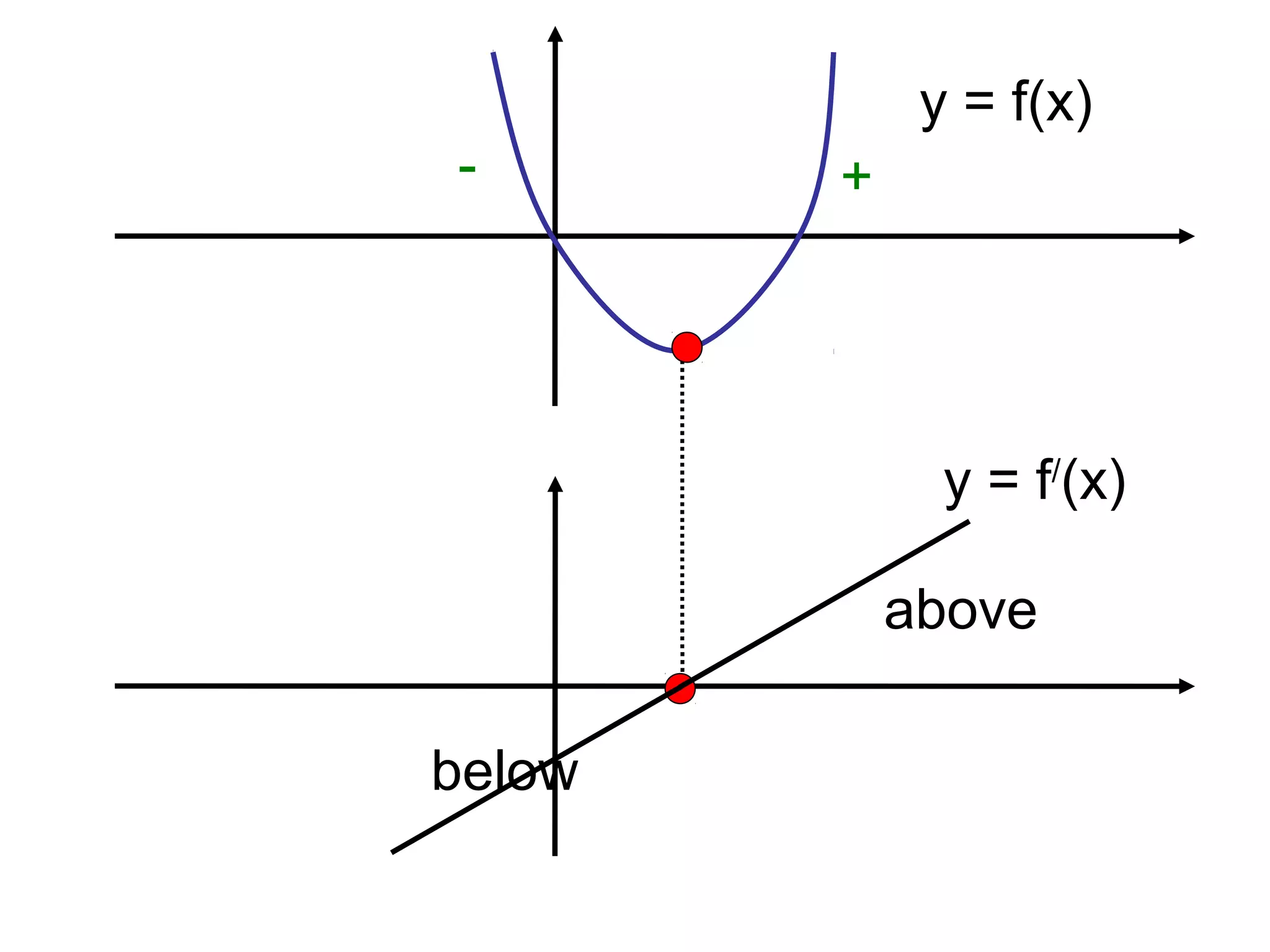
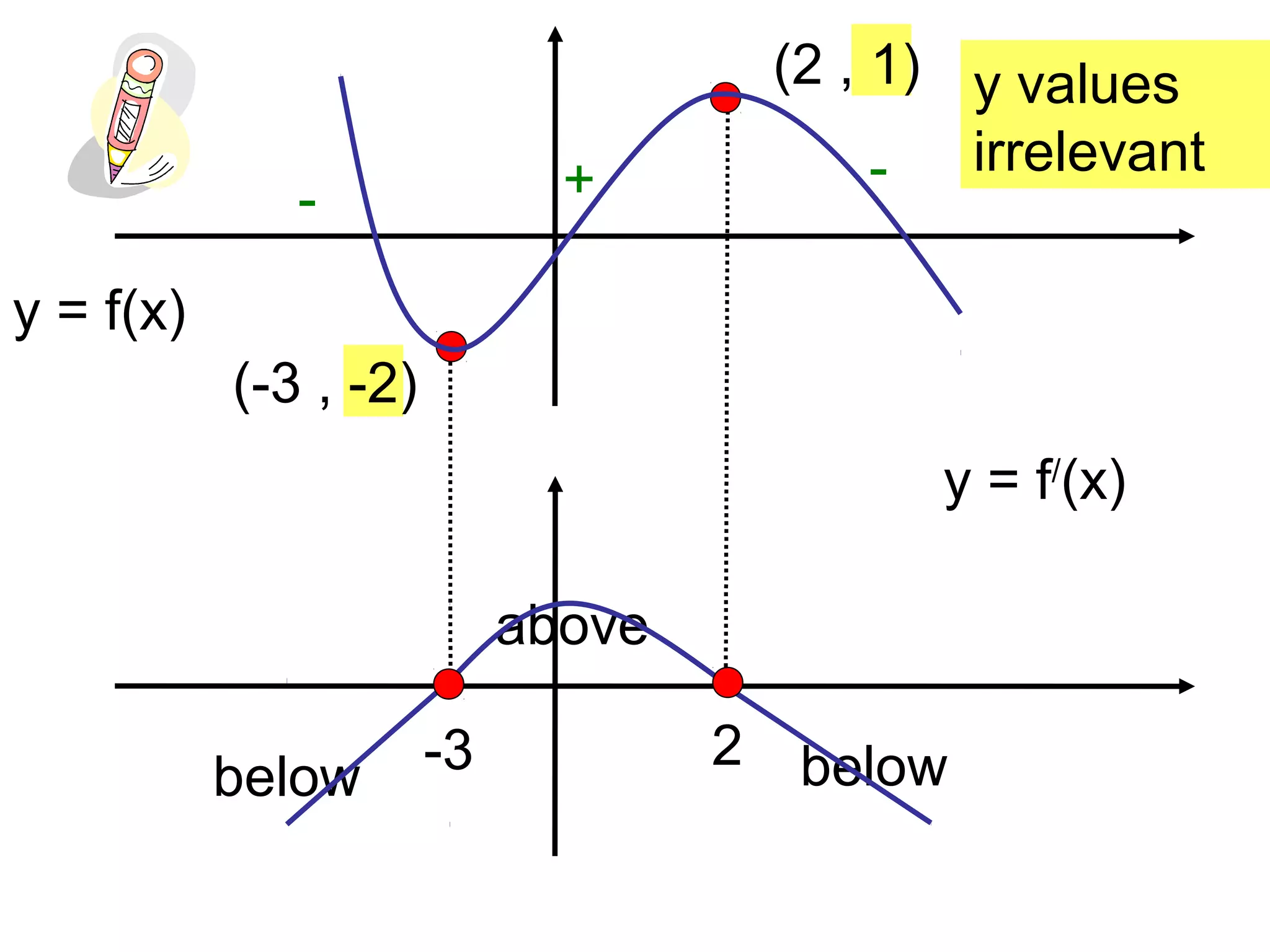
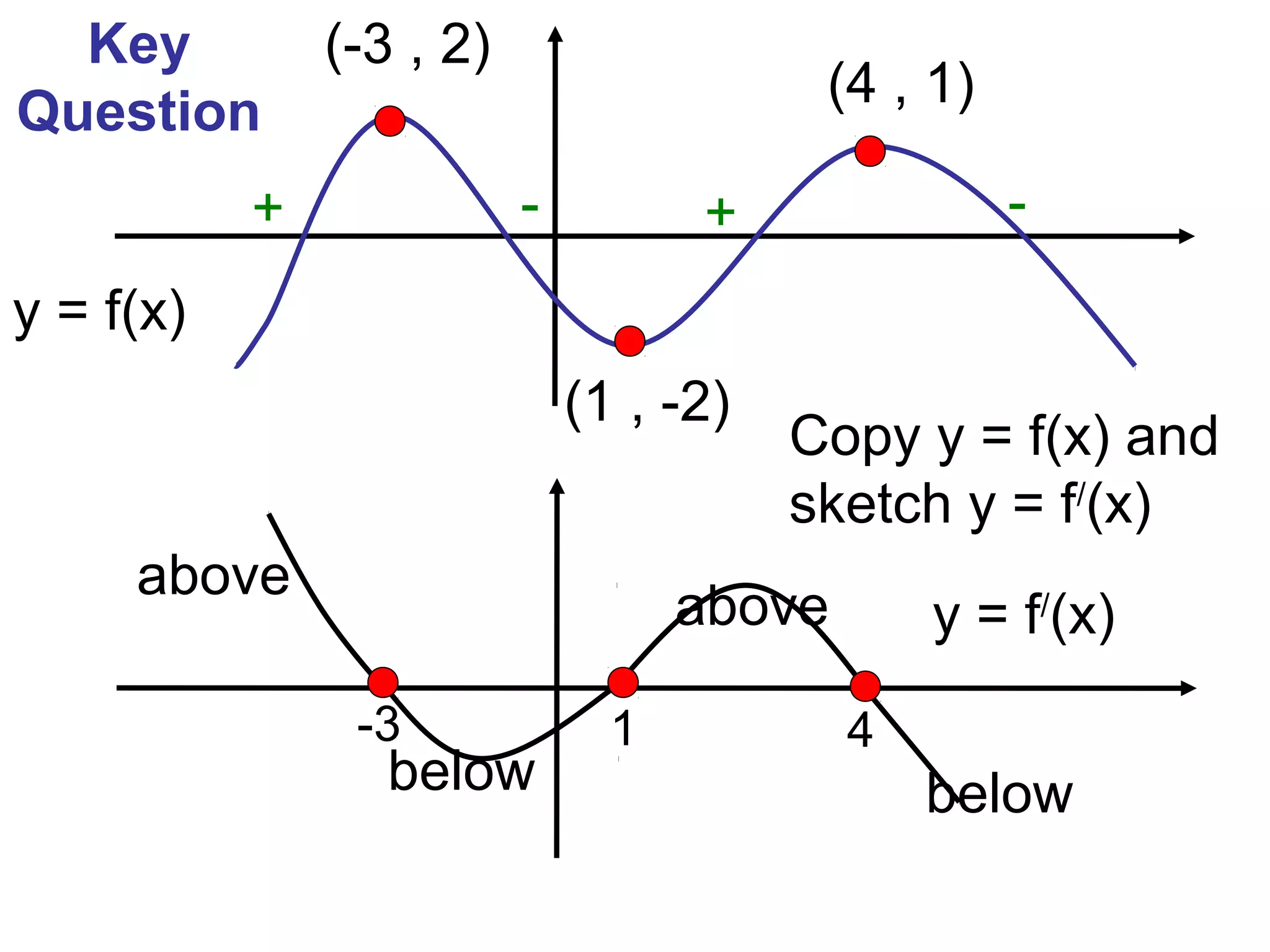
This document provides instructions for sketching the derivative graph y = f'(x) given an original function graph y = f(x). It explains that the derivative graph is drawn directly below the original function graph. Points where the original function has positive slope will result in the derivative graph being above the x-axis, and points with negative slope will produce a derivative graph below the x-axis. Examples are given to demonstrate how to copy the original function and sketch the derivative based on the signs of slopes.

1. Block 1
Derivative Graphs

2. What is to be learned?
• How to sketch y = f/
(x) if given y = f(x)

3. y = f(x)
f/
(x) = 0
y = f/
(x)
m is
positive
f/
(x) above
axis
m is
negative
f/
(x) below
axis
m is
positive
f/
(x) above
axis
m is
negative
f/
(x) below
axis

4. y = f(x)
y = f/
(x)
+
above
-
below
above
below
+ -

5. y = f(x)
y = f/
(x)
+-
above
below

6. Sketching y = f/
(x)
• Draw directly below y = f(x)
• SVs on y = f(x) →
• +ve gradient on y = f(x) →
• -ve gradient on y = f(x) →
zero on y = f/
(x)
(on x axis)
above x axis
below x axis

7. y = f(x)
y = f/
(x)
-
below
above
below
+ -
(-3 , -2)
(2 , 1)
-3 2
y values
irrelevant

8. y = f(x)
y = f/
(x)
+
above
-
below
above
below
+ -
(-3 , 2)
(1 , -2)
(4 , 1)
-3 1 4
Key
Question
Copy y = f(x) and
sketch y = f/
(x)