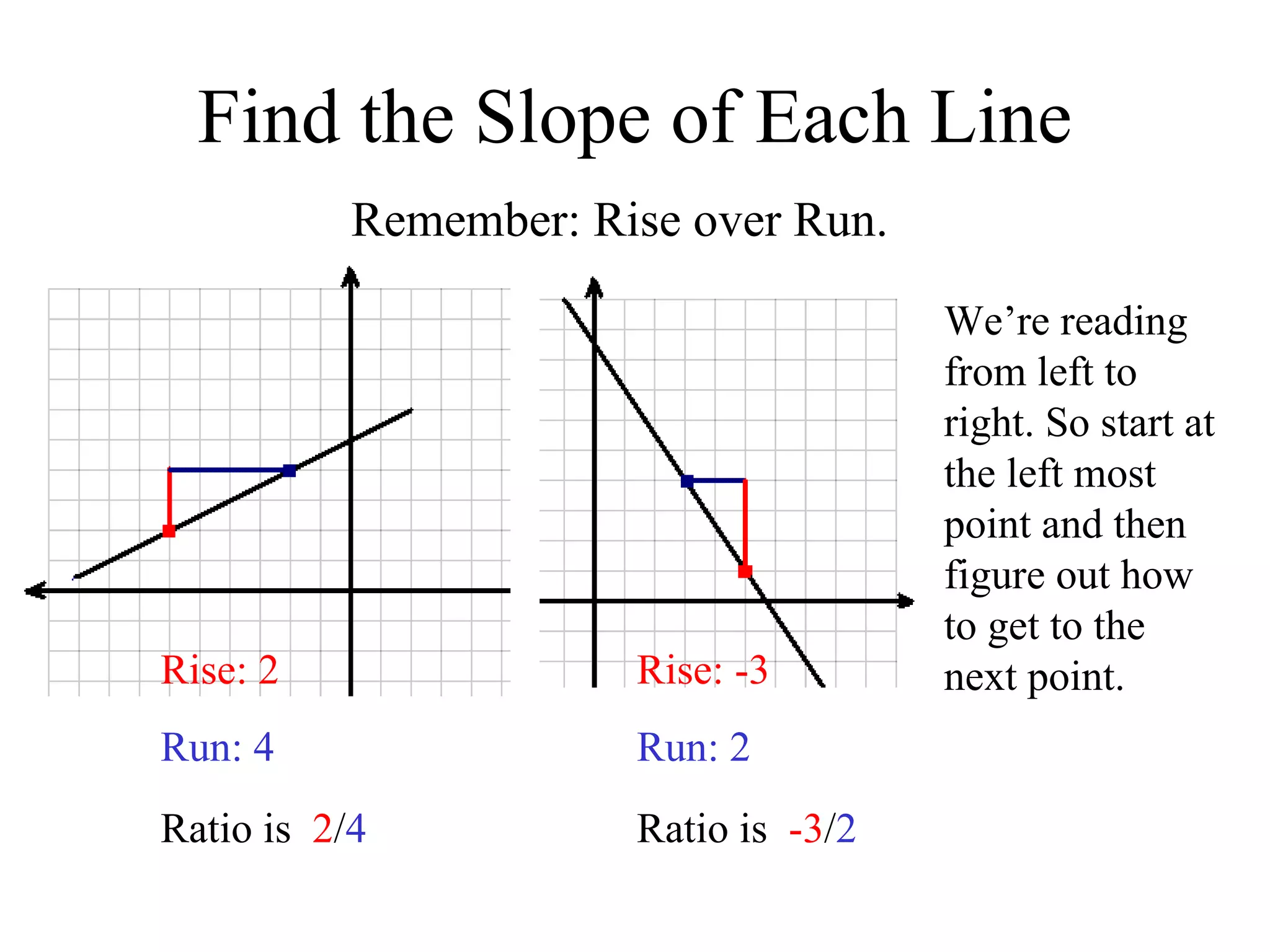
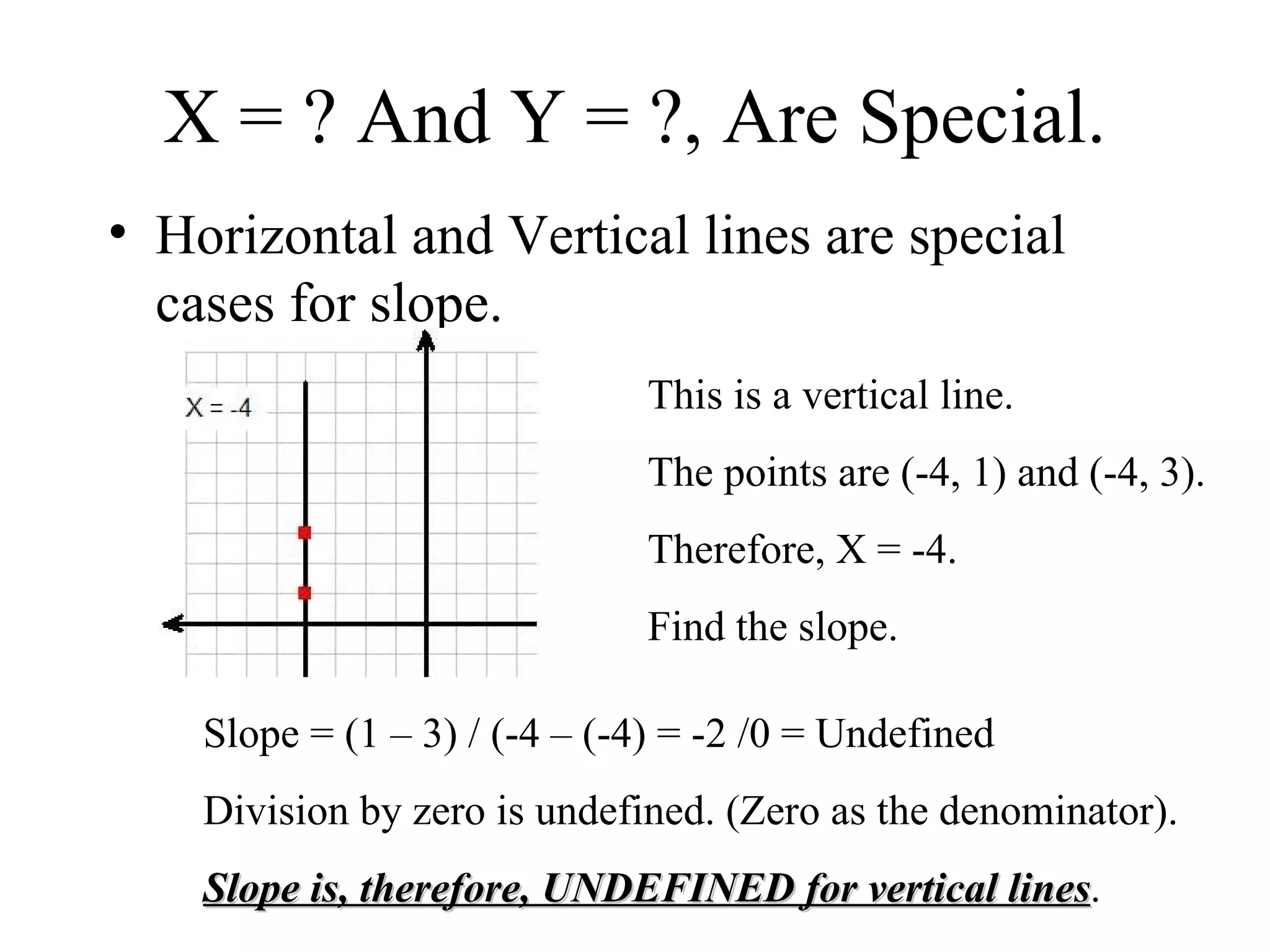
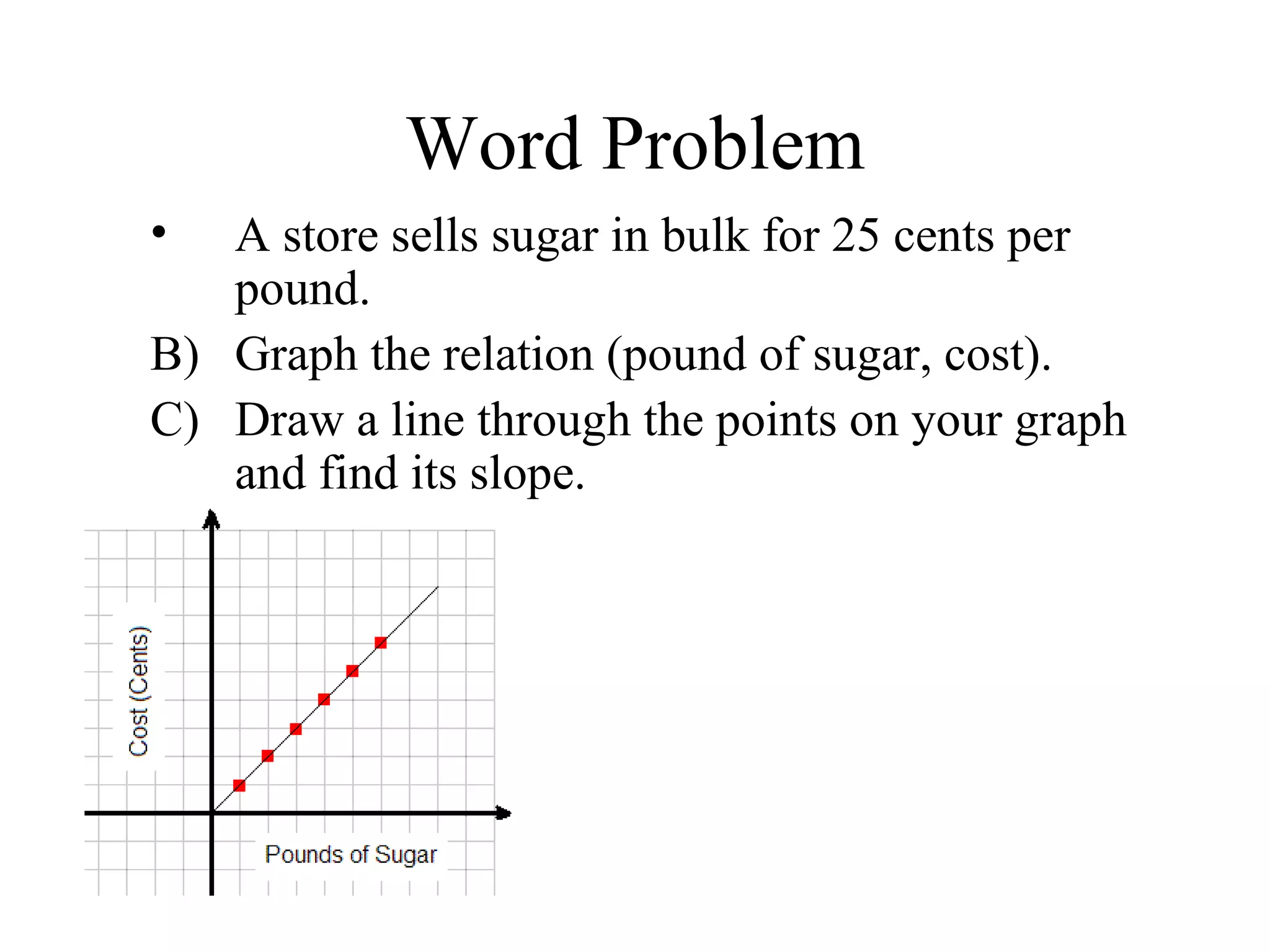
The document discusses slope and the slope-intercept form of linear equations. It defines slope as the ratio of the rise over the run between two points on a line. Slope can be calculated using two points or using the difference of the y-coordinates over the difference of the x-coordinates. Horizontal and vertical lines have special cases for slope calculations. The slope-intercept form is defined as y=mx+b, where m is the slope and b is the y-intercept. Using this form, lines can be graphed by plotting the y-intercept and using the slope to find the second point and draw the line.

1. Chapter 8 Section 3 Slope and Y-Intercept February 9 th , 2009 I suggest you write EVERY THING down in your notes.

2. Warm Up Solve for y: 9x + y = 7 6x – 3y = 12 11 – y = x x = 14 – 7y Write each ration in Simplest Form. (8-2)/(5-3) (1-3)/(6-0) (6 – (-2))/(5 – 9) (-2 – (-3))/(7 – 10)

3. Slope The ratio that describes the tilt of a line is its slope. To calculate slope, you use this ratio. Slope = (Vertical Change)/(Horizontal Change) Slope = Rise/Run (Rise over Run).

4. Slope Rise shows vertical change. Run shows horizontal change. Up means positive. Down means negative. Right is positive. Left is negative.

5. Find the Slope of Each Line Remember: Rise over Run. Rise: 2 Run: 4 Rise: -3 Run: 2 Ratio is 2 / 4 Ratio is -3 / 2 We’re reading from left to right. So start at the left most point and then figure out how to get to the next point.

6. If You Know Two Points: You can find the slope of the line using the ratio. The difference of y – coordinates OVER the difference of x – coordinates. The y -coordinate you use first in the numerator must correspond to the x -coordinate you use first in the denominator. P.S.: Difference means to subtract!

7. Find the slope of the line through C( -2, 6 ) and D( 4, 3 ). Slope = difference in y-coordinates difference in x-coordinates = ( 3 – 6 )  y-coordinates ( 4 – ( -2 ))  x-coordinates Slope = -3 / 6 = -1/2 Down 1, to the Right 2. Cause of Rise (of –1) over Run (+2).

8. Find the Slope of the Line through each pair of points: V(8, -1) and Q(0, -7) S(-4, 3) and R(-10, 9) 3/4: Rise = 3, Run = 4 -1 or (1/-1): Rise = 1, Run = -1

9. X = ? And Y = ?, Are Special. Horizontal and Vertical lines are special cases for slope. This is a horizontal line. The points are (-3, 2) and (1, 2). Therefore, Y = 2. Find the slope. Slope = (2 – 2) / (1 – (-3) = 0 /4 = 0 The slope for a horizontal line (or anything Y = ?) is zero.

10. X = ? And Y = ?, Are Special. Horizontal and Vertical lines are special cases for slope. This is a vertical line. The points are (-4, 1) and (-4, 3). Therefore, X = -4. Find the slope. Slope = (1 – 3) / (-4 – (-4) = -2 /0 = Undefined Division by zero is undefined. (Zero as the denominator). Slope is, therefore, UNDEFINED for vertical lines .

11. Word Problem A store sells sugar in bulk for 25 cents per pound. Graph the relation (pound of sugar, cost). Draw a line through the points on your graph and find its slope.

12. Using Slope to Graph Linear Equations This is the graph of y=(-1/2)x + 3. The slope of the line is (-2/4) or (-1/2). The Y-INTERCEPT of the line is the point where the line crosses the Y-AXIS. The CONSTANT in the equation is the same as the y-intercept .

13. Using Slope to Graph Linear Equations This is the graph of y=(-1/2)x + 3. The slope of the line is (-2/4) or (-1/2). y = (-1/2) x + 3 Slope = always a ratio Y-Intercept = Constant

14. Slope-Intercept Form Using the Slope-Intercept Form, you can graph without having to pick points and make a table. y = mx + b = Slope-Intercept Form M = Slope of the line. (Ratio) B = Y-Intercept. (Constant) Linear Equations will always be in this format, or at least, be able to be made into this format. Like solving for y.

15. To Graph with y = mx + b Start with b. Since b is where the line of the equation hits the y-axis, its your first point. Point = (0, b) Take the slope, or m. Starting at b, move along the RISE and RUN of the ratio. Where you end up is your second point. Connect the two dots with a line. (This is the graph of your linear equation).

16. Lets Graph Together! y = (-1/3)x + 2 If you can’t tell where the negative goes, always put it on the numerator. b = 2 so, (0, 2) Rise: -1, Run: +3 Graph next dot. Connect dots with straight line.

17. Assignment #3 Pages 400-401: 1-41 odd numbered problems.