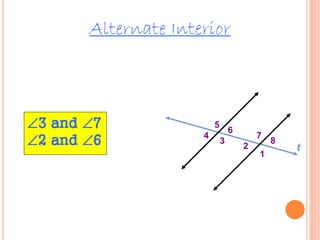
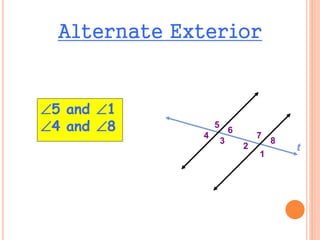
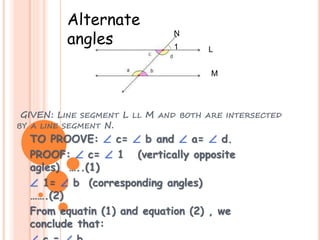
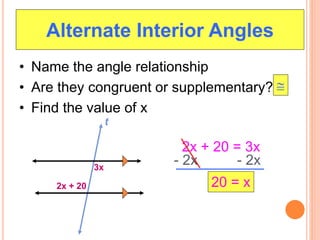
The document presents a proof that alternate angles are equal. It defines two types of alternate angles: alternate interior angles and alternate exterior angles. It gives an example of two lines intersected by a transversal line to represent the angles. The proof uses vertically opposite angles and corresponding angles properties to show that alternate interior angles are congruent. It also asks to identify angle relationships and find values of variables in examples of alternate exterior and interior angles.

1. PRESENTATION TO PROOF THAT ALTERNATE
ANGLES ARE EQUAL

2. ALTERNATE ANGLES:
Alternate Exterior Angles: Nonadjacent exterior angles that lie on opposite
sides of the transversal.
THE ALTERNTE ANGLES ARE
OF 2 TYPES:
Alternate Interior Angles: Nonadjacent interior
angles that lie on opposite sides of the
transversal.

3. Alternate Interior
3 and 7
2 and 6
1
2
3
4
5
6
7
8
t

4. Alternate Exterior
5 and 1
4 and 8
1
2
3
4
5
6
7
8
t

5. GIVEN: LINE SEGMENT L LL M AND BOTH ARE INTERSECTED
BY A LINE SEGMENT N.
TO PROOVE:  c=  b and  a=  d.
PROOF:  c=  1 (vertically opposite
agles) …..(1)
 1=  b (corresponding angles)
…….(2)
From equatin (1) and equation (2) , we
conclude that:
1
Alternate
angles
L
M
N

6. FIND ALL
ANGLE
MEASURES

7. ALTERNATE EXTERIOR ANGLES
 Name the angle relationship
 Are they congruent or supplementary?
 Find the value of x
125 
t
5x 
5x = 125
5 5
x = 25


8. Alternate Interior Angles
• Name the angle relationship
• Are they congruent or supplementary?
• Find the value of x
3x
t
2x + 20

20 = x
2x + 20 = 3x
- 2x - 2x

10. SUBMIITED BY:
SHEENAM
9TH KAVERI
18
SUBMITTEDTO:
MRS. MEENU MAM