This document discusses the treatment of compressible flow in computational fluid dynamics (CFD). It covers the basics of compressible flow including conservation laws, the governing equations in conservation form, and the wave theory known as the CFL condition. It also discusses schemes for solving the equations, including flux vector splitting schemes, Roe averaged schemes, and AUSM schemes. The document emphasizes that compressible flow equations are hyperbolic and describes how characteristics and eigenvalues relate to the equation types.

1. ©ZeusNumerix
Defense | Nuclear Power | Aerospace | Infrastructure | Industry
Treatment of compressible flow in CFD
Abhishek Jain
abhishek@zeusnumerix.com
Compressible Flow: Basics

2. ©ZeusNumerix
2
Overview
 Conservation Laws
 Conservation form of equations
 Governing equations: Hyperbolic
 The Wave theory: CFL Condition
 Schemes and their types
 Eigen values
 Boundary conditions

3. ©ZeusNumerix
Conservation Laws
 Mass is Conserved
 Net mass flowing out of the system = Net mass decreased in
the system
 Momentum is Conserved
 Rate of change of momentum = Momentum transfer through
the surfaces – Forces (surface and body)
 Surface forces – Shear stress, pressure, surface tension
 Body forces – Gravity, centrifugal or electromagnetic etc
 Energy is Conserved
 Rate of change of energy = Neat heat flux + work done by
body and surface forces
3

4. ©ZeusNumerix
The Equations
 Equations in Conservation form (Differential)
4
Similarly for
y and z direction

5. ©ZeusNumerix
Conservation and Non-
Conservation Forms
 Conservation Form
 Easy to code as all equations look similar
 More physical as “can be simply stated in English”
 Primary variable are calculated from the flux variables
 Captures the shock; (shock produced by solution)
 Non-Conservation Form
 Equation given above are expanded
 Has a shock fitting approach; solution is a forethought i.e.
shock location must be approximately known
 Captures the shock better
 There have been instances where shock fitting and
capturing methods have been used with either forms
5

6. ©ZeusNumerix
Integral Form of Equations
 Conservation form
 F, G, H are similar
 S depends on the type of flow solved
6
U =
ρ
ρu
ρv
ρw
ρE
F =
ρu
ρ u2 + p
ρuv + p
ρuw + p
(ρE + p)u

7. ©ZeusNumerix
Difference
 Integral form means that if we were to add up the
properties in the whole domain there will be an equilibrium
 Does not assume if quantities are a part of continuous function
or discontinuous
 Differential means the function is continuous
 Not able to capture physical discontinuities like shock wave
 Integral form there is called more fundamental
7

8. ©ZeusNumerix
Completing the Loop
 The number of equations is FIVE
 Assuming calorically perfect gas E=CvT
 Number of unknowns
 ρ, u, v, w, p, T
 Hence the thermal equation of state is used for closure
 p= ρRT
 R is the Gas Constant
 Please remember that the above equation was not used in
incompressible flow
8

9. ©ZeusNumerix
Equation Types
 Eigen values are calculated using the coefficients of the
equations
 In case the Eigen values of the equations are
 Real and distinct – equation is Hyperbolic
 Real and Zero – equation is Parabolic
 Imaginary – equation is elliptic
 Characteristic lines are curves where slope of dependent
variable is indeterminant
 Slope of the characteristic line can be real, zero or
imaginary making the equations Hyperbolic, parabolic or
elliptic
9

10. ©ZeusNumerix
Equations
 Hyperbolic
 Disturbance propagates from domain of dependence (Brown)
to range of influence (Gray)
 Characteristics APC and BPD
10
P
C
D
B
A

11. ©ZeusNumerix
Mach Cone
 Supersonic flow means signal does not travel in all directions
 Signal does not reach upstream
11
Zone of Silence
Mach Cone
Motion
Zone of Silence

12. ©ZeusNumerix
Equations
 Parabolic – Effect travels through one direction only
 Elliptic – Effect travels in all directions
 For complex equations like Navier Stokes the behavior may
be mixed
 Examples
 Supersonic inviscid flow – hyperbolic
 Subsonic inviscid flow – elliptic
 Boundary layer flow – parabolic
 Scheme that works for one set fails for another
12

13. ©ZeusNumerix
The Time Marching
 Supersonic blunt body problem
 Flow inside blue circle is subsonic
 At other places supersonic
 Problem is elliptic in circle & hyperbolic outside
 First technique to make problem hyperbolic
 Introduce time derivative in steady problem
 March in time to ‘reach’ at steady state
 Most widely used method (Finite Volume)
 Marching explicit or implicit (next lecture)
13

14. ©ZeusNumerix
The Wave Theory
 Flow is traveling of waves
 Slope of the wave matters
14
X
Time
i i+1 i+2 i+3 i+4 i+5 i+6
n+4
n+3
n+2
n+1
n
Area of physical domain
covered

15. ©ZeusNumerix
CFL Condition
 Stencil are the points used for simulation of flow
 In case below it is i(n), i+1(n) and i(n+1)
 For stable simulation Numerical domain must be greater
than physical domain
 Δt = CFL * Δx/Wave speed (CFL acts as a factor of safety)
15
Numerical domain of
dependence
True domain
of dependence
True wave
direction
i i+1

16. ©ZeusNumerix
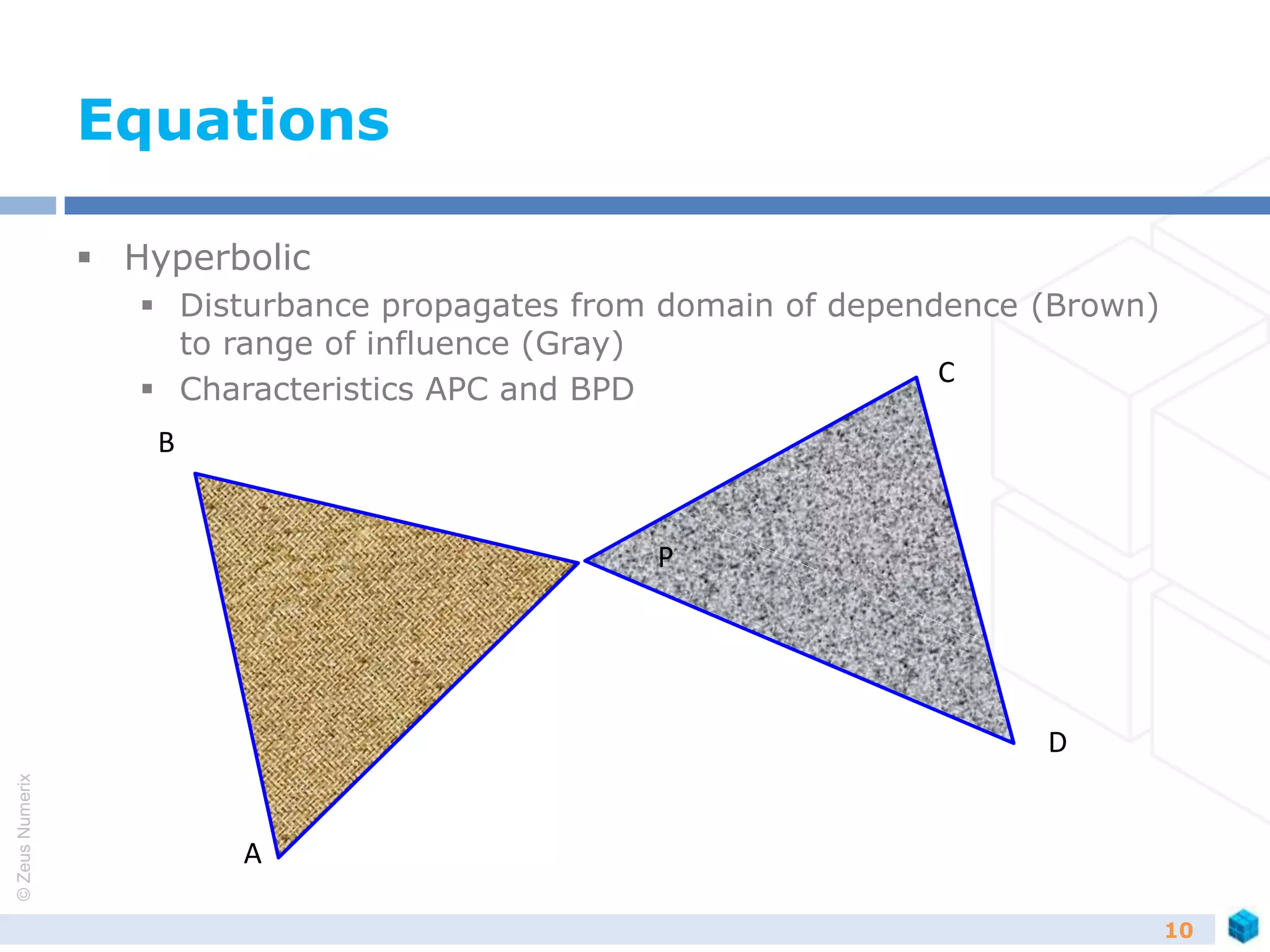
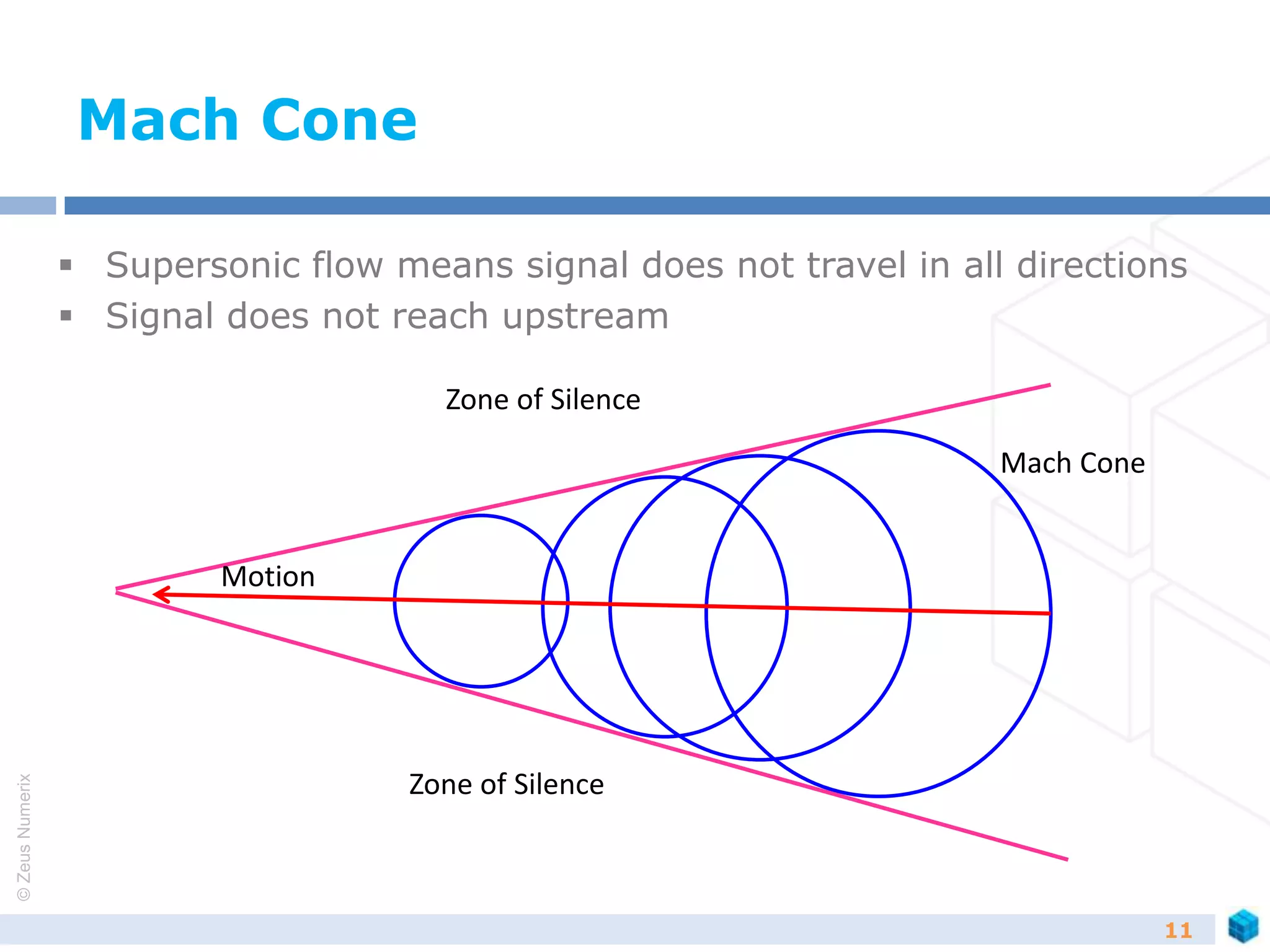
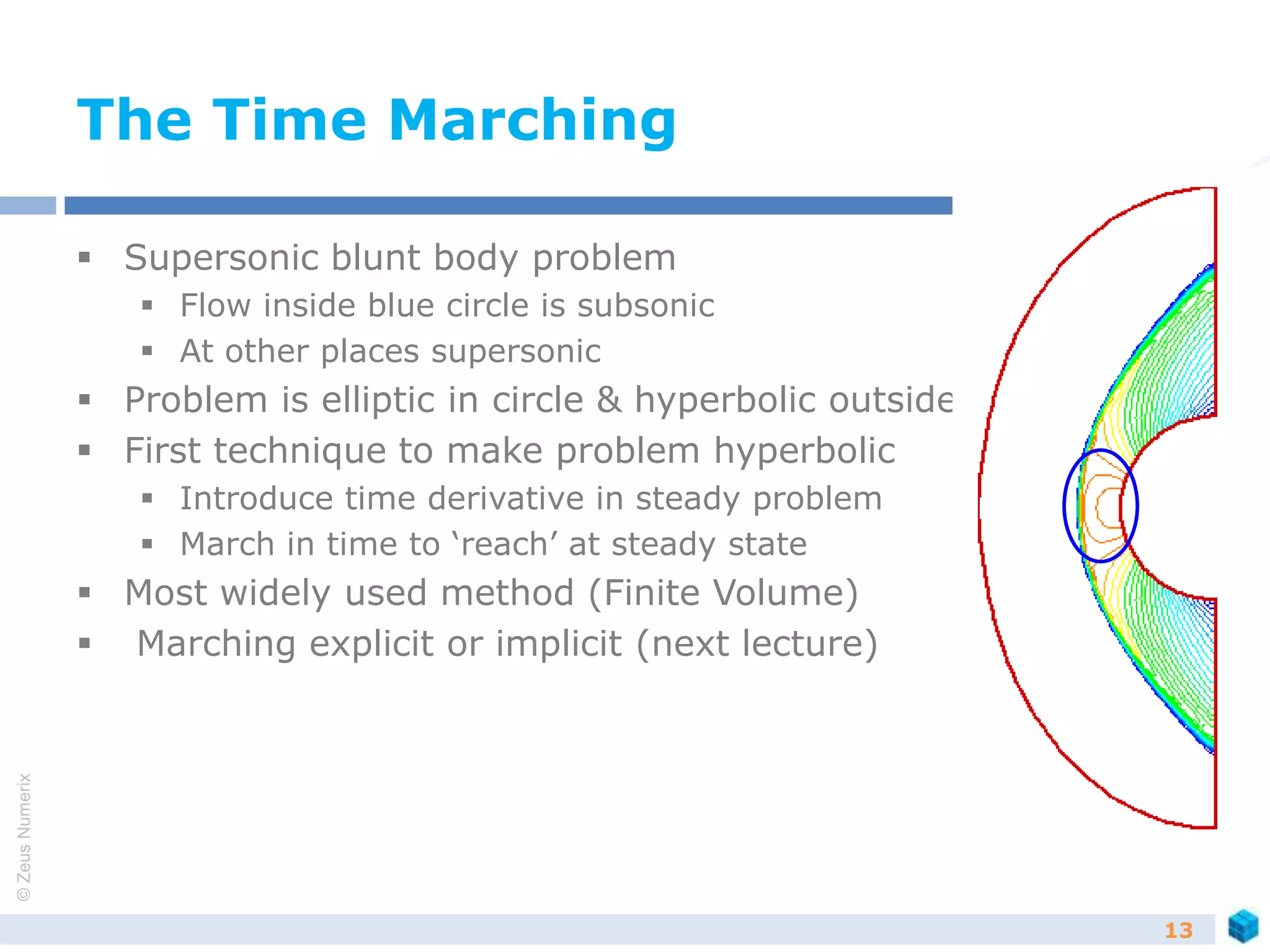
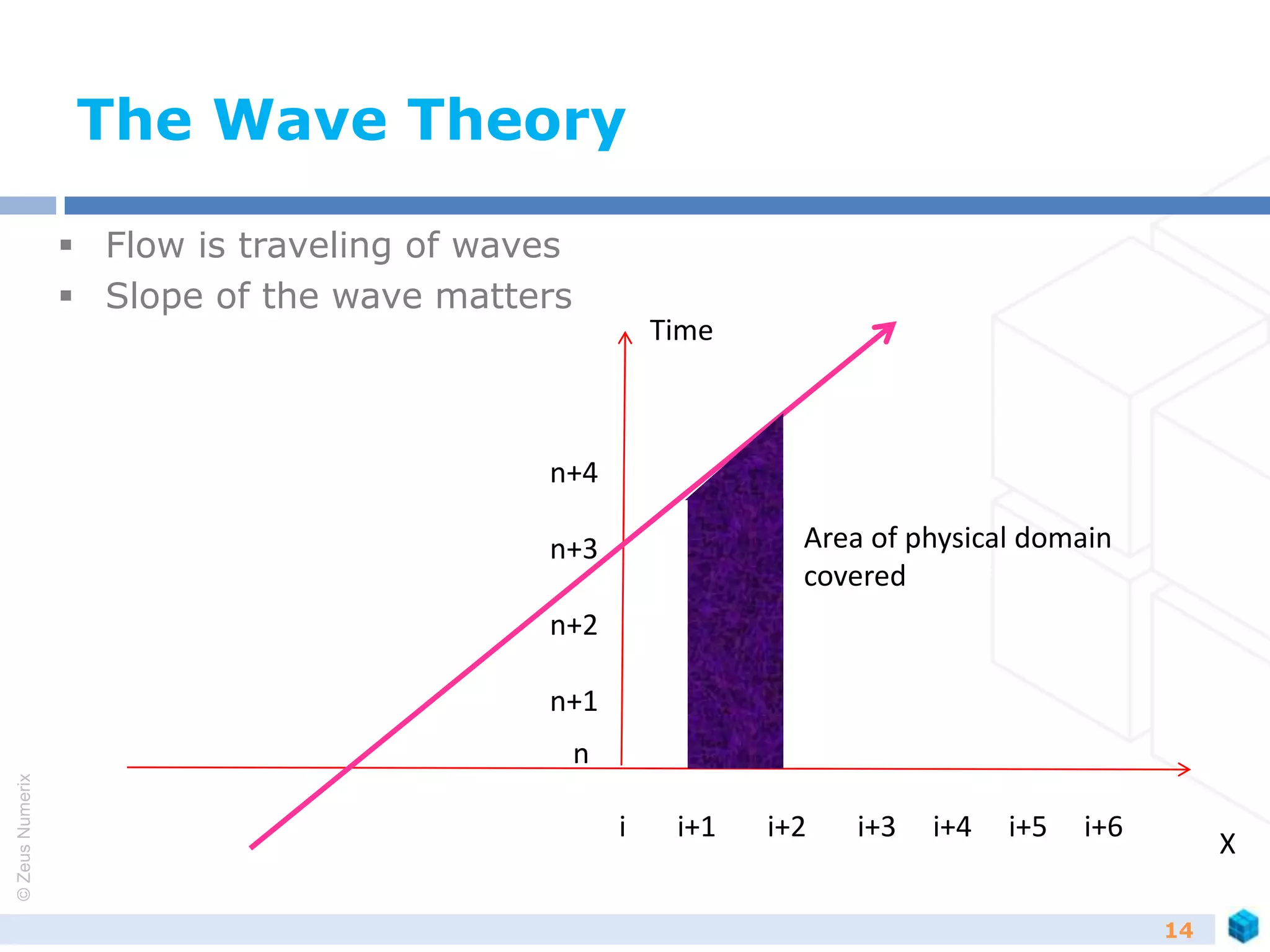
Schemes
 Problems in CFD can be finally simplified to
 dU/dt +dF/dx = 0
 Method of solving for [F] is called a scheme
 Flux vector splitting schemes
 Equations contains waves that travel in forward and backward
direction
 Flux vector split in such a fashion that waves are split in
forward moving and backward moving
 Solved independently to get solution
 Van Leer scheme – M = M++M-
 Steger Warming Method – Λ = Λ++Λ-
 van Leer better at sonic points as M is second derivative
16

17. ©ZeusNumerix
Schemes
 Flux vector splitting schemes are diffusive and do not
capture boundary layer properly
 Easy to code with faster turn around time
 Roe Averaged – solves a local Reimann problem and give
better result at boundary layer but produces expansion
shock
 Entropy Fix Roe – Forced condition put on such that
Entropy never decreases
 AUSM – Combines the goodness of flux vector splitting
schemes and Roe type schemes
 Has many modifications for time decrease or better
performance
17

18. ©ZeusNumerix
Thank You!
3 November 2014 18