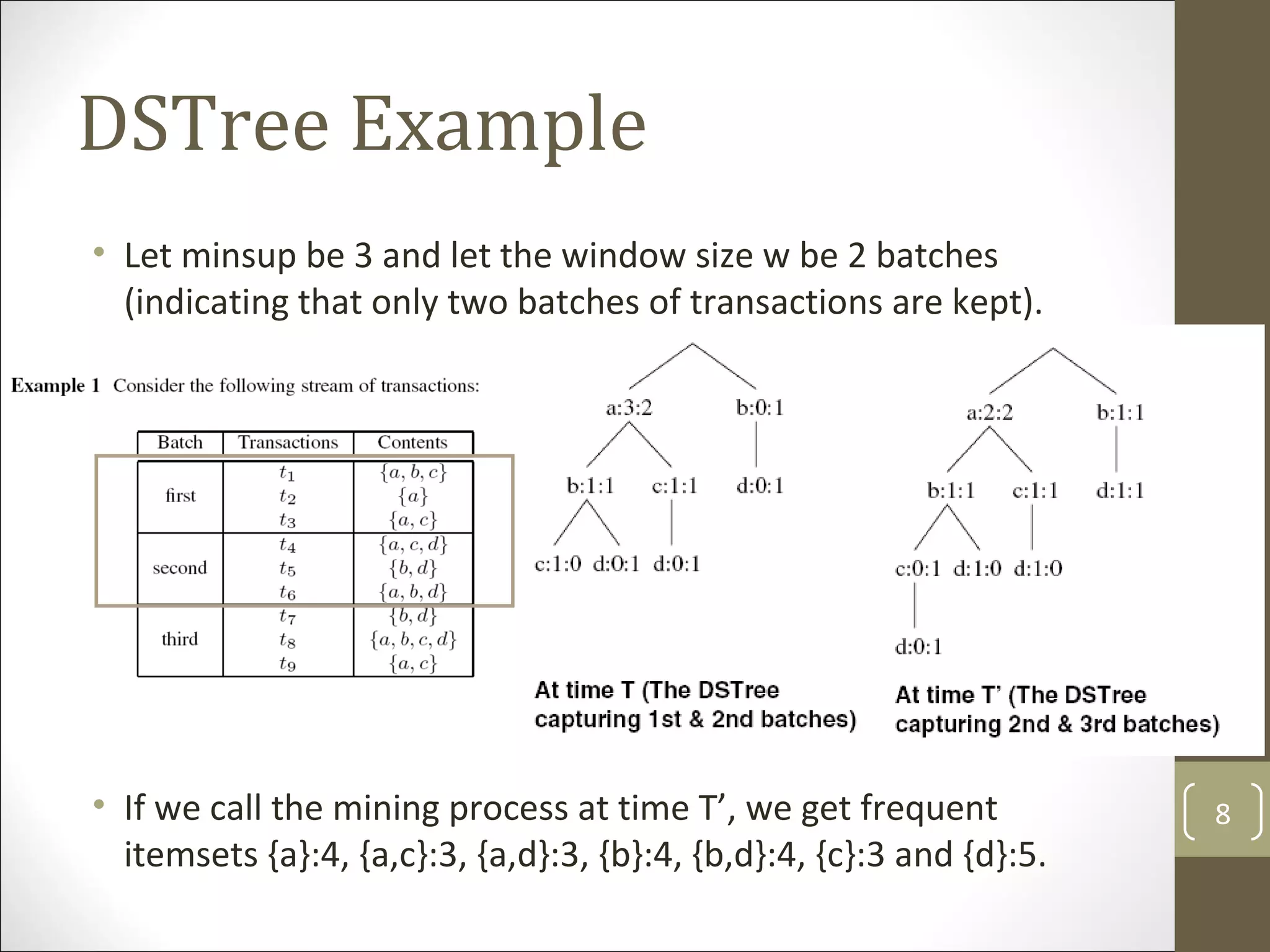
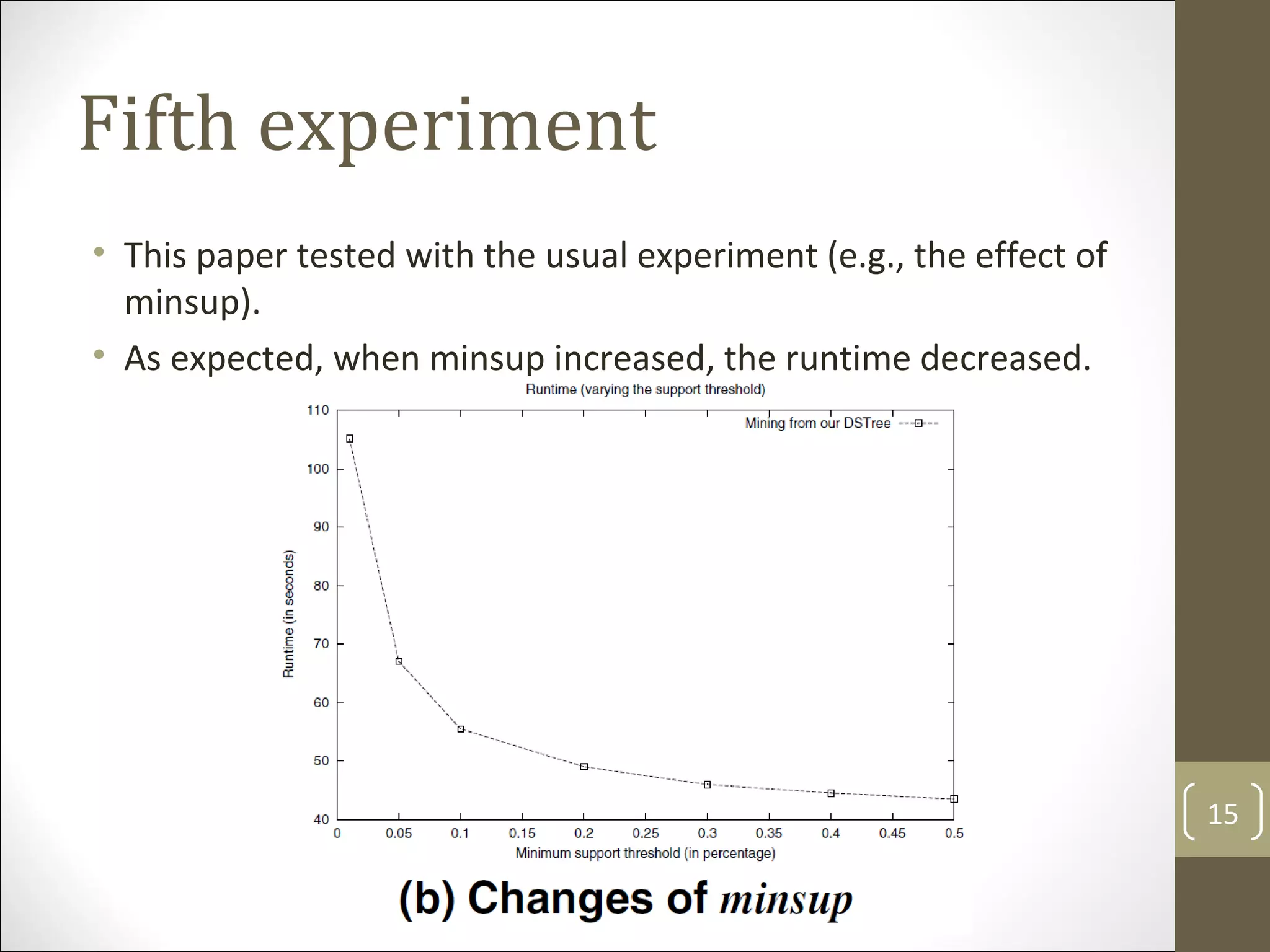
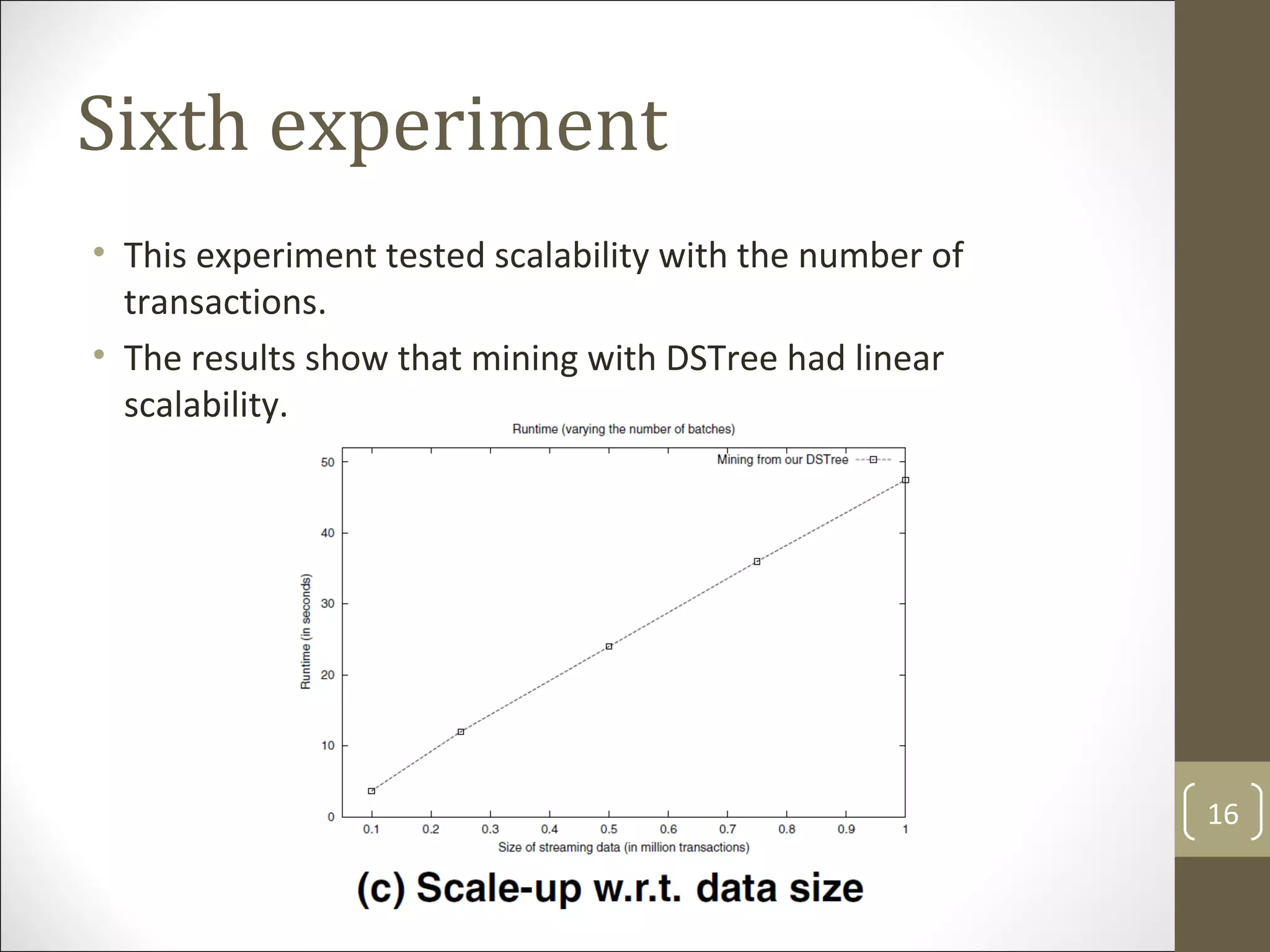
The document presents dstree, a novel data structure designed for exact stream mining of frequent itemsets in data streams. It compares dstree against existing algorithms like cantree and fp-streaming, demonstrating its efficiency, accuracy, and lower maintenance costs. The experimental results confirm that dstree maintains linear scalability and offers better performance in terms of memory usage and result accuracy compared to approximate mining techniques.

1. DSTree: A Tree Structure for the Mining of Frequent Sets from Data Streams Presenter / Meng-Lun Wu Source / ICDM’06, IEEE Author / Carson Kai-Sang Leung, Quamrul I. Khan

2. Outline Introduction Related Work DSTree Discussion Experimental Results Conclusions

3. Introduction With advances in technology, a flood of data can be produced in many applications. Ex. Sensor networks and Web click streams. This calls for efficient techniques for extracting useful information from streams of data. Mining from data streams is more challenging due to Property 1: Data streams are continuous and unbounded. Property 2: Data in the streams are not necessarily uniformly distributed; their distributions are usually changing with time.

4. Introduction (cont.) Several stream mining algorithms can be broadly categorized into two classes. Exact algorithms Finding truly frequent itemsets, especially for maximal, closed, or “short” itemsets. i.e., itemsets with frequency  user-defined minimum support threshold minsup. Approximate algorithms Finding “frequent” itemsets by using approximate procedures, which may lead to some false positives or false negatives. The key contribution of this work is called DSTree (Data Stream Tree), which is designed for exact stream mining of regular frequent itemsets.

5. Related Work In this section, we briefly discuss some data structures that are relevant to our work. CanTree (proposed in ICDM’05) vs. DSTree CanTree is designed for incremental mining, whereas DSTree is designed for stream mining. Each node in the CanTree keeps just one frequency count, whereas each node in the DSTree keeps a list of frequency counts. Transactions are deleted from the CanTree, the frequency counts of the affected nodes get decremented while in the DSTree, the list of frequency counts at each affected node just shifts.

6. Related Work (cont.) FP-streaming (FP-tree and FP-stream) vs. DSTree FP-streaming DSTree Algorithm type Approximate stream mining Exact stream mining Constructing tree One batch built one FP-tree Several batch in one transaction built one DSTree Store counts Keep just one frequency counts Keeps a list of frequency counts Support threshold Yes No Each path Represents an itemset Represents a transaction in the current window Window Titled-time windowing sliding window

7. DSTree Due to Property 1 of data streams, The DSTree is desinged for (exact) stream mining. The construction of the DSTree only requires one scan of the streaming data. The tree captures the contents of transactions in each batch of streaming data. Due to the dynamic nature and Property 2 of data streams We arrange transaction items according to some canonical order. E.g. lexicographic order or alphabetical order. The frequency of a node in DSTree is at least as high as the sum of frequencies of its children. The ordering of items is unaffected by the continuous changes in item frequencies.

8. Let minsup be 3 and let the window size w be 2 batches (indicating that only two batches of transactions are kept). If we call the mining process at time T’, we get frequent itemsets {a}:4, {a,c}:3, {a,d}:3, {b}:4, {b,d}:4, {c}:3 and {d}:5. DSTree Example

9. Discussion (a) Applicability for finding other patterns: DSTree also provides users with such functionalities as stream mining of maximal, closed, and constrained itemsets. A frequent itemset is maximal if none of its proper supersets is frequent. A frequent itemset X is closed if none of proper supersets of X has the same frequency as X. DSTree can provide users with additional functionality to these algorithms. These algorithms can use DSTree and arrange tree items according to some cannonical order. C succ  max (S.Price)  30 C conv  avg (S.Price)  7

10. Discussion (cont.) (b)Extensions – different windowing techniques It is important to note that the sliding window is not confined. Tiled-time window: more weights can be put on recent data and less weights on older data. (c) Efficiency and memory issues: DSTree do not need to keep any extra tree structures as in the FP-streaming algorithm, where space is required for both the FP-tree and the FP-stream structure.

11. Experimental Results & First Experiment Experiment Data IBM Almaden Research Center: 1 M records with an average transaction length of 10 items, and a domain of 1,000 items. Each batch contain 0.1 M transactions and the window size is set to w=5 batches. This experiments mainly evaluated the accuracy and efficiency of DSTree. First Experiment Accuracy: Comparing the frequent itemsets returned by mining directly from these transactions with those returned by mining from our DSTree. Accuracy: 100%

12. Second Experiment We compared the runtime of mining from DSTree with that of using the FP-streaming mining algorithm.

13. Third Experiment We compared the DSTree with its relevant structures (e.g., CanTree, FP-tree and FP-stream structure). When minsup=0.05%, the size of DSTree is about 1.25X that of the FP-stream; when minsup=0.01%, the size of the DSTree <0.90X that of the stream. The results also confirmed that the size of the DSTree did not depend on minsup whereas that of the FP-stream did. Among the two structures, the former kept transactions while the latter kept itemsets. Thus mining from the DSTree gave exact results, but mining with FP-streaming gave approximate results.

14. Fourth Experiment It show that the sizes of both DSTree and CanTree were unaffected by changes in minsup. The size of the DSTree is smaller than that of the CanTree because the latter keeps all transactions whereas the former only keeps transactions in the current window. The size of DSTree  0.5X that of the CanTree. The DSTree required a lower maintenance cost than the CanTree. Whenever transactions were deleted from the CanTree, it needed to either decrement the frequency count of nodes or remove the nodes corresponding to the deleted transactions. In contrast, DSTree did not require expensive deletion of transactions; it just shifted the frequency lists.

15. Fifth experiment This paper tested with the usual experiment (e.g., the effect of minsup). As expected, when minsup increased, the runtime decreased.

16. Sixth experiment This experiment tested scalability with the number of transactions. The results show that mining with DSTree had linear scalability.

17. Conclusions A key contribution of this paper is to propose the novel structure of DSTree (Data Stream Tree). This tree captures the contents of transactions in a window, and arranges tree nodes according to some canonical order. By exploiting its nice properties, DSTree can be easily maintained when the window slides. It can also be used for efficient stream mining of maximal itemsets, closed itemsets, as well as constrained itemsets.