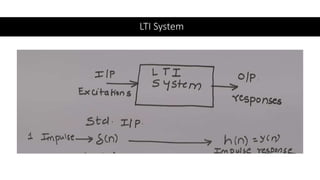
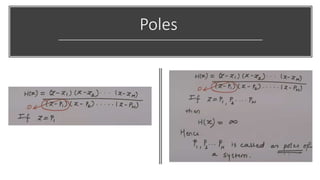
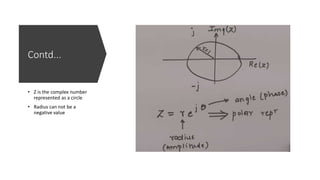
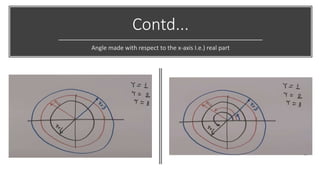
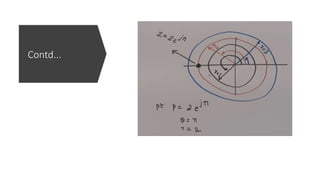
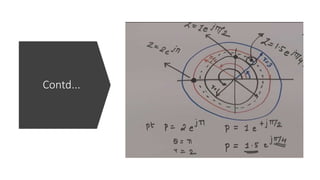
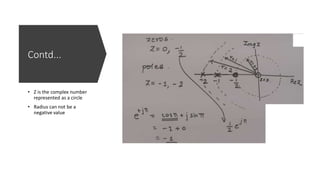
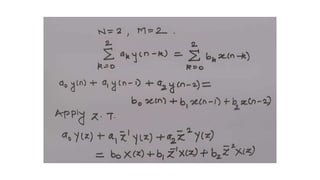The document discusses the z-transform and its application to linear time-invariant (LTI) systems. It covers difference equations, system transfer functions, pole-zero representations, and the significance of poles and zeros. Poles and zeros are represented as points in the z-plane. Poles cause the transfer function to approach infinity while zeros cause it to approach zero. The locations of poles and zeros determine how a system responds to different input frequencies.

1. Z-Transform

2. LTI System

3. Difference
Equation

4. Z-Transform

6. Linearity and Scaling property

7. System Transfer Functions

9. • Assume Z1, Z2 and P1, P2 are the roots of the ploynomial with degree two.

10. Pole Zero representation of the System

11. Poles

12. Representation
of Zero and
Pole entity in
Z-plane

13. Significance of Poles and
Zeros in Transfer
function

14. Significance of Poles and Zeros in Transfer function

15. Contd...
• Z is the complex number
represented as a circle
• Radius can not be a
negative value

16. Contd...
Angle made with respect to the x-axis I.e.) real part

17. Contd...

18. Contd...

19. Contd...

20. Contd...
• Z is the complex number
represented as a circle
• Radius can not be a
negative value

21. Problem 1:
Pole Zero
Representation

22. Contin...

23. Contin...

24. Contin...

25. Problem 2:
Pole Zero
Representation

26. Contin...

27. Contin...

28. Contin...

29. Summary

30. How poles and Zeros affects H(Z)? Why do we
need to calculate this for a system?
• Zeros makes the H(Z) to go to Zero
• Poles makes the H(Z) to go to infinity
• If you want to Block certain input at the output side, then
make the H(Z) to Zero
• If you want to make certain input to get highest amplitude or
highest system response , then make the H(Z) to Infinity.
• Poles are the representatives for passing certain values
• Zeros are the representatives for rejecting certain values
• Poles and zeros can take real or imaginary values
• Poles and zeros depends on both radius and angle/phase