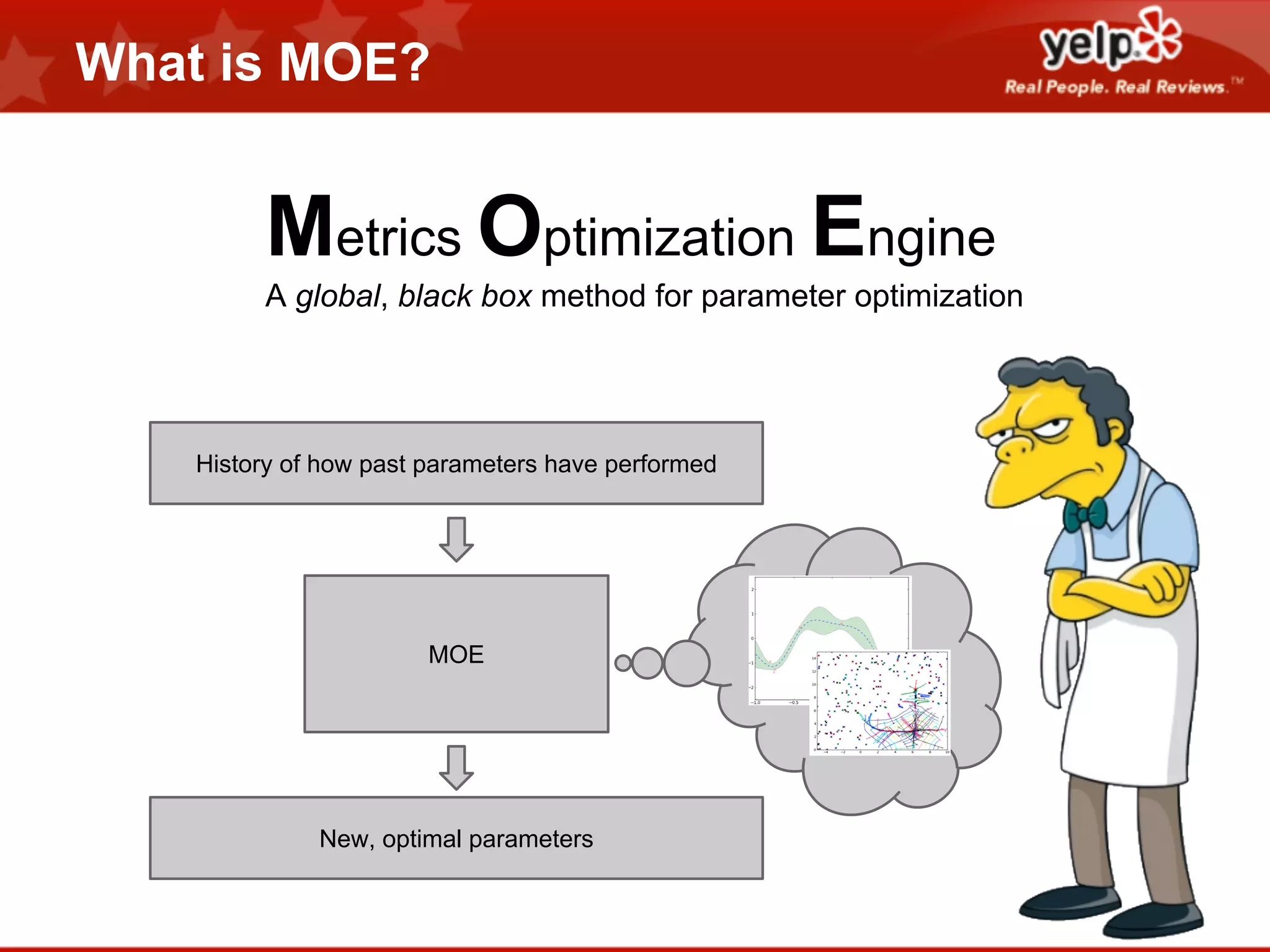
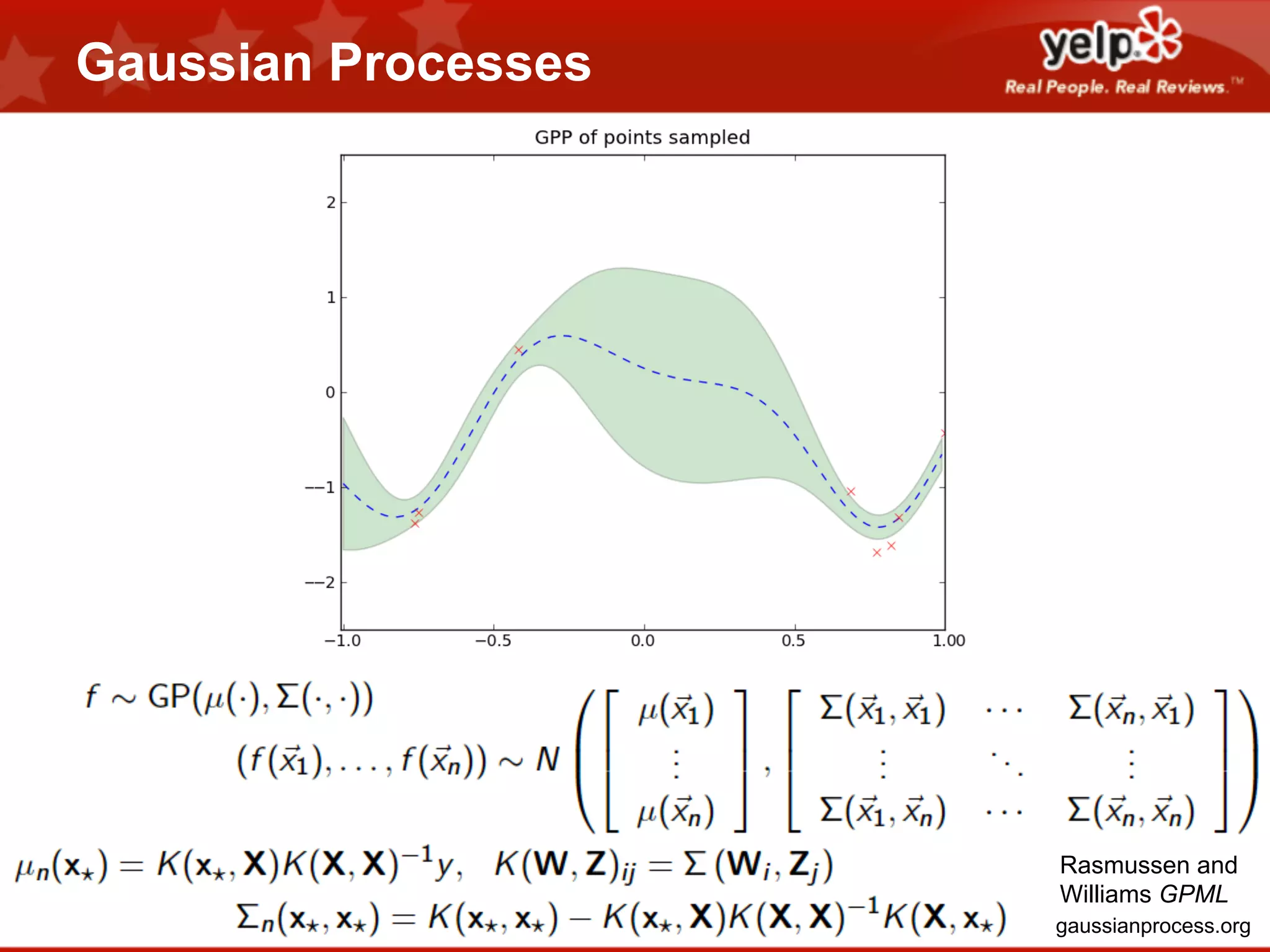
Scott Clark gave a presentation on optimal learning techniques. He discussed multi-armed bandits, which address the challenge of collecting information efficiently from multiple options with unknown outcomes. He provided an example of exploring various slot machines to maximize rewards. Clark also discussed Bayesian global optimization and Yelp's Metrics Optimization Engine (MOE), which uses Gaussian processes to suggest optimal parameters for A/B tests based on past experiment results, in order to efficiently optimize metrics. MOE is now being used in Yelp's live experiments to continuously improve performance.

1. Optimal Learning
for Fun and Profit
Scott Clark, Ph.D.
Yelp Open House
11/20/13
sclark@yelp.com
@DrScottClark

2. Outline of Talk
● Optimal Learning
○ What is it?
○ Why do we care?
● Multi-armed bandits
○ Definition and motivation
○ Examples
● Bayesian global optimization
○ Optimal experiment design
○ Uses to extend traditional A/B testing

3. What is optimal learning?
Optimal learning addresses the challenge of
how to collect information as efficiently as
possible, primarily for settings where
collecting information is time consuming
and expensive.
Source: optimallearning.princeton.edu

4. Part I:
Multi-Armed Bandits

5. What are multi-armed bandits?
THE SETUP
●
●
●
●
Imagine you are in front of K slot machines.
Each one is set to "free play" (but you can still win $$$)
Each has a possibly different, unknown payout rate
You have a fixed amount of time to maximize payout
GO!

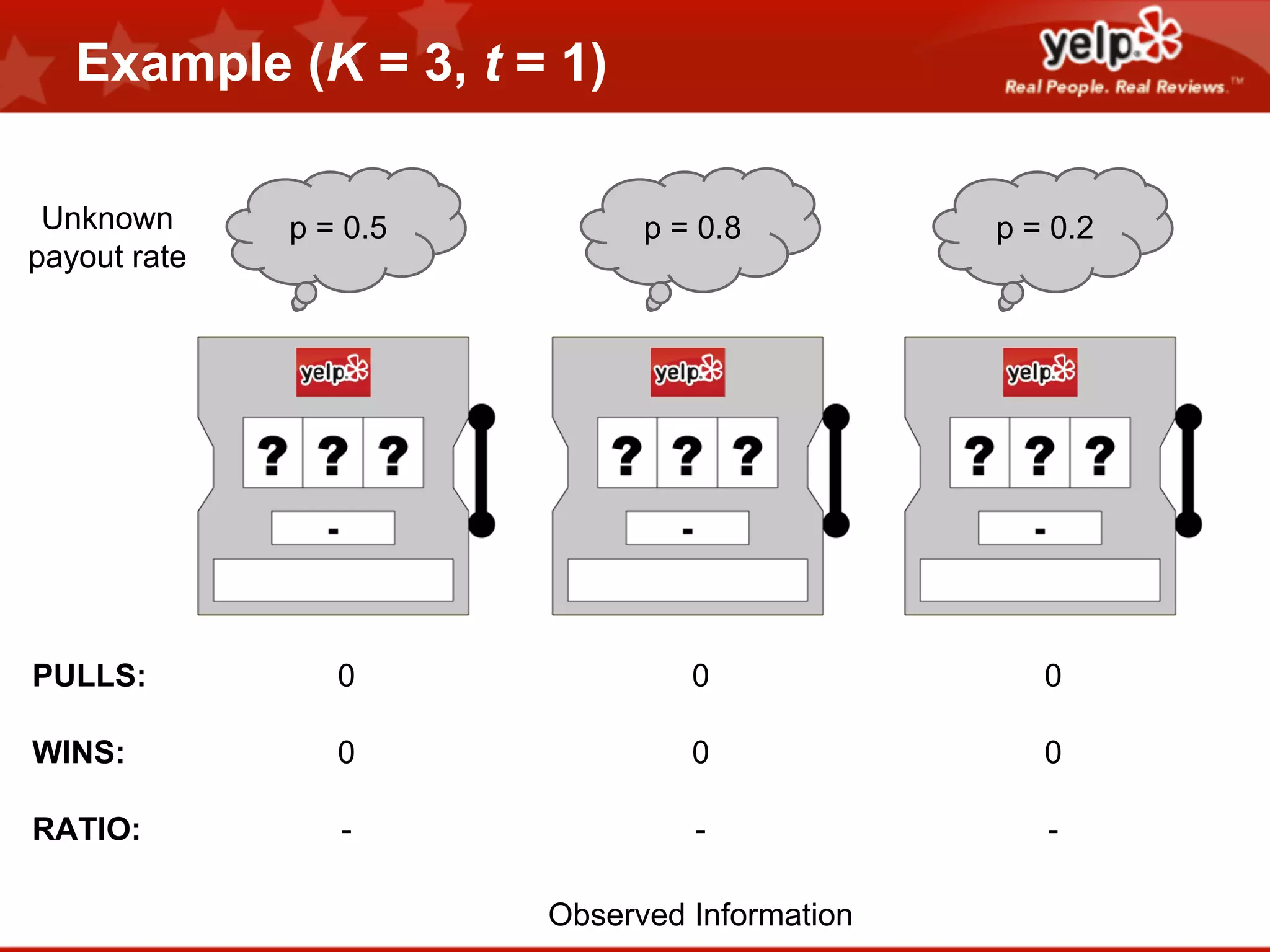
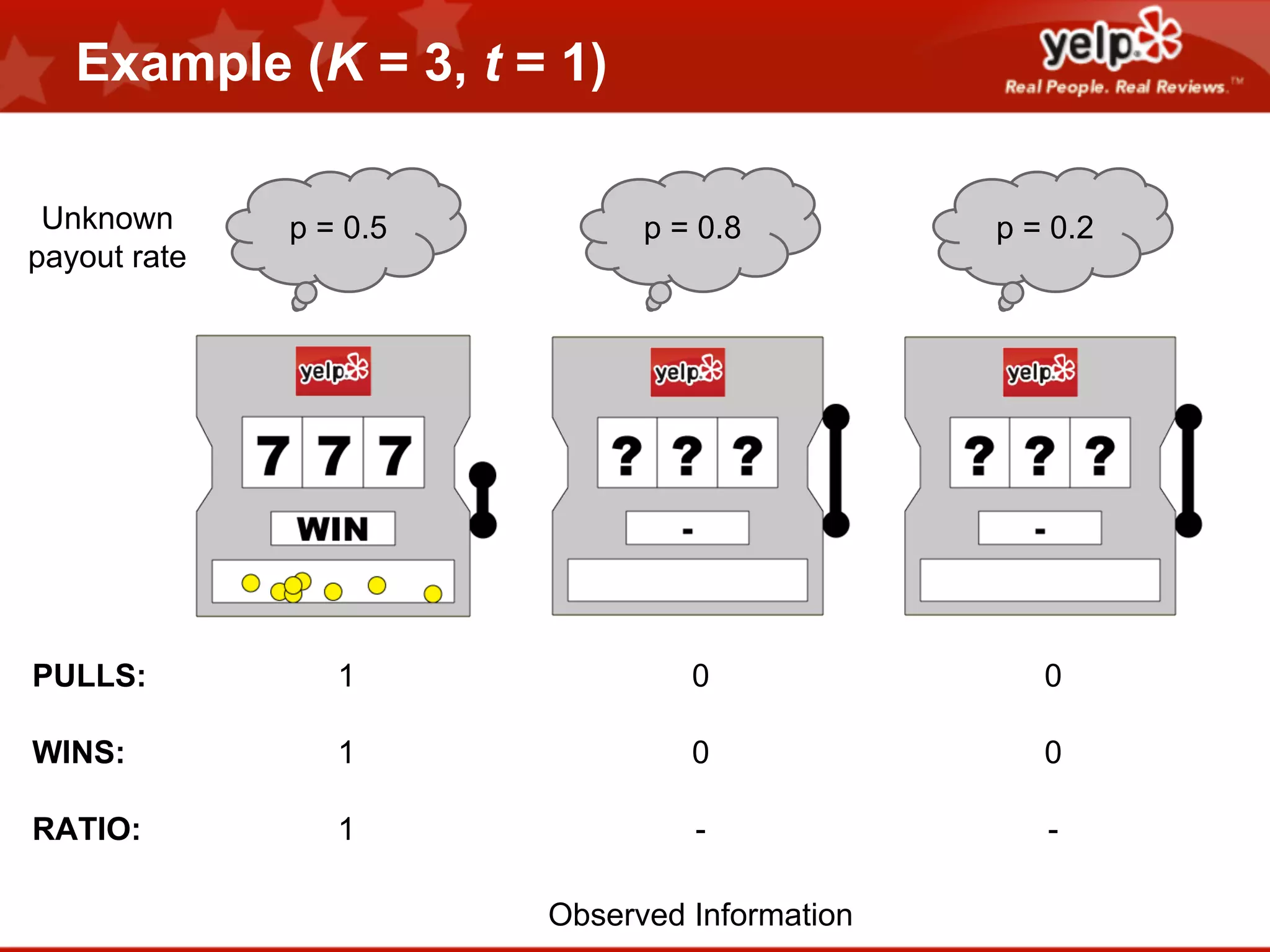
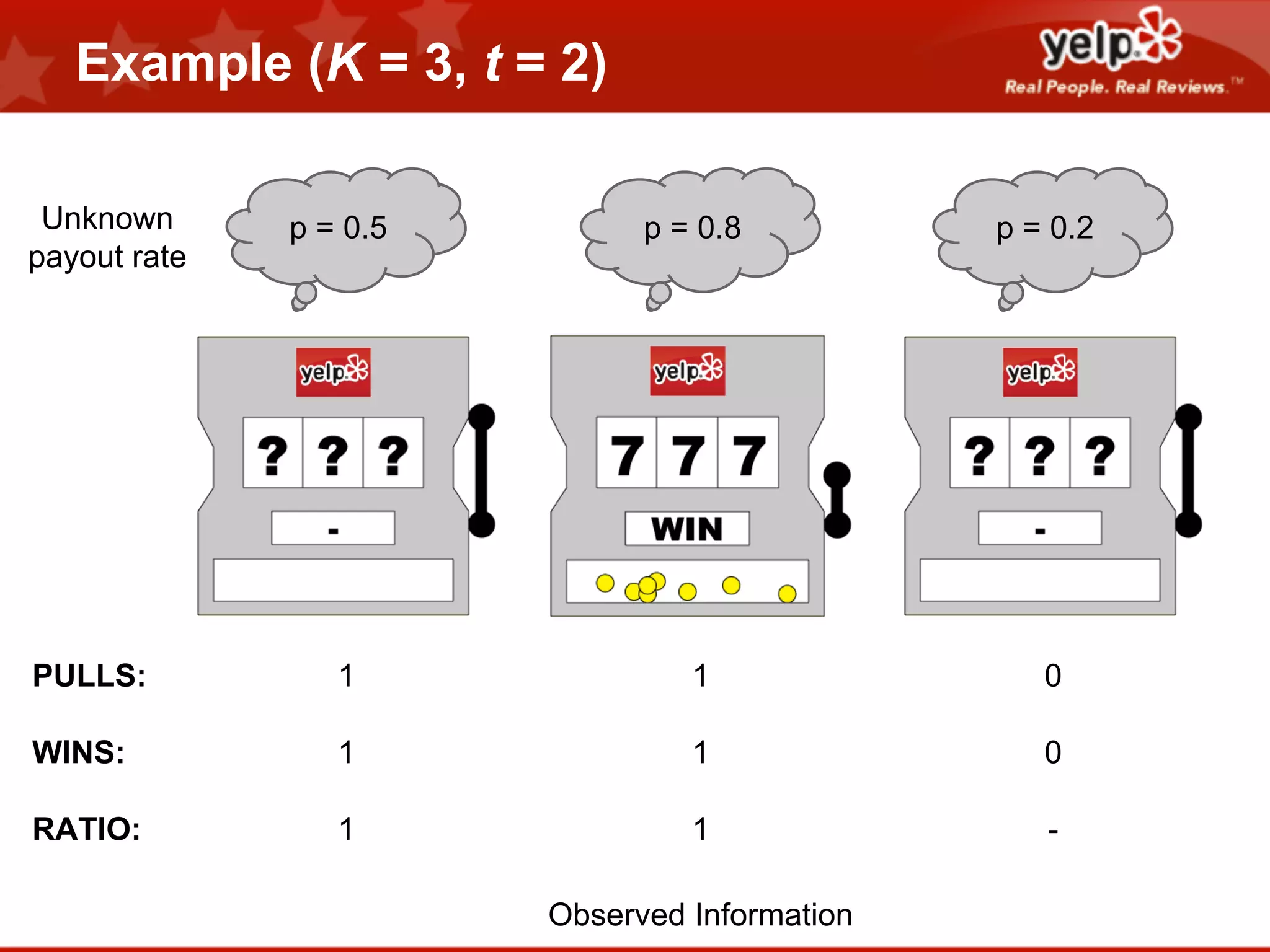
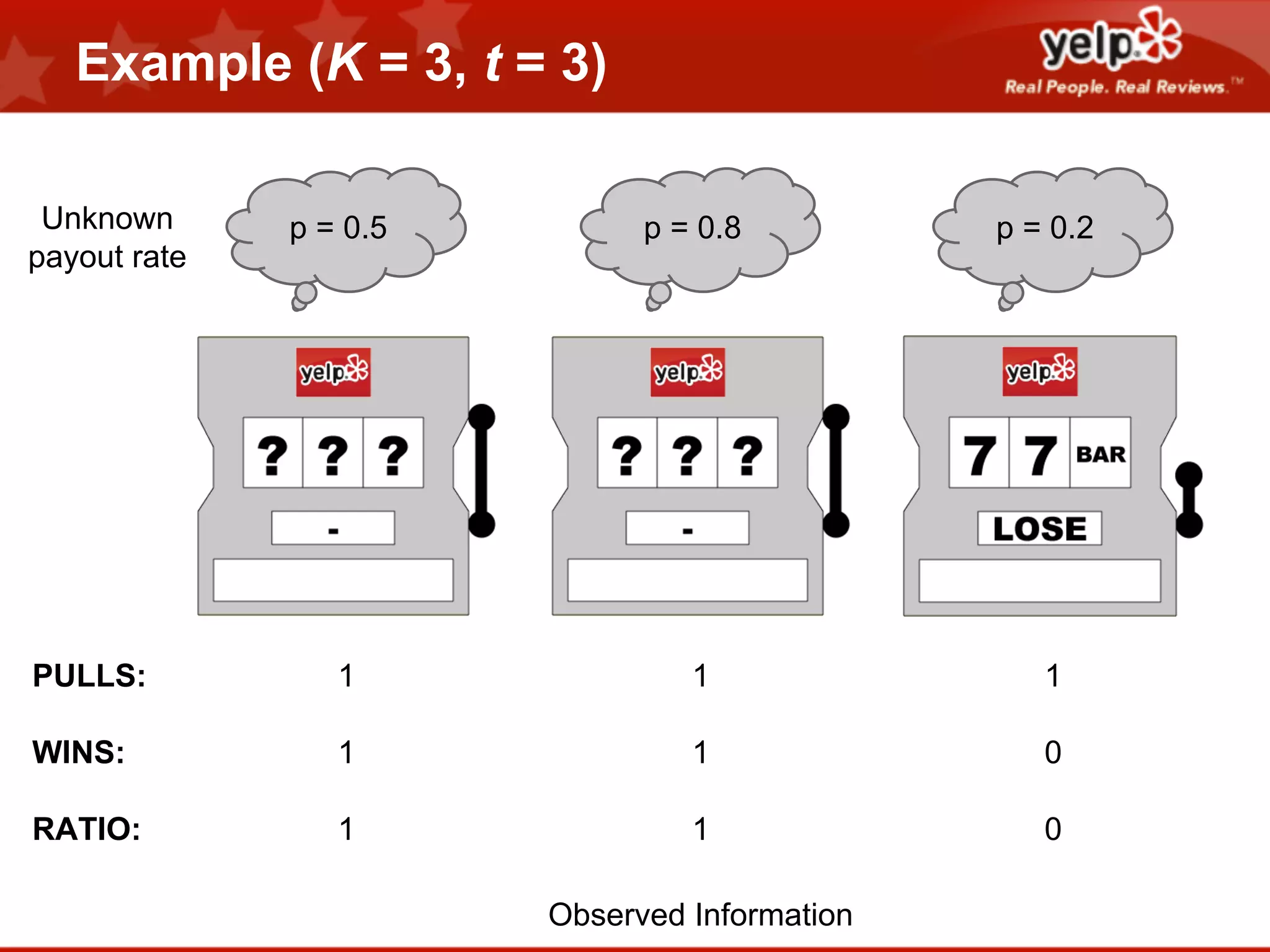
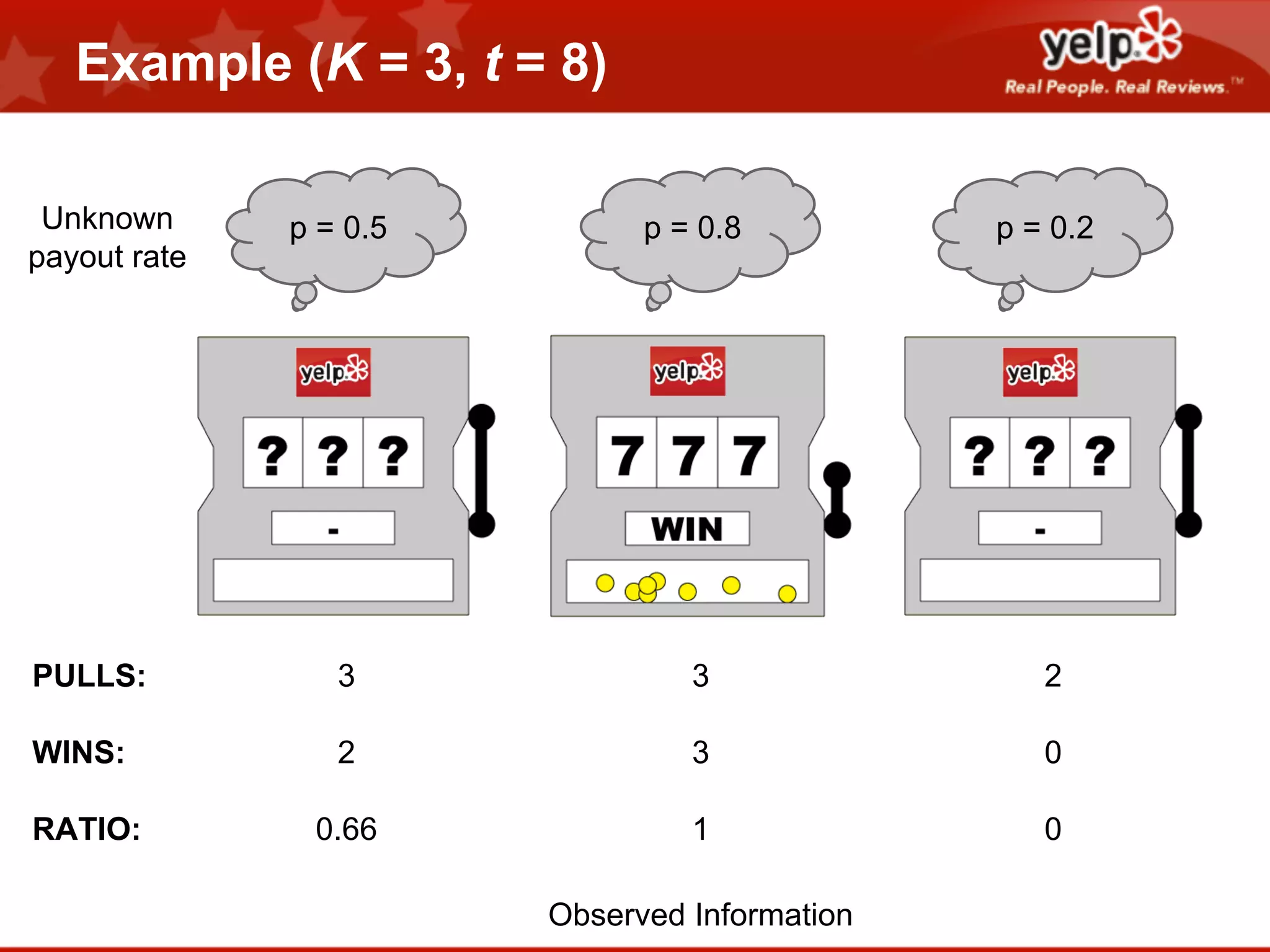
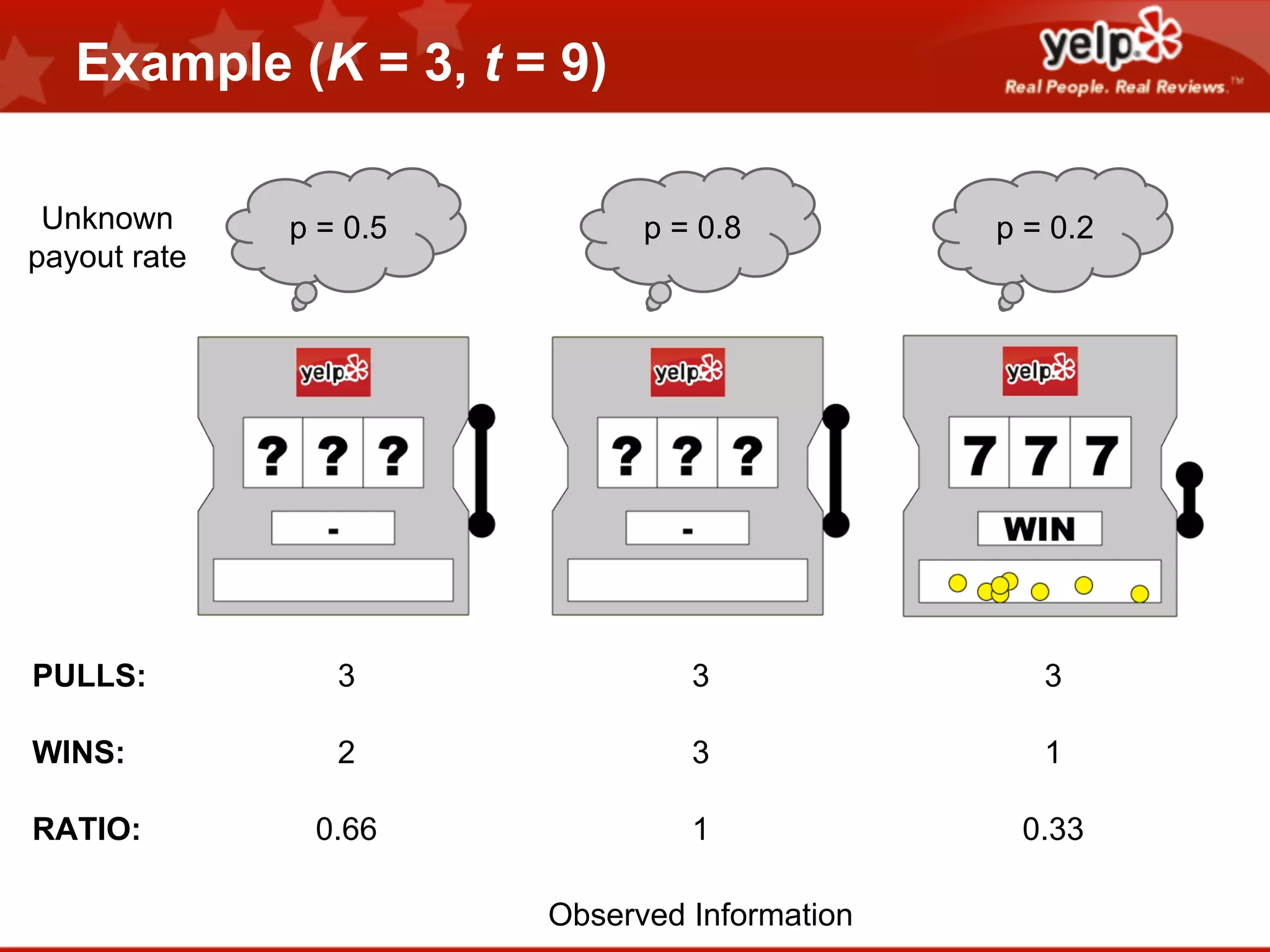
6. What are multi-armed bandits?
THE SETUP
(math version)
[Robbins 1952]

7. Modern Bandits
Why do we care?
● Maps well onto Click Through Rate (CTR)
○ Each arm is an ad or search result
○ Each click is a success
○ Want to maximize clicks
● Can be used in experiments (A/B testing)
○ Want to find the best solutions, fast
○ Want to limit how often bad solutions are used

8. Tradeoffs
Exploration vs. Exploitation
Gaining knowledge about the system
vs.
Getting largest payout with current knowledge

9. Naive Example
Epsilon First Policy
● Sample sequentially εT < T times
○ only explore
● Pick the best and sample for t = εT+1, ..., T
○ only exploit

10. Example (K = 3, t = 1)
Unknown
payout rate
p = 0.5
p = 0.8
p = 0.2
PULLS:
0
0
0
WINS:
0
0
0
RATIO:
-
-
-
Observed Information

11. Example (K = 3, t = 1)
Unknown
payout rate
p = 0.5
p = 0.8
p = 0.2
PULLS:
1
0
0
WINS:
1
0
0
RATIO:
1
-
-
Observed Information

12. Example (K = 3, t = 2)
Unknown
payout rate
p = 0.5
p = 0.8
p = 0.2
PULLS:
1
1
0
WINS:
1
1
0
RATIO:
1
1
-
Observed Information

13. Example (K = 3, t = 3)
Unknown
payout rate
p = 0.5
p = 0.8
p = 0.2
PULLS:
1
1
1
WINS:
1
1
0
RATIO:
1
1
0
Observed Information

14. Example (K = 3, t = 4)
Unknown
payout rate
p = 0.5
p = 0.8
p = 0.2
PULLS:
2
1
1
WINS:
1
1
0
RATIO:
0.5
1
0
Observed Information

15. Example (K = 3, t = 5)
Unknown
payout rate
p = 0.5
p = 0.8
p = 0.2
PULLS:
2
2
1
WINS:
1
2
0
RATIO:
0.5
1
0
Observed Information

16. Example (K = 3, t = 6)
Unknown
payout rate
p = 0.5
p = 0.8
p = 0.2
PULLS:
2
2
2
WINS:
1
2
0
RATIO:
0.5
1
0
Observed Information

17. Example (K = 3, t = 7)
Unknown
payout rate
p = 0.5
p = 0.8
p = 0.2
PULLS:
3
2
2
WINS:
2
2
2
RATIO:
0.66
1
0
Observed Information

18. Example (K = 3, t = 8)
Unknown
payout rate
p = 0.5
p = 0.8
p = 0.2
PULLS:
3
3
2
WINS:
2
3
0
RATIO:
0.66
1
0
Observed Information

19. Example (K = 3, t = 9)
Unknown
payout rate
p = 0.5
p = 0.8
p = 0.2
PULLS:
3
3
3
WINS:
2
3
1
RATIO:
0.66
1
0.33
Observed Information

20. Example (K = 3, t > 9)
Exploit!
Profit!
Right?

21. What if our ratio is a poor approx?
Unknown
payout rate
p = 0.5
p = 0.8
p = 0.2
PULLS:
3
3
3
WINS:
2
3
1
RATIO:
0.66
1
0.33
Observed Information

22. What if our ratio is a poor approx?
Unknown
payout rate
p = 0.9
p = 0.5
p = 0.5
PULLS:
3
3
3
WINS:
2
3
1
RATIO:
0.66
1
0.33
Observed Information

23. Fixed exploration fails
Regret is unbounded!
Amount of exploration
needs to depend on data
We need better policies!

24. What should we do?
Many different policies
● Weighted random choice (another naive approach)
● Epsilon-greedy
○ Best arm so far with P=1-ε, random otherwise
● Epsilon-decreasing*
○ Best arm so far with P=1-(ε * exp(-rt)), random otherwise
● UCB-exp*
● UCB-tuned*
● BLA*
● SoftMax*
● etc, etc, etc (60+ years of research)
*Regret bounded as t->infinity

25. Extensions and complications
What if...
● Hardware constraints limit real-time knowledge? (batching)
● Payoff noisy? Non-binary? Changes in time? (dynamic content)
● Parallel sampling? (many concurrent users)
● Arms expire? (events, news stories, etc)
● You have knowledge of the user? (logged in, contextual history)
● The number of arms increases? Continuous? (parameter search)
Every problem is different.
This is an active area of research.

26. Part II:
Global Optimization

27. What is global optimization?
THE GOAL
●
●
●
Optimize some objective function
○ CTR, revenue, delivery time, or some combination thereof
given some parameters
○ config values, cuttoffs, ML parameters
CTR = f(parameters)
○ Find best parameters
(more mathy version)

28. What is MOE?
Metrics Optimization Engine
A global, black box method for parameter optimization
History of how past parameters have performed
MOE
New, optimal parameters

29. What does MOE do?
● MOE optimizes a metric (like CTR) given some
parameters as inputs (like scoring weights)
● Given the past performance of different parameters
MOE suggests new, optimal parameters to test
MOE
Results of A/B
tests run so far
New, optimal
values to A/B test

30. Example Experiment
Biz details distance in ad
●
●
Setting a different distance cutoff for each category
to show “X miles away” text in biz_details ad
For each category we define a maximum distance
Parameters + Obj Func
distance_cutoffs = {
‘shopping’: 20.0,
‘food’: 14.0,
‘auto’: 15.0,
…
}
objective_function = {
‘value’: 0.012,
‘std’: 0.00013
}
MOE
MapReduce, MongoDB, python
New Parameters
distance_cutoffs = {
‘shopping’: 22.1,
‘food’: 7.3,
‘auto’: 12.6,
…
}

31. Why do we need MOE?
● Parameter optimization is hard
○ Finding the perfect set of parameters takes a long time
○ Hope it is well behaved and try to move in the right direction
○ Not possible as number of parameters increases
● Intractable to find best set of parameters in all situations
○ Thousands of combinations of program type, flow, category
○ Finding the best parameters manually is impossible
● Heuristics quickly break down in the real world
○ Dependent parameters (changes to one change all others)
○ Many parameters at once (location, category, map, place, ...)
○ Non-linear (complexity and chaos break assumptions)
MOE solves all of these problems in an optimal way

32. How does it work?
MOE
1. Build Gaussian Process (GP)
with points sampled so far
2. Optimize covariance
hyperparameters of GP
3. Find point(s) of highest
Expected Improvement
within parameter domain
4. Return optimal next best
point(s) to sample

33. Gaussian Processes
Rasmussen and
Williams GPML
gaussianprocess.org

34. Optimizing Covariance Hyperparameters
Finding the GP model that fits best
●
All of these GPs are created with the same initial data
○ with different hyperparameters (length scales)
●
Need to find the model that is most likely given the data
○ Maximum likelihood, cross validation, priors, etc
Rasmussen and Williams Gaussian Processes for Machine Learning

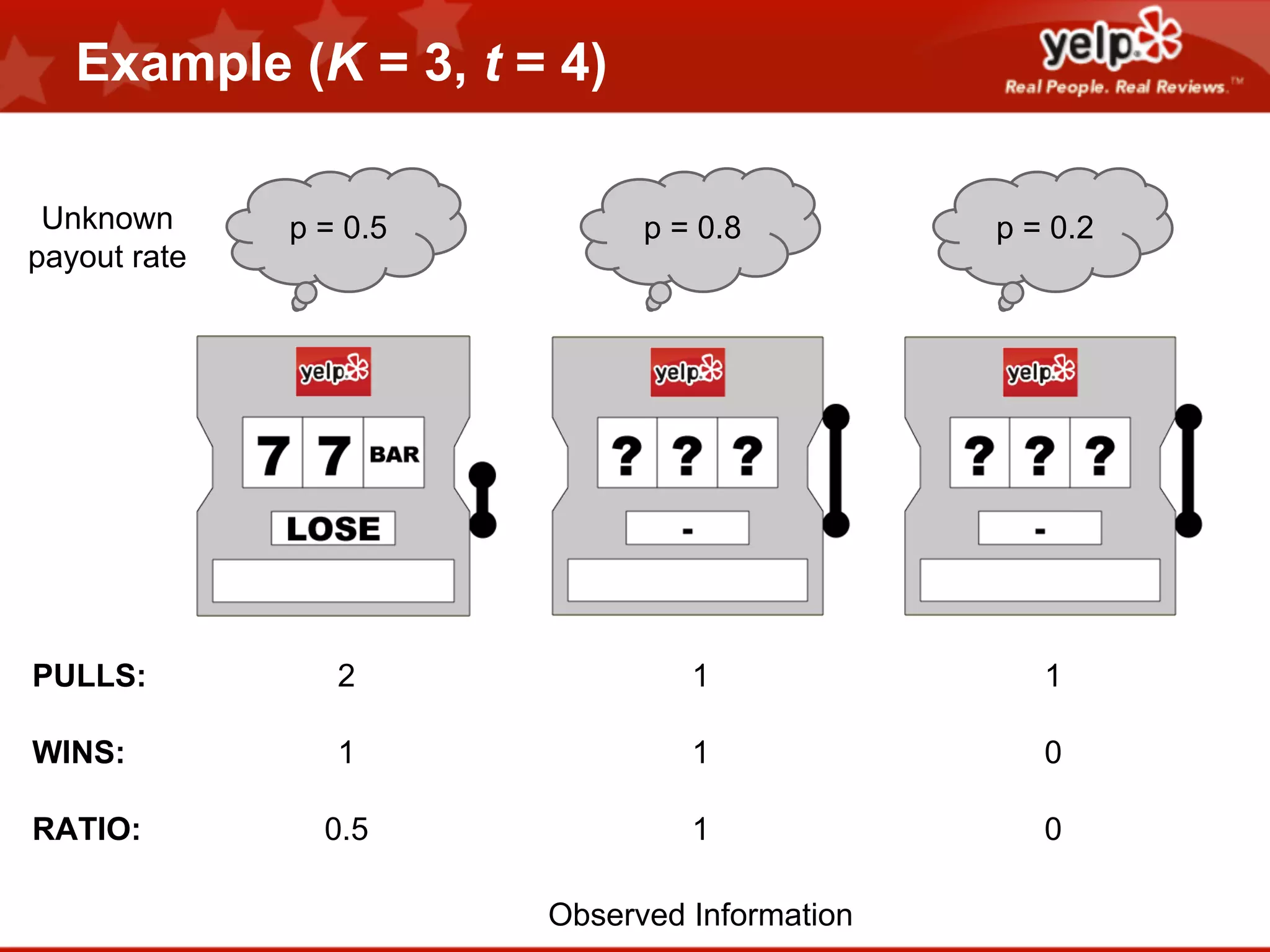
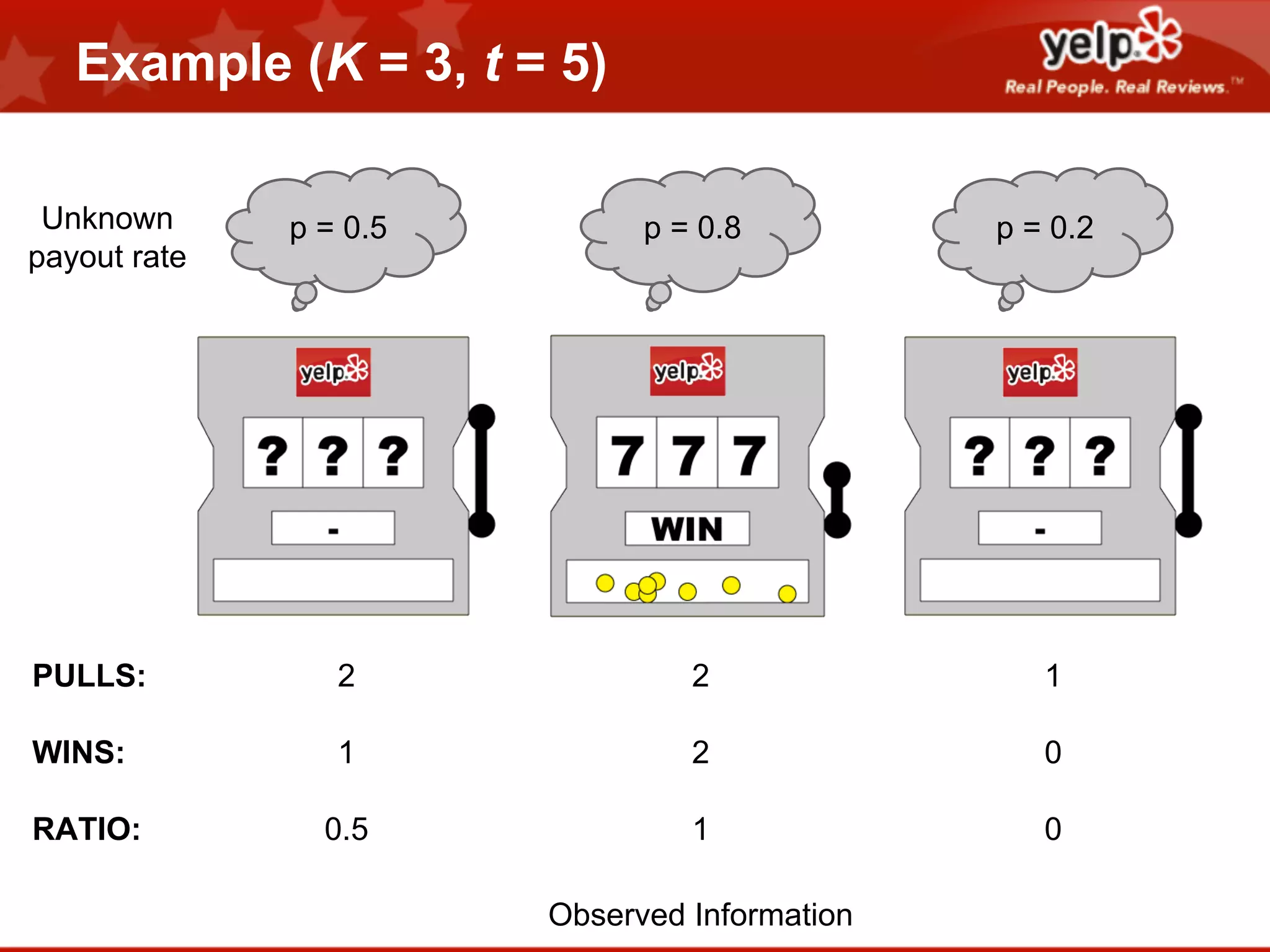
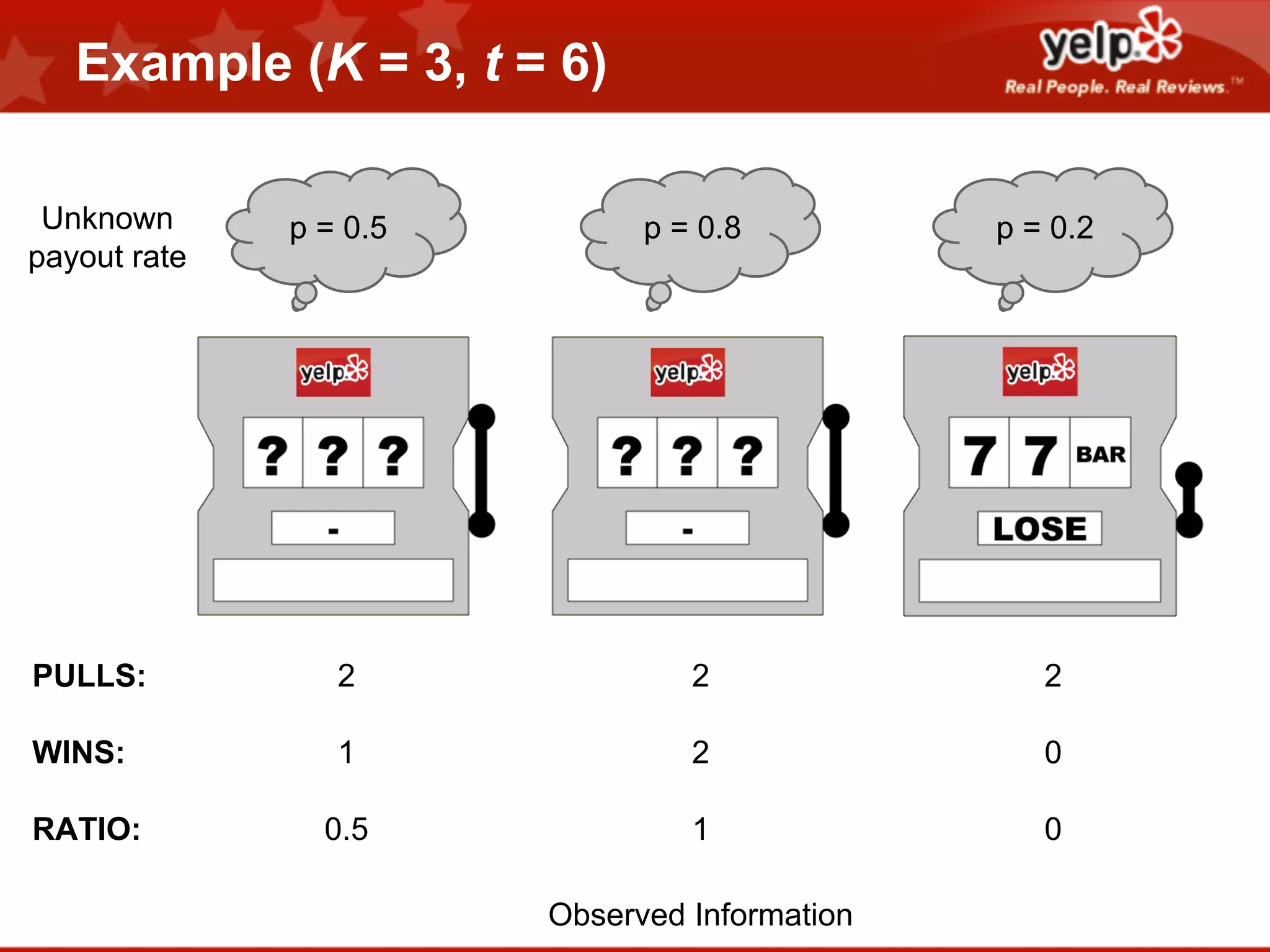
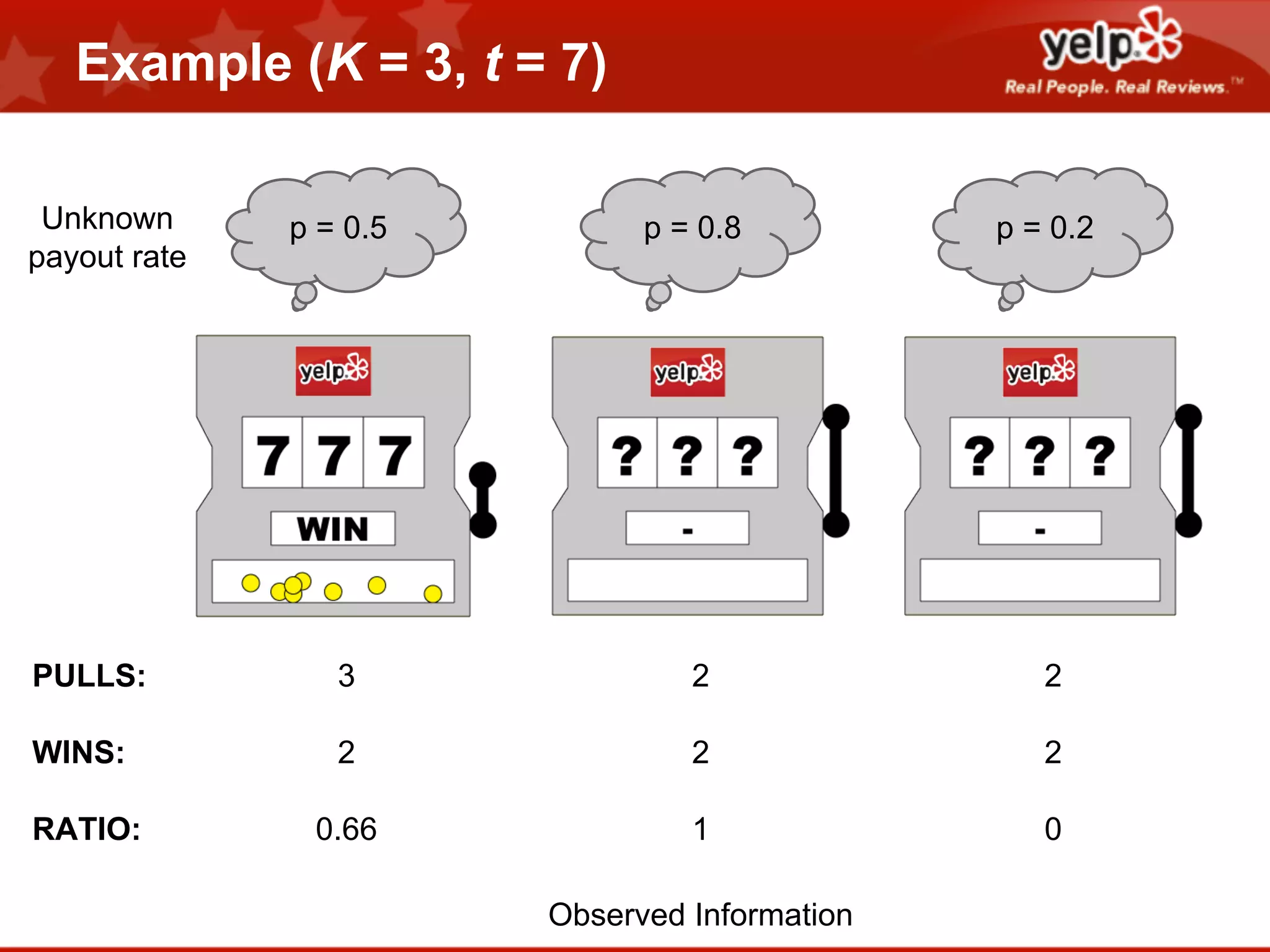
35. Find point(s) of highest expected improvement
Expected Improvement of sampling two points
We want to find the point(s) that are expected to beat the best point seen so far the most.
[Jones, Schonlau, Welsch 1998]
[Clark, Frazier 2012]

36. What is MOE doing right now?
MOE is now live in production
● MOE is informing active experiments
● MOE is successfully optimizing towards all given metrics
● MOE treats the underlying system it is optimizing as a black box,
allowing it to be easily extended to any system
Ongoing:
● Looking into best path towards contributing it back to the
community, if/when we decide to open source.
● MOE + bandits = <3

37. Questions?
Questions?
sclark@yelp.com
@DrScottClark