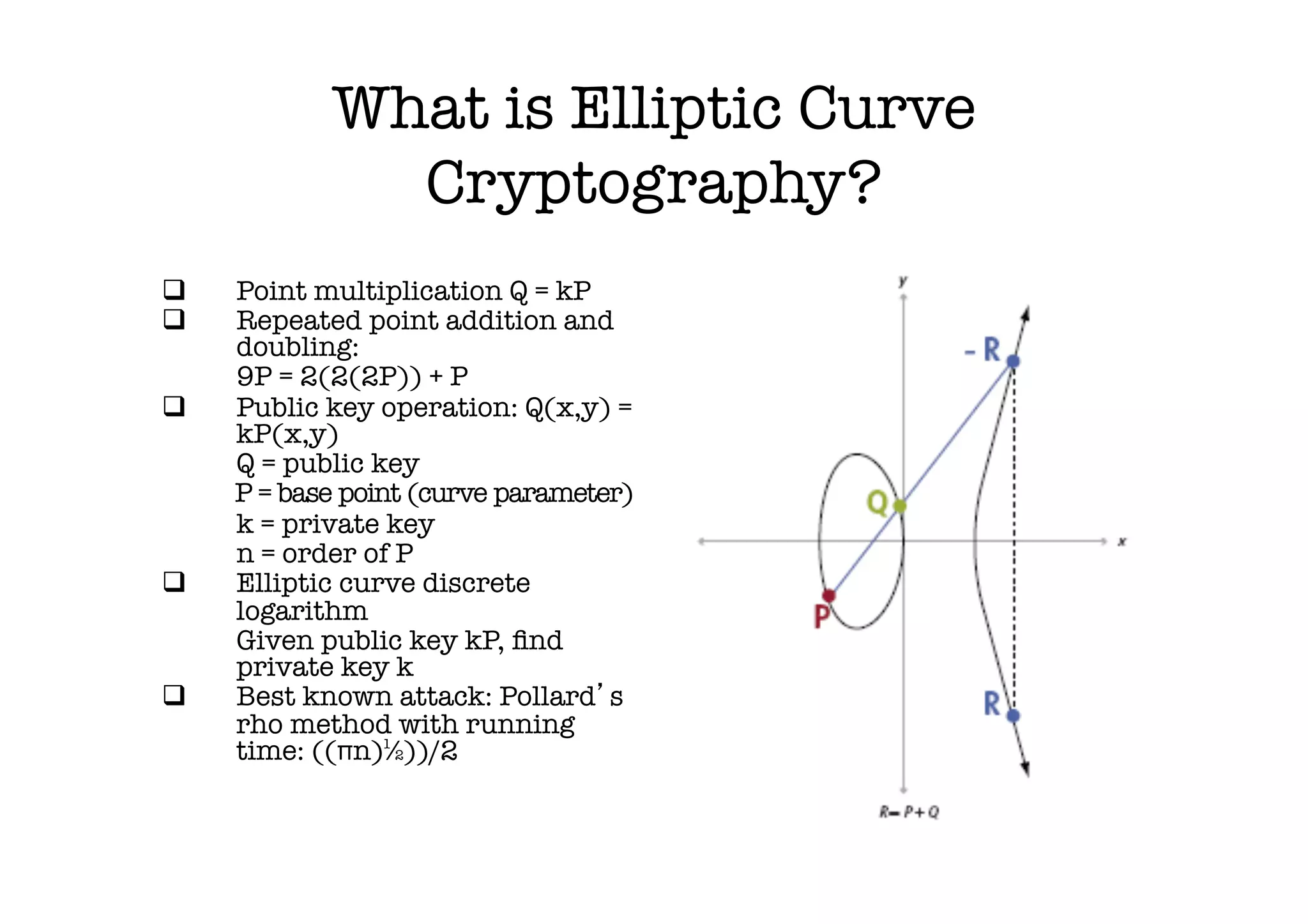
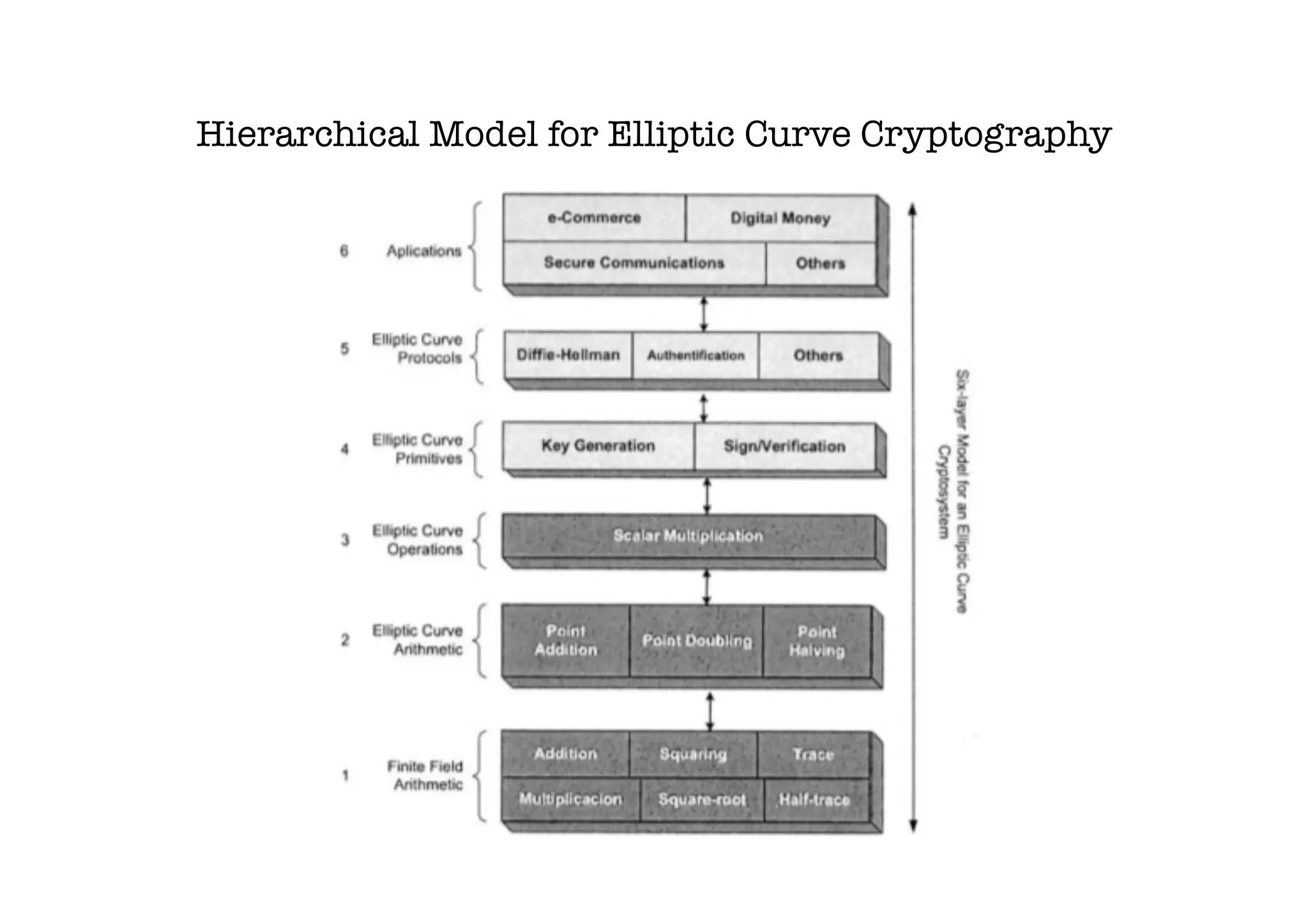
The document discusses the need for a PhD student to learn advanced mathematics for research into implementing elliptic curve cryptography on constrained devices. The research aims to develop efficient and secure implementations of elliptic curve cryptography algorithms for tiny spaces around 1mm2. This requires knowledge of number theory, finite fields, algebra, groups, rings, fields, polynomials and their properties to understand elliptic curve cryptography and implement the algorithms securely while targeting constrained devices. The student hopes to improve architectures, develop configurable ECC modules, and create efficient software and hardware implementations to measure the security, efficiency and performance of different approaches.

1. Why I need to learn so much
math for my PhD research
Marisa W. Paryasto
School of Electrical Engineering and
Informatics
ITB
July 23rd, 2009

2. My Research
q Title: Elliptic Curve Cryptography
Algorithm Implementation and
Design for Constrained Devices
q Target: Make it fits constrained
devices [constrained devices = some
tiny little spaces about 1mm2]

3. Math Foundation needed
q Number Theory
q Finite Fields
q Algebra
⣄ Basic Properties
⣄ Groups
⣄ Field Extensions
⣄ Rings
⣄ Roots of
⣄ Fields
Irreducible
Polynomials
⣄ Polynomial
⣄ Bases of Finite
Fields
⣄ Finite Fields GF
(2m)

4. What is Elliptic Curve
Cryptography?
q Point multiplication Q = kP
q Repeated point addition and
doubling:
9P = 2(2(2P)) + P
q Public key operation: Q(x,y) =
kP(x,y)
Q = public key
P = base point (curve parameter)
k = private key
n = order of P
q Elliptic curve discrete
logarithm
Given public key kP, find
private key k
q Best known attack: Pollard s
rho method with running
time: ((πn)½))/2

5. Hierarchical Model for Elliptic Curve Cryptography

6. Research Questions
q Implementing ECC is not simple.
Especially in constrained devices.
q How do you know that it s secure and
being implemented securely?

7. More problems
q There is no guide yet for
implementing ECC efficiently
q There is no tools to predict certain
configurations of ECC and its level of
security

8. Hypothesis
q There is exist some (generic)
algorithm to implement ECC.
q Different implementation algorithms
determine different level of security.
(Notes: metric of security?)

9. Methods (to solve the problems)
q
Improve an architecture to be
resistance against side channel
attacks
⣄ Asynchronous circuits implementation
q Develop a configurable, integrated
ECC modules (to measure security/
efficiency/space/speed)

10. Contribution
Efficient
software Attack of ECC
Hardware
implementati hardware
Efficient implementati
on of ECC/ implementati
implementati on of ECC on
Reconfigurabl on on
on of ECC
constrained
e ECC constrained
devices
implementati device
on
basis various
smart attack
conversion
library
circuit
algorithm
synthesis
math
software
hardware
math / foundation