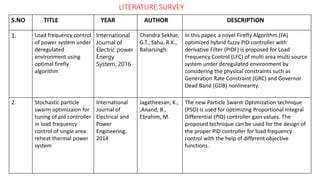
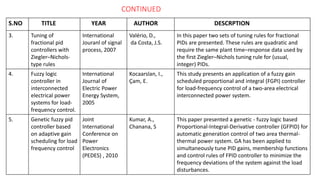
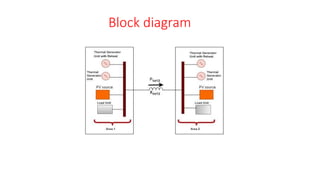
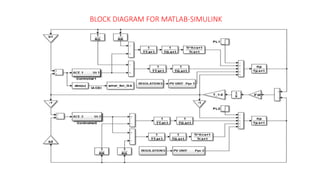
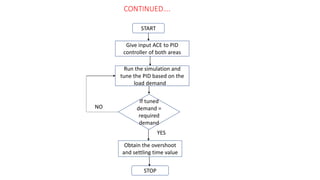
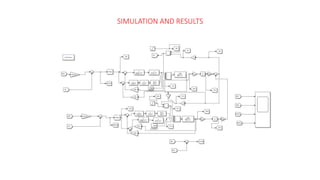
This document presents a study on load frequency control (LFC) for a two-area interconnected power system incorporating a photovoltaic solar power plant. The proposed PID controller achieves improved performance with low overshoot and short settling time, as validated through MATLAB-Simulink simulations. The results indicate beneficial operating characteristics for systems that utilize solar power, suggesting the PID controller's effectiveness in maintaining frequency stability.

1. PRESENTED BY,
M.NIVEDHA(91762225001)
M.E-I YEAR(PED)
DEPT OF EEE,
ACGCET,KARAIKUDI.
ALAGAPPA CHETTIAR GOVERNMENT COLLEGE OF
ENGINEERING& TECHNOLOGY
(An Autonomous Institution affiliated to Anna University, Chennai)
Karaikudi-630 003.
UNDER THE GUIDANCE OF,
DR.K.BASKARAN,
PROFESSOR AND HEAD,
DEPT OF EEE,
ACGCET,KARAIKUDI.

2. CONTENTS
• Abstract
• Literature survey
• Introduction
• Block Diagram
• Two area interconnected power system
• Controller used
• Block diagram of MATLAB-Simulink
• Working
• Simulation and results
• Conclusion
• Reference

3. ABSTRACT
• In this study, in order to solve the LFC problem, control method was applied to a
two area interconnected power system.
• A photovoltaic solar power plant (PV-SPP) was also connected, in order to identify
the harmful effects on the frequency of the system.
• The control method exhibited a better performance because of the low overshoot
and short settling time.

4. LITERATURE SURVEY
S.NO TITLE YEAR AUTHOR DESCRIPTION
1. Load frequency control
of power system under
deregulated
environment using
optimal firefly
algorithm
International
Journal of
Electric power
Energy
System, 2016
Chandra Sekhar,
G.T., Sahu, R.K.,
Baliarsingh.
In this paper, a novel Firefly Algorithm (FA)
optimized hybrid fuzzy PID controller with
derivative Filter (PIDF) is proposed for Load
Frequency Control (LFC) of multi area multi source
system under deregulated environment by
considering the physical constraints such as
Generation Rate Constraint (GRC) and Governor
Dead Band (GDB) nonlinearity.
2. Stochastic particle
swarm optimizaion for
tuning of pid controller
in load frequency
control of single area
reheat thermal power
system
International
Journal of
Electrical and
Power
Engineering,
2014
Jagatheesan, K.;
,Anand, B.,
Ebrahim, M.
The new Particle Swarm Optimization technique
(PSO) is used for optimizing Proportional Integral
Differential (PID) controller gain values. The
proposed technique can be used for the design of
the proper PID controller for load frequency
control with the help of different objective
functions.

5. CONTINUED
S.NO TITLE YEAR AUTHOR DESCRPTION
3. Tuning of
fractional pid
controllers with
Ziegler–Nichols-
type rules
International
Jouranl of signal
process, 2007
Valério, D.,
da Costa, J.S.
In this paper two sets of tuning rules for fractional
PIDs are presented. These rules are quadratic and
require the same plant time–response data used by
the first Ziegler–Nichols tuning rule for (usual,
integer) PIDs.
4. Fuzzy logic
controller in
interconnected
electrical power
systems for load-
frequency control.
International
Journal of
Electric Power
Energy System,
2005
Kocaarslan, I.,
Çam, E.
This study presents an application of a fuzzy gain
scheduled proportional and integral (FGPI) controller
for load-frequency control of a two-area electrical
interconnected power system.
5. Genetic fuzzy pid
controller based
on adaptive gain
scheduling for load
frequency control
Joint
International
Conference on
Power
Electronics
(PEDES) , 2010
Kumar, A.,
Chanana, S
This paper presented a genetic - fuzzy logic based
Proportional-Integral-Derivative controller (GFPID) for
automatic generation control of two area thermal-
thermal power system. GA has been applied to
simultaneously tune PID gains, membership functions
and control rules of FPID controller to minimize the
frequency deviations of the system against the load
disturbances.

6. INTRODUCTION
• In the case of large frequency or voltage changes, the network is in danger of
collapse. One way to eradicate this kind of problem is through load frequency control
(LFC).
• In particular, it is quite difficult to stabilize the frequency in each area, because of the
increase of the multi area.
• The most common control strategy for such systems is the PID controller.

7. Block diagram

8. TWO AREA INTERCONNECTED POWER SYSTEM
• In this study, a two area three source interconnected renewable energy power system
was modelled, which is shown in the block diagram.
• A Thermal Unit (TU), a Thermal generator unit with a Reheat Unit (RTU), and a PV-unit
were connected to the system as energy resources.
• Since the use of PV-units in grids has gradually increased in the last few years, a PV-unit
was incorporated into the system.

9. CONTROLLER USED
PID Controller
• Proportional-integral-derivative (PID) control method was preferred for load-frequency
control in power systems.
• In this study, a PID control has been applied to the system and is simulated by MATLAB-
Simulink.
• The output power of PV-unit was modelled to take into account climatic conditions.
• The LFC was achieved when the power obtained from the PV-unit changed.

10. CONTINUED….
• The outputs are the generator frequency Δf and area control error (ACE) given by below
equation,
ACE = B Δ f + ΔPtie ,
• The error input to the controllers is the respective ACE given by,
𝑒1 (𝑡) = 𝐴𝐸𝐶1 = 𝐵1∆𝑓1 + ∆𝑃t𝑖𝑒
𝑒2 (𝑡) = 𝐴𝐸𝐶2 = 𝐵2∆𝑓2 −∆𝑃t𝑖𝑒
• The Ziegler-Nichols (ZN) method is used for calculating the optimum values of the
parameters of the PID controller.
• “Ku” is defined as the constant value of oscillation of the system and “Tu” is the oscillation
frequency. Their formulas are given in Table below

11. CONTINUED….
CONTROLLER Kp Ki Kd
PID 3×𝐾𝑢
5
6×𝐾𝑢
5×𝑇𝑢
3×𝐾𝑢×𝑇𝑢
40
ZN method of detection parameters

12. BLOCK DIAGRAM FOR MATLAB-SIMULINK

13. CONTINUED….
START
Give input ACE to PID
controller of both areas
Run the simulation and
tune the PID based on the
load demand R
If tuned
demand =
required
demand
Obtain the overshoot
and settling time value
STOP
YES
NO

14. Continued….
Parameters of two-area power system with PV-unit
• B1, B2: 0.425 pu TR: 10
• RG: 2.43 Hz/pu KR: 0.3
• RR: 2.43 Hz/pu KP: 120
• TG: 0.3 TP: 20
• TT: 0.08 Tc : 20 C
• e: 1.6021917 10^-19 (C) T1-2: 0.086
• k: 1.380622 10^-23 (J/K) I0: 0.0002 (A)
• A: 100 Rs : 0.0001 (W)
• NS: 10 Iph : ISC: 5 (A)
• NP: 7 Sc : 100

15. WORKING
• Stable operation of power system requires matching between total load generation with total load
demand and system losses.
• Due to rising and failing of load demand, the real and reactive power balance is disturbed.
• This results in deviation of system frequency and tie-line interchange power from their scheduled
value.
• High deviation of system frequency may lead to system collapse.

16. CONTINUED….
• Load frequency control is one of the major requirements in providing reliable and quality
operation in multi-area power systems.
• LFC is continuously monitoring the system frequency and tie-line power and calculate net
changes (known as area control error, ACE).
• Control the value settings of generators so as to keep ACE to its minimum value.

17. SIMULATION AND RESULTS

18. CONTINUED….
• In this study, a PV-unit was added to the two area multi source interconnected power system.
• The LFC of the system was carried out to perform the PID controller.
• The results obtained by the PID controller for area 1 is settling time of 16.1 s and overshoot
value of -0.0044 Pu as indicated in table below.
• When the situation at the 5th s is examined for area 2, the settling time value obtained is 11.3
s and the overshoot value is -0.0081 Pu as indicated in table below.

19. CONTINUED….
Changes of ACE1 in the area 1
The detailed display of frequency, ∆F1 change in area 1.

20. CONTINUED….
Design controllers Area 1 Load increase
Overshoots Settling time(s)
Area 2 Load increase
Overshoots Settling time(s)
PID -0.0044 16.1 -0.0081 11.3
The obtained results.

21. CONCLUSION
• In this project, a PID controller was proposed for frequency stability problems in a two area
multi source interconnected power system.
• The systems and controller was designed andsimulated with the MATLAB-Simulink
program.
• Ultimately, since the overshoot values and the settling time values directly affect the
operating lifetimes, operating costs, and efficiencies of the grid, the proposed PID controller
would be beneficial and advisable for an interconnected power system with solar power
sources.
• Because the overshoot and settling time value obtained are low sich as -0.0044 and 16.1s for
area 1 and -0.0081 and -11.3s for area 2.

22. REFERENCE
1. Goksenli, N.; Akbaba, M. Development of a new microcontroller based mppt method for
photovoltaic generators using akbaba model with implementation and simulation. Sol. Energy 2016,
136, 622–628.
2. Chandra Sekhar, G.T.; Sahu, R.K.; Baliarsingh, A.K.; Panda, S. Load frequency control of power
system under deregulated environment using optimal firefly algorithm. Int. J. Electr. Power Energy
Syst. 2016, 74, 195–211.
3. Sahu, B.K.; Pati, T.K.; Nayak, J.R.; Panda, S.; Kar, S.K. A novel hybrid lus–tlbo optimized fuzzy-pid
controller for load frequency control of multi-source power system. Int. J. Electr. Power Energy Syst.
2016, 74, 58–69.
4. Rahmann, C.; Castillo, A. Fast frequency response capability of photovoltaic power plants: The
necessity ofnew grid requirements and definitions. Energies 2014, 7, 6306–6322.
5. Khooban, M.H.; Niknam, T. A new intelligent online fuzzy tuning approach for multi-area load
frequency control: Self adaptive modified bat algorithm. Int. J. Electr. Power Energy Syst. 2015, 71,
254–261.

23. THANK YOU