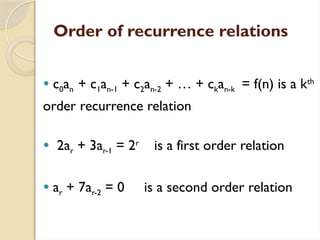
The document explains recurrence relations, focusing on their definitions, methods to find homogeneous and particular solutions, and provides examples to illustrate the concepts. A recurrence relation is defined as a recursive formula for a numeric function, with linear recurrence relations being characterized by constant coefficients. The total solution combines the homogeneous solution obtained from the characteristic equation and a particular solution based on the right-hand side of the relation.

1. Recurrence Relations
Courtesy: Prof. Sheetal Iyer, Comp Dept, SAE, Kondhwa

2. What is recurrence relation ?
Consider Fibonacci series
0 1 1 2 3 5 8 13 ……………….
This is a recursive function.
We can represent it in a numeric function as,
an = an-1 + an-2
This is a recurrence relation

3. Recurrence Relation
 Definition : The recursive formula for
defining the numeric function is called a
recurrence relation.
 A recurrence relation of the form
c0an + c1an-1 + c2an-2 + … + ckan-k = f(n)
for n≥k
where c0 , c1 , c2 , …., ck are constants is
called a linear recurrence relation.

4. Order of recurrence relations
 c0an + c1an-1 + c2an-2 + … + ckan-k = f(n) is a kth
order recurrence relation
 2ar + 3ar-1 = 2r
is a first order relation
 ar + 7ar-2 = 0 is a second order relation

5. Homogeneous Equation
 Every linear recurrence relation is associated
with its homogeneous equation.
 The solution of homogeneous equation is
called homogeneous solution of the given
recurrence relation.
 Homogeneous recurrence relation is obtained
by substituting the right-hand side with zero.
 Thus
c0an + c1an-1 + c2an-2 + … + ckan-k = 0

6. Method to find homogeneous solution of
recurrence relation
 Define the characteristic equation of the
homogeneous equation.
c0αk
+ c1αk-1
+ c2αk-2
+ …. + ck = 0
This is kth
degree polynomial equation. Hence it
has k roots.

7. Method to find homogeneous
solution of recurrence relation
 Suppose α1 , α2 ,….., αk are roots of the
characteristic equation and all roots are
distinct then (Below is generalized form of
homogenous solution of recurrence relation if roots are
different)
an = A1α1
n
+ A2α2
n
+ …… + Akαk
n
Where A1, A2, ….. ,Ak are constants which are
to be determined by initial conditions.

8. Method to find homogeneous
solution of recurrence relation
 If any root is repeated (say α1) m times then
the term A1 α1
n
is replaced by (Below is
generalized form of homogenous solution of
recurrence relation if roots are same)
(A1nm-1
+ A2nm-2
+ ….. + Am-1n + Am) α1
n
Where Ai ‘s are to be calculated using initial
conditions.

9. Example 1
Q . Find the solution of the given recurrence
relation ar – 10ar-1 + 9ar-2 = 0 with initial
conditions a0 = 3 and a1 = 11.
A. Characteristic equation of the given
recurrence relation is
α2
- 10 α +9 = 0
Therefore (α-1)(α-9)=0
Hence α = 1, 9 i.e α1 =1 and α2=9
Thus solution of homogeneous equation is
ar= A11r
+ A29r

10. Example 1 (contd..)
To find A1 and A2
put r = 0 in the homogenous solution
a0 = A110
+ A290
3 = A1 + A2 ……………………….(1)
put r =1 in the homogenous solution
a1 = A111
+ A291
11 = A1 + 9A2 .....................(2)
Solving equation (1) and (2) we get
A1 = 2 and A2 = 1
Hence solution of homogeneous equation is
ar= (2)1r
+ (1)9r
ar= 2 + 9r

11. Example 2
Q . Find the solution of the given recurrence
relation ar – 8ar-1 + 16ar-2 = 0 with initial
conditions a2 = 16 and a3 = 8.
A. Characteristic equation of the given
recurrence relation is
α2
- 8α + 16 = 0
Therefore (α – 4)2
= 0
α = 4 repeated twice
Thus,
ar= (A1r + A2)4r

12. Example 2(contd..)
To find A1 and A2
put r = 2 in the homogenous solution
a2 = (2A1 + A2 )42
16 = 32A1 + 16A2 ……………………….(1)
put r =3 in the homogenous solution
a3 = ( 3A1 + A2 )43
8 = 192A1 + 64A2 .....................(2)
Solving equation (1) and (2) we get
A1 = ¼ and A2 = ½
Hence solution of homogeneous equation is
ar= (¼ r + ½)4r

13. Total Solutions
 Definition: The total solution of a linear
recurrence relation with constant co-efficients
is the sum of two parts, the homogenous
solution and the particular/heterogenous
solution which satisfies the recurrence
relation with f(n) on the right hand side
 Thus, an = an + an
(h) (p)

14. Method to find particular solution
 Particular solution can be found by method of
inspection
F(n) Right Hand Side Form of Particular Solution
A constant d A constant P
A linear function
d0 + d1n
A linear function
P0 + P1n
A kth
degree polynomial
d0 + d1n + d2n2
+ …… + d2nk
A kth
degree polynomial
P0 + P1n + P2n2
+ …… + P2nk
An exponential function dbn
provided b is not the characteristic root
An exponential function Pbn
An exponential function dbn
provided b is the characteristic root of the
expression with multiplicity (m-1)
An exponential function Pnm-1
bn

15. Example 1
Q . Solve the recurrence relation
an – an-1 - 6an-2 = -30 given a0 = 20 and a1 = -5.
A. Part 1 : Solution of the Homogeneous recurrence
relation
an – an-1 - 6an-2 = 0
Characteristic equation of the above relation
α2
– α – 6 =0
Therefore (α-3)(α+2)=0
Hence α = -2, 3 i.e α1 = -2 and α2 = 3
Thus, an= A1 (α1)n
+ A2 (α2)n
an= A1 (-2)n
+ A2 (3)n
………………(1)

16. Example 1 (contd..)
Part 2 : Solution of Particular Solution
The R.H.S is a constant , Hence from the
previous table substitute an, an-1 and an-2 in the
given recurrence relation by P.
P – P – 6P = -30
-6P = -30
P = 5
Thus, an = 5 …………………….(2)
Total Solution of recurrence relation is
Part 1 + Part 2

17. Example 1 (contd..)
an = A1 (-2)n
+ A2 3n
+ 5
To find A1 and A2
put r = 0
20 = A1 (-2)0
+ A2 30
+ 5
15 = A1 + A2 …………………(3)
and r = 1
-5 = A1 (-2)1
+ A2 31
+ 5
-10 = -2A1 + 3A2 ………………..(4)
Solving equations (3) and (4), we get
A1 = 11 and A2 = 4
Hence, an = 11 (-2)n
+ 4 (3)n
+ 5

18. Example 2
Q . Solve the recurrence relation
an – 7an-1 + 10an-2 = 6+8n given a0 = 1 and a1 = 2.
A. Part 1 : Solution of the Homogeneous recurrence
relation
an – 7an-1 + 10an-2 = 0
Characteristic equation of the above relation
α2
– 7α + 10 =0
Therefore (α-3)(α-2)=0
Hence α = 5, 2 i.e α1 = 5 and α2 = 2
Thus, an= A1 (α1)n
+ A2 (α2)n
an= A1 (5)n
+ A2 (2)n
………………(1)

19. Example 2 (contd..)
Part 2 : Solution of Particular Solution
The R.H.S is a linear equation, Hence from the previous table substitute an
by P0 + P1n,
an-1 by P0 + P1(n-1) and an-2 by P0 + P1(n-2) in the given recurrence relation.
P0 + P1n – 7(P0 + P1(n-1)) + 10(P0 + P1(n-2)) = 6 + 8n
(4P0 – 13P1) + 4 P1n = 6 + 8n
On comparing the co-efficients of polynomials
4P0 – 13P1 = 6 ……………… (2)
4 P1 = 8 …………….(3)
Solving equations (2) and (3)
P0 = 8 and P1 = 2

20. Example 2 (contd..)
Hence , an = 8 + 2n ……………………….(4)
Total Solution of recurrence relation is
Part 1 + Part 2
an= A1 (5)n
+ A2 (2)n
+ 8 +2n
To find A1 and A2
Put n=0
1 = A1 (5)0
+ A2 (2)0
+ 8 +2(0)
-7 = A1 + A2 ………………….(5)
Put n=1
2 = A1 (5)1
+ A2 (2)1
+ 8 +2(1)
-8 = 5 A1 + 2 A2 …………………….(6)

21. Example 2 (contd..)
Solving equations (5) and (6) to get
A1 = 2 and A2 = -9
Thus,
an= 2 (5)n
- 9(2)n
+ 8 +2n