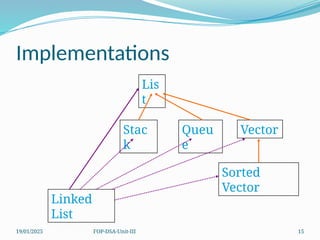
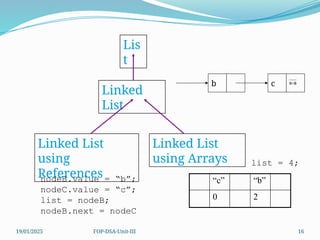
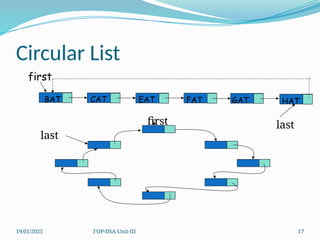
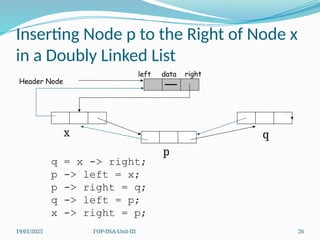
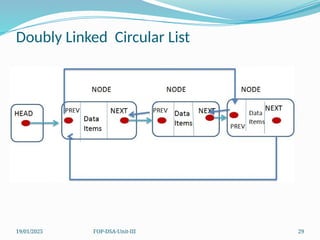
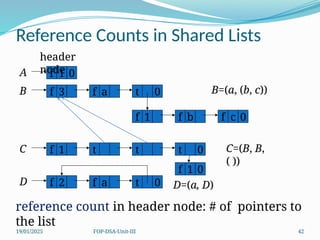
The document outlines concepts related to linked lists including their types, operations, and implementations using C++. It discusses various data manipulation techniques such as insertion, deletion, and memory management strategies, along with polynomial manipulations and generalized linked lists. Furthermore, it touches on advanced topics like dynamic memory management and strategies for optimizing performance in memory use.